ЗНО онлайн 2016 року з математики – основна сесія
Тестові завдання основної сесії ЗНО 2016 року з математики
ТЕМА: Геометрія. Планіметрія. Найпростіші фігури на площині. Вертикальні та суміжні кути.
Це завдання перевіряє вміння визначати невідомий кут, використовуючи означення суміжних кутів і властивості вертикальникх кутів.
Зображені на рисунку кути
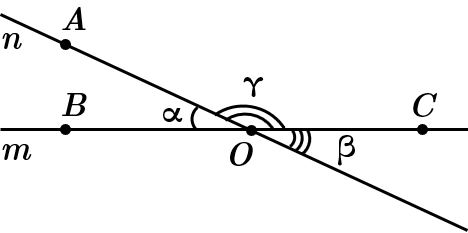
Вертикальні кути рівні, тому
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Раціональні нерівності.
Це завдання перевіряє знання означення розв'язку нерівності з однією змінною.
ОДЗ:
Розв'яжемо нерівність:
Розв'яжемо методом інтервалів:
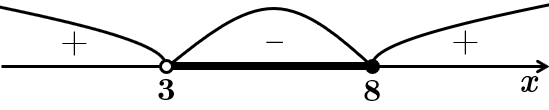
З наведених чисел, лише
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Перетворення виразів із степенями.
Це завдання перевіряє вміння зводити одночлен до стандартного вигляду. Для цього треба знайти добуток коефіцієнтів:
Тоді
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Означення розв'язку системи рівнянь з двома змінними та методи їх розв'язування.
Це завдання перевіряє вміння розв'язувати системи рівнянь мішаного типу.
Друге рівняння системи, що містить лише одну змінну
Отже, пара чисел
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Графік функції.
Це завдання перевіряє знання графіків основних елементарних функцій.
Пряма є графіком лінійної функції, тобто функції, заданої рівнянням
Цю функцію отримаємо, якщо в рівняння
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Трикутники. Нерівність трикутника.
Це завдання перевіряє вміння визначати можливе значення невідомої сторони трикутника.
Використаємо нерівність трикутника: будь-яка сторона довільного трикутника менша за суму двох інших його сторін та більша за їх різницю. Оскільки сторони трикутника
Цю умову задовольняє лише варіант Г –
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Вирази з коренями. Формули скороченого множення.
Це завдання перевіряє вміння виконувати арифметичні дії з дробовими виразами.
Щоб спростити вираз, зведемо дроби до спільного знаменника. На практиці дроби з різними знаменниками зводять до найпростішого (найменшого) спільного знаменника. Найпростішим спільним знаменником дробів є вираз
також є спільним знаменником, проте він ділиться на спільний знаменник
Скористаємось основною властивістю дробів: дріб не зміниться, якщо його чисельник і знаменник домножити на один і той самий ненульовий вираз. Тоді чисельник і знаменник першого дробу домножимо на
Тоді
Розкладемо чисельник на множники, скориставшись формулою різниці квадратів, і скоротимо отриманий дріб:
Запропонований спосіб розв'язання не є єдиноможливим. Вираз можна спростити, виконавши ще такі перетворення:
Тоді
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Прямокутна система координат у просторі.
Це завдання перевіряє вміння визначати координати точки, зображеної на рисунку.
Оскільки точка

Серед наведених цій умові задовільняє лише відповідь В.
Відповідь: В.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Арифметична прогресія.
Це завдання перевіряє знання формули
Запишемо формулу
тоді для
Підставивши відомі значення різниці прогресії
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи статистики. Графічне подання статистичної інформації.
Це завдання перевіряє вміння аналізувати статистичну інформацію, наведену у вигляді графіків або діаграм.
Щоб відповідсти на запитання, потрібно визначити на осі "роки" рік, в якому точка, що йому відповідає, віддалена від точки, що відповідає попередньому року, по вертикалі на найбільшу відстань.
З діаграми видно, що найбільші по вертикалі відстані спостерігаються між точками, що відповідають
Знайдемо різниці між річними мінімумами:
Оскільки
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі.
Це завдання перевіряє знання означення мимобіжних прямих і вміння його використовувати до розв'язування задач.
I. Оскільки через дві прямі, що перетинаються, можна провести єдину площину, а мимобіжні прямі не перетинаються, тому твердження є неправильним.
II. Прямі, які не лежать в одній площині, називаються мимобіжними. Тому твердження є неправильним.
III. Оскільки прямі
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Ірраціональні вирази та їх перетворення.
Це завдання перевіряє вміння оцінювати значення ірраціонального виразу, використовуючи властивості функції.
Оскільки виконується нерівність
Оскільки
то
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Логарифмічні вирази та їх перетворення.
Це завдання перевіряє знання формули суми логарифмів та вміння її застосовувати до розв'язування задач.
Оскільки
при
то
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Подібність фігур.
Це завдання перевіряє вміння знаходити подібні фігури та використовувати пропорційність їх відповідних лінійних елементів для знаходження відношення площ цих фігур.
Подібними називаються фігури однакової форми. Коефіцієнтом подібності називається відношення відповідних лінійних елементів цих фігур. Оскільки у зображених на рисунку телевізорів екрани мають форму прямокутників, відповідні сторони яких пропорційні, то ці прямокутники подібні.
Коефіцієнт подібності дорівнює відношенню діагоналей цих прямокутників, тобто діагоналей екранів телевізорів:
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і почати аналізу. Числа і вирази. Тригонометричні вирази та їх перетворення.
Це завдання перевіряє знання основної тригонометричної тотожності та вміння її застосовувати до перетворення тригонометричних виразів.
Для будь-якого кута
I спосіб. Домножимо обідві частини цієї рівності на
звідси
Оскільки за умовою
то отримаємо:
II спосіб. Виразимо з основної тригонометричної тотожності
Зауваження. Правильну відповідь до завдання можна отримати, якщо навіть не знати (чи не пам'ятати) основної тригонометричної тотожності. Якщо знати, що
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Первісна та визначений інтеграл. Формула Ньютона - Лейбніца.
Це завдання перевіряє знання таблиці первісних основних елементарних функцій та вміння застосовувати формулу Ньютона - Лейбніца для знаходження визначеного інтеграла.
За формулою Ньютона - Лейбніца:
де
Нагадаємо, що функція
Визначимо одну з первісних функції
Правило знаходження первісних. Якщо
Отже,
Однією з первісних степеневої функції
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники. Пряма трикутна призма. Об'єм призми.
Це завдання перевіряє вміння обчислювати об'єм призми. Для виконання завдання потрібно знати формули об'єму призми, площі рівностороннього трикутника, означення квадрата та периметра рівностороннього трикутника.
Нехай
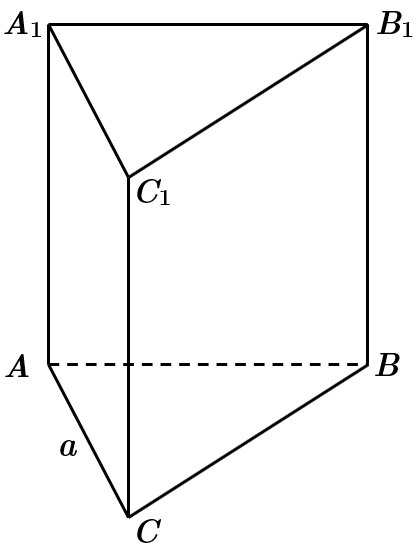
Оскільки периметр правильного трикутника зі стороною
Оскільки бічні грані призми за умовою є квадратами, то
Об'єм призми визначається за формулою
Площа правильного трикутника зі стороною
Оскільки
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Графік функції.
Це завдання перевіряє вміння визначати графік аналітично заданої функції.
Графіком квадратичної функції
З наведених рисунків цю умову задовольняють варіанти А, В і Д. Оскільки за умовою рівняння
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Тригонометричні рівняння.
Це завдання перевіряє знання співвідношень між тригонометричними функціями одного аргумента та вміння розв'язувати тригонометричні рівняння.
Оскільки
Розв'язком такого рівняння є
Оскільки
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Логарифмічні нерівності.
Це завдання перевіряє вміння розв'язувати логарифмічні нерівності.
Запишемо ОДЗ цєї нерівності:
Запишемо
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Графік функції. Основні властивості функцій: монотонність, парність та непарність.
Це завдання перевіряє вміння встановлювати властивості числових функцій, заданих графічно та належність точки графіку заданої функції.
Щоб розв'язати це завдання, потрібно знати означення зростаючої (спадної) функції, парної та непарної функцій, властивості та графік логарифмічної функції
Функція
Функція
Функція
Функція
Область визначення і парної, і непарної функції симетрична відносно точки
Доберемо до кожного із запитань (1 – 4) правильну відповідь.
1. Точка
2. Оскільки графік парної функції симетричний відносно осі
3. Щоб вказати графік функції, що має дві спільні точки з графіком логарифмічної функції
Зауважимо, що графік функції
Графік цієї функції перетинає графіки функцій, зображених на рисунках 1 – 3, по одному разу, не має жодної спільної точки з графіком, зображеним на рисунку 5, і дві спільні точки, – з графіком, зображеним на рисунку 4. Отже, 3 – Г.
4. Графік функції, що зростає на відрізку
Відповідь: 1 – A, 2 – Б, 3 – Г, 4 – B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Раціональні числа та дії з ними. Означення степеня з раціональним показником. Модуль дійсного числа.
Це завдання перевіряє вміння виконувати дії з раціональними числами, записаними у вигляді звичайних дробів, знаходити значення степеневого виразу, виразу, що містить знак модуля.
Для розв'язання завдання потрібно знати правила дій із звичайними дробами, означення степеня з раціональним показником та правила дій зі степенями, а саме:
то значення модуля дійсного числа.
Нагадаємо, що за означенням модулем числа
Обчислимо значення виразів (1 – 4).
1.
Отже, 1 – Д.
2.
3.
Отже, 3 – Г.
4.
Або
Отже, 4 – Б.
Відповідь: 1 – Д, 2 – А, 3 – Г, 4 – Б.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Описане коло, дотична до кола та її властивості. Трикутники (рівносторонній та прямокутний трикутники). Тригонометричні співвідношення в прямокутному трикутнику.
Це завдання перевіряє вміння визначати довжини відрізків, використовуючи властивості дотичної до кола, елементів кола, вписаних у коло кутів та співвідношень у прямокутному трикутнику.
Обчислимо довжини відрізків (1 – 4).
1. Оскільки діаметр кола вдвічі більший за його радіус, то згідно умови
2. Розглянемо трикутник
Такий же результат отримаємо, якщо скористаємось тим фактом, що у прямокутному трикутнику
Отже, 2 – Б.
3. Відрізок
Отже, 3 – A.
4. Розглянмо вписаний у коло трикутник
Або за теоремою Піфагора отримуємо:
Отже, 4 – Г.
Відповідь: 1 – B, 2 – Б, 3 – A, 4 – Г.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники, тіла й поверхні обертання (куб, куля, циліндр, конус). Формули для обчислень площ поверхонь многогранників і тіл обертання.
Це завдання перевіряє вміння визначати площу повної поверхні куба, кулі, циліндра та конуса.
Обчислимо площу повної поверхні кожного геометричного тіла (1 – 4).
1. Площа повної поверхні циліндра, радіус основи якого дорівнює
За умовою
Отже, 1 – Г.
2. Щоб визначити площу повної поверхні конуса, потрібно знати радіус його основи
Оскільки
Отже, 2 – Б.
3. Площу повної поверхні куба із ребром
Отже, 3 – А.
4. Площа поверхні кулі радіуса
Отже, 4 – Д.
Відповідь: 1 – Г, 2 – Б, 3 – А, 4 – Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Текстові задачі.
Це завдання перевіряє вміння розв'язувати текстові задачі на відношення, пропорції та відсотки.
1. За діаграмою визначаємо, що підручники становлять
2. Визначаємо кількість довідників
Нехай додатково придбано
Відповідь: 1.
2.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Квадрат та його властивості. Трапеція та її властивості. Прямокутний трикутник. Теорема Піфагора.
Це завдання перевіряє вміння обчислювати довжини відрізків як елементи відповідних геометричних фігур, використовуючи властивості середньої лінії трапеції та означення квадрата.
1. Оскільки чотирикутник
тоді
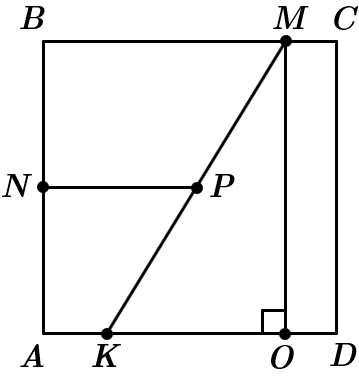
2. Опустимо з точки
За теоремою Піфагора отримуємо:
Відповідь: 1.
2.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Похідна функції. Правило знаходження похідної складеної функції.
Це завдання перевіряє вміння обчислювати значення похідної складеної функції у заданій точці.
Нехай
Якщо функція
Функцію
Обчислюємо значення похідної в точці
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи. Застосування рівнянь та їхніх систем до розв'язування текстових задач.
Це завдання перевіряє вміння розв'язувати текстові задачі за допомогою рівнянь та їх систем.
І спосіб. Позначимо кількість тримісних номерів через
В одномісних номерах при повному заповненні проживає
Складаємо рівняння
звідки отримуємо
Отже, у готелі було всього
ІІ спосіб. Якщо ввести позначення:
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Паралелограм та його властивості. Координати та вектори на площині. Скалярний добуток векторів та його властивості. Теорема косинусів.
Це завдання перевіряє вміння застосовувати координати й вектори до розв'язування планіметричних задач.
Нагадаємо, що скалярним добутком векторів
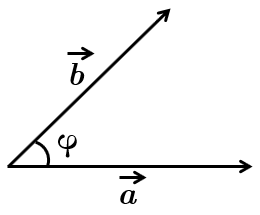
Довжину вектора
На рисунку
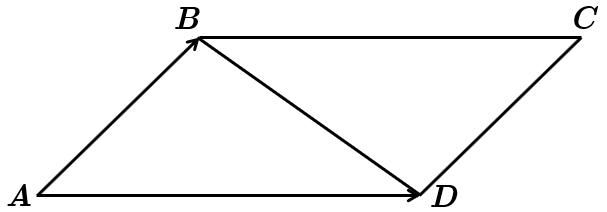
За умовою
Визначаємо довжину вектора
Діагональ
Звідки отримуємо
Отже, довжина діагоналі
Знаючи довжини сторін
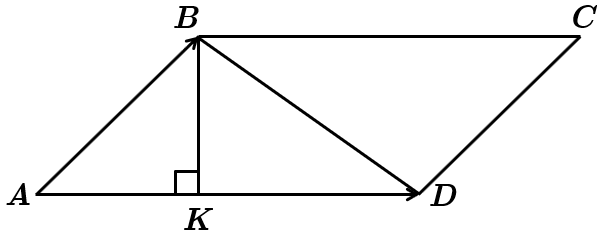
Прямокутні трикутники
З прямокутного трикутника
Тоді
Отже,
тоді
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Комбінаторика, теорія ймовірностей і статистика. Комбінаторні правила суми та добутку.
Це завдання перевіряє вміння розв'язувати комбінаторні задачі з практичним змістом, використовуючи комбінаторні формули.
Оскільки серед трьох різних видів чаю, які обирає покупець, обов'язково є вид "чорна перлина", то шукана кількість варіантів вибору трьох коробок чаю дорівнює кількості варіантів вибору двох коробок різних видів з
Наведені міркування можна обґрунтувати ще так.
Правило добутку. Якщо елемент
Розділимо
Зауваження. Важливо розрізняти, у яких випадках потрібно застосовувати формулу для обчислення кількості комбінацій:
У нашому випадку, під час формування наборів чаю не важливим є порядок вибору виду чаю, тому використано формулу для обчислення кількості комбінацій.
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Побудова графіків функцій.
Це завдання перевіряє вміння будувати графіки функцій.
Щоб виконати це завдання, потрібно вміти розкладати квадратний тричлен на лінійні множники, знати означення модуля числа та вміти розкрити модуль лінійного виразу, будувати графік лінійної функції, знати означення області значень функції та вміти визначати її за графіком функції.
Розв'язання завдання слушно розбити на такі кроки.
Перший крок. Спростимо задану функцію.
Спочатку розкладемо на лінійні множники квадратичний вираз
в якій
У нашому випадку
Можна розкласти квадратичний вираз на множники, використовуючи метод групування, наприклад, так:
За означенням модулем числа
Отже,
тобто
Враховуємо, що знаменник будь-якого дробу не може дорівнювати нулю. Отже, область визначення функції задається умовою
Другий крок. Будуємо графік заданої функції. Він є об'єднанням графіків лінійних функцій

Областю значень функції
Нагадаємо, що область значень функції
Геометрично, щоб визначити область значень функції, потрібно спроектувати її графік на вісь ординат.
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники. Чотирикутна піраміда. Кут між прямою та площиною, площинами. Планіметрія. Ромб та його властивості.
Це завдання перевіряє вміння застосовувати означення та властивості основних видів многогранників до розв'язування стереометричних задач, зокрема, знаходити міру кута між площинами.
Для розв'язання завдання потрібно перш за все правильно побудувати рисунок, важливо правильно показати положення висоти піраміди, знати означення кута між площинами, двогранного кута та його лінійного кута, вміти визначати довжини відрізків, використовуючи теорему Піфагора чи тригонометричні співвідношення між сторонами і кутами прямокутного трикутника.

1) Нехай
Отже,
Розглянемо прямокутний трикутник
Тоді
У трикутнику
Зауваження. Оскільки відрізок
Відповідь:
Знайшли помилку? Пишіть на
33
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Рівняння мішаного типу з параметром.
Це завдання перевіряє вміння розв'язувати рівняння залежно від значення параметра.
Задане рівняння
ріносильне системі
Знайдемо корені рівняння
Для цього запишемо це рівняння у вигляді
тобто
і розглянемо його як квадратне відносно
Тоді:
1)
Оскільки завжди
2)
Рівняння
Отже, рівняння
має єдиний корінь
виконується для всіх
Рівняння
рівносильно системі
тобто
Зауваження. Окремо розв'язувати нерівність
залежно від значень
яка, в свою чергу, рівносильна кожній із систем
На практиці з останніх двох систем розглядаємо ту, у якій нерівність
Розв'яжемо квадратне рівняння
причому
Зауваження. Квадратне рівняння
можна розв'язати, виконавши низку наступних перетворень:
звідси отримуємо
Залишилося врахувати обмеження на параметр
Значення
Значення
При
а при
Позначимо область існування коренів на числовій прямій:


Відповідь: рівняння не має змісту, якщо
Знайшли помилку? Пишіть на




