Розділ: Планіметрія
Тема: Паралелограм. Ромб. Трапеція
Кількість завдань: 86
ТЕМА: Трикутники. Чотирикутники.
Завдання скеровано на перевірку знання властивостей трапеції, рівнобедреного трикутника.
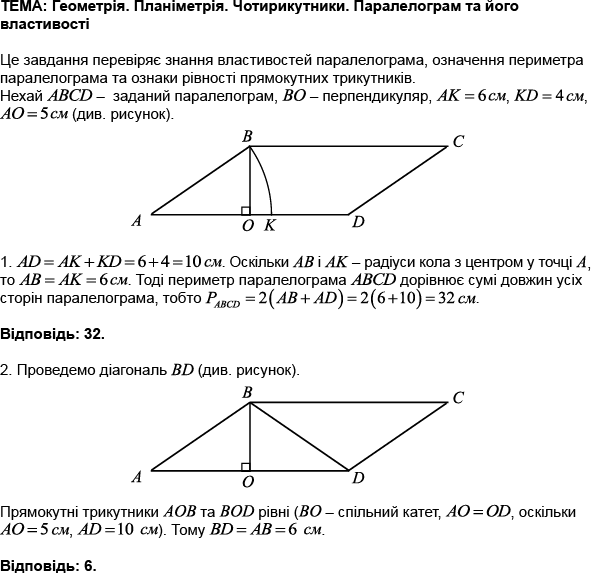
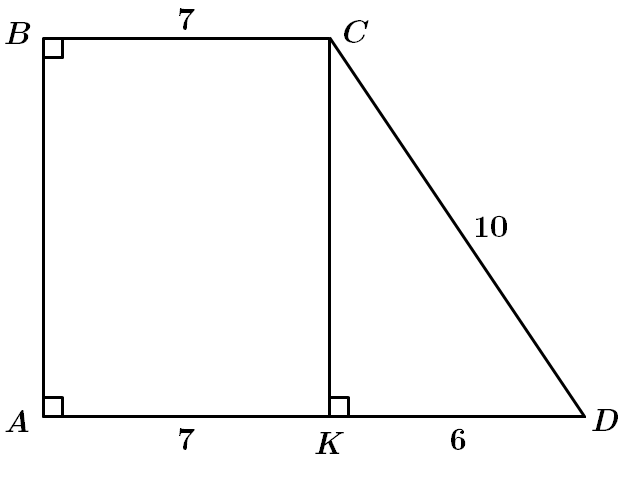
1. Відстань від
За теоремою Піфагора в
Правильна відповідь – Г.
2. Побудуємо
3.
Правильна відповідь – Б.
Відповідь: 1 – Г, 2 – А, 3 – Б.
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивостей ромба, середньої лінії трапеції, рівностороннього трикутника.
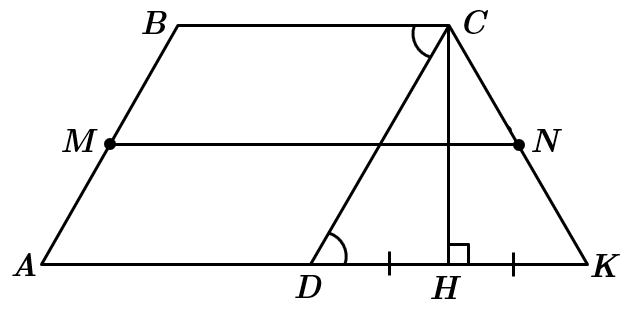
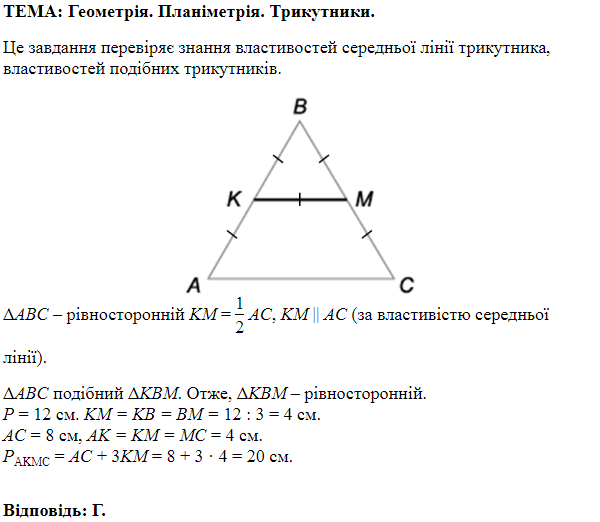
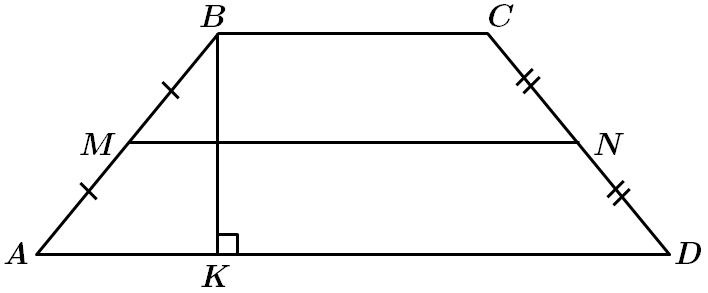
1. Висота
У
Правильна відповідь – Г.
2.
У ромбі
Правильна відповідь – Б.
3.
Середнія лінія
Правильна відповідь – B.
Відповідь: 1 – Г, 2 – Б, 3 – B.
ТЕМА: Чотирикутники.
Завдання скеровано на перевірку знань властивостей ромба та його елементів.
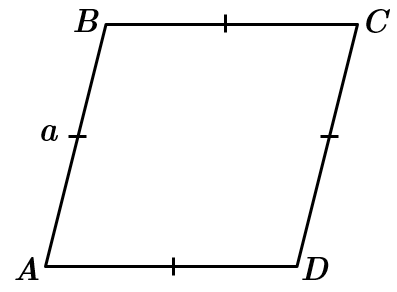
Ромб – це чотирикутник, у якого всі сторони рівні.
Периметр ромба – це сума довжин усіх його сторін:
За умовою, довжина сторони
З запропонованих чисел лише
Відповідь: В.
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивостей трапеції, трикутників, уміння застосовувати теорему косинусів.
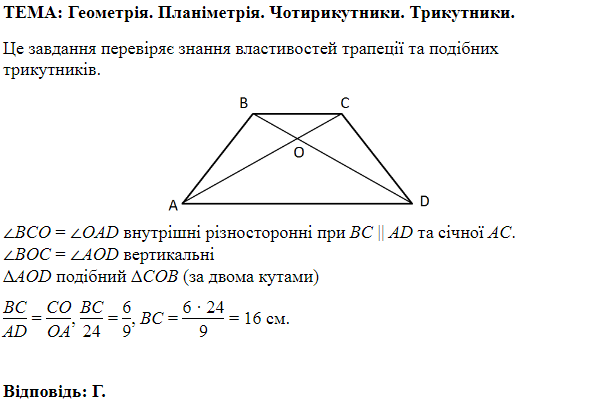
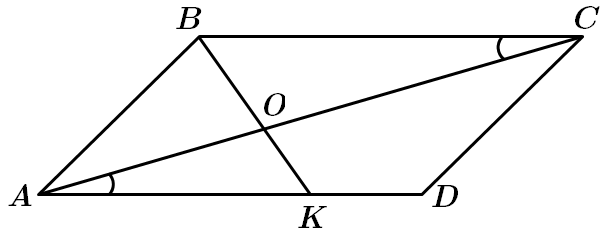
1. Оскільки точка
Отже, 1 – А.
2. Розгляньмо прямокутний трикутник
Отже, 2 – Д.
3.
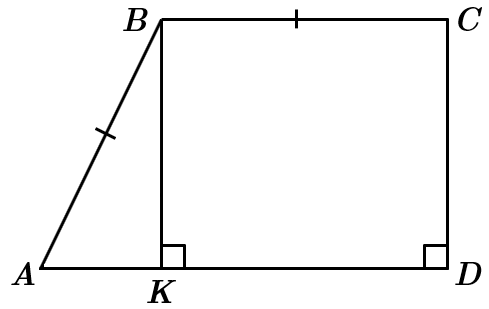
Нехай
Оскільки
Проведімо висоту з точки
Оскільки
У прямокутному трикутнику
Отже, 3 – B.
Відповідь: 1 – A, 2 – Д, 3 – В.
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивостей трапеції, її середньої лінії, співвідношення між сторонами й кутами прямокутного трикутника.
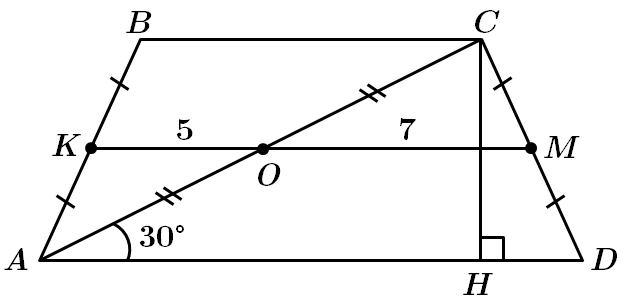
За властивістю середньої лінії трапеції:
У
У
Побудуймо
У
Площа трапеції
Відповідь: Г.
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знань властивостей ромба та рівнобедреного трикутника.
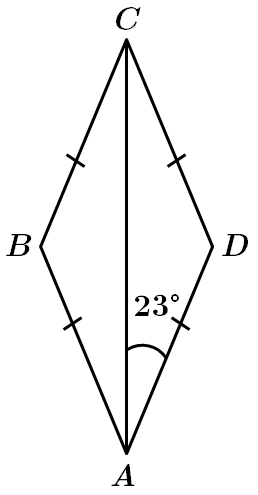
Отже,
Або можна обчислити більший кут ромба іншим способом. За властивістю ромба,
Сума сусідніх кутів будь-якого паралелограма (ромб – паралелограм) дорівнює
Відповідь: B.
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знань властивостей паралелограмів, теореми косинусів, уміння розв’язувати трикутники.
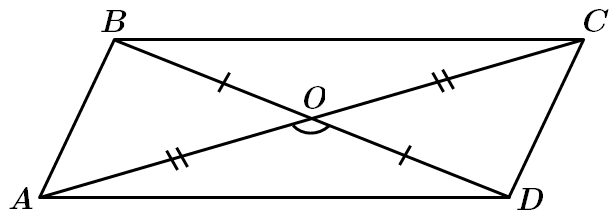
За властивістю паралелограма
У
Відповідь: A.
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивостей трапеції, прямокутного трикутника, уміння визначати площу трапеції.
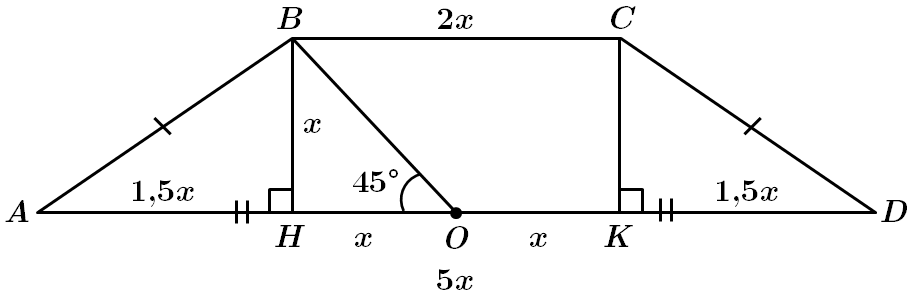
Нехай
Побудуймо висоти
Точка
У
Площу трапеції визначмо за формулою:
Якщо
Відповідь: Г.
ТЕМА: Чотирикутники.
Завдання скеровано на перевірку знань властивостей паралелограмів, зокрема прямокутника.
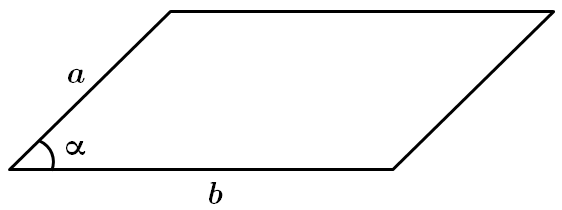
I. Периметром паралелограма називають суму довжин всіх його сторін.
Отже, твердження правильне.
II. Площу паралелограма визначають за формулою:
III. Рівні діагоналі прямокутника не означають рівності сторін. Тільки за умови, що протилежні сторони також рівні, інші сторони прямокутників також будуть рівними між собою.
Отже, твердження неправильне.
Відповідь: А.
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивостей трапеції, її середньої лінії, трикутників, уміння застосовувати теорему синусів.
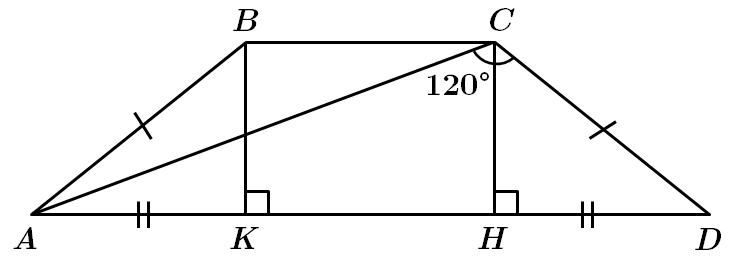
1. Середню лінію трапеції визначають за формулою
Правильна відповідь – В.
2.
Рівні похилі
Правильна відповідь – А.
3. Коло, описане навколо трапеції
За наслідком з теореми синусів:
Правильна відповідь – Г.
Відповідь: 1 – В, 2 – А, 3 – Г.
ТЕМА: Чотирикутники.
Завдання скеровано на перевірку знання властивостей чотирикутників, зокрема ромба.

I. Ромб – паралелограм, тому всі властивості паралелограма є властивостями ромба.
Отже, у будь-якому ромбі діагоналі точкою перетину діляться навпіл.
II. Периметр ромба не дорівнює сумі його діагоналей. Якби це твердження було правильним, то в
III. Твердження правильне. Висота ромба
Відповідь: Г.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання скеровано на перевірку вміння застосовувати властивості трапеції та квадрата, розв’язування трикутників.
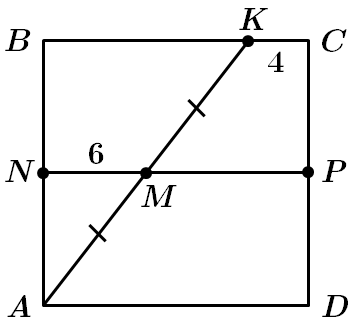
1 – В. Точка
У
2 – A.
У трапеції
За властивістю середньої лінії:
3 – Г.
За теоремою Піфагора:
Відповідь: 1В, 2А, 3Г.
ТЕМА: Геометрія. Планіметрія.
Завдання скеровано на перевірку знання властивостей трапеції та трикутника.
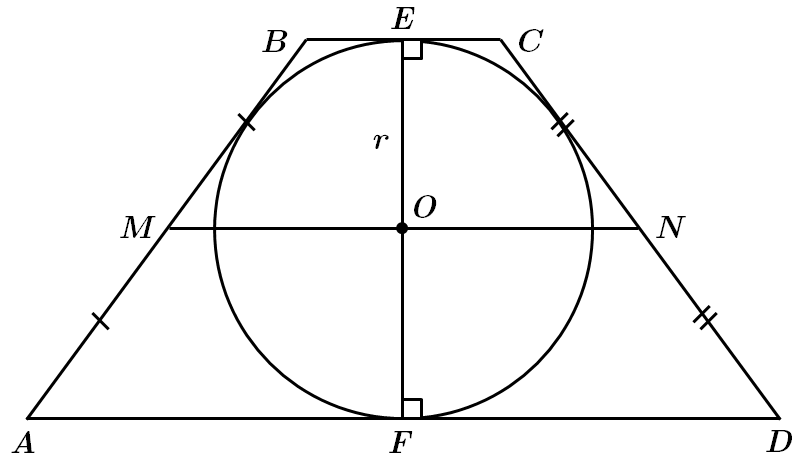
I. Якщо в трапецію можна вписати коло, то воно буде дотикатись до всіх її сторін, а отже, до основ.
II, III твердження не є правильними, бо точка перетину діагоналей не належить середній лінії, та центр описаного кола не обов'язково лежить на більшій основі.
Відповідь: Б.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Геометричні величини та вимірювання їх.
Завдання скеровано на перевірку знань властивостей паралельних прямих та паралелограмів, умінь розв’язувати планіметричні задачі.
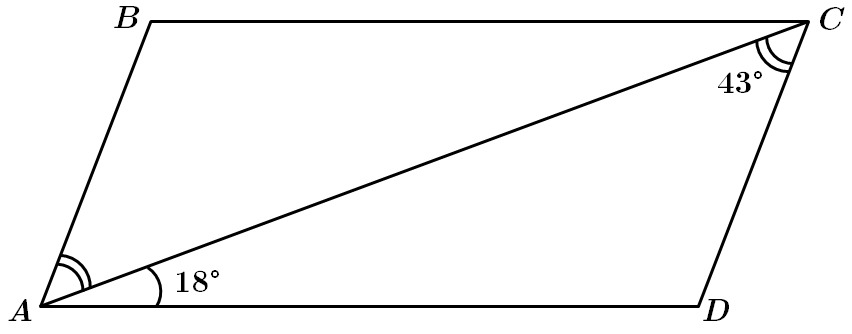
Відповідь: A.
ТЕМА: Геометрія. Планіметрія.
Завдання скеровано на перевірку властивостей трапеції та трикутника, їх властивостей.
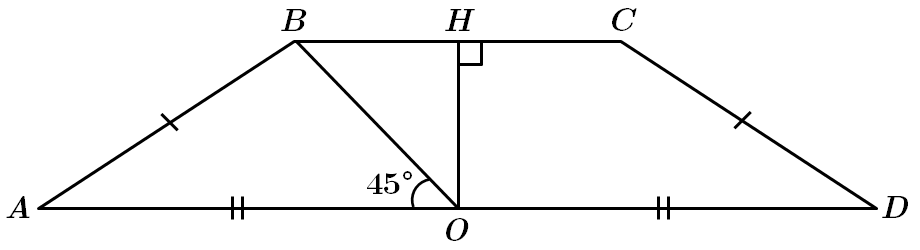
1.
2. Трапеція
3.
4. Площу трапеції знаходимо за формулою:
Відповідь: A.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Завдання скеровано на перевірку вміння застосовувати властивості трикутників до розв’язування планіметричних задач, знаходити довжину середньої лінії трапеції.
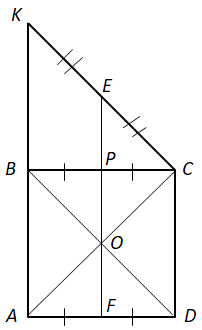
1 – A.
2 – Г.
3 – Б. Центр кола, описаного навколо квадрата, – це точка перетину діагоналей – точка
Центр кола, описаного навколо прямокутного трикутника, – середина гіпотенузи – точка
Відповідь: 1A, 2Г, 3Б.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивості трапеції, прямокутного трикутника.
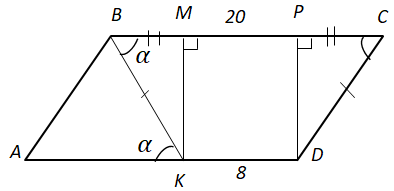
У
Площу паралелограма знаходимо за формулою:
Відповідь: Б.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Завдання скеровано на перевірку вміння застосовувати властивості трикутників до розв’язування планіметричних задач, знаходити довжину середньої лінії трапеції, знання теореми Піфагора, описані навколо кола чотирикутники.
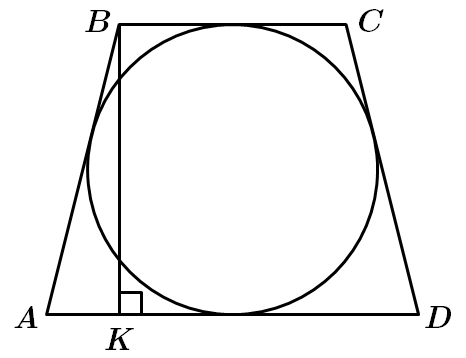
Якщо у чотирикутник можна вписати коло, то сума довжин протилежних сторін рівна.
1 – В. Середня лінія трапеції дорівнює
2 – Г. За умовою
3 – Б.
за теоремою Піфагора:
Відповідь: 1В, 2Г, 3Б.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання скеровано на перевірку знання про паралелограм, ромб, квадрат та їх властивості.
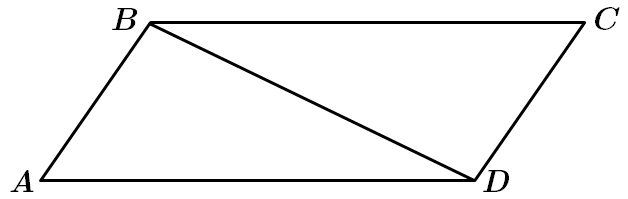
I. Твердження неправильне. Сума двох сусідніх сторін паралелограма не може дорівнювати його діагоналі, тому що за нерівністю трикутника
II. Твердження правильне. Існує паралелограм, в якому один з кутів вдвічі більше за інший. Наприклад, з кутами
III. Твердження правильне. Існує паралелограм – ромб, у якого діагоналі перпендикулярні.
Відповідь: В.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання скеровано на перевірку знання властивостей квадрата та трапеції, площ чотирикутників.
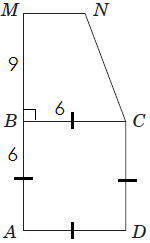
1 – Г.
2 – Д.
3 – A.
Відповідь: 1Г, 2Д, 3A.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання теореми синусів, властивостей паралельних прямих.
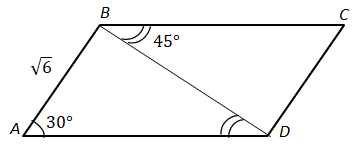
За теоремою синусів у
Відповідь: Д.
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.
Завдання перевіряє вміння застосовувати означення та властивості прямокутного трикутника, знаходження площі паралелограма, до розв'язування планіметричних задач.
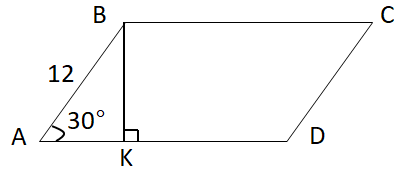
За умовою
У
Площа паралелограма
Відповідь: B.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання перевіряє знання властивостей трапеції.
Правильне лише ІІІ твердження.
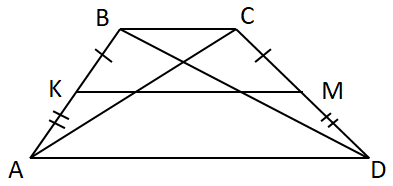
I. Середня лінія трапеції не проходить через точку перетину її діагоналей.
II. Діагональ трапеції не ділить її на два рівних трикутники
III.
Відповідь: А.
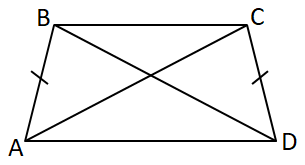
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання перевіряє знання паралелограма, ромба, квадрата та їх властивостей.
I. Діагоналі будь-якого ромба ділять його кути навпіл (властивість ромба).
IІ. Неправильне твердження.
IІІ. Діагоналі будь-якого квадрата взаємно перпендикулярні (це властивість ромба, а квадрат є ромбом із прямими кутами).
Отже, правильна відповідь – Д.
Відповідь: Д.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Перевіряє знання властивостей трапеції та її середньої лінії, вміння застосовувати означення та властивості різних видів трикутників до розв'язування планіметричних задач.
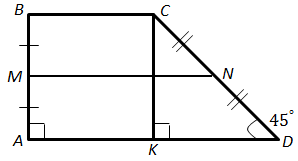
1.
2. Отже,
3. Проведемо
4.
5.
Відповідь: 8.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання перевіряє вміння застосовувати властивості трапеції, властивостей паралельних прямих.
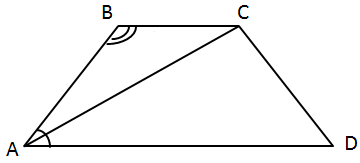
I.
II.
III.
Відповідь: Б.
ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури на площині та їхні властивості.
Завдання перевіряє знання властивостей суміжних кутів та паралелограма.
За властивістю паралелограма
Відповідь: B.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання скеровано на перевірку знання властивостей паралелограма, ромба; вміння використовувати формули площ геометричних фігур для розв’язування планіметричних задач.
1. На рис. 1 зображено ромб. За властивістю ромба діагоналі перетинаються під прямим кутом. Отже, 1 – A.
2.
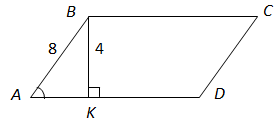
У
3.
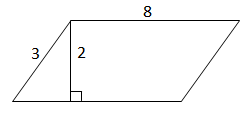
За формулою
Відповідь: 1А, 2Б, 3Д.
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.
Завдання скеровано на перевірку знання властивостей трикутника, трапеції; вміння розв’язувати задачі практичного змісту.
Побудуємо математичну модель задачі:

Відстань між паралельними сторонами
У
Уздовж сторін
Всього стовпчиків має бути
Відповідь: Б.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання скеровано на перевірку знання властивостей квадрата, трапеції; вміння використовувати формули площ геометричних фігур для розв’язування планіметричних задач.
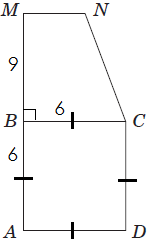
1.
2. У прямокутній трапеції
3.
Відповідь: 1Г, 2Д, 3A.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання скеровано на перевірку знання властивостей та ознак ромба.
І. Навколо чотирикутника можна описати коло, якщо сума протилежних кутів дорівнює 180°. Ця властивість у будь-якому ромбі не виконується. Отже, твердження неправильне.
ІІ. Діагоналі ромба взаємно перпендикулярні (властивість ромба). Правильне твердження.
ІІІ. У будь-якому ромбі всі сторони рівні (означення ромба). Правильне твердження.
Відповідь: Г.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання скеровано на перевірку знання формули суми кутів чотирикутника.
Сума кутів будь-якого чотирикутника 360°. Сума трьох кутів – 280°, тому четвертий кут:
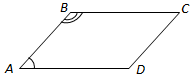
Якщо гострі кути паралелограма
Сума кутів, прилеглих до будь-якої сторони паралелограма, дорівнює 180° (як внутрішні односторонні при паралельних прямих і січної).
Відповідь: A.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивостей ромба, подібних трикутників, теореми Піфагора.
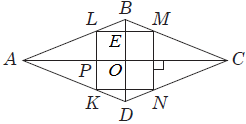
1. За теоремою Піфагора,
2.
Відповідь: 1. 12. 2. 21.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання скеровано на перевірку знання властивостей та ознак паралелограма.
З наведених тверджень привильними є твердження II i III.
Протилежні кути паралелограма рівні (властивість).
Відстані від точки перетину діагоналей до протилежних сторін рівні.
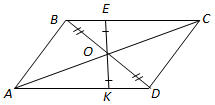
Відповідь: Д.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання скеровано на перевірку вміння застосовувати означення та властивості трапеції.
І спосіб:
ІІ спосіб:
За властивістю трапеції
Відповідь: A.
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.
Завдання перевіряє знання про подібні трикутники, властивість середньої лінії трапеції, властивості паралелограма.
1.
Отже, 1 – Б.
2.
Отже, 2 – B.
3.
Середня лінія трапеції дорівнює
Відповідь: 1 – Б, 2 – B, 3 – Г.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання перевіряє знання властивостей ромба, трапеції, прямокутника, властивостей чотирикутників, вписаних в коло.
Навколо чотирикутника можна описати коло, якщо сума протилежних кутів дорівнює
Відповідь: B.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Завдання перевіряє вміння застосовувати властивості трикутників до розв’язування планіметричних задач, знаходити довжину середньої лінії трапеції, знання теореми Піфагора.
1.
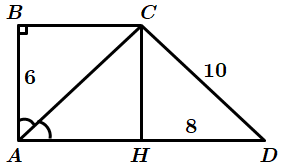
Отже, 1 – A.
2.
У
Отже, 2 – Б.
3.
Cередня лінія трапеції
Відповідь: 1 – A, 2 – Б, 3 – Г.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання перевіряє знання паралелограма, ромба, квадрата та їх властивостей.
I правильне. Діагоналі ромба є бісектрисами його кутів.
II неправильне. Діагоналі точкою перетину діляться навпіл – властивість паралелограма.
III правильне. Діагоналі перпендикулярні – властивість будь-якого квадрата.
Відповідь: Д.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання перевіряє вміння застосовувати властивості паралелограма до розв'язування планіметричних задач.
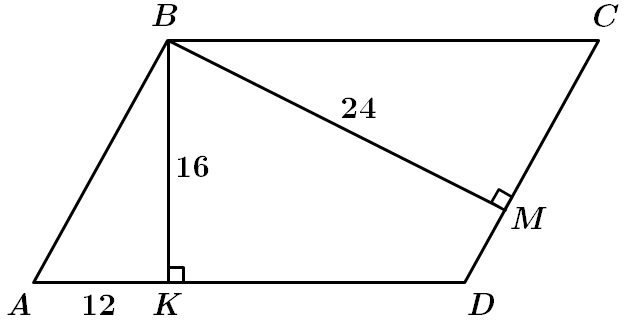
1. У
2. За формулою
Відповідь: 1.
2.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання перевіряє знання властивостей ромба.
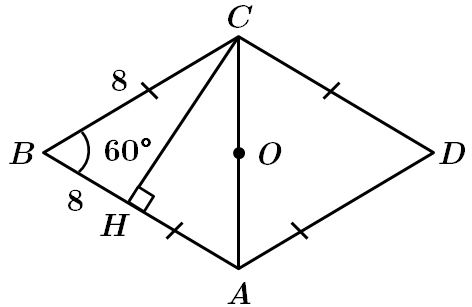
1.
2.
3. Центр кола, вписаного в ромб – точка перетину діагоналей точка
За властивістю ромба
Відповідь: 1 – B, 2 – Б, 3 – A.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання перевіряє знання властивостей трапеції.
I – неправильне твердження. Трапеція – це чотирикутник, у якого дві сторони паралельні (основи), а дві інші – ні (бічні).
IІ – правильне твердження. Основи трапеції – паралельні відрізки, бічна сторона – січна. Кути, прилеглі до бічної сторони – внутрішні односторонні кути, і за властивістю паралельних прямих їх сума дорівнює
III – неправильне твердження. Наведемо контрприклад. У прямокутній трапеції сума протилежних кутів не дорівнює
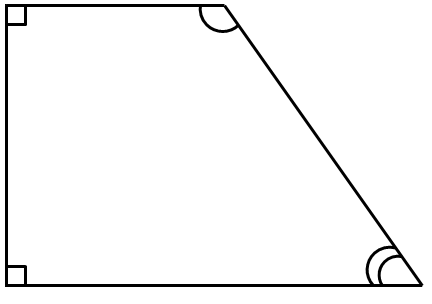
Відповідь: Б.
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.
Це завдання перевіряє знання властивостей ромба, прямокутного трикутника, вміння розв’язувати прямокутні трикутники.
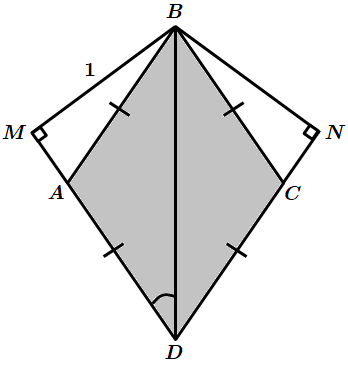
кута
За властивістю катета, протилеглого до кута
Відповідь, найближча до точної
Відповідь: Б.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Це завдання перевіряє знання властивостей паралелограмів, нерівності трикутника.
I. Протилежні сторони будь-якого паралелограма рівні (властивість параллелограма).
II. Довжина сторони будь-якого трикутника менша за суму довжин двох інших сторін (нерівність трикутника).
III. Твердження неправильне.
Відповідь: B.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Це завдання перевіряє знання властивостей паралелограмів, суміжних кутів.
За властивістю суміжних кутів
За властивістю паралелограма
Відповідь: Д.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Геометричні величини та їх вимірювання.
Це завдання перевіряє знання про середню лінію трапеції, вміння застосовувати властивості трапеції до розв'язування планіметричних задач.
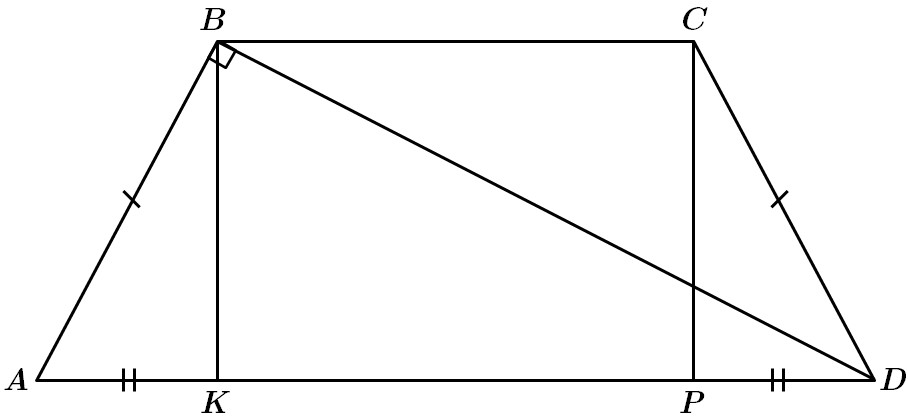
1. Довжина середньої лінії трапеції дорівнює:
Отже, 1 – Г.
2.
Отже, 2 – А.
3.
За властивістю висоти прямокутного трикутника, проведеної до гіпотенузи:
Отже, 3 – Б.
4. У
Отже, 4 – В.
Відповідь: 1 – Г, 2 – А, 3 – Б, 4 – В.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Це завдання перевіряє вміння застосовувати властивості ромба до розв'язування планіметричних задач; знання теореми Піфагора, формули площі трикутника.
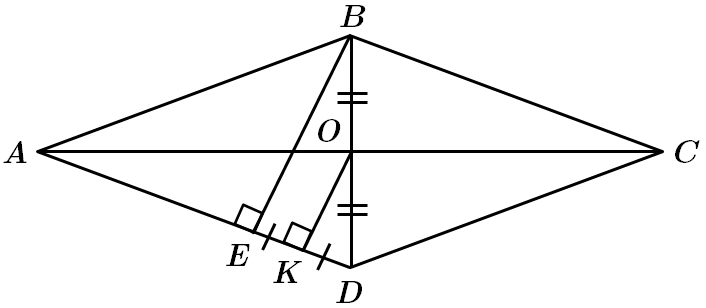
1.
2.
У
Відповідь: 1.
2.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Це завдання перевіряє знання про трапецію та її властивості; середню лінію трапеції, вписані в коло та описані навколо кола чотирикутники, теореми Піфагора.
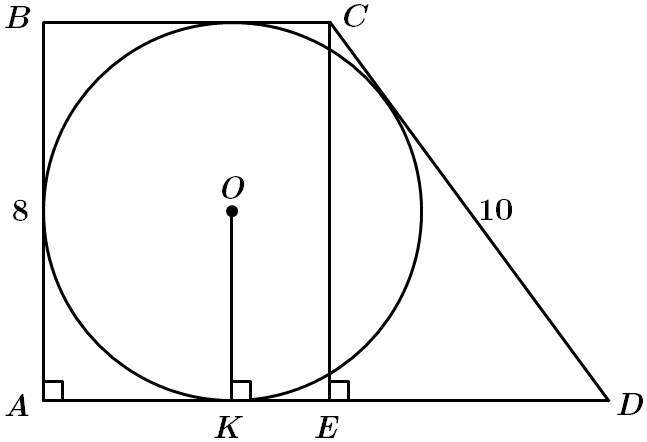
1. Висота трапеції – діаметр кола
Отже, 1 – Б.
2.
3. За властивістю чотирикутника, описаного навколо кола
4. Середня лінія трапеції дорівнює
Відповідь: 1 – Б, 2 – A, 3 – Г, 4 – B.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Це завдання перевіряє знання властивостей паралелограма.
I. Сума кутів, прилеглих до будь-якої сторони паралелограма, дорівнює
II. Протилежні сторони паралелограма рівні. Отже, твердження ІІ правильне.
III.
Відповідь: B.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Це завдання перевіряє вміння застосовувати означення, ознаки та властивості різних видів чотирикутників до розв'язування планіметричних задач.
1.
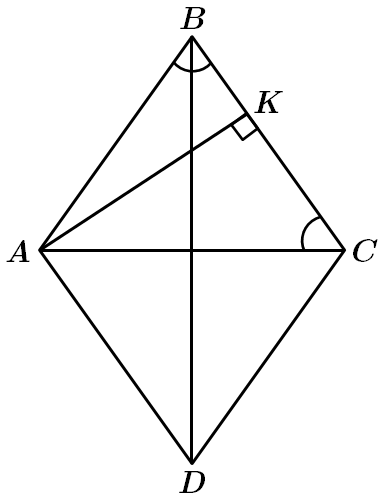
Отже, 1 – Г.
2.
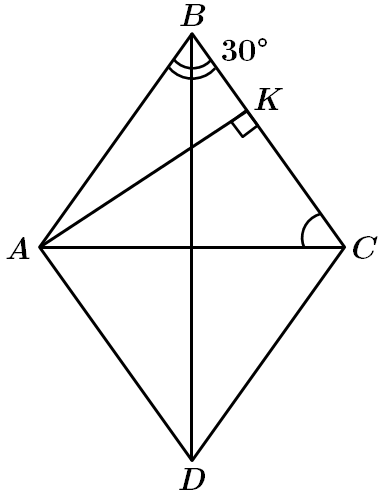
Отже, 2 – В.
3.
Додаткова побудова
Отже, 3 – Б.
4.
Отже, 4 – Д.
Відповідь: 1 – Г, 2 – В, 3 – Б, 4 – Д.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Геометричні перетворення.
Це завдання перевіряє вміння застосовувати означення паралелограма, ознак подібності трикутників до розв'язування планіметричних задач.
Розглянемо
Отже,
Відповідь: Б.
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники. Геометричні перетворення.
Це завдання перевіряє знання співвідношення між сторонами і кутами прямокутного трикутника, ознаки та властивості подібних фігур; уміння застосовувати властивості трикутників та чотирикутників до розв'язування планіметричних задач.
1.
За властивостю катета, який лежить напроти кута
2.
Відповідь: 1.
2.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Це завдання перевіряє знання теореми косинусів, властивостей ромба, уміння розв'язувати планіметричні задачі.
Дано: ромб
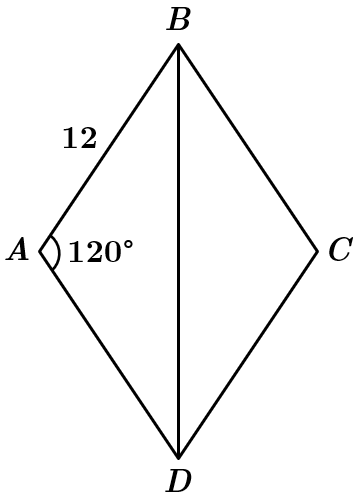
Більша діагональ лежить напроти більшого кута ромба
У трикутнику
Отже,
Відповідь: Г.
ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості. Трикутники. Чотирикутники.
Це завдання перевіряє знання теореми Фалеса, властивостей середньої лінії трикутника, трапеції, теореми Піфагора, уміння застосовувати властивості геометричних фігур до розв'язання планіметричних задач.
1. Оскільки площа квадрата
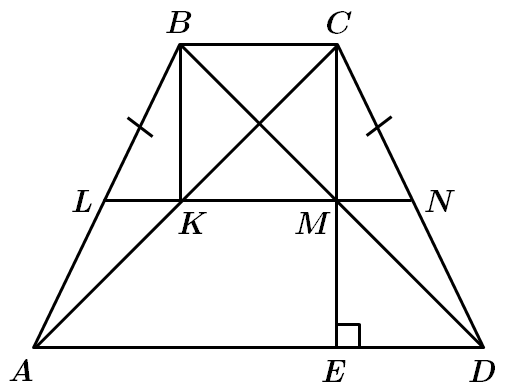
За теоремою Фалеса
За теоремою Піфагора
2. Оскільки
Відповідь: 1.
2.
ТЕМА: Геометрія. Планіметрія. Координати та вектори на площині.
Це завдання перевіряє вміння виконувати дії з векторами, знаходити скалярний добуток векторів.
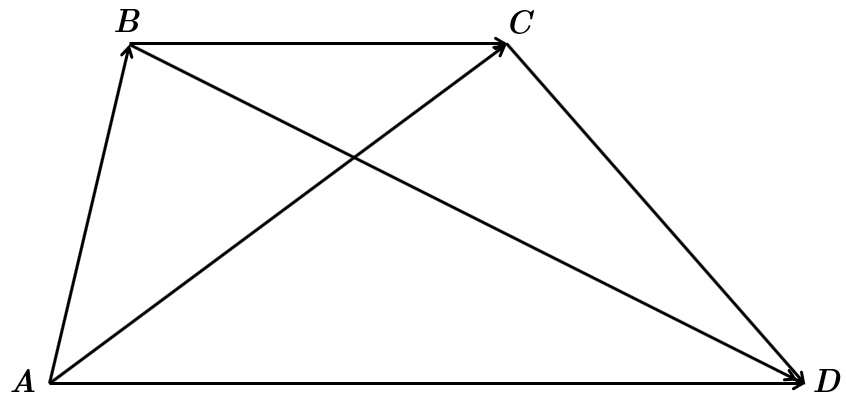
1.
2.
3.
4. Знаходимо скалярний добуток векторів:
Відповідь:
ТЕМА: Геометрія. Коло та круг. Чотирикутники. Геометричні величини та їх вимірювання.
Це завдання перевіряє знання про коло та його елементи, уміння застосовувати властивості ромба, використовувати формули площ геометричних фігур до розв'язування планіметричних задач.
1. Довжина кола
2. Нехай
Площу ромба знайдемо за формулою:
Відповідь: 1.
2.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Паралелограм та його властивості. Координати та вектори на площині. Скалярний добуток векторів та його властивості. Теорема косинусів.
Це завдання перевіряє вміння застосовувати координати й вектори до розв'язування планіметричних задач.
Нагадаємо, що скалярним добутком векторів
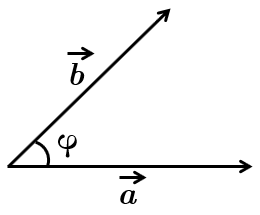
Довжину вектора
На рисунку
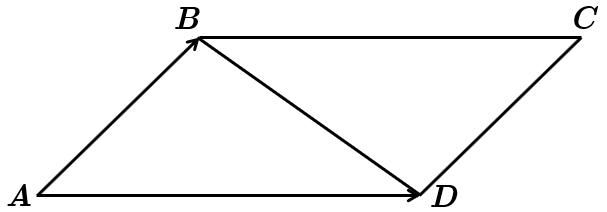
За умовою
Визначаємо довжину вектора
Діагональ
Звідки отримуємо
Отже, довжина діагоналі
Знаючи довжини сторін
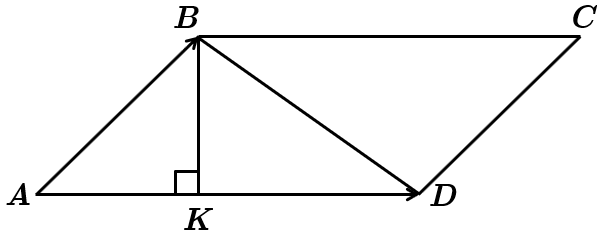
Прямокутні трикутники
З прямокутного трикутника
Тоді
Отже,
тоді
Відповідь: