Алгебра і початки аналізу – Дійсні числа

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє вміння порівнювати дійсні числа.

Запишімо подвійною нерівністю: \begin{gather*} -2{,}07\lt x\lt 15{,}9. \end{gather*}

Першим цілим числом, яке більше за \(-2{,}07\), є \(-2.\) Останнім цілим числом, яке менше за \(15{,}9\), є \(15.\)

Кількість цілих чисел:

• від \(1\) до \(15\) – це п`ятнадцять чисел;
• число \(0\) – це ще одне число;
• числа \(-1\) та \(-2\) – це ще два числа.

Всього: \(15 + 1 + 2 = 18.\)

Відповідь: Д.

ТЕМА: Дійсні числа та дії з ними.

Завдання скеровано на перевірку вміння виконувати дії з дійсними числами.

1. \(\cos \frac{\pi}{2}=0.\)

Число \(0\) належить проміжку \((-\infty; 0].\) Отже, правильна відповідь – А.

2. \(\pi\approx 3{,}14\)

Число \(1{,}86\) належить проміжку \((0; 2).\) Отже, правильна відповідь – Б.

3. Оскільки \(\pi\gt 3\), то

Отже, правильна відповідь – Д.

Відповідь: 1 – А, 2 – Б, 3 – Д.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа.

Завдання скеровано на перевірку знання властивостей степенів із цілим показником, тотожних перетворень раціональних і логарифмічних виразів.

1. Оскільки \(9=3^2\), то

Отже, \(a=m+2n.\) Правильна відповідь – Д.

2. Скористаймося формулою скороченого множення:

Отже, \(a=2mn.\) Правильна відповідь – Г.

3. Скористаймося властивостями логарифма:

Отже, \(a=3mn.\) Правильна відповідь – B.

Відповідь: 1 – Д, 2 – Г, 3 – В.

ТЕМА: Дійсні числа та дії з ними.

Завдання скеровано на перевірку вміння виконувати дії з раціональними числами, використовувати властивості модуля.

Спростімо вираз

за формулою різниці квадратів $$ (a-b)(a+b)=a^2-b^2. $$

Підставимо в умову:

За властивістю модуля числа:

Відповідь: Д.

ТЕМА: Дійсні числа. Логарифмічні вирази та їх перетворення.

Завдання скеровано на перевірку знання властивостей степенів, логарифмів, уміння виконувати тотожні перетворення їх.

1. \(\frac{m}{4}=1\), \(m=4.\)

Отже, правильна відповідь – B.

2.

Отже, правильна відповідь – Г.

3. \(\log_{16}2+\log_{16}m=\log_{16}(2m)=1.\)

За властивістю логарифмів: $$ \log_ab+\log_ac=\log_a(bc). $$

За означенням логарифма:

Отже, правильна відповідь – Д.

Відповідь: 1 – В, 2 – Г, 3 – Д.

ТЕМА: Дійсні числа та дії з ними.

Завдання скеровано на перевірку знання властивостей коренів, уміння виконувати дії з ірраціональними числами.

Спростімо вираз:

Використали властивість кореня: \(\sqrt{a\cdot b}=\sqrt{a}\cdot \sqrt{b},\) де \(a\), \(b\gt 0.\)

Відповідь: B.

ТЕМА: Дійсні числа та дії з ними.

Завдання скеровано на перевірку вміння виконувати дії з дійсними числами, тотожні перетворення ірраціональних і логарифмічних виразів.

1. \(\ln\frac 1e=\ln e^{-1}=-1\cdot \ln e=-1\) є від'ємним цілим числом.

Застосували формули:

Отже, правильна відповідь – Б.

2. \(e+1\approx 2\mathord{,}7+1\approx 3\mathord{,}7\) є ірраціональним числом. Отже, правильна відповідь – Д.

Вираз \((e-1)^2\) спростили за формулою квадрата різниці: \((a-b)^2=a^2-2ab+b^2.\)

Відповідь: 1 – Б, 2 – Д, 3 – А.

ТЕМА: Дійсні числа та дії з ними.

Завдання скеровано на перевірку вміння виконувати дії з дійсними числами, знання властивостей модуля числа.

За властивістю модуля числа

Отже, \(|2\sqrt{2}-3|=-(2\sqrt{2}-3)=3-2\sqrt{2}.\)

Відповідь: A.

ТЕМА: Дійсні числа та дії з ними.

Завдання скеровано на перевірку вміння виконувати дії з дійсними числами.

1. \(\sin\left(-\frac{\mathbf{\pi}}{6}\right)=-\sin\frac{\mathbf{\pi}}{6}=-\frac 12.\)

Функція \(y=\sin x\) – непарна, тому \(\sin (-x)=-\sin (x).\) Отже, правильна відповідь – А.

За властивістю модуля числа: $$ |a|=\left\{\begin{array}{l} a,\ \text{якщо}\ a\ge 0,\\ -a,\ \text{якщо}\ a\lt 0. \end{array}\right. $$ \(\mathbf{\pi}+2\gt 0\), тому \(|\mathbf{\pi}+2|=\mathbf{\pi}+2.\)

Отже, правильна відповідь – Г.

3. \(\left(-\frac{1}{\sqrt{2}}\right)^2=\left(\frac{1}{\sqrt{2}}\right)^2=\frac{1^2}{(\sqrt{2})^2}=\frac 12.\) Отже, правильна відповідь – Б.

Відповідь: 1 – A, 2 – Г, 3 – Б.

ТЕМА: Алгебра і початки аналізу. Дійсні числа та дії з ними.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення ірраціональних, логарифмічних та степеневих виразів.

1. \(\mathbf{\varphi}^0=\left(\frac{\sqrt{5}+1}{2}\right)^0=1\in (0; 1].\)

Отже, правильна відповідь – B.

2. \((\sqrt{5}-1)\cdot \frac{\sqrt{5}+1}{2}=\frac{(\sqrt{5}-1)(\sqrt{5}+1)}{2}=\frac{5-1}{2}=2\in (1; 2].\)

Отже, правильна відповідь – Г.

3.

Отже, правильна відповідь – Б.

При спрощенні виразу застосовували формули:

Відповідь: 1В, 2Г, 3Б.

ТЕМА: Алгебра і початки аналізу. Дійсні числа.

Завдання скеровано на перевірку знання означення степеня з натуральним показником, його властивостей.

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Дійсні числа та дії з ними.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення раціональних виразів.

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Дійсні числа та дії з ними.

Завдання скеровано на перевірку знання означення модуля числа та його властивостей.

З наведених чисел – це \(-1\mathord{,}9.\)

Відповідь: В.

ТЕМА: Алгебра і початки аналізу. Дійсні числа та дії з ними.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення тригонометричних, ірраціональних виразів, знання модуля числа та його властивостей.

1. \(\sin \left(-\frac{\mathbf{\pi}}{6}\right)=-\sin\frac{\mathbf{\pi}}{6}=-\frac 12.\)

\(y=\sin x\) – непарна, тому

Отже, правильна відповідь – Г.

Отже, правильна відповідь – Б.

3. \(\left(-\frac{1}{\sqrt{2}}\right)^2=\left(\frac{1}{\sqrt{2}}\right)^2=\frac 12.\)

Отже, правильна відповідь – A.

Відповідь: 1Г, 2Б, 3A.

ТЕМА: Алгебра і початки аналізу. Дійсні числа.

Завдання скеровано на перевірку знання означення степеня з натуральним показником, його властивостей.

Використали властивість степеня з натуральним показником. При множенні степенів з однаковими основами показники додаються, а основа залишається без змін: $$ a^n\cdot a^m=a^{n+m}, $$ (де \(a\) – будь-яке число, \(n\) i \(m\) – натуральні числа).

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення раціональних виразів.

Якщо $$ m=n-1, $$ то

Отже, правильна відповідь – B.

Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання перевіряє знання властивостей дійсних чисел.

1. Дільником числа \(8\) є числа, на які \(8\) ділиться без остачі. Серед наведених чисел – це \(8.\) Отже, правильна відповіль – A.

2. Просте число – це число, яке має тільки два дільники – \(1\) та саме число. Серед наведених – це \(17.\) Отже, правильна відповідь – B.

3. Квадратом натурального числа є число \(16=4^2.\) Отже, правильна відповідь – Б.

Відповідь: 1А, 2В, 3Б.

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє вміння використовувати властивості модуля, виконувати тотожні перетворення ірраціональних, тригонометричних виразів, розрізняти види чисел та числових проміжків.

Знайдемо значення виразу

1. \(|-1,6|+2=1,6+2=3,6\in [3;\ +\infty)\) Д.

2. \begin{gather*} \frac{\sqrt{24}}{\sqrt{3}}=\sqrt{\frac{24}{3}}=\sqrt{8}\\[7pt] \sqrt{4}\lt \sqrt{8}\lt\sqrt{9}\\[7pt] 2\lt\sqrt{8}\lt 3. \end{gather*} Отже, \(\sqrt{8}\in [2;\ 3)\) – Г.

3. \(2\cos\frac{\mathbf{\pi}}{3}=2\cdot \frac 12=1\in [1;\ 2)\) – B.

Відповідь: 1Д 2Г 3В.

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє вміння порівнювати дійсні числа.

Запишемо подвійною нерівністю: \begin{gather*} \sqrt{8}\lt x\lt \sqrt{81}\\[7pt] \sqrt{8}\lt \sqrt{9}=3,\ \ \sqrt{81}=9\\[7pt] 3\le x\lt 9 \end{gather*} \(x=3\), \(4\), \(5\), \(6\), \(7\), \(8\) – шість цілих чисел.

Відповідь: B.

Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє знання правил округлення цілих чисел.

В числі \(1265\): цифра "\(2\)", позначає сотні, а наступна цифра "\(6\)" – позначає десятки.

Округлення до сотень означає, що ми дивимося на число, яке позначає десятки, щоб вирішити – збільшувати сотні чи залишити як є. Оскільки \(6 \gt 5 \rightarrow\) округлюємо вгору. Отже, \(1265 \approx 1300\) км.

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа. Числові множини та співвідношення між ними.

Це завдання перевіряє вміння виконувати дії з дійсними числами та порівнювати їх.

Оцінимо вираз. \begin{gather*} \sqrt{25}\lt \sqrt{27}\lt \sqrt{36},\\[7pt] 5\lt\sqrt{27}\lt 6,\\[7pt] 4\lt \sqrt{27}-1\lt 5,\\[6pt] 2\lt \frac{\sqrt{27}-1}{2}\lt 2\mathord{,}5. \end{gather*} Отже, значення виразу належить проміжку \([2; 3).\)

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа.

Це завдання перевіряє вміння виконувати тотожні перетворення раціональних виразів.

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа.

Це завдання перевіряє вміння розрізняти види чисел.

1. \(\frac 35\) правильний дріб. Отже, 1 – Б.

2. \(\frac 65=1\frac 15=1\mathord{,}2\in (1; 1\mathord{,}5).\)
Отже, 2 – Д.

3. \(\frac 85=1\frac 35=1\mathord{,}6=7^{\log_7 1\mathord{,}6}.\)
Отже, 3 – Г.

4. \(\sqrt[3]{\frac 18}+\sqrt{\frac{25}{9}}=\frac 12+\frac 53=\frac{13}{6}.\)
Отже, 4 – A.

Відповідь: 1 – Б, 2 – Д, 3 – Г, 4 – A.

ТЕМА: Алгебра та початки аналізу. Числа і вирази. Дійсні числа.

Це завдання перевіряє знання означення кореня \(n\text{-го}\) степеня, властивості коренів, уміння використовувати властивості модуля до розв'язування задач.

\begin{gather*} \sqrt{(\sqrt{3}-2)^2}+\sqrt{(\sqrt{3}+2)^2}=|\sqrt{3}-2|+|\sqrt{3}+2|=2-\sqrt{3}+\sqrt{3}+2=4,\\[7pt] \sqrt{3}-2\lt 0,\ \text{тому} |\sqrt{3}-2|=2-\sqrt{3},\\[7pt] \sqrt{3}+2\gt 0,\ \text{тому} |\sqrt{3}+2|=\sqrt{3}+2. \end{gather*}

Відповідь: Г.

ТЕМА: Алгебра та початки аналізу. Числа та вирази. Дійсні числа.

Це завдання перевіряє вміння виконувати дії з дійсними числами.

$$ 3(a-1)=3(0\mathord{,}7-1)=2\mathord{,}1-3=-0\mathord{,}9. $$

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа. Логарифмічні вирази.

Це завдання перевіряє знання означення та властивості кореня n-го степеня, степеня з натуральним показником, основної логарифмічної тотожності.

1. $$ (3a^3)^2=3^2\cdot (a^3)^2=9a^6. $$ Отже, 1 – A.

2. $$ \sqrt[3]{27a^6}=\sqrt[3]{27}\cdot \sqrt[3]{a^6}=3a^2. $$ Отже, 2 – Д.

3. $$ \frac{27a^6}{9a^3}=3a^3. $$ Отже, 3 – Г.

Відповідь: 1 – А, 2 – Д, 3 – Г, 4 – Б.

ТЕМА: Алгебра. Числа і вирази. Дійсні числа.

Це завдання перевіряє вміння використовувати ознаки подільності до розв'язування задач.

Якщо цукерки можна поділити між двома або трьома дітьми, то їх кількість визначається числом, кратним \(6\).

Якщо цукерки не можна поділити порівну між чотирма дітьми, то їх кількість не є кратною \(4.\)

З наведених чисел кратні \(6\) – це \(36\), \(42\) та \(48.\) З них тільки \(42\) не є кратним \(4.\) Отже, відповідь \(42.\)

Відповідь: B.

ТЕМА: Алгебра. Числа і вирази. Дійсні числа та дії з ними.

Це завдання перевіряє вміння виконувати дії з дійсними числами.

Якщо \(\frac ab=\frac 27\), то число \(\frac ba\), яке є взаємно оберненим до числа \(\frac ab\), дорівнює \(\frac 72.\)

Відповідь: Б.

ТЕМА: Числа і вирази. Дійсні числа.

Це завдання перевіряє знання властивостей степеня з цілим показником, уміння використовувати властивості модуля числа.

1. \(a^0=1\), отже, правильна відповідь – Б.

2. \(a^2=(-3)^2=9\gt 1\), отже, правильна відповідь – A.

3. \(\frac{|a|}{a}\) при \(a\lt 0\ |a|=-a\).

\(\frac{-a}{a}=-1\), отже, правильна відповідь – Г.

4. \(\sqrt[3]{a}=\sqrt[3]{-3}\lt \sqrt[3]{-1}\), отже, правильна відповідь – Д.

Відповідь: 1 – Б, 2 – А, 3 – Г, 4 – Д.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа (натуральні, цілі, раціональні та ірраціональні).

Це завдання перевіряє вміння виконувати дії з дійсними числами, використовувати ознаки подільності, знаходити найменше спільне кратне кількох чисел, розрізняти види чисел.

1. \(32+18=50\) є числом, що ділиться націло на \(10.\)

Отже, правильна відповідь – Б.

2. \(32\cdot 18=16\cdot 2\cdot 2\cdot 9=16\cdot 4\cdot 9\) є квадратом натурального числа.

Отже, правильна відповідь – A.

3. \(32:18=\frac{32}{18}=\frac{16}{9}\) є раціональним числом, яке не є цілим.

Отже, правильна відповідь – Г.

4. \(32-18=14\) є дільником числа \(84\ (84:14=6).\)

Отже, правильна відповідь – Д.

Відповідь: 1 – Б, 2 – А, 3 – Г, 4 – Д.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа.

Це завдання перевіряє знання означення степеня з натуральним показником, їхні властивості, властивості та означення кореня \(n\text{-го}\) степеня. $$ a^4\cdot \sqrt{a^6}=a^4\cdot \sqrt{(a^3)^2}=a^4\cdot |a^3|. $$

При \(a\ge 0\ |a^3|=a^3\), тому \(a^4\cdot a^3=a^7.\)

Використали властивість степеня з натуральним показником: $$ a^{mn}=(a^m)^n, $$ та властивість кореня \(n\text{-го}\) степеня:

Відповідь: Г.

ТЕМА: Числа та вирази. Дійсні числа.

Це завдання перевіряє знання властивостей дій з дійсними числами, уміння округлювати десяткові дроби.

Для того, щоб округлити дріб до десятих, необхідно знати цифру, яка стоїть у розряді сотих.

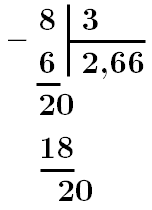
Якщо ця цифра \(5\) або більше, то цифра, яка стоїть в розряді десятих, збільшується на один.

\(2\mathord{,}66\approx 2\mathord{,}7.\)

Відповідь: Г.

ТЕМА: Алгебра та початки аналізу. Числа і вирази. Раціональні вирази та їх перетворення.

Це завдання перевіряє вміння виконувати дії з раціональними числами, виконувати тотожні перетворення раціональних виразів і знаходити їхнє числове значення при заданих значеннях змінної.

1. \(\frac 73a=\frac 73\cdot 15=\frac{7\cdot 15}{3}=35\)

ділиться націло на \(5.\) Отже, 1 – Д.

2. \(2a-1=2\cdot 15-1=29\)

є простим числом. Отже, 2 – Б.

3. \(a^2+12a+36=(a+6)^2=(15+6)^2=21^2\)

ділиться націло на \(3.\) Отже, 3 – Г.

4. \(a^2+13^2=15^2+13^2=225+169=394\)

є парним числом. Отже, 4 – В.

Відповідь: 1 – Д, 2 – Б, 3 – Г, 4 – В.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа.

Це завдання перевіряє знання модуля дійсного числа та його властивостей.

За властивістю модуля дійсного числа

Спрощуємо вираз:

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа, порівняння чисел.

Це завдання перевіряє вміння порівнювати дійсні числа.

З двох дробів з однаковими чисельниками більший той, у якого менший знаменник.

Отже, \(\frac{5}{18}\lt \frac{5}{17}.\)

З двох дробів з однаковими знаменниками більший той, у якого більший чисельник.

Отже, \(\frac{5}{17}\lt \frac{6}{17}.\)

Маємо \(\frac{5}{18}\lt \frac{5}{17}\lt \frac{6}{17}.\)

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа, порівняння чисел та дії над ними.

Це завдання перевіряє знання означення кореня n-го степеня та його властивостей; означення степеня з натуральним, цілим та раціональним показниками, їхні властивості.

Доберемо до кожного із запитань 1 – 4 правильну відповідь.

1. \((a^m)^n=a^4\), то \(a^{mn}=a^4\), \(mn=4.\) Отже, 1 – B.

2. \(a^m\cdot a^n=a^4\), то \(a^{m+n}=a^4\), \(m+n=4.\) Отже, 2 – A.

3. \(\sqrt[8]{a^m}=\sqrt{a^n}\), то \(a^{\frac m8}=a^{\frac n2}\), \(\frac m8=\frac n2\), \(2m=8n\), \(m=4n.\) Отже, 3 – Г.

4. \(\frac{a^n}{a^m}=\frac{1}{a^4}\), то \(a^{n-m}=a^{-4}\), \(n-m=-4\), \(m-n=4.\) Отже, 4 – Б.

Відповідь: 1 – B, 2 – А, 3 – Г, 4 – Б.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа, порівняння чисел та дії з ними. Числові множини та співвідношення між ними.

Це завдання перевіряє знання властивостей модуля дійсного числа.

За властивістю модуля:

\(a-2\lt 0\) при \(a\lt 2\), тому розкривши модуль, отримаємо

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв’язувати рівняння першого степеня, застосовувати загальні методи та прийоми в процесі розв’язання рівнянь.

Розв’яжемо рівняння першого степеня відносно \(y:\)

Відповідь: B.

ТЕМА: Алгебра та початки аналізу. Числа і вирази. Раціональні, ірраціональні, степеневі, показникові, логаримфічні вирази та їхні перетворення.

Це завдання перевіряє вміння виконувати тотожні перетворення ірраціональних, степеневих, логарифмічних виразів, використовувати властивості модуля до розв'язування задач.

1. Щоб розв'язати це завдання, достатньо скористатися формулою: \begin{gather*} \sqrt{a^2}=|a|,\\[6pt] \sqrt{\left(-\frac 12\right)^2}=\left|-\frac 12\right|=\frac 12=0\mathord{,}5\\[6pt] 0\mathord{,}5\in [0; 1). \end{gather*} Отже, 1 – B.

2. Щоб розв'язати це завдання, достатньо скористатися формулою: \begin{gather*} (a^x)^y=a^{x\cdot y},\\[6pt] 8^{\frac 23}=(2^3)^{\frac 23}=2^2=4,\\[6pt] 4\in [3; +\infty). \end{gather*} Отже, 2 – Д.

3. Щоб розв'язати це завдання, достатньо скористатися формулами: \begin{gather*} \log_a b^n=n\cdot \log_a b,\\[7pt] \log_{a^k} b=\frac 1k\cdot \log_a b. \end{gather*}

\(\log_{\frac 12} 10\lt \log_{\frac 12} 8\)
\(\log_{\frac 12} x\) – спадна функція, тому більшому значенню аргументу відповідає менше значення функції. $$ \log_{\frac 12} 8=-3, $$ тому $$ \log_{\frac 12}10\lt -3\ \ (-\infty; -3). $$ Отже, 3 – A.

4.За означенням модуля числа: \begin{gather*} |a|=\left\{\begin{array}{l} a,\ \text{якщо}\ a\ge 0, \\ -a,\ \text{якщо}\ a\lt 0. \end{array}\right.\\[6pt] \left|\frac 12-2\right|=\left|-1\frac 12\right|=1\frac 12=1\mathord{,}5\\[6pt] 1\mathord{,}5\in [1; 3). \end{gather*} Отже, 4 – Г.

Відповідь: 1 – B, 2 – Д, 3 – A, 4 – Г.

ТЕМА: Алгебра та початки аналізу. Числа і вирази. Раціональні вирази та їхні перетворення.

Це завдання перевіряє вміння порівнювати дійсні числа, знаходити відношення чисел.

Число \(a\) в \(5\) разів більше, ніж додатне число \(b.\) Тоді $$ a=5b. $$ Отже, правильна відповідь – Г.

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Раціональні числа та дії з ними. Означення степеня з раціональним показником. Модуль дійсного числа.

Це завдання перевіряє вміння виконувати дії з раціональними числами, записаними у вигляді звичайних дробів, знаходити значення степеневого виразу, виразу, що містить знак модуля.

Для розв'язання завдання потрібно знати правила дій із звичайними дробами, означення степеня з раціональним показником та правила дій зі степенями, а саме:

то значення модуля дійсного числа.

Нагадаємо, що за означенням модулем числа \(x\) називають саме це число, якщо воно є невід'ємним, і протилежне до \(x\) число, якщо воно є від'ємним, тобто

Обчислимо значення виразів (1 – 4).

1.

Отже, 1 – Д.

2. $$ \frac 1a=\frac{1}{\frac{25}{4}}=\frac{4}{25}. $$ Отже, 2 – A.

3.

Отже, 3 – Г.

4.

Або

Отже, 4 – Б.

Відповідь: 1 – Д, 2 – А, 3 – Г, 4 – Б.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Степеневі вирази та їхні перетворення.

Це завдання перевіряє вміння перетворювати степеневі вирази та знаходити їхні значення. Для розв'язання завдання потрібно знати означення степеня з натуральним, цілим, раціональним показниками та правила дій зі степенями, а саме:

Обчислимо значення виразів (1–4).

1.

Отже, 1 – A.

2.

Отже, 2 – B.

3.

Отже, 3 – Д.

4. \begin{gather*} 2^{3\mathord{,}5}\cdot 2^{1\mathord{,}5}=2^{3\mathord{,}5+1\mathord{,}5}=2^5=32. \end{gather*} Отже, 4 – Г.

Відповідь: 1 – А, 2 – В, 3 – Д, 4 – Г.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Арифметичні дії з дробами.

Це завдання перевіряє вміння виконувати додавання двох дробів із різними знаменниками.

Щоб додати два дроби із різними знаменниками, треба звести їх до спільного знаменника. Знайдемо спільний знаменник дробів \(\frac{5}{12}\) i \(\frac 78\), він є найменшим спільним кратним знаменників цих дробів: НСК \((8; 12)=24\) – це найменше число, що кратне числам \(8\) і \(12.\) Тоді

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Подільність чисел.

Це завдання перевіряє вміння знаходити дільники чисел, знання означень простого числа і числа, кратного іншому числу.

1. Серед наведених чисел квадратом натурального числа є число \(16 =4^{2}\), отже, 1 – Б.

2. Натуральне число, більше за одиницю, називається простим, якщо воно має лише два дільники: одиницю та саме число. Іншими словами, просте число ділиться націло лише на \(1\) та на себе. Усі парні натуральні числа більше \(2\) не є простими, оскільки, крім \(1\) та самого числа, вони обов’язково мають дільник \(2.\) Отже, парні числа \(8\), \(16\) та \(56\) не є простими. Число \(27\) також не є простим, воно ділиться націло на \(1\), \(3\), \(9\) і \(27.\) Залишається число \(17.\) Воно має лише два дільники: \(1\) та \(17\), тобто є простим. Отже, 2   В.

3. Число \(a\) називається дільником числа \(c\), якщо \(c\) ділиться на \(a\) націло. Серед наведених чисел на \(8\) націло ділиться тільки число \(8.\) Зауважимо також, що дільник числа не може бути більшим за саме число. Отже, 3 – А.

4. Число \(c\) називають кратним числу \(a\), якщо \(c\) ділиться націло на \(a.\) Серед наведених чисел на \(7\) націло ділиться тільки число \(56\), отже 4 – Д.

Відповідь: 1 – Б, 2 – В, 3 – A, 4 – Д.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа та дії з ними.

Це завдання перевіряє знання означень оберненого дробу до даного, неправильного дробу, скороченого дробу.

Розглянемо кожен із дробів (А – Д).

А. Дріб \(\frac{5}{7}\) є оберненим до дробу \(\frac{7}{5} = 1\frac{2}{5}\), оскільки \(\frac{5}{7} \cdot \frac{7}{5} = 1.\) Отже, 4 – А.

Б. Дріб \(\frac{13}{27}\) менший за \(0{,}5\), оскільки \(\frac{13}{27} = \frac{26}{54} \lt \frac{27}{54}=\frac{1}{2}.\) Отже, 3 – Б.

В. Дріб \(\frac{41}{10}\) більший за \(1\), тому цей дріб є неправильним. Отже, 2 – В.

Г. Дріб \(\frac{7}{10}\) не задовольняє жодне з тверджень (1–4).

Д. Чисельник і знаменник дробу \(\frac{34}{51}\) діляться на \(17\), тому цей дріб скоротний. Отже, 1 – Д.

Відповідь: 1 – Д, 2 – B, 3 – Б, 4 – A.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Формули скороченого множення. Модуль числа.

Це завдання перевіряє вміння спрощувати вираз, що містить під знаком модуля раціональний дріб.

Для розв’язання цього завдання потрібно знати формули скороченого множення: $$ a^2-b^2=(a-b)(a+b) $$ та означення модуля. Модулем (абсолютною величиною) числа \(a\) називається саме число \(a\), якщо воно невід’ємне, та протилежне число \(-a\), якщо \(a\) – від’ємне, тобто

Спочатку спростимо заданий вираз:

За означенням,

Оскільки за умовою \(a\lt -7\), то

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Ірраціональні вирази.

Це завдання перевіряє розуміння означення арифметичного кореня \(n\text{-го}\) степеня (зокрема, кубічного кореня) та вміння його добувати.

Оскільки \(64=4^3\), то $$ \frac{\sqrt[3]{64}}{64}=\frac{\sqrt[3]{4^3}}{64}=\frac{4}{64}=\frac{1}{16}. $$

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Арифметичні дії.

Це завдання перевіряє вміння виконувати арифметичні дії з буквениими виразами.

Під час виконання завдання важливо правильно розкрити дужки, перед якими стоїть знак «–». Якщо перед дужками стоїть знак «–», то дужки можна прибрати, змінивши знак всіх доданків, що стоять у дужках, на протилежні. Підставимо у вираз \(7-m\) замість \(m\) вираз \(n-1{:}\)

Відповідь: B.