Елементарні геометричні фігури на площині. Геометричні величини – тести ЗНО/НМТ

Предмет: Геометрія
Розділ: Планіметрія
Тема: Елементарні геометричні фігури на площині. Геометричні величини
Кількість завдань: 42

123456789101112131415161718192021222324252627282930313233343536373839404142

Зачекайте, йде розрахунок...

Завдання 1 з 42

Три промені зі спільним початком лежать в одній площині (див. рисунок). Визначте градусну міру кута $\gamma$, якщо $\alpha=20^\circ$, $\beta=50^\circ.$

А$330^\circ$

Б$290^\circ$

В$250^\circ$

Г$160^\circ$

Д$110^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їх властивості. Геометричні величини та їх вимірювання. Величини кута, вимірювання кутів.

Це завдання перевіряє вміння вимірювати кути, знання аксіом планіметрії.

Градусна міра повного кута $360^\circ.$

\begin{gather*} \alpha+\beta+\gamma= 360^\circ,\\[7pt] \gamma=360^\circ - \alpha-\beta=360^\circ - 20^\circ - 50^\circ = 290^\circ. \end{gather*}

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 2. Завдання: 5315

Завдання 2 з 42

Пряма $c$ перетинає паралельні прямі $a$ i $b$ (див. рисунок). Які з наведених тверджень є правильними для кутів $1$, $2$, $3$?

I. $\angle 1$ i $\angle 3$ – суміжні.

II. $\angle 1=\angle 2$.

III. $\angle 2+ \angle 3=180^\circ$.

Алише I

Блише I i III

Влише IІІ

Глише I i ІІ

ДІ, ІІ та ІІІ

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Прямі на площині.

Це завдання перевіряє знання властивостей паралельних прямих.

$a\ ||\ b$, $c$ – січна.

За властивістю паралельних прямих:

I. $\angle 1$ i $\angle 3$ суміжні (за означенням суміжних кутів).

II. $\angle 1=\angle 2$ як відповідні при паралельних прямих.

IІІ. $\angle 1=\angle 2$, $\angle 1+\angle 3=180^\circ$ (за властивістю суміжних кутів).

Отже, $\angle 2+\angle 3=180^\circ$.

Усі з наведених тверджень є правильними.

Відповідь: Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 3. Завдання: 6080

Завдання 3 з 42

Пряма $n$ перетинає перпендикулярні прямі $l$ i $m$ (див. рисунок). Визначте градусну міру кута $\alpha.$

А$34^\circ$

Б$46^\circ$

В$54^\circ$

Г$56^\circ$

Д$58^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Трикутники.

Це завдання перевіряє знання теореми про суму кутів трикутника, властивостей суміжних та вертикальних кутів.

$\angle DAC + \angle CAB = 180^\circ$ як суміжні.

$\angle DAC = 146^\circ$, $\angle CAB = 180^\circ - 146^\circ = 34^\circ.$

У $\Delta ABC$ $(\angle B = 90^\circ).$ $\angle A + \angle C = 90^\circ$, $\angle C = 90^\circ - 34^\circ = 56^\circ.$ $\angle ACB = \alpha = 56^\circ$ (як вертикальні).

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 126. Завдання: 6285

Завдання 4 з 42

Три прямі, що розміщені в одній площині, перетинаються в одній точці (див. рисунок). Визначте градусну міру кута $\alpha$.

А$101^\circ$

Б$99^\circ$

В$81^\circ$

Г$79^\circ$

Д$69^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їх властивості.

Це завдання перевіряє знання про суміжні та вертикальні кути.

Кути $\alpha$ та $\beta$ – вертикальні.

За властивістю вертикальних кутів $\alpha = \beta.$

За аксіомою вимірювання кутів:

\begin{gather*} 52^\circ + \beta + 49^\circ = 180^\circ;\\[7pt] \beta = 180^\circ - (52^\circ + 49^\circ) = 180^\circ - 101^\circ = 79^\circ;\\[7pt] \alpha = \beta = 79^\circ. \end{gather*}

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 127. Завдання: 6316

Завдання 5 з 42

Прямі $a$, $b$, $c$ попарно перетинаються в точках $A$, $B$, $C$ (див. рисунок). За даними, вказаними на рисунку, знайдіть градусну міру кута $ABC$.

А$70^\circ$

Б$80^\circ$

В$140^\circ$

Г$100^\circ$

Д$40^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Трикутники. Найпростіші геометричні фігури на площині.

Це завдання перевіряє знання суміжних та вертикальних кутів, теореми про суму кутів трикутника.

Кут $30^\circ$ та $\angle BCA$ – вертикальні, отже, рівні. Зовнішній кут трикутника $110^\circ$ дорівнює сумі внутрішніх кутів, не суміжних з даним.

\begin{gather*} \angle B = 110^\circ – 30^\circ = 80^\circ. \end{gather*}

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 128. Завдання: 6347

Завдання 6 з 42

Які з наведених тверджень є правильними?

I. Сума двох будь-яких вертикальних кутів дорівнює $180^\circ.$

II. Сума двох будь-яких суміжних кутів дорівнює $180^\circ.$

III. Сума будь-якого гострого кута та будь-якого тупого кута дорівнює $180^\circ.$

Алише І

Блише ІI

Влише І i III

Глише ІI i ІІI

ДI, II i III

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Найпростіші фігури на площині. Вертикальні кути. Суміжні кути.

Це завдання перевіряє знання основних властивостей вертикальних та суміжних кутів, які відносяться до найпростіших геометричних фігур на площині.

Нагадаємо, що суміжними називають два кути, у яких одна сторона спільна, а інші є доповняльними променями. На рис. 1 кути $AOC$ та $COB$ є суміжними.

Вертикальними називаються два кути, в яких сторони одного кута є доповнювальними променями сторін другого. На рис. 2 кути $AOB$ та $COD$ є вертикальними. Вертикальними також є кути $AOD$ та $BOC.$

Проаналізуємо наведені твердження.

I. Вертикальні кути є рівними, але їх сума дорівнює $180^\circ$ лише тоді, коли ці кути прямі. Тому твердження I не є правильним.

II. Суміжні кути в сумі утворюють розгорнутий кут, градусна міра якого дорівнює $180^\circ.$ Отже, твердження II є правильним.

III. Кут називається гострим, якщо його градусна міра менше $90^\circ$, і тупим, якщо його градусна міра більше $90^\circ$ і менше $180^\circ.$ Їх сума не обов’язково дорівнює $180^\circ$, а дорівнює $180^\circ$ лише тоді, коли вони суміжні. Отже, твердження III не є правильним.

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 138. Завдання: 6876

Завдання 7 з 42

Відрізок, довжина якого дорівнює $60$ см, розділений точками на чотири рівні відрізки. Визначте відстань між серединами отриманих крайніх відрізків.

А$36$ см

Б$40$ см

В$45$ см

Г$48$ см

Д$50$ см

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Найпростіші фігури на площині. Довжина відрізка.

Це завдання перевіряє вміння знаходити довжини відрізків, використовуючи основну властивість вимірювання відрізків.

Довжина відрізка дорівнює сумі довжин частин, на які відрізок ділиться будь-якою його точкою.

Розділимо відрізок $AB$ точками $K$, $L$, $M$ на рівні відрізки $AK$, $KL$, $LM$ та $MB$ (див. рисунок).

Тоді довжина кожного з цих відрізків дорівнює $$ \frac{1}{4} AB = \frac{1}{4} \cdot 60 = 15\ \text{см}. $$ Нехай точки $C$ і $D$ – середини крайніх відрізків $AK$ і $MB$ відповідно. Тоді

\begin{gather*} AC = CK = MD = DB = \frac{15}{2} = 7{,}5\ \text{см}\ \text{і}\\[6pt] CD = CK + KL + LM + MD = 7{,}5 + 15 + 15 + 7{,}5 = 45\ \text{см}. \end{gather*}

Відповідь: B.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 142. Завдання: 7072

Завдання 8 з 42

Прямі $k$, $l$, $m$ i $n$ лежать в одній площині (див. рисунок). Визначте градусну міру кута $\alpha.$

А$15^\circ$

Б$25^\circ$

В$35^\circ$

Г$45^\circ$

Д$55^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Суміжні кути. Трикутники. Зовнішній кут трикутника. Теорема про суму кутів трикутника.

Це завдання перевіряє вміння знаходити градусні міри кутів.

Для розв’язання завдання потрібно знати такі теореми.

Теорема 1. Сума внутрішніх кутів трикутника дорівнює $180^\circ.$

Теорема 2. Сума суміжних кутів дорівнює $180^\circ.$

Наведемо декілька способів розв’язання цього завдання.

Перший спосіб. Розглянемо трикутник $ABC$ (див. рисунок), у якого $\angle B=85^\circ$, $\angle MAB$ – зовнішній кут трикутника, суміжний з кутом $A$, тоді $$ \angle A=180^\circ-\angle MAB=40^\circ. $$ Знаючи два внутрішніх кути трикутника $ABC$, можемо визначити градусну міру його третього кута: $$ \angle C=180^\circ-(40^\circ+85^\circ)=55^\circ. $$ Оскільки за умовою $\angle ACN=90^\circ$, то $$ 55^\circ+\alpha=90^\circ, $$ звідки $\alpha=35^\circ.$

Другий спосіб. Опустимо з вершини $B$ трикутника $ABC$ на сторону $AC$ перпендикуляр $AD$ (див. рисунок). З паралельності прямих $BD$ і $CN$ випливає, що $\angle DBC=\angle BCN$ як внутрішні різносторонні. Тому шуканий кут $\alpha$ дорівнює куту $DBC.$ Маємо:

\begin{gather*} \angle A=180^\circ-\angle MAB=40^\circ,\\[7pt] \angle ABD=90^\circ-\angle A=90^\circ-40^\circ=50^\circ,\\[7pt] \alpha=\angle DBC=\angle ABC-\angle ABD=85^\circ-50^\circ=35^\circ. \end{gather*}

Третій спосіб. Скористаємось теоремою. Зовнішній кут трикутника дорівнює сумі двох внутрішніх, не суміжних з ним. Отже, $\angle BCP=\angle A+\angle B$ (див. рисунок). Оскільки

\begin{gather*} \angle BCP=90^\circ+\alpha,\\[7pt] \angle A=180^\circ-140^\circ=40^\circ, \end{gather*}

то

$$ 90^\circ+\alpha=40^\circ+85^\circ. $$

Звідки одержуємо:

$$ \alpha=125^\circ-90^\circ=35^\circ. $$

Відповідь: B.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 144. Завдання: 7170

Завдання 9 з 42

Прямі $AB$ i $CK$ паралельні, $CB$ – бісектриса кута $ACK.$ Визначте градусну міру кута $ABC$, якщо $\angle BAC=52^\circ.$

А$38^\circ$

Б$52^\circ$

В$64^\circ$

Г$69^\circ$

Д$128^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Кути при паралельних прямих. Бісектриса кута.

Це завдання перевіряє знання властивостей кутів, що утворюються при перетині двох паралельних прямих січною та означення бісектриси кута.

Кути $\angle BAC$ та $\angle ACK$ – внутрішні односторонні кути при паралельних прямих $AB$ i $CK$ та січній $AC.$ Сума внутрішніх односторонніх кутів при паралельних прямих дорівнює $180^\circ.$ Отже, $$ \angle BAC+\angle ACK=180^\circ, $$ звідки

$$ \angle ACK=180^\circ-\angle BAC=180^\circ-52^\circ=128^\circ. $$

Оскільки $BC$ є бісектрисою кута $\angle ACK$, то за означенням бісектриси, вона ділить цей кут навпіл, отже,

$$ \angle ACB=\angle BCK=\frac{128^\circ}{2}=64^\circ. $$

Кути $\angle BCK$ i $\angle ABC$ – внутрішні різносторонні кути при паралельних прямих $AB$ i $CK$ та січній $BC$, тому вони рівні. Отже, $\angle ABC=64^\circ.$

Відповідь: B.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 187. Завдання: 9240

Завдання 10 з 42

На рисунку зображено прямі $m$ i $n$, що перетинаються. Визначте градусну міру кута $\gamma$, якщо $\alpha+\beta=50^\circ.$

А$310^\circ$

Б$155^\circ$

В$145^\circ$

Г$140^\circ$

Д$130^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Найпростіші фігури на площині. Вертикальні та суміжні кути.

Це завдання перевіряє вміння визначати невідомий кут, використовуючи означення суміжних кутів і властивості вертикальникх кутів.

Зображені на рисунку кути $\alpha$ i $\beta$ є вертикальними, тому що утворені при перетині двох прямих $m$ i $n.$

Вертикальні кути рівні, тому $$ \alpha=\beta=\frac{50^\circ}{2}=25^\circ. $$ Кути $\alpha$ i $\gamma$ є суміжними, оскільки промінь $OA$, що лежить на прямій $n$, є спільною стороною цих кутів, а сторони $OB$ та $OC$, що лежать на прямій $m$, є доповняльними променями. Оскільки сума суміжних кутів дорівнює $180^\circ$, то $$ \gamma=180^\circ-\alpha=180^\circ-25^\circ=155^\circ. $$

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 191. Завдання: 9427

Завдання 11 з 42

На відрізку $AB$ вибрано точку $M$ так, що довжина відрізка $AM$ утричі більша за довжину $MB.$ Визначте довжину відрізка $AB$, якщо $MB=12$ см.

А$48$ см

Б$36$ см

В$24$ см

Г$42$ см

Д$54$ см

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їх властивості. Аксіоми планіметрії.

Це завдання перевіряє вміння застосовувати властивості найпростіших геометричних фігур до розв’язування планіметричних задач.

\begin{gather*} AM=3MB=3\cdot 12=36\ \textit{см},\\[7pt] AB=AM+MB=36+12=48\ \textit{см}. \end{gather*}

Відповідь: A.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 247. Завдання: 12066

Завдання 12 з 42

Усі зображені на рисунку прямі лежать в одній площині, прямі $m$ i $n$ є паралельними. Визначте градусну міру кута $\mathbf{\alpha}.$

А$20^\circ$

Б$50^\circ$

В$60^\circ$

Г$70^\circ$

Д$110^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їх властивості.

Це завдання перевіряє знання аксіом стереометрії, властивостей паралельних прямих, уміння застосовувати властивості найпростіших геометричних фігур до розв’язування планіметричних задач.

$\angle ABC+\angle CBD+\angle DBE=180^\circ$, $\angle CBD=\angle BDE=70^\circ$, як внутрішні різносторонні при $m\ ||\ n$ та січною $BD.$ Кут $\mathbf{\alpha}=180^\circ-60^\circ-70^\circ=50^\circ.$

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 247. Завдання: 12072

Завдання 13 з 42

Точка $B$ належить відрізку $AC.$ Визначте відстань між серединами відрізків $AB$ і $BC$, якщо $AB=10\ \textit{см}$, $BC=5\mathord{,}2\ \textit{см}.$

А$2\mathord{,}4$ см

Б$2\mathord{,}6$ см

В$5\mathord{,}0$ см

Г$7\mathord{,}6$ см

Д$10\mathord{,}2$ см

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості.

Це завдання перевіряє знання аксіом планіметрії, уміння застосовувати властивості найпростіших геометричних фігур до розв'язування планіметричних задач.

Нехай точка $K$ – середина $AB$, а точка $M$ – середина $BC.$

\begin{gather*} KM=KB+BM=\frac 12AB+\frac 12BC=\\[6pt] =\frac 12(AB+BC)=(10+5\mathord{,}2):2=7\mathord{,6}\ \textit{см}. \end{gather*}

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 256. Завдання: 12505

Завдання 14 з 42

Рівносторонній трикутник $ABC$ та пряма $KM$, що проходить через точку $B$, лежать в одній площині (див. рисунок). Визначте градусну міру кута $KBA$, якщо $\angle CBM=85^\circ.$

А$45^\circ$

Б$35^\circ$

В$30^\circ$

Г$25^\circ$

Д$15^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості. Трикутники.

Це завдання перевіряє вміння застосовувати властивості найпростіших геометричних фігур, різних видів трикутників до розв'язування планіметричних задач.

$\Delta ABC$ – рівносторонній, тому $$ \angle A=\angle B=\angle C=60^\circ. $$

$\angle KBM=180^\circ$ – розгорнутий. $$ \angle KBA+\angle ABC+\angle CBM=180^\circ. $$

Отже,

$$ \angle KBA=180^\circ-\angle MBC-\angle ABC=180^\circ-85^\circ-60^\circ=35^\circ. $$

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 290. Завдання: 14238

Завдання 15 з 42

На рисунку зображено ескіз емблеми. Емблема має форму кола радіуса $2$ м, усередині якого розміщено $6$ однакових півкіл. Один кінець кожного півкола збігається із центром кола, інший кінець лежить на колі. Для виготовлення емблеми (з усіма елементами включно) потрібен гнучкий матеріал вартістю $200$ грн за $1$ м довжини. Укажіть з-поміж наведених сум грошей найменшу, якої достатньо, щоб придбати цей матеріал для виготовлення емблеми. Уважайте, що на з’єднання елементів емблеми не потрібно додаткових витрат матеріалу.

А$4000$ грн

Б$5000$ грн

В$6000$ грн

Г$7000$ грн

Д$8000$ грн

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Геометричні величини та їх вимірювання.

Це завдання перевіряє вміння обчислювати довжину кола та його дуг, використовувати формули знаходження довжини кола до розв'язування планіметричних задач і задач практичного змісту.

Знаходимо довжини $6$ півкіл, які знаходяться усередині кола радіуса $2$ м, за формулою $$ 6C_1=6\mathbf{\pi}R, $$ де $R$ – радіус кола та $R=1$ м.

$$ 6C_1=6\cdot \mathbf{\pi}\cdot 1=6\mathbf{\pi}\ \textit{м}. $$

Емблема також складається ще з одного кола, радіусом $2$ м, тому

$$ C_2=2\cdot \mathbf{\pi}\cdot 2=4\mathbf{\pi}\ \textit{м}. $$

Довжина матеріалу складає

$$ 6\mathbf{\pi}+4\mathbf{\pi}=10\mathbf{\pi}\ \textit{м}. $$

Вартість матеріалу

$$ 10\mathbf{\pi}\cdot 200=2000\mathbf{\pi}\ \textit{грн}. $$

$\mathbf{\pi}\approx 3\mathord{,}14$, тому

$$ 2000\cdot 3\mathord{,}14=6280\ \textit{грн}. $$

З-поміж наведених сум грошей найменша, якої достатньо, щоб придбати матеріал це $7000$ грн.

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 290. Завдання: 14252

Завдання 16 з 42

У прямокутній системі координат на площині задано трапецію $ABCD$ $(AD\ ||\ BC$, $AD\gt BC).$ Площа трапеції дорівнює $42.$ Визначте абсцису вершини $D$, якщо $A(-1; 3)$, $B(1; 6)$, $C(7; 6).$

Впишіть відповідь:

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Координати та вектори на площині. Геометричні величини та їх вимірювання.

Це завдання перевіряє знання прямокутної системи координат на площині, координати точки, формули площі трапеції.

Позначимо задані точки на координатній площині.

Задано трапеція $ABCD.$ Точки $B$ та $C$ мають однакову ординату, тому пряма $BC$ паралельна осі $Ox.$

$BC\ ||\ AD$, тому точка $D$ має з точкою $A$ однакову ординату $y=3.$ Площа трапеції $42$, тому $$ S=\frac{BC+AD}{2}\cdot h, $$ де $h$ – висота трапеції, складемо рівняння.

\begin{gather*} BC=6,\\[7pt] h=BK=3,\\[7pt] S=42,\\[6pt] \frac{6+AD}{2}\cdot 3=42, \end{gather*}

звідси $AD=22.$

Так як точка $A$ має абсцису $-1$, то точка $D$ буде мати абсцису $21.$

Відповідь: $21.$

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 290. Завдання: 14264

Завдання 17 з 42

Три прямі, розміщені в одній площині, перетинаються в одній точці (див. рисунок). Визначте градусну міру кута $\mathbf{\alpha}.$

А$80^\circ$

Б$50^\circ$

В$90^\circ$

Г$100^\circ$

Д$70^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Найпростіші геометричні фігури на площині та їхні властивості.

Це завдання перевіряє вміння застосовувати властивості найпростіших геометричних фігур до розв'язування планіметричних задач, знання властивості вертикальних кутів.

$\angle \mathbf{\beta}=60^\circ$ як вертикальний з даним кутом $60^\circ.$

$\mathbf{\alpha}+\mathbf{\beta}+40^\circ=180^\circ$ оскільки складають розгорнутий кут.

Тому $\mathbf{\alpha}=180^\circ-40^\circ-\mathbf{\beta}=180^\circ-40^\circ-60^\circ=80^\circ.$

Відповідь: A.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 298. Завдання: 14597

Завдання 18 з 42

Ha рисунку зображено паралельні прямі $a$ i $b$ тa січну $CD.$ Знайдіть відстань між прямими $a$ i $b$, якщо $CK=5$ см, $KD=2$ см, a відстань від точки $K$ до прямої $a$, дорівнює $1$ см.

А$2\mathord{,}5$ см

Б$3$ см

В$3\mathord{,}5$ см

Г$4$ см

Д$4\mathord{,}5$ см

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості. Трикутники. Суміжні та вертикальні кути, паралельні та перпендикулярні прямі. Геометричні перетворення.

Це завдання перевіряє вміння застосовувати властивості паралельних прямих, ознаки подібності трикутників до розв'язування планіметричних задач.

Зробимо додаткову побудову і терез точку $K$ проведемо пряму $AB$, перпендикулярну до прямих $a$ i $b.$

Розглянемо трикутники $ADK$ та $BCK.$ Вони подібні за двома кутами: $\angle ADK=\angle BCK$ як внутрішні різносторонні при $a\ ||\ b$ та січною $CD.$

$\angle DAK=\angle KBC=90^\circ$ за побудовою.

У подібних трикутниках відповідні сторони пропорційні, отже $$ \frac{AK}{KB}=\frac{KD}{CK}. $$

Відстань від точки $K$ до прямої $a$ – це довжина перпенидкуляра $KA=1$ см \begin{gather*} \frac{1}{KB}=\frac 25,\\[6pt] KB=2\mathord{,}5\ \textit{см}. \end{gather*}

Відстань між прямими $a$ i $b$ – це довжина спільного перпендикуляра

$AB=AK+KB=1+2\mathord{,}5=3\mathord{,}5$ см.

Відповідь: B.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 298. Завдання: 14606

Завдання 19 з 42

Дві дороги розходяться на рівнинній місцевості як промені $OA$ та $OB$, позначені на рисунку. Перша дорога (промінь $OA$) утворює кут $40^\circ$ з напрямком «схід», а друга (промінь $OB$) – кут $20^\circ$ з напрямком «південь». Який кут утворюють ці дороги між собою?

А$90^\circ$

Б$100^\circ$

В$110^\circ$

Г$120^\circ$

Д$130^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості.

Це завдання перевіряє вміння застосовувати означення, ознаки та властивості найпростіших геометричних фігур до розв'язування задач практичного змісту.

Кут $COD$ – прямий.

\begin{gather*} \angle COB=\angle COD-\angle BOD=90^\circ-20^\circ=70^\circ,\\[7pt] \angle AOB=\angle AOC+\angle COB=40^\circ+70^\circ=110^\circ. \end{gather*}

Відповідь: B.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 310. Завдання: 15236

Завдання 20 з 42

На рисунку зображено паралелограм $ABCD$, точка $B$ лежить на прямій $MC.$
Визначте градусну міру кута $CDA$, якщо $\angle MBA=25^\circ.$

А$115^\circ$

Б$65^\circ$

В$175^\circ$

Г$165^\circ$

Д$155^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Чотирикутники.

Це завдання перевіряє знання властивостей паралелограмів, суміжних кутів.

За властивістю суміжних кутів $$ \angle ABM+\angle CBA=180^\circ. $$

$$ \angle CBA=180^\circ-\angle ABM=180^\circ-25^\circ=155^\circ. $$

За властивістю паралелограма $\angle B=\angle D=155^\circ$ як протилежні.

Відповідь: Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 384. Завдання: 18979

Завдання 21 з 42

Прямі $l$, $m$ і $n$ лежать в одній площині (див. рисунок). Визначте градусну міру
кута $\mathbf{\alpha}.$

А$110^\circ$

Б$50^\circ$

В$60^\circ$

Г$70^\circ$

Д$80^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

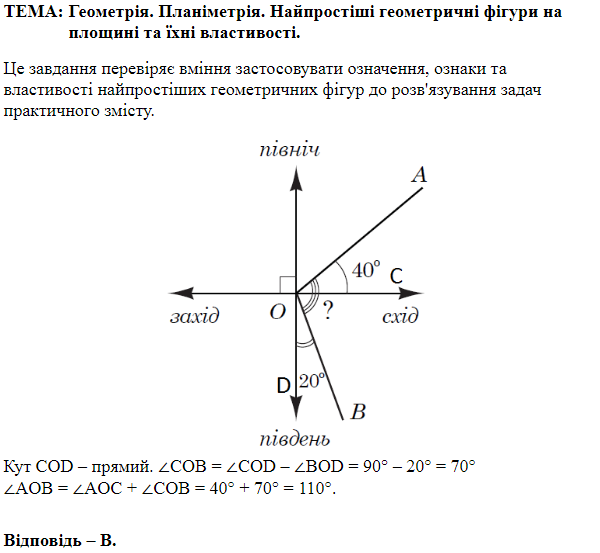
ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури на площині та їхні властивості.

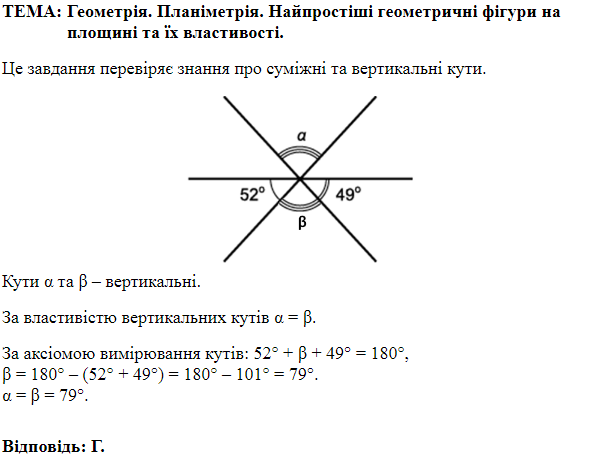
Завдання перевіряє знання властивостей суміжних та вертикальних кутів, теореми про суму кутів трикутника.

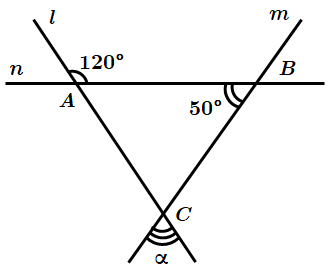
$\angle BAC=180^\circ-120^\circ=60^\circ$ – суміжний до кута $120^\circ.$

$\angle ACB=\mathbf{\alpha}$ – вертикальні кути.

Сума кутів $\Delta ABC$ дорівнює $180^\circ$, тому $$ \mathbf{\alpha}=180^\circ-(50^\circ+60^\circ)=70^\circ. $$

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 400. Завдання: 19946

Завдання 22 з 42

Пряма $l$ перетинає паралельні прямі $m$ та $n$ (див. рисунок). Визначте градусну міру кута $\mathbf{\alpha}$, якщо $\mathbf{\beta} = 125^\circ.$

А$35^\circ$

Б$45^\circ$

В$55^\circ$

Г$65^\circ$

Д$75^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури та їхні властивості.

Завдання перевіряє знання властивостей вертикальних i суміжних кутів, паралельних прямих.

$\angle\mathbf{\beta}=\angle\mathbf{\gamma}$ як вертикальний. $\mathbf{\alpha}+\mathbf{\gamma}=180^\circ.$ За властивістю паралельних прямих. $\mathbf{\alpha}$, $\mathbf{\gamma}$ – внутрішні односторонні. $$ \mathbf{\alpha}=180^\circ-\mathbf{\gamma}=180^\circ-125^\circ=55^\circ. $$

Відповідь: B.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 425. Завдання: 21208

Завдання 23 з 42

Вершина $B$ паралелограма $ABCD$ лежить на прямій $MC$ (див. рисунок). Визначте градусну міру кута $CDA$, якщо $\angle MBA=25^\circ$.

А$65^\circ$

Б$115^\circ$

В$155^\circ$

Г$165^\circ$

Д$175^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури на площині та їхні властивості.

Завдання перевіряє знання властивостей суміжних кутів та паралелограма.

$\angle ABM+\angle ABC=180^\circ$ за властивістю суміжних кутів.

$$ \angle ABC=180^\circ-\angle ABM=180^\circ-25^\circ=155^\circ. $$

За властивістю паралелограма $$ \angle B=\angle D=155^\circ. $$

Відповідь: B.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 516. Завдання: 25996

Завдання 24 з 42

Прямі $AB$ і $CK$ паралельні, $CB$ – бісектриса кута $ACK$. Визначте градусну міру кута $ABC$, якщо $\angle BAC = 52^\circ.$

А$38^\circ$

Б$52^\circ$

В$64^\circ$

Г$69^\circ$

Д$128^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури та їхні властивості.

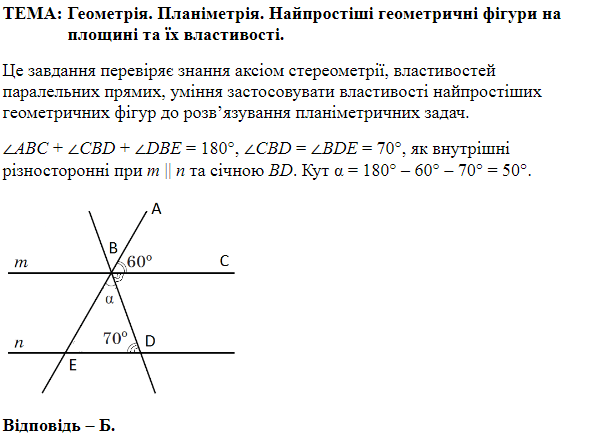
Перевіряє знання властивостей, паралельних прямих, суми кутів трикутника.

$$ \angle BAC+\angle ACK=180^\circ $$ за властивістю паралельних прямих сума внутрішніх односторонніх кутів $180^\circ.$ $$ \angle ACK=180^\circ-52^\circ=128^\circ. $$ $CB$ – бісектриса, тому $$ \angle ACB=\angle BCK=128^\circ:2=64^\circ. $$ Сума кутів трикутника $180^\circ.$ Отже, \begin{gather*} \angle ABC=180^\circ-(\angle BAC +\angle ACB)=\\[7pt] =180^\circ-(52^\circ+64^\circ)=180^\circ-116^\circ=64^\circ. \end{gather*} Або в такий спосіб: $\angle ABC=\angle BCK=64^\circ$ як внутрішні різносторонні при $AB\ ||\ CK$ та січної $BC.$

Відповідь: B.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 521. Завдання: 26118

Завдання 25 з 42

На рисунку зображено відрізок $d$ на координатній площині. Установіть відповідність між відрізком (1–3) та рисунком (А – Д), на якому він зображений.

Відрізок

1відрізок, симетричний відрізку $d$ відносно oсі $x$

2відрізок, симетричний відрізку $d$ відносно осі $y$

3відрізок, симетричний відрізку $d$ відносно точки $O$

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

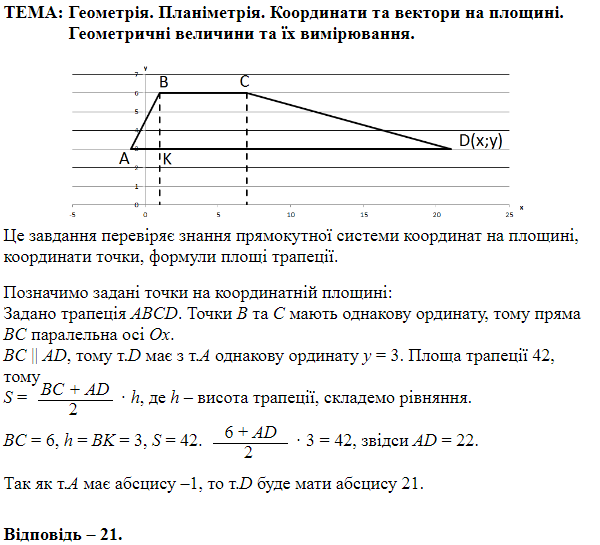
ТЕМА: Геометрія. Планіметрія. Геометричні перетворення.

Завдання перевіряє знання геометричних перетворень на площині: симетрії відносно прямої та точки.

1 – Б. симетрія відносно осі $x.$

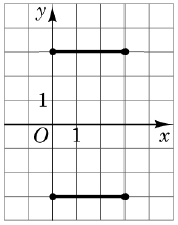
2 – Г. симетрія відносно осі $y.$

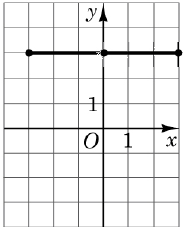
3 – Д. симетрія відносно точки $O.$

Відповідь: 1Б, 2Г, 3Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 523. Завдання: 26201

Завдання 26 з 42

Із точки $O,$ яка лежить на прямій $AB,$ проведено промені $OM$ і $OK$ (див. рисунок). Відомо, що $\angle BOM = 30^\circ,$ $\angle MOK = 80^\circ.$ Визначте градусну міру кута $AOK.$ Уважайте, що промені $OK,\ OM$ і пряма $AB$ лежать в одній площині.

А$60^\circ$

Б$70^\circ$

В$80^\circ$

Г$150^\circ$

Д$170^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури на площині та їх властивості.

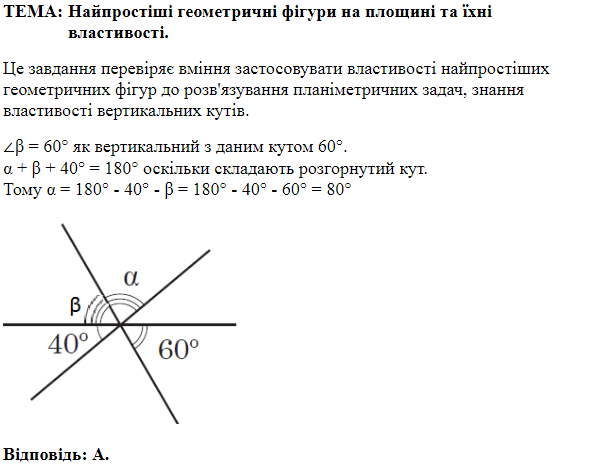
Завдання перевіряє знання аксіом планіметрії.

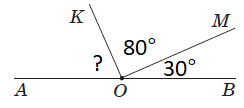
$\angle AOK+\angle KOM+\angle MOB=180^\circ.$

$\angle AOK=180^\circ-(30^\circ+80^\circ)=70^\circ.$

Отже, правильна відповідь – Б.

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 547. Завдання: 26824

Завдання 27 з 42

Зовнішній кут при вершині $A$ трикутника $ABC$ дорівнює $100^\circ,$ $\angle C=20^\circ$ (див. рисунок). Визначте градусну міру кута $B.$

А$100^\circ$

Б$90^\circ$

В$120^\circ$

Г$80^\circ$

Д$70^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія.

Завдання скеровано на перевірку знання властивості зовнішнього кута трикутника.

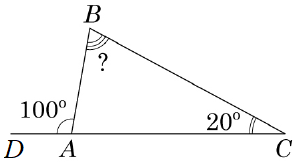
За властивістю зовнішнього кута трикутника:

\begin{gather*} \angle DAB=\angle B+\angle C. \end{gather*}

Отже, $\angle B=100^\circ-20^\circ=80^\circ.$

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 585. Завдання: 28355

Завдання 28 з 42

Відомо, що вісь $AO$ Пізанської вежі натепер відхилена від вертикалі $BO$ на кут $4^\circ$ (див. рисунок). Визначте градусну міру кута $AOC,$ який утворює вісь вежі з горизонтальною поверхнею $OC.$

А$176^\circ$

Б$94^\circ$

В$104^\circ$

Г$86^\circ$

Д$96^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури на площині та їхні властивості.

Завдання скеровано на перевірку знання властивостей кутів, аксіом планіметрії.

$\angle BOC=90^\circ, \angle BOA=4^\circ.$ Отже,

$$ \angle AOC=\angle BOC-\angle BOA=90^\circ-4^\circ=86^\circ. $$

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 606. Завдання: 28379

Завдання 29 з 42

На рисунку зображено дві прямі, що перетинаються.

Визначте градусну міру кута $\mathbf{\alpha}$, якщо $\mathbf{\beta}+\mathbf{\varphi}=70^\circ.$

А$145^\circ$

Б$135^\circ$

В$125^\circ$

Г$110^\circ$

Д$290^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Елементарні геометричні фігури на площині та їхні властивості.

Завдання скеровано на перевірку знання властивостей суміжних і вертикальних кутів.

Кути $\mathbf{\beta}$ i $\mathbf{\varphi}$ – вертикальні. За їхньою властивістю $\mathbf{\beta}=\mathbf{\varphi}.$

За умовою $\mathbf{\beta}+\mathbf{\varphi}=70^\circ$, тому $$ \mathbf{\beta}=\mathbf{\varphi}=70^\circ:2=35^\circ. $$

Кути $\mathbf{\alpha}$ i $\mathbf{\beta}$ – суміжні. За властивістю суміжних кутів:

\begin{gather*} \mathbf{\alpha}+\mathbf{\beta}=180^\circ,\\[7pt] \mathbf{\alpha}=180^\circ - \mathbf{\beta}=180^\circ-35^\circ=145^\circ. \end{gather*}

Відповідь: A.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 699. Завдання: 35325

Завдання 30 з 42

Пряма $l$ перетинає паралельні прямі $m$ і $n.$ Визначте градусну міру кута $\mathbf{\beta}$, якщо $\mathbf{\alpha}=35^\circ.$

А$135^\circ$

Б$125^\circ$

В$155^\circ$

Г$55^\circ$

Д$145^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Елементарні геометричні фігури на площині та їхні властивості.

Завдання скеровано на перевірку знання властивостей суміжних і вертикальних кутів, паралельних прямих.

Кути $\mathbf{\gamma}$ i $\mathbf{\beta}$ – вертикальні. За властивістю вертикальних кутів $\mathbf{\beta} = \mathbf{\gamma}.$

Кути $\mathbf{\alpha}$ i $\mathbf{\gamma}$ – внутрішні односторонні. За їхньою властивістю:

\begin{gather*} \mathbf{\alpha}+ \mathbf{\gamma}=180^\circ,\\[7pt] \mathbf{\alpha}=35^\circ,\\[7pt] \mathbf{\gamma}=180^\circ - 35^\circ=145^\circ. \end{gather*}

Отже, $\mathbf{\beta}=145^\circ.$

Відповідь: Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 700. Завдання: 35346

Завдання 31 з 42

На рисунку зображено елемент декору паркану, що складається з п’яти довгих і чотирьох коротких стрілок, які виходять з вершини розгорнутого кута та поділяють його на рівні частини. Знайдіть градусну міру кута між двома довгими сусідніми стрілками.

А$18^\circ$

Б$20^\circ$

В$30^\circ$

Г$36^\circ$

Д$40^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Елементарні геометричні фігури на площині та їхні властивості.

Завдання скеровано на перевірку знання властивостей і видів кутів.

Розгорнутий кут поділено на $10$ рівних частин. Градусна міра кожного з-поміж цих кутів $$ 180^\circ: 10=18^\circ. $$

Градусна міра кута між довгими стрілками складається з двох градусних мір кутів між довгою і короткою стрілкою.

Отже,

$$ 18^\circ\cdot 2=36^\circ. $$

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 701. Завдання: 35369

Завдання 32 з 42

Драбина $BC$ приставлена до вертикальної стіни $AB$ й спирається на горизонтальну поверхню $AC$ (див. рисунок). За наведеними на рисунку даними визначте градусну міру кута $BCA$ нахилу драбини до поверхні $AC.$

А$18^\circ$

Б$82^\circ$

В$72^\circ$

Г$12^\circ$

Д$78^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія.

Завдання скеровано на перевірку знання властивості зовнішнього кута трикутника.

За властивістю зовнішнього кута трикутника: \begin{gather*} \angle KBC=\angle A+\angle C,\\[7pt] \angle C=\angle KBC-\angle A,\\[7pt] \angle C=162^\circ-90^\circ,\\[7pt] \angle C=72^\circ. \end{gather*}

Відповідь: B.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 712. Завдання: 35424

Завдання 33 з 42

Визначте радіанну міру кута $\beta$, якщо суміжний із ним кут $\alpha=\frac{\pi}{5}.$

А$\frac{\pi}{5}$

Б$\frac{7\pi}{10}$

В$\frac{4\pi}{5}$

Г$\frac{9\pi}{5}$

Д$\frac{3\pi}{10}$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Найпростіші фігури на площині. Вертикальні кути. Суміжні кути.

Завдання спрямовано на перевірку знань про суміжні та вертикальні кути як основні геометричні фігури на площині.

Суміжними називають два кути, у яких одна сторона спільна, а інші є доповняльними променями. На рис. 1 кути $AOC$ та $COB$ суміжні.

Рис. 1

Сума суміжних кутів дорівнює $180^\circ.$ Оскільки в умові міру кута наведено в радіанах, скористаймось еквівалентом: \begin{gather*} \alpha+\beta=\pi. \end{gather*}

Відомо, що кут \begin{gather*} \alpha=\frac{\pi}{5}. \end{gather*}

Щоб визначити міру кута $\beta$, віднімімо від $\pi$ відомий кут: \begin{gather*} \beta=\pi-\frac{\pi}{5}. \end{gather*}

Зведімо до спільного знаменника:

\begin{gather*} \beta=\frac{5\pi}{5}-\frac{\pi}{5}=\frac{5\pi-\pi}{5}=\frac{4\pi}{5}. \end{gather*}

Відповідь: B.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 731. Завдання: 36326

Завдання 34 з 42

З точки $O$, яка лежить на прямій $AB$, проведено промені $OM$ і $OK$ (див. рисунок). Відомо, що $\angle BOM=30^\circ$, $\angle MOK=80^\circ$. Визначте градусну міру кута $AOK$. Уважайте, що промені $OK$, $OM$ і пряма $AB$ лежать в одній площині.

А$50^\circ$

Б$60^\circ$

В$80^\circ$

Г$70^\circ$

Д$110^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури на площині та їх властивості.

Завдання перевіряє знання аксіом планіметрії.

\begin{gather*} \angle AOK+\angle KOM+\angle MOB=180^\circ;\\[7pt] \angle AOK=180^\circ-(30^\circ+80^\circ)=70^\circ. \end{gather*}

Отже, правильна відповідь – Г.

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 735. Завдання: 36904

Завдання 35 з 42

На рисунку зображено прямі, що перетинаються. Визначте градусну міру кута $\beta$, якщо $\alpha=25^\circ.$

А$145^\circ$

Б$155^\circ$

В$115^\circ$

Г$65^\circ$

Д$165^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Найпростіші фігури на площині. Суміжні кути.

Завдання перевіряє вміння визначати невідомий кут, використовуючи означення і властивість суміжних кутів.

Кути $\alpha$ та $\beta$ суміжні, оскільки мають спільну сторону, а інші їхні сторони є доповняльними променями. Сума суміжних кутів завжди дорівнює $180^\circ.$ Тому

\begin{gather*} \beta=180^\circ-\alpha=180^\circ-25^\circ=155^\circ. \end{gather*}

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 736. Завдання: 37099

Завдання 36 з 42

На відрізку $AB$ вибрано точку $C$ так, що $AC:CB=2:3.$ Визначте довжину відрізка $AC$, якщо $CB=12$ см.

А$4$ см

Б$18$ см

В$6$ см

Г$12$ см

Д$8$ см

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Відрізок $AC$ складається з $2$ частин, отже: $AC=2x.$

Відрізок $CB$ складається з $3$ частин, отже: $CB=3x.$

За умовою $CB=12$ см. Тоді

\begin{gather*} 3x=12;\\[7pt] x=4\ \text{см}. \end{gather*}

Підставимо це значення у вираз для $AC{:}$

\begin{gather*} AC=2x=2\cdot 4=8\ \text{см}. \end{gather*}

Відповідь: Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 737. Завдання: 37161

Завдання 37 з 42

На відрізку $AB$ вибрано точку $M$ (див. рисунок). Визначте відстань між серединами відрізків $AM$ i $MB$, якщо $AM=12$ см, $MB=2AM.$

А$9$ см

Б$24$ см

В$12$ см

Г$18$ см

Д$16$ см

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості.

Завдання перевіряє знання аксіом планіметрії, уміння застосовувати властивості найпростіших геометричних фігур у розв'язуванні планіметричних задач.

За умовою $MB=2AM$, отже $MB=2\cdot 12=24$ см.

Нехай точка $K$ – середина $AM$, а точка $C$ – середина $MB.$

\begin{gather*} KC=KM+MC=\frac 12 AM+\frac 12 MB;\\[6pt] KC=\frac 12(AM+MB)=\frac 12(12+24)=\frac 12\cdot 36=18\ \text{см}. \end{gather*}

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 739. Завдання: 37381

Завдання 38 з 42

З вершини зображеного на рисунку розгорнутого кута $AOB$ проведено два промені $OK$ i $OM$ так, що $\angle KOB=110^\circ$, $\angle MOB=30^\circ.$ Обчисліть градусну міру кута $KOM.$

А$140^\circ$

Б$80^\circ$

В$60^\circ$

Г$70^\circ$

Д$90^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури на площині та їхні властивості.

Завдання перевіряє знання аксіом планіметрії.

$\angle KOB=\angle KOM+\angle MOB.$

Підставмо відомі значення:

\begin{gather*} 110^\circ=\angle KOM+30^\circ;\\[7pt] \angle KOM=110^\circ-30^\circ;\\[7pt] \angle KOM=80^\circ. \end{gather*}

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 741. Завдання: 37506

Завдання 39 з 42

На відрізку $AB$ вибрано точку $M$ (див. рисунок). Обчисліть відстань від середини відрізка $AM$ до точки $B$, якщо $AB=26$ см, $AM=8$ см.

А$17$ см

Б$22$ см

В$18$ см

Г$24$ см

Д$20$ см

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості.

Оскільки точка $M$ лежить на відрізку $AB$, загальна довжина складається з двох частин:

\begin{gather*} AB=AM+MB;\\[7pt] MB=AB-AM=26-8=18\ \text{см}. \end{gather*}

Нехай точка $K$ – середина відрізка $AM.$ Тоді відстань від $K$ до $M$ дорівнює половині довжини $AM{:}$

\begin{gather*} KM=AM:2=8:2=4\ \text{см}. \end{gather*}

Відстань від середини відрізка $AM$ (точки $K$) до точки $B$ складається з відрізків $KM$ та $MB{:}$

\begin{gather*} KB=KM+MB=4+18=22\ \text{см}. \end{gather*}

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 743. Завдання: 37687

Завдання 40 з 42

З вершини зображеного розгорнутого кута $AOB$ проведено два промені $OK$ i $OM$ так, що $\angle KOB=115^\circ$, $\angle MOB=35^\circ.$ Обчисліть градусну міру кута $KOM.$

А$140^\circ$

Б$120^\circ$

В$60^\circ$

Г$70^\circ$

Д$80^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури на площині та їх властивості.

Завдання перевіряє знання аксіом планіметрії.

$\angle KOB=\angle KOM+\angle MOB.$

Підставмо відомі значення:

\begin{gather*} 115^\circ=\angle KOM+35^\circ;\\[7pt] \angle KOM=115^\circ-35^\circ;\\[7pt] \angle KOM=80^\circ. \end{gather*}

Відповідь: Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 749. Завдання: 38250

Завдання 41 з 42

На рисунку зображено елемент декору паркану, що складається з дев’яти стрілок, які виходять із вершини розгорнутого кута й поділяють його на рівні частини. Обчисліть градусну міру кута між двома сусідніми стрілками.

А$20^\circ$

Б$18^\circ$

В$15^\circ$

Г$10^\circ$

Д$9^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури на площині та їхні властивості.

Завдання перевіряє знання видів і властивостей кутів.

Розгорнутий кут поділено на $10$ рівних частин. Обчислімо градусну міру кожного із цих кутів:

\begin{gather*} 180^\circ:10=18^\circ. \end{gather*}

Отже, градусна міра кута між двома сусідніми стрілками становить $18^\circ.$

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 804. Завдання: 38367

Завдання 42 з 42

Група туристів рухається в напрямку $OA$, який утворює кут $15^\circ$ із напрямком північ (див. рисунок). На який кут треба змінити напрямок руху цій групі, щоб рухатися в напрямку південний схід?

А$75^\circ$

Б$85^\circ$

В$110^\circ$

Г$120^\circ$

Д$125^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Показати відповідь Читати пояснення

Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості.

Завдання перевіряє вміння застосовувати означення, ознаки та властивості найпростіших геометричних фігур для розв'язання задач практичного змісту.

Напрямки північ і схід перпендикулярні, тому кут між ними дорівнює $90^\circ.$ Кут між напрямком північ і напрямком $OA$ дорівнює $15^\circ$, тому:

\begin{gather*} \angle AOB=90^\circ-15^\circ=75^\circ. \end{gather*}

Напрямок південний схід є бісектрисою прямого кута між напрямками схід і південь, тобто

\begin{gather*} \angle BOC=\angle COD=90^\circ: 2=45^\circ. \end{gather*}

Обчислімо шуканий кут повороту:

\begin{gather*} \angle AOC=\angle AOB+\angle BOC=75^\circ+45^\circ=120^\circ. \end{gather*}

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 806. Завдання: 38594

Новини

Розпочався додатковий набір студентів на контракт
Максимальні розміри освітніх грантів для вступників у 2026 році
Кількість вступників на бакалаврат зросла приблизно на 10%

Інформація

Усі завдання ЗНО з математики за темами
Усі тести ЗНО з математики онлайн
Завдання й відповіді ЗНО з математики минулих років
Усе про тест ЗНО з математики
Програма ЗНО з математики
Тести ЗНО онлайн з інших предметів
Дорожня карта учасника ЗНО
Дорожня карта вступника на бакалавра

Геометрія – Елементарні геометричні фігури на площині. Геометричні величини