Геометрія – Коло та круг. Многокутники

ТЕМА: Геометрія. Чотирикутники.

Завдання скеровано на перевірку знання властивості чотирикутника, у який можна вписати коло.

Периметр чотирикутника – це сума довжин усіх його сторін:

Обчислімо суму довжин двох відомих протилежних сторін заданого чотирикутника:

Відомо, що в цей чотирикутник вписано коло. У чотирикутник можна вписати коло тоді й лише тоді, коли суми його протилежних сторін рівні:

Тоді сума двох інших протилежних сторін \(BC\) й \(AD\) заданого чотирикутника також дорівнюватиме \(27\) см:

Уже відомі суми протилежних сторін чотирикутника: \(AB\), \(CD\) і \(BC\), \(AD.\) Щоб обчислити його периметр, треба додати дві відомі суми:

Відповідь: Г.

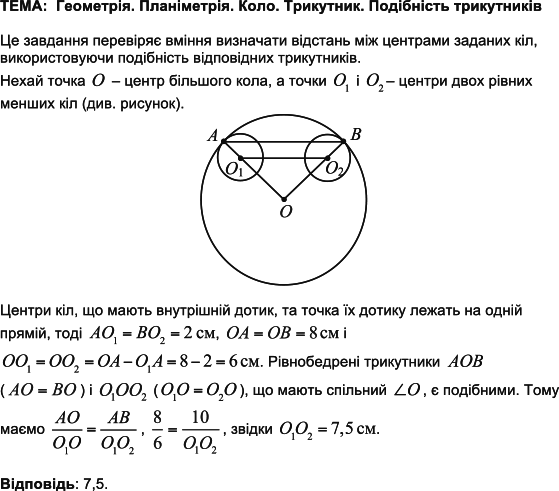
ТЕМА: Коло та круг.

Завдання скеровано на перевірку знань про коло та його елементи.

Якщо точки \(A\), \(B\), \(C\) поділяють коло на три рівні частини, то

Звідси

Відповідь: Г.

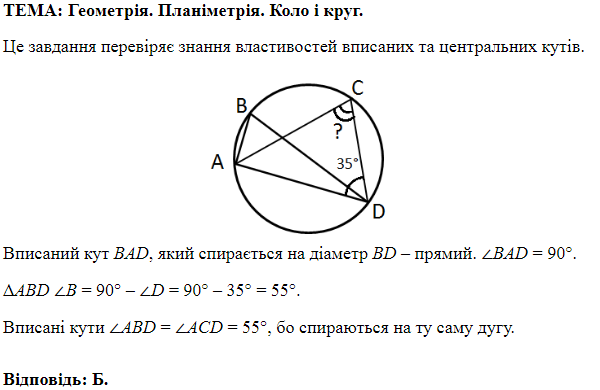
ТЕМА: Геометрія. Планіметрія. Коло та круг.

Завдання скеровано на перевірку знання властивостей вписаного та центрального кутів, уміння визначати довжину дуги кола.

Точка \(O\) – центр кола. За властивістю вписаного кута \begin{gather*} \angle ACB=\frac 12\angle AOB, \end{gather*} \(O\) – центр кола. Вписаний кут у колі дорівнює половині дуги, на яку він спирається, або половині відповідного центрального кута.

Градусна міра дуги \(AB\) дорівнює \(60^\circ.\) За формулою довжини дуги

де \(L\) – довжина кола, \(n\) – градусна міра центрального кута (градусна міра дуги).

Тобто

Відповідь: A.

ТЕМА: Чотирикутники. Коло та круг.

Завдання скеровано на перевірку знання властивостей кола, круга та їхніх елементів, властивостей прямокутника.

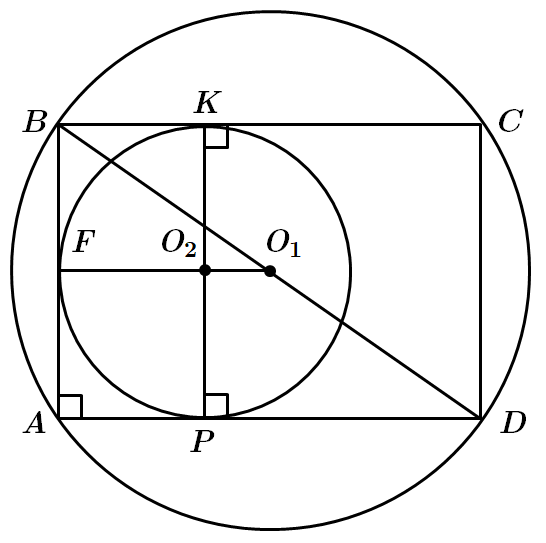
Площа круга із центром у точці \(O_1\) дорівнює \(625\mathbf{\pi}\) см\(^2.\)

1. Відстань від \(O_2\) до сторони \(BC{:}\) $$ O_2K=\frac 12BA=\frac 12\cdot 30=15\ \text{см}. $$

\(O_2K\ \perp\ BC\), а \(KP\) – діаметр кола.

Правильна відповідь – B.

2. Центр кола \(O_1\), описаного навколо прямокутника \(ABCD\), лежить на середині діагоналі \(BD.\)

У \(\Delta ABD\) \((\angle A=90^\circ)\) за теоремою Піфагора:

Правильна відповідь – Д.

3. Відстань $$ O_1O_2=FO_1-FO_2, $$ де \(FO_2\) – радіус кола із центром у точці \(O_2.\)

Правильна відповідь – A.

Відповідь: 1 – B, 2 – Д, 3 – A.

ТЕМА: Коло та круг. Чотирикутники. Трикутники.

Завдання скеровано на перевірку знання властивостей чотирикутників, зокрема прямокутника, кола, прямокутного трикутника, уміння застосовувати теорему Піфагора для розв’язування прямокутного трикутника.

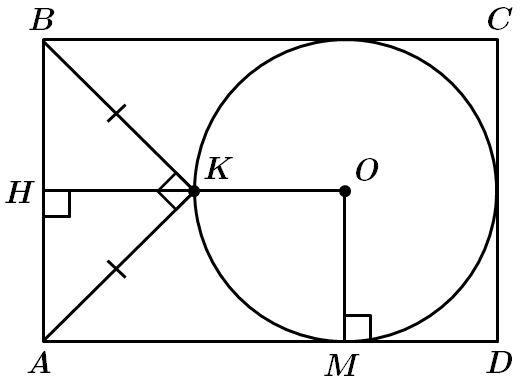
1. Коло дотикається до сторін \(BC\) i \(AD\), тому діаметр кола дорівнює стороні \(AB.\) Отже, довжина радіуса \(OK=\frac 12AB=6\) см.

Правильна відповідь – А.

2. У \(\Delta ABK\ (\angle K=90^\circ)\), \(BK=AK.\) За теоремою Піфагора:

Правильна відповідь – B.

3. У \(\Delta ABK\ KH\ \perp\ AB\) і є медіаною. За властивістю медіани проведеної до гіпотенузи:

У \(\Delta AOM\ (\angle M=90^\circ)\), \(OM=6\) см, \(AM=OH=12\) см. За теоремою Піфагора:

Правильна відповідь – Г.

Відповідь: 1 – A, 2 – B, 3 – Г.

ТЕМА: Коло та круг.

Завдання скеровано на перевірку вміння застосовувати властивості кола для розв’язування планіметричних задач практичного змісту.

Градусна міра повного кута дорівнює \(360^\circ.\) Якщо поділити його на \(12\) рівних частин, то кожна з них дорівнюватиме \(30^\circ.\)

Кут між хвилинною і годинниковою стрілками на циферблаті містить \(5\) таких кутів $$30^\circ\cdot 5=150^\circ.$$

Відповідь: Б.

ТЕМА: Геометрія. Геометричні величини та вимірювання їх.

Завдання скеровано на перевірку вміння знаходити величини кутів, розв’язувати планіметричні задачі.

Повний кут має градусну міру \(360^\circ.\) Радіуси \(OA\), \(OB\), \(OC\) поділяють кут на \(3\) рівних частини.

Отже, \(\angle AOB=360^\circ :3=120^\circ.\)

Відповідь: Г.

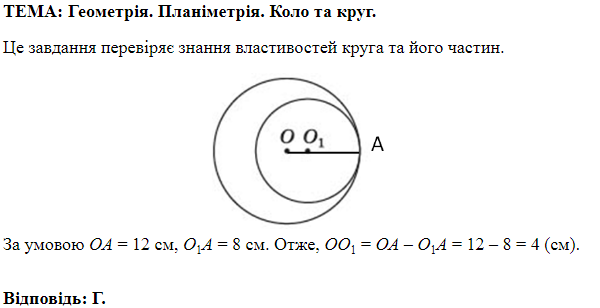
ТЕМА: Геометрія. Планіметрія. Коло та круг.

Завдання скеровано на перевірку знання властивостей кола та його елементів.

\(OA=12\ \text{см},\ O_1A=8\ \text{см}.\) $$ OO_1=OA-O_1A=12-8=4\ (\text{см}). $$

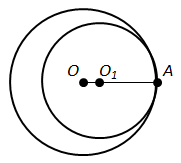
Отже, правильна відповідь – Г.

Відповідь: Г.

ТЕМА: Геометрія. Планіметрія. Коло та круг.

Завдання перевіряє знання властивостей кола та його елементів, хорд.

I.   Пряма, що проходить через центр кола, містить діаметр кола. Отже, має з ним дві спільні точки.

II.  \(AB\perp CD.\) \(\Delta COD\) – рівнобедрений, \(OC=OD.\) Отже, висота \(OK,\) проведена до основи, є медіаною. \(K\) – середина хорди \(CD.\)

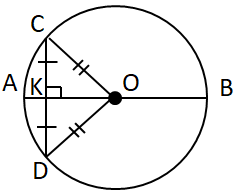
III. Діаметри кола проходять через центр кола, а отже, мають завжди спільну точку – центр кола.

Правильні твердження лише І та ІІ, тому відповідь Г.

Відповідь: Г.

ТЕМА: Геометрія. Планіметрія. Коло та круг.

Завдання перевіряє знання властивостей кола та хорд.

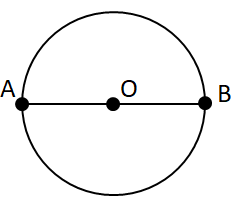
Відрізок, що сполучає дві точки кола, називається хордою. Найбільша за довжиною хорда – діаметр кола.

Отже, \(AB=32,\) тому що радіус кола дорівнює \(16\ (d=2R).\)

Відповідь: Г.

ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники. Круг.

Завдання скеровано на перевірку знання основних властивостей геометричних фігур.

\(\angle KAD=90^\circ,\ S_{\text{сектора}}=100\mathbf{\pi}\ \text{см}^2,\) \(BM=16\ \text{см}.\)

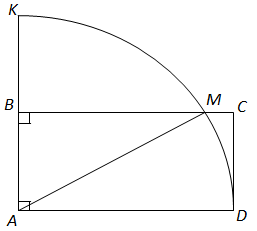
1. Площа сектора \(KAD\) становить \(\frac 14\) площі круга.

Площа круга \(S=\mathbf{\pi}R^2\). Отже, \(S_{\text{сектора}}=\frac 14\mathbf{\pi}R^2=100\mathbf{\pi}.\)

2. \(AM=AD=20\ \text{см}\) (як радіуси)
\(BM=16\ \text{см}\) (за умовою).

У \(\triangle ABM\ (\angle B=90^\circ)\) за теоремою Піфагора \begin{gather*} AM^2=AB^2+BM^2;\\[7pt] AB^2=20^2-16^2=(20-16)(20+16)=\\[7pt] =4\cdot 36\\[7pt] AB=\sqrt{4\cdot 36}=2\cdot 6=12\ \text{см}\\[7pt] S=AB\cdot AD=12\cdot 20=240\ \ \text{см}^2 \end{gather*}

Відповідь: 1. 20. 2. 240.

ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.

Завдання скеровано на перевірку знання властивостей трикутників та їх основних властивостей.

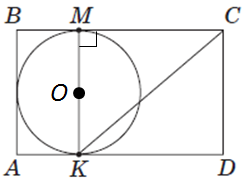
\(P_{ABMK}=24\ \text{см}\ \ KC=17\ \text{см}.\)

1.

2. \(2OM=MK=8\ \text{см}, \triangle MKC\ (\angle M=90^\circ)\) - за теоремою Піфагора

Відповідь: 1. 4. 2. 152.

ТЕМА: Геометрія. Планіметрія. Чотирикутники. Коло та круг.

Завдання перевіряє вміння застосовувати властивості різних видів трикутників до розв'язування планіметричних задач.

\(BK=8\) см, \(KM=10\) см – діаметр.

1. \(BK=MD=8\) см, \(KM=10\) см.

За властивістю прямокутника, діагоналі рівні. \begin{gather*} AC=BD=BK+KM+MD=8+10+8=26\ \textit{см}. \end{gather*}

2. \(P_{ABCD}=2(AB+BC)\), \(AB=KM=10\) см.

\(\Delta ABD (\angle A=90^\circ)\) за теоремою Піфагора

Відповідь: 1. \(26.\)
                   2. \(68.\)

ТЕМА: Геометрія. Планіметрія. Чотирикутники.

Завдання перевіряє знання властивостей ромба, трапеції, прямокутника, властивостей чотирикутників, вписаних в коло.

Навколо чотирикутника можна описати коло, якщо сума протилежних кутів дорівнює \(180^\circ.\) Отже, навколо ромба та довільної трапеції не можна описати коло, але навколо довільного прямокутника – так.

Відповідь: B.

ТЕМА: Геометрія. Планіметрія. Коло і круг. Чотирикутники. Трикутники.

Завдання перевіряє знання про коло та його елементи, теореми Піфагора, знання формули для обчислення площі трикутника.

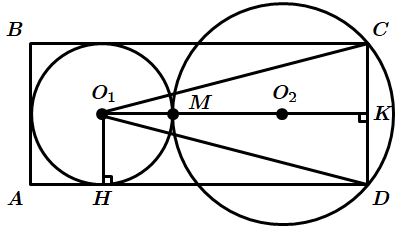
1. \(O_2C=20\) см, \(O_2K\perp CD\), \(O_2K=12\) см.

За теоремою Піфагора \begin{gather*} \Delta O_2KC\ (\angle K=90^\circ),\\[7pt] O_2C^2=O_2K^2+CK^2,\\[7pt] CK=\sqrt{400-144}=\sqrt{256}=16\ \textit{см},\\[7pt] O_1H=CK=16\ \textit{см}. \end{gather*}

2. \(S_{DO_1C}=\frac 12CD\cdot O_1K\),

Відповідь: 1. \(16.\)
                   2. \(768.\)

ТЕМА: Геометрія. Планіметрія. Коло та круг.

Завдання перевіряє вміння знаходити довжину кола та його дуги.

Довжина кола \(C=2\mathbf{\pi}R\), \(R=27\) м. Отже, довжина всього кола $$ C=2\mathbf{\pi}\cdot 27=54\mathbf{\pi}\ \textit{м}. $$

Оскільки до каркаса прикрілено \(18\) кабінок, то довжина дуги \(AB\) дорівнює

Найближча до точної відповідь Б.

Відповідь: Б.

ТЕМА: Геометрія. Стереометрія. Тіла обертання.

Завдання перевіряє вміння розв’язувати задачі на обчислення об’ємів і площ поверхонь конуса.

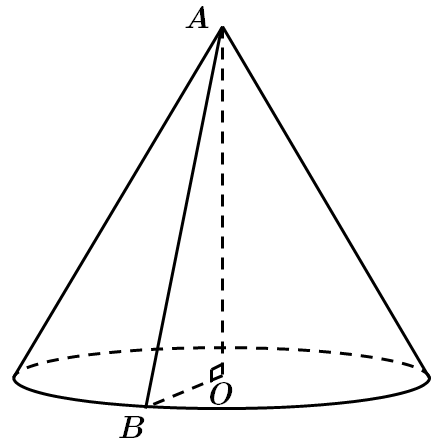
Площа основи конуса – \(S_\text{основи}=\mathbf{\pi}R^2=100\mathbf{\pi}\) см\(^2\), \(R^2=100\), \(R=10\) см. \(OB=10\) см.

Об'єм конуса знаходимо за формулою:

\(V=\frac 13S_\text{основи}H,\) де \(S_\text{основи}=100\mathbf{\pi}\) см\(^2\), \(H=AO.\)

\(\frac 13\cdot 100\mathbf{\pi}\cdot H=800\mathbf{\pi}\), \(H=24\) см.

У \(\Delta AOB\ (\angle O=90^\circ)\) за теоремою Піфагора:

\(AB=26\) см – твірна конуса.

Відповідь: \(26.\)

ТЕМА: Геометрія. Планіметрія. Чотирикутники.

Завдання перевіряє знання властивостей ромба.

\(ABCD\) – ромб, \(\angle B=60^\circ\), \(AB=BC=CD=DA=8.\)

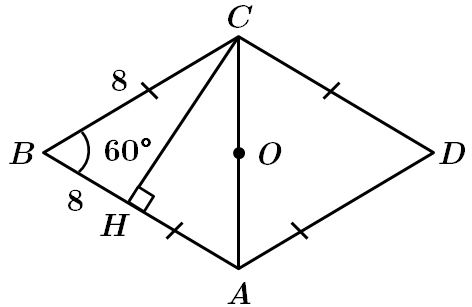
1. \(\Delta ABC\) – рівносторонній, \(AC=8.\) Отже, 1 – B.

3. Центр кола, вписаного в ромб – точка перетину діагоналей точка \(O.\)

За властивістю ромба \(AO=OC=\frac 12AC=4.\) Отже, 3 – A.

Відповідь: 1 – B, 2 – Б, 3 – A.

ТЕМА: Геометрія. Планіметрія. Геометричні величини та їх вимірювання.

Завдання перевіряє вміння знаходити довжини відрізків, розв'язувати задачі практичного змісту.

У \(\Delta BOC\ (\angle O=90^\circ)\ OB=OC\) як радіуси.
\(BC=6\) м. За теоремою Піфагора

Ширина смуги

Відповідь: Г.

ТЕМА: Геометрія. Планіметрія. Коло та круг.

Це завдання перевіряє знання властивостей вписаного та центрального кутів, уміння знаходити довжину дуги кола.

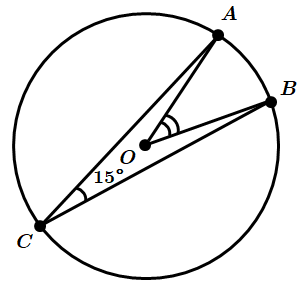
1. За властивістю вписаного кута \(\angle ACB=\frac 12\angle AOB.\)
\(\angle AOB=2\cdot \angle ACB=2\cdot 15^\circ=30^\circ.\) Градусна міра дуги \(AB\) дорівнює \(30^\circ.\)

2. \(l_{AB}=8\mathbf{\pi}\) см. За формулою довжини дуги $$l=\frac{\mathbf{\pi}R}{180^\circ}\cdot n^\circ,$$ де \(R\) – радіус кола, \(n\) – градусна міра центрального кута (градусна міра дуги).

Відповідь: 1. \(30.\)
                   2. \(48.\)

ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.

Це завдання перевіряє знання властивостей прямокутника, прямокутного та рівнобедреного трикутників, теореми Піфагора.

1. За умовою завдання у прямокутник \(ABCD\) (\(AD=BC=12\) см) вписано рівнобедрений трикутник \(AKD.\) Якщо трикутник рівнобедрений, то $$ BK=KC=\frac 12BC=\frac 12\cdot 12=6\ \textit{см}. $$ \(\Delta ABK\ (\angle B=90^\circ)\) – єгипетський, \(AB=8\) см. Отже, 1 – Б.

2. Центр кола, описаного навколо прямокутника, лежить на перетині діагоналей. Радіус кола – половина діагоналі \(BD.\) У \(\Delta ABD\ (\angle A=90^\circ).\) За теоремою Піфагора:

Отже, 2 – A.

3. \(ABKD\) – трапеція. Довжина середньої лінії $$ \frac{AD+BK}{2}=\frac{12+6}{2}=9\ \textit{см}. $$ Отже, 3 – В.

Відповідь: 1 – Б, 2 – A, 3 – В.

ТЕМА: Геометрія. Планіметрія. Многокутники.

Це завдання перевіряє знання про вписані в коло та описані навколо кола многокутники.

У будь-який трикутник можна вписати коло. Отже, I твердження правильне.

У чотирикутник можно вписати коло, якщо суми протилежних сторін рівні. Отже, в прямокутник не можна вписати коло, але у ромб – так.

Отже, ІІ твердження – неправильне, ІІІ – правильне.

Відповідь: Г.

ТЕМА: Геометрія. Планіметрія. Коло та круг. Координати та вектори на площині.

Це завдання перевіряє знання про коло, круг та їхні елементи, прямокутну систему координат; уміння застосовувати координати до розв'язування планіметричних задач.

Рівняння кола зведемо до стандартного вигляду: \begin{gather*} (x+3)^2+y^2-4y=21,\\[7pt] (x+3)^2+y^2-4y+4=25,\\[7pt] (x+3)^2+(y-2)^2=25. \end{gather*}

Коло з центром у точці \(A(-3; 2)\) та радіусом \(5.\ 3AC=BC.\)

\(AC\ ||\ Oy\), тому \(x_c=-3\).
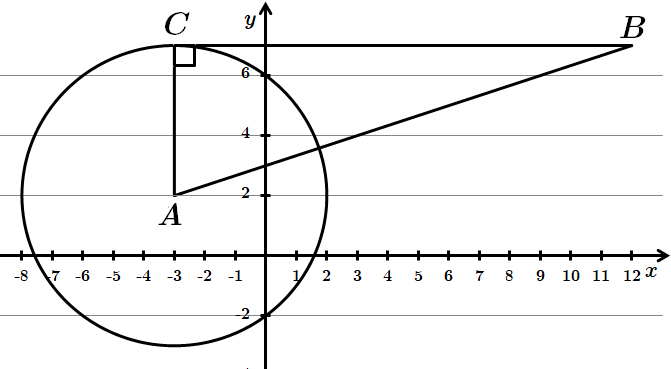
\(AC=5\), \(y_c=7.\) Отже, \(C(-3; 7).\)

\(\Delta ACB,\) \(\angle C=90^\circ\), \(BC\ ||\ Ox\), \(BC=3AC=15.\)
Отже, \(x_\text{в}=12\), \(y_\text{в}=7.\)
\(B(12; 7)\), \(12+7=19.\)

Відповідь: \(19.\)

ТЕМА: Геометрія. Планіметрія. Чотирикутники.

Це завдання перевіряє знання про трапецію та її властивості; середню лінію трапеції, вписані в коло та описані навколо кола чотирикутники, теореми Піфагора.

\(OK=4\), \(CD=10.\)

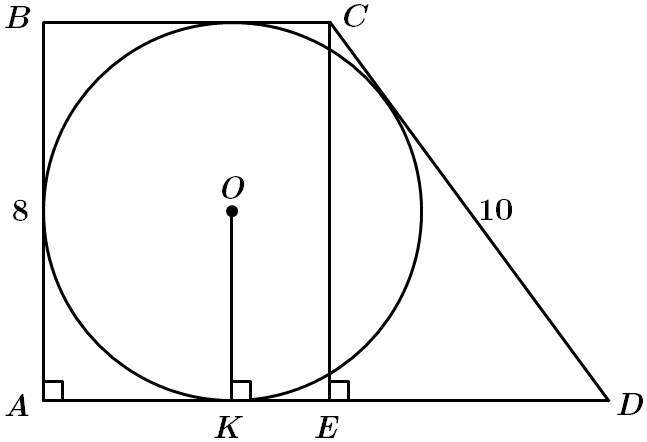
1. Висота трапеції – діаметр кола \(AB=8.\)
Отже, 1 – Б.

2. \(CE\ \perp\ AD\), \(ED\) – проекція сторони \(CD\) на \(AD.\)

\(\Delta CED\ (\angle E=90^\circ)\) за теоремою Піфагора $$ ED=\sqrt{CD^2-CE^2}=\sqrt{100-64}=\sqrt{36}=6. $$ Отже, 2 – A.

3. За властивістю чотирикутника, описаного навколо кола $$ AB+CD=BC+AD=18. $$ Нехай \(BC=AE=x\), тоді \begin{gather*} BC+AD=x+x+6=18,\\[7pt] 2x=12,\ \ x=6,\\[7pt] AD=AE+ED=6+6=12. \end{gather*} Отже, 3 – Г.

4. Середня лінія трапеції дорівнює $$ \frac{BC+AD}{2}=\frac{18}{2}=9. $$ Отже, 4 – B.

Відповідь: 1 – Б, 2 – A, 3 – Г, 4 – B.

ТЕМА: Геометрія. Планіметрія. Коло та круг.

Це завдання перевіряє знання кола та його елементів.

\begin{gather*} OA=12\ \textit{см},\\[7pt] O_1A=8\ \textit{см},\\[7pt] OO_1=OA-O_1A=12-8=4\ \textit{см}. \end{gather*}

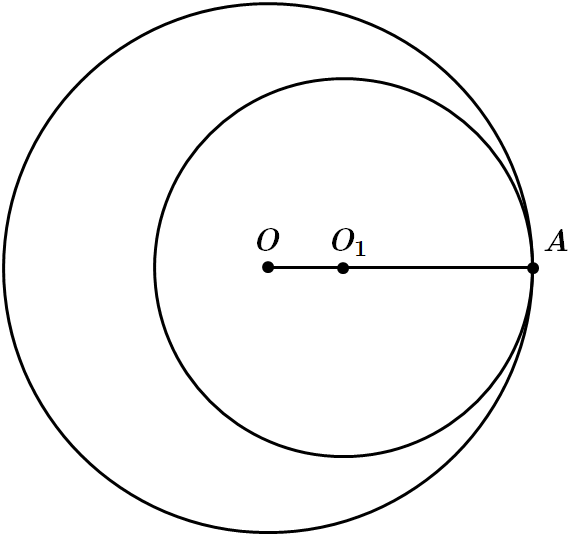
Відповідь: Г.

ТЕМА: Геометрія. Планіметрія. Чотирикутники. Коло та круг.

Це завдання перевіряє знання про центральні та вписані кути, прямокутник, формули для обчислення площі трикутників.

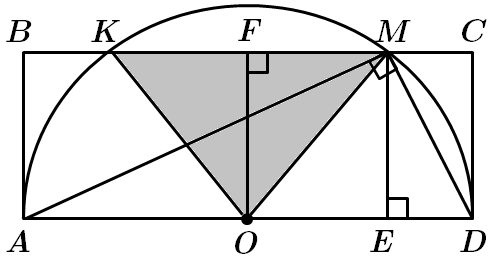
1. \(\angle AMD\) – вписаний, який спирається на діаметр. \(\angle AMD=90^\circ.\) \(ME\ \perp\ AD.\)

За властивістю висоти до гіпотенузи:

\(ME^2=AE\cdot ED.\)

Нехай \(BK=MC=x\ \textit{см}\), \(KM=3x\ \textit{см}\), \(ME=AB=4\ \textit{см}\), \(AE=BM=4x\ \textit{см}\), \(DE=MC=x\ \textit{см}.\)

\(16=4x\cdot x\), \(x=2\ \textit{см}.\)

\(AD=5x=5\cdot 2=10\ \textit{см}\) – діаметр.

\(R=5\ \textit{см}.\)

2. \(OF\ \perp\ KM\), \(\Delta OFM\ (\angle F=90^\circ)\), \(OM=R=5\ \textit{см}\), \(OF=AB=4\ \textit{см}\), \(FM=3\ \textit{см}\) (єгипетський).

\(S_{OKM}=\frac 12KM\cdot OF=FM\cdot OF=3\cdot 4=12\ \textit{см}^2.\)

Відповідь: 1. \(5.\)
                   2. \(12.\)

ТЕМА: Геометрія. Планіметрія. Трикутники.

Це завдання перевіряє вміння класифікувати трикутники за сторонами та кутами, знання теореми про суму кутів трикутника, кола, описаного навколо трикутника.

Якщо \(\angle B\) – тупий, а сума кутів трикутника \(180^\circ\), то \(\angle B\gt 90^\circ\), \(\angle A+\angle C\lt 90^\circ.\)

За нерівністю трикутника \(AC\lt AB+BC.\) Отже, твердження ІІ неправильне.

Центр кола, описаного навколо тупокутного трикутника \(ABC\) лежить поза його межами.

Отже, правильна відповідь – Д.

Відповідь: Д.

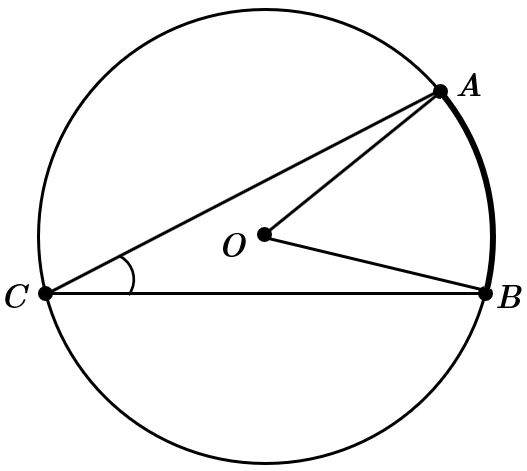
ТЕМА: Геометрія. Планіметрія. Коло та круг.

Це завдання перевіряє знання про коло та його елементи, центральні кути, дуги.

\(AB\) становить \(\frac 16\) довжини кола, тому центральний кут \(AOB\) також становить \(\frac 16\) від повного кута \(360^\circ.\)

$$ \angle AOB=\frac 16\cdot 360^\circ=60^\circ. $$

Відповідь: B.

ТЕМА: Геометрія. Планіметрія. Трикутники. Коло. Круг. Координати та вектори на площині.

Це завдання перевіряє знання кола, круга та їхніх елементів; теореми синусів, рівняння кола.

Запишемо рівняння кола в канонічному вигляді

Центр кола \((2; 0)\) та радіус \(\sqrt{72}=6\sqrt{2}.\)

За наслідком з теореми синусів

Відповідь: \(12.\)

ТЕМА: Геометрія. Планіметрія. Коло та круг. Чотирикутники. Геометричні величини та їх вимірювання.

Це завдання перевіряє знання дотичної до кола та її властивості, формули довжини кола; уміння застосовувати ознаки та властивості різних видів чотирикутників до розв'язування планіметричних задач.

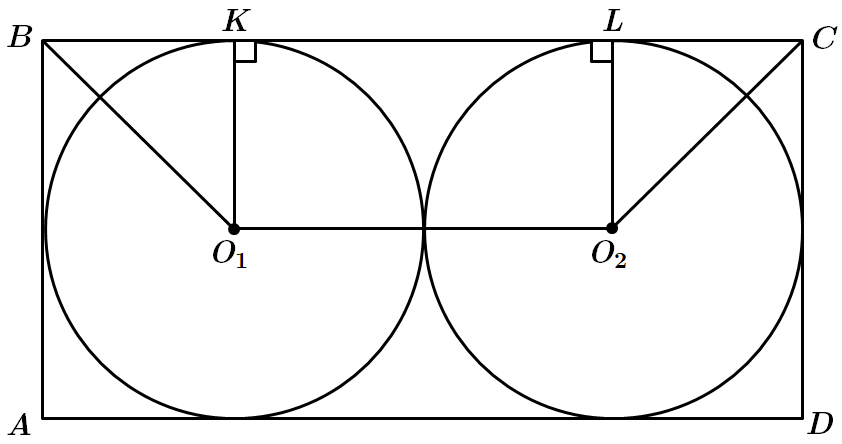
1.Довжина кола знаходиться за формулою \(C=2\mathbf{\pi}R.\)

\(O_1O_2=2R=8.\)

2. У прямокутник \(ABCD\) вписано два кола, тому \(BC=4R=16.\)

\(OO_1=2R=8.\)

\(O_1K\ \perp\ BC\) (за властивістю дотичної)

\(O_1K=4.\)

\(O_2L\ \perp\ BC\) \(O_1K=O_2L=R\), тому \(O_1O_2\ ||\ BC\), отже \(BO_1O_2C\) – трапеція.

Відповідь: 1. \(8.\)
                   2. \(48.\)

ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники. Коло та круг.

Це завдання перевіряє знання властивості дотичної до кола, вміння застосовувати набуті знання до розв'язування планіметричних задач та задач практичного змісту.

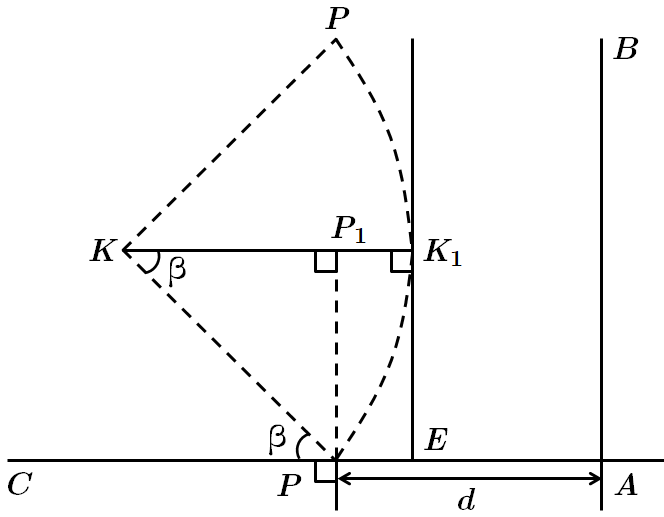
Проведемо \(K_1E\ ||\ AB\) дотичну до кола.

За властивістю дотичної до кола \(KK_1\ \perp\ K_1E.\)

\(\angle CPK=\angle PKP_1=\mathbf{\beta}\) як внутрішні різносторонні при \(KK_1\ ||\ CE\) та січної \(KP.\)

У \(\Delta KP_1P\ (\angle P_1=90^\circ)\), \(KP=0\mathord{,}9\) м, \(\angle K=\mathbf{\beta}.\)

Серед наведених відстаней найменша \(0\mathord{,}7\) м.

Відповідь: Г.

ТЕМА: Трикутники.

Це завдання перевіряє знання властивостей медіани, середньої лінії трикутника, уміння застосовувати властивості різних видів трикутників до розв'язання планіметричних задач.

\(BM\) – медіана, точка \(K\) – середина медіани.

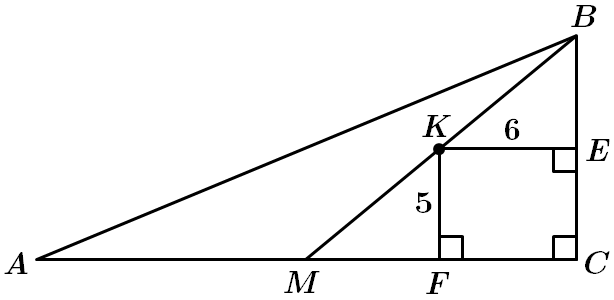
1. Відстань від точки \(K\) до \(AC\) – це \(KF=5\) см, \(KF\ \perp\ AC.\)

Відповідно, \(KE\ \perp\ BC,\) \(KE=6\) см.

\(KE\ \perp \ BC\), \(AC\ \perp\ BC\rightarrow\ KE\ ||\ AC.\)

За теоремою Фалеса, точка \(E\) – середина \(BC\), тому \(KE\) – середня лінія \(\Delta MBC.\)

За властивістю середньої лінії, \begin{gather*} KE=\frac 12MC,\\[6pt] MC=2KE=2\cdot 6=12\ \textit{см}. \end{gather*} Оскільки \(BM\) – медіана, то \(AC=2MC=24\) см.

Отже, довжина катета \(AC=24\) см.

2. Аналогічно, \(KF\) – середня лінія \(\Delta CMB\), тому \(BC=2KF=10\) см.

За теоремою Піфагора, у \(\Delta ABC\ (\angle C=90^\circ)\)

За властивістю прямокутного трикутника, радіус описаного кола дорівнює половині гіпотенузи. Отже, радіус кола $$ 26 : 2 = 13\ \textit{см}. $$

Відповідь: 1. \(24\) см.
                   2. \(13\) см.

ТЕМА: Геометрія. Планіметрія. Коло та круг. Трикутники.

Це завдання перевіряє знання властивостей дотичної до кола, центральних та вписаних кутів, видів трикутників та їхніх основних властивостей.

1. За властивістю дотичної до кола \(OC\ \perp\ MP\), тому \(\angle OCM=90^\circ.\)

Отже, 1 – В.

2. \(\angle BAC=80^\circ\), \(AK\) – діаметр, тому \(AK\) – бісектриса \(\angle BAC\), \(\angle BAK=\angle KAC=40^\circ.\)

\(\Delta AOC\) рівнобедрений (\(OA=OC\) як радіуси) \(\angle A=\angle C=40^\circ.\)

Отже, 2 – A.

3. Градусна міра дуги \(\overset{\smile}{AB}\) дорівнює градусній мірі центрального кута \(\angle AOB.\)

\(\Delta AOB=\Delta AOC\) (за трьома сторонами).

У \(\Delta AOB\ \angle A=\angle B=40^\circ\), \(\angle O=180^\circ-80^\circ=100^\circ.\)

Градусна міра дуги \(\overset{\smile}{AB}=100^\circ.\)

Отже, 3 – Г.

4. За властивістю вписаного кута: \(\angle CAK=\frac 12\) дуги \(KC\), дуга \(KC=2\angle CAK=2\cdot 40^\circ=80^\circ.\)

Отже, 4 – Б.

Відповідь: 1 – В, 2 – A, 3 – Г, 4 – Б.

26

ТЕМА: Геометрія. Планіметрія. Коло та круг. Чотирикутники. Геометричні величини та їхні вимірювання. Трикутники.

Це завдання перевіряє знання про коло, круг та їхні елементи, формул для обчислення площі кругового сектора, прямокутника.

1. Площу кругового сектора знаходимо за формулою $$ S_\text{сек}=\frac{\mathbf{\pi}R^2}{360^\circ}\cdot \mathbf{\alpha}, $$ де \(\mathbf{\alpha}\) – центральний кут.

2. Нехай \(a\) – спільна дотична до секторів. За властивістю дотичної до кола \(AO\ \perp\ a\), \(CO\ \perp\ a\), тому точка \(O\) лежить на прямій \(AC.\)

У \(\Delta ABC\ (\angle B=90^\circ)\) – єгипетський, тому \(AB=8\) см.

Відповідь: 1. \(6.\)
                   2. \(48.\)

ТЕМА: Геометрія. Стереометрія. Многогранники, тіла й поверхні обертання. Планіметрія. Трикутники.

Це завдання перевіряє вміння розв'язувати задачі на обчислення площ поверхонь, знання формул для обчислення площ поверхонь тіл обертання, знання теореми Піфагора, співвідношення між сторонами та кутами прямокутного трикутника.

Доберемо до кожного із запитань 1 – 4 правильну відповідь.

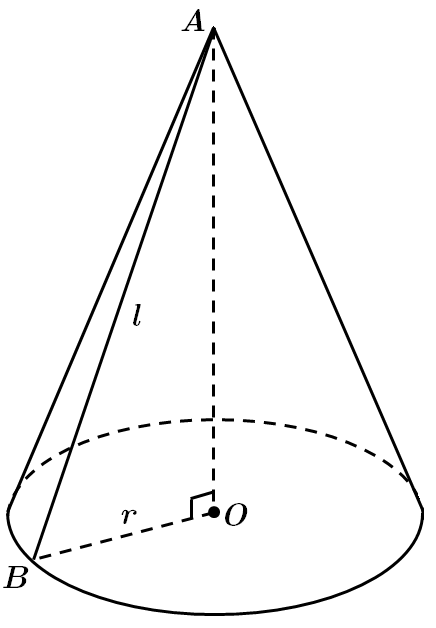
1. Якщо \(S_\text{б.п.}=3S_\text{осн}\), то \(S_\text{б.п.}=\mathbf{\pi}rl\), \(S_\text{осн}=\mathbf{\pi}r^2\), \(\mathbf{\pi}rl=3\mathbf{\pi}r^2\), \(l=3r.\) Отже, 1 – B.

2. Якщо висота конуса дорівнює радіусу основи, то \(AO=OB=r\), \(\Delta AOB\) – прямокутний рівнобедрений, за теоремою Піфагора \(AB^2=OB^2+AO^2\), \(l^2=r^2+r^2\), \(l=r\sqrt{2}.\) Отже, 2 – Б.

3. Якщо проекція твірної на площину основи конуса удвічі менша за твірну, то \(l=2r.\) \(OB\) – проекція твірної \(AB\) на площину основи. Отже, 3 – А.

4. Якщо площа повної поверхні конуса дорівнює \(5\mathbf{\pi}r^2\)

Отже, 4 – Г.

Відповідь: 1 – В, 2 – Б, 3 – А, 4 – Г.

ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості. Коло та круг. Трикутники. Чотирикутники.

Це завдання перевіряє вміння застосовувати означення, ознаки та властивості геометричних фігур до розв'язування планіметричних задач та задач практичного змісту; уміння застосовувати теорему Піфагора до розв'язування прямокутного трикутника, властивості прямокутника.

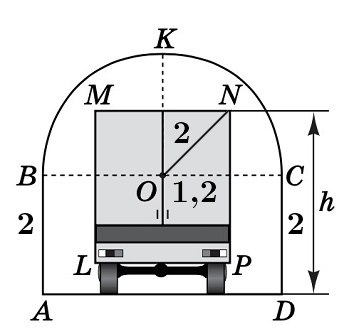
Розглянемо випадок, коли вантажівка дотикається аркового проїзду. При цьому \(ON=OC=2\) м (радіус аркового проїзду).

Оскільки \(MN=2\mathord{,}4\) м, а \(MF=FN=1\mathord{,}2\) м. \(FN=OE=1\mathord{,}2\) м. Значення \(NE\) знайдемо за теоремою Піфагора з \(\Delta NEO\ (\angle E=90^\circ).\)

Висота \(h\) вантажівки складається з суми

При значенні \(3\mathord{,}6\) м вантажівка дотикається арки, тому максимально можливе значення – \(3\mathord{,}5\) м.

Відповідь: Г.

ТЕМА: Геометрія. Коло та круг. Чотирикутники. Геометричні величини та їх вимірювання.

Це завдання перевіряє знання про коло та його елементи, уміння застосовувати властивості ромба, використовувати формули площ геометричних фігур до розв'язування планіметричних задач.

1. Довжина кола $$ C=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}R=12\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}. $$ Отже,

2. Нехай $$ AK=MC=x, $$ тоді $$ KM=6x=2R=12. $$ Отже, \(x=2.\)

Площу ромба знайдемо за формулою: $$ S=\frac 12d_1d_2, $$ де \(d_1\), \(d_2\) – довжини діагоналей.

Відповідь: 1. \(12.\)
                   2. \(96.\)

ТЕМА: Геометрія. Планіметрія. Описане коло, дотична до кола та її властивості. Трикутники (рівносторонній та прямокутний трикутники). Тригонометричні співвідношення в прямокутному трикутнику.

Це завдання перевіряє вміння визначати довжини відрізків, використовуючи властивості дотичної до кола, елементів кола, вписаних у коло кутів та співвідношень у прямокутному трикутнику.

Обчислимо довжини відрізків (1 – 4).

1. Оскільки діаметр кола вдвічі більший за його радіус, то згідно умови $$ BK=2\cdot 6=12. $$ Отже, 1 – B.

2. Розглянемо трикутник \(ABO.\) Оскільки пряма \(AB\) є дотичною до кола, то \(\angle ABO=90^\circ.\) У прямокутному трикутнику \(ABO\) катет \(BO=6\), а гіпотенуза \(AO=2AB.\) За теоремою Піфагора отримаємо

Такий же результат отримаємо, якщо скористаємось тим фактом, що у прямокутному трикутнику \(ABO\ \angle AOB=30^\circ\) (оскільки вказано, що гіпотенуза вдвічі більша за протилежний до цього кута катет). Тоді

Отже, 2 – Б.

Отже, 3 – A.

4. Розглянмо вписаний у коло трикутник \(BCK.\) Оскільки вписаний кут \(BCK\) спирається на діаметр кола, то \(\angle BCK=90^\circ\), тобто трикутник \(BCK\) є прямокутним. У цьому трикутнику \(BK=12\), \(\angle CBK=60^\circ\), тоді

Або за теоремою Піфагора отримуємо:

Отже, 4 – Г.

Відповідь: 1 – B, 2 – Б, 3 – A, 4 – Г.