Геометрія – Координати та вектори на площині. Геометричні переміщення

ТЕМА: Координати і вектори в просторі.

Завдання скеровано на перевірку вміння додавати і віднімати вектори, визначати модуль вектора.

Визначмо різницю векторів за формулами:

Визначимо модуль вектора \(\overrightarrow{c}\) за формулою:

Відповідь: Б.

ТЕМА: Координати і вектори на площині.

Завдання скеровано на перевірку знання рівняння кола, властивостей прямокутної системи координат на площині, уміння застосовувати координати для розв’язання планіметричних задач.

За умовою:

Рівняння кола: \((x-x_0)^2+(y-y_0)^2=R^2.\)

Дано коло із центром у точці \((11+3a; -2)\) i радіусом \(7.\)

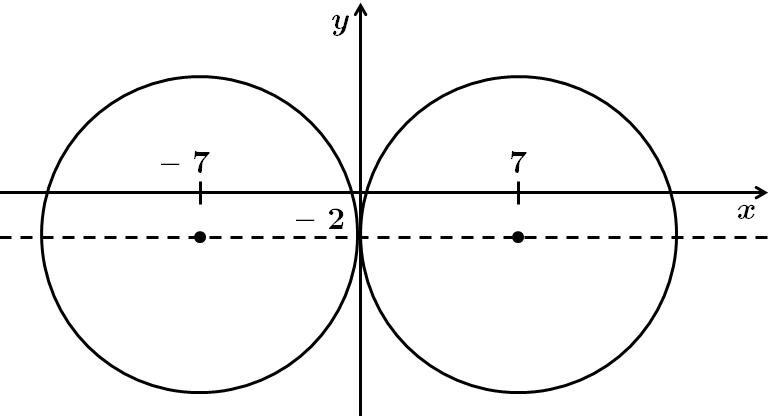
Унаслідок зміни параметра \(a\) коло переміщується вздовж прямої \(y=-2.\)

Для того, щоб коло дотикалося до осі \(Oy\), центр кола повинен бути в точці \((7; -2)\) або \((-7; -2).\)

Щоб коло перетинало двічі вісь ординат, абсциса \(a\) центра кола повинна бути цілим числом – розв'язком нерівності:

Найменше ціле значення \(a=-5.\)

Відповідь: \(-5.\)

ТЕМА: Координати і вектори в просторі. Геометричні переміщення.

Завдання скеровано на перевірку вміння визначати координати середини відрізка, знання основних видів геометричних переміщень, зокрема симетрії відносно точки.

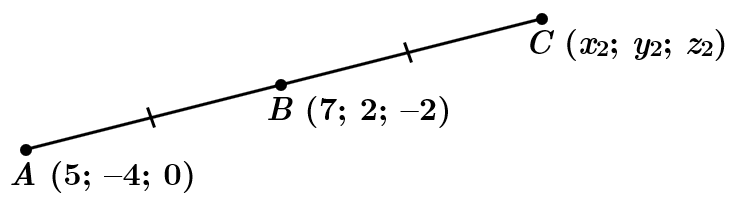
Точка \(C\) симетрична точці \(A\) відносно точки \(B\), якщо точки лежать на одній прямій і \(AB=BC.\)

Скористаймося формулою визначення координат середини відрізка:

де кінці відрізка мають координати: \((x_1; y_1; z_1)\), \((x_2; y_2; z_2).\)

\(A(5; -4; 0)\), \(B(7; 2; -2)\), \(C(x_2; y_2; z_2).\)

Отже, правильна відповідь – \(C(9; 8; -4).\)

Відповідь: Д.

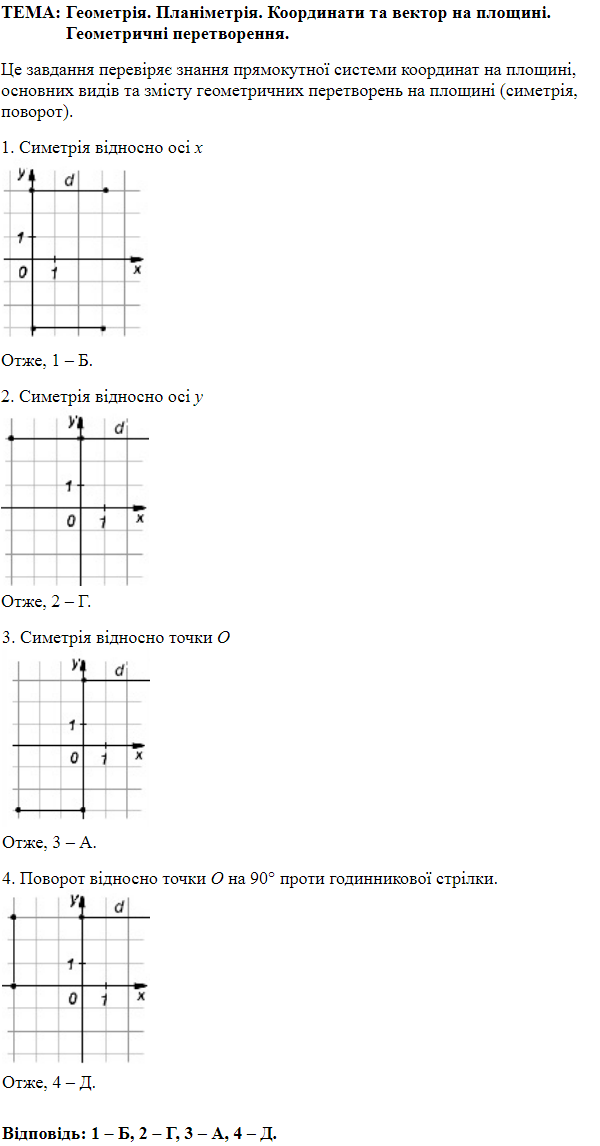
ТЕМА: Геометрія. Планіметрія. Геометричні перетворення.

Завдання перевіряє знання геометричних перетворень на площині: симетрії відносно прямої та точки.

1 – Б. симетрія відносно осі \(x.\)

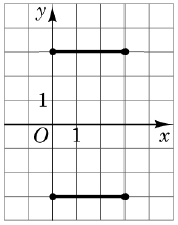
2 – Г. симетрія відносно осі \(y.\)

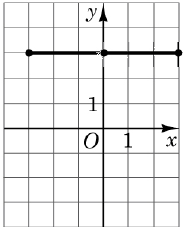
3 – Д. симетрія відносно точки \(O.\)

Відповідь: 1Б, 2Г, 3Д.

ТЕМА: Геометрія. Планіметрія. Трикутники. Координати та вектори на площині.

Завдання перевіряє вміння застосовувати властивості рівнобедреного трикутника, знаходити площу трикутника.

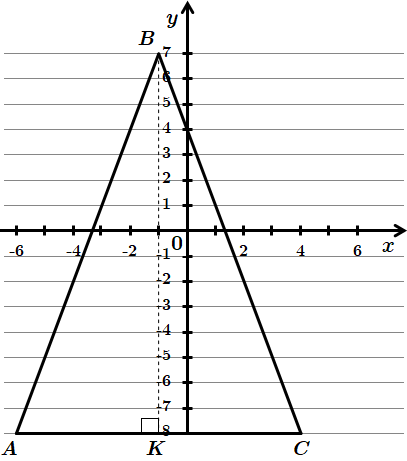
Накреслимо трикутник \(ABC. AB=BC.\) Отже, точка \(B\) має абсцису \(-1.\) \((AC=10).\) Нехай координати точки \(B(-1; y).\)

Точка \(B\) лежить на прямій \(y=2x+9,\) тому \(y=2(-1)+9=7,\) \(B(-1; 7).\) \(BK\perp AC.\) \(BK=15\) висота та медіана.

Відповідь: \(75.\)

ТЕМА: Геометрія. Планіметрія. Координати та вектори на площині.

Завдання перевіряє знання властивості рівних векторів, координат вектора; уміння складати рівняння кола, знаходити координати середини відрізка.

Коло задано рівнянням $$ x^2-4x+y^2+12y=9. $$

Запишемо в стандартному вигляді:

Точка \(O(2; -6)\) – центр кола, \(R=7.\)

Нехай точка \(A(x_\text{A}; y_\text{A})\), \(\overrightarrow{OA}(x_\text{A}-2; y_\text{A}+6)\), \(\overrightarrow{OA}(-1; 2).\)

Отже,

Точка \(O\) середина відрізка \(AC.\)

За формулами $$ x=\frac{x_1+x_2}{2},\ \ y=\frac{y_1+y_2}{2} $$ знаходимо координати точки \(C:\)

Відповідь: \(-24.\)

ТЕМА: Геометрія. Планіметрія. Коло та круг. Трикутники. Координати та вектори на площині.

Завдання перевіряє вміння знаходити координати середини відрізка, складати рівняння кола, застосовувати властивості прямокутного трикутника, використовувати формули площі трикутника.

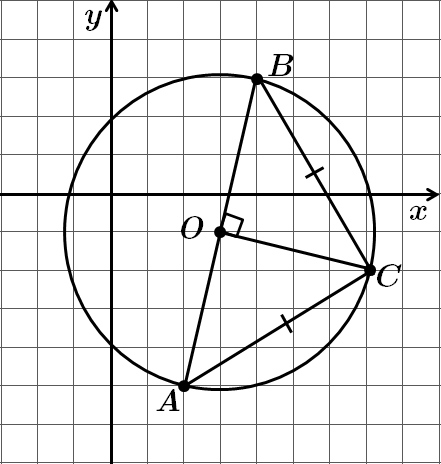
Коло задане рівнянням \((x-3)^2+y^2+2y=16.\)

Запишемо у стандартному вигляді
\((x-a)^2+(y-b)^2=R^2\), де \((a; b)\) – центр кола, \(R\) – радіус
\((x-3)^2+y^2+2y+1=16+1\)
\((x-3)^2+(y+1)^2=17.\)
\((3; -1)\) – центр кола, \(R=\sqrt{17}.\)

Точка \(A(2; -5)\), \(B(4; 3).\) Центр кола \(O(3; -1)\) є серединою відрізка \(AB\) $$ x=\frac{2+4}{2}=3;\ \ y=\frac{-5+3}{2}=-1. $$

Отже, \(\Delta ABC\) – рівнобедрений прямокутний з гіпотенузою \(AB=2\sqrt{17}.\)

Висота, проведена до гіпотенузи, – медіана та радіус описаного кола.

Отже, \(S_{ABC}=\frac 12 AB\cdot OC\), \(OC=R=\sqrt{17}.\)

\(S_{ABC}=\frac 12\cdot 2\sqrt{17}\cdot \sqrt{17}=17.\)

Відповідь: \(17.\)

ТЕМА: Геометрія. Планіметрія. Координати та вектори на площині.

Це завдання перевіряє вміння знаходити координати середини відрізка, виконувати дії з векторами, знаходити скалярний добуток векторів.

Запишемо рівняння кола у вигляді:

\((x-a)^2+(y-b)^2=R^2\), де \((a; b)\) – центр кола, \(R\) – радіус.
\((x^2-8x+16)+y^2-16+7=0\),
\((x-4)^2+y^2=9\), \(O(4; 0)\) – центр кола.

За формулою знаходження координат середини відрізка знаходимо координати точки \(D:\)

Знайдемо координати векторів \(\overline{AB}\) та \(\overline{AD}:\)

\(\overline{AB}(0-(-4); 3-(-3))\), \(\overline{AB}(4; 6)\), \(\overline{AD}(12; 0).\)

Знайдемо довжини векторів:

Відповідь: \(72.\)

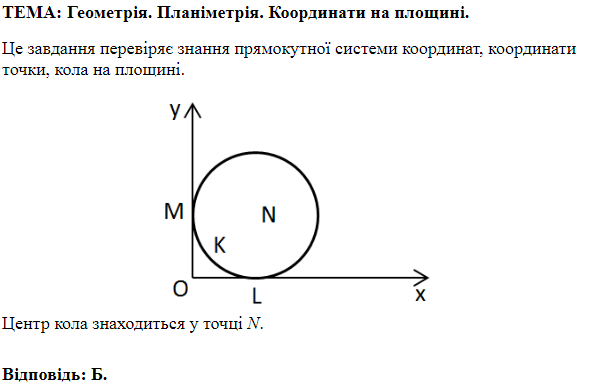
ТЕМА: Геометрія. Планіметрія. Коло та круг. Координати та вектори на площині.

Це завдання перевіряє знання про коло, круг та їхні елементи, прямокутну систему координат; уміння застосовувати координати до розв'язування планіметричних задач.

Рівняння кола зведемо до стандартного вигляду: \begin{gather*} (x+3)^2+y^2-4y=21,\\[7pt] (x+3)^2+y^2-4y+4=25,\\[7pt] (x+3)^2+(y-2)^2=25. \end{gather*}

Коло з центром у точці \(A(-3; 2)\) та радіусом \(5.\ 3AC=BC.\)

\(AC\ ||\ Oy\), тому \(x_c=-3\).
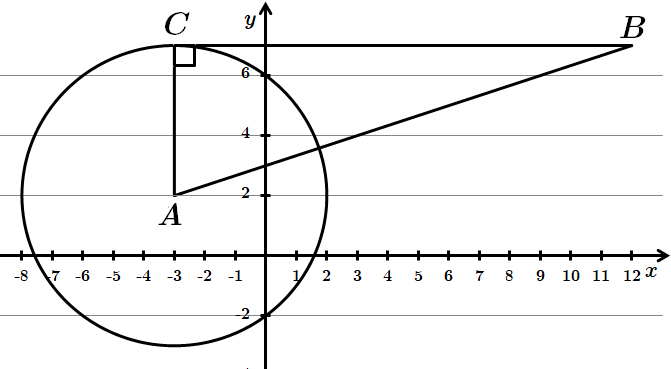
\(AC=5\), \(y_c=7.\) Отже, \(C(-3; 7).\)

\(\Delta ACB,\) \(\angle C=90^\circ\), \(BC\ ||\ Ox\), \(BC=3AC=15.\)
Отже, \(x_\text{в}=12\), \(y_\text{в}=7.\)
\(B(12; 7)\), \(12+7=19.\)

Відповідь: \(19.\)

ТЕМА: Планіметрія. Координати і вектори на площині.

Це завдання перевіряє вміння виконувати дії з векторами, знаходити скалярний добуток, координати вектора.

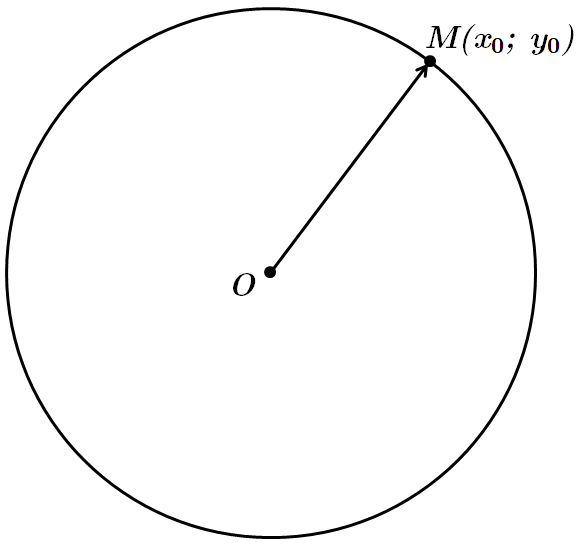
Коло із центром в точці \(O\) задано рівнянням \(x^2+y^2=80.\)

\(M(x_0; y_0)\) лежить на колі, тому \(x_0^2+y_0^2=80.\)

\(O(0; 0)\), \(M(x_0; y_0)\) отже, \(\overline{OM}(x_0; y_0).\)

За умовою \(\overline{a}\ \perp\ \overline{OM}\), тому \(\overline{a}\cdot \overline{OM}=0\), \(\overline{a}(-2; 1)\), \(-2x_0+1\cdot y_0=0.\)

Складемо систему рівнянь:

За умовою \(x_0\lt 0\), а отже, \(x_0=-4.\)

Відповідь: \(-4.\)

ТЕМА: Геометрія. Планіметрія. Трикутники. Коло. Круг. Координати та вектори на площині.

Це завдання перевіряє знання кола, круга та їхніх елементів; теореми синусів, рівняння кола.

Запишемо рівняння кола в канонічному вигляді

Центр кола \((2; 0)\) та радіус \(\sqrt{72}=6\sqrt{2}.\)

За наслідком з теореми синусів

Відповідь: \(12.\)

ТЕМА: Планіметрія. Координати та вектори на площині.

Це завдання перевіряє знання поняття колінеарних векторів, координат вектора, уміння застосовувати вектори до розв'язування планіметричних задач.

За умовою задачі, \(\overrightarrow{AB}\ ||\ \overrightarrow{a}.\)

Нехай абсциса точки \(B\) буде \(x\), тоді точка \(B(x; 3).\) Ордината дорівнює \(3\) тому, що точка \(B\) лежить на прямій \(y=3.\)

У колінеарних векторів відповідні координати пропорційні, тому

Відповідь: \(-5\mathord{,}2.\)

ТЕМА: Геометрія. Планіметрія. Координати та вектори на площині. Геометричні величини та їх вимірювання.

Це завдання перевіряє знання прямокутної системи координат на площині, координати точки, формули площі трапеції.

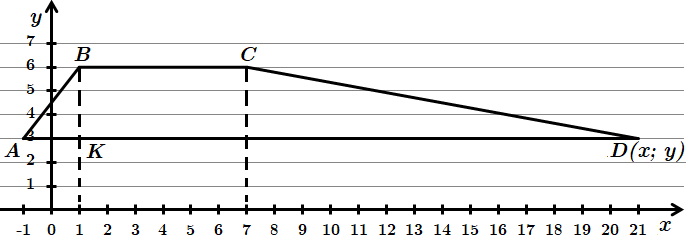
Позначимо задані точки на координатній площині.

Задано трапеція \(ABCD.\) Точки \(B\) та \(C\) мають однакову ординату, тому пряма \(BC\) паралельна осі \(Ox.\)

\(BC\ ||\ AD\), тому точка \(D\) має з точкою \(A\) однакову ординату \(y=3.\) Площа трапеції \(42\), тому $$ S=\frac{BC+AD}{2}\cdot h, $$ де \(h\) – висота трапеції, складемо рівняння.

звідси \(AD=22.\)

Так як точка \(A\) має абсцису \(-1\), то точка \(D\) буде мати абсцису \(21.\)

Відповідь: \(21.\)

ТЕМА: Геометрія. Планіметрія. Координати та вектори на площині.

Це завдання перевіряє вміння виконувати дії з векторами.

На рисунку зображено квадрат \(ABCD.\) Вектори \(\overrightarrow{AB}\) та \(\overrightarrow{AD}\) із спільним початком. Їх сума зображується діагоналлю паралелограма, побудованого на цих векторах.

Отже, \(\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}.\)

Відповідь: B.

ТЕМА: Геометрія. Планіметрія. Координати та вектори на площині.

Це завдання перевіряє вміння виконувати дії з векторами, знаходити скалярний добуток векторів, знання правил додавання векторів, множення вектора на число.

Умова перпендикулярності векторів – їх скалярний добуток дорівнює нулю.

Відповідь: \(-0\mathord{,}6.\)

ТЕМА: Геометрія. Планіметрія. Координати та вектори на площині.

Це завдання перевіряє вміння знаходити координати вектора, знаходити скалярний добуток векторів, застосовувати координати й вектори до розв'язування планіметричних задач.

\(\overrightarrow{AB}\ \perp \overrightarrow{a}\), \(\ \overrightarrow{a}(4;3).\) Точка \(A(-2; 0)\), а точка \(B\) лежить на прямій \(y=2x\), тому \(B(x; 2x).\)

Координати вектора \(\overrightarrow{AB}(x+2; 2x).\) Координати \(\overrightarrow{a}\) та \(\overrightarrow{AB}\) взаємно перпендикулярні, тому скалярний добуток їх дорівнює нулю.

Відповідь: \(-0\mathord{,}8.\)

ТЕМА: Геометрія. Планіметрія. Координати та вектори на площині.

Це завдання перевіряє вміння виконувати дії з векторами, знаходити скалярний добуток векторів.

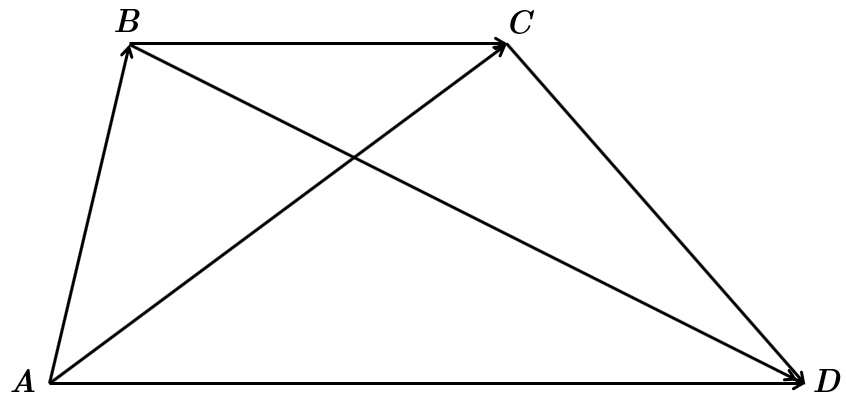
1. \(AD\ ||\ BC.\) Отже,

2. \(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\) (за правилом трикутника). Отже, \(\overrightarrow{AC}(-2; 12).\)

3. \(\overrightarrow{BD}=\overrightarrow{AD}-\overrightarrow{AB}\), \(\overrightarrow{BD}(-10; -3).\)

4. Знаходимо скалярний добуток векторів:

Відповідь: \(-16.\)

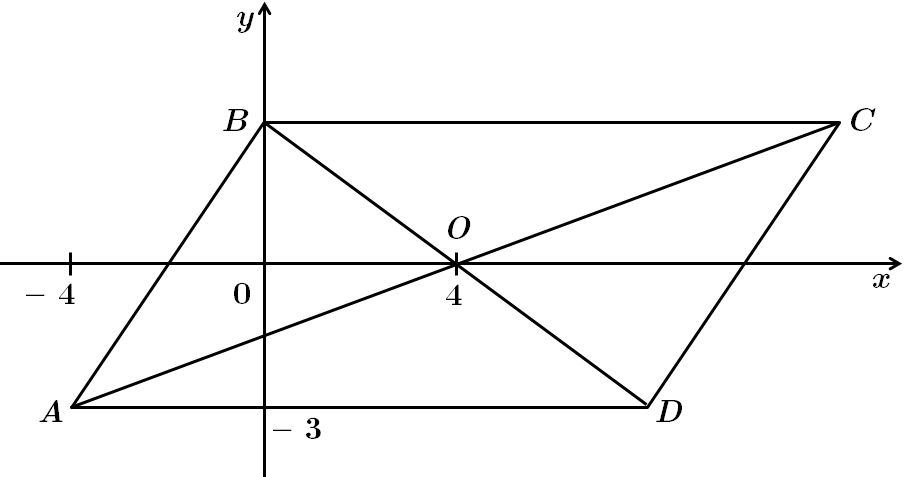
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Паралелограм та його властивості. Координати та вектори на площині. Скалярний добуток векторів та його властивості. Теорема косинусів.

Це завдання перевіряє вміння застосовувати координати й вектори до розв'язування планіметричних задач.

Нагадаємо, що скалярним добутком векторів \(\overrightarrow{a}\) i \(\overrightarrow{b}\) називають число, яке дорівнює добутку довжин цих векторів на косинус кута між ними: $$ \overrightarrow{a}\cdot \overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\cos \varphi, $$ де \(\varphi\) – кут між векторами \(\overrightarrow{a}\) i \(\overrightarrow{b}\).

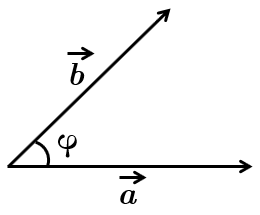
Довжину вектора \(\overrightarrow{a}(a_x; a_y)\) обчислюють за формулою $$ |\overrightarrow{a}|=\sqrt{a_x^2+a_y^2}. $$

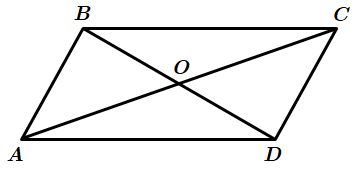
На рисунку \(ABCD\) – паралелограм, \(\overrightarrow{AB}(6; -8)\), \(\cos A=0\mathord{,}44.\)

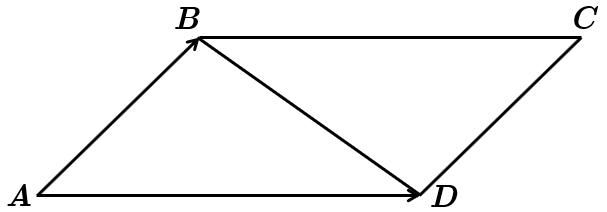
За умовою $$ \overrightarrow{AB}\cdot \overrightarrow{AD}=88, $$ тобто $$ |\overrightarrow{AB}||\overrightarrow{AD}|\cos A=88. $$ Оскільки вектор \(\overrightarrow{AB}(6; -8)\) відомий, то його довжина

Визначаємо довжину вектора \(\overrightarrow{AD}\mathord{:}\)

Діагональ \(BD\) паралелограма \(ABCD\) є стороною трикутника \(ABD.\) У цьому трикутнику відомі довжини сторін \(AB\) та \(AD\), що дорівнюють довжинам векторів \(\overrightarrow{AB}\) та \(\overrightarrow{AD}\) відповідно, та косинус кута між ними. За теоремою косинусів

Звідки отримуємо $$ BD=\sqrt{324}=18. $$

Отже, довжина діагоналі \(BD\) дорівнює \(18.\)

Знаючи довжини сторін \(AB\) та \(AD\) і косинус кута між ними, довжину діагоналі \(BD\) можна визначати ще так. Опустимо з вершини \(B\) на сторону \(AD\) перпендикуляр \(BK\).

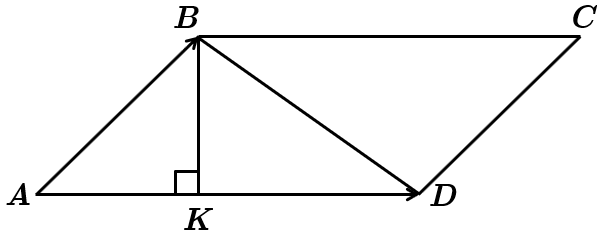
Прямокутні трикутники \(AKB\) та \(BKD\) мають спільний катет, тоді виконується рівність

З прямокутного трикутника \(AKB\) визначаємо

Тоді

Отже, $$ 10^2-4\mathord{,}4^2=BD^2-15\mathord{,}6^2 $$ звідки отримуємо

тоді $$ BD=\sqrt{324}=18. $$

Відповідь: \(18.\)

ТЕМА: Геометрія. Планіметрія. Трикутники. Середня лінія трикутника. Вектори. Множення вектора на число.

Це завдання перевіряє знання означення і властивостей середньої лінії трикутника, а також уміння множити вектор на число.

Якщо точки \(K\) і \(M\) є серединами сторін \(AB\) і \(BC\) відповідно, то \(KM\) – середня лінія трикутника \(ABC\), яка паралельна стороні \(AC\), причому \(KM\ ||\ AC\), \(KM = \frac{1}{2}AC\), тоді \(AC = 2KM.\)

Вектори \(\overrightarrow{MK}\) і \(\overrightarrow{AC}\) лежать на паралельних прямих, отже, є колінеарними. Їх напрямки протилежні, а довжина вектора \(\overrightarrow{AC}\) вдвічі більша за довжину вектора \(\overrightarrow{MK}\), тому \(\overrightarrow{AC} = -2\overrightarrow{MK}.\)

Оскільки \(\overrightarrow{MK} = a\), то \(\overrightarrow{AC} = -2a.\)

Відповідь: Д.

ТЕМА: Геометрія. Стереометрія. Координати та вектори у просторі. Формула для обчислення відстані між двома точками.

Це завдання перевіряє розуміння декартової системи координат у просторі, а також уміння визначати відстань від заданої точки до геометричних об’єктів (точки, прямої та площини).

Нагадаємо, що відстань \(d\) між точками \(M_1(x_1; y_1; z_1)\) та \(M_2(x_2; y_2; z_2)\) можна обчислити за формулою:

1. Відстань від точки \(M(1; -4; 8)\) до площини \(xy\) дорівнює відстані від точки \(M\) до її проєкції на цю площину, тобто до точки \((1; -4; 0)\). Ця відстань дорівнює \(8.\) Отже, 1 – Г.

У загальному випадку відстань від точки \(M_1(x_1; y_1; z_1)\) до площини \(xy\) дорівнює \(|z_1|\), до площини \(xz\) — \(|y_1|\), до площини \(yz\) — \(|x_1|\).

2. Відстань від точки \(M\) до початку координат – це відстань від проекції точки \(M\) до точки \((0; 0; 0)\) і дорівнює

Отже, 2 – Д.

3. Відстань від точки \(M\) до осі \(z\) – це відстань від проєкції точки \(M\) на площину \(xy\) до початку координат, тобто точки \((0; 0; 0)\). Отже, шуканa відстань – це відстань між точками \((1; -4; 0)\) та \((0; 0; 0)\) і дорівнює

Отже, 3 – В.

4. Відстань від точки \(M\) до точки \(N(1; 0; 8)\) дорівнює

Отже, 4 – Б.

Відповідь: 1 – Г, 2 – Д, 3 – В, 4 – Б.

ТЕМА: Геометрія. Планіметрія. Вектори. Сума векторів. Теорема Піфагора.

Це завдання перевіряє вміння визначати довжину вектора, що є сумою зображених на рисунку векторів.

Для розв’язання завдання необхідно вміти виконувати операцію додавання двох векторів, використовувати теорему Піфагора для знаходження невідомих елементів прямокутних трикутників.

Для визначення суми зображених на рисунку векторів скористаємося правилом паралелограма. Побудуємо паралелограм \(ABCD\), причому \(\overrightarrow{a} = \overrightarrow{AB}\), \(\overrightarrow{b} = \overrightarrow{AD}.\) Тоді сумою векторів \(\overrightarrow{a}\) і \(\overrightarrow{b}\) є вектор \(\overrightarrow{c} = \overrightarrow{AC}\mathord{:}\) $$ \overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b},\ \text{або} $$ $$ \overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{AD} $$ (див. рисунок).

Оскільки за умовою вектори \(\overrightarrow{a}\) і \(\overrightarrow{b}\) перпендикулярні, то паралелограм \(ABCD\) є прямокутником, довжина вектора \(\overrightarrow{a} + \overrightarrow{b}\) дорівнює довжині гіпотенузи \(AC\) прямокутного трикутника \(ADC\) з катетами \(AD = 8\) та \(DC = 6\) (див. рисунок).

За теоремою Піфагора

Отже, довжина вектора \(\overrightarrow{a} + \overrightarrow{b}\) дорівнює \(10.\)

Відповідь: Г.

ТЕМА: Геометрія. Планіметрія. Декартова система координат на площині. Теорема Піфагора.

Це завдання перевіряє знання прямокутної системи координат на площині, координат точок та вміння визначати координати точки, розташованої на координатній осі.

Згідно з умовою точка \(C\) лежить на осі \(x\), тому її координати \((x_0; 0)\). Оскільки відрізок \(AC\) перетинає вісь \(y\), то \(x_0\gt 0\) і відрізок розташований так, як показано на рисунку. Трикутник \(AKC\) є прямокутним із катетом \(AK=4\) (довжина \(AK\) дорівнює модулю ординати точки \(A\)) і гіпотенузою \(AC=5\), тобто його другий катет \(KC\) можна визначити за теоремою Піфагора:

Додавши до \(-2\) число \(3\), дістанемо абсцису \(x_0=1\) точки \(C.\) Тоді \(C(1; 0)\) – шукана точка.

Це завдання можна розв’язати, використовуючи лише формулу довжини відрізка за заданими координатами його кінцевих точок.

Оскільки точка \(C\) лежить на осі абсцис, то її ордината дорівнює нулю, тобто \(C(x; 0)\). Тоді, довжина відрізка \(AC{:}\)

Розв’язавши це рівняння, одержимо два корені: \(x=-5\) та \(x=1.\) Значення \(x=-5\) не може бути абсцисою точки \(C\), оскільки в цьому випадку відрізок \(AC\) не перетинатиме вісь ординат. Отже, \(C(1; 0).\)

Відповідь: A.

ТЕМА: Геометрія. Планіметрія. Координати та вектор на площині. Геометричні перетворення.

Це завдання перевіряє знання прямокутної системи координат на площині, основних видів та змісту геометричних перетворень на площині (симетрія, поворот).

1. Симетрія відносно осі \(x\)

Отже, 1 – Б.

2. Симетрія відносно осі \(y\)

Отже, 2 – Г.

3. Симетрія відносно точки \(O\)

Отже, 3 – А.

4. Поворот відносно точки \(O\) на \(90^\circ\) проти годинникової стрілки.

Отже, 4 – Д.

Відповідь: 1 – Б, 2 – Г, 3 – А, 4 – Д.

ТЕМА: Геометрія. Планіметрія. Коло та круг. Координати та вектори на площині.

Це завдання перевіряє знання властивостей кола та круга, їхніх елементів; формули для обчислення відстані між двома точками, рівняння кола.

Коло задано рівнянням \(x^2+y^2=9\). Точки, які належать кругу, обмеженого цим колом, розташовані на відстані, не більшій, ніж радіус від центра кола. \((0; 0)\) – центр кола, \(R=3.\)

Отже, умова виконується, якщо координати точки \((x_0, y_0)\) задовольняють умові $$ x_0^2+y_0^2\le 9. $$

а) \((\sqrt{2})^2+5^2\gt 9.\)

б) \(1^2+3^2\gt 9.\)

в) \(4^2+5^2\gt 9.\)

г) \(3^2+2^2\gt 9.\)

д) \(2^2+(\sqrt{3})^2\le 9,\ 7\le 9.\)

Відповідь: Д.

ТЕМА: Геометрія. Планіметрія. Координати та вектори на площині.

Це завдання перевіряє знання колінеарних векторів.

Колінеарні вектори – це вектори, які лежать на паралельних прямих або на одній прямій. Напрямок та довжина для визначення їх колінеарності не важливі.

\(\overrightarrow{BO}\parallel\overrightarrow{BD}\).

Відповідь: Г.