Завдання за темою з математики

ТЕМА: Геометрія. Стереометрія. Координати і вектори у просторі.

Завдання скеровано на перевірку вміння виконувати дії з векторами, знаходити координати та модуль вектора.

1. Нехай \(\text{т.}\ B(x;\ y;\ z).\ \overline{AB}(x-3;\ y+7;\ z-11)\). Отже, \begin{gather*} x-3=9,\ x=12,\\[7pt] y+7=12,\ y=5,\\[7pt] z-11=-8,\ z=3. \end{gather*} ордината \(\text{т.}\ B\ y_B=5\).

2.

Відповідь: 1. 5. 2. 51.

ТЕМА: Геометрія. Стереометрія. Координати і вектори у просторі.

Завдання скеровано на перевірку вміння виконувати дії з векторами, знаходити координати та скалярний добуток векторів.

1. \begin{gather*} A(x;\ y;\ z)\ \ \overline{AB}(7-x;\ -2-y;\ 0-z)\\[7pt] \overline{AB}(7-x;\ -2-y;\ -z)\\[7pt] \overline{AB}(-3;\ 8;\ 1)\\[7pt] 7-x=-3,\ x=10,\\[7pt] -2-y=8,\ y=-10,\\[7pt] -z=1,\ z=-1. \end{gather*} ордината \(\text{т.}\ A\ =\ -10\).

2.

За формулою скалярного добутку:

Відповідь: 1. –10. 2. –111.

ТЕМА: Геометрія. Стереометрія. Координати і вектори у просторі.

Завдання скеровано на перевірку вміння виконувати дії з векторами, знаходити координати та скалярний добуток векторів.

1. \begin{gather*} \overline{a}(2;\ -9;\ 3)\\[7pt] \overline{b}=-2\overline{a}(-4;\ 18;\ -6) \end{gather*} Сума координат \(-4+18+(-6)=8\).

2.

$$ \overline{a}(a_1;\ a_2;\ a_3),\ \overline{b}(b_1;\ b_2;\ b_3) $$ За формулою \(\overline{a}\cdot \overline{b}=a_1b_1+a_2b_2+a_3b_3\) знаходимо скалярний добуток векторів:

Відповідь: 1. 8. 2. –188.

ТЕМА: Геометрія Стереометрія. Координати у просторі.

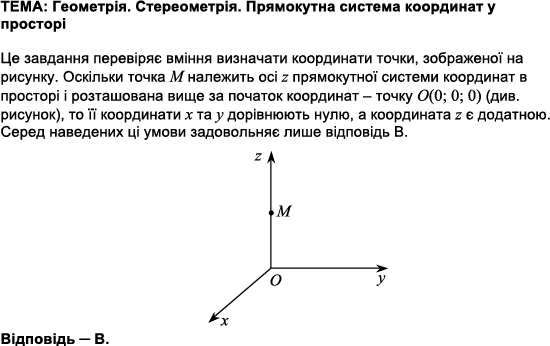
Перевіряє знання прямокутної системи координат у просторі, координати точки.

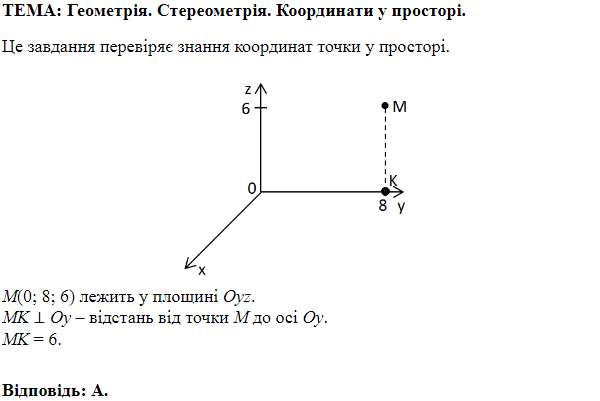
1. Точка на осі \(y\) має нульові координати \(x\) та \(z.\) Довжина відрізка \(BC\) – \(8\) одиниць, звідси серединою відрізка є точка з координатами \((0;\ 4;\ 0).\) Отже, 1 – Г.

2. Точки, що належить відрізку \(DD_1\) мають координати \(x=4;\ y=8\) (як у точки \(D_1).\) Точка, що належить відрізку \(DD_1\) і віддалена від точки \(D\) на \(4\) одиниці, має координати \((4;\ 8;\ 4).\) Отже, 2 – Д.

3. Точка \(C_1\) лежить в площині \(yz,\) тому має \(x=0.\) Координати \(y\) та \(z\) співпадають з координатами точки \(D_1.\) Отже, координати точки \(C_1(0;\ 8;\ 12).\) Отже, 3 – A.

Відповідь: 1Г, 2Д, 3А.