Алгебра і початки аналізу – Лінійні, квадратні, раціональні рівняння та системи рівнянь

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лінійні, квадратні, раціональні, ірраціональні, показникові, логарифмічні, тригонометричні рівняння, нерівності та їх системи. Рівняння з однією змінною, означення кореня (розв'язку) рівняння з однією змінною. Методи розв'язування раціональних, ірраціональних, показникових, логарифмічних, тригонометричних рівнянь.

Це завдання перевіряє вміння розв'язувати квадратні рівняння, розкладати многочлен на множники.

\begin{gather*} 2x(x + 2) = 5(x + 2),\\[7pt] 2x(x + 2) - 5(x + 2) = 0,\\[7pt] (x + 2)(2x - 5) = 0,\\[7pt] \left[\begin{array}{l} x + 2 = 0,\\ 2x - 5 = 0, \end{array}\right.\ \ \left[\begin{array}{l} x = -2,\\ 2x = 5, \end{array}\right.\\[7pt] \left[\begin{array}{l} x = -2,\\ x = 2{,}5. \end{array}\right. \end{gather*}

Відповідь: Д.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лінійні, квадратні, раціональні, ірраціональні, показникові, логарифмічні, тригонометричні рівняння, нерівності та їх системи. Означення розв'язку системи рівнянь з двома змінними та методи їх розв'язань.

Це завдання перевіряє вміння розв'язувати системи лінійних рівнянь.

Складемо рівняння почленно: \(x = 9.\)

Відповідь: A.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лінійні, квадратні, раціональні, ірраціональні, показникові, логарифмічні, тригонометричні рівняння, нерівності та їх системи.

Це завдання перевіряє вміння розв’язувати системи рівнянь.

Розв'яжемо методом підстановки

\begin{gather*} \begin{cases} y = 3 - x,\\ x^2 + 4 = 8(3 - x), \end{cases}\ \ \begin{cases} y = 3 - x,\\ x^2 + 4 = 24 - 8x, \end{cases}\\[7pt] \begin{cases} y = 3 - x,\\ x^2 + 8x - 20 = 0. \end{cases}\\[7pt] x^2 + 8x - 20 = 0.\\[7pt] D = 64 - 4\cdot(-20) = 144;\\[6pt] x_1 = \frac{-8 + 12}{2} = 2;\\[6pt] x_2 = \frac{-8 - 12}{2} = -10. \end{gather*}

Отримали:

\begin{gather*} x_1 = 2;\\[7pt] y_1 = 3 - 2 = 1;\\[7pt] x_2 = -10;\\[7pt] y_2 = 3 - (-10) = 13. \end{gather*}

Розв'язок системи: \((2; 1)\), \((-10; 13).\)

У відповідь запишемо найменший з добутків \(x_0\cdot y_0{:}\)

\begin{gather*} -10\cdot 13 = -130. \end{gather*}

Відповідь: \(-130.\)

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння і нерівності. Лінійні, квадратні, раціональні, ірраціональні, показникові, логарифмічні, тригонометричні рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв'язувати лінійні рівняння.

\begin{gather*} \frac 2x=5;\\[6pt] x=\frac 25;\\[6pt] x=0{,}4. \end{gather*}

Відповідь: Г.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв’язувати лінійні рівняння з модулем.

За властивістю модуля:

\begin{gather*} \left[\begin{array}{l} |2x-1|-3=5,\\ |2x-1|-3=-5, \end{array}\right.\ \ \left[\begin{array}{l} |2x-1|=8,\\ |2x-1|=-2. \end{array}\right. \end{gather*}

Рівняння \(|2x - 1| = -2\) не має коренів, тому розв’язуємо тільки перше рівняння сукупності:

\begin{gather*} |2x - 1| = 8,\\[7pt] \left[\begin{array}{l} 2x-1=8,\\ 2x-1=-8, \end{array}\right.\ \ \left[\begin{array}{l} 2x=9,\\ 2x=-7, \end{array}\right.\\[7pt] \left[\begin{array}{l} x_1=4{,}5,\\ x_2=-3{,}5. \end{array}\right. \end{gather*}

Рівняння має два корені. У відповідь запишемо добуток коренів:

\begin{gather*} x_1 \cdot x_2 = 4{,}5 \cdot (-3{,}5) = -15{,}75. \end{gather*}

Відповідь: \(-15{,}75.\)

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лінійні, квадратні, раціональні, ірраціональні, показникові, логарифмічні, тригонометричні рівняння, нерівності та їх системи.

Це завдання перевіряє вміння розв’язувати системи рівнянь.

ОДЗ: \begin{gather*} 2y - 5 \ne 0,\\[7pt] 2y \ne 5,\\[7pt] y \ne 2{,}5. \end{gather*}

Розв'яжемо методом підстановки:

\begin{gather*} \left\{\begin{array}{l} x = y - 9,\\ \dfrac{y - 9 + 8}{2y - 5} = 2, \end{array}\right.\\[7pt] \left\{\begin{array}{l} x = y - 9,\\ \dfrac{y - 1}{2y - 5} = 2, \end{array}\right.\\[7pt] \left\{\begin{array}{l} x = y - 9,\\ 4y - 10 = y - 1, \end{array}\right.\\[7pt] \left\{\begin{array}{l} x = y - 9,\\ 3y = 9, \end{array}\right.\ \ \left\{\begin{array}{l} x = -6,\\ y = 3. \end{array}\right. \end{gather*}

\((-6; 3)\) – розв'язок системи.

Добуток \(x_0\cdot y_0 = -6\cdot 3 = -18.\)

Відповідь: \(-18.\)

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв’язувати лінійні нерівності.

Додамо почленно рівняння

\begin{gather*} +\begin{cases} 3x - 2y = 9, \\ \underline{x + 2y = -5,} \end{cases}\\[7pt] 4x = 4;\\[7pt] x = 1. \end{gather*}

Підставимо значення \(x = 1\) у друге рівняння:

\begin{gather*} 1 + 2y = -5;\\[7pt] 2y = -6;\\[7pt] y = -3;\\[7pt] (1; -3). \end{gather*}

У відповідь запишемо

\begin{gather*} x_{0} + y_{0} = 1 + (-3) = -2. \end{gather*}

Відповідь: A.

Пояснення

ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Лінійні рівняння.

Це завдання перевіряє уміння розв’язувати лінійні рівняння.

Помножимо обидві частини рівняння на \(6{:}\) \begin{gather*} \frac{x}{2}+\frac{x}{3}=2\ \big|\cdot 6,\\[6pt] 3x+2x=12,\\[6pt] 5x=12,\\[7pt] x=12:5,\\[7pt] x=2{,}4. \end{gather*}

Відповідь: Г.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лінійні, квадратні, раціональні, ірраціональні, показникові, логарифмічні, тригонометричні рівняння, нерівності та їх системи.

Це завдання перевіряє вміння розв'язувати лінійні рівняння.

\begin{gather*} \frac{2x - 3}{3} = \frac{x + 1}{6}. \end{gather*}

Помножимо обидві частини рівняння на \(6{:}\) \begin{gather*} 2(2x - 3) = x + 1,\\[7pt] 4x - 6 = x + 1,\\[7pt] 3x = 7,\\[6pt] x = \frac{7}{3}. \end{gather*}

Відповідь: Д.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лінійні, квадратні, раціональні, ірраціональні, показникові, логарифмічні, тригонометричні рівняння, нерівності та їх системи.

Це завдання перевіряє вміння розв'язувати текстові задачі за допомогою складання рівнянь та їх систем.

Нехай пострілів у «десятку» було \(x\), а у «дев'ятку» – \(y.\)

Усього пострілів зроблено \(10.\) Отже, \(x + y = 10.\)

Усього спортсмен набрав \(94\) очки, отже, \(10x + 9y = 94.\)

Розв'яжемо систему рівнянь методом додавання:

\begin{gather*} \left\{\begin{array}{l} x + y = 10,\ |\ \cdot (-10)\\ 10x + 9y = 94, \end{array}\right.\\[7pt] \underline{\left\{\begin{array}{l} -10x - 10y = -100, \\ 10x + 9y = 94, \end{array}\right.}\\[7pt] -y=-6,\\[7pt] y=6. \end{gather*}

Отже, у «дев'ятку» спортсмен влучив \(6\) разів.

Відповідь: \(6.\)

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лінійні, квадратні, раціональні, ірраціональні, показникові, логарифмічні, тригонометричні рівняння, нерівності та їх системи.

Це завдання перевіряє вміння розв’язувати лінійні рівняння.

Помножимо обидві частини рівняння на \(4.\)

\begin{gather*} 4 \cdot 0{,}5(3x - 4) = \frac{(x + 1) \cdot 4}{4};\\[6pt] 2(3x - 4) = x + 1;\\[7pt] 6x - 8 = x + 1;\\[7pt] 5x = 9;\\[6pt] x = \frac{9}{5}. \end{gather*}

Відповідь: Г.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лінійні, квадратні, раціональні, ірраціональні, показникові, логарифмічні, тригонометричні рівняння, нерівності та їх системи.

Це завдання перевіряє вміння розв’язувати системи рівнянь.

Розв’яжемо методом додавання:

\begin{gather*} +\begin{cases} x^2 - y^2 = -5, \\ \underline{x^2 + y^2 = 3,} \end{cases}\\ 2x^2=-2,\\[7pt] x^2=-1. \end{gather*}

Дане рівняння не має жодного розв’язку.

Відповідь: A.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лінійні, квадратні, раціональні, ірраціональні, показникові, логарифмічні, тригонометричні рівняння, нерівності та їх системи.

Це завдання перевіряє вміння розв’язувати лінійні рівняння з модулем.

За означенням модуля:

\begin{gather*} \left[\begin{array}{l} x-1=6,\\ x-1=-6, \end{array}\right.\ \ \left[\begin{array}{l} x_1=7,\\ x_2=-5. \end{array}\right. \end{gather*}

Cума коренів рівняння:

\begin{gather*} x_1 + x_2 = 7 + (-5) = 2. \end{gather*}

Відповідь: B.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лінійні, квадратні, раціональні, ірраціональні, показникові, логарифмічні, тригонометричні рівняння, нерівності та їх системи.

Це завдання перевіряє вміння розв'язувати раціональні рівняння з параметрами.

\begin{gather*} \left\{\begin{array}{l} x^2-x+a=0,\\ 2x+3\ne 0, \end{array}\right.\ \ \left\{\begin{array}{l} x^2-x+a=0,\\ x\ne -1{,}5. \end{array}\right. \end{gather*}

Рівняння буде мати один корінь у двох випадках:

1) рівняння \(x^2-x+a=0\) має один корінь \((D=0)\) та він не дорівнює \(-1{,}5.\)

2) рівняння \(x^2-x+a=0\) має два корені \((D\gt 0)\), але один з коренів дорівнює \(-1{,}5.\)

Розглянемо кожний випадок: \begin{gather*} \text{1)}\ x^2-x+a=0;\\[7pt] D=1-4a=0;\\[7pt] a=\frac 14;\\[7pt] x=\frac 12. \end{gather*}

Отже, при \(a=\frac 14\) рівняння має один корінь.

\begin{gather*} \text{2)}\ x^2-x+a=0;\\[7pt] D=1-4a\gt 0;\\[6pt] x_1=\frac{1+\sqrt{1-4a}}{2};\\[6pt] x_2=\frac{1-\sqrt{1-4a}}{2}. \end{gather*}

\(x_1\gt 0\), отже, не може дорівнювати \(-1{,}5.\)

Знайдемо значення \(a\), при якому \(x_2=-1{,}5.\)

\begin{gather*} \frac{1-\sqrt{1-4a}}{2}=-\frac 32;\\[6pt] 1-\sqrt{1-4a}=-3;\\[6pt] \sqrt{1-4a}=4;\\[7pt] 1-4a=16;\\[7pt] -4a=15;\\[6pt] a=-\frac{15}{4};\\[6pt] a=-3{,}75. \end{gather*}

Отже, при \(a=-3{,}75\) рівняння має один корінь.

У відповідь запишем найменше значення \(a.\)

Відповідь: \(-3{,}75.\)

Пояснення

ТЕМА: Алгебра і початки аналізу. Функції. Рівняння, нерівності та їхні системи.

Це завдання перевіряє знання властивостей функцій, уміння розв'язувати рівняння графічним методом, рівнянь з параметром.

Розв'яжемо рівняння графічно.

Побудуємо графік \(y=\left|x^2-3|x|-4\right|.\)

\begin{gather*} x_0=\frac 32=1{,}5;\\[6pt] y_0=1{,}5^2-3\cdot 1{,}5-4=-6{,}25. \end{gather*}

\((1{,}5; -6{,}25)\) – вершина параболи.

Точки перетину з осями:

– з \(Ox{:}\)

\begin{gather*} y=0;\\[7pt] x^2-3x-4=0;\\[7pt] D=9+16=25;\\[6pt] x_1=\frac{3+5}{2}=4;\\[6pt] x_2=\frac{3-5}{2}=-1. \end{gather*}

– з \(Oy{:}\)

\begin{gather*} x=0;\\[7pt] y=-4. \end{gather*}

\(a=1\) гілки напрямлені вгору.

\(y=a\) – пряма, паралельна осі \(Ox.\) Кількість розв'язків рівняння \(\left|x^2-3|x|-4\right|=a\) – кількість точок перетину графіків.

Найбільше значення \(a\), при якому рівняння має чотири корені: \(a=6{,}25.\)

Відповідь: \(6{,}25.\)

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв'язувати системи рівнянь графічним методом, рівняння з параметром.

Розв'яжемо рівняння графічно. Розв'язок системи рівнянь – точки перетину графіків.

1) \(x^2+y^2=81\) коло з центром \((0; 0)\) та радіусом \(9.\)

2) \((x+2)^2+y^2=a^2\) коло з центром \((-2; 0)\) та радіусом \(a.\)

 

Система має єдиний розв'язок за умови внутрішнього або зовнішнього дотику двох кіл.

 

Найбільше значення параметра \(a\), за якого система має єдиний розв'язок \(a=11.\)

Відповідь: \(11.\)

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Корінь рівняння.

Це завдання перевіряє знання та розуміння означення кореня рівняння.

Число \(a\) є коренем рівняння \(f(x)=g(x)\), якщо при його підстановці у рівняння замість змінної \(x\) отримаємо числову тотожність: \(f(a)=g(a)\), тобто ліва і права частини рівняння набувають однакових значень. Щоб отримати відповідь на запитання завдання, можна розв’язувати окремо кожне з наведених рівнянь, або ж скористатися означенням кореня рівняння. Підставимо число \(2\) у кожне з наведених рівнянь.

А. Дріб \(\frac{a}{b}\) дорівнює нулю лише тоді, коли чисельник \(a=0\) і знаменник \(b\ne 0.\) Чисельник рівняння \(\frac{1}{x-2}=0\) дорівнює \(1\) незалежно від значення \(x.\) Отже, це рівняння коренів не має.

Б. \(2^2+4=4+4=8\ne 0.\) Це означає, що число \(2\) не є коренем рівняння \(x^2+4=0.\) Окрім цього зазначимо, що вираз \(x^2+4\) за будь-яких \(x\) набуває лише додатних значень, точніше, дорівнює \(4\), якщо \(x=0\), та більше \(4\), якщо \(x\ne 0.\)

В. \(5\cdot 2+12=10+12=22\ne 2\) – число \(2\) не є коренем рівняння.

Г. \(\frac{3\cdot 2-6}{2}=\frac{6-6}{2}=0=0\) – число \(2\) є коренем рівняння.

Д. \(2+2=4\ne 2\) – число \(2\) не є коренем рівняння.

Відповідь: Г.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Квадратні рівняння. Теорема Вієта.

Це завдання перевіряє вміння знаходити добуток коренів квадратного рівняння.

Перший спосіб. За теоремою Вієта, якщо зведене квадратне рівняння $$ x^{2} + px + q = 0 $$ має корені \(x_{1}, x_{2}\), то \begin{gather*} x_{1} + x_{2} = -p,\\[7pt] x_{1} \cdot x_{2} = q. \end{gather*} Задане рівняння $$ x^{2} + 6x - 55 = 0 $$ має два корені, оскільки його дискримінант

Тоді за теоремою Вієта їх добуток дорівнює \(-55.\)

Другий спосіб. Можна розв’язувати це завдання, не використовуючи теорему Вієта. Знайдемо корені заданого квадратного рівняння:

\begin{gather*} x_{1} = \frac{-p - \sqrt{D}}{2} = \frac{-6 - 16}{2} = -11,\\[6pt] x_{2} = \frac{-p + \sqrt{D}}{2} = \frac{-6 + 16}{2} = 5. \end{gather*}

Тоді \(x_{1}\cdot x_{2} = (-11)\cdot 5 = -55.\)

Відповідь: A.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Раціональні рівняння.

Це завдання перевіряє вміння розв’язувати раціональні рівняння зі змінною у знаменнику дробу.

При розв’язанні таких рівнянь треба враховувати ОДЗ (область допустимих значень) рівняння: $$ 2x\ne 0{,}2-3x\ne 0. $$ Два дроби з однаковими чисельниками є рівними, якщо рівні їхні знаменники. Отже, початкове рівняння на його ОДЗ еквівалентне рівнянню $$ 2-3x=2x, $$ звідки \begin{gather*} 5x=2,\\[6pt] x=\frac{2}{5}=0{,}4. \end{gather*} Цей корінь задовольняє ОДЗ, отже є коренем початкового рівняння.

Зауважимо, що задане рівняння можна розглядати як пропорцію. Враховуючи, що добуток крайніх членів пропорції дорівнює добутку її середніх членів, отримаємо: $$ 1\cdot (2-3x)=2x\cdot 1, $$ тобто $$ 2-3x=2x. $$

Відповідь: Г.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Означення розв’язку системи рівнянь з двома змінними та методи їх розв’язування.

Це завдання перевіряє вміння розв’язувати системи рівнянь.

З першого рівняння системи виразимо змінну \(y\) через змінну \(x{:}\) $$ y=\frac{3x}{2}. $$

Підставимо цей вираз замість змінної \(y\) у друге рівняння системи: $$ x-\frac{3x}{2}=12. $$

Розв’яжемо отримане рівняння: \begin{gather*} 2x-3x=24,\\[7pt] -x=24,\\[7pt] x=-24. \end{gather*} Тоді $$ y=\frac{3}{2}\cdot(-24)=-36. $$ Отже, пара \((-24; -36)\) є розв’язком заданої системи. Тому \(x_0=-24.\)

Зазначимо, що для отримання правильної відповіді не обов’язково систему розв’язувати повністю, достатньо лише виразити з першого (другого) рівняння змінну \(y\) через змінну \(x\), отриманий вираз підставити замість змінної \(y\) у друге (перше) рівняння системи, після чого розв’язати отримане рівняння. Його корінь \(x=x_0\) і буде відповіддю до завдання.

Другий спосіб. Спочатку помножимо обидві частини другого рівняння на \(4{:}\) $$ 4x-4y=48, $$ після чого додамо рівняння $$ 4y=6x $$ та $$ 4x-4y=48. $$ Одержимо: \begin{gather*} 4x=6x+48,\\[7pt] -2x=48,\\[7pt] x=-24. \end{gather*}

Відповідь: A.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Рівняння, що містять змінну під знаком модуля.

Це завдання перевіряє вміння розв’язувати рівняння з модулем.

Домножимо обидві частини рівняння \(\frac{|x|}{10} = 2\) на 10, отримаємо \(|x| = 20.\) Модуль числа – це відстань на координатній осі \(x\) від цього числа до початку координат, звідси \(x = \pm 20.\)

Відповідь: Б.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Лінійні рівняння.

Це завдання перевіряє вміння розв’язувати лінійні рівняння: щоб вказати проміжок, якому належить корінь заданого лінійного рівняння, потрібно спочатку його знайти.

Розділимо обидві частини рівняння на \(0{,}5\mathord{:}\) \begin{gather*} 0{,}5(x - 4) = 1{,}5,\\[6pt] x - 4 = \frac{1{,}5}{0{,}5},\\[6pt] x - 4 = 3. \end{gather*}

Перенесемо \(-4\) в праву частину рівняння, змінивши знак на протилежний: $$ x = 3 + 4, $$ \(x = 7\) – корінь рівняння, він належить проміжку \((4; 8]\).

Зазначимо, що розділити вираз на \(0{,}5\) – це рівносильно множенню його на \(2\), тому обидві частини заданого рівняння можна спочатку не розділити на \(0{,}5\), а помножити на \(2\mathord{:}\) $$ 2 \cdot 0{,}5(x - 4) = 2 \cdot 1{,}5, $$ звідки \begin{gather*} x - 4 = 3, \\[7pt] x = 7. \end{gather*}

Відповідь: Г.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Рівняння, що містять змінну під знаком модуля.

Це завдання перевіряє вміння розв’язувати дробово-раціональні рівняння зі змінною під знаком модуля.

Задане рівняння рівносильне рівнянню \(|x|= \frac{4}{3}.\)

Геометрично модуль числа – це відстань на координатній прямій від точки, що зображує це число, до початку відліку. На відстані \(\frac{4}{3}\) від початку відліку знаходяться два числа: \(x_{1} = \frac{4}{3}\) і \(x_{2} = -\frac{4}{3}.\) Обидва ці числа і є коренями заданого рівняння.

Відповідь: Д.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Означення розв'язку системи рівнянь з двома змінними та методи їх розв'язування.

Це завдання перевіряє вміння розв'язувати системи рівнянь.

Додамо почленно обидва рівняння системи:

$$ 2x+x+(-3y)+3y=14+(-11). $$

Звівши подібні доданки, отримаємо:

\begin{gather*} 3x=3,\\[7pt] x=1. \end{gather*}

Пiдставимо отримане значення \(x=1\) в будь-яке з рівнянь системи, наприклад, в друге рівняння:

\begin{gather*} 1+3y=-11,\\[7pt] 3y=-12,\\[7pt] y=-4. \end{gather*}

Отже, пара чисел \((1; -4)\) є розв'язком \((x_0; y_0)\) системи рівнянь. Визначимо суму:

$$ x_0+y_0=1+(-4)=-3. $$

Відповідь: Д.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи. Рівняння з модулем.

Це завдання перевіряє вміння розв'язувати рівняння, що містить невідоме під знаком модуля (абсолютної величини).

Геометрично модуль числа – це відстань по координатній прямій від нього до початку координат. Тому якщо модуль числа дорівнює \(6\), то це число дорівнює \(6\) або \(-6\). Отже, задане рівняння рівносильне сукупності двох рівнянь: $$ \left[\begin{array}{l} 2x-1=6,\\ 2x-1=-6. \end{array}\right. $$

Розв'яжемо кожне з рівнянь окремо:

\begin{gather*} 2x=6+1,\\[7pt] 2x=7,\\[7pt] x_1=3\mathord{,}5;\\[7pt] 2x=-6+1,\\[7pt] 2x=-5,\\[7pt] x_2=-2\mathord{,}5. \end{gather*}

Отже, рівняння має два корені \(x_1=3\mathord{,}5\), \(x_2=-2\mathord{,}5.\)

Відповідь: Г.

Пояснення

ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Квадратні рівняння.

Це завдання перевіряє вміння розв'язувати неповні квадратні рівняння.

\begin{gather*} 4x^2=1\\[6pt] x^2=\frac 14\\[6pt] x=\pm\sqrt{\frac 14}\\[6pt] x_1=0\mathord{,}5\\[7pt] x_2=-0\mathord{,}5. \end{gather*}

Отже, правильна відповідь – Д.

Відповідь: Д.

Пояснення

ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Лінійні, квадратні, раціональні рівняння та їхні системи.

Це завдання перевіряє вміння розв'язувати рівняння та системи рівнянь першого та другого степеня.

\begin{gather*} \left\{\begin{array}{l} xy=12,\\ x(y+2)=6, \end{array}\right.\ \ \left\{\begin{array}{l} xy=12,\\ xy+2x=6. \end{array}\right. \end{gather*}

Почленно віднімемо рівняння системи:

\begin{gather*} -\underline{\left\{\begin{array}{l} xy=12,\\ xy+2x=6, \end{array}\right.}\\[7pt] \ \ \ \ \ \ \ \ \ \ \ \ -2x=6,\\[7pt] \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x=-3. \end{gather*}

Підставимо значення \(x=-3\) в перше рівняння: \begin{gather*} -3\cdot y=12,\\[6pt] y=-\frac{12}{3},\\[6pt] y=-4. \end{gather*}

Розв'язок системи \((-3; -4).\)

Отже, правильна відповідь $$ x_0+y_0=-3+(-4)=-7. $$

Відповідь: A.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв’язувати рівняння першого степеня, застосовувати загальні методи та прийоми в процесі розв’язання рівнянь.

Розв’яжемо рівняння першого степеня відносно \(y:\)

\begin{gather*} 2y+4=x,\\[7pt] 2y=x-4,\\[6pt] y=\frac{x-4}{2}. \end{gather*}

Відповідь: B.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв'язувати рівняння другого степеня.

\begin{gather*} x^2-10=5x+14,\\[7pt] x^2-5x-24=0,\\[7pt] D=(-5)^2-4\cdot (-24)=25+96=121,\\[6pt] x_1=\frac{5+11}{2}=8,\\[6pt] x_2=\frac{5-11}{2}=-3. \end{gather*}

Відповідь: B.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Рівняння, нерівності та їхні системи.

Це завдання перевіряє знання модуля дійсного числа та його властивості; вміння розв'язувати рівняння першого ступеня.

За властивістю модуля дійсного числа, рівняння \(|x-1|=6\) рівносильне сукупності таких рівнянь:

\begin{gather*} \left[\begin{array}{l} x-1=6,\\ x-1=-6, \end{array}\right.\ \ \left[\begin{array}{l} x=7,\\ x=-5. \end{array}\right. \end{gather*}

Сума коренів рівняння дорівнює \(7+(-5)=2.\)

Відповідь: B.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв'язувати системи рівнянь другого степеня.

Розв'яжемо способом додавання

\begin{gather*} + \left\{\begin{array}{l} x^2-y^2=-4,\\ \underline{x^2+y^2=4,} \end{array}\right.\\[3pt] 2x^2=0.\ \ \ \ \\[7pt] x^2=0,\\[7pt] x=0. \end{gather*}

Підставимо \(x=0\) в перше рівняння

\begin{gather*} 0-y^2=-4,\\[7pt] y^2=4,\\[7pt] y=\pm 2. \end{gather*}

Розв'язок системи рівнянь \((0; 2)\) та \((0; -2).\) Отже рівняння має два розв'язки.

Відповідь: B.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв’язувати квадратні нерівності з модулем.

\begin{gather*} \begin{cases} x^2 - 6x = 9, \\ x^2 - 6x = -9, \end{cases} \ \ \begin{cases} x^2 - 6x - 9 = 0, \\ x^2 - 6x + 9 = 0. \end{cases} \end{gather*}

1) \(x^2 - 6x - 9 = 0\)

2) \(x^2 - 6x + 9 = 0\)

\begin{gather*} (x - 3)^2 = 0;\\[7pt] x_3 = 3. \end{gather*}

Корінь, який належить проміжку \((-2; 1]\ x = 3 - 3\sqrt{2}.\)

Відповідь: A.

Пояснення

ТЕМА: Алгебра і початки аналізу. Функції. Рівняння та їхні системи.

Це завдання перевіряє вміння розв'язувати рівняння та їхні системи, зокрема графічно.

Система має єдиний розв'язок за умови однієї спільної точки графіка рівняння \begin{gather*} |x-12|+|y|=1 \end{gather*} та кола \begin{gather*} (x-a)^2+y^2=4. \end{gather*}

Центр кола \((a; 0).\) Радіус кола – \(2.\)

На рисунку зображено можливі чотири варіанти розташування кола відносно графіку рівняння.

\(a=9\); \(11\); \(13\); \(15.\)

Сума значень параметра \(a{:}\)

\begin{gather*} 9+11+13+15=48. \end{gather*}

Відповідь: \(48.\)

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв'язувати рівняння з параметрами, зокрема графічно.

Розв'яжемо графічно:

\begin{gather*} \left\{\begin{array}{l} y-x=a,\\ x^2+y^2=1, \end{array}\right.\ \ \left\{\begin{array}{l} y=x+a,\\ x^2+y^2=1. \end{array}\right. \end{gather*}

\(x^2+y^2=1\) – рівняння кола, з центром в точці \((0; 0)\) та радіусом \(R=1.\)

\(y=x+a\) – пряма \(y=x\), яка переміщується вздовж осі \(Oy\) на \(a\) одиниць.

Кількість розв'язків системи – кількість точок перетину графіків.

Найбільше ціле значення параметра \(a=1\) при якому система має два розв'язки.

Відповідь: \(1.\)

Пояснення

ТЕМА: Рівняння, нерівності та їхні системи. Лінійні, квадратні рівняння та їхні системи.

Це завдання перевіряє вміння розв'язувати системи рівнянь першого та другого степеня, застосовувати загальні методи та прийоми в процесі розв'язування систем рівнянь.

З першого рівняння добуток \(xy=-12.\)

Отримаємо:

\begin{gather*} 2\cdot(-12)-x=-18,\\[7pt] -24-x=-18,\\[7pt] x=-24+18,\\[7pt] x=-6. \end{gather*}

Якщо \((x_0; y_0)\) – розв'язок системи, то \(x_0=-6.\)

Відповідь: A.

Пояснення

ТЕМА: Рівняння, нерівності та їхні системи. Лінійні рівняння.

Це завдання перевіряє вміння розв'язувати лінійні рівняння.

\begin{gather*} 2x-3=4,\\[7pt] 2x=4+3,\\[7pt] 2x=7,\\[7pt] x=7:2,\\[7pt] x=3\mathord{,}5. \end{gather*}

Значення \(x\) належить проміжку \([2; 4).\)

Відповідь: Г.

Пояснення

ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Лінійні рівняння.

Це завдання перевіряє вміння розв'язувати рівняння, що містять змінну під знаком модуля.

\begin{gather*} 2|x|=2,\\[7pt] |x|=1,\\[7pt] x=\pm 1. \end{gather*}

Отже, за наведених чисел коренем рівняння є \(x=-1.\)

Відповідь: Г.

Пояснення

ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Раціональні рівняння.

Це завдання перевіряє вміння розв'язувати раціональні рівняння.

\begin{gather*} \frac{3x-2}{x+1}=7,\\[6pt] \frac{3x-2}{x+1}-7=0 \end{gather*}

зводимо до спільного знаменника:

\begin{gather*} \frac{3x-2-7(x+1)}{x+1}=0,\\[6pt] \frac{3x-2-7x-7}{x+1}=0,\\[6pt] \frac{-4x-9}{x+1}=0,\\[6pt] \left\{\begin{array}{l} -4x-9=0,\\ x+1\ne 0, \end{array}\right.\ \ \left\{\begin{array}{l} x=-2\mathord{,}25,\\ x\ne -1. \end{array}\right. \end{gather*}

Корінь рівняння \(x=-2\mathord{,}25\) належить проміжку \((-\infty; -2).\)

Відповідь: A.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння.

Це завдання перевіряє вміння розв'язувати рівняння з однією змінною, використовувати методи розв'язування раціональних рівнянь.

Якщо рівняння має вигляд добутку множників, що дорівнює нулю, то принаймні один з множників повинен дорівнювати нулю.

\begin{gather*} \left[\begin{array}{l} x+1=0,\\ 2x-3=0, \end{array}\right.\ \ \left[\begin{array}{l} x=-1,\\ 2x=3, \end{array}\right.\ \ \left[\begin{array}{l} x=-1,\\ x=1\mathord{,}5. \end{array}\right. \end{gather*}

Відповідь: Д.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння та їхні системи.

Це завдання перевіряє вміння розв'язувати системи рівнянь першого степеня.

\begin{gather*} \left\{\begin{array}{l} 2y=5x,\\ x+y=14, \end{array}\right.\ \ \left\{\begin{array}{l} y=\frac 52x,\\ x+\frac 52x=14, \end{array}\right.\ \ \left\{\begin{array}{l} y=\frac 52x,\\ \frac 72x=14, \end{array}\right. \\[7pt] \left\{\begin{array}{l} y=\frac 52x,\\ x=14:\frac 72, \end{array}\right.\ \ \left\{\begin{array}{l} y=\frac 52x,\\ x=4, \end{array}\right.\ \ \left\{\begin{array}{l} y=10,\\ x=4. \end{array}\right. \end{gather*}

Розв'язок \((4; 10).\) Відповідь: \(4\cdot 10=40.\)

Відповідь: Г.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лiнiйнi, квaдpaтні, рацiональнi, iррацiональнi, показникові, логарифмiчнi, тригонометричні рівняння, неpiвності та їx системи.

Це завдання перевіряє вміння розв'язувати системи лінійних рівнянь.

Почленно додамо рівняння: \begin{gather*} \left\{\begin{array}{l} 2x+5y=5\\ x-2y=7\ |\ \cdot (-2) \end{array}\right.\\[7pt] \ +\ \left\{\begin{array}{l} 2x+5y=5\\ \underline{-2x+4y=-14} \end{array}\right.\\[7pt] 9y=-9,\ y=-1 \end{gather*} Підставимо \(y=-1\) у друге рівняння: \begin{gather*} x-2(-1)=7,\\[7pt] x+2=7,\\[7pt] x=5. \end{gather*}

Розв'язок системи \((x_0; y_0)\) це \((5; -1).\) Сума \(x_0+y_0=5+(-1)=4.\)

Відповідь: Д.

Пояснення

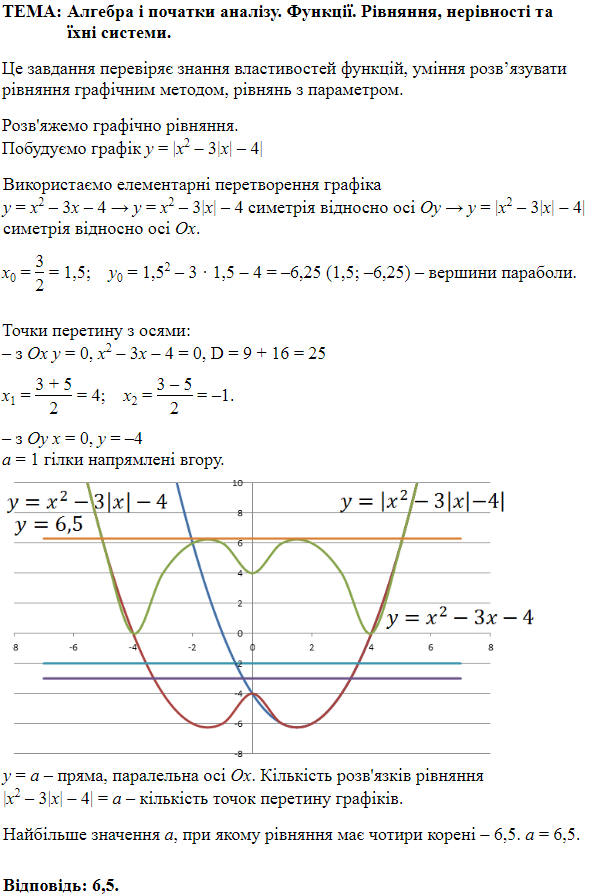
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв’язувати квадратні рівняння.

Розв'яжемо квадратне рівняння: \begin{gather*} x^2-8x+15=0,\\[6pt] D=(-8)^2-4\cdot 1\cdot 15=4,\\[6pt] x_1=\frac{8+2}{2\cdot 1}=5,\\[6pt] x_2=\frac{8-2}{2\cdot 1}=3. \end{gather*}

Відповідь: A.

Пояснення

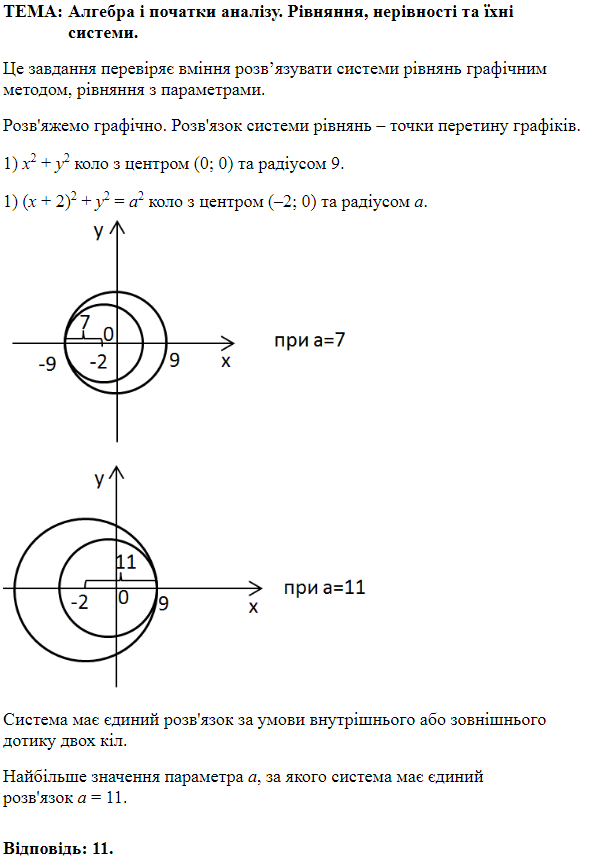
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв’язувати системи лінійних рівнянь.

Розв'яжемо систему лінійних рівнянь методом додавання: \begin{gather*} +\left\{\begin{array}{l} 10x-4y=26,\\ 6x+4y=6, \end{array}\right.\\[0pt] \ \ \ \ \ \ \overline{16x=32,}\\[7pt] x=32:16,\ \ x=2. \end{gather*}

Підставимо значення \(x=2\) в друге рівняння: \begin{gather*} 6\cdot 2+4y=6,\\[7pt] 12+4y=6,\\[7pt] 4y=6-12,\\[7pt] 4y=-6,\\[7pt] y=-6: 4,\\[7pt] y=-1\mathord{,}5. \end{gather*}

Розв'язок системи \((2; -1\mathord{,}5).\)
Обчислимо добуток \(x_0\cdot y_0=2\cdot (-1\mathord{,}5)=-3.\)

Відповідь: A.

Пояснення

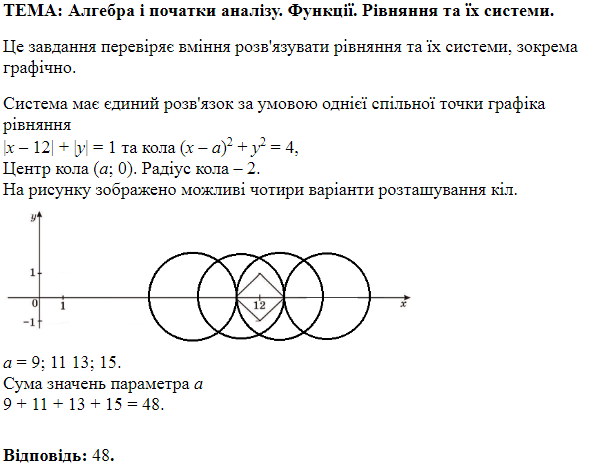
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв’язувати лінійні рівняння з модулем.

За властивістю модуля

У відповідь запишемо суму розв'язків: \(0\mathord{,}5+2=2\mathord{,}5.\)

Відповідь: \(2\mathord{,}5.\)

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання перевіряє вміння розв’язувати лінійні рівняння.

Помножимо обидві частини рівняння на \(3.\)

\(5x+8=3\), \(5x=-5\), \(x=-1.\)

Відповідь: Д.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання перевіряє вміння розв’язувати квадратні рівняння.

Розв'яжемо квадратне рівняння:

\begin{gather*} x^2-4x+3=0,\\[7pt] D=(-4)^2-4\cdot 1\cdot 3=16-12=4,\\[7pt] x_1=\frac{4+2}{2}=3;\ \ x_2=\frac{4-2}{2}=1. \end{gather*}

Відповідь: Б.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє відношення та пропорції. Перевіряє знання основної властивості пропорції.

Розв'яжемо рівняння, використавши основну властивість пропорції: \begin{gather*} \frac 8x=\frac 25,\\[6pt] 2\cdot x=8\cdot 5,\\[6pt] x=20. \end{gather*}

Відповідь: A.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв'язувати квадратні рівняння.

Розв'яжемо рівняння:

\begin{gather*} x^2=25x,\\[7pt] x^2-25x=0,\\[7pt] x(x-25)=0,\\[7pt] \left[\begin{array}{l} x_1=0,\\ x_2=25. \end{array}\right. \end{gather*}

Відповідь: Б.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати рівняння першого степеня.

\begin{gather*} \frac{x}{10}=2,5;\\[6pt] x=2,5\cdot 10=25. \end{gather*}

Відповідь: Г.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати системи лінійних рівнянь.

Розв'яжемо систему рівнянь методом додавання: \begin{gather*} \left\{ \begin{array}{l l} 6(x+5)+10y=3 & \\ 2x=y+4& \end{array}\right. \left\{ \begin{array}{l l} 6x+30+10y=3 & \\ 2x-y=4& \end{array}\right. \\[7pt] \left\{ \begin{array}{l l} 6x+10y=-27 & \\ 2x-y=4\ \ |\cdot (-3)& \end{array}\right. \left\{ \begin{array}{l l} 6x+10y=-27 & \\ -6x+3y=-12& \end{array}\right. \\[7pt] 13y=-39,\ \ y=-3. \end{gather*}

Підставимо значення \(y=-3\) у друге рівняння: \begin{gather*} 2x-(-3)=4;\ \ 2x+3=4; \\[6pt] 2x=1;\ \ x=\frac 12\\[6pt] x_0=\frac 12;\ \ y_0=-3. \end{gather*}

У відповідь запишемо суму $$ x_0+y_0=\frac 12+(-3)=-2,5. $$

Відповідь: А.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати рівняння, використовуючи означення та властивості модуля.

Якщо \(x\geq 0\), то \(|x|=x\). Отже, \(x+4x=3,\ 5x=3,\ x=0,6\).

Якщо \(x\lt 0\), то \(|x|=-x\). Отже, \(x-4x=3,\ -3x=3,\ x=-1\).

У відповідь запишемо їхню суму \(0,6+(-1)=-0,4\).

Відповідь: –0,4.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати рівняння першого степеню.

Розв'яжемо лінійне рівняння:

\begin{gather*} 1-5x=0\\[7pt] -5x=-1\\[6pt] x=\frac{-1}{-5}\\[6pt] x=\frac 15 \end{gather*}

Відповідь: B.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати рівняння, що зводяться до квадратних.

Рівняння \(x^4-x^2-20=0\) – біквадратне. Розв'яжемо заміною:

Повернемось до заміни:

\begin{gather*} x^2=5\\[7pt] \left [ \begin{array}{l l} x_1=\sqrt{5} & \\ x_2=-\sqrt{5}& \end{array}\right. \end{gather*}

Добуток його дійсних коренів: $$ x_1\cdot x_2=\sqrt{5}\cdot (-\sqrt{5})=-5. $$

Відповідь: –5.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати рівняння другого степеня, знання теореми Вієта.

І спосіб: заходимо корні рівняння

ІІ спосіб: за теоремою Вієта: $$ x_1+x_2=-b=-3 $$

Відповідь: Б.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати раціональні рівняння.

Розв'яжемо рівняння $$ \frac{x}{9-x}=\frac 12;\ \ x\ne 9 $$

Використаємо властивість пропорції

належить проміжку \((2;\ 5]\).

Відповідь: Г.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання перевіряє вміння розв’язувати лінійні рівняння.

Розв'яжемо лінійне рівняння:

\begin{gather*} 2x-3=4\\[7pt] 2x=4+3\\[7pt] 2x=7\\[7pt] x=3,5 \end{gather*}

Відповідь: Б.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння.

Перевіряє вміння розв'язувати квадратні рівняння, знання теореми Вієта.

Добуток коренів рівняння за теоремою Вієта для зведеного квадратного рівняння:

\begin{gather*} x^2+px+q=0\\[7pt] x_1\cdot x_2=q\\[7pt] x_1\cdot x_2=-55. \end{gather*}

Відповідь: A.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання перевіряє вміння розв’язувати лінійні рівняння.

$$ \frac x2 +\frac x3= 2, $$ зведемо до спільного знаменника: \begin{gather*} \frac{3x+2x}{6}=2,\\[6pt] \frac{5x}{6}=2,\\[6pt] 5x=12,\\[6pt] x=2,4. \end{gather*}

Відповідь: B.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати системи лінійних та раціональних рівнянь.

Розв'яжемо систему рівнянь:

\begin{gather*} \left\{ \begin{array}{l} \frac{1}{3y}=\frac 2x, \\ x-y=30. \end{array} \right. \end{gather*}

Застосуємо основну властивість пропорції до першого рівняння:

\begin{gather*} \left\{ \begin{array}{l} 1\cdot x=2\cdot 3y, \\ x-y=30, \end{array} \right. \ \ \ \left\{ \begin{array}{l} x=6y, \\ x-y=30. \end{array} \right. \end{gather*}

Методом підстановки маємо:

\begin{gather*} \left\{ \begin{array}{l} x=6y, \\ 6y-y=30, \end{array} \right. \ \ \ \left\{ \begin{array}{l} x=6y, \\ 5y=30, \end{array} \right. \\[7pt] \left\{ \begin{array}{l} x=6y, \\ y=6, \end{array} \right. \ \ \ \left\{ \begin{array}{l} x=6\cdot 6, \\ y=6, \end{array} \right. \\[7pt] \left\{ \begin{array}{l} x=36, \\ y=6. \end{array} \right. \end{gather*}

\((36;\ 6)\) – розв'язок системи, тому \(36+6=42\) – правильна відповідь.

Відповідь: Г.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати квадратні рівняння, аналізувати та досліджувати рівняння, розв’язувати рівняння з параметром.

Дано рівняння \(x^2-4ax+4a^2-25=0.\) Корені квадратного рівняння задовольняють умову \(x_1\lt 1\lt x_2.\)

Знайдемо \(a,\) при яких

\begin{gather*} \left\{ \begin{array}{l} 2a-5\lt 1,\\ 2a+5\gt 1, \end{array} \right. \\[7pt] \left\{ \begin{array}{l} 2a\lt 6,\\ 2a\gt -4, \end{array} \right. \ \ \ \left\{ \begin{array}{l} a\lt 3,\\ a\gt -2. \end{array} \right. \end{gather*}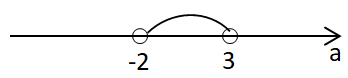

Цілі значення \(a\in (-2;\ 3)\) це \(a=-1;\ 0;\ 1;\ 2.\)

Таких значень \(4.\)

Відповідь: 4.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання перевіряє вміння розв’язувати лінійні рівняння.

Розв'яжемо лінійне рівняння \(0,01x=-1,\) \begin{gather*} x=-1:0,01;\\[7pt] x=-100. \end{gather*}

Отже, правильна відповідь – Б.

Відповідь: Б.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати квадратні рівняння, аналізувати та досліджувати рівняння, розв’язувати рівняння з параметром.

\(x^2-(2m-4)x+16=0,\ \ x_1\gt x_2\ \text{на}\ 6.\)

Знайдемо дискримінант рівняння:

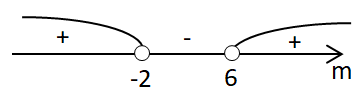
Додатнє значення \(m,\) при якому рівняння має два різних кореня \(m\gt 6.\)

За теоремою Вієта і враховуючи умову завдання:

\begin{gather*} \left\{ \begin{array}{l} x_1+x_2=2m-4,\\ x_1\cdot x_2=16,\\ x_1-x_2=6, \end{array} \right. \ \ \ \left\{ \begin{array}{l} x_2+6+x_2=2m-4,\\ (x_2+6)x_2=16,\\ x_1=x_2+6, \end{array} \right. \\[7pt] 2x_2=2m-10,\ \ x_2=m-5. \end{gather*}

Підставимо значення \(x_2\) у друге рівняння:

\begin{gather*} (m-5+6)(m-5)=16,\ \ (m+1)(m-5)=16,\\[7pt] m^2-5m+m-5-16=0,\ \ m^2-4m-21=0. \end{gather*}

Корені рівняння:

\begin{gather*} \left\{ \begin{array}{l} m_1=7,\\ m_2=-3\ \ne\ m\gt 6. \end{array} \right. \end{gather*}

Отже, додатнє значення \(m=7.\)

Відповідь: 7.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання скеровано на перевірку вміння розв’язувати рівняння першого степеня, використовуючи означення та властивості модуля.

\begin{gather*} |3x+2|=2\\[7pt] 3x+2=2\\[7pt] 3x=0\\[7pt] x=0\\[7pt] \text{або}\\[7pt] 3x+2=-2\\[7pt] 3x=-4\\[6pt] x=-\frac 43. \end{gather*}

З наведених чисел \(-\frac 43\) є коренем рівняння.

Відповідь: Б.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання скеровано на перевірку вміння розв’язувати раціональні рівняння, аналізувати та досліджувати рівняння, розв’язувати рівняння з параметром.

$$\frac{x^2-ax+4}{x-5}=0.$$ ОДЗ:

Рівняння буде мати один корінь за умов:
1) \(D=0\) та \(x\ne 5;\)
2) \(D\gt 0,\) але один з коренів дорівнює \(5.\)

Розглянемо обидва випадки: \begin{gather*} \text{1)}\ \ D=0,\ \ a^2-16=0,\ \ a^2=16,\\[7pt] a=4\ \text{або}\ a=-4\\[6pt] x=\frac a2=\frac 42=2\ \text{або}\ x=-2. \end{gather*} Отже, корінь один. \begin{gather*} \text{2)}\ \ D\gt 0,\ \ a^2-16=0,\\[7pt] a\in (-\infty; -4)\cup (4; +\infty) \end{gather*}

 

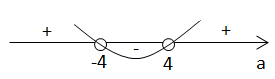
\begin{gather*} x_1=\frac{a+\sqrt{a^2-16}}{2},\\[6pt] x_2=\frac{a-\sqrt{a^2-16}}{2}. \end{gather*}

 

Нехай \(x_1=5,\) тоді

Нехай \(x_2=5,\) отже

Отже, рівняння має один корінь при \(a=4,\ a=-4, a=5\mathord{,}8.\) Добуток усіх значень \(a\) дорівнює: $$4\cdot (-4)\cdot 5\mathord{,}8=-92\mathord{,}8.$$

Відповідь: -92,8.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання скеровано на перевірку вміння розв’язувати системи лінійних рівнянь.

Розв'яжемо систему: \begin{gather*} \left\{ \begin{array}{l} 2x-\frac y3=7,\\ 4x+\frac{2y}{3}=6\ | : 2, \end{array} \right. \ \ \ \ \left\{ \begin{array}{l} 2x-\frac y3=7,\\ 2x+\frac y3=3. \end{array} \right. \end{gather*}

Почленно додамо рівняння: $$ 4x=10,\ \ x=10:4,\ \ x=2,5. $$ Підставимо значення \(x\) у перше рівняння: \begin{gather*} 2\cdot 2,5-\frac y3=7,\ \ 5-\frac y3=7,\\[6pt] -\frac y3=2,\ \ y=-6. \end{gather*} \((2,5; -6)\) – розв'язок системи.

Отже, \(x_0+y_0=2,5+(-6)=-3,5.\)

Відповідь: A.

Пояснення

ТЕМА: Алгебра. Лінійні рівняння.

Завдання скеровано на перевірку вміння розв’язувати лінійні рівняння, знання основної властивості пропорції.

$$ \frac{2x-7}{3}=\frac{5x+4}{2}. $$

Застосуємо основну властивість пропорції:

\begin{gather*} \frac ab=\frac cd,\\[6pt] a\cdot d=b\cdot c,\\[7pt] 2(2x-7)=3(5x+4),\\[7pt] 4x-14=15x+12,\\[7pt] 4x-15x=12+14,\\[7pt] -11x=26,\\[6pt] x=-\frac{26}{11},\\[6pt] x=-2\frac{4}{11}. \end{gather*}

Відповідь: B.

Пояснення

ТЕМА: Алгебра і початки аналізу. Розв’язування показникових, раціональних рівнянь.

Завдання скеровано на перевірку вміння розв’язувати показникові, раціональні і ірраціональні рівняння й нерівності та їх системи з параметрами.

1. Область допустимих значень

\begin{gather*} \left\{ \begin{array}{l} x\ge 0,\\ 3-x\ge 0,\\ \sqrt{x}+\sqrt{3-x}\ne 0, \end{array} \right.\\[7pt] \left\{ \begin{array}{l} x\ge 0,\\ x\le 3. \end{array} \right.\\[7pt] x\in [0; 3]. \end{gather*}

2. Розв'яжемо рівняння:

\begin{gather*} 3^{2a-5x+2}-\sqrt{27}=0,\\[7pt] 3^{2a-5x+2}=3\sqrt{3},\\[7pt] 3^{2a-5x+2}=3^{1\mathord{,}5},\\[7pt] 2a-5x+2=1\mathord{,}5,\\[7pt] 5x=2a+0\mathord{,}5,\\[7pt] x=0\mathord{,}4a+0\mathord{,}1. \end{gather*}

Для того, щоб рівняння мало корінь

\begin{gather*} 0\le 0\mathord{,}4a+0\mathord{,}1\le 3,\\[7pt] -0\mathord{,}1\le 0\mathord{,}4a\le 2\mathord{,}9,\\[6pt] -\frac 14\le a\le \frac{29}{4},\\[6pt] -\frac 14\le a\le 7\frac 14. \end{gather*}

Найбільше значення \(a=7\frac 14=7\mathord{,}25.\)

Відповідь: \(7\mathord{,}25.\)

Пояснення

ТЕМА: Алгебра і початки аналізу. Розв’язування раціональних рівнянь.

Завдання скеровано на перевірку вміння розв’язувати раціональні рівняння, та їх системи з параметрами.

\begin{gather*} \left\{ \begin{array}{l} y+(x-1)^2=5a,\\ x^2-2x+y^2+8y=47, \end{array} \right.\ \ \left\{ \begin{array}{l} (x-1)^2+y=5a,\\ (x^2-2x+1)+(y^2+8y+16)=64, \end{array} \right.\\[7pt] \left\{ \begin{array}{l} y=-(x-1)^2+5a,\\ (x-1)^2+(y+4)^2=64. \end{array} \right. \end{gather*}

Розв'яжемо систему графічним способом.

\((x-1)^2+(y+4)^2=64\) – рівняння кола з центром \((1; -4)\) і радіусом \(8.\)

\(y=-(x-1)^2+5a\) – квадратична функція з вершиною в точці \((1; 5a)\) з вітками вниз.

Для того, щоб система мала єдиний розв'язок, треба, щоб графіки мали одну спільну точку.

Отже,

\begin{gather*} 5a=-12,\\[7pt] a=-12:5=-2\mathord{,}4. \end{gather*}

Відповідь: \(-2\mathord{,}4.\)

Пояснення

ТЕМА: Лінійні, показникові та раціональні рівняння.

Завдання скеровано на перевірку вміння розв’язувати показникові та раціональні рівняння та їх системи.

Рівняння \(5^x=\sqrt{5}\) містить одну змінну. Розв'яжімо його, зводячи до однакової основи:

\begin{gather*} \sqrt{5}=5^{\frac 12},\\[6pt] \text{тому}\ 5^x=5^{\frac 12},\\[6pt] x=\frac 12. \end{gather*}

Підставмо значення \(x\) у друге рівняння:

\begin{gather*} \frac{y+1}{2\cdot \frac 12+3}=\frac{1-4\cdot \frac 12}{2},\\[6pt] \frac{y+1}{1+3}=\frac{1-2}{2},\\[6pt] \frac{y+1}{4}=\frac{-1}{2}. \end{gather*}

За основною властивістю пропорції: $$ \frac ab=\frac cd \rightarrow a\cdot d=b\cdot c. $$ Тому запишімо:

\begin{gather*} 2(y+1)=4\cdot (-1),\\[7pt] 2y+2=-4,\\[7pt] 2y=-4-2,\\[7pt] 2y=-6,\\[7pt] y=-6:2,\\[7pt] y=-3. \end{gather*}

Маємо розв'язок \((x_0; y_0)\) як \(\left(\frac 12; -3\right).\)

Підставмо його у вираз:

Відповідь: А.

Пояснення

ТЕМА: Лінійні і раціональні рівняння та їх системи.

Завдання скеровано на перевірку вміння розв’язувати лінійні і раціональні рівняння.

Розв'яжімо систему рівнянь методом додавання:

\begin{gather*} \left\{\begin{array}{l} x-\frac 3y=3\ |\cdot (-1),\\ x+\frac 1y=11. \end{array}\right.\\[7pt] + \left\{\begin{array}{l} -x+\frac 3y=-3,\\ \underline{x+\frac 1y=11,} \end{array}\right.\\[6pt] \frac 3y+\frac 1y=8,\\[6pt] \frac 4y=8,\\[6pt] y=\frac 12. \end{gather*}

Підставмо значення \(y=0\mathord{,}5\) у перше рівняння:

\begin{gather*} x-\frac{3}{0\mathord{,}5}=3,\\[6pt] x-6=3,\\[7pt] x=9. \end{gather*}

Розв'язком системи є пара чисел \((9; 0\mathord{,}5)\mathord{:}\)

$$ x_0+y_0=9+0\mathord{,}5=9\mathord{,}5. $$

Відповідь: Г.

Пояснення

ТЕМА: Квадратні рівняння.

Завдання скеровано на перевірку вміння розв’язувати квадратні рівняння.

А

\begin{gather*} x^2+2x+1=0,\\[7pt] (x+1)^2=0,\\[7pt] x=-1 \end{gather*}

Рівняння має один корінь.

Б

\begin{gather*} x^2+2x+3=0,\\[7pt] x^2+2x+1+2=0,\\[7pt] x^2+2x+1=-2,\\[7pt] (x+1)^2=-2,\\[7pt] x\in \varnothing. \end{gather*}

Рівняння коренів не має.

В

\begin{gather*} x^2+2x=0,\\[7pt] x(x+2)=0,\\[7pt] x=0\ \text{або}\ x=-2 \end{gather*}

Рівняння має два різні дійсні корені.

Г

\begin{gather*} x^2+4=0,\\[7pt] x^2=-4,\\[7pt] x\in \varnothing. \end{gather*}

Рівняння коренів не має.

Д

\begin{gather*} -x^2-2x-1=0,\\[7pt] x^2+2x+1=0,\\[7pt] x=1. \end{gather*}

Рівняння має один корінь.

Відповідь: В.

Пояснення

ТЕМА: Лінійні рівняння.

Завдання скеровано на перевірку вміння розв’язувати лінійні рівняння з параметром.

Розв'яжімо лінійне рівняння:

\begin{gather*} ax-5=a+2x,\\[7pt] ax-2x=a+5,\\[7pt] x(a-2)=a+5. \end{gather*}

Якщо \(a=2\), рівняння не має коренів \((x\cdot 0=7).\)

Якщо \(a\ne 2\), корінь є. Його визначають так: $$ x=\frac{a+5}{a-2}. $$

Корінь рівняння буде додатним, якщо $$ \frac{a+5}{a-2}\gt 0. $$

Розв'яжімо методом інтервалів:

На проміжку \(a\in [-9; 9]\) рівняння має розв'язок, якщо \(a\in [-9; -5)\cup (2; 9].\)

Цілі значення \(a\) із цього проміжку: \(-9\), \(-8\), \(-7\), \(-6\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\), \(9.\) Тобто цілих значень \(a\) \(11.\)

Відповідь: \(11.\)

Пояснення

ТЕМА: Показникові. Раціональні рівняння.

Завдання скеровано на перевірку вміння розв’язувати показникові та квадратні рівняння, рівняння з параметром.

Замінімо змінну. Нехай \(3^x=t.\) Оскільки показникова функція завжди набуває лише додатних значень: \(t\gt 0.\) Рівняння набуває вигляду:

\begin{gather*} t+\frac{4a^2+10a}{t}=4a+5. \end{gather*}

Помножмо все на \(t\ (t\ne 0){:}\)

Оскільки \(D\gt 0\), маємо два корені:

Щоб рівняння не мало коренів, необхідно, щоб \(t_1\le 0\) i \(t_2\le 0{:}\)

\begin{gather*} 1.\ 2a+5\le 0,\\[7pt] 2a\le -5,\\[7pt] a\le -2{,}5.\\[7pt] 2.\ 2a\le 0,\\[7pt] a\le 0. \end{gather*}

Спільна умова: \(a\le -2{,}5.\)

Найбільше значення \(a\) з проміжку \((-\infty; -2{,}5]\) це \(-2{,}5.\)

Відповідь: \(-2{,}5.\)

Пояснення

ТЕМА: Раціональні рівняння.

Завдання скеровано на перевірку вміння розв’язувати раціональні рівняння з параметром.

Область допустимих значень:

\begin{gather*} 3x-a\ne 0,\\[7pt] 3x\ne a,\\[6pt] x\ne \frac a3. \end{gather*}

Прирівняймо чисельники рівних дробів:

\(x_1=6\mathord{,}5\) не буде коренем рівняння за умови:

\begin{gather*} x_1=\frac a3=6\mathord{,}5\\[6pt] a=19\mathord{,}5. \end{gather*}

Рівняння має один корінь \(x_2=-3.\)

\(x_2=-3\) не буде коренем рівняння за умови, що

\begin{gather*} x_2=\frac a3=-3,\\[7pt] a=-9. \end{gather*}

Рівняння має один корінь \(x_1=6{,}5.\)

Отже, рівняння має один корінь за \(a=19\mathord{,}5\) або \(a=-9.\)

У відповіді запишімо їхню суму: $$ 19\mathord{,}5+(-9)=10\mathord{,}5. $$

Відповідь: \(10\mathord{,}5.\)

Пояснення

ТЕМА: Лінійні й раціональні рівняння та їх системи.

Завдання скеровано на перевірку вміння розв’язувати лінійні й раціональні рівняння.

ОДЗ: \(x\ne 0.\)

Розв’яжімо методом підставлення:

\begin{gather*} \left\{\begin{array}{l} \frac{2x+y}{x}=5,\\ 4x-y=-2, \end{array}\right.\ \ \left\{\begin{array}{l} 2x+y=5x,\\ 4x-y=-2, \end{array}\right.\\[7pt] \left\{\begin{array}{l} y=3x,\\ 4x-y=-2, \end{array}\right.\ \ \left\{\begin{array}{l} y=3x,\\ 4x-3x=-2, \end{array}\right.\\[7pt] \left\{\begin{array}{l} y=3x,\\ x=-2, \end{array}\right.\ \ \left\{\begin{array}{l} y=3\cdot (-2),\\ x=-2, \end{array}\right.\\[7pt] \left\{\begin{array}{l} y=-6,\\ x=-2. \end{array}\right. \end{gather*}

\((-2; -6)\) – розв'язок системи.

Відповідь: Б.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання спрямовано на перевірку навичок розв’язання квадратних рівнянь, їхнього аналізу та дослідження рівнянь із параметрами.

\begin{gather*} x^2-4ax+4a^2-25=0;\\[7pt] x_1\lt 1\lt x_2. \end{gather*}

Визначмо дискримінант рівняння:

Підставмо вирази для коренів у подвійну нерівність:

\begin{gather*} 2a-5\lt 1\lt 2a+5. \end{gather*}

Ця нерівність рівносильна системі нерівностей:

\begin{gather*} \left\{\begin{array}{l} 2a-5\lt 1\\ 2a+5\gt 1, \end{array}\right.\ \ \left\{\begin{array}{l} 2a\lt 1+5,\\ 2a\gt 1-5, \end{array}\right.\\[7pt] \left\{\begin{array}{l} 2a\lt 6,\\ 2a\gt -4, \end{array}\right.\ \ \left\{\begin{array}{l} a\lt 3,\\ a\gt -2. \end{array}\right. \end{gather*}

Отже, значення \(a\) має перебувати в межах \(-2\lt a\lt 3.\)

Випишімо всі цілі числа, що входять у цей проміжок: \(-1\), \(0\), \(1\), \(2.\)

Усього таких значень чотири.

Відповідь: \(4.\)

Пояснення

ТЕМА: Лінійні та раціональні рівняння і їх системи.

Завдання скеровано на перевірку вміння розв’язувати лінійні та раціональні рівняння.

Розв'яжімо систему рівнянь методом додавання:

\begin{gather*} \left\{\begin{array}{l} x+2y=8,\\ x-2y=-4, \end{array}\right.\\[7pt] x+2y+x-2y=8+(-4);\\[7pt] 2x=4;\\[7pt] x=2. \end{gather*}

Підставмо значення \(x=2\) в перше рівняння:

\begin{gather*} 2+2y=8;\\[7pt] 2y=8-2;\\[7pt] 2y=6;\\[7pt] y=3. \end{gather*}

Розв'язком системи є пара чисел \((2; 3){:}\)

\begin{gather*} x_0\cdot y_0=2\cdot 3=6. \end{gather*}

Відповідь: Д.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати квадратні рівняння, зокрема з параметрами, а також аналізувати та досліджувати їхні властивості.

Два числа називають протилежними, якщо їхня сума дорівнює нулю (наприклад, \(5\) і \(-5\)). Отже, для коренів рівняння має виконуватися умова: \begin{gather*} x_1+x_2=0. \end{gather*}

Для зведеного квадратного рівняння \(x^2+px+q=0\) за теоремою Вієта сума коренів дорівнює другому коефіцієнту, узятому з протилежним знаком: \begin{gather*} x_1+x_2=-p. \end{gather*}

У рівнянні

зведімо подібні доданки:

Коефіцієнт:

\begin{gather*} p=(a-1)^2+6(a-1). \end{gather*}

Отже, має виконуватися умова:

\begin{gather*} (a-1)^2+6(a-1)=0;\\[7pt] (a-1)(a-1+6)=0;\\[7pt] (a-1)(a+5)=0. \end{gather*}

Отримуємо два значення: \(a=1\) та \(a=-5.\)

Перевірка існування коренів (дискримінант): числа є коренями рівняння, якщо дискримінант \(D\ge 0.\)

Оскільки за \(x_1+x_2=0\) рівняння набуває вигляду \(x^2+q=0\), то корені існують, якщо \(q\le 0.\)

Якщо \(a=1{:}\) \(q=a+2=1+2=3\gt 0.\) Рівняння \(x^2+3=0\) не має дійсних коренів, тобто \(a=1\) не підходить.

Якщо \(a=-5{:}\) \(q=a+2=-5+2=-3\lt 0.\) Рівняння \(x^2-3=0\) має корені \(\sqrt{3}\) та \(-\sqrt{3}.\) Тож \(a=-5\) підходить.

Оскільки умову задовольняє лише одне значення \(a=-5\), то сума значень дорівнює самому числу \(-5.\)

Відповідь: \(-5.\)

Пояснення

ТЕМА: Алгебра і початки аналізу. Квадратні рівняння.

Завдання скеровано на перевірку вміння розв'язувати квадратні рівняння.

Більший корінь \(2{,}5\) належить проміжку \((0; 3].\)

Відповідь: B.

Пояснення

ТЕМА: Лінійні і раціональні рівняння та їх системи.

Завдання скеровано на перевірку вміння розв’язувати лінійні й раціональні рівняння.

Розв'яжімо систему рівнянь методом підстановки:

\begin{gather*} \left\{\begin{array}{l} \frac x4=3y-1,\\ x-2y=1. \end{array}\right. \end{gather*}

Помножмо перше рівняння на \(4{:}\)

\begin{gather*} \left\{\begin{array}{l} x=12y-4,\\ x-2y=1. \end{array}\right. \end{gather*}

Підставмо \(x=12y-4\) в друге рівняння:

\begin{gather*} 12y-4-2y=1;\\[7pt] 10y=1+4;\\[7pt] 10y=5;\\[7pt] y=5:10;\\[7pt] y=0{,}5. \end{gather*}

Обчислімо \(x{:}\)

\begin{gather*} x=12\cdot 0{,}5-4=6-4=2. \end{gather*}

Отже, розв'язком системи є пара чисел \((2; 0{,}5){:}\)

\begin{gather*} x_0+y_0=2+0{,}5=2{,}5. \end{gather*}

Відповідь: B.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати квадратні рівняння, аналізувати та досліджувати рівняння, розв'язувати рівняння з параметром.

\begin{gather*} x^2-(2m-4)x+16=0;\\[7pt] x_1\gt x_2\ \text{на}\ 6. \end{gather*}

 

Знайдемо дискримінант рівняння:

 

 

 

Додатне значення \(m\), при якому рівняння має два різних кореня \(m\gt 6.\)

 

За теоремою Вієта і враховуючи умову завдання:

 

 

Підставмо значення \(x_2\) у друге рівняння:

\begin{gather*} (m-5+6)(m-5)=16;\\[7pt] (m+1)(m-5)=16;\\[7pt] m^2-5m+m-5-16=0;\\[7pt] m^2-4m-21=0. \end{gather*}

Корені рівняння:

\begin{gather*} \left\{\begin{array}{l} m_1=7,\\ m_2=-3\ne m\gt 6. \end{array}\right. \end{gather*}

Отже, додатне значення \(m=7.\)

 

Відповідь: \(7.\)

 

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати квадратні рівняння, зокрема з параметрами, а також аналізувати та досліджувати їхні властивості.

Для зведеного квадратного рівняння \(x^2+px+q=0\) за теоремою Вієта сума коренів \(x_1+x_2=-p\), а добуток \(x_1\cdot x_2=q.\)

У цьому завданні \(x_1+x_2=8\) та \(x_1\cdot x_2=4a-1.\)

Треба визначити \(x_1^2+x_2^2.\) Використаймо формулу квадрата суми:

\begin{gather*} (x_1+x_2)^2=x_1^2+2x_1x_2+x_2^2. \end{gather*}

Звідси:

\begin{gather*} x_1^2+x_2^2=(x_1+x_2)^2-2x_1x_2. \end{gather*}

За умовою сума квадратів дорівнює \(38{:}\)

\begin{gather*} 8^2-2(4a-1)=38;\\[7pt] 64-8a+2=38;\\[7pt] 66-8a=38;\\[7pt] -8a=38-66;\\[7pt] -8a=-28;\\[6pt] a=\frac{28}{8}=3{,}5. \end{gather*}

Перевірка існування коренів:

Щоб корені взагалі існували, дискримінант має бути \(D\ge 0.\)

Якщо \(a=3{,}5\), то

Оскільки \(D\gt 0\), корені існують.

Відповідь: \(3{,}5.\)

Пояснення

ТЕМА: Лінійні й раціональні рівняння та їх системи.

Завдання перевіряє вміння розв’язувати лінійні й раціональні рівняння.

ОДЗ:

\begin{gather*} x+y\ne 0;\\[7pt] x\ne -y. \end{gather*}

Спростімо перше рівняння, скориставшись властивістю пропорції:

\begin{gather*} \frac ab=\frac cd\Rightarrow a\cdot d=b\cdot c;\\[6pt] x+y=3\cdot (-2);\\[7pt] x+y=-6. \end{gather*}

Розв’яжімо методом додаванням отриману систему:

\begin{gather*} \left\{\begin{array}{l} x+y=-6,\\ 2x-y=12. \end{array}\right.\\[7pt] x+y+2x-y=-6+12;\\[7pt] 3x=6;\\[7pt] x=2. \end{gather*}

Підставмо \(x=2\) у перше рівняння:

\begin{gather*} 2+y=-6;\\[7pt] y=-8. \end{gather*}

\((2; -8)\) – розв'язок системи, задовільняє ОДЗ.

Обчислімо добуток

\begin{gather*} x_0\cdot y_0=2\cdot (-8)=-16. \end{gather*}

Відповідь: Д.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати квадратні рівняння, аналізувати та досліджувати рівняння, розв’язувати рівняння з параметром.

\(ax^2+bx+c=0\), де \(a\), \(b\), \(c\) – коефіцієнти квадратного рівняння.

\(D=b^2-4ac\) – дискримінант.

Якщо \(D\gt 0\), то

\begin{gather*} x_1=\frac{-b-\sqrt{D}}{2a};\\[6pt] x_2=\frac{-b+\sqrt{D}}{2a}. \end{gather*}

У заданому рівнянні \(2x^2-(4a+9)x+6a+9=0\) маємо коефіцієнти:

\begin{gather*} a_\text{коеф.}=2;\\[7pt] b_\text{коеф.}=-(4a+9);\\[7pt] c_\text{коеф.}=6a+9. \end{gather*}

Обчислімо дискримінат заданого рівняння:

\begin{gather*} D=(-(4a+9))^2-4\cdot 2\cdot (6a+9);\\[7pt] D=(16a^2+72a+81)-8(6a+9);\\[7pt] D=16a^2+72a+81-48a-72;\\[7pt] D=16a^2+24a+9;\\[7pt] 16a^2+24a+9=(4a+3)^2;\\[7pt] \sqrt{D}=|4a+3|. \end{gather*}

Тобто

За умовою задачі перший корінь належить проміжку \((-8; 0)\), а другий – проміжку \((1; 5).\)

\(x_1=1{,}5\) належить проміжку \((1; 5).\)

Отже, \(x_2=2a+3\) має належати проміжку \((-8; 0).\)

Складімо нерівність:

\begin{gather*} -8\lt 2a+3\lt 0;\\[7pt] -8-3\lt 2a\lt 0-3;\\[7pt] -11\lt 2a\lt -3;\\[6pt] \frac{-11}{2}\lt a\lt \frac{-3}{2};\\[6pt] -5{,}5\lt a\lt -1{,}5. \end{gather*}

Тобто \(a\in (-5{,}5; -1{,}5).\)

Цілі числа, які належать цьому проміжку: \(\{-5\), \(-4\), \(-3\), \(-2\}.\)

У відповіді запишімо їхню суму:

\begin{gather*} -5+(-4)+(-3)+(-2)=-14. \end{gather*}

Відповідь: \(-14.\)

Пояснення

ТЕМА: Лінійні та раціональні рівняння, їхні системи.

Завдання перевіряє вміння розв’язувати лінійні та раціональні рівняння.

Розв'яжімо систему рівнянь методом підстановки:

\begin{gather*} \left\{\begin{array}{l} \frac{x}{2y}=-3,\\ x+y=10. \end{array}\right. \end{gather*}

Помножмо обидві частини першого рівняння на \(2y\), щоб позбутися знаменника:

\begin{gather*} x=-3\cdot 2y;\\[7pt] x=-6y. \end{gather*}

Підставмо \(x=-6y\) у друге рівняння:

\begin{gather*} -6y+y=10;\\[7pt] -5y=10;\\[7pt] y=-2. \end{gather*}

Обчислімо \(x{:}\)

\begin{gather*} x=-6y=-6\cdot (-2)=12. \end{gather*}

Отже, розв'язком системи є пара чисел \((12; -2).\)

\(x_0=12.\)

Відповідь: Г.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати квадратні рівняння, аналізувати їхні властивості та досліджувати рівняння з параметрами.

\begin{gather*} x^2+(a-2)x+28-4a=0. \end{gather*}

Для зведеного квадратного рівняння \(x^2+px+q=0\) за теоремою Вієта сума коренів \(x_1+x_2=-p\), а добуток \(x_1\cdot x_2=q.\)

У цьому завданні \(x_1+x_2=-(a-2)\) та \(x_1\cdot x_2=28-4a.\)

За умовою:

\begin{gather*} x_1+x_2=x_1\cdot x_2+1;\\[7pt] -(a-2)=28-4a+1;\\[7pt] -a+2=29-4a;\\[7pt] -a+4a=29-2;\\[7pt] 3a=27;\\[7pt] a=27:3;\\[7pt] a=9. \end{gather*}

Перевірка існування коренів:

Щоб корені взагалі існували, дискримінант має бути \(D\ge 0.\)

\begin{gather*} D=(a-2)^2-4\cdot 1\cdot (28-4a). \end{gather*}

Якщо \(a=9\), то

Оскільки \(D\gt 0\), корені існують.

Відповідь: \(9.\)

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати квадратні рівняння, аналізувати та досліджувати рівняння, розв'язувати рівняння з параметром.

Розкриємо дужки та перенесемо всі доданки з \(x\) в один бік, а числа та параметри — в інший.

\begin{gather*} a^2x-a=x(a^2-a)-10;\\[7pt] a^2x-a=a^2x-ax-10;\\[7pt] a^2x-a^2x+ax=a-10;\\[7pt] ax=a-10;\\[7pt] a\ne 0;\\[6pt] x=\frac{a-10}{a}. \end{gather*}

 

 

 

За умовою корінь рівняння має бути від’ємним числом \((x\lt 0){:}\)

 

\begin{gather*} \frac{a-10}{a}\lt 0. \end{gather*}

 

Розв`яжемо нерівність методом інтервалів:

 

 

 

 

 

 

Отже, \(x\lt 0\) при \(a\in (0; 10).\)

 

 

 

Найбільше ціле число \(a\) з інтервалу \((0; 10)\) це \(9.\)

 

 

 

Відповідь: \(9.\)