Геометрія – Призма

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники.

Завдання перевіряє знання властивостей призми та вміння розв'язувати стереометричні задачі.

Площу бічної поверхні призми визначмо за формулою:

\begin{gather*} S_\text{біч}=P_\text{осн}\cdot H. \end{gather*}

В основі правильної чотирикутної призми лежить квадрат зі стороною \(\sqrt{a}\), тож його периметр:

\begin{gather*} P=4\sqrt{a}. \end{gather*}

За умовою задачі висота \(H=3\sqrt{a}.\)

Отже,

\begin{gather*} S_\text{біч}=4\sqrt{a}\cdot 3\sqrt{a}=12(\sqrt{a})^2=12a. \end{gather*}

Відповідь: A.

Пояснення

ТЕМА: Геометрія. Стереометрія. Прямі та площини в просторі. Многогранники.

Завдання перевіряє вміння розв’язувати стереометричні задачі, обчислювати об’єм призми.

Обчислімо довжину сторони квадрата – перерізу правильної чотирикутної призми, площа якої 64:

\begin{gather*} BD=BB_1=\sqrt{64}=8. \end{gather*}

Обчислімо висоту призми:

\begin{gather*} H=BB_1=8. \end{gather*}

В основі призми лежить квадрат \(ABCD\) з діагоналлю \(BD=8.\) Обчислімо його площу:

Підставмо обчислені значення площі основи та висоти у формулу для обчислення об'єму:

\begin{gather*} V=S_\text{осн}\cdot H=32\cdot 8=256. \end{gather*}

Відповідь: \(256.\)

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники.

Завдання перевіряє знання властивостей призми та вміння розв'язувати стереометричні задачі.

Площу бічної поверхні призми визначмо за формулою:

\begin{gather*} S_\text{біч}=P_\text{осн}\cdot H. \end{gather*}

В основі правильної чотирикутної призми лежить квадрат зі стороною \(a\), тож його периметр:

\begin{gather*} P=4a. \end{gather*}

 

У правильній призмі бічне ребро – її висота, отже \(H=b.\)

\begin{gather*} S_\text{біч}=4a\cdot b=4ab. \end{gather*}

Відповідь: Д.

Пояснення

ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Многогранники.

Завдання перевіряє вміння розв’язувати стереометричні задачі, обчислювати об’єм призми.

В основі прямокутного паралелепіпеда лежить прямокутник. Оскільки його діагоналі рівні, за умовою вони становлять \(12\) см, що вдвічі більше за одну зі сторін основи.

У прямокутному \(\Delta ABD\ (\angle A=90^\circ)\) за теоремою Піфагора:

Площа прямокутника \(ABCD\) (основи паралелепіпеда):

\begin{gather*} S_\text{осн}=AB\cdot AD=6\cdot 6\sqrt{3}=36\sqrt{3}. \end{gather*}

Діагональний переріз \(BB_1D_1D\) – прямокутник зі сторонами \(BD\) і \(DD_1\) де (\(DD_1=H\) – висота паралелепіпеда).

За умовою:

\begin{gather*} S_{BB_1D_1D}=72\sqrt{3};\\[7pt] S_{BB_1D_1D}=BD\cdot H;\\[7pt] 12\cdot H=72\sqrt{3};\\[7pt] H=72\sqrt{3}:12=6\sqrt{3}. \end{gather*}

Об'єм прямокутного паралелепіпеда обчислімо за формулою:

Відповідь: \(648.\)

Пояснення

ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Многогранники.

Завдання перевіряє вміння розв’язувати стереометричні задачі, обчислювати об’єм призми.

Обчислімо площу ромба за формулою:

Порівняймо \(20\) та \(8\sqrt{3}.\)

\begin{gather*} 8\sqrt{3}=\sqrt{64\cdot 3}=\sqrt{192};\\[7pt] 20=\sqrt{400}. \end{gather*}

Отже, більша діагональ основи дорівнює \(20.\)

Більша діагональ \(A_1C\) призми утворює прямокутний трикутник \(CAA_1\ (\angle A=90^\circ)\) із більшою діагоналлю основи \((AC=20)\) і висотою призми \((H=AA_1).\)

Оскільки кут нахилу \(30^\circ\ (\angle ACA_1=30^\circ)\), то

Обчислімо об’єм призми:

Відповідь: \(1600.\)

 

 

 

Пояснення

ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Многогранники.

Завдання перевіряє вміння розв’язувати стереометричні задачі, обчислювати об’єм призми.

 

Обчислімо меншу діагональ \((BD)\) основи.

Діагональний переріз прямої призми – прямокутник, сторонами якого є діагональ основи та висота призми \((H=DD_1=7\sqrt{3}).\) Оскільки переріз менший, він проходить через меншу діагональ ромба \((BD).\)

Формула для обчислення площі перерізу:

\begin{gather*} S_{BB_1D_1D}=BD\cdot DD_1. \end{gather*}

Звідси обчислімо меншу діагональ:

\begin{gather*} BD=\frac{ S_{BB_1D_1D}}{DD_1}=\frac{140\sqrt{3}}{7\sqrt{3}}=20. \end{gather*}

У ромбі з гострим кутом \(60^\circ\) менша діагональ ділить його на два рівносторонні трикутники. Отже, сторона ромба дорівнює меншій діагоналі \(AD=BD=20\) см (оскільки \(\Delta ABD\) рівносторонній).

Обчислімо площу основи \((S_\text{осн}){:}\)

Площу ромба обчислімо за формулою через сторону \((a)\) та синус кута між ними:

Об'єм призми обчислімо за формулою:

Відповідь: \(4200.\)

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники.

Завдання перевіряє знання властивостей призми та вміння розв’язувати стереометричні задачі.

Площу бічної поверхні призми визначмо за формулою: \begin{gather*} S_\text{біч}=P_\text{осн}\cdot H. \end{gather*}

В основі правильної чотирикутної призми лежить квадрат зі стороною \(a\), тож його периметр: \begin{gather*} P=4a. \end{gather*}

За умовою задачі висота \(H=2a.\)

Отже,

\begin{gather*} S_\text{біч}=4a\cdot 2a=8a^2. \end{gather*}

Відповідь: Г.

Пояснення

ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Многогранники.

Завдання перевіряє вміння розв’язувати стереометричні задачі, обчислювати об’єм призми.

 

Діагональний переріз прямої призми — це прямокутник. Його сторони — це діагональ ромба \((d)\) та висота призми \((H).\) Периметр цього прямокутника розраховується за формулою:

\begin{gather*} P_\text{пер}=2(d+H). \end{gather*}

 

 

 

Підставмо відомі значення:

\begin{gather*} 58=2(d+5);\\[7pt] 29=d+5;\\[7pt] d_1=24. \end{gather*}

 

 

Діагоналі ромба перетинаються під кутом \(90^\circ\) і діляться навпіл. Розгляньмо прямокутний трикутник \(\Delta COD\), де: \(CD=20\) (сторона ромба), \(OD=24:2 = 12\) (половина відомої діагоналі \((d_1)\) ромба).

 

 

 

За теоремою Піфагора:

 

\begin{gather*} CD^2=OD^2+OC^2;\\[7pt] 20^2=12^2+OC^2;\\[7pt] 400=144+OC^2;\\[7pt] OC^2=400-144=256;\\[7pt] OC=\sqrt{256}=16. \end{gather*}

 

Отже друга діагональ ромба

 

\begin{gather*} d_2=AC=2\cdot OC=2\cdot 16=32. \end{gather*}

 

Формула об’єму призми:

 

\begin{gather*} V=S_\text{осн}\cdot H. \end{gather*}

 

Площа основи (ромба):

 

 

 

 

 

 

Відповідь: \(1920.\)

 

 

 

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники.

Завдання перевіряє вміння розв’язувати стереометричні задачі, знання властивостей призми.

Об'єм призми визначаємо за формулою:

\begin{gather*} V=S_\text{осн}\cdot H. \end{gather*}

В основі правильної чотирикутної призми лежить квадрат зі стороною \(a\), тож його площа:

\begin{gather*} S_\text{осн}=a^2. \end{gather*}

За умовою задачі висота \(H=3a.\)

Отже,

\begin{gather*} V=a^2\cdot 3a=3a^3. \end{gather*}

Відповідь: Б.

Пояснення

ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Многогранники.

Завдання перевіряє вміння розв’язувати стереометричні задачі, обчислювати площу бічної поверхні призми.

 

Діагоналі ромба перетинаються під прямим кутом і діляться навпіл. Розгляньмо прямокутний трикутник \(\Delta COD\), катетами якого є половини діагоналей:

\begin{gather*} CO=3\sqrt{3};\\[7pt] DO=3. \end{gather*}

 

 

 

За теоремою Піфагора обчислімо гіпотенузу (сторону ромба):

 

 

 

 

 

Більша діагональ \(A_1C\) призми утворює прямокутний трикутник \(CAA_1\) \((\angle A=90^\circ)\) з більшою діагоналлю основи \((AC=6\sqrt{3})\) і висотою призми.

 

 

 

Оскільки кут нахилу \(30^\circ\ (\angle ACA_1=30^\circ)\), то

\begin{gather*} H=AC\cdot \mathrm{tg}\ 30^\circ=6\sqrt{3}\cdot \frac{1}{\sqrt{3}}=6. \end{gather*}

 

 

Формула бічної поверхні призми:

 

\begin{gather*} S_\text{біч}=P_\text{осн}\cdot H;\\[7pt] P_\text{осн}=4\cdot CD=4\cdot 6=24;\\[7pt] S_\text{біч}=24\cdot 6=144. \end{gather*}

 

Відповідь: \(144.\)

 

 

 

Пояснення

ТЕМА: Геометрія. Стереометрія. Прямі та площини в просторі. Многогранники.

Завдання перевіряє вміння розв’язувати стереометричні задачі, обчислювати об’єм призми.

 

У паралелограмі менша діагональ лежить навпроти гострого кута. Використаймо теорему косинусів:

 

Менший діагональний переріз прямої призми – це прямокутник зі сторонами \(BB_1D_1D.\) Сторона \(BD=13\) см, а висота \(DD_1=H.\) Його площа за умовою дорівнює \(260\) см\(^2{:}\)

\begin{gather*} S_{BB_1D_1D}=BD\cdot DD_1;\\[7pt] 260=13\cdot H;\\[6pt] H=\frac{260}{13}=20\ \text{см}. \end{gather*}

 

Обчислімо площу основи призми (паралелограма \(ABCD\)) за формулою \(S=ab\sin \gamma{:}\)

 

 

Обчислімо об’єм призми:

\begin{gather*} V=S_\text{осн}\cdot H;\\[7pt] V=60\sqrt{3}\cdot 20=1200\sqrt{3}\ \text{см}^3. \end{gather*}

За умовою треба обчислити \(\frac{V}{\sqrt{3}}{:}\)

\begin{gather*} \frac{1200\sqrt{3}}{\sqrt{3}}=1200\ \text{см}^3. \end{gather*}

Відповідь: \(1200.\)

 

Пояснення

ТЕМА: Геометрія. Стереометрія. Прямі та площини в просторі. Многогранники.

Завдання перевіряє вміння розв’язувати стереометричні задачі, обчислювати площу діагонального перерізу призми.

Основою призми є паралелограм зі сторонами \(AB = 8\) і \(AD = 15\), \(\angle A = 60^\circ.\)

Діагональний переріз прямої призми – прямокутник, сторонами якого є висота призми та діагональ основи.

Невідомий діагональний переріз меншої площі буде побудовано на меншій діагоналі основи. У паралелограмі менша діагональ завжди лежить навпроти гострого кута. Отже, треба визначити довжину діагоналі \(BD.\)

Розгляньмо трикутник \(ABD.\) За теоремою косинусів:

Меншим діагональним перерізом є прямокутник \(DBB_1D_1\) зі сторонами \(BD = 13\) см і висотою \(BB_1 = 20\) см.

Обчислімо його площу \(S{:}\)

Відповідь: \(260.\)

Пояснення

ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Многогранники.

Завдання перевіряє вміння розв’язувати стереометричні задачі, обчислювати об’єм призми.

1. Визначмо більшу діагональ \((AC)\) основи .

Діагональний переріз прямої призми – це прямокутник, сторонами якого є діагональ основи та висота призми \((H=AA_1=8\sqrt{3}).\) Оскільки переріз більший, він проходить через більшу діагональ ромба \((AC).\)

Формула площі перерізу:

\begin{gather*} S_{AA_1C_1C}=AC\cdot AA_1. \end{gather*}

Звідси обчислімо більшу діагональ:

\begin{gather*} AC=\frac{S_{AA_1C_1C}}{AA_1}=\frac{240\sqrt{3}}{8\sqrt{3}}=30. \end{gather*}

2. Визначмо меншу діагональ \((BD)\) ромба .

У ромбі з гострим кутом \(60^\circ\) діагоналі розбивають його на чотири прямокутні трикутники, або менша діагональ ділить ромб на два рівносторонні трикутники. Сторона ромба дорівнює меншій діагоналі \(CD=BD\) (бо трикутник \(\Delta BCD\) рівносторонній). Визначмо сторону \(CD\) ромба:

3. Площа повної поверхні:

Відповідь: \(960.\)

Пояснення

ТЕМА: Тіла обертання. Многогранники.

Завдання скеровано на перевірку знання властивостей призми й циліндра, формул для обчислення площі поверхні циліндра й об’єму призми.

Пряма призма, в основі – ромб. \(AC=16\) см, \(BD=12\) см.

Радіус основи ціліндра \(OK=AD\), \(S_\text{бічн.}=400\pi\) см\(^2.\)

У ромбі діагоналі \(AC\ \perp\ BP\) й діляться точкою перетину \(P\) навпіл: \begin{gather*} AP=PC=\frac 12AC=8\ \text{см},\\[6pt] BP=PD=\frac 12BD=6\ \text{см}. \end{gather*}

У \(\Delta APD\ (\angle P=90^\circ)\) за теоремою Піфагора:

Площа бічної поверхні циліндра \(S_\text{бічн.}=2\pi RH\), де \(R=OK=AD=10\) см, \(H=OO_1=AA_1\) (за умовою задачі).

\begin{gather*} 2\pi\cdot 10\cdot H=400\pi,\\[7pt] H=20\ (\text{см}). \end{gather*}

Об'єм призми визначмо за формулою: $$ V=S_\text{осн.}\cdot H, $$ де \begin{gather*} S_\text{осн.}=S_{ABCD}=96\ \text{см}^2,\\[7pt] H=AA_1=20\ \text{см},\\[7pt] V=96\cdot 20=1920\ (\text{см}^3). \end{gather*}

Відповідь: \(1920.\)

Пояснення

ТЕМА: Геометрія. Стереометрія. Прямі та площини ву просторі. Многогранники.

Завдання перевіряє вміння розв’язувати стереометричні задачі, задачі на обчислення об’єму призми.

 

1. Визначмо більшу діагональ основи \((AC).\)

 

Діагональний переріз прямої призми – це прямокутник, сторонами якого є діагональ основи та висота призми \((H=AA_1=8\sqrt{3}).\) Оскільки переріз більший, він проходить через більшу діагональ ромба \((AC).\)

Формула площі перерізу: \(S_{AA_1C_1C}=AC\cdot AA_1.\)

Звідси визначмо більшу діагональ:

\begin{gather*} AC=\frac{S_{AA_1C_1C}}{AA_1}=\frac{240\sqrt{3}}{8\sqrt{3}}=30. \end{gather*}

 

2. Визначмо меншу діагональ ромба \((BD).\)

 

У ромбі з гострим кутом \(60^\circ\) діагоналі розбивають його на чотири прямокутні трикутники, або менша діагональ ділить ромб на два рівносторонні трикутники. Сторона ромба дорівнює меншій діагоналі \(CD=BD\) (бо трикутник \(\Delta BCD\) рівносторонній). Визначмо сторону \(CD\) ромба:

 

 

 

3. Обчислімо площу основи \((S_\text{осн}).\)

 

Обчислімо площу ромба через його діагоналі: \begin{gather*} S=\frac 12d_1d_2, \end{gather*} \(d_1\), \(d_2\) – діагоналі ромба.

 

 

4. Обчислімо об'єм \((V)\) призми за формулою:

 

 

Відповідь: \(3600.\)

 

Пояснення

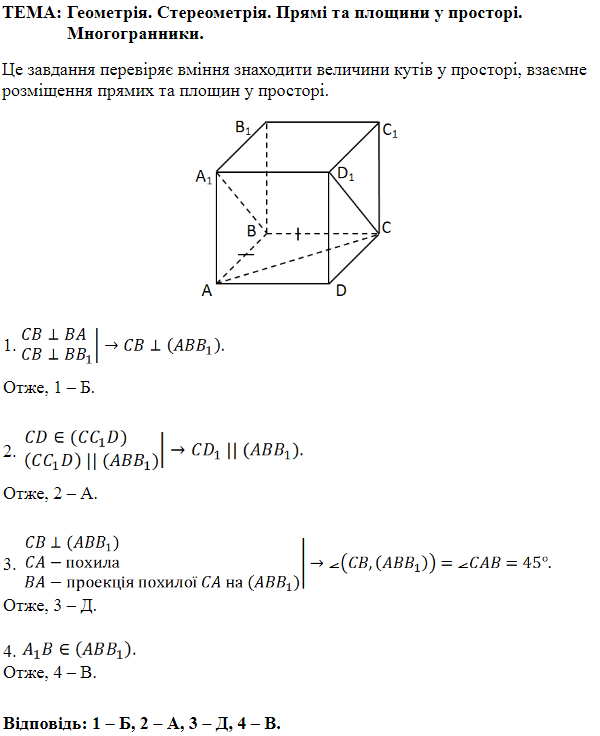
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Многогранники.

Завдання скеровано на перевірку знань ознаки паралельності прямої та площини, властивостей призми.

За ознакою паралельності прямої і площини, якщо пряма \(AB\), що не лежить у площині \((CDD_1)\), паралельна прямій \(CD\), яка лежить в цій площині, то \(AB\ || (CDD_1).\)

Аналогічно, \(AB\) не лежить у площині \((A_1B_1C_1)\), але паралельна прямій \(A_1B_1\), яка лежить в цій площині, то \(AB\ ||\ (A_1B_1C_1).\)

Отже, таких площин лише дві.

Відповідь: В.

Пояснення

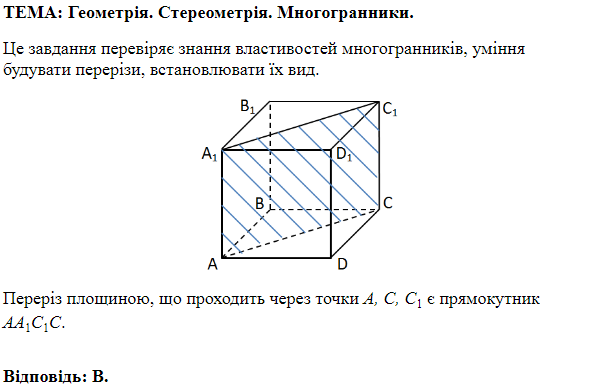
ТЕМА: Геометрія. Стереометрія. Многогранники, тіла обертання.

Завдання скеровано на перевірку знань властивостей призми та циліндра, вміння розв’язувати задачі на обчислення об’ємів і площ поверхонь геометричних тіл.

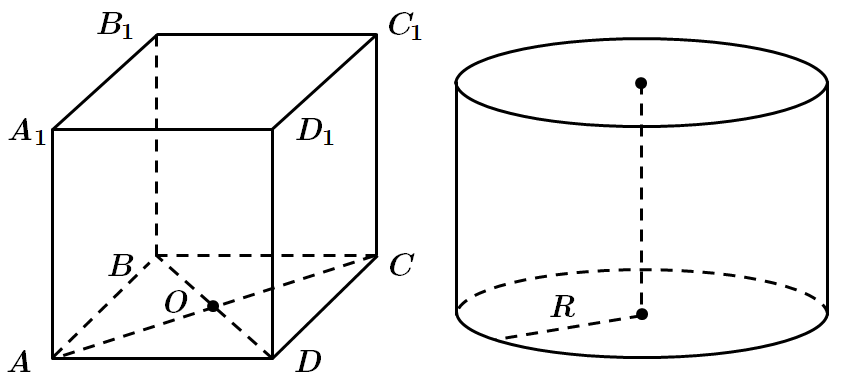
1. В основі призми – ромб з діагоналями \(12\) см і \(16\) см.

\(AO=OC=8\) см, \(BO=OD=6\) см. \(AC\ \perp\ BD.\) \(\Delta AOD\) – прямокутний. За теоремою Піфагора

2. Радіус основи циліндра \(R=AD=10\) см.

3. Площа поверхні циліндра

\begin{gather*} S_\text{б}=2\mathbf{\pi}RH,\\[7pt] 2\mathbf{\pi}\cdot 10\cdot H=400\mathbf{\pi},\\[7pt] H=20\ \textit{см}. \end{gather*}

4. Висота призми дорівнює висоті циліндра \(H=20\) см.

5. Об'єм призми

\begin{gather*} V=S_\text{осн}\cdot H. \end{gather*}

Площу ромбу можна знайти за формулою:

\begin{gather*} S_\text{осн}=\frac 12d_1d_2,\\[6pt] S_\text{осн}=\frac 12\cdot 12\cdot 16=96\ \textit{см}^2,\\[6pt] V=96\cdot 20=1920\ \textit{см}^3. \end{gather*}

Відповідь: 1920.

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники.

Завдання скеровано на перевірку знання про многогранники та їхні елементи, ознаки паралельності прямої та площини.

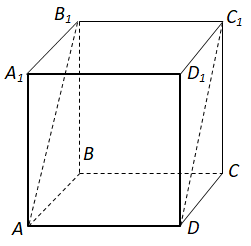
Протилежні грані куба – паралельні площини. \(C_1D\subset (DD_1C_1)\) \((AA_1B)\ ||\ (DD_1C_1).\) Отже, \(C_1D\ ||\ (AA_1B_1).\)

Відповідь: Б.

Пояснення

ТЕМА: Геометрія. Стереометрія. Планіметрія. Многогранники. Трикутники. Чотирикутники.

Завдання скеровано на перевірку вміння розв’язувати задачі на обчислення

\(A(4; \sqrt{10}; 3),\ M(-2; 0; 1).\) Призма правильна, тому \(ABCD\) – квадрат.

 

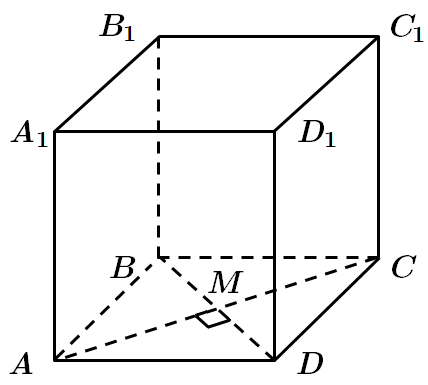
Діагоналі квадрата перпендикулярні. У \(\Delta AMD (\angle M=90^\circ)\) \(AM=MD=\sqrt{50}.\) За теоремою Піфагора

Висота \(AA_1=3AB=30.\) $$V=S_\text{осн}H,$$ де \(S_\text{осн}\) – площа квадрата, \(H\) – висота.

\begin{gather*} S_\text{осн}=AD^2=100.\\[7pt] V=100\cdot 30=3000. \end{gather*}

Відповідь: 3000.

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники.

Завдання скеровано на перевірку знань про многогранники та їхні елементи.

Бічною гранню прямої призми є прямокутник.

Отже, правильна відповідь – Б.

Відповідь: Б.

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники.

Завдання перевіряє вміння розв’язувати стереометричні задачі, задачі на обчислення об’єму призми, побудови перерізів.

\(ABCD\) – ромб, \(AB=20,\) \(P_{AA_1C_1C}=58,\) \(AA_1=5.\) \(AA_1=CC_1=5,\) то \(A_1C_1=AC=(58-2\cdot 5):2=24.\)

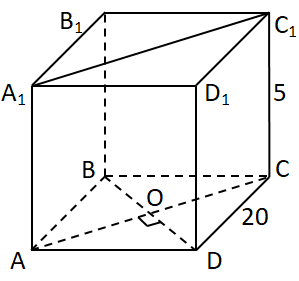
За властивістю ромба \(AC\perp BD,\ AO=OC,\ BO=OD.\) Отже, у \(\Delta COD\ (\angle O=90^\circ)\) \(CD=20,\ OC=12\) за теоремою Піфагора

\begin{gather*} OD^2+OC^2=CD^2,\\[7pt] OD=\sqrt{20^2-12^2}=\sqrt{400-144}=\sqrt{256}=16.\\[7pt] BD=2\cdot OD=32. \end{gather*}

Площу ромбу можна знайти за формулою

\begin{gather*} S=\frac 12d_1d_2\ \ S=\frac 12\cdot 32\cdot 24=16\cdot 24,\\[7pt] V=S_\text{осн}\cdot H,\ \text{де}\ S_\text{осн}=16\cdot 24,\ H=AA_1=5.\\[7pt] \end{gather*}

Отже,

$$ V=16\cdot 24\cdot 5=16\cdot 120=1920. $$

Відповідь: 1920.

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники.

Завдання перевіряє знання про многогранники та їхні елементи.

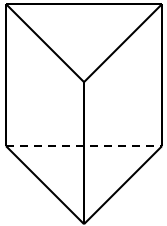
У трикутної призми \(3\) бічні грані та \(2\) грані основ.

Отже, кількість граней призми – \(5.\)

Відповідь: B.

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники.

Перевіряє знання про многогранники та їхні елементи, основні види многогранників: призму, паралелепіпед, піраміду.

На рисунку зображена розгортка чотирикутної піраміди. Отже, правильна відповідь – Б.

Відповідь: Б.

Пояснення

ТЕМА: Геометрія Стереометрія. Прямі та площини у просторі. Многогранники.

Завдання перевіряє вміння розв’язувати стереометричні задачі, задачі на обчислення площі поверхні призми.

\(BD=6\ \ AC=8\).

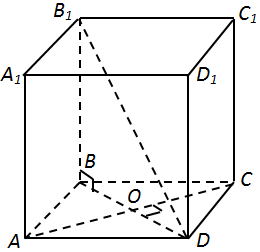
1. Діагональ призми – це похила на площину основи. Отже, меншій похилій відповідає менша проекція. \(BD\) – менша проекція, отже, \(B_1D\) – менша похила. \(B_1D=10.\)

2. \(\Delta BB_1D\ \ (\angle B=90^\circ)\ BB_1^2+BD^2=B_1D^2\) за теоремою Піфагора $$ BB_1=\sqrt{100-36}=8 $$

3. Діагоналі ромба перетинаються під кутом \(90^\circ.\) \begin{gather*} AC\cap BD=0\\[7pt] \Delta COD\ (\angle O=90^\circ)\\[6pt] OC=\frac 12 AC=4,\ \ OD=\frac 12 BD=3 \end{gather*} за теоремою Піфагора \begin{gather*} CD=\sqrt{CO^2+OD^2}=\sqrt{3^2+4^2}=5. . \end{gather*}

4. За формулою \(S_\text{бічної}=P_\text{основи}\cdot H\) \begin{gather*} P_\text{основи}=4\cdot CD=20,\ \ H=BB_1=8\\[7pt] S_\text{бічної}=20\cdot 8=160. \end{gather*}

Відповідь: 160.

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники. Прямі та площини у просторі.

Завдання скеровано на перевірку знання поняття відстані від точки до площини, між паралельними площинами.

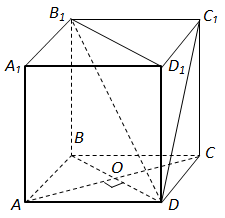
1. Довжина діагоналі куба дорівнює \begin{gather*} B_1D^2=AD^2+DC^2+DD_1^2=\\[7pt] =2^2+2^2+2^2=12\\[7pt] B_1D=\sqrt{12}=\sqrt{4\cdot 3}=2\sqrt{3} \end{gather*} Отже, 1 - В.

2. Бічне ребро \(AA_1\perp (A_1B_1C_1)\), а отже, й прямій \(A_1C_1\), яка міститься в цій площині $$ AA_1=\mathbf{\rho}(A, A_1C_1)=2 $$ отже, 2 - A.

3. Осьовий переріз куба \(BB_1D_1D\) перпендикулярний площині основи. \(AO\perp BD\) за властивістю квадрата. Отже, \begin{gather*} \mathbf{\rho}(A,\ (BB_1D_1))=AO\\[7pt] AC=2\sqrt{2},\\[7pt] AO=\frac 12 AC=\frac 12\cdot 2\sqrt{2}=\sqrt{2}. \end{gather*} отже, 3 - Д

Відповідь: 1В, 2А, 3Д.

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники. Прямі та площини у просторі.

Завдання скеровано на перевірку знання поняття відстані від точки до площини, між паралельними площинами.

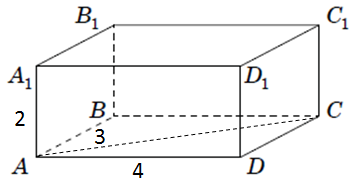
Усі грані цього прямокутного паралепіпеда – прямокутники.

1. \(CB\perp (AA_1B_1)\) – відстань від т.\(C\) до \((AA_1B_1),\ CB=4\), отже, 1 - B.

2. \(CC_1\perp (ABC),\ AC\subset\ (ABC)\rightarrow\) відстань від т.\(A\) до \(CC_1\) – це відрізок \(AC.\)
\(AC^2=AD^2+DC^2,\ AC=\sqrt{3^2+4^2}=5\). Oтже, 2 - Г.

3. \((ABC)||(A_1B_1C_1)\). Отже, відстань між ними – це довжина бічного ребра. \(AA_1=2\). Отже, 3 – A.

Відповідь: 1B, 2Г, 3A.

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники.

Завдання скеровано на перевірку знання про многогранники та їх основні елементи, вміння розв’язування задач, зокрема практичного змісту.

Якщо радіус кульки 6 см, то діаметр – 12 см.

Для того, щоб кульки помістилися у шухлядці, її висота може бути 13 см.

Відповідь: Г.

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники. Тіла обертання.

Завдання скеровано на перевірку вміння розв’язувати задачі, зокрема практичного змісту на обчислення площ поверхонь геометричних тіл.

\(AB=10\ \text{см},\ OK=1\ \text{см}\).

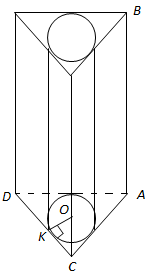
Бічні грані правильної трикутної призми виготовлені з паперу.

Площу паперу, витраченого на виготовлення коробки, визначимо за формулою площі бічної поверхні призми.

Радіус основи вписаного циліндра - це радіус кола, вписаного в правильний трикутник, \(OK=r=1\ \text{см}\).

Сторону трикутника знайдемо за формулою:

Відповідь, найближча до точної, – \(105\ \text{см}^2\).

Відповідь: B.

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники.

Завдання скеровано на перевірку знання про многогранники та їх основні елементи.

\begin{gather*} AA_1=BB_1=CC_1=DD_1\\[7pt] AB=CD=C_1D_1=A_1B_1\\[7pt] AD=BC=B_1C_1=A_1D_1. \end{gather*} Сума усіх ребер дорівнює $$ 4(AA_1+AB+AD)=4\cdot 60=240\ (\text{см}) $$

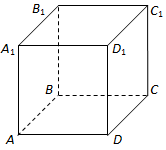
Відповідь: Б.

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники.

Завдання перевіряє знання формул для обчислення площ поверхонь призми, площі трикутника.

\(\Delta ABC\) – рівнобедрений. \(AB=AC=13\) см, \(BC=10\) см.

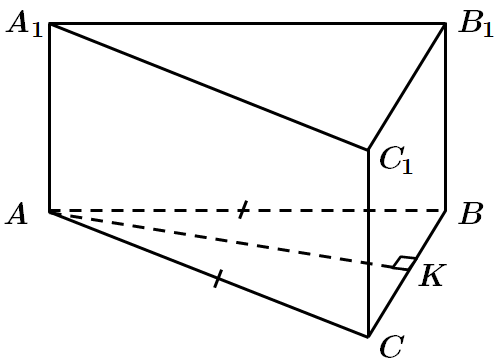
Бічні грані – прямокутники. Найбільша за площею бічна грань \(AA_1C_1C\) або \(A_1B_1BA.\)

\begin{gather*} S_{AA_1C_1C}=260\ \text{см}^2=AC\cdot CC_1,\\[7pt] CC_1=260:13=20\ \text{см}. \end{gather*}

У \(\Delta ABC\ AK\perp BC\) – висота та медіана. \(KC=5\) см.

У \(\Delta AKC\ (\angle K=90^\circ)\) за теоремою Піфагора

\begin{gather*} AC^2=AK^2+KC^2,\\[7pt] AK=\sqrt{13^2-5^2}=\sqrt{8\cdot 18}=\sqrt{4\cdot 36}=2\cdot 6=12\ \text{см}.\\[6pt] S_{ABC}=\frac 12BC\cdot AK=\frac 12\cdot 10\cdot 12=60\ \text{см}^2.\\[6pt] S_\text{бічна}=P_\text{основи}\cdot H,\ \ \text{де}\ \ P_\text{основи}=13+13+10=36\ \text{см}.\\[7pt] H=CC_1=20\ \text{см}.\\[7pt] S_\text{бічна}=36\cdot 20=720\ \text{см}^2.\\[7pt] S_\text{поверні}=S_\text{бічна}+2S_\text{основи}=720+2\cdot 60=720+120=840\ \text{см}^2. \end{gather*}

Відповідь: Г.

Пояснення

ТЕМА: Геометрія. Планіметрія. Стереометрія. Трикутники. Многогранники.

Завдання перевіряє знання про призму та її елементи, вміння знаходити площу трикутника.

\(ACDE\) – прямокутник, \(P=38\) см, \(AE=CD=11\) см.

$$AC=DE=(38-11\cdot 2):2=8\ \textit{см}.$$

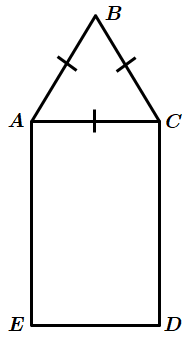
Площа основи призми – площа \(\Delta ABC (AB=BC=AC).\)

За формулою $$ S=\frac{a^2\sqrt{3}}{4}, $$ де \(a\) – довжина сторони, знаходимо площу $$ S=\frac{8^2\sqrt{3}}{4}=16\sqrt{3}\ \textit{см}^2. $$

Відповідь: A.

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники.

Завдання перевіряє знання про многогранники та їхні елементи.

Довжина всіх ребер куба \(72\) см.

Усього в куба \(12\) ребер, тому довжина ребра дорівнює
\(72 : 12 = 6\) см.

Відповідь: A.

Пояснення

ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі.

Завдання перевіряє вміння застосовувати означення та властивості паралельних прямих і площин.

1. Точка \(C_1\) симетрична точці \(A_1\) відносно площини \((BB_1D_1).\) Отже, 1 – Д.

2. \(A_1D_1\in (A_1B_1C_1)\), \(A_1D_1\ ||\ AD\), звідси \(AD\ ||\ (A_1B_1C_1).\) Отже, 2 – B.

3. \((BB_1C_1)\cap (DD_1C_1)=CC_1.\) Отже, 3 – Б.

Відповідь: 1 – Д, 2 – B, 3 – Б.

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники.

Завдання перевіряє знання властивостей призми.

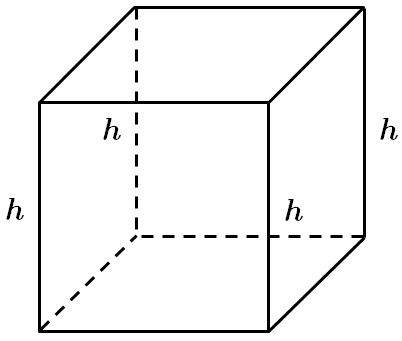
У прямокутному паралелепіпеді бічні ребра є висотами. Отже, \begin{gather*} 4h=120,\\[7pt] h=120:4,\\[7pt] h=30\ \text{см}. \end{gather*}

Відповідь: Б.

Пояснення

ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі.

Це завдання перевіряє знання ознак паралельності прямої та площини, аксіом стереометрії.

1. Точки \(B, D\in (ABC)\rightarrow BD\in (ABC).\) Отже, 1 – Б.

Відповідь: 1 – Б, 2 – A, 3 – Г.

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники.

Це завдання перевіряє вміння застосовувати властивості многогранників.

Прямою трикутною призмою є призма, основою якої є трикутник, а бічні ребра перпендикулярні до площини основи. Це означає, що всі бічні грані - прямокутники.

Відповідь: Г.

Пояснення

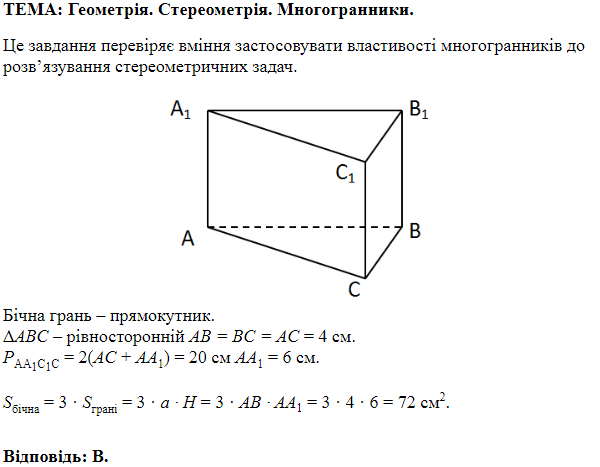
ТЕМА: Геометрія. Стереометрія. Многогранники, тіла і поверхні обертання. Тіла і поверхні обертання та їх елементи, основні види тіл і поверхонь обертання: циліндр, конус, зрізаний конус, куля, сфера.

Це завдання перевіряє вміння застосовувати означення та властивості призми, знання формули площі бічної поверхні призми.

\(ABCA_1B_1C_1\) – правильна призма. \(\Delta ABC\) – рівносторонній.

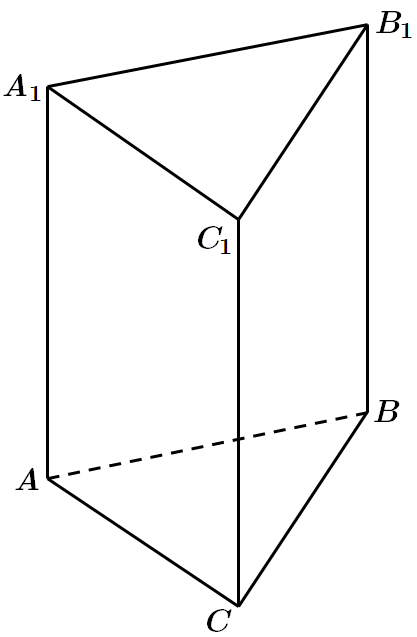
Відповідь: B.

Пояснення

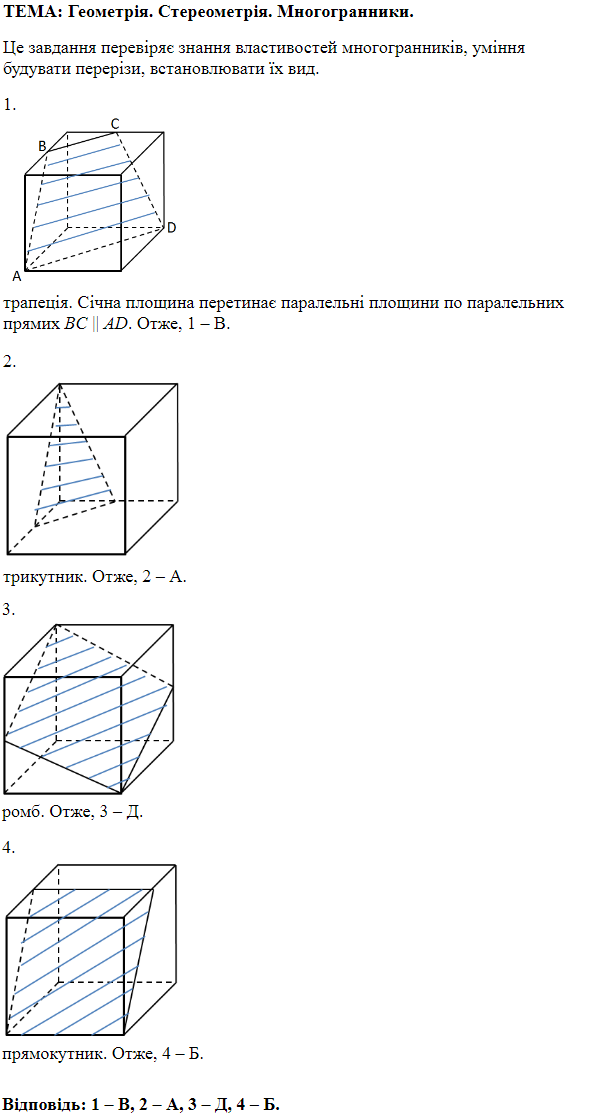
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Многогранники.

Це завдання перевіряє знання про взаємне розміщення прямих у просторі, площин у просторі, многогранників та їхніх елементів.

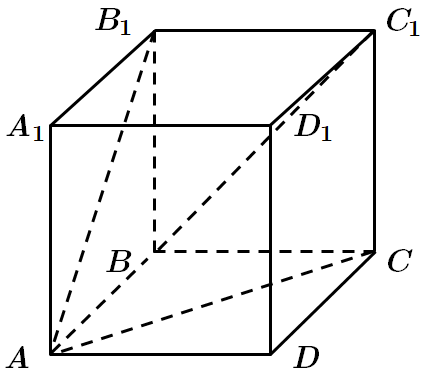
1. \(AC\cup CC_1\), \(AC\ \perp\ CC_1\),

\(\left.\begin{array}{l} CC_1\ \perp\ (ABC),\\ AC \in (ABC), \end{array}\right| \rightarrow CC_1\ \perp\ AC.\)
Отже, 1 – B.

2. Прямі \(AB_1\) та \(CD_1\) мимобіжні, не лежать в одній площині та не перетинаються.
Отже, 2 – Б.

3. \(\Delta ACD_1\) – рівносторонній, так як \(AC=CD_1=AD_1\) (діагоналі рівних квадратів).
\(\angle(AC\), \(CD_1)=\angle ACD_1=60^\circ.\)
Отже, 3 – Д.

4. \(AB_1\ ||\ C_1D\) не перетинаються та лежать в одній площині \((AB_1C_1).\)
Отже, 4 – A.

Відповідь: 1 – B, 2 – Б, 3 – Д, 4 – A.

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники.

Це завдання перевіряє вміння застосовувати означення та властивості прямокутного паралелепіпеда до розв'язування стереометричних задач і задач практичного змісту.

Площа плівки, якою обгорнута коробка – це площа поверхні прямокутного паралелепіпеда.

Основа паралелепіпеда – прямокутник зі сторонами \(30\) мм та \(75\) мм. Висота паралелепіпеда – \(10\) см.

\(S_\text{пп}=S_\text{бп}+2S_\text{осн}.\)

\(S_\text{бп}=P_\text{осн}\cdot H=(3\cdot 7\mathord{,}5)\cdot 2\cdot 10=210\) см\(^2.\)

\(30\ \textit{мм}=3\ \textit{см}\), \(75\ \textit{мм}=7\mathord{,}5\ \textit{см}.\) \(S_\text{осн}=3\cdot 7\mathord{,}5=22\mathord{,}5\ \textit{см}^2.\)

\(S_\text{пп}=210+2\cdot 22\mathord{,}5=210+45=255\ \textit{см}^2.\)

Відповідь: Б.

Пояснення

ТЕМА: Стереометрія. Многограники.

Це завдання перевіряє вміння розв'язувати задачі на обчислення об'ємів геометричних тіл, знання формул для обчислення площ трикутників.

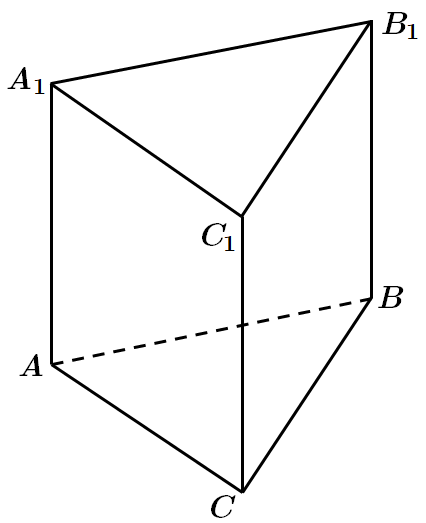
Дана трикутна призма \(ABCA_1B_1C_1\).

Усі бічні грані – квадрати, тому основа призми – рівносторонній трикутник. Площу рівностороннього трикутника можна знайти за формулою $$ S_{\Delta}=\frac{a^2\sqrt{3}}{4}, $$ де \(a\) – сторона трикутника.

За умовою $$ S_{\Delta}=9\sqrt{3}\ \textit{см}^2. $$ Звідси, \(a^2\sqrt{3}=36\sqrt{3}\), \(a^2=36\), \(a=6\) см.

\(AA_1C_1C\) – квадрат, тому \(AA_1=6\) см.

Об'єм призми

Відповідь: A.

Пояснення

ТЕМА: Стереометрія. Многогранники.

Це завдання перевіряє вміння розв'язувати задачі на обчислення площ поверхонь, встановлювати за розгорткою поверхні вид геометричного тіла.

На рисунку зображена розгортка правильної призми, тому основа – правильний трикутник. \(P_\text{осн}=12\) см, тому сторона основи \(4\) см.

Бічне ребро позначимо через \(H.\) Периметр розгортки складається з

\begin{gather*} 6\cdot H+4\cdot 4=52,\\[7pt] 6H=36,\\[7pt] H=6\ \textit{см}. \end{gather*}

За формулою $$ S_\text{біч.пов.}=P_\text{осн}\cdot H $$ знаходимо $$ S_\text{біч.пов.}=12\cdot 6 =72\ \textit{см}^2. $$

Відповідь: Г.

Пояснення

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники.

Це завдання перевіряє вміння застосовувати означення та властивості основних видів многогранників до розв'язування стереометричних задач; знання формул для обчислення площ поверхонь.

Данo куб, тому грань – квадрат, площею \(12\) см\(^2.\) Ребро куба \(\sqrt{12}=2\sqrt{3}\) см.

Діагональ куба знаходимо за формулою \(d=a\sqrt{3}\), де \(a\) – ребро куба.

Отже, \(d=2\sqrt{3}\cdot \sqrt{3}=2\cdot 3=6\) см.

Відповідь: A.

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники.

Це завдання перевіряє знання формули для обчислення площі поверхні призми, уміння встановлювати за розгорткою поверхні вид геометричного тіла.

Фрагмент розгортки правильної чотирикутної призми утворений з двох її сусідніх граней.

$$ S_\text{б}=2S_{ABCD}=2\cdot 6^2=72\ \text{см}^2. $$

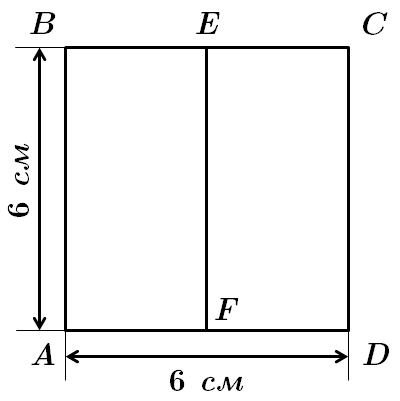
Основа призми – квадрат зі стороною \(AF=3\) см.

Відповідь: Г.

Пояснення

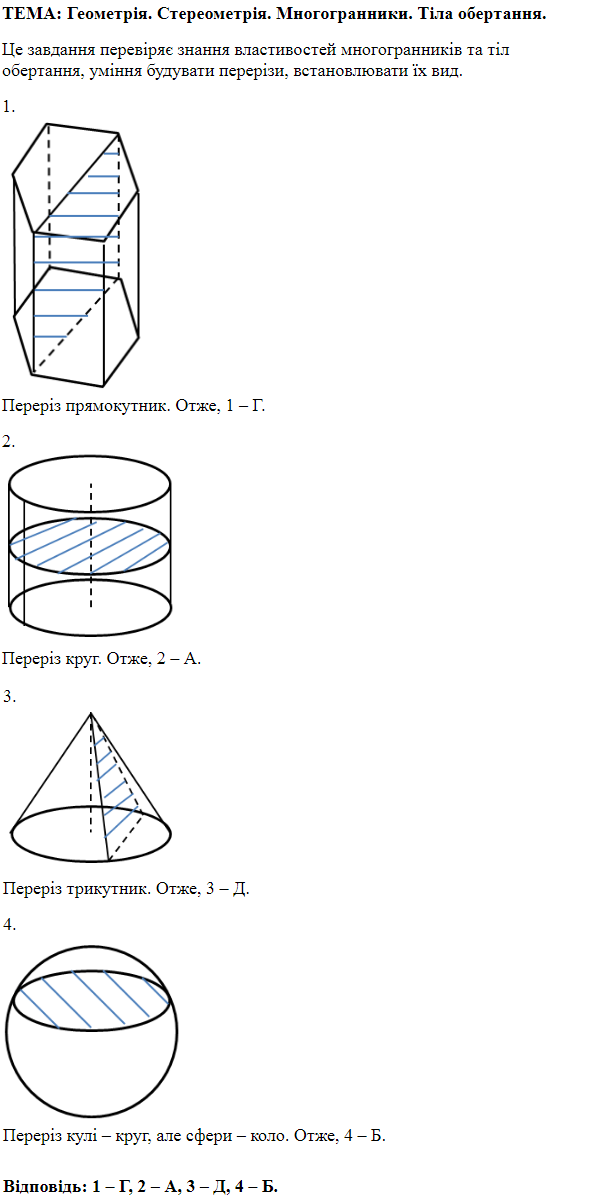
ТЕМА: Геометрія. Стереометрія. Многогранники, тіла й поверхні обертання (куб, куля, циліндр, конус). Формули для обчислень площ поверхонь многогранників і тіл обертання.

Це завдання перевіряє вміння визначати площу повної поверхні куба, кулі, циліндра та конуса.

Обчислимо площу повної поверхні кожного геометричного тіла (1 – 4).

1. Площа повної поверхні циліндра, радіус основи якого дорівнює \(R\), а висота – \(H\), обчислюється за формулою

За умовою \(R=3\), \(H=4\), тоді

$$ S_\text{повн.}=2\pi\cdot 3(3+4)=42\pi. $$

Отже, 1 – Г.

2. Щоб визначити площу повної поверхні конуса, потрібно знати радіус його основи \(R\) та твірну \(L\mathord{:}\)

Оскільки \(R=3\), \(L=5\), то

$$ S_\text{повн.}=3\pi(5+3)=24\pi. $$

Отже, 2 – Б.

3. Площу повної поверхні куба із ребром \(a=\sqrt{3\pi}\) обчислюємо за формулою

Отже, 3 – А.

4. Площа поверхні кулі радіуса \(R\) визначається за формулою $$ S_\text{повн.}=4\pi R^2. $$ За умовою \(R=2\sqrt{3}\), тому

Отже, 4 – Д.

Відповідь: 1 – Г, 2 – Б, 3 – А, 4 – Д.

Пояснення

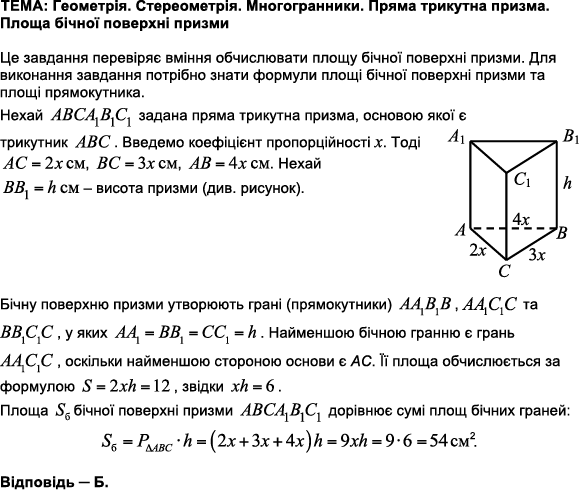
ТЕМА: Геометрія. Стереометрія. Многогранники. Пряма трикутна призма. Об'єм призми.

Це завдання перевіряє вміння обчислювати об'єм призми. Для виконання завдання потрібно знати формули об'єму призми, площі рівностороннього трикутника, означення квадрата та периметра рівностороннього трикутника.

Нехай \(ABCA_1B_1C_1\) – задана правильна трикутна призма, основою якої є рівносторонній трикутник \(ABC\), \(AB=BC=AC=a.\)

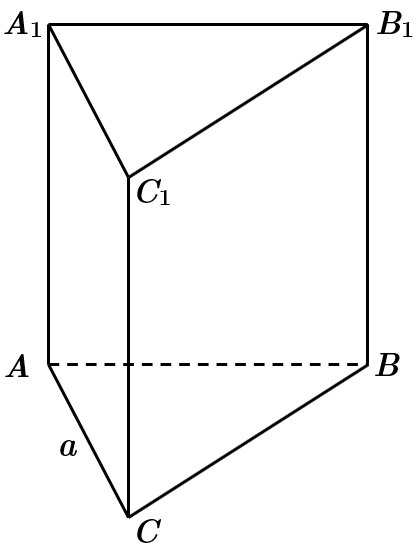
Оскільки периметр правильного трикутника зі стороною \(a\) дрівнює \(3a\), то \(3a=12\) (за умовою), звідки \(a=4.\)

Оскільки бічні грані призми за умовою є квадратами, то \(AA_1=AB=4.\)

Об'єм призми визначається за формулою $$ V=S_\text{осн}\cdot h, $$ де \(S_\text{осн}\) – площа основи призми, \(h\) – висота призми.

Площа правильного трикутника зі стороною \(a\) визначається за формулою $$ S=\frac{a^2\sqrt{3}}{4}. $$ Тоді

$$ S_\text{осн}=\frac{4^2\sqrt{3}}{4}=4\sqrt{3}. $$

Оскільки \(ABCA_1B_1C_1\) – пряма призма, то її висота дорівнює бічному ребру: $$ h=AA_1=4. $$ Тоді $$ V=4\sqrt{3}\cdot 4=16\sqrt{3}. $$

Відповідь: A.

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники. Пряма трикутна призма. Площа бічної поверхні призми.

Це завдання перевіряє вміння обчислювати площу бічної поверхні призми. Для виконання завдання потрібо знати формули площі бічної поверхні призми та площі прямокутника.

Нехай \(ABCA_1B_1C_1\) – задана правильна трикутна призма, основою якої є рівносторонній трикутник \(ABC\), \(AB=BC=AC=a\) (див. рисунок).

Нехай \(CB_1=d\) – діагональ бічної грані. Визначимо з прямокутного трикутника \(CBB_1\ (\angle B=90^\circ)\) за теоремою Піфагора висоту призми \(BB_1\mathord{:}\)

Оскільки сторони основи рівні, то бічні грані призми – рівні прямокутники, тоді площа \(S_\text{б}\) бічної поверхні призми \(ABCA_1B_1C_1\) дорівнює площі бічної грані \(BB_1C_1C\), помноженої на \(3\mathord{:}\)

Відповідь: A.

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники.

Це завдання перевіряє знання формул площі поверхні паралелепіпеда, вміння розв'язувати текстові задачі.

Площа бічної поверхні

\begin{gather*} S_\text{біч}=P_\text{осн}\cdot H=P_{ABCD}\cdot CC_1=(5+4)\cdot 2\cdot 2{,}5=45\ \text{м}^2. \end{gather*}

Площа стін становить \(0{,}8\) від площі бічної поверхні:

\begin{gather*} S_\text{стін}=45\cdot 0{,}8=36\ \text{м}^2. \end{gather*}

Площі стелі:

\begin{gather*} S_\text{стелі}=4\cdot 5=20\ \text{м}^2. \end{gather*}

Площа, яку треба пофарбувати:

\begin{gather*} S=36+20=56\ \text{м}^2. \end{gather*}

На \(1\) м\(^2\) витрачається \(0{,}25\) кг фарби, отже,

\begin{gather*} 56\cdot 0{,}25=14\ \text{кг} \end{gather*}

потрібно для того, щоб повністю пофарбувати стіни та стелю.

Відповідь: \(14.\)

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники.

Це завдання перевіряє знання формул об'ємів куба та піраміди.

Об'єм куба

\begin{gather*} V_\text{куба}=a^3=216;\\[6pt] a=6\ \text{см}. \end{gather*}

Об'єм піраміди

Відповідь: \(36.\)

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники. Пряма трикутна призма. Площа бічної поверхні призми.

Це завдання перевіряє вміння обчислювати площу бічної поверхні призми. Для виконання завдання потрібно знати формули площі бічної поверхні призми та площі прямокутника.

Нехай \(ABCA_1B_1C_1\) задана пряма трикутна призма, основою якої є трикутник \(ABC.\) Введемо коефіцієнт пропорційності \(x.\) Тоді \(AC=2x\) см, \(BC=3x\) см, \(AB=4x\) см. Нехай \(BB_1=h\) см – висота призми (див. рисунок).

Бічну поверхню призми утворюють грані (прямокутники) \(AA_1B_1B\), \(AA_1C_1C\) та \(BB_1C_1C\), у яких $$ AA_1=BB_1=CC_1=h. $$ Найменшою бічною гранню є грань \(AA_1C_1C\), оскільки найменшою стороною основи є \(AC.\) Її площа обчислюється за формулою $$ S=2xh=12, $$ звідки \(xh=6\).

Площа \(S_\text{б}\) бічної поверхні призми \(ABCA_1B_1C_1\) дорівнює сумі площ бічних граней:

$$ S_\text{б}=P_{\Delta ABC}\cdot h=(2x+3x+4x)h=9xh=9\cdot 6=54\ \text{см}^2. $$

Відповідь: Б.

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники. Прямокутний паралелепіпед. Розгортка прямокутного паралелепіпеда. Об’єм прямокутного паралелепіпеда.

Це завдання перевіряє вміння за розгорткою многогранника визначати його об’єм.

Основою прямокутного паралелепіпеда, розгортка якого зображена на рисунку, є прямокутник із сторонами \(3\ \text{см}\) і \(4\ \text{см}.\) Сума довжин бічного ребра паралелепіпеда і більшої сторони його основи дорівнює \(12\ \text{см}\), тому довжина бічного ребра дорівнює $$ 12 - 4 = 8\ \text{см}. $$ Отже, висота паралелепіпеда дорівнює \(8\ \text{см}.\)

Об’єм паралелепіпеда визначається за формулою: $$ V = abc, $$ де \(a, b, c\) – виміри прямокутного паралелепіпеда, тобто довжина і ширина його основи та висота. Тоді

$$ V = 3 \cdot 4 \cdot 8 = 96\ \text{см}^{3}. $$

Відповідь: A.

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники. Об’єм прямокутного паралелепіпеда.

Це завдання практичного змісту перевіряє вміння розв’язувати стереометричні задачі з використанням формули об’єму прямокутного паралелепіпеда.

Зображена на рисунку ємність для квітів є прямокутним паралелепіпедом, з якого вирізаний менший паралелепіпед. Отже, об’єм цієї ємності шукатимемо як різницю об’ємів двох паралелепіпедів. Об’єм паралелепіпеда знаходиться за формулою $$ V=abc, $$ де \(a\), \(b\) і \(c\)   виміри паралелепіпеда. Виміри першого паралелепіпеда задані: \(40\) см, \(40\) см, \(50\) см, а виміри другого паралелепіпеда (порожня частина) знаходимо:

\begin{gather*} 40-10=30\ \text{см},\\[7pt] 40-5-5=30\ \text{см},\\[7pt] 50-5-5=40\ \text{см}. \end{gather*}

Об’єм однієї ємності:

Тоді об’єм \(10\) таких ємностей дорівнює \(440000\) см\(^3\) або \(0{,}44\) м\(^3.\)

Тут враховано, що \(1\) м\(=100\) см, \(1\) м\(^3=1000000\) см\(^3.\)

Відповідь: Г.

Пояснення

Пояснення

Пояснення

Пояснення

Пояснення

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники.

Це завдання перевіряє вміння встановлювати властивості многогранників за їх розгорткою.

На рисунку фігури з номерами \(2\) і \(3\) є розгортками куба.

Відповідь: Г.

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники та тіла обертання.

Це завдання перевіряє знання властивостей призми та кулі, формули об'єму призми, вміння застосовувати властивості геометричних фігур до розв'язування стереометричних задач.

Дана призма \(ABCA_1B_1C_1\) – правильна призма, вписана у сферу. Отже, основи призми – правильні трикутники \(ABC\), \(A_1B_1C_1\) вписані у кола.

Точка \(O\) – центр сфери. Проведемо \(OO_1\!\perp\!(ABC)\), \(ON\!\perp\!BB_1.\)

Точка \(O_1\) – центр кола, описаного навколо \(\Delta ABC.\)

\(ONBO_1\) – прямокутник.

За умовою \(\angle OBN=30^\circ.\) Отже, \(\angle OBO_1=60^\circ.\) Точка \(N\) – середина ребра \(BB_1.\) \(OB=6\) см.

У \(\Delta OBO_1\ (\angle O_1=90^\circ)\),

\begin{gather*} O_1B=OB\cos 60^\circ=6\cdot \frac 12=3\ \text{см};\\[6pt] OO_1=OB\sin 60^\circ =6\cdot \frac{\sqrt{3}}{2}=3\sqrt{3}\ \text{см}. \end{gather*}

У \(\Delta ABC\ O_1B=3\) см – радіус описаного кола, отже,

\begin{gather*} AB=R\sqrt{3}=3\sqrt{3}\ \text{см}. \end{gather*}

\begin{gather*} S_{ABC}=\frac{a^2\sqrt{3}}{4}, \end{gather*} де \(a=AB\) – сторона правильного трикутника.

\begin{gather*} S_{ABC}=\frac{(3\sqrt{3})^2\sqrt{3}}{4}=\frac{27\sqrt{3}}{4}\ \text{см}^2;\\[6pt] BB_1=2OO_1=6\sqrt{3}\ \text{см};\\[6pt] V=S_\text{осн.}\cdot H,\ \text{де}\\[6pt] S_\text{осн.}=S_{ABC}=\frac{27\sqrt{3}}{4}\ \text{см}^2;\\[6pt] H=BB_1=6\sqrt{3}\ \text{см};\\[6pt] V=\frac{27\sqrt{3}\cdot 6\sqrt{3}}{4}=\frac{243}{2}=121{,}5\ \text{см}^3. \end{gather*}

Відповідь: \(121{,}5.\)

Пояснення

ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі.

Це завдання перевіряє знання ознаки паралельності прямої та площини у просторі.

Використаємо ознаку паралельності прямої та площини: якщо пряма, яка не лежить у площині, паралельна прямій, що лежить у площині, то ця пряма паралельна площині.

1. \(BC\!\parallel\!B_1C_1\) та \(B_1C_1 \in (AB_1C_1D)\), звідси \(BC\!\parallel\!(AB_1C_1D).\) Отже, 1 – A.

2. \(D_1C\!\parallel\!A_1B\) та \(D_1C \in (DCC_1D_1)\), звідси \(A_1B\!\parallel\!(DCC_1D_1).\) Отже, 2 – B.

3. \(DD_1\!\parallel\!AA_1\) та \(AA_1 \in (AA_1C_1C)\), звідси \(DD_1\!\parallel\!(AA_1C_1C).\) Отже, 3 – Д.

4. \(BD\!\parallel\!B_1D_1\) та \(B_1D_1 \in (AB_1D_1)\), звідси \(BD\!\parallel\!(AB_1D_1).\) Отже, 4 – Г.

Відповідь: 1 – А, 2 – В, 3 – Д, 4 – Г.

Пояснення

ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Многогранники.

Це завдання перевіряє знання формули для обчислення об’ємів многогранників, уміння знаходити зазначені відстані та величини кутів у просторі.

\(ABCDA_1B_1C_1D_1\) – призма, \(BB_1\) – висота призми. \(AC = 17\) см.

1. \((AB_1C) \cap (AA_1B_1) = AB_1\), \((AB_1C) \cap (BCC_1) = B_1C\). Отже, \(\Delta AB_1C\) – даний переріз.

2. \(BO\!\perp\!AC\) (властивість діагоналей ромба). \(B_1O\!\perp\!AC\) (за теоремою про три перпендикуляри). \((BOB_1)\!\perp\!AC.\) Отже, \(\angle B_1OB = \alpha\) – лінійний кут відповідного двогранного кута між площинами \((AB_1C)\) і \((ABC).\)

3. \(\Delta B_1BO\) \((\angle B = 90^\circ)\),

4.

\begin{gather*} V = S_{основи} \cdot H = S_{ABCD} \cdot BB_1,\\[6pt] S_{ABCD} = \frac{1}{2}AC \cdot BD = \frac{17}{2}BD,\\[6pt] BB_1 = 1{,}2BD. \end{gather*}

За умовою, \(V = 1020\ \text{см}^3.\) Отже,

\begin{gather*} \frac{17}{2}BD \cdot 1{,}2BD = 1020,\\[6pt] BD^2 = 100,\\[7pt] BD = 10\ \text{см},\\[6pt] BO = \frac{1}{2}BD = 5\ \text{см}. \end{gather*}

5. \(BB_1 = 1{,}2BD = 1{,}2 \cdot 10 = 12\) см.

6. \(\Delta B_1BO\) \((\angle B = 90^\circ)\) за теоремою Піфагора:

Відповідь: \(110{,}5.\)

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники. Прямі та площини у просторі.

Це завдання перевіряє вміння знаходити відстань від точки до прямої, знання теореми про три перпендикуляри.

\(ABCDA_1B_1C_1D_1\) – куб, ребро якого \(1\) см.

Відстань від точки \(A\) до прямої \(B_1C_1\) – довжина перпендикуляра з точки \(A\) до прямої \(B_1C_1.\)

\(AB\ \perp\ (BB_1C_1)\), \(AB_1\) – похила на \((BB_1C_1)\), \(BB_1\) – проекція \(AB_1\) на \((BB_1C_1).\)

За теоремою про три перпендикуляри: якщо проекція \(BB_1\ \perp\ B_1C_1\), то й похила \(AB_1\ \perp\ B_1C_1\), а отже, \(AB_1\) – відстань від \(A\) до \(B_1C_1.\)

У \(\triangle ABB_1\) (\(\angle B=90^\circ\)) \(AB=BB_1=1\) см.

За теоремою Піфагора

\begin{gather*} AB_1^2=AB^2+BB_1^2=1^2+1^2=2,\\[7pt] AB_1=\sqrt{2}\ \text{см}. \end{gather*}

Відповідь: B.

Пояснення

Пояснення

Пояснення

Пояснення

ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Многогранники.

Це завдання перевіряє знання формули для обчислення об'ємів многогранників, уміння будувати перерізи многогранників, ознак паралельності прямої та площини у просторі.

\(ABCDA_1B_1C_1D_1\) – пряма призма, тому \(CC_1 \perp (ABC)\), \(ABCD\) – трапеція, \(AB=CD.\)

Додаткова побудова: \(CK\ ||\ AB.\)

\(CC_1\ ||\ BB_1\), \(CK\ ||\ AB\), \(CK\cap CC_1\), \(AB\cap BB_1\), звідси, за ознакою паралельності площин \((CKC_1)\ ||\ (ABB_1).\)

Січна площина \((CC_1K)\) перетинає паралельні площини по паралельних прямих. Отже, \(KK_1\ ||\ AA_1\), \(C_1K_1\ ||\ CK.\)

\(AB\ ||\ CK\), \(CK\in (CC_1K)\Rightarrow AB\ ||\ (CC_1K).\)

Прямокутник \(KCC_1K_1\) – шуканий переріз.

\begin{gather*} V=S_\text{основи}\cdot H=S_{ABCD}\cdot CC_1;\\[7pt] CC_1=8\ \text{см};\\[7pt] V=672\ \text{см}^3. \end{gather*}

Отже,

\begin{gather*} S_\text{основи}=\frac{672}{8}=84\ \text{см}^2. \end{gather*}

Нехай \(BC=x\) см, тоді \(AD=CE=6x\) см.

\begin{gather*} S_\text{основи}=S_{ABCD}=\frac{BC+AD}{2}\cdot CE, \end{gather*}

де \(CE \perp AD\) – висота трапеції.

\begin{gather*} \frac{x+6x}{2}\cdot 6x=84;\\[6pt] 21x^2=84;\\[7pt] x^2=4;\\[7pt] x=2;\\[7pt] BC=2\ \text{см};\\[7pt] AD=CE=12\ \text{см}. \end{gather*}

\(\Delta CED\ (\angle E=90^\circ)\) за теоремою Піфагора:

\(AB=CD\) (за умовою), \(AB=CK\) (протилежні сторони паралелограма).

Отже, \(CK=13\) см.

Відповідь: \(104.\)

Пояснення

ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Многогранники.

Це завдання перевіряє вміння знаходити величини кутів у просторі, взаємне розміщення прямих та площин у просторі.

1. \begin{gather*} \left.\begin{array}{l} CB\!\perp\!BA,\\ CB\!\perp\!BB_1, \end{array}\right| \Rightarrow CB\!\perp\!(ABB_1). \end{gather*}

Отже, 1 – Б.

Отже, 2 – А.

Отже, 3 – Д.

4. \(A_1B \in (ABB_1).\)

Отже, 4 – В.

Відповідь: 1 – Б, 2 – А, 3 – Д, 4 – В.

Пояснення

Пояснення

Пояснення

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники і тіла обертання, їх види і властивості.

Це завдання перевіряє вміння застосовувати властивості призми до розв’язування стереометричних задач.

\(BB_1D_1D\) – прямокутник, який є перерізом правильної чотирикутної призми.

\begin{gather*} S_{BB_1D_1D} = 40\ \text{см}^2.\\[7pt] P_{ABCD} = 20\sqrt{2}\ \text{см}. \end{gather*}

Призма правильна, тому \(ABCD\) – квадрат.

У \(\Delta ABD\ (\angle A = 90^\circ)\) за теоремою Піфагора

\begin{gather*} AB^2 + AD^2 = BD^2;\\[7pt] 2 \cdot (5\sqrt{2})^2 = BD^2;\\[7pt] BD = 10\ \text{см}.\\[7pt] S_{BB_1D_1D} = BD \cdot BB_1;\\[7pt] 10 \cdot BB_1 = 40;\\[7pt] BB_1 = 4\ \text{см}. \end{gather*}

Відповідь: B

Пояснення

ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Многогранники.

Це завдання перевіряє знання формули для обчислення об'ємів многогранників, уміння будувати перерізи многогранників, ознак перпендикулярності прямої та площини у просторі.

\(ABCA_1B_1C_1\) – пряма призма \(\Delta ABC\) – рівнобедрений, \(AB=BC=25\) см, \(AC=30\) см.

Додаткова побудова:
\(AK\ \perp\ BC\) (у \(\Delta ABC\)),
\(KK_1\ \perp BC\ (BCC_1).\)

За ознакою перпендикулярності прямої та площини \(BC\ \perp\ (AKK_1).\)

Отже, \(AKK_1A_1\) – переріз призми, який проходить через ребро \(AA_1\) та перпендикуляра \(BC.\) \(AKK_1A_1\) – прямокутник.

Розглянемо \(\Delta ABC.\) \(BE\ \perp\ AC\), \(AK\ \perp\ BC.\) \(\Delta ABE\) \((\angle E=90^\circ)\), \(AB=25\) см.

\(AE=\frac 12 AC=15\) см (\(BE\) – висота та медіана). За теоремою Піфагора

Відповідь: \(900.\)