Алгебра і початки аналізу – Нерівності та системи нерівностей

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Квадратні нерівності та їх системи.

Це завдання перевіряє вміння розв'язувати квадратні нерівності.

Для розв’язання квадратної нерівності використаймо ескіз графіка квадратичної функції \(y=ax^2+bx+c.\) Для побудови ескізу достатньо знати, куди напрямлені вітки параболи – вгору \((a\gt 0)\) чи вниз \((a\lt 0)\), та абсциси точок перетину з віссю \(Ox:\)

Отже, вітки параболи напрямлені вгору.

Розв’яжімо рівняння \(x^2-9=0.\)

Розкладімо на множники за формулою різниці квадратів:

\begin{gather*} a^2-b^2=(a-b)(a+b);\\[7pt] (x-3)(x+3)=0;\\[7pt] x_1=3\ \text{та}\ x_2=-3.\end{gather*}

Це – нулі функції \(y=x^2-9.\)

Побудуймо ескіз графіка функції.

\begin{gather*} x\in\ (-3; 3). \end{gather*}

З наведених чисел лише число \(2\in (-3; 3).\)

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Лінійні нерівності.

Завдання перевіряє вміння розв’язувати системи лінійних нерівностей.

Розв'яжімо систему нерівностей:

Зобразімо множину розв'язків кожної нерівності на одній координатній прямій:

Розв'язком системи є проміжок \(x\in [-4; 2{,}5).\)

Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Лінійні нерівності.

Завдання перевіряє знання властивостей нерівностей і вміння розв’язувати лінійні нерівності.

\begin{gather*} x\in (-\infty; -3]. \end{gather*}

Відповідь: Б.

ТЕМА: Показникові нерівності.

Завдання скеровано на перевірку вміння розв'язувати показникові нерівності, знання властивостей показникової функції.

Функція \(y=\left(\dfrac 15\right)^x\) – спадна, тому більшому значенню функції відповідає менше значення аргументу:

\begin{gather*} a^{f(x)}\gt a^{g(x)};\\[7pt] 0\lt a\lt 1\Leftrightarrow f(x)\lt g(x). \end{gather*}

Отже, \(x\lt 2.\)

\begin{gather*} x\in (-\infty; 2). \end{gather*}

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати квадратні рівняння, аналізувати та досліджувати рівняння, розв'язувати рівняння з параметром.

Розкриємо дужки та перенесемо всі доданки з \(x\) в один бік, а числа та параметри — в інший.

За умовою корінь рівняння має бути від’ємним числом \((x\lt 0){:}\)

\begin{gather*} \frac{a-10}{a}\lt 0. \end{gather*}

Розв`яжемо нерівність методом інтервалів:

Отже, \(x\lt 0\) при \(a\in (0; 10).\)

Найбільше ціле число \(a\) з інтервалу \((0; 10)\) це \(9.\)

Відповідь: \(9.\)

ТЕМА: Алгебра і початки аналізу. Лінійні нерівності.

Завдання скеровано на перевірку вміння розв'язувати системи лінійних нерівностей.

Зобразимо множину розв'язків кожної нерівності на одній координатній прямій:

Розв'язком системи є проміжок \(x\in (-2; 9].\) З наведених чисел, лише число \(6\) належить даному проміжку.

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Логарифмічні нерівності.

Завдання скеровано на перевірку вміння розв’язувати логарифмічні нерівності, знання властивостей логарифмічної функції.

Використаймо властивість логарифма:

Тоді

Функція \(y=\log_{0{,}7}x\) спадна, тому \(x\lt 0{,}7.\)

Логарифмічна функція має область визначення \(x\gt 0.\)

Отже, розв'язком нерівності буде розв'язок системи:

Отже, \(x\in (0; 0{,}7).\)

Відповідь: Д.

ТЕМА: Лінійні нерівності.

Завдання скеровано на перевірку вміння розв’язувати лінійні нерівності, знання властивостей нерівностей.

\begin{gather*} x\in \left(-\infty; -\frac 14\right). \end{gather*}

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Квадратні нерівності.

Завдання скеровано на перевірку вміння розв’язувати нерівності другого степеня, наведені у вигляді добутку лінійних множників.

Визначмо корені рівняння, прирівнявши ліву частину до нуля: \((x+3)(x-2)=0.\)

Звідси:
1) \(x+3=0\Rightarrow x=-3;\)
2) \(x-2=0\Rightarrow x=2.\)

Визначмо знаки виразу \((x+3)(x-2)\) на кожному з отриманих проміжків за допомогою методу інтервалів (див. рисунок).

Отже, \(x\in(-3; 2)\) – множина розв'язків заданої нерівності.

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Лінійні нерівності.

Завдання спрямоване на перевірку навичок розв’язання лінійних нерівностей і застосування властивостей числових нерівностей.

\begin{gather*} x\in (-\infty; -3]. \end{gather*}

Відповідь: A.

ТЕМА: Показникові нерівності.

Завдання скеровано на перевірку вміння розв’язувати показникові нерівності, знання властивостей показникової функції.

За властивістю степенів:

Функція \(y=a^x\) за \(a\gt 1\) є зростаючою, тому

$$ x\in [6; +\infty). $$

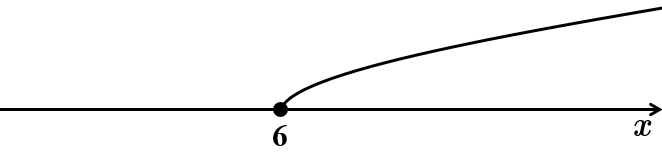
Відповідь: B.

ТЕМА: Лінійні нерівності.

Завдання скеровано на перевірку вміння розв’язувати лінійні нерівності, знання властивостей нерівностей.

$$ x\in (-9; +\infty). $$

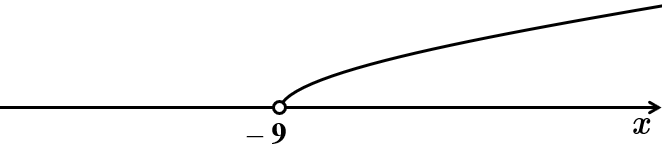
Відповідь: Д.

ТЕМА: Системи лінійних нерівностей.

Завдання скеровано на перевірку вміння розв’язувати системи лінійних нерівностей, знання властивостей нерівностей.

Розв'яжімо систему лінійних нерівностей:

За властивістю нерівностей, під час ділення нерівності на від'ємне число знак нерівності треба замінити на протилежний.

Зобразімо розв'язок на числовій прямій:

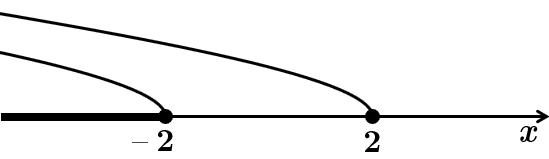
Спільний розв'язок \(x\in (-\infty; -2].\)

Відповідь: Г.

ТЕМА: Показникові нерівності.

Завдання скеровано на перевірку вміння розв'язувати показникові нерівності, знання властивостей показникової функції.

Функція \(y=\left(\frac 14\right)^x\) – спадна, тому більшому значенню функції відповідає менше значення аргументу:

$$ x\in (-\infty; 4). $$

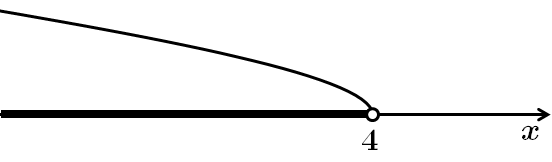
Відповідь: Д.

ТЕМА: Лінійні нерівності.

Завдання скеровано на перевірку вміння розв’язувати найпростіші лінійні нерівності.

$$ x\in [0\mathord{,}5; +\infty). $$

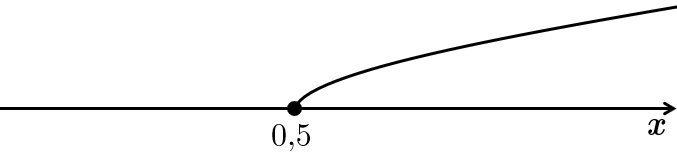
Відповідь: Б.

ТЕМА: Алгебра і початки аналізу Логарифмічні нерівності.

Завдання скеровано на перевірку вміння розв’язувати логарифмічні нерівності, знання властивостей логарифмічної функції.

Функція \(y=\log_3x\) є зростаючою, тому \(1-2x\lt 9.\) Логарифмічна функція має область визначення \(1-2x\gt 9.\)

Отже, розв'язком нерівності буде розв'язок системи:

$$ x\in \left(-4; \frac 12\right). $$

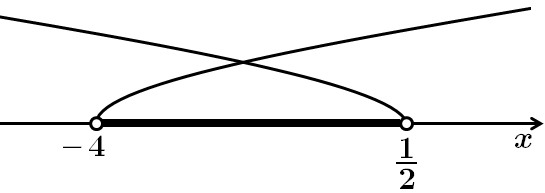
Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Лінійні нерівності.

Завдання скеровано на перевірку вміння розв’язувати системи лінійних нерівностей.

Зобразимо множину розв'язків кожної нерівності на одній координатній прямій:

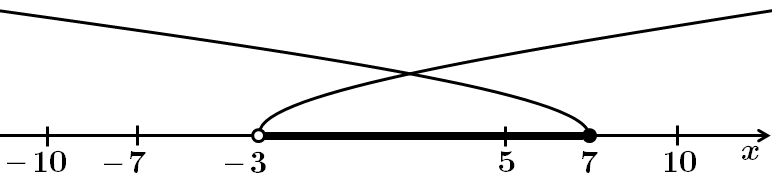
Розв'язком системи є проміжок \(x\in (-3; 7].\) З наведених чисел, лише число \(5\) належить даному проміжку.

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання скеровано на перевірку вміння порівнювати дійсні числа, знання властивостей модуля.

Розв'язком нерівності \(|-2x-3|\gt 5\) з наведених чисел є \(2.\) \begin{gather*} |-2\cdot 2-3|\gt 5,\ \ |-4-3|\gt 5,\\[7pt] |-7|\gt 5,\ \ 7\gt 5. \end{gather*}

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання скеровано на перевірку вміння розв’язувати системи лінійних та показникових нерівностей.

Розв'яжемо систему нерівностей: \begin{gather*} \left\{ \begin{array}{l} 5^x\lt 25,\\ 2-x\lt 8, \end{array} \right. \ \ \ \ \left\{ \begin{array}{l} 5^x\lt 5^2,\\ x\gt -6, \end{array} \right. \\[7pt] \left\{ \begin{array}{l} x\lt 2,\\ x\gt -6. \end{array} \right. \end{gather*}

\(x\in (-6; 2).\)

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати рівняння першого степеня.

Розв'яжемо нерівність \(0,2x-54\lt 0\): \begin{gather*} 0,2x\lt 54\\[6pt] x\lt \frac{54}{0,2}\\[6pt] x\lt 270\\[7pt] x\in(-\infty; 270). \end{gather*}

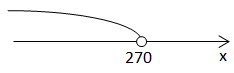
Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

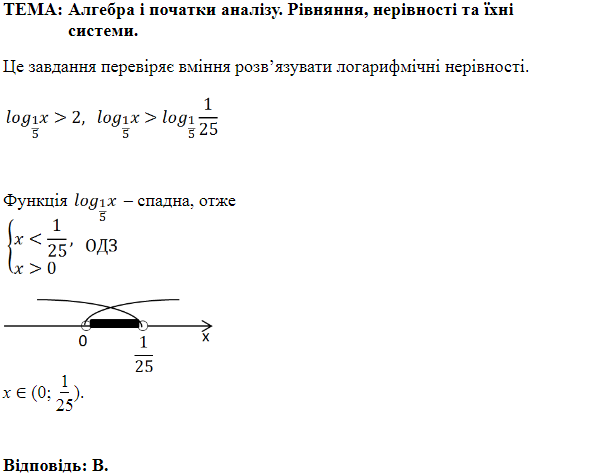
Завдання перевіряє вміння розв’язувати логарифмічні нерівності.

Розв'яжемо тригонометричну нерівність \(\log_{0,3}(x+3)\gt \log_{0,3}4.\)

Функція є спадною, бо основа логарифма \(0,3\lt 1.\) Отже, \(x+3\lt 4\) та за ОДЗ \(x+3\gt 0.\)

Розв'язком нерівності буде розв'язок системи лінійних нерівностей:

\(x\in (-3;\ 1).\)

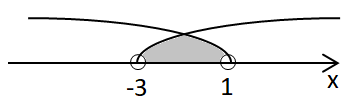
Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати лінійні нерівності.

Розв'яжемо лінійну нерівність: \begin{gather*} x+3\le0,\\[7pt] x\le -3. \end{gather*} Зобразимо розв'язок на координатній прямій:

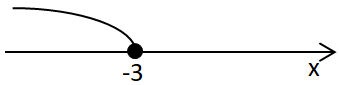
Отже, правильна відповідь – В.

Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати показникові нерівності, нерівності з модулем.

\begin{gather*} \left\{ \begin{array}{l} \left(\frac 13\right)^x\lt 81,\\ |x|\le 5; \end{array} \right. \ \ \ \ \left\{ \begin{array}{l} \left(\frac 13\right)^x\lt \left(\frac 13\right)^{-4},\\ -5\le x\le 5; \end{array} \right. \end{gather*} функція \(y=\left(\frac 13\right)^x\) складна, оскільки основа степені \(\frac 13\lt 1.\)

Отже, \begin{gather*} \left\{ \begin{array}{l} x\gt -4,\\ -5\le x\le 5. \end{array} \right. \end{gather*}

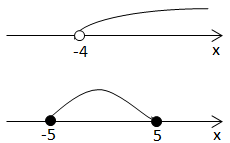
Розв'язок системи – спільний розв'язок двох нерівностей. Отже, \(x\in (-4;\ 5].\)

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Перевіряє вміння розв’язувати показникові нерівності.

Зведемо до однакової основи: \begin{gather*} 10^{x+1}\gt 10^{-2}. \end{gather*} Функція \(y=10^x\) – зростаюча, тому \begin{gather*} x+1\gt -2,\\[7pt] x\gt -3. \end{gather*} Отже, \(x\in (-3;\ +\infty).\)

Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати системи лінійних нерівностей.

Розв'яжемо систему лінійний нерівностей: \begin{gather*} \left\{ \begin{array}{ l l} 3x-5\lt 2x, & \\ 12-9x\le 3x, & \end{array}\right. \ \ \left\{ \begin{array}{ l l} 3x-2x\lt 5, & \\ -9x-3x\le -12, & \end{array}\right. \\[7pt] \left\{ \begin{array}{ l l} x\lt 5, & \\ -12x\le -12 & \end{array}\right. \ \ \left\{ \begin{array}{ l l} x\lt 5, & \\ x\ge 1. & \end{array}\right. \end{gather*}

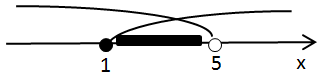
Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати нерівності з модулем.

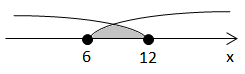
Сума всіх цілих розв'язків: $$ 6+7+8+9+10+11+12=63 $$ Всі розв'язки містяться на проміжку \([-15;\ 15]\).

Відповідь: 63.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати показникові нерівності.

Розв'яжемо показникову нерівність:

Функція \(y=3^x\) зростає, отже, \begin{gather*} x\lt 3-x;\ \ 2x\lt 3;\ \ x\lt \frac 32.\\[7pt] x\in (-\infty;\ \frac 32). \end{gather*}

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати логарифмічні нерівності.

Функція \(y=\log_{0,9}(3x)\) – спадна, отже, знак нерівності змінюємо на протилежний. Враховуючи ОДЗ, отримаємо: \begin{gather*} \left\{ \begin{array}{l l} 3x\gt 0 & \\ 3x\lt 0,9^2& \end{array}\right. \left\{ \begin{array}{l l} x\gt 0 & \\ 3x\lt 0,81& \end{array}\right. \left\{ \begin{array}{l l} x\gt 0 & \\ x\lt 0,27& \end{array}\right. \end{gather*}

\(x\in\ (0;\ 0,27)\)

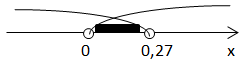
Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати показникові нерівності.

Розв'яжемо нерівність: \begin{gather*} 4\cdot 3^x\lt 3^x + 6,\\[7pt] 4\cdot 3^x-3^x\lt 6,\\[7pt] 3\cdot 3^3 \lt 6,\\[7pt] 3^x \lt 2,\\[7pt] x\lt \log_3 2,\\[7pt] x\in (-\infty;\ \log_3 2). \end{gather*}

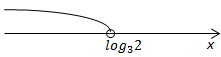
Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв'язувати систему лінійних нерівностей.

Розв'яжемо системи лінійних нерівностей:

\begin{gather*} \left\{\begin{array}{l} 4x-7\ge 2x+1,\\ x\ge -3, \end{array}\right.\ \ \left\{\begin{array}{l} 4x-2x\ge 1+7,\\ x\ge -3, \end{array}\right.\\[7pt] \left\{\begin{array}{l} 2x\ge 8,\\ x\ge -3, \end{array}\right.\ \ \left\{\begin{array}{l} x\ge 4,\\ x\ge -3. \end{array}\right. \end{gather*}

Отже, розв'язок нерівності \(x\in [4; +\infty).\)

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати системи лінійних нерівностей.

Розв'яжемо систему нерівностей \begin{gather*} \left\{\begin{array}{l} 6\gt 2x,\\ 7x-28\le 0, \end{array}\right.\ \ \left\{\begin{array}{l} x\lt 3,\\ 7x\le 28, \end{array}\right.\ \ \left\{\begin{array}{l} x\lt 3,\\ x\le 4. \end{array}\right.\\[7pt] x\in (-\infty; 3). \end{gather*}

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Рівняння і нерівності.

Завдання перевіряє вміння розв'язувати систему лінійних нерівностей.

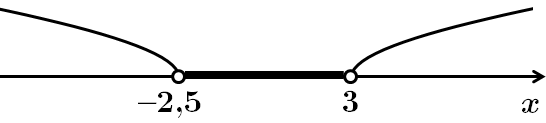
Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв’язувати показникові нерівності.

Функція \(y=10^x\) – зростаюча, тому \(x+1\gt 2\), \(x\gt -2-1\), \(x\gt -3.\)

$$ x\in (-3; +\infty). $$

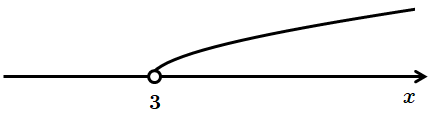
Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лiнiйнi, квaдpaтні, рацiональнi, iррацiональнi, показникові, логарифмiчнi, тригонометричні рівняння, неpiвності та їx системи.

Це завдання перевіряє вміння розв'язувати показникові нерівності.

Розв'яжемо показникову нерівність:

\(2^{4x-5}\ge 2.\) Функція \(y=2^x\) – зростає, отже,

\(x\in [1\mathord{,}5; +\infty).\)

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лiнiйнi, квaдpaтні, рацiональнi, iррацiональнi, показникові, логарифмiчнi, тригонометричні рівняння, неpiвності та їx системи.

Це завдання перевіряє вміння розв'язувати квадратні нерівності.

Розв'яжемо методом інтервалів:

\(x=3\), \(x=-3\) – нулі функції

\(x\in (-3; 3).\)

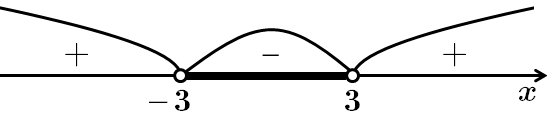
З наведених чисел лише число \(-2\in (-3; 3).\)

Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв'язувати нерівності, що містять змінну під знаком модуля.

Використовуючи геометричну інтерпритацію модуля отримаємо розв'зок нерівності \(|x|\lt 3:\)

\(x\in (-\infty; -3)\cup (3; +\infty).\)

Отже, з наведених чисел \(x=-8\) є розв'язком нерівності.

Відповідь: Д.

ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Лінійні нерівності.

Це завдання перевіряє вміння розв'язувати лінійні нерівності, використовувати формули скороченого множення для тотожного перетворення виразів.

Використаємо формулу \(a^3+b^3=(a+b)(a^2-ab+b^2)\) для спрощення правої частини нерівності:

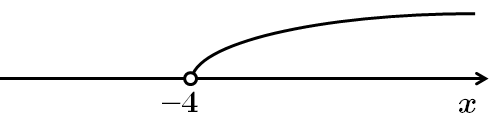
Отже, \(x\in (-4; +\infty).\)

Відповідь: A.

ТЕМА: Алгебра, початки аналізу. Рівняння, нерівності та їхні системи. Лінійні нерівності та їхні системи.

Це завдання перевіряє вміння розв'язувати нерівності першого степеня, нерівності, що містять змінну під знаком модуля.

\(|x+4|(x-1)\lt 0.\)

Цю нерівність можна розв'язати двома способами:

І спосіб.

Вираз \(|x+4|\ge 0\) при будь-яких значеннях змінної, тому розв'язком нерівності є розв'язок системи:

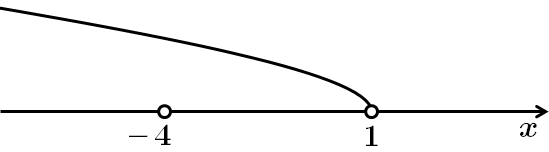
ІІ спосіб.

Розв'язуємо методом інтервалів:

\(|x+4|(x-1)\lt 0\)

$$ x\in (-\infty; -4)\cup (-4; 1). $$

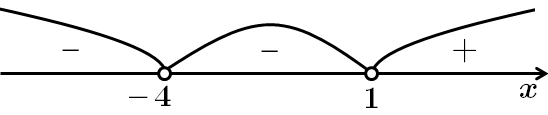
Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи. Раціональні нерівності.

Це завдання перевіряє знання методів розв'язування раціональних нерівностей.

Зведемо до спільного знаменника

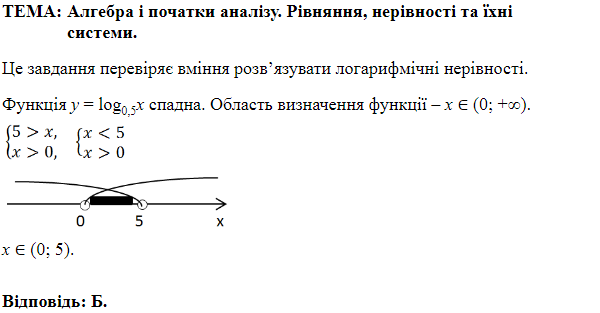
Розв'яжемо методом інтервалів:

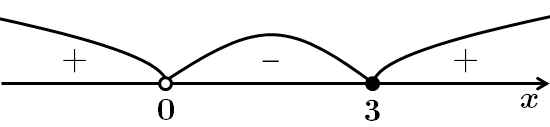
Отже, \(x\in (-\infty; 0)\cup [3; +\infty).\)

Відповідь: A.

ТЕМА: Алгебра та початки аналізу. Функції. Нерівності. Функціональна залежність.

Це завдання перевіряє вміння знаходити область визначення функції, розв'язувати лінійні нерівності.

Область визначення знаходимо з розв'язку нерівності: \begin{gather*} 50-3x\ge 0,\\[7pt] -3x\ge -50,\\[7pt] 3x\le 50,\\[7pt] x\le 50:3,\\[7pt] x\le 16\frac 23. \end{gather*}

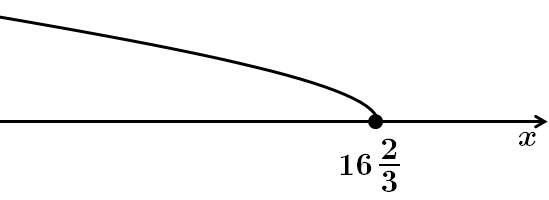
Найбільше ціле двоцифрове число, що належить області визначення – це число \(16.\)

Відповідь: \(16.\)

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Це завдання перевіряє знання методів розв'язування раціональних нерівностей, уміння застосовувати методи та прийоми в процесі розв'язування нерівностей.

\begin{gather*} \frac{2x-4}{x+1}\lt 0,\\[6pt] \frac{2(x-2)}{x+1}\lt 0,\\[6pt] \frac{x-2}{x+1}\lt 0. \end{gather*}

Розв'яжемо методом інтервалів: $$(x-2)(x+1)\lt 0.$$

 $$x\in (-1; 2).$$

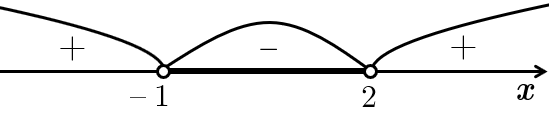
Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа, порівняння чисел. Числові множини та співвідношення між ними.

Це завдання перевіряє вміння порівнювати дійсні числа.

Подвійна нерівність \(5\le 3^x\le 15\) буде вірною при \(x=2:\)

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння застосовувати загальні методи та прийоми в процесі розв'язування рівнянь, нерівностей та систем.

\(x^2+64\gt 0\) при будь-яких значеннях \(x\), тому, щоб добуток \((x^2+64)(x-5)\) був більше нуля, необхідно, щоб другий множник \((x-5)\) був більшим за нуль.

Відповідь: A.

ТЕМА: Алгебра і почати аналізу. Функції. Логарифмічна функція. Рівняння, нерівності та їхні системи.

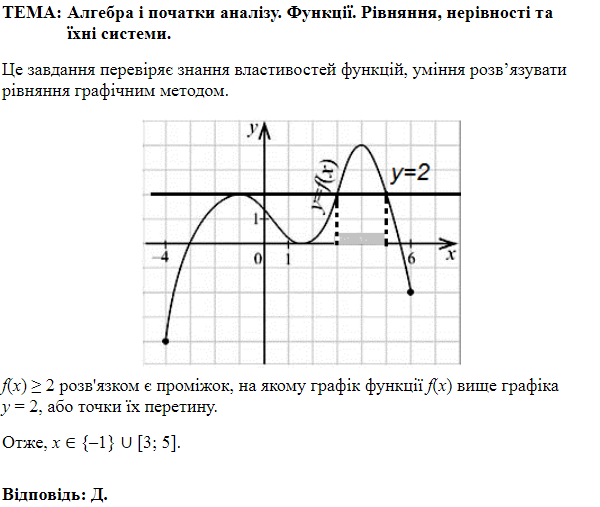
Це завдання перевіряє знання властивостей логарифмічної функції, уміння користуватися графічним методом розв’язування і дослідження нерівностей.

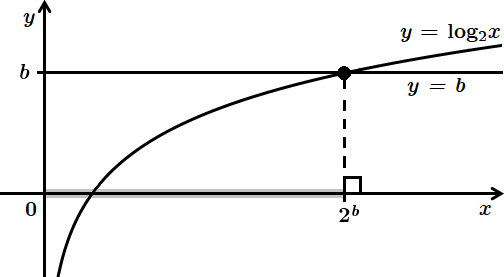
Точка перетину графіків функцій \(y=\log_2x\) та \(y=b\) буде точка з координатами \((2^b; b).\)

Розв’язуючи графічно нерівність \(\log_2x\lt b\), знаходимо частину графіка \(y=\log_2x\), яка знаходиться нижче прямої \(y=b\) та значення \(x\), яке відповідає даній частині графіка. Це \(x\in (0; 2^b).\)

Відповідь: A.

ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Раціональні нерівності.

Це завдання перевіряє знання методів розв'язування раціональних нерівностей.

$$ \frac{x+3}{x-2}\gt 0 $$ розв'яжемо методом інтервалів:

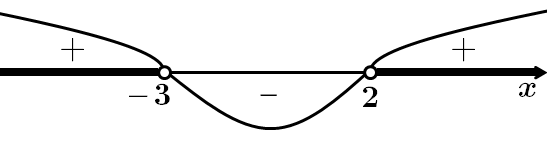
Отже, \(x\in (-\infty; -3)\cup (2; +\infty).\)

Відповідь: Д.

ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Показникові нерівності.

Це завдання перевіряє вміння розв'язувати показникові нерівності.

Функція $$ y=\left(\frac 37\right)^x $$ спадна, тому

Отже, \(x\in (-\infty; 6).\)

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Логарифмічні нерівності.

Це завдання перевіряє вміння розв'язувати логарифмічні нерівності.

Запишемо ОДЗ цєї нерівності: \(x\gt 0\), оскільки логарифмічна функція визначена лише для додатного аргумента.

Запишемо \(-1\) у вигляді логарифма з основою \(3\mathord{:}\) $$ -1=\log_3 3^{-1}=\log_3 \frac 13. $$ Тоді вихідна нерівність матиме вигляд: $$ \log_3 x\lt \log_3 \frac 13. $$ Оскільки функція $$ y=\log_3 x $$ є зростаючою ще раз підкреслимо, що вона існує лише для \(x\gt 0,\) то отримана нерівність рівносильна нерівності $$ 0\lt x\lt \frac 13. $$

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Раціональні нерівності.

Це завдання перевіряє знання означення розв'язку нерівності з однією змінною.

ОДЗ: \(x-3\ne 0.\)

Розв'яжемо нерівність:

Розв'яжемо методом інтервалів:

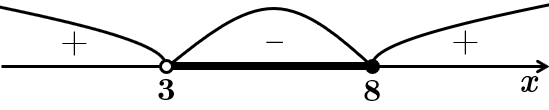
З наведених чисел, лише \(4\) належить даному проміжку.

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи. Раціональні нерівності.

Це завдання перевіряє вміння розв'язувати раціональні нерівності.

Розв'яжемо нерівність "методом інтервалів". Запишемо нерівність у вигляді \(f(x)\ge 0\), де $$ f(x)=\frac{(5-x)^2}{x^2+x-6}. $$

Знайдемо область визначення функції \(f(x).\) Раціональний дріб існує, якщо його знаменник відмінний від нуля, тому \(x^2+x-6\ne 0.\) Квадратне рівння \(x^2+x-6=0\) має два корені \(x=-3\) та \(x=2.\) Отже, область визначення функції \(f(x)\) містить всі точки числової прямої, крім двох точок \(x=-3\) та \(x=2\), тобто

Знайдемо нулі функції \(f(x)\), тобто корені рівняння $$ \frac{(5-x)^2}{x^2+x-6}=0. $$

Нагадаємо, що дріб дорівнює нулю, якщо його чисельник дорівнює нулю, а знаменник – ні. Рівняння \((5-x)^2=0\) має корінь \(x=5\), який належить \(D(f).\) Оскільки $$ (5-x)^2=(5-x)(5-x), $$ то кажуть, що \(x=5\) є коренем кратності \(2.\)

Відмітимо на числовій прямій нуль \(x=5\) та точки, в яких \(f(x)\) не існує, тобто точки \(x=-3\), \(x=2\) та визначимо знак функції \(f(x)\) на кожному інтервалі:

Зазначимо, що при переході через точку \(x=5\) знак функції \(f(x)\) не змінюється.

Об'єднуючи проміжки \((-\infty; -3)\), \((2; 5)\), \((5; +\infty)\), на яких виконується нерівність \(f(x)\gt 0\), та точку \(x=5\), в якій \(f(x)=0\), записуємо множину розв'язків заданої нерівності: $$ x\in (-\infty; -3)\cup (2; +\infty). $$

Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Метод інтервалів.

Це завдання перевіряє вміння розв’язувати раціональні нерівності.

Розв’яжемо нерівність методом інтервалів. Для цього перенесемо всі вирази у ліву частину нерівності: $$ (x + 4)(x - 8) - 3(x - 8) \gt 0 $$ і винесемо за дужки спільний множник \((x - 8).\) Отримаємо: \begin{gather*} (x - 8)((x + 4) - 3) \gt 0,\\[7pt] (x - 8)(x + 1) \gt 0. \end{gather*}

Визначимо нулі функції $$ y = (x - 8)(x + 1), $$ тобто корені рівняння $$ (x - 8)(x + 1) = 0. $$ Добуток дорівнює нулю, коли хоча б один із множників дорівнює нулю: \begin{gather*} x - 8 = 0,\\[7pt] x_1 = 8, \\[7pt] x + 1 = 0,\\[7pt] x_2 = -1. \end{gather*}

Позначимо на числовій осі \(x\) нулі \(x_{1} = 8\) та \(x_{2} = -1\) та визначимо знаки виразу \((x - 8)(x + 1)\) на кожному з отриманих проміжків.

Отже, \((-\infty; -1) \cup (8; +\infty)\) – множина розв’язків заданої нерівності.

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Показникові нерівності.

Це завдання перевіряє вміння розв’язувати показникові нерівності.

Запишемо число \(\frac{1}{36}\) як степінь з основою \(6\mathord{:}\) $$ \frac{1}{36} = \frac{1}{6^{2}} = 6^{-2}. $$ Отримуємо нерівність: \(6^{x} \lt 6^{-2}\).

Оскільки основа \(6 \gt 1\), то задана нерівність рівносильна нерівності \(x \lt -2\). Запишемо множину розв’язків нерівності у вигляді інтервалу: \(x \in (-\infty; -2).\)

Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Метод інтервалів.

Це завдання перевіряє вміння розв’язувати нерівності методом інтервалів.

Розв’яжемо нерівність «методом інтервалів». Для цього визначимо нулі функції $$ y = \frac{(x - 6)(x + 2)^{2}}{x - 3} $$ та точки, де функція не існує. Прирівняємо \(y\) до нуля:

Дріб дорівнює нулю, коли чисельник дорівнює нулю, а знаменник не дорівнює нулю. Тоді \begin{gather*} (x - 6)(x + 2)^{2} = 0,\\[7pt] x - 3 \ne 0. \end{gather*} Тоді \begin{gather*} x = 6,\\[7pt] x = -2,\\[7pt] x \ne 3. \end{gather*} Нанесемо точки на числову вісь \(x.\)

Визначимо знаки виразу $$ \frac{(x - 6)(x + 2)^{2}}{x - 3} $$ на кожному з отриманих проміжків (див. рисунок).

Отже, \(\{-2\} \cup (3; 6]\) – множина розв’язків заданої нерівності.

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Нерівність з однією змінною.

Це завдання перевіряє вміння розв’язувати нерівності.

Розділимо обидві частини нерівності на \(0{,}2\): \begin{gather*} 0{,}2x \lt 54,\\[6pt] x\lt \frac{54}{0{,}2},\\[6pt] x\lt 270. \end{gather*}

Або: \begin{gather*} 5 \cdot 0{,}2x \lt 5 \cdot 54,\\[7pt] x \lt 5 \cdot 54,\\[6pt] x\lt 270. \end{gather*} Запишемо у вигляді інтервалу: \(x \in (-\infty; 270).\)

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Метод інтервалів. Основна логарифмічна тотожність.

Це завдання перевіряє вміння застосовувати основну логарифмічну тотожність для спрощення виразів, що містять логарифмічну функцію, та розв’язувати нерівності, що зводяться до раціональних.

Враховуючи, що аргументом логарифмічної функції може бути лише додатне число, запишемо ОДЗ цієї нерівності: \(-2x\gt 0\), звідки \(x\lt 0.\) Скористаємося основною тригонометричною тотожністю: $$ 2^{\log_2(-2x)}=-2x, $$ тоді нерівність набуває вигляду $$ x^2-2x-15\lt 0. $$ Розв’яжемо отриману нерівність методом інтервалів.

Знайдемо нулі функції \begin{gather*} y=x^2-2x-15{:}\\[7pt] x_1=-3,\\[7pt] x_2=5. \end{gather*} Тоді нерівність можна записати у вигляді $$ (x+3)(x-5)\lt 0. $$ Визначимо знаки функції $$ y=x^2-2x-15 $$ на проміжках \((-\infty; -3)\), \((-3; 5)\) та \((5; +\infty)\) (див. діаграму), звідки \(x\in(-3; 5).\)

Зауважимо, що на діаграмі точки \(x=-3\) та \(x=5\) не зафарбовані з тих міркувань, що ці точки не є розв’язками строгої нерівності $$ x^2-2x-15\lt 0. $$ Ураховуючи ОДЗ початкової нерівності, тобто нерівність \(x\lt 0\), отримаємо множину її розв’язків \((-3; 0).\) Ця множина містить два цілі розв’язки \(x=-2\) та \(x=-1.\) Тому сума всіх цілих розв’язків заданої нерівності дорівнює $$ -2-1=-3. $$

Відповідь: \(-3.\)

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Метод інтервалів.

Це завдання перевіряє вміння розв’язувати раціональні нерівності.

Перший спосіб. Розв’яжемо нерівність методом інтервалів. Для цього перенесемо всі доданки у ліву частину нерівності: $$ x^3-x^2\ge 0 $$ і винесемо за дужки спільний множник: $$ x^2(x-1)\ge 0. $$

Визначимо нулі функції $$ y=x^2(x-1), $$ тобто корені рівняння $$ x^2(x-1)=0, $$ \(x_1=0\) і \(x_2=1\). Зазначимо, що корінь \(x_1=0\) має кратність \(2.\)

Позначимо на числовій осі \(x\) нулі \(x_1=0\) і \(x_2=1\) та визначимо знаки виразу $$ x^2(x-1) $$ на кожному з отриманих проміжків (див. діаграму).

Отже, \(x\in\{0\}\cup [1; +\infty)\) – множина розв’язків заданої нерівності.

Другий спосіб. При \(x=0\) нерівність \(x^3\ge x^2\) є правильною: \(0\ge 0.\) Отже, \(x=0\) – один з розв’язків нерівності. Нехай \(x\ne 0\). Тоді \(x^2\gt 0\), тому, поділивши обидві частини нерівності \(x^3\ge x^2\) на \(x^2\), отримаємо нерівність \(x\ge 1\), рівносильну заданій. Об’єднавши множини \(x\in\{0\}\) та \(x\in [1; +\infty)\), отримаємо відповідь: \(x\in\{0\}\cup [1; +\infty).\)

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Логарифмічні нерівності.

Це завдання перевіряє вміння розв’язувати логарифмічні рівняння.

Перший спосіб. Оскільки $$ \lg \frac{4}{2x - 3} = \lg 4 - \lg (2x - 3), $$ то перепишемо нерівність у вигляді \begin{gather*} \lg 4 - \lg (2x - 3) \ge 0,\ \text{або}\\[7pt] \lg (2x - 3) \le \lg 4. \end{gather*} Ураховуючи, що логарифмічна функція \(y = \lg x\) (тут основа дорівнює \(10 \gt 1\)) є зростаючою, то задана нерівність рівносильна системі нерівностей $$ \left\{\begin{array}{l} 2x - 3 \le 4,\\ 2x-3\gt 0, \end{array}\right. $$ звідки отримуємо: \begin{gather*} \left\{\begin{array}{l} 2x \le 7,\\ 2x \gt 3, \end{array}\right.\\[7pt] x \in (1{,}5; 3{,}5]. \end{gather*} Отже, найбільший розв’язок цієї нерівності – це число \(x = 3{,}5.\)

Другий спосіб. Ураховуючи, що \(0 = \lg 1\), перепишемо нерівність у вигляді $$ \lg \frac{4}{2x - 3} \ge \lg 1, $$ після чого переходимо до рівносильної нерівності

звідки \(x \in (1{,}5; 3{,}5].\)

Відповідь: \(3{,}5.\)

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Показникові нерівності.

Це завдання перевіряє вміння розв’язувати показникові нерівності.

Поділимо обидві частини нерівності на \(2\mathord{:}\) $$ (0{,}3)^{x} \lt 0{,}09 $$ (оскільки \(2 \gt 0\), то знак нерівності не змінюється). Запишемо число \(0{,}09\) як степінь з основою \(0{,}3\mathord{:}\) $$ 0{,}09 = 0{,}3^{2}. $$ Отримаємо нерівність: $$ (0{,}3)^{x} \lt (0{,}3)^{2}. $$

Оскільки \(0{,}3 \lt 1\), то функція \(y = (0{,}3)^{x}\) є спадною на всій області визначення, і нерівність $$ (0{,}3)^{x} \lt (0{,}3)^{2} $$ рівносильна нерівності \(x \gt 2\), тобто \(x \in (2; +\infty).\)

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Модуль числа. Раціональні нерівності.

Це завдання перевіряє знання означення модуля числа та вміння розкривати модуль буквенного виразу.

За означенням модулем числа \(x\) називають саме це число, якщо воно є невід’ємним, і протилежне до \(x\) число, якщо воно є від’ємним, тобто

Отже,

Визначимо проміжки знакосталості виразу \(a^{2}-a-6.\) Для цього визначимо нулі цього тричлена, прирівнявши його до нуля: \(a^{2}-a-6=0\), звідки \(a_{1}=-2\), \(a_{2}=3.\) Визначимо знак виразу \(a^{2}-a-6\) на проміжках \((-\infty; -2)\), \((-2; 3)\) і \((3; +\infty) \) (див. рисунок).

Оскільки на проміжку \((-2; 3)\) вираз \(a^{2}-a-6\) набуває лише від’ємних значень, то на цьому проміжку

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Нерівності мішаного типу. Методи інтервалів.

Це завдання перевіряє вміння розв’язувати нерівності мішаного типу.

Виконаємо рівносильні перетворення: \begin{gather*} \frac{10^x-16\cdot 5^x}{x+2}\ge 0,\\[6pt] \frac{5^x(2^x-16)}{x+2}\ge 0,\\[6pt] \frac{5^x(2^x-2^4)}{x+2}\ge 0. \end{gather*}

Оскільки для всіх \(x\in(-\infty; +\infty)\) \(5^x\gt 0\), то $$ \frac{2^x-2^4}{x+2}\ge 0. $$

Останню нерівність, яка рівносильна початковій, розв’яжемо методом інтервалів на заданому проміжку \([-3; 7].\) Знайдемо нулі функції $$ y=\frac{2^x-2^4}{x+2} $$ та точки, в яких вона не визначена. Функція дорівнює нулю, якщо $$ 2^x-2^4=0, $$ звідки \(x=4\). Функція не визначена в точці \(x=-2.\) Нанесемо ці точки на числову вісь, враховуючи, що задана нерівність є нестрогою (знак «\(\ge\)»), отже, точка \(x=4\) – зафарбована. Визначимо знаки виразу $$ \frac{2^x-2^4}{x+2} $$ на цьому проміжку (див. рисунок).

Отже, \([-3; -2)\cup [4; 7]\) – множина розв’язків заданої нерівності на проміжку \([-3; 7].\)

З рисунка видно, що цілими розв’язками нерівності $$ \frac{2^x-2^4}{x+2}\ge 0 $$ на проміжку \([-3; 7]\) є числа \(-3\), \(4\), \(5\), \(6\) та \(7.\) Їх сума дорівнює \(19.\)

Відповідь: \(19.\)

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Раціональні нерівності.

Це завдання перевіряє вміння розв’язувати раціональні нерівності.

Застосуємо метод інтервалів. Для цього піднесемо ліву частину до квадрата, а праву – перенесемо у ліву частину, змінивши знак: $$ x^2+8x+16-16\le 0, $$ звідси $$ x^2+8x\le 0. $$

Винесемо за дужки спільний множник \(x{:}\) $$ x(x+8)\le 0. $$ Таку ж нерівність отримаємо, якщо скористаємося формулою різниці квадратів:

Визначимо нулі функції $$ y=x(x+8). $$ Прирівняємо \(y\) до нуля: $$ x(x+8)=0. $$ Добуток дорівнює нулю, якщо хоча б один з множників дорівнює нулю, отже \(x=-8\), \(x=0.\) Нанесемо їх на числову вісь \(x.\) Визначимо знаки виразу \(x(x+8)\) на кожному з отриманих проміжків (див. рисунок).

Отже, \(x\in[-8; 0]\) – множина розв’язків заданої нерівності.

Зауваження. Можна спочатку зробити заміну \(x+4=t\) і розв’язати нерівність $$ t^2\le 16, $$ звідки $$ -4\le t\le 4, $$ тоді \begin{gather*} -4\le x+4\le 4,\\[7pt] -8\le x\le 0. \end{gather*}

Відповідь: Д.

ТЕМА: АЛгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв'язувати раціональні нерівності.

Розв'яжемо методом інтервалів.

ОДЗ: \(x\ne 0.\)

\(x\in (-\infty; 0)\cup [3; +\infty).\)

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лінійні, квадратні, раціональні, ірраціональні, показникові, логарифмічні, тригонометричні рівняння, нерівності та їх системи.

Це завдання перевіряє вміння розв'язувати показникові та раціональні нерівності та їхні системи.

Функція \(y = 0{,}5^x\) спадна, тому

\begin{gather*} x \in \left(-2\frac{1}{3};\ 5\right). \end{gather*}

Цілі розв'язки: \(-2\); \(-1\); \(0\); \(1\); \(2\); \(3\); \(4.\)

Отже, кількість цілих розв'язків – \(7.\)

Відповідь: \(7.\)

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лінійні, квадратні, раціональні, ірраціональні, показникові, логарифмічні, тригонометричні рівняння, нерівності та їх системи.

Це завдання перевіряє вміння розв’язувати раціональні нерівності.

Квадратична функція \(y = f(x)\) має від'ємний коефіцієнт \(a\) у формулі \begin{gather*} y = ax^2 + bx + c. \end{gather*}

Розкладемо на множники \begin{gather*} x \cdot f(x) \lt 0,\\[7pt] -x(x - 1)(x - 4) \lt 0,\\[7pt] x(x - 1)(x - 4) \gt 0. \end{gather*} Розв'яжемо методом інтервалів

\begin{gather*} x \in (0; 1) \cup (4; +\infty). \end{gather*}

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лінійні, квадратні, раціональні, ірраціональні, показникові, логарифмічні, тригонометричні рівняння, нерівності та їх системи.

Це завдання перевіряє знання методів розв'язування квадратних нерівностей.

\(x = 0\), \(x = 2\) – нулі функції. Розв'яжемо методом інтервалів.

\begin{gather*} x \in [0; 2]. \end{gather*}

Відповідь: Б.

ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Раціональні нерівності.

Це завдання перевіряє вміння розв'язувати нерівності методом інтервалів, застосовувати методи та прийоми у процесі розв'язування нерівностей.

Розкладемо на множники квадратний тричлен за формулою:

де \(x_1\), \(x_2\) – корені тричлена.

Отже,

Розв'яжемо методом інтервалів. Нулі функції: \(x=-9\), \(x=-3\), \(x=-5.\)

Сума цілих розв'язків: $$ -5+(-4)+(-3)+(-9)=-21. $$

Відповідь: \(-21.\)

ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Логарифмічні нерівності.

Це завдання перевіряє вміння розв’язувати логарифмічні нерівності.

Відповідь: A.

ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Системи лінійних нерівностей.

Це завдання перевіряє вміння розв'язувати системи нерівностей першого степеня.

$$ -3\lt 2-5x\lt 6 $$

Ця нерівність рівносильна системі нерівностей: $$ \left\{ \begin{array}{l} 2-5x\gt -3,\\ 2-5x\lt 6, \end{array} \right.\ \ \left\{ \begin{array}{l} -5x\gt -5,\\ -5x\lt 4, \end{array} \right.\ \ \left\{ \begin{array}{l} x\lt 1,\\ x\gt -\frac 45. \end{array} \right. $$

\(-0\mathord{,}8\lt x\lt 1.\)

Відповідь: Б.