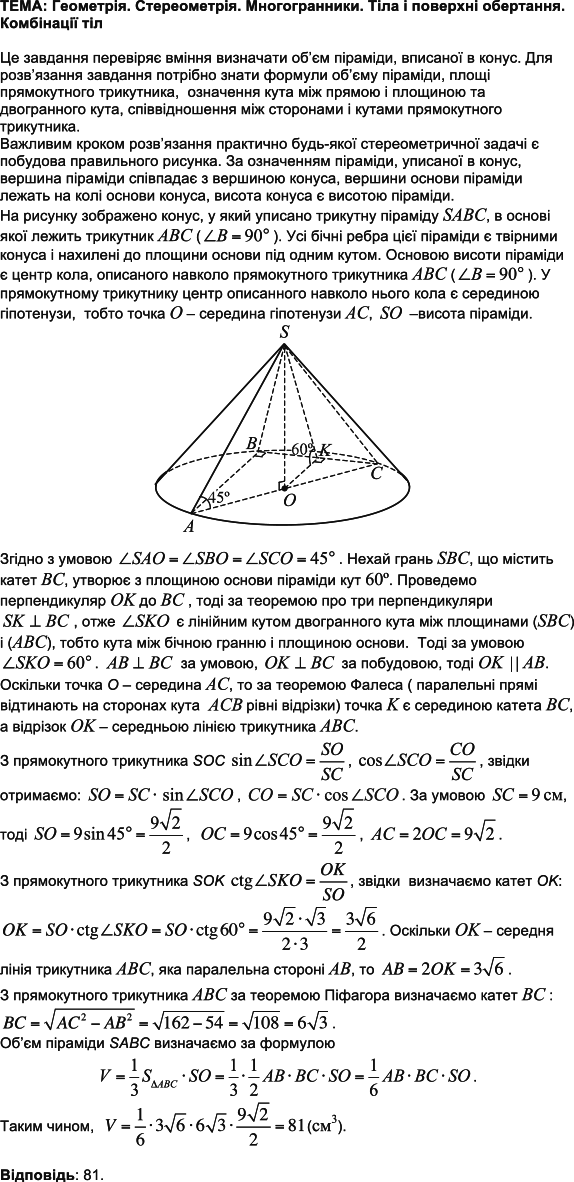
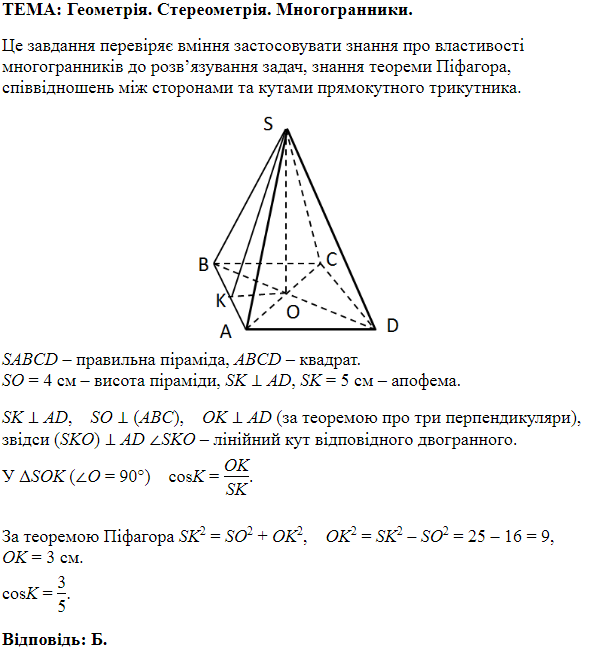
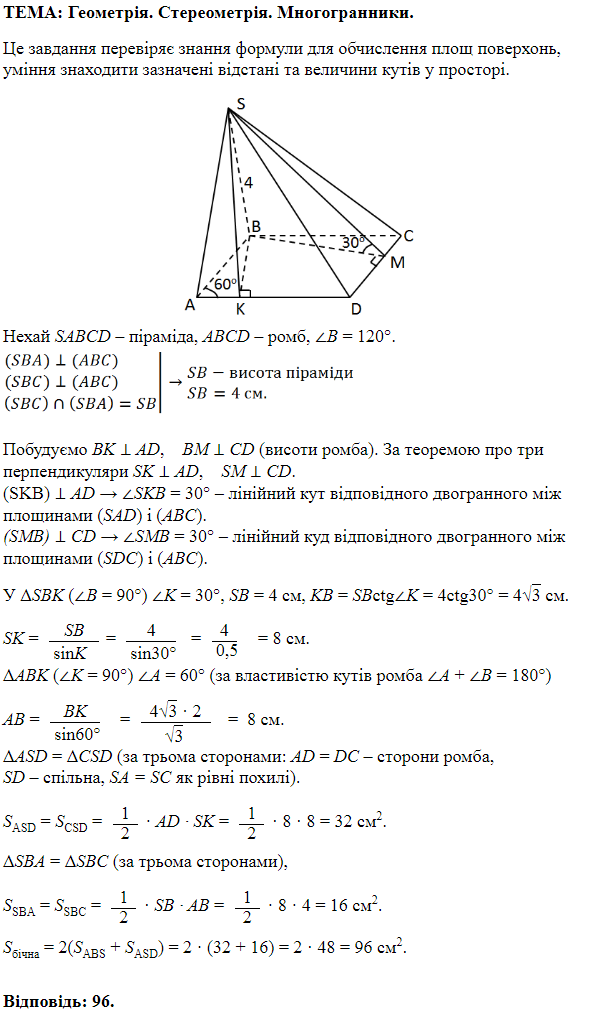
Розділ: Стереометрія
Тема: Піраміда
Кількість завдань: 45
ТЕМА: Прямі та площини в просторі. Многогранники.
Завдання скеровано на перевірку знання взаємного розміщення прямих і площин у просторі, властивостей піраміди.
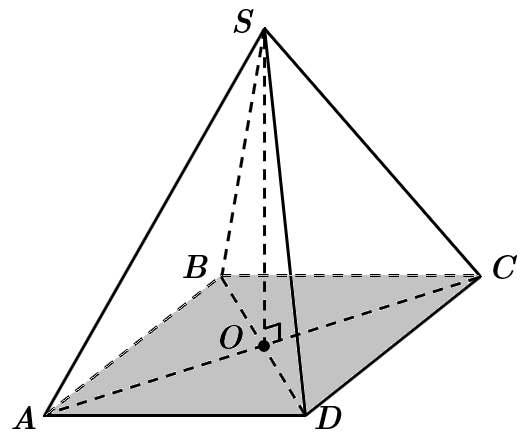
Висота піраміди
Відповідь: Д.
ТЕМА: Тіла обертання. Многогранники.
Завдання скеровано на перевірку знання властивостей піраміди та сфери, формул для обчислення площі поверхні сфери й об’єму піраміди.
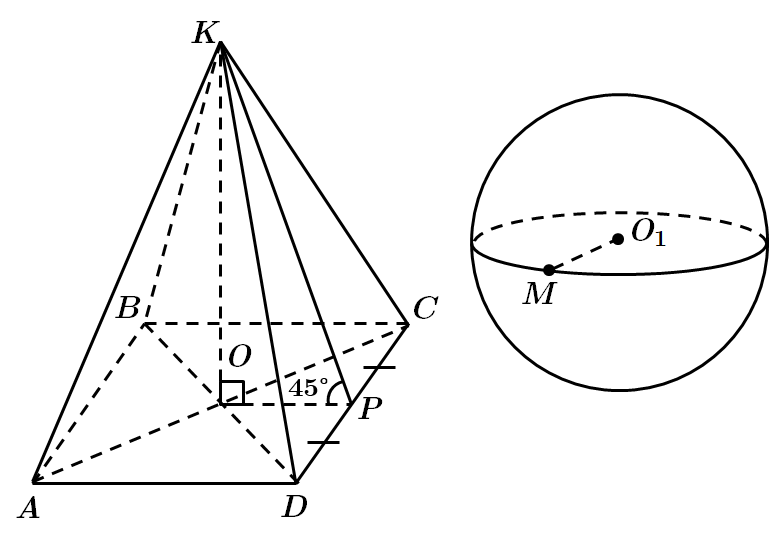
За умовою, радіус кола, описаного навколо квадрата
Об'єм піраміди
У
Відповідь:
ТЕМА: Многогранники.
Завдання скеровано на перевірку знання про піраміду та її елементи.
У піраміді
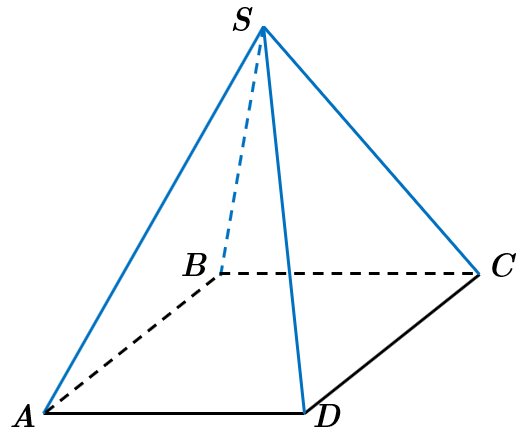
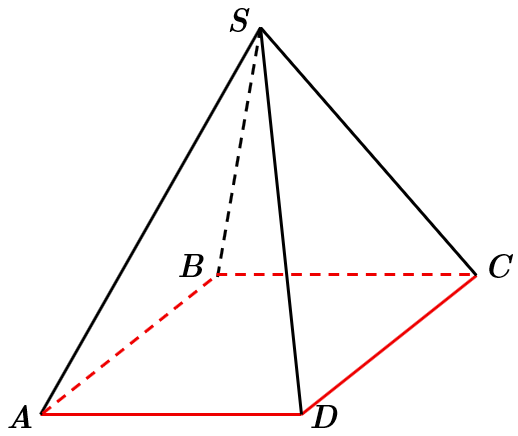
Відповідь: Г.
ТЕМА: Геометрія. Стереометрія. Многогранники, тіла обертання.
Завдання скеровано на перевірку знань властивостей піраміди та конуса, вміння розв’язувати задачі на обчислення площ поверхонь геометричних тіл.
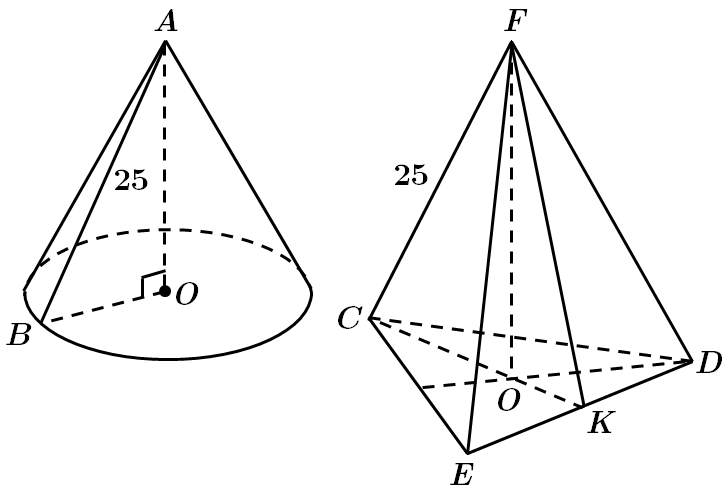
Твірна консуса
Площа бічної поверхні конуса
У піраміді
Площа бічної поверхні піраміди
Відповідь:
ТЕМА: Геометрія. Планіметрія. Стереометрія. Чотирикутники. Многогранники.
Завдання скеровано на перевірку знання про піраміду та її елементи, вміння знаходити площу ромба та об’єм піраміди.
Об'єм піраміди обчислуємо за формулою:
За умовою завдання основою піраміди є ромб, діагоналі якого
Відповідь: Д.
ТЕМА: Геометрія. Стереометрія. Многогранники.
Завдання скеровано на перевірку знання формул для обчислення площ поверхонь піраміди.
Сторона основи піраміди
За формулою
Відповідь: Г.
ТЕМА: Геометрія. Стереометрія. Многогранники. Піраміда.
Завдання скеровано на перевірку знань властивостей піраміди та її елементів, розв’язування задач на трикутники.
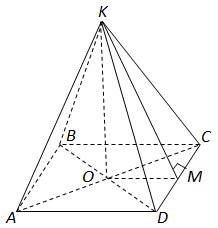
1. Піраміда правильна – в основі лежить квадрат
2.
За теоремою про три перпендикуляри
4.
Відповідь: Г.
ТЕМА: Геометрія. Стереометрія. Многогранники.
Завдання перевіряє вміння розв’язувати стереометричні задачі, знання властивостей піраміди.
Об'єм піраміди знаходимо за формулою
Піраміда правильна, тому в основі лежить квадрат. Сторона квадрата –
Отже,
Відповідь: Г.
ТЕМА: Геометрія. Стереометрія. Планіметрія. Многогранники. Трикутники. Чотирикутники.
Завдання перевіряє вміння розв’язувати стереометричні задачі на обчислення невідомих елементів піраміди, знання теореми Піфагора та властивості квадрата.
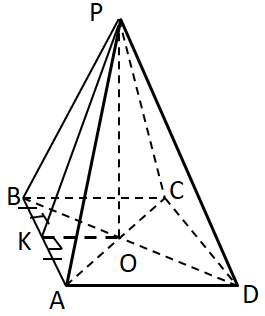
Відповідь: Г.
ТЕМА: Геометрія. Стереометрія. Многогранники.
Перевіряє знання про многогранники та їхні елементи, основні види многогранників: призму, паралелепіпед, піраміду.
На рисунку зображена розгортка чотирикутної піраміди. Отже, правильна відповідь – Б.
Відповідь: Б.
ТЕМА: Геометрія. Стереометрія. Планіметрія. Многогранники. Трикутники. Чотирикутники.
Завдання перевіряє вміння розв’язувати стереометричні задачі, знання теореми Піфагора та властивості квадрата.
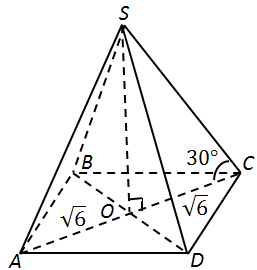
1.
2.
Oтже, 2 – A.
3. У правильній піраміді бічні ребра рівні
Oтже, 3 – Б.
Відповідь: 1Г, 2А, 3Б.
ТЕМА: Геометрія. Стереометрія. Многогранники.
Завдання скеровано на перевірку вміння розв’язувати задачі на обчислення площ поверхонь геометричних тіл.
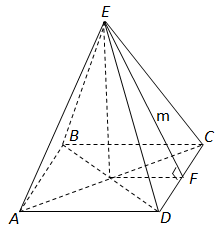
За формулою
запишемо площу бічної поверхні (де
Отже,
Відповідь: В.
ТЕМА: Геометрія. Стереометрія. Многогранники.
Завдання скеровано на перевірку вміння розв’язувати задачі на обчислення площ поверхонь геометричних тіл.
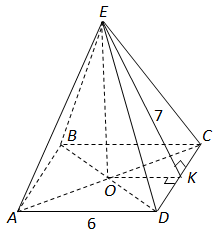
Відповідь: Д.
ТЕМА: Геометрія. Стереометрія. Многогранники. Прямі та площини у просторі.
Завдання скеровано на перевірку вміння знаходити кути у просторі, знання про двогранний кут, лінійний кут двогранного кута.
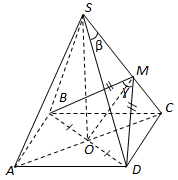
1.
2. 1)
2)
3)
4)
Відповідь:
ТЕМА: Геометрія. Стереометрія. Многогранники.
Завдання скеровано на перевірку вміння розв’язувати задачі на обчислення об’ємів геометричних тіл, знання основних властивостей піраміди.
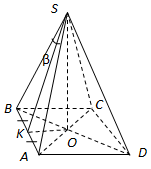
1.
2.
3.
Відповідь: 2.
3.
ТЕМА: Геометрія. Стереометрія. Многогранники.
Завдання перевіряє вміння розв’язувати задачі на обчислення об’ємів піраміди.
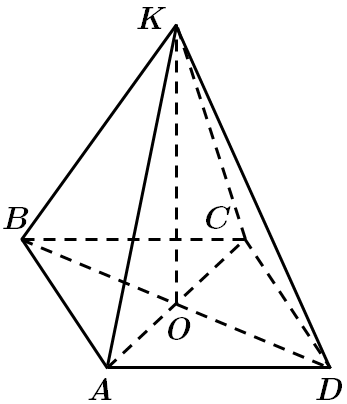
У квадраті
У
Об'єм піраміди знаходимо за формулою:
Відповідь:
ТЕМА: Геометрія. Стереометрія. Планіметрія. Многогранники. Трикутники. Чотирикутники.
Завдання перевіряє вміння розв’язувати задачі на обчислення об’єму піраміди, знання теореми Піфагора та властивості квадрата.
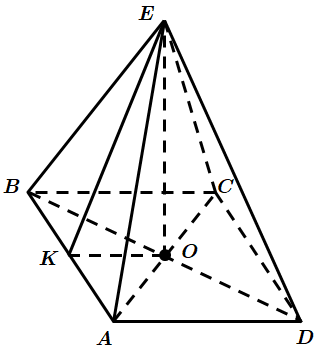
У
Відповідь:
ТЕМА: Геометрія. Стереометрія. Многогранники.
Завдання перевіряє знання властивостей піраміди, означення кута між прямою та площиною.
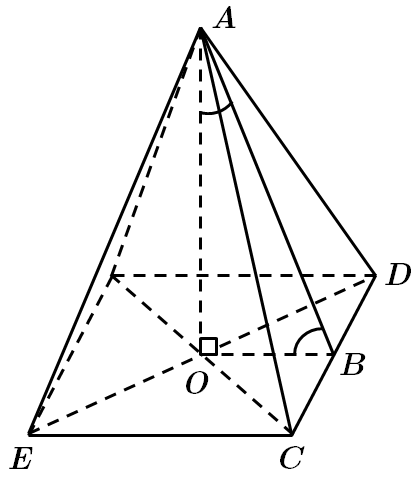
Висота піраміди
Отже,
Відповідь: Г.
ТЕМА: Геометрія. Стереометрія. Многогранники.
Це завдання перевіряє вміння розв'язувати задачі на обчислення площ поверхонь геометричних тіл, знання многогранників та їхніх елементів.
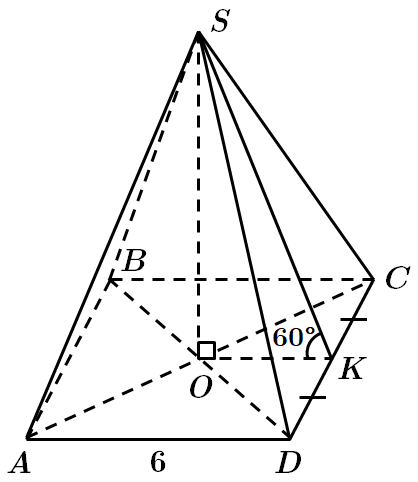
Відповідь: A.
ТЕМА: Геометрія. Стереометрія. Многогранники.
Це завдання перевіряє знання про піраміду, формулу об'єму піраміди.
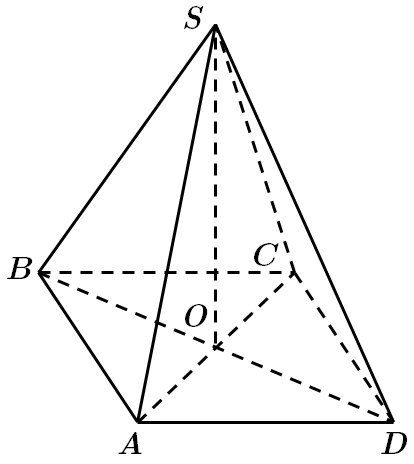
Піраміда
Відповідь: Б.

ТЕМА: Геометрія. Стереометрія. Многогранники.
Це завдання перевіряє вміння розв'язувати задачі на обчислення площ поверхонь геометричних тіл.
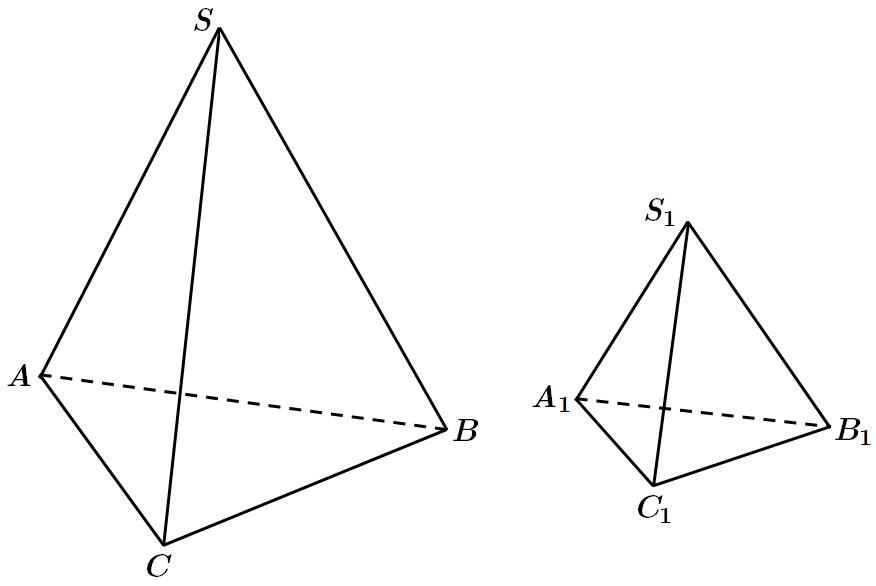
Дано
Відношення площ подібних трикутників дорівнює квадрату відношення відповідних сторін:
Площа бічної поверхні піраміди
Відповідь: Д.
ТЕМА: Геометрія. Стереометрія. Многогранники.
Це завдання перевіряє вміння застосовувати означення та властивості основних видів многогранників, знання формули для обчислення площі поверхні.
Дано: правильна трикутна піраміда, тому основа – правильний трикутник, основа висоти – центр трикутника.
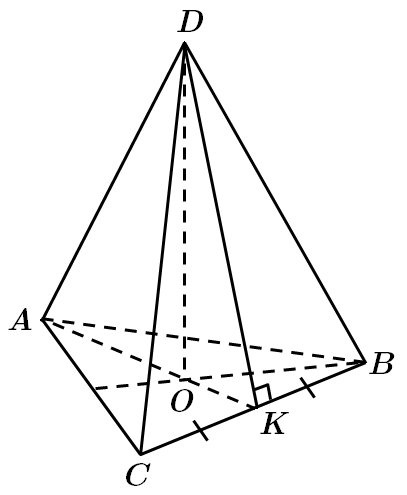
У
Відповідь: A.
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Многогранники, тіла й поверхні обертання.
Це завдання перевіряє вміння застосовувати означення та властивості піраміди до розв’язування стереометричних задач, знаходити відстані в просторі, використовувати пряму та обернену теореми про три перпендикуляри.
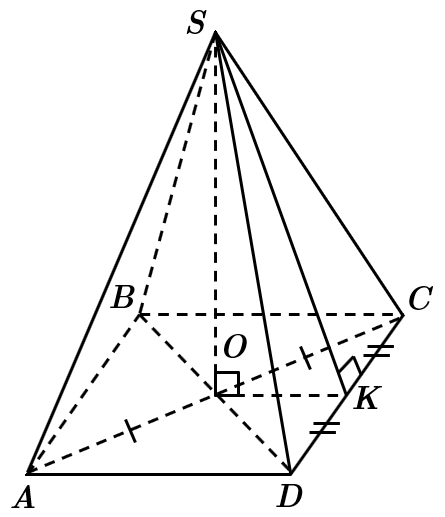
Піраміда – правильна, тому основа – квадрат, основа висоти – центр квадрата (точка перетину діагоналей).
Відповідь: Г.