Алгебра і початки аналізу – Показникові, логарифмічні рівняння та системи рівнянь

ТЕМА: Показникові. Раціональні рівняння.

Завдання скеровано на перевірку вміння розв’язувати показникові та раціональні рівняння, рівняння з параметром.

Область допустимих значень:

Дріб дорівнює нулю за умови, що чисельник дорівнює нулю, а знаменник – ні.

За умовою корінь \(x\) має бути додатним і задовольняти ОДЗ. Тобто \(x\gt 0\) та \(x\lt 2.\) Отже, \(0\lt x\lt 2.\)

Підставмо \(x\) у нерівність:

Оскільки \(a\) – ціле число, то \(a=5\mathord{,}\ 6\mathord{,}\ 7\mathord{,}\ 8.\)

Сума значень \(a:\) $$ 5+6+7+8=26. $$

Відповідь: \(26.\)

ТЕМА: Логарифмічні рівняння.

Завдання скеровано на перевірку вміння розв’язувати логарифмічні рівняння.

Застосуймо властивості алгоритмів:

Зведімо обидві сторони рівняння до логарифмів з однаковою основою:

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Показникові рівняння.

Завдання скеровано на перевірку вміння розв’язувати показникові рівняння, виконувати тотожні перетворення степеневих виразів.

Зведемо до однакової основи ліву та праву частину показникового рівняння:

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Логарифмічні рівняння.

Завдання скеровано на перевірку вміння розв’язувати логарифмічні рівняння.

Використали означення логарифма: \(\log_ab=c\), \(a^c=b\) та застосували формулу: $$ a^{-n}=\frac{1}{a^n}. $$

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання скеровано на перевірку вміння розв’язувати логарифмічні рівняння, аналізувати та досліджувати рівняння, розв’язувати рівняння з параметром.

$$ \lg(2ax+5-a)=\lg(4x) $$ ОДЗ:

Лінійне рівняння не має коренів при \(a=2.\)

При \(a\ne 2\ \ x=\frac{a-5}{2a-4}.\)

Логарифмічне рівняння не буде мати розв'язок, якщо \(x\le 0.\) Знайдемо такі значення:

$$ \frac{a-5}{2a-4}\le 0, $$

$$a\in (2; 5].$$ Отже, рівняння не буде мати розв'язків, якщо \(a\in [2; 5],\) включаючи значення \(2.\) Сума всіх цілих значень \(a\) $$ 2+3+4+5=14. $$

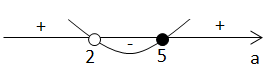
Відповідь: 14.

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання скеровано на перевірку вміння розв’язувати показникові рівняння.

Зведемо до однакової основи: \begin{gather*} 3^{x^2}=3^4,\ \ x^2=4,\\[7pt] x=2\ \ \text{або}\ \ x=-2. \end{gather*}

Рівняння має два корені. Найменший з них \(x=-2.\) Він належить проміжку \([-2; 0).\)

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати логарифмічні рівняння.

\(\log_{\frac 13}(x+1)=-2.\) За означенням логарифма \begin{gather*} x+1=\left(\frac 13\right)^{-2},\ \ x+1=3^2,\\[6pt] x+1=9,\ \ x=8 \in (7; 9]. \end{gather*}

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати системи рівнянь першого степеня та показникових.

Розв'яжемо систему рівнянь: \begin{gather*} \left\{ \begin{array}{l} x+y=5,\\ 4^x=16^{-1}; \end{array} \right. \ \ \ \ \left\{ \begin{array}{l} x+y=5,\\ 4^x=4^{-2}; \end{array} \right. \\[7pt] \left\{ \begin{array}{l} -2+y=5,\\ x=-2; \end{array} \right. \ \ \ \ \left\{ \begin{array}{l} y=7,\\ x=-2. \end{array} \right. \end{gather*} \(x_0=-2;\ y_0=7.\) Отже $$ x_0\cdot y_0=-2\cdot 7=-14. $$

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати логарифмічні рівняння, аналізувати та досліджувати рівняння, розв’язувати рівняння з параметром.

\(\log_2^2x-(a-1)\log_2x-a=0.\)

ОДЗ: \(x\gt 0.\)

Зробимо заміну: \(\log_2x=t.\)

Корені квадратного рівняння:

\begin{gather*} t_1=\frac{(a-1)+(a+1)}{2}=a\\[6pt] t_2=\frac{a-1-(a+1)}{2}=-1. \end{gather*}

Повертаємось до заміни:

\begin{gather*} \left[ \begin{array}{l} \log_2x=-1,\\ \log_2x=a; \end{array} \right. \ \ \ \left[ \begin{array}{l} x_1=\frac 12,\\ x_2=2^a. \end{array} \right. \end{gather*}

\(x_1\notin (30;\ 100),\) тому даному проміжку повинен належати \(x_2.\)

\begin{gather*} 30\lt x_2\lt 100,\ \ 30\lt 2^a\lt 100.\\[7pt] \text{при}\ a=5\ (a\in \mathbb{Z}). \end{gather*}

Наймеше значення \(a=5.\)

Відповідь: 5.

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання перевіряє вміння розв’язувати показникові рівняння.

Розв'яжемо показникове рівняння: \begin{gather*} \left(\frac 13\right)^{2x-1}=9. \end{gather*}

Зведемо до однакової основи: \begin{gather*} \left(\frac 13\right)^{2x-1}=\left(\frac 13\right)^{-2}\\[6pt] 2x-1=-2,\ \ 2x=-2+1,\\[6pt] 2x=-1,\ \ x=-\frac 12. \end{gather*}

Корінь рівняння \(x=-0,5\) належить проміжку \((-1;\ 0].\)

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати показникові, квадратні рівняння та рівняння з параметрами.

1. Розв'яжемо систему, якщо \(a=0\).

2. Визначимо всі розв'язки системи:

Розв'яжемо квадратне рівняння:

\(D\geq 0\) при будь-якому значенні \(a\).

Знайдемо значення \(y\): \begin{gather*} \text{якщо}\ x_2=-1,\ \text{то}\ 3^{y^2}=\frac{8-(-1)}{3}=3\\[6pt] y^2=1,\ \ y=1\ \text{або}\ y=-1. \end{gather*}

Отже, \((-1;\ 1),\ (-1;\ -1)\) – розв'язки системи при всіх значеннях \(a\).

якщо \(x_1=\frac 3a\), то

Якщо \(y^2\geq 0\), то \(3^{y^2}\geq 1\).

Отже, розв'язки \(\left(\frac 3a;\ \sqrt{\log_3\frac{8a-3}{3a}}\right)\) та \(\left(\frac 3a;\ -\sqrt{\log_3\frac{8a-3}{3a}}\right)\) будуть розв'язками системи за умови \begin{gather*} \frac{8a-3}{3a}\geq 1,\ \ \frac{8a-3-3a}{3a}\geq 0,\\[6pt] \frac{5a-3}{3a}\geq 0,\ \ \frac{5(a-0,6)}{3a}\geq 0 \end{gather*}

розв'яжемо методом інтервалів:

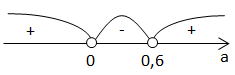
Відповідь:
1. \((-1;\ -1)\ (-1;\ 1)\)
2. якщо \(a\in [0;\ 0,6)\), то розв'язком є \((-1;\ 1)\) i \((-1;\ 1)\)
якщо \(a\in (-\infty;\ 0)\cup [0,6;\ +\infty)\), то розв'язками системи є \((-1;\ 1);\ (-1;\ -1); \left(\frac 3a;\ \sqrt{\log_3\frac{8a-3}{3a}}\right);\) \(\left(\frac 3a;\ -\sqrt{\log_3\frac{8a-3}{3a}}\right)\).

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати показникові, квадратні рівняння та рівняння з параметрами.

1. Розв'яжемо систему, якщо \(a=0\).

Підставимо у друге рівняння замість \(4^{\sqrt{y}}\) число 2.

Отже, за \(a=0\) розв'язком системи є \((-3;\ 0,25)\).

2. Нехай \(a\ne 0\).

Почленно додамо рівняння \begin{gather*} ax^2+3ax+4\cdot 4^{\sqrt{y}}-2x-4\cdot 4^{\sqrt{y}}+2=8\\[7pt] ax^2+3ax-2x-6=0,\\[7pt] ax^2+(3a-2)x-6=0. \end{gather*}

Отримаємо квадратне рівняння.

Система рівносильна сукупності систем:

Оскільки \(4^{\sqrt{y}}\geq 1\ \left(y\geq 0,\ \sqrt{y}\geq 0,\ 4^{\sqrt{y}}\geq 4^0\right)\), отримуємо

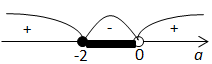
Тоді \begin{gather*} \left\{ \begin{array}{l l} x=\frac 2a, & \\ \sqrt{y}=\log_4\frac{a-2}{2a}, & \end{array}\right. \left\{ \begin{array}{l l} x=\frac 2a, & \\ y=\log^2_4\frac{a-2}{2a}. & \end{array}\right. \end{gather*}

Відповідь:
1. \((-3;\ 0,25)\)
2. якщо \(a\in (-\infty;\ -2)\cup [0;\ +\infty)\), то розв'язком є \((-3;\ 0,25)\)
якщо \(a\in [-2;\ 0)\), то розв'язками є \((-3;\ 0,25)\) та \(\left(\frac 2a;\ \log^2_4\frac{a-2}{2a}\right)\).

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати логарифмічні, квадратні рівняння та рівняння з параметрами.

1. Знайдемо множину допустимих значень змінної \(x\):

2. Розв'яжемо рівняння залежно від значень \(a\): \begin{gather*} \left\{ \begin{array}{ l l} \left[ \begin{array}{l l} x-2=0 & \\ x^2-3(a-1)x+2a^2-3a=0& \end{array}\right. &\\ x\in (-\infty;\ -0,5)\cup (-0,5;\ 1,5) & \end{array}\right. \end{gather*}

1) \(x-2=0,\ \ x=2\ \notin\) ОДЗ.

2) \(x^2-3(a-1)x+2a^2-3a=0\).

Розв'яжемо квадратне рівняння: \begin{gather*} D=\left(-3(a-1)\right)^2-4(2a^2-3a)=\\[7pt] =9(a^2-2a+1)-8a^2+12a=(a-3)^2\\[6pt] x_1=\frac{3(a-1)+(a-3)}{2}=2a-3;\\[6pt] x_2=\frac{3(a-1)-(a-3)}{2}=a. \end{gather*}

Знайдемо значення переметра \(a\), при яких \(x_1=2a-3\) належить ОДЗ: \begin{gather*} \left[ \begin{array}{l l} 2a-3\lt -0,5 & \\ -0,5\lt 2a-3\lt 1,5& \end{array}\right. \left[ \begin{array}{l l} a\lt 1,25 & \\ 1,25\lt a\lt 2,25& \end{array}\right. \\[7pt] a\in (-\infty;\ 1,25)\cup (1,25;\ 2,25). \end{gather*} Для кореня \(x_2=a\) \begin{gather*} \left[ \begin{array}{l l} a\lt -0,5 & \\ a\in (-0,5;\ 1,5)& \end{array}\right. \\[7pt] a\in (-\infty;\ -0,5)\cup (-0,5;\ 1,5). \end{gather*}

Відповідь:
якщо

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання перевіряє вміння розв'язувати логарифмічні рівняння, знання числових проміжків.

За означенням логарифма \begin{gather*} \log_ab=c,\ \ b=a^c,\\[6pt] \log_{\frac 13}(x+1)=-2,\ \ x+1=\left(\frac 13\right)^{-2},\\[6pt] x+1=3^2,\ \ x+1=9,\ \ x=8.\\[7pt] 7\lt 8\le 9. \end{gather*} Отже, \(x\in (7; 9].\)

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати логарифмічні рівняння, порівнювати дійсні числа.

За означенням логарифма $$ x=64^{\frac 12}=\sqrt{64}=8 $$ \(6\lt 8\lt 32\) – проміжок, якому належить корінь.

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Рівняння і нерівності.

Завдання перевіряє вміння розв'язувати логарифмічн рівняння.

\begin{gather*} 4+\log_{\frac 12}x=0,\\[6pt] \log_{\frac 12}x=-4. \end{gather*} За означенням логарифма $$ x=\left(\frac 12\right)^{-4}=2^4=16. $$

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Рівняння.

Це завдання перевіряє вміння розв'язувати показникові рівняння.

Корінь рівняння належить проміжку \([1; 2).\) Отже, правильна відповідь Г.

Відповідь: Г.

ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Показникові рівняння.

Це завдання перевіряє вміння розв'язувати показникові рівняння.

\(3^{7x}=9,\) \(3^{7x}=3^2\), \(7x=2.\)

\(x=2:7\), \(x=0\mathord{,}28\text{...}\), \(x\approx 0\mathord{,}3\) якщо округлити до десятих.

Відповідь: B.

ТЕМА: Рівняння, нерівності та їхні системи. Логарифмічні рівняння.

Це завдання перевіряє вміння розв'язувати рівняння, що містять логарифмічні вирази, знання властивостей логарифма.

Застосуємо означення логарифма

Відповідь: Г.

ТЕМА: Рівняння, нерівності та їхні системи. Показникові нерівності.

Це завдання перевіряє вміння розв'язувати нерівності, що містять показникові вирази, застосовувати загальні методи та прийоми (застосування властивостей функцій) у процесі розв'язування нерівності.

Винесемо спільний множник \(2^x\) за дужки:

Функція \(y=2^x\) зростаюча, тому \(x\ge 4\), \(x\in [4; +\infty).\)

Відповідь: Б.

ТЕМА: Рівняння, нерівності та їхні системи. Логарифмічні рівняння. Функціональна залежність. Логарифмічна функція.

Це завдання перевіряє вміння розв'язувати логарифмічні рівняння.

\(\log_4(x-1)=3.\) За означенням логарифма можна записати \(x-1=4^3.\)

Звідси \(x-1=64\), \(x=65.\)

Відповідь: Г.

ТЕМА: Рівняння, нерівності та їхні системи. Показникові рівняння.

Це завдання перевіряє вміння розв'язувати показникові рівняння.

Отже, корінь рівняння \(x=4.\)

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи. Логарифмічні рівняння.

Це завдання перевіряє вміння розв'язувати логарифмічні рівняння.

Використаємо властивість логарифма: $$ \log_a b^n=n\cdot \log_a b, $$

Звідси, \(x=9\) корінь рівняння. Проміжок, якому належить корінь рівняння \((8; 10].\)

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Рівняння, нерівності та їхні системи.

Це завдання перевіряє знання означення степеня з раціональним показником, уміння розв’язувати показникові та лінійні рівняння.

Відповідь: B.