Розділ: Функції
Тема: Степеневі, показникові, логарифмічні та тригонометричні функції
Кількість завдань: 59
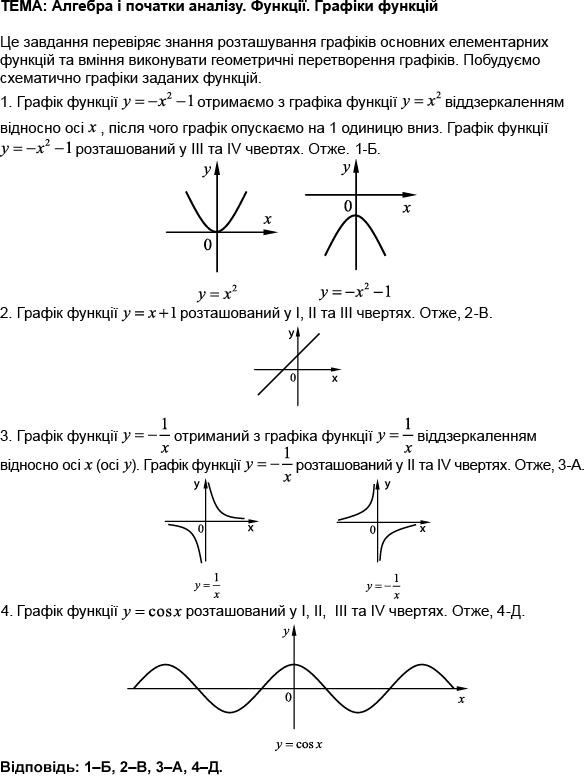
ТЕМА: Функціональна залежність. Степеневі, тригонометричні функції.
Завдання скеровано на перевірку вміння встановлювати властивості числових функцій, заданих формулою.
1.
Отже, правильна відповідь – Д.
2.
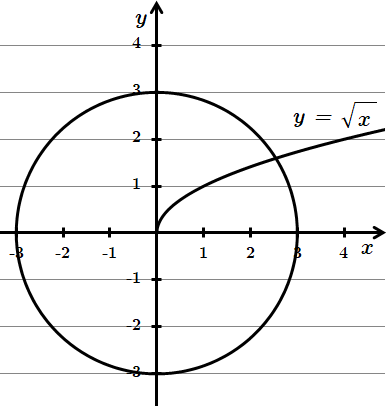
Отже, правильна відповідь – Б.
3.
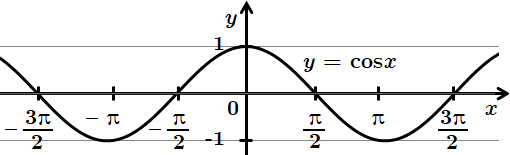
Функція
Відповідь: 1 – Д, 2 – Б, 3 – А.
ТЕМА: Показникова функція.
Завдання скеровано на перевірку вміння застосовувати властивості перетворення графіків функцій, знання властивостей показникової функції.
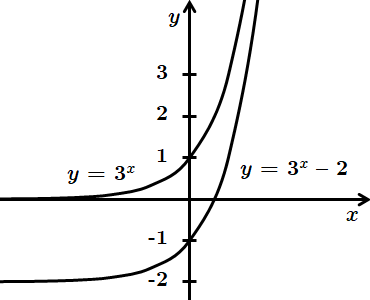
Графік функції
За властивістю елементарних перетворень переміщення вздовж осі
Запис
Відповідь: А.
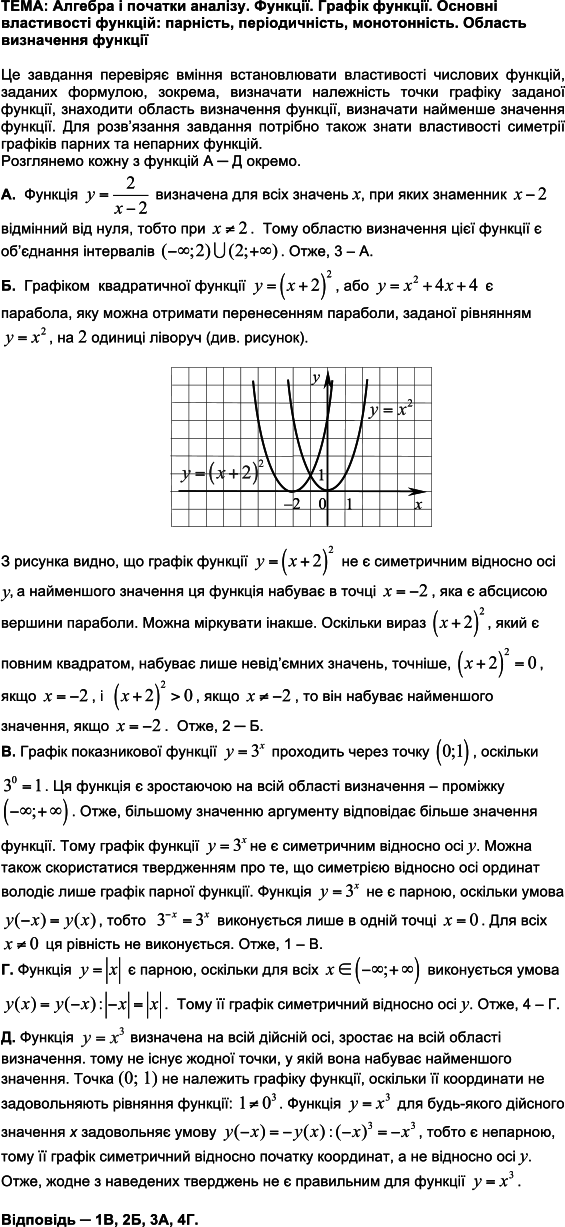
ТЕМА: Алгебра і початки аналізу. Функціональна залежність.
Завдання скеровано на перевірку вміння будувати графіки функцій, встановлювати властивості числових функцій.
1. Набуває всіх значень з проміжку
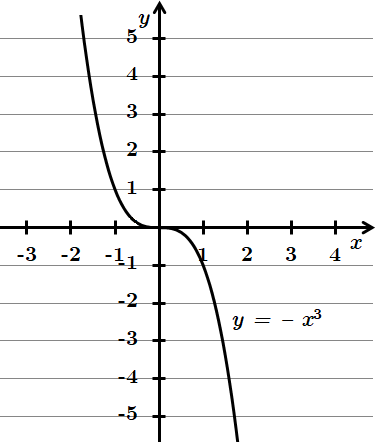
Отже, 1 – Г.
2. Графік функції має з графіком рівняння
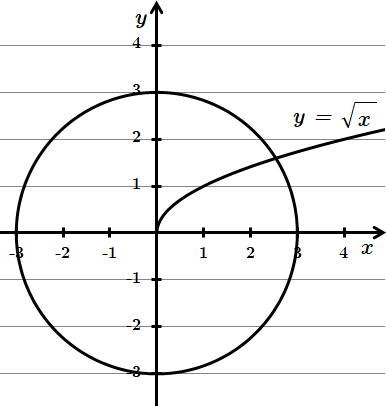
Отже, 2 – Б.
3.
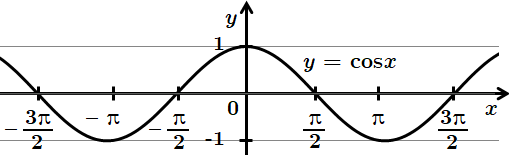
Відповідь: 1Г, 2Б, 3В.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння встановлювати властивості числових функцій, заданих графіком.
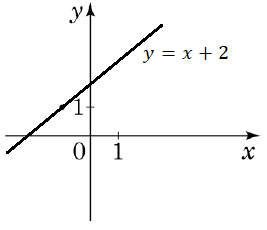
Графік лінійної функції
Відповідь: В.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння встановлювати властивості числових функцій, заданих графіком.
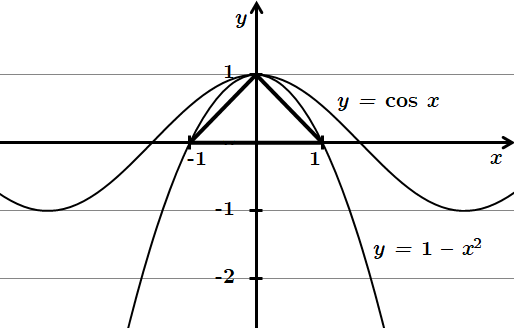
1.
2. Спільних точок параболи
3. Спільних точок функції
Відповідь: 1Д 2Г 3Б.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння встановлювати властивості числових функцій, заданих формулою чи графіком.
1.
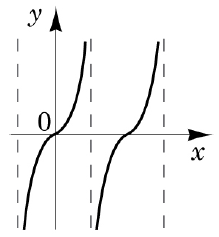
2.
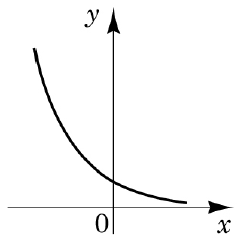
3.
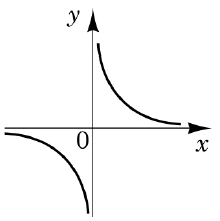
Відповідь: 1Г 2Д 3А.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння виконувати перетворення графіків функцій.
Графік функції
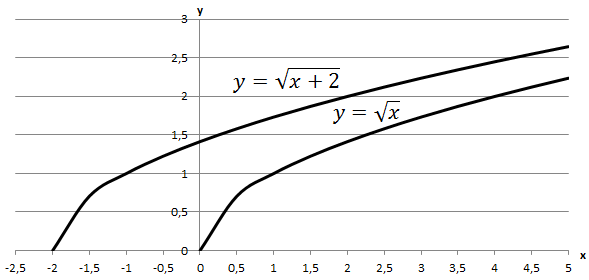
Відповідь: Г.
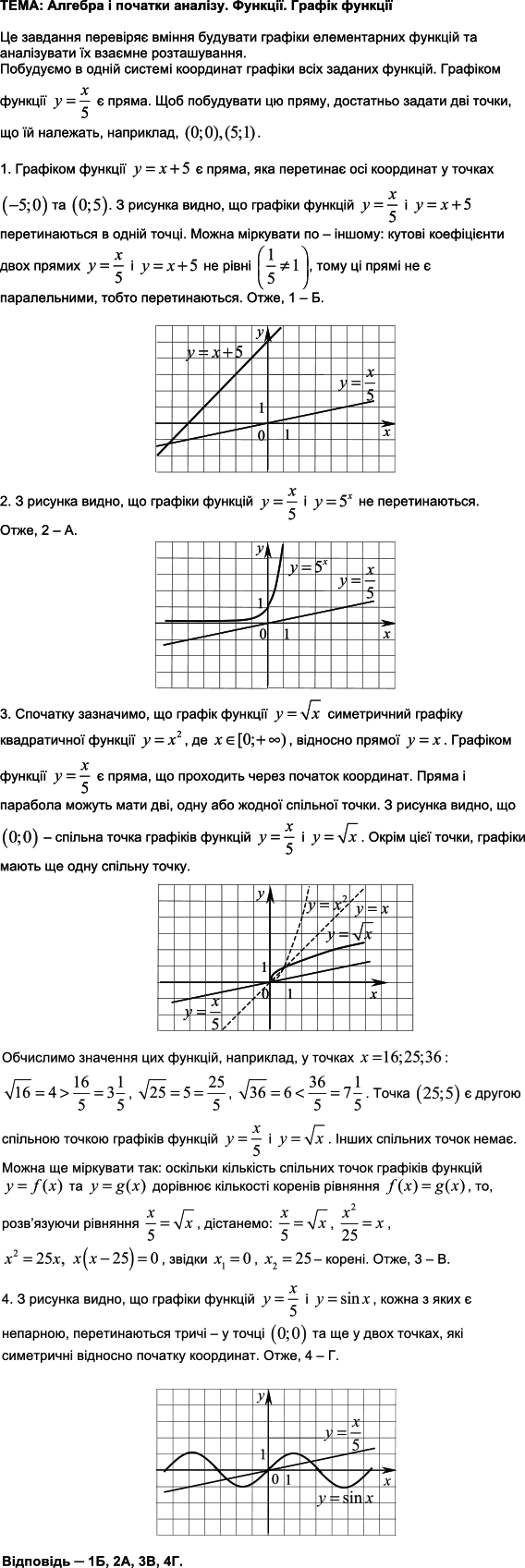
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння установлювати властивості числових функцій, заданих формулою або графіком.
Побудуємо задані графіки функцій
1.
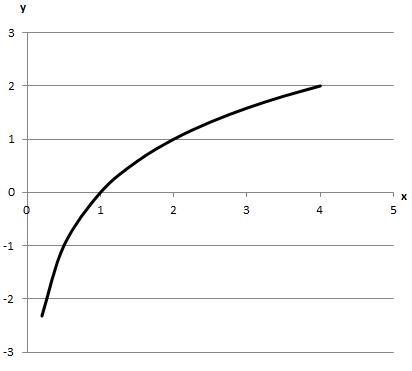
Не перетинає вісь
2.
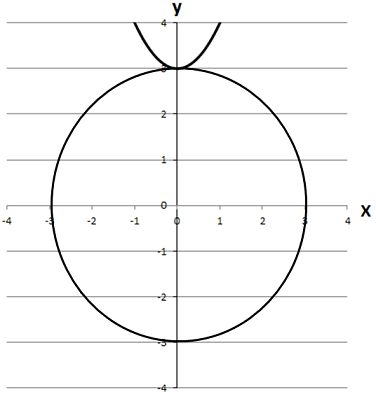
Має лише одну спільну точку з графіком рівняння
3.
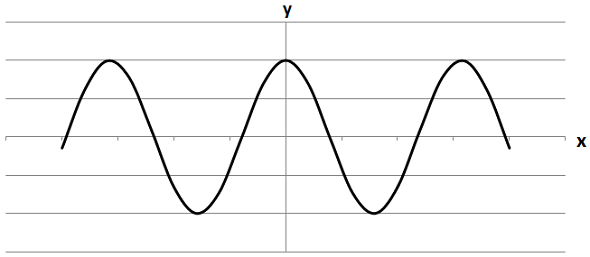
Розташований у всіх координатних чвертях. Отже, 3 - В.
Відповідь: 1А, 2Г, 3В.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння встановлювати властивості числових функцій, заданих формулою.
1.
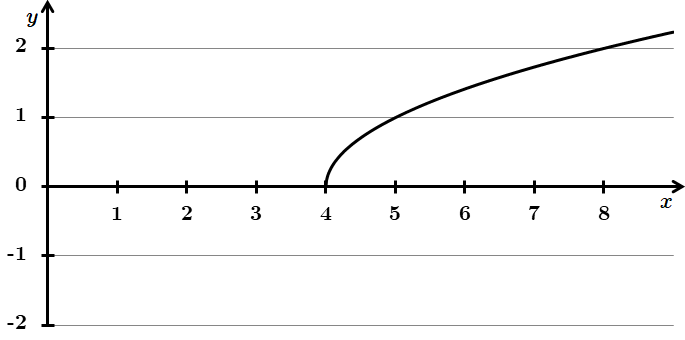
Отже, 1 – Б.
2.
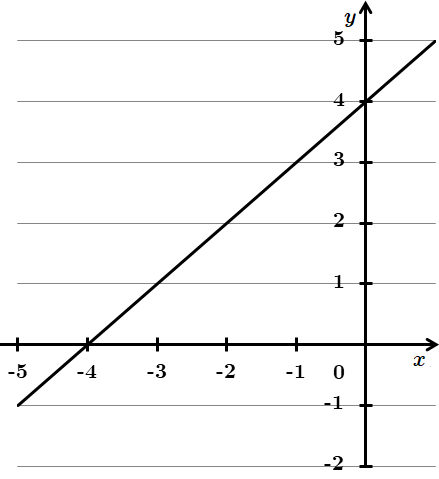
Отже, 2 – Г.
3.
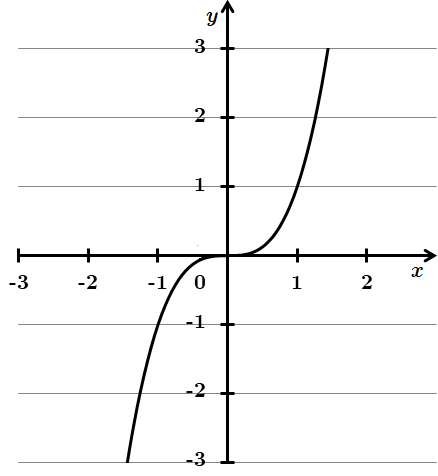
Отже, 3 – Д.
Відповідь: 1 – Б, 2 – Г, 3 – Д.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння встановлювати властивості числових функцій, заданих формулою або графіком.
1.
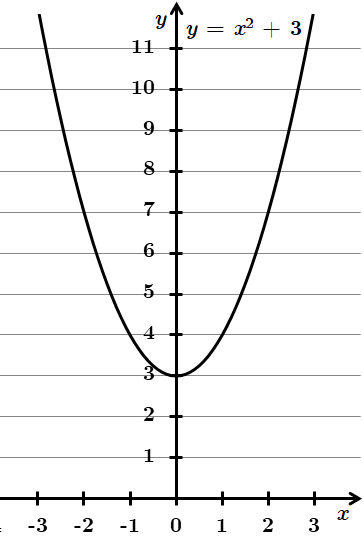
Симетричний відносно осі y. Отже, 1 – A.
2.
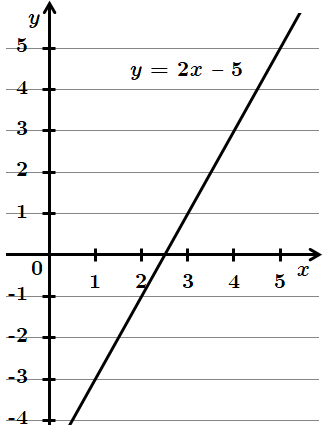
Набуває від'ємного значення в точці
3.
Симетричний відносно початку координат. Отже, 3 – Д.
Відповідь: 1 – A, 2 – B, 3 – Д.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє знання властивостей тригонометричної функції.
Відповідь: B.
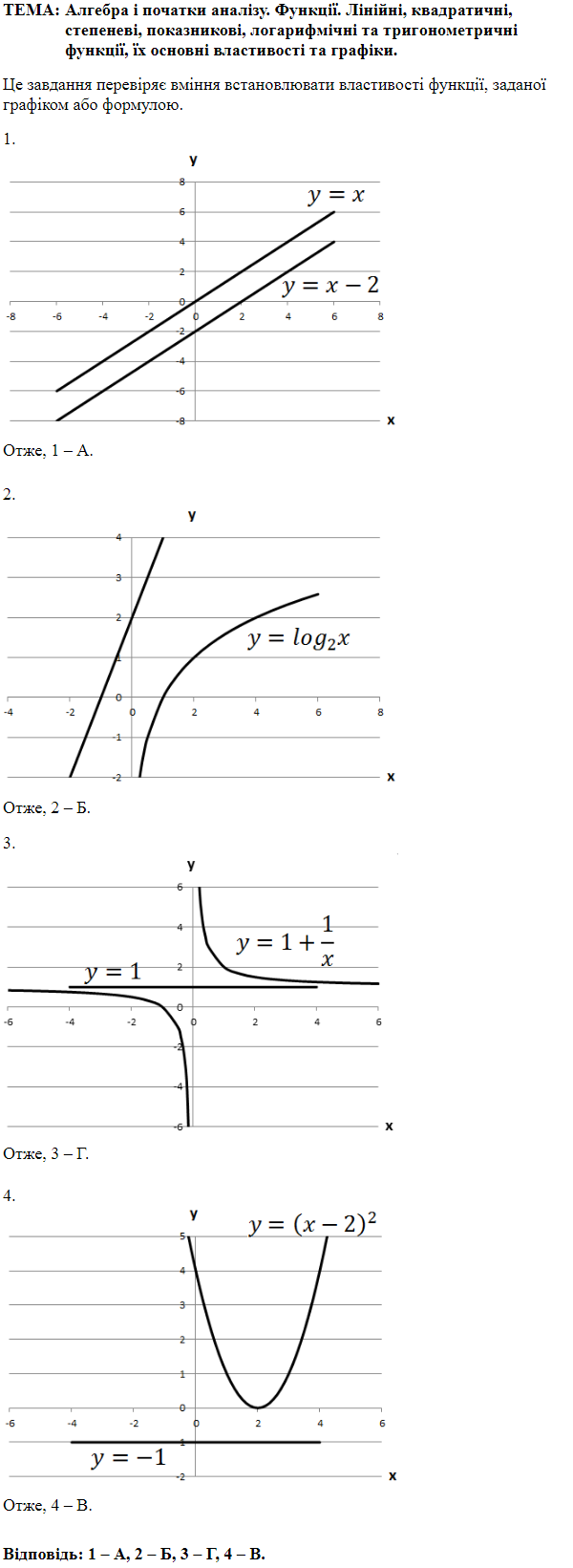
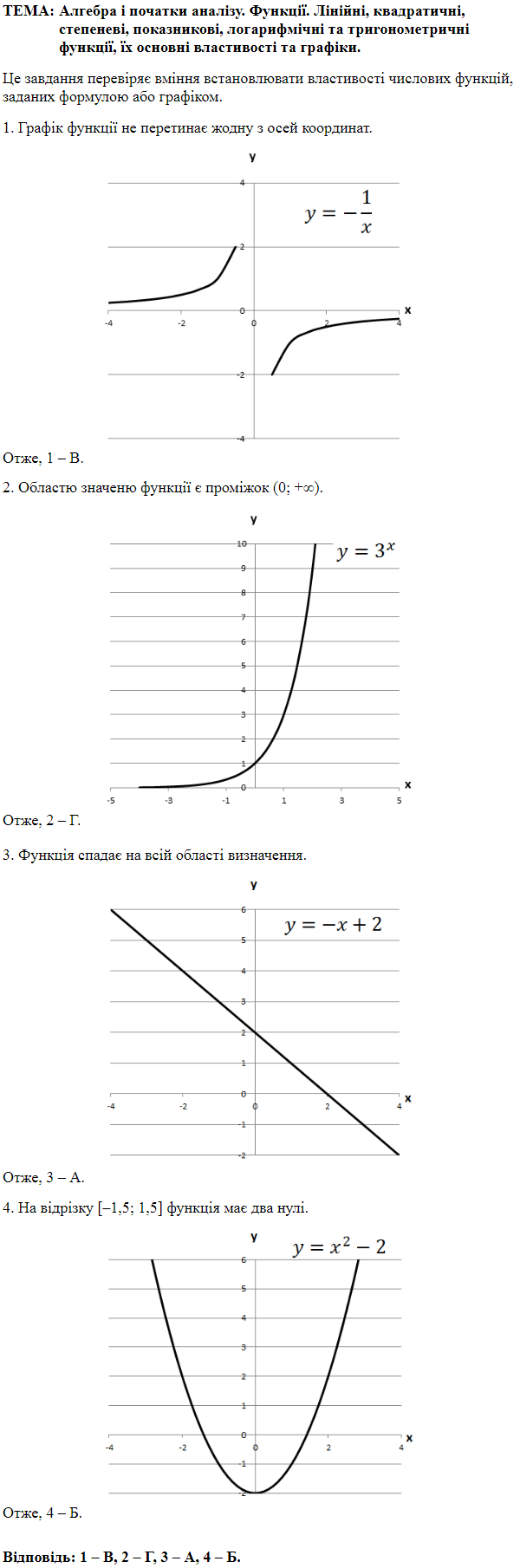
ТЕМА: Алгебра і початки аналізу. Функції. Лiнiйнi, квадратичні, степеневі, показникові, логарифмiчнi та триroнометричнi функції, їх основні властивості та графіки.
Це завдання перевіряє вміння встановлювати властивості функції, заданої графіком.
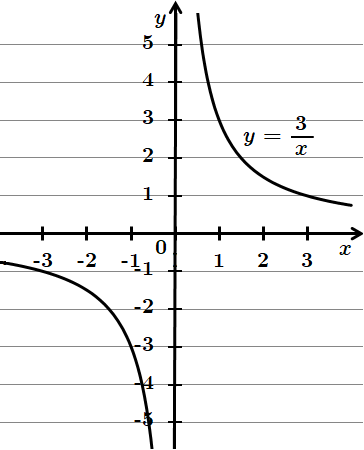
1.
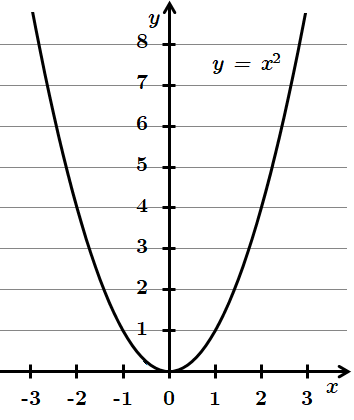
2.
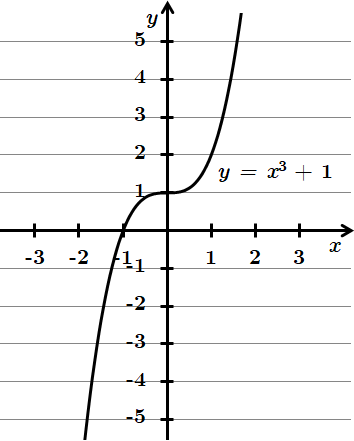
3.
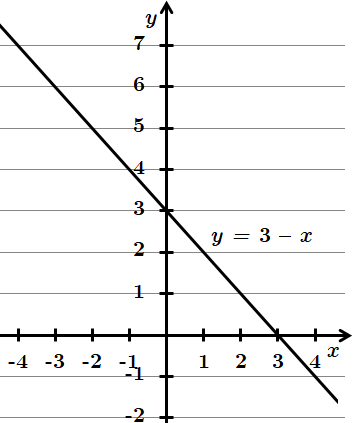
4.
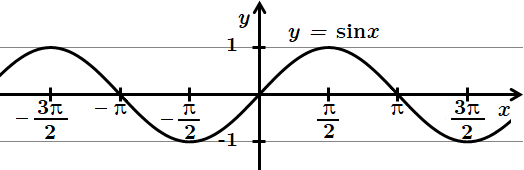
Відповідь: 1 – Г, 2 – Б, 3 – А, 4 – B.
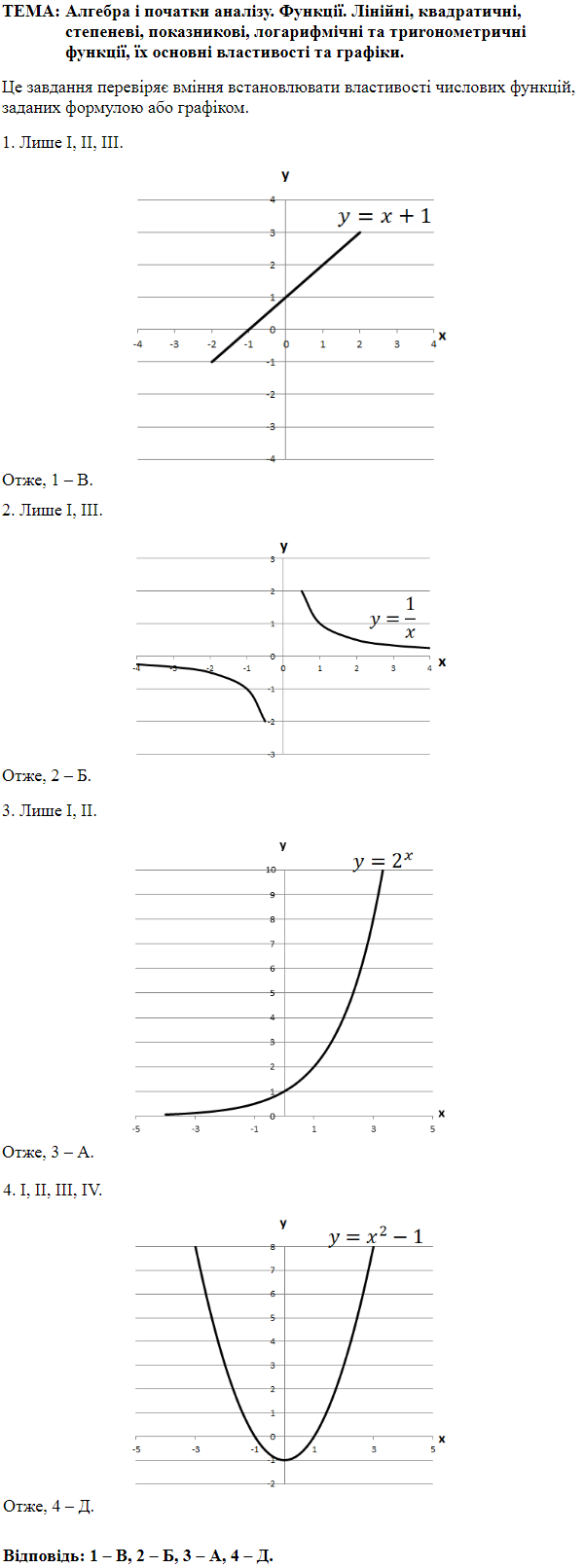
ТЕМА: Алгебра і початки аналізу. Функції. Лінійні, квадратичні, тригонометричні, логарифмічні функції.
Це завдання перевіряє вміння будувати графіки елементарних функцій, встановлювати властивості числових функцій, заданих формулою або графіком.
1.
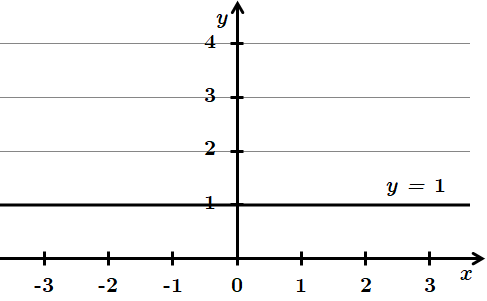
Не має спільних точок з віссю
2.
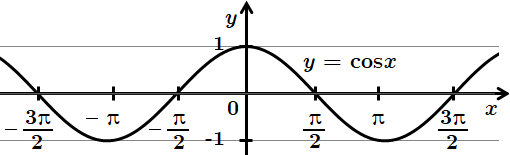
Має безліч спільних точок з віссю
3.
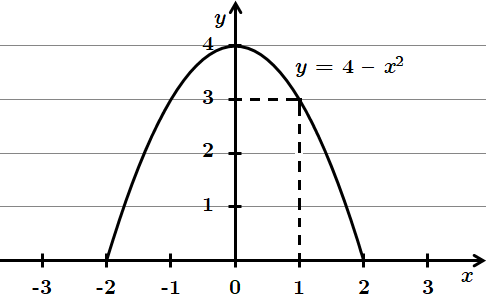
Проходить через точку
4.
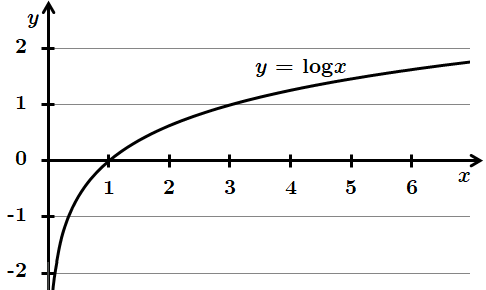
Не перетинає вісь
Відповідь: 1 – Г, 2 – B, 3 – Д, 4 – A.
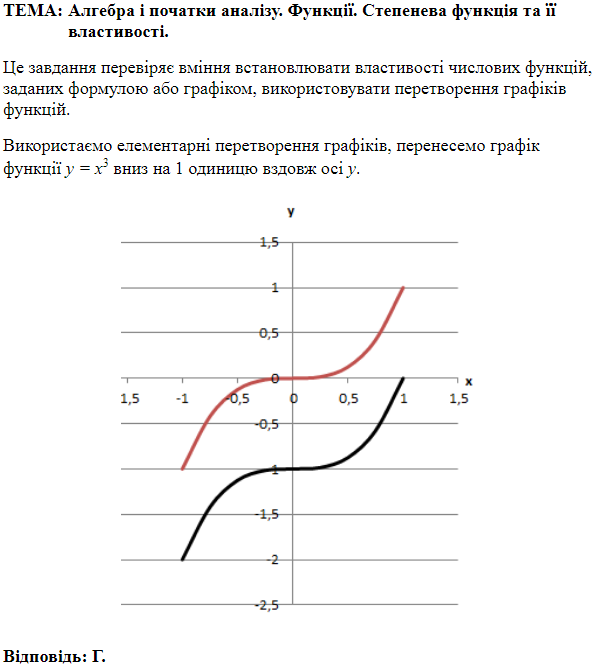
ТЕМА: Алгебра і початки аналізу. Функції. Степенева функція.
Це завдання перевіряє вміння встановлювати властивості числових функцій, заданих формулою або графіком.
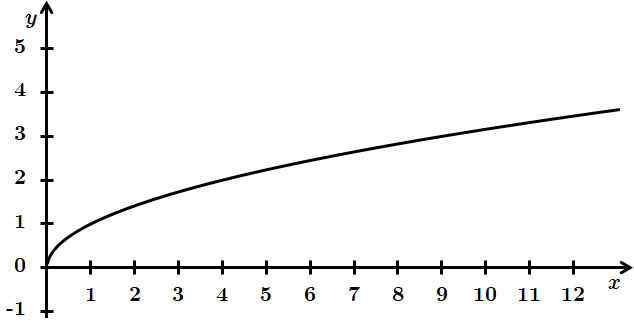
Ця функція зростає на всій області визначення, не є парною, періодичною, не має точок екстремуму.
Функція набуває лише невід'ємних значень.
Відповідь: A.
ТЕМА: Алгебра та початки аналізу. Функції. Степенева, показникова, тригонометрична функції.
Це завдання перевіряє вміння встановлювати властивості числових функцій, заданих формулою або графіком.
1.
Отже, 1 – B.
2.
Отже, 2 – Б.
3.
Отже, 3 – A.
4.
Отже, 4 – Д.
Відповідь: 1 – В, 2 – Б, 3 – А, 4 – Д.
ТЕМА: Алгебра. Функції. Функціональа залежність. Лінійні, квадратичні, степеневі, показникові, логарифмічні та тригонометричні функції, їхні основні властивості.
Це завдання перевіряє вміння встановлювати властивості числових функцій, заданих формулою або графіком, досліджувати на парність (непарність).
Для наведених функцій область визначення не є симетричною у функції
Серед інших умова
Така властивість є у функції
Відповідь: Д.
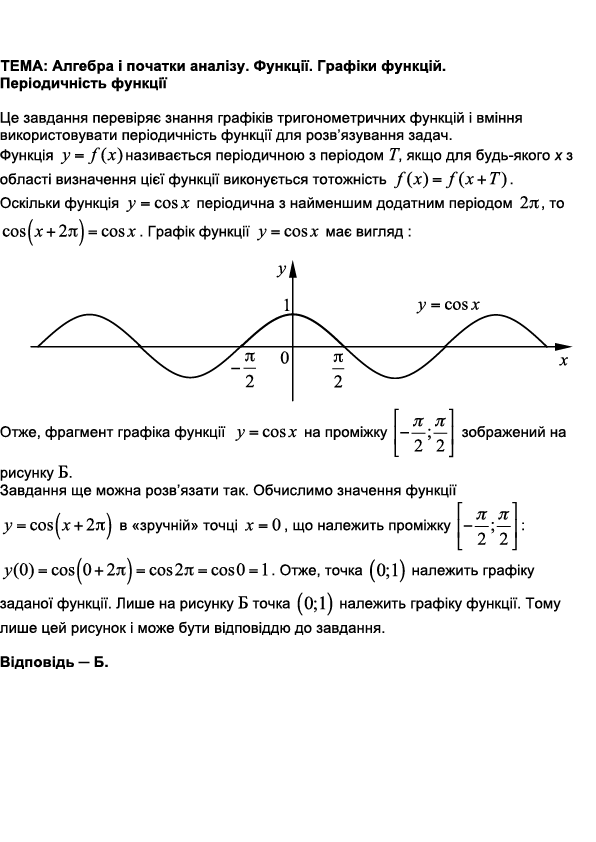
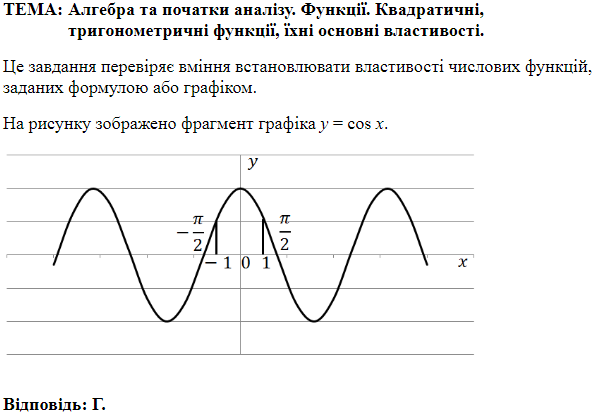
ТЕМА: Функції. Функціональна залежність. Тригонометричні функції, їхні основні властивості.
Це завдання перевіряє вміння встановлювати властивості тригонометричних функцій, заданих графіком.
Задана функція з періодом
Область значень функції
Нулі функції
Значення
Отже, відповідь
Відповідь: Д.




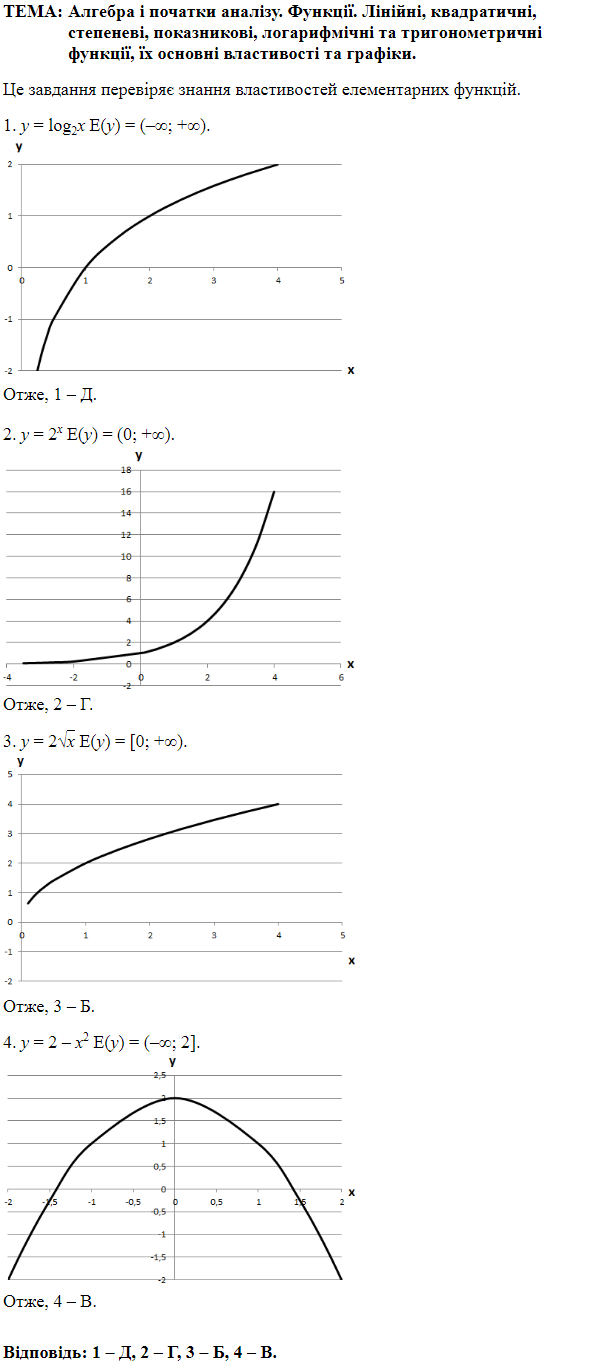
ТЕМА: Алгебра і початки аналізу. Функції. Функціональна залежність. Квадратична, показникова, логарифмічна та степенева функції, їхні основні властивості.
Це завдання перевіряє вміння знаходити область значень функцій.
Область значень функції — це множина всіх можливих значень, які приймає функція при всіх допустимих значеннях аргументу.
Зобразимо схематично графіки функцій та визначимо область значень кожної з них.
1.
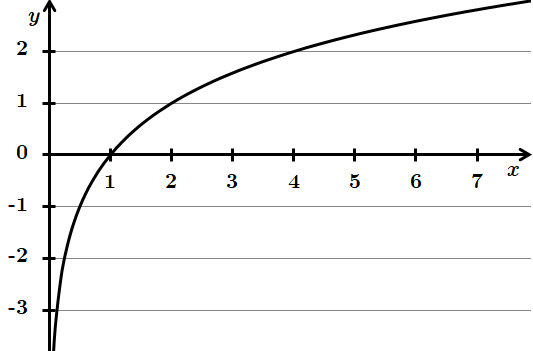
Отже, 1 – Д.
2.
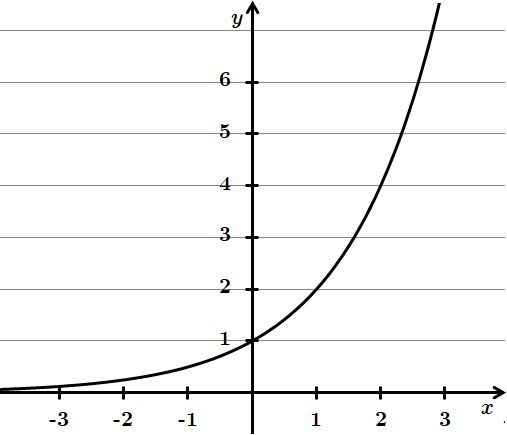
Отже, 2 – Г.
3.
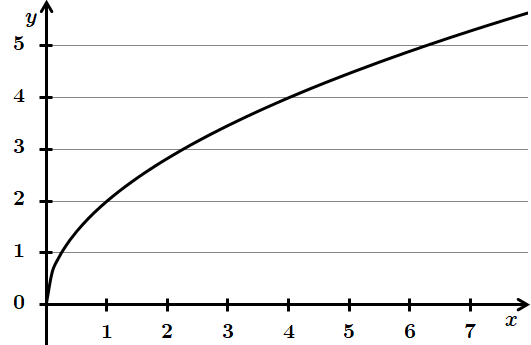
Отже, 3 – B.
4.
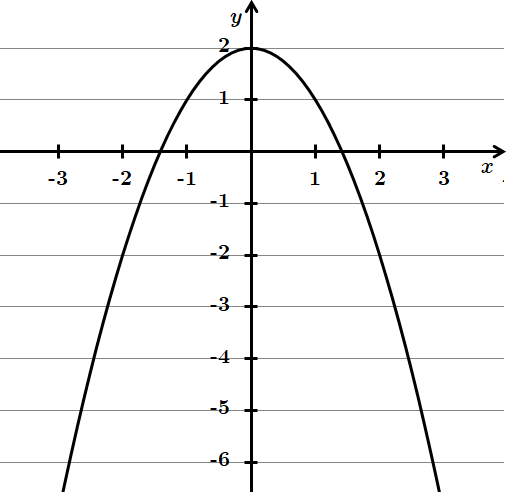
Отже, 4 – A.
Відповідь: 1 – Д, 2 – Г, 3 – В, 4 – А.
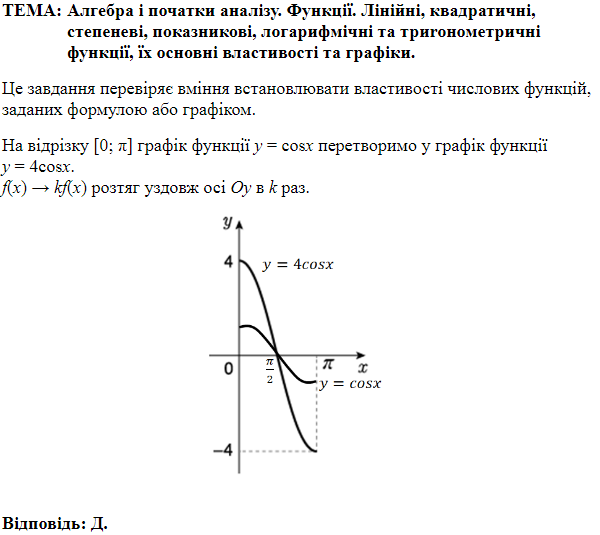
ТЕМА: Алгебра і початки аналізу. Функції. Тригонометричні функції, їхні основні властивості.
Це завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком, використовувати перетворення графіків функцій.
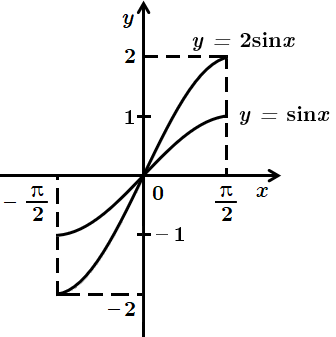
На рисунку зображено перетворення графіка функції
Перетворення графіка
Відповідь: A.
ТЕМА: Алгебра та початки аналізу. Функції. Лінійні, степеневі, показникові функції, їхні основні властивості.
Це завдання перевіряє вміння будувати графіки елементарних функцій, встановлювати властивості числових функцій, заданих формулою або графіком, використовувати перетворення графіків функцій.
Дано графік функції
1.
2.
3.
При
тому абсциса точки перетину
Отже, 3 – Б.
4.
Відповідь: 1 – Д, 2 – Г, 3 – Б, 4 – В.
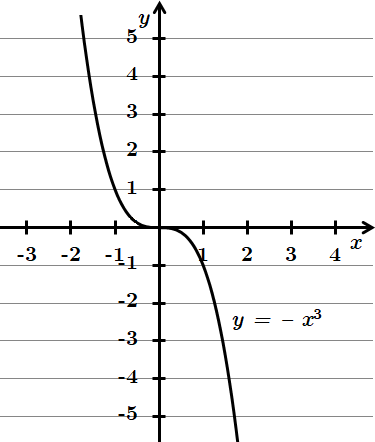
ТЕМА: Алгебра та початки аналізу. Функції. Тригонометричні функції.
Це завдання перевіряє вміння встановлювати властивості числових функцій, заданих формулою або графіком, використовувати перетворення графіків функцій.
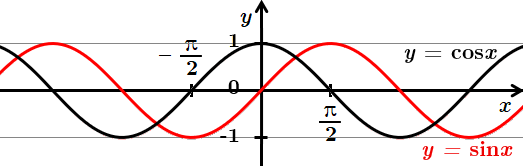
Графік
Отже, правильна відповідь – А.
Відповідь: A.