Розділ: Планіметрія
Тема: Прямокутні трикутники
Кількість завдань: 61
ТЕМА: Коло та круг. Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивостей чотирикутників, зокрема прямокутника, кола, прямокутного трикутника, уміння застосовувати теорему Піфагора для розв’язування прямокутного трикутника.
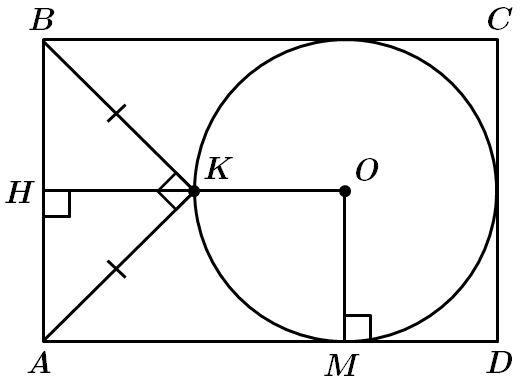
1. Коло дотикається до сторін
Правильна відповідь – А.
2. У
Правильна відповідь – B.
3. У
У
Правильна відповідь – Г.
Відповідь: 1 – A, 2 – B, 3 – Г.
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивостей трапеції, прямокутного трикутника, уміння визначати площу трапеції.
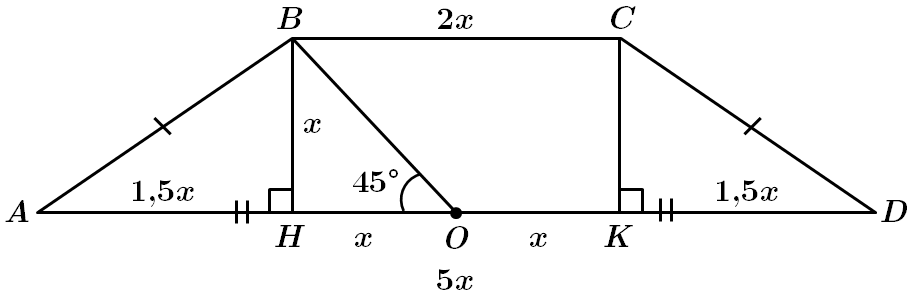
Нехай
Побудуймо висоти
Точка
У
Площу трапеції визначмо за формулою:
Якщо
Відповідь: Г.
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивостей чотирикутників, зокрема квадрата, прямокутного трикутника, а також теореми Піфагора.
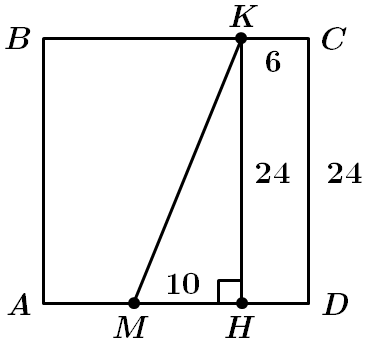
У квадраті
Нехай
Отже,
Побудуймо
Розгляньмо
Визначмо довжину гіпотенузи:
Відповідь: В.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Завдання скеровано на перевірку вміння застосовувати властивості прямокутника та прямокутного трикутника.
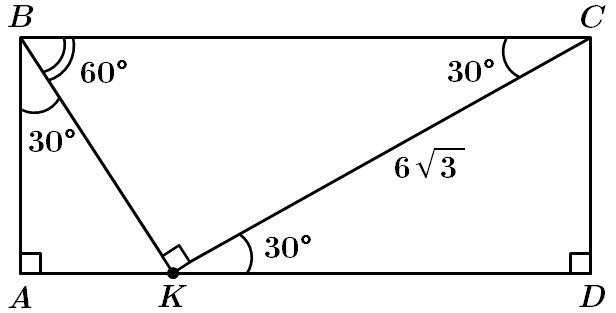
У
У прямокутнику
Відповідь: B.
ТЕМА: Геометрія. Планіметрія. Трикутники.
Завдання перевіряє вміння застосовувати означення та властивості різних видів трикутників до розв'язування планіметричних задач.
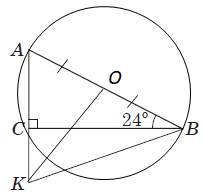
1 – Г. У
2 – B.
3 – A.
Відповідь: 1Г, 2В, 3А.
ТЕМА: Геометрія. Планіметрія.
Завдання перевіряє знання властивості трикутника про суму кутів.
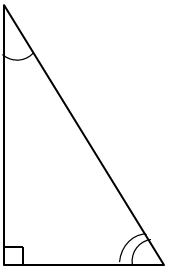
Сума кутів трикутника –
Отже,
Гострі кути
Найменший кут цього трикутника
Відповідь: B.
ТЕМА: Геометрія. Планіметрія. Трикутники.
Завдання перевіряє вміння застосовувати означення та властивості різних видів трикутників до розв'язування планіметричних задач.
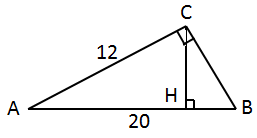
1. За теоремою Піфагора:
2. Радіус кола, описаного навколо прямокутного трикутника, дорівнює половині гіпотенузи. Отже,
3.
Висоту
Або знайти висоту за допомогою метричних співвідношень у прямокутному трикутнику:
Отже, правильна відповідь – Б.
Відповідь: 1Д, 2В, 3Б.
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.
Завдання скеровано на перевірку знання властивостей трикутників та їх основних властивостей.
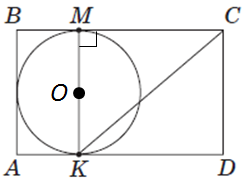
1.
2.
Відповідь: 1. 4. 2. 152.
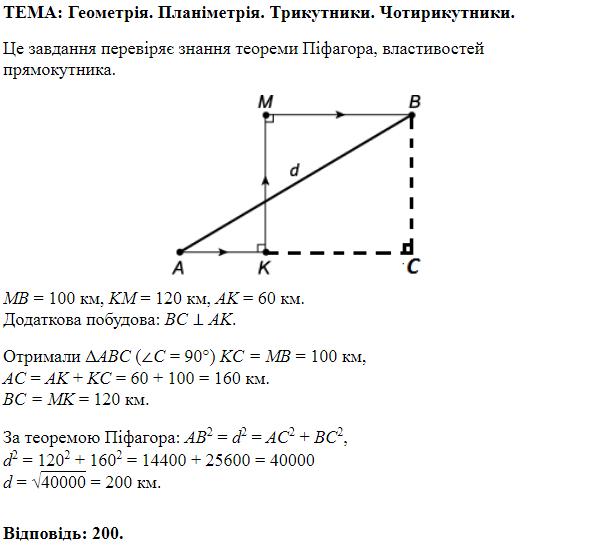
ТЕМА: Геометрія. Планіметрія. Трикутники.
Завдання скеровано на перевірку знання властивостей трикутника, вміння розв’язувати задачі практичного змісту.
Побудуємо математичну модель задачі:
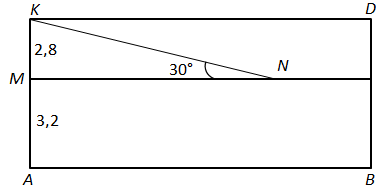
Катет
Відповідь: Г.
ТЕМА: Геометрія. Стереометрія. Многогранники.
Завдання перевіряє вміння розв’язувати задачі на обчислення об’ємів піраміди.
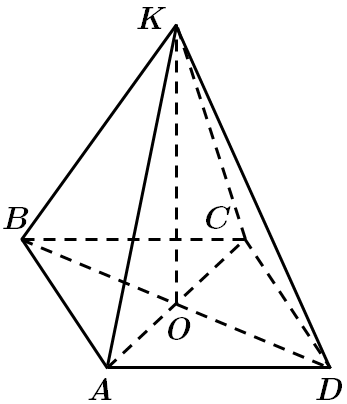
У квадраті
У
Об'єм піраміди знаходимо за формулою:
Відповідь:
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Коло та круг.
Завдання перевіряє вміння застосовувати властивості різних видів трикутників до розв'язування планіметричних задач.
1.
За властивістю прямокутника, діагоналі рівні.
2.
Відповідь: 1.
2.
ТЕМА: Геометрія. Планіметрія.
Завдання перевіряє вміння застосовувати означення та властивості різних видів трикутників до розв'язування планіметричних задач практичного змісту.
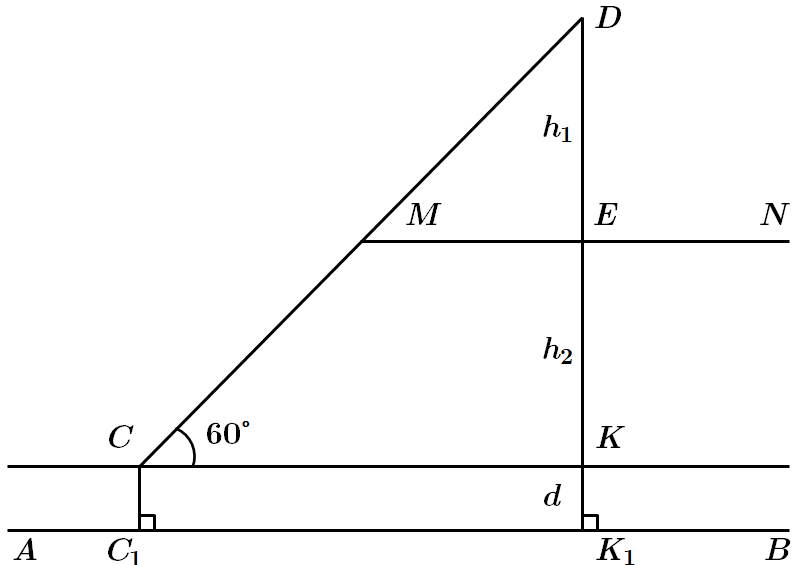
Відповідь: Г.
ТЕМА: Геометрія. Планіметрія. Коло і круг. Чотирикутники. Трикутники.
Завдання перевіряє знання про коло та його елементи, теореми Піфагора, знання формули для обчислення площі трикутника.
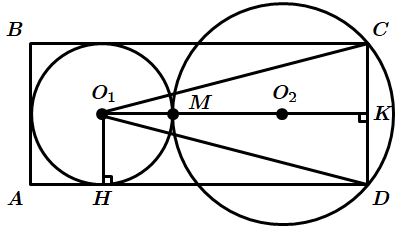
1.
За теоремою Піфагора
2.
Відповідь: 1.
2.
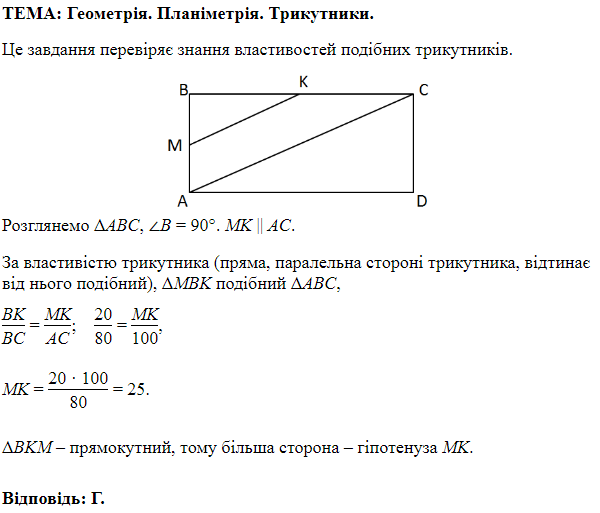
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Завдання перевіряє вміння застосовувати властивості трикутників до розв’язування планіметричних задач, знаходити довжину середньої лінії трапеції, знання теореми Піфагора.
1.
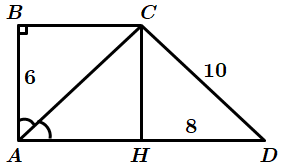
Отже, 1 – A.
2.
У
Отже, 2 – Б.
3.
Cередня лінія трапеції
Відповідь: 1 – A, 2 – Б, 3 – Г.
ТЕМА: Геометрія. Стереометрія. Тіла обертання.
Завдання перевіряє вміння розв’язувати задачі на обчислення об’ємів і площ поверхонь конуса.
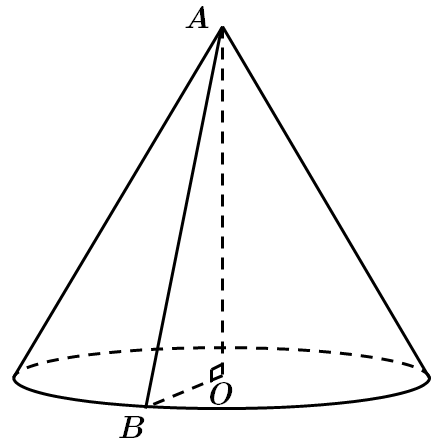
Площа основи конуса –
Об'єм конуса знаходимо за формулою:
У
Відповідь:
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання перевіряє вміння застосовувати властивості паралелограма до розв'язування планіметричних задач.
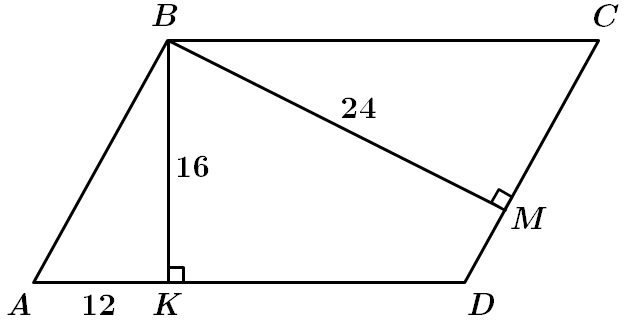
1. У
2. За формулою
Відповідь: 1.
2.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання перевіряє знання властивостей ромба.
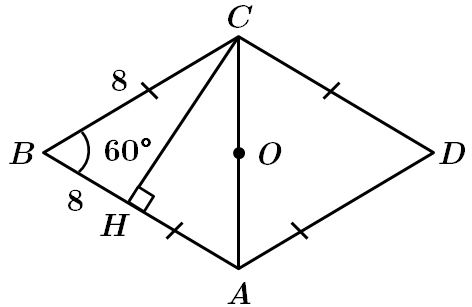
1.
2.
3. Центр кола, вписаного в ромб – точка перетину діагоналей точка
За властивістю ромба
Відповідь: 1 – B, 2 – Б, 3 – A.
ТЕМА: Геометрія. Планіметрія. Геометричні величини та їх вимірювання.
Завдання перевіряє вміння знаходити довжини відрізків, розв'язувати задачі практичного змісту.
У
Ширина смуги
Відповідь: Г.
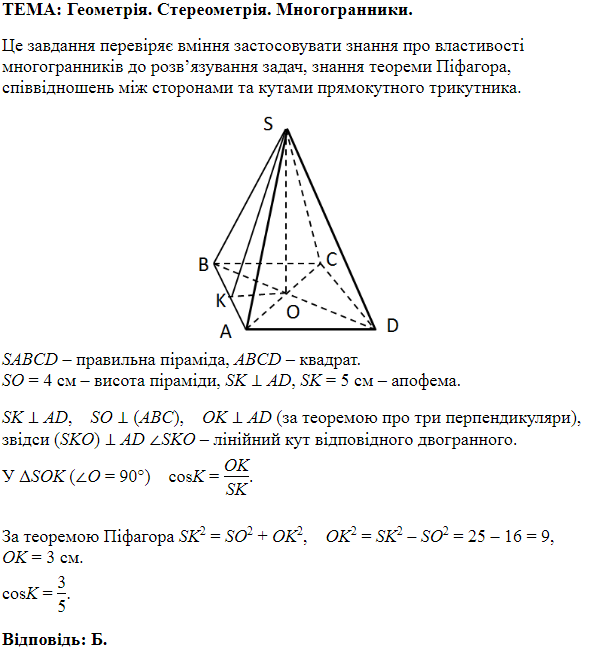
ТЕМА: Геометрія. Стереометрія. Многогранники.
Завдання перевіряє знання властивостей піраміди, означення кута між прямою та площиною.
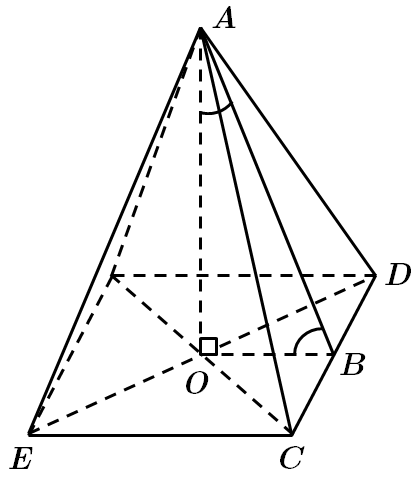
Висота піраміди
Отже,
Відповідь: Г.
ТЕМА: Геометрія. Планіметрія. Трикутники.
Це завдання перевіряє вміння застосувати означення та властивості різних видів трикутників до розв'язання задач практичного змісту.
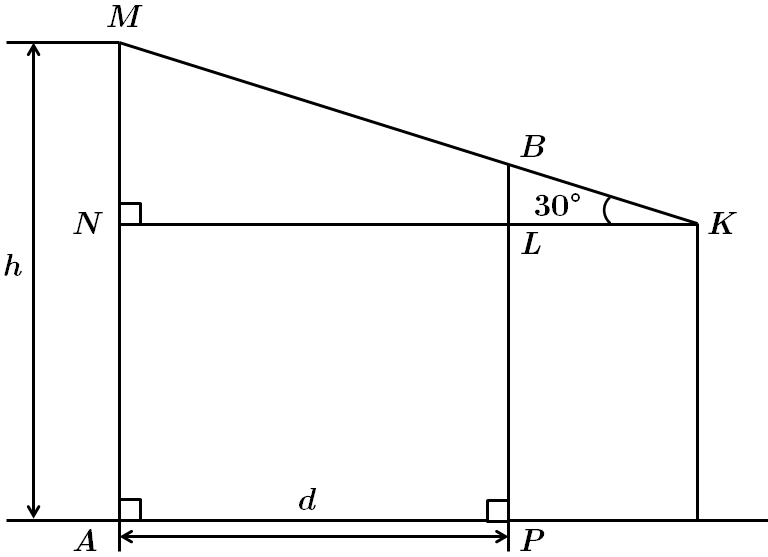
З-поміж наведених відстаней найменша
Відповідь: Г.
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.
Це завдання перевіряє знання теореми про суму кутів трикутника, властивостей суміжних та вертикальних кутів, властивості прямокутника.
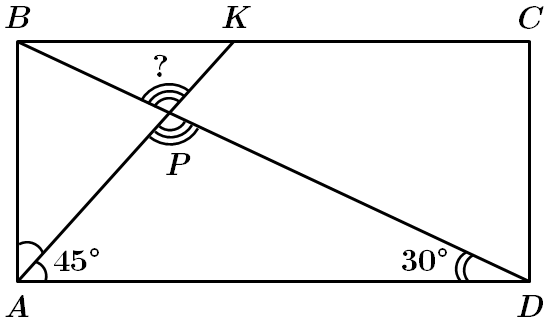
У трикутнику
Звідси
Відповідь: A.
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.
Це завдання перевіряє вміння застосовувати властивості різних видів трикутників до розв'язування планіметричних задач та задач практичного змісту.
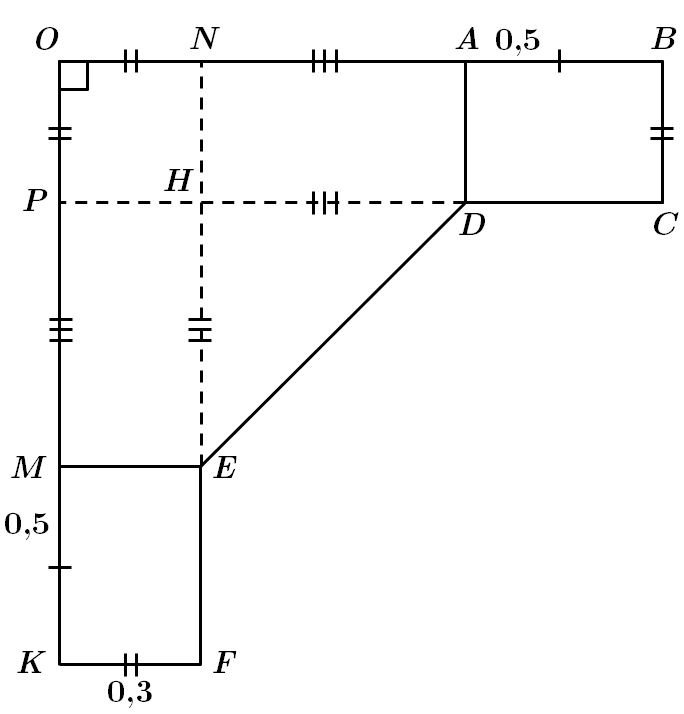
За теоремою Піфагора
Число
Серед відповідей цю нерівність задовольняє число
Відповідь: Б.
ТЕМА: Геометрія. Стереометрія. Многогранники.
Це завдання перевіряє вміння розв'язувати задачі на обчислення площ поверхонь геометричних тіл, знання многогранників та їхніх елементів.
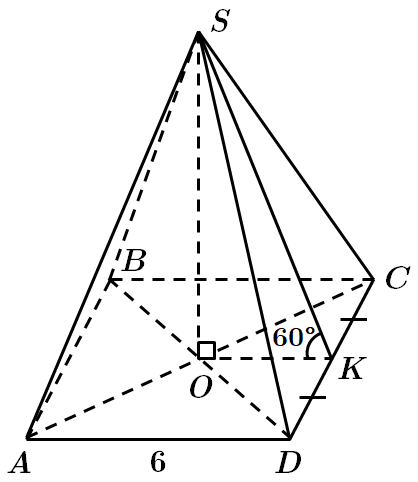
Відповідь: A.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Це завдання перевіряє вміння застосовувати означення, ознаки та властивості різних видів чотирикутників до розв'язування планіметричних задач.
1.
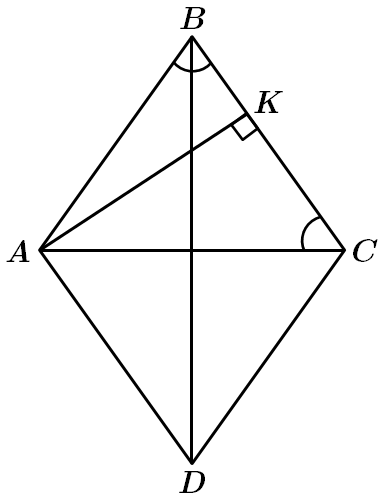
Отже, 1 – Г.
2.
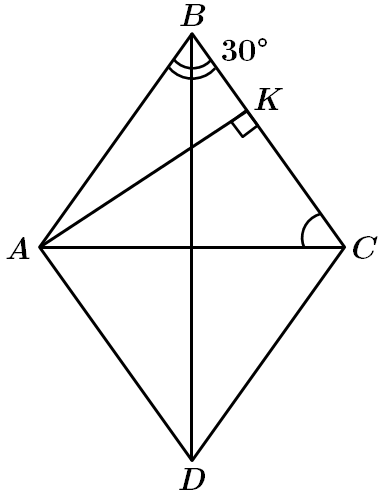
Отже, 2 – В.
3.
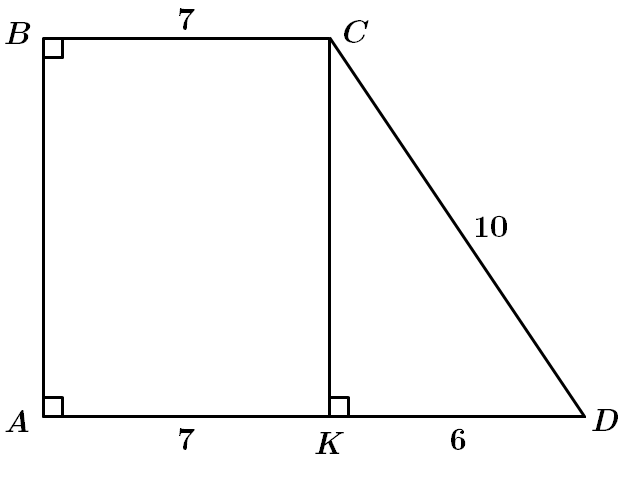
Додаткова побудова
Отже, 3 – Б.
4.
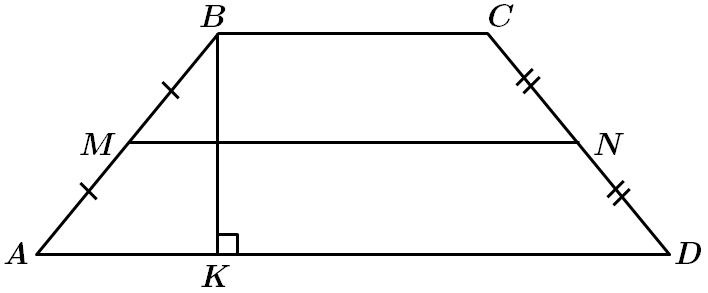
Отже, 4 – Д.
Відповідь: 1 – Г, 2 – В, 3 – Б, 4 – Д.
ТЕМА: Геометрія. Стереометрія. Многогранники, тіла й поверхні обертання.
Це завдання перевіряє вміння застосовувати властивості конуса до розв'язування стереометричних задач.
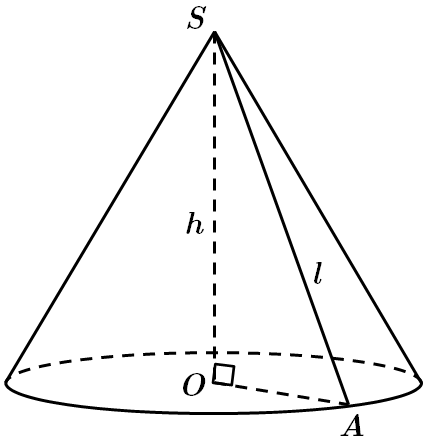
У
Отже, правильна відповідь А.
Відповідь: A.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Це завдання перевіряє вміння застосовувати означення, ознаки та властивості різних видів чотирикутників до розв'язування планіметричних задач.
Відповідь: Г.
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.
Це завдання перевіряє знання співвідношення між сторонами і кутами прямокутного трикутника, теореми косинусів; уміння застосовувати властивості різних видів чотирикутників до розв'язування планіметричних задач.
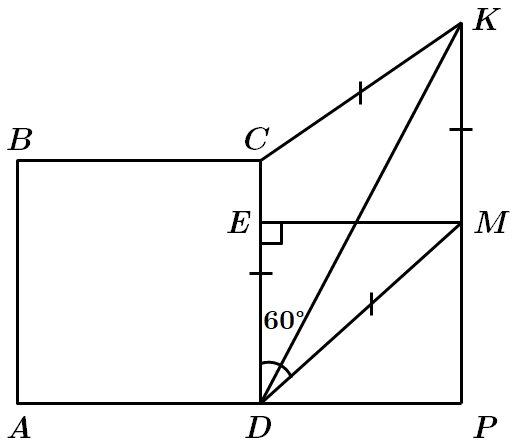
1. Периметр ромба
Отже, 1 – В.
2. Більша діагональ ромба лежить напроти більшого кута ромба.
У
Отже, 2 – Г.
3.Відстань від точки
У
Отже, 3 – Б.
4.
Отже, 4 – Д.
Відповідь: 1 – В, 2 – Г, 3 – Б, 4 – Д.
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники. Коло та круг.
Це завдання перевіряє знання властивості дотичної до кола, вміння застосовувати набуті знання до розв'язування планіметричних задач та задач практичного змісту.
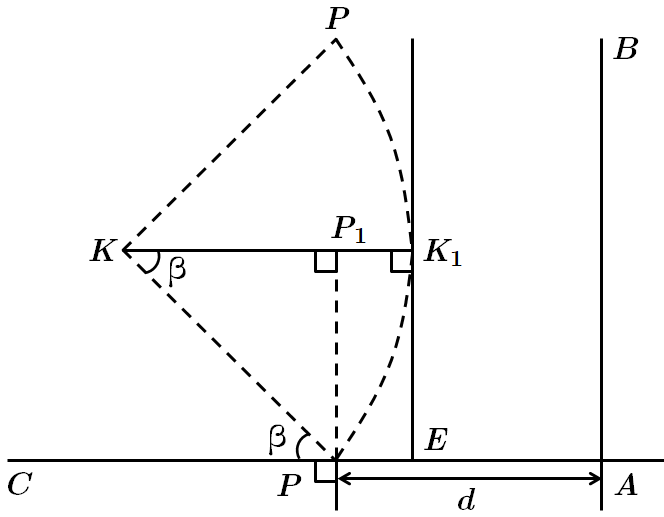
Проведемо
За властивістю дотичної до кола
У
Серед наведених відстаней найменша
Відповідь: Г.
ТЕМА: Трикутники.
Це завдання перевіряє знання властивостей медіани, середньої лінії трикутника, уміння застосовувати властивості різних видів трикутників до розв'язання планіметричних задач.
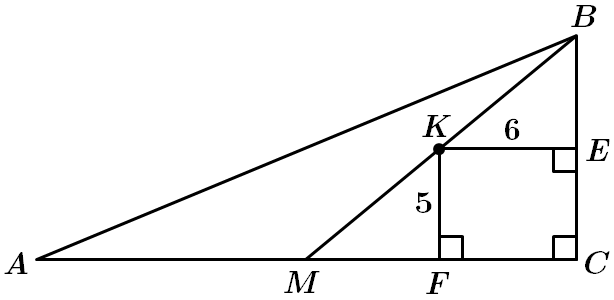
1. Відстань від точки
Відповідно,
За теоремою Фалеса, точка
За властивістю середньої лінії,
Отже, довжина катета
2. Аналогічно,
За теоремою Піфагора, у
За властивістю прямокутного трикутника, радіус описаного кола дорівнює половині гіпотенузи. Отже, радіус кола
Відповідь: 1.
2.
ТЕМА: Планіметрія. Коло та круг. Трикутники. Чотирикутники.
Це завдання перевіряє вміння застосовувати властивості різних видів трикутників та чотирикутників до розв'язування планіметричних задач та задач практичного змісту.
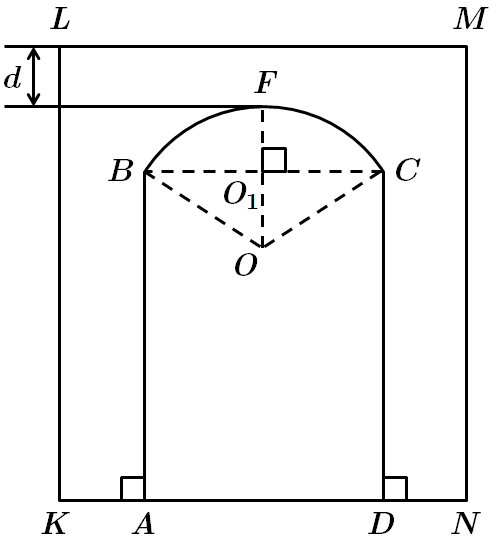
Нехай точка
Радіус кола –
Відповідь: Г.


ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Це завдання перевіряє знання теореми косинусів, властивостей ромба, уміння розв'язувати планіметричні задачі.
Дано: ромб
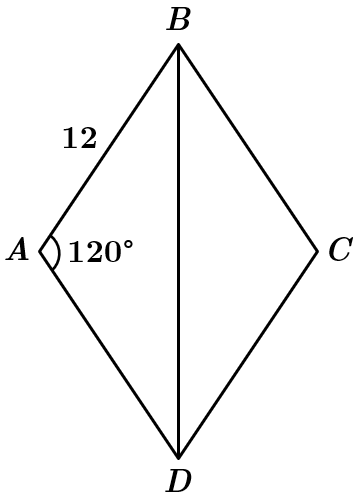
Більша діагональ лежить напроти більшого кута ромба
У трикутнику
Отже,
Відповідь: Г.
ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості. Трикутники. Чотирикутники.
Це завдання перевіряє знання теореми Фалеса, властивостей середньої лінії трикутника, трапеції, теореми Піфагора, уміння застосовувати властивості геометричних фігур до розв'язання планіметричних задач.
1. Оскільки площа квадрата
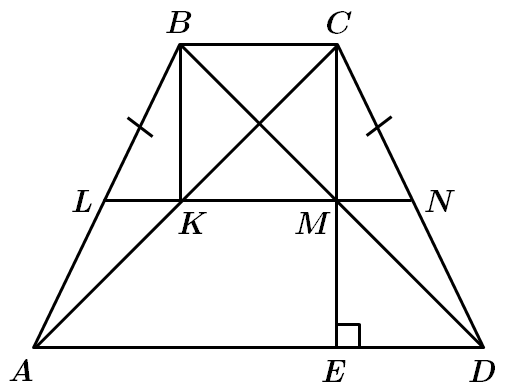
За теоремою Фалеса
За теоремою Піфагора
2. Оскільки
Відповідь: 1.
2.
ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості. Коло та круг. Трикутники. Чотирикутники.
Це завдання перевіряє вміння застосовувати означення, ознаки та властивості геометричних фігур до розв'язування планіметричних задач та задач практичного змісту; уміння застосовувати теорему Піфагора до розв'язування прямокутного трикутника, властивості прямокутника.
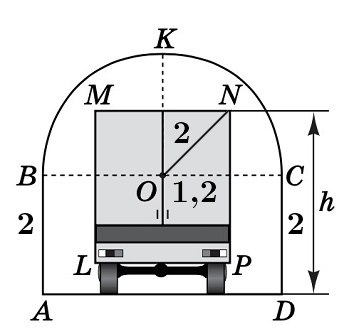
Розглянемо випадок, коли вантажівка дотикається аркового проїзду. При цьому
Оскільки
Висота
При значенні
Відповідь: Г.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Це завдання перевіряє знання про прямокутник та його властивості, середню лінію трикутника та її властивості.
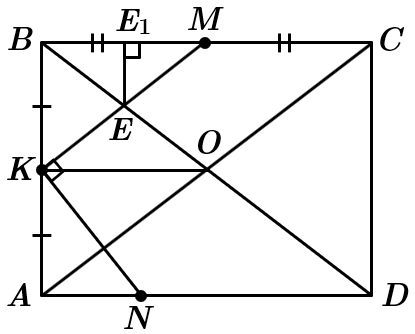
1. У
(за властивістю середньої лінії).
Отже, 1 – A.
2.
Отже, 2 – B.
3. У
Отже, 3 – Б.
4. Нехай
Отже, 4 – Г.
Відповідь: 1 – A, 2 – B, 3 – Б, 4 – Г.
ТЕМА: Геометрія. Планіметрія. Трикутники.
Це завдання перевіряє вміння застосовувати означення та властивості різних видів трикутників до розв'язування планіметричних задач та задач практичного змісту.
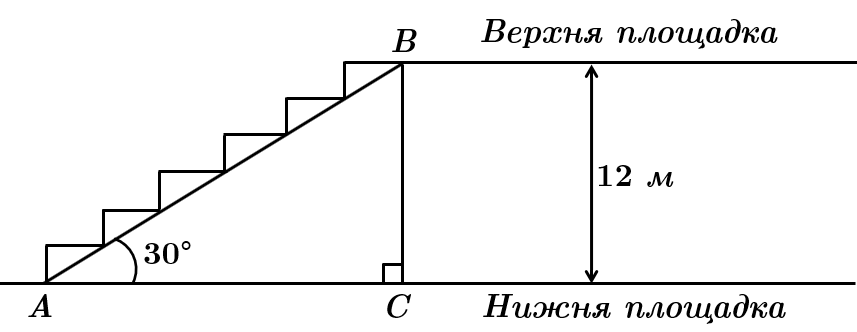
Довжина ескалатора
Відповідь: Б.