Розділ: Стереометрія
Тема: Прямі та площини у просторі
Кількість завдань: 38
ТЕМА: Прямі та площини в просторі. Многогранники.
Завдання скеровано на перевірку знання взаємного розміщення прямих і площин у просторі, властивостей піраміди.
За властивістю паралельних площин: через точку, яка не лежить у площині, можна провести площину, паралельну заданій, і до того ж тільки одну.
Через точку
Відповідь: Б.
ТЕМА: Прямі та площини в просторі. Многогранники.
Завдання скеровано на перевірку знання взаємного розміщення прямих і площин у просторі, властивостей піраміди.
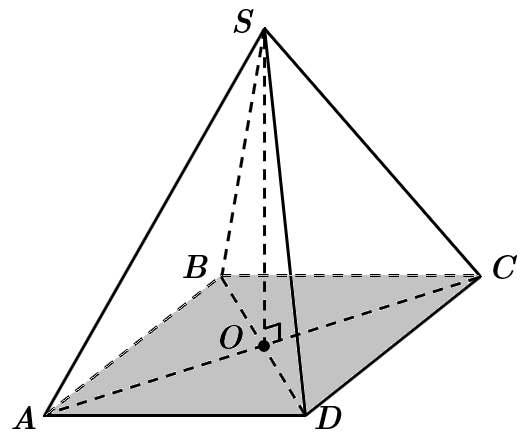
Висота піраміди
Відповідь: Д.
ТЕМА: Прямі та площини в просторі.
Завдання скеровано на перевірку знання аксіом стереометрії, взаємного розміщення прямих у просторі.
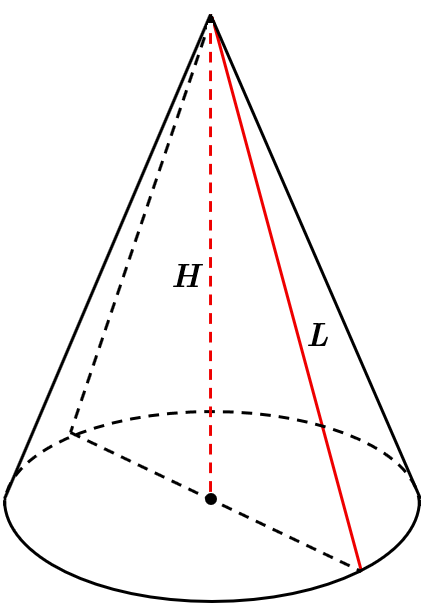
Висота конуса
Оскільки висота й твірна конуса мають спільну точку (перетинаються у вершині), вони, за визначенням, лежать в одній площині.
За аксіомою стереометрії, якщо дві прямі мають спільну точку, то через них можна провести площину, і до того ж тільки одну.
Відповідь: Д.
ТЕМА: Прямі та площини в просторі.
Завдання скеровано на перевірку вміння застосовувати означення, ознаки та властивості паралельних прямих.
За властивістю паралельності прямих
Отже, прямих, що проходять через ребра куба і є паралельними прямій
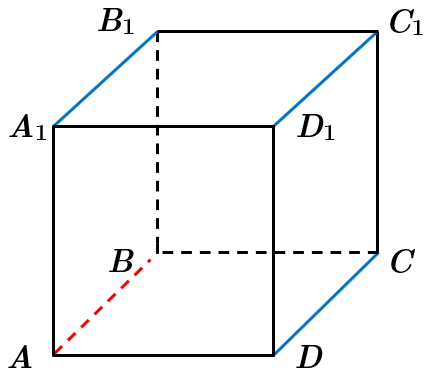
Відповідь: Г.
ТЕМА: Прямі та площини у просторі.
Завдання скеровано на перевірку знання аксіом стереометрії, взаємного розміщення прямих у просторі.
Застосуймо аксіому стереометрії: якщо дві прямі мають спільну точку, то через них можна провести лише одну площину.
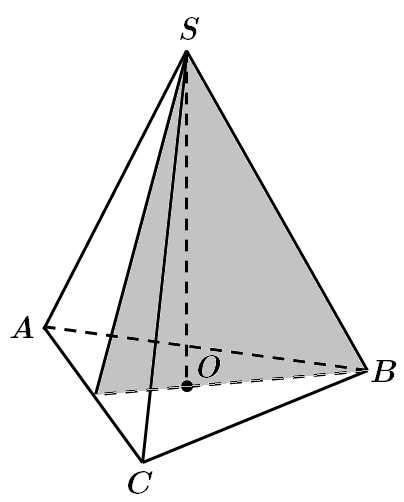
Отже, прямі
За аксіомою стереометрії якщо дві прямі мають спільну точку, то через них можна провести площину, і до того ж, тільки одну.
Відповідь: Д.
ТЕМА: Прямі та площини в просторі.
Завдання скеровано на перевірку знання аксіом стереометрії, взаємного розміщення прямих у просторі.

Скористаймося аксіомою паралельності: через точку, що не лежить на прямій, можна провести лише одну пряму, паралельну даній. Отже, через точку
Відповідь: Б.
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Многогранники.
Завдання скеровано на перевірку знань ознаки паралельності прямої та площини, властивостей призми.
За ознакою паралельності прямої і площини, якщо пряма
Аналогічно,
Отже, таких площин лише дві.
Відповідь: В.
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі.
Завдання скероване на перевірку розуміння властивостей паралельних площин.
У піраміді
Через точку, яка не лежить у площині, можна провести тільки одну площину, паралельну даній.
Отже, через точку
Відповідь: Б.
ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури на площині та їх властивості.
Завдання скеровано на перевірку знання аксіом планіметрії, нерівності трикутника, рівності трикутників.
Точки
I.

точка
II.
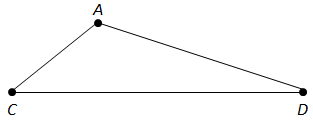
точка
III.
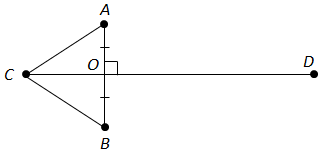
Правильними є твердження І та ІІІ.
Відповідь: В.
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі.
Завдання перевіряє вміння застосовувати означення та властивості паралельних прямих і площин.
1. Точка
2.
3.
Відповідь: 1 – Д, 2 – B, 3 – Б.
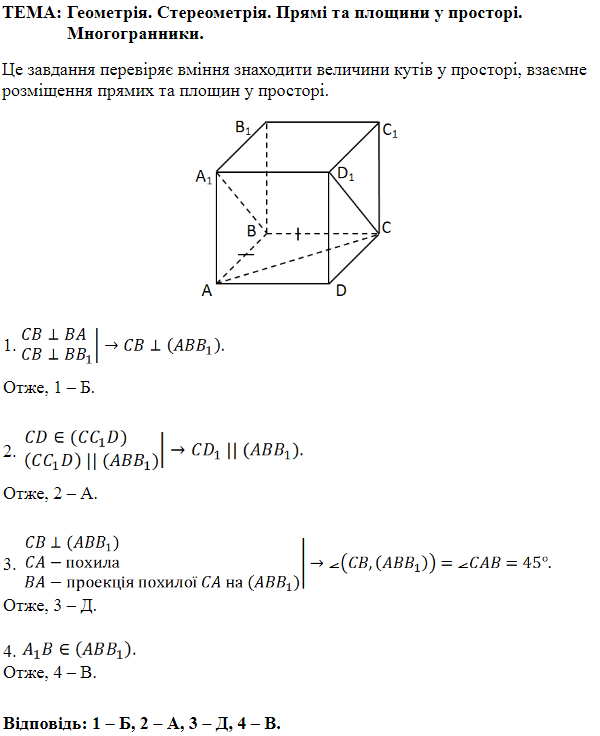
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі.
Це завдання перевіряє знання ознак паралельності прямої та площини, аксіом стереометрії.
1. Точки
2.
3.
Відповідь: 1 – Б, 2 – A, 3 – Г.
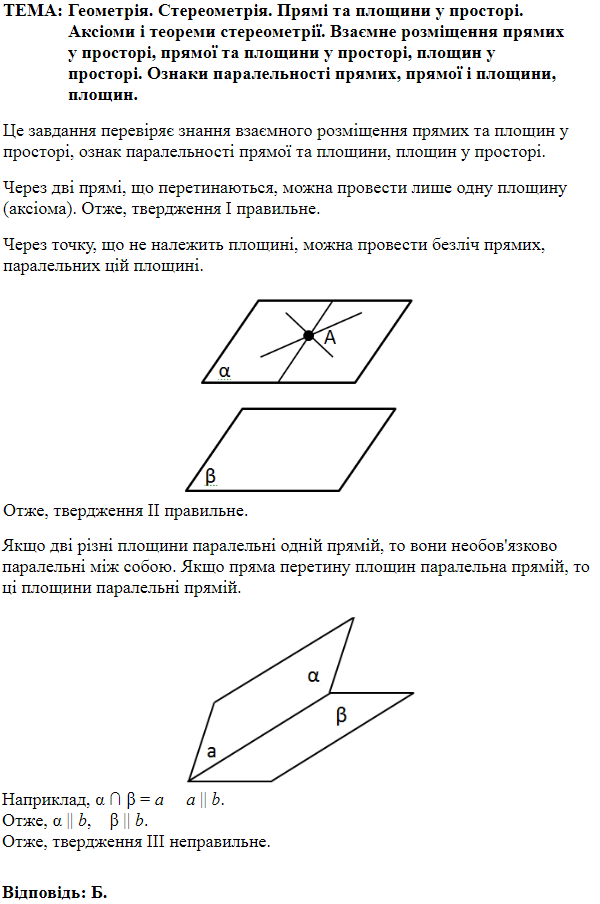
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Аксіоми і теореми стереометрії. Взаємне розміщення прямих у просторі, прямої та площини у просторі, площин у просторі.
Це завдання перевіряє знання взаємного розміщення прямих та площин у просторі.
1.
2.
Отже, 2 – A.
3.
4.
Відповідь: 1 – Б, 2 – A, 3 – Д, 4 – B.
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Многогранники.
Це завдання перевіряє знання про взаємне розміщення прямих у просторі, площин у просторі, многогранників та їхніх елементів.
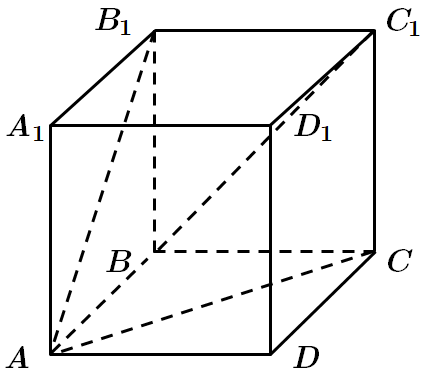
1.
Отже, 1 – B.
2. Прямі
Отже, 2 – Б.
3.
Отже, 3 – Д.
4.
Отже, 4 – A.
Відповідь: 1 – B, 2 – Б, 3 – Д, 4 – A.
ТЕМА: Стереометрія. Прямі та площини у просторі.
Це завдання перевіряє знання взаємного розміщення прямої та площини у просторі.
За наслідками з аксіом стереометрії: через пряму і точку, яка їй належить, проходить площина, і до того ж тільки одна.
Через точку
Відповідь: Б.
ТЕМА: Стереометрія. Прямі та площини у просторі. Взаємне розміщення прямих у просторі.
Це завдання перевіряє знання означення паралельних прямих.
У просторі задано паралельні прямі
Через дві прямі в площині можна провести пряму, що перетинає обидві прямі
Отже, правильні твердження І та ІІ.
Відповідь: Д.
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі.
Це завдання перевіряє знання аксіом стереометрії, ознаки паралельності прямої та площини, ознаку мимобіжності прямих.
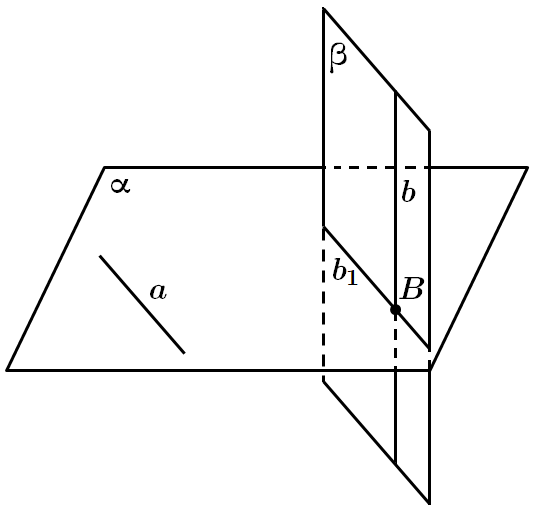
Задано дві мимобіжні прямі
Проведемо в площині
Відповідь: Б.
ТЕМА: Геометрія. Стереометрія. Прямі і площини у просторі.
Це завдання перевіряє вміння застосовувати означення, ознаки та властивості паралельних і перпендикулярних прямих і площин.
I. Твердження хибне, тому що, якщо пряма лежить і в площині
II. Твердження є правильним. Пряма, перпендикулярна до площини
III. Твердження хибне, тому що пряма, що лежить в одній з паралельних площин, може бути паралельною або мимобіжною з прямими, які лежать в іншій паралельній площині.
Відповідь: B.
ТЕМА: Геометрія. Стереометрія. Паралельність і перпендикулярність прямої і площини. Паралельність площин.
Це завдання перевіряє знання можливого взаємного розташування прямих та площин у просторі.
I. Твердження є правильним, достатньо щоб пряма
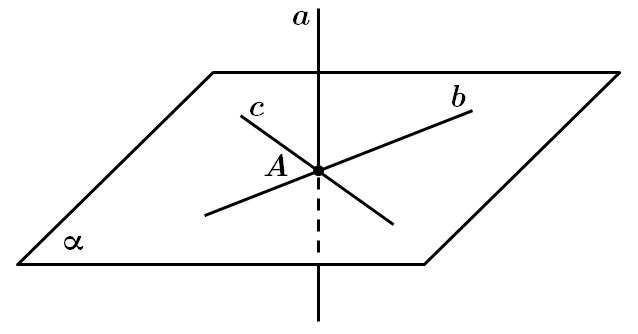
II. Твердження є правильним, через точку
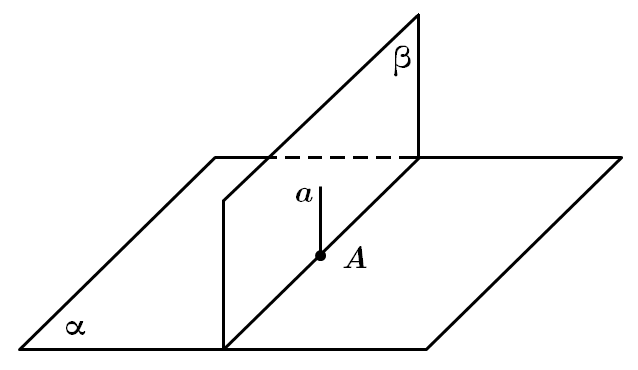
III. Твердження є неправильним. Згідно з аксіомою стереометрії: якщо дві площини мають спільну точку, то вони або збігаються, або перетинаються по прямій, яка проходить через цю точку. Тобто якщо провести через точку
Відповідь: Г.
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі.
Це завдання перевіряє знання взаємного розміщення прямих у просторі, уміння застосовувати означення, ознаки та властивості перпендикулярних прямих.
I. Твердження не правильне. Якщо
II.
III.
Відповідь: Г.
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі.
Це завдання перевіряє знання означення мимобіжних прямих і вміння його використовувати до розв'язування задач.
I. Оскільки через дві прямі, що перетинаються, можна провести єдину площину, а мимобіжні прямі не перетинаються, тому твердження є неправильним.
II. Прямі, які не лежать в одній площині, називаються мимобіжними. Тому твердження є неправильним.
III. Оскільки прямі
Відповідь: Г.