Розділ: Стереометрія
Тема: Тіла обертання
Кількість завдань: 82
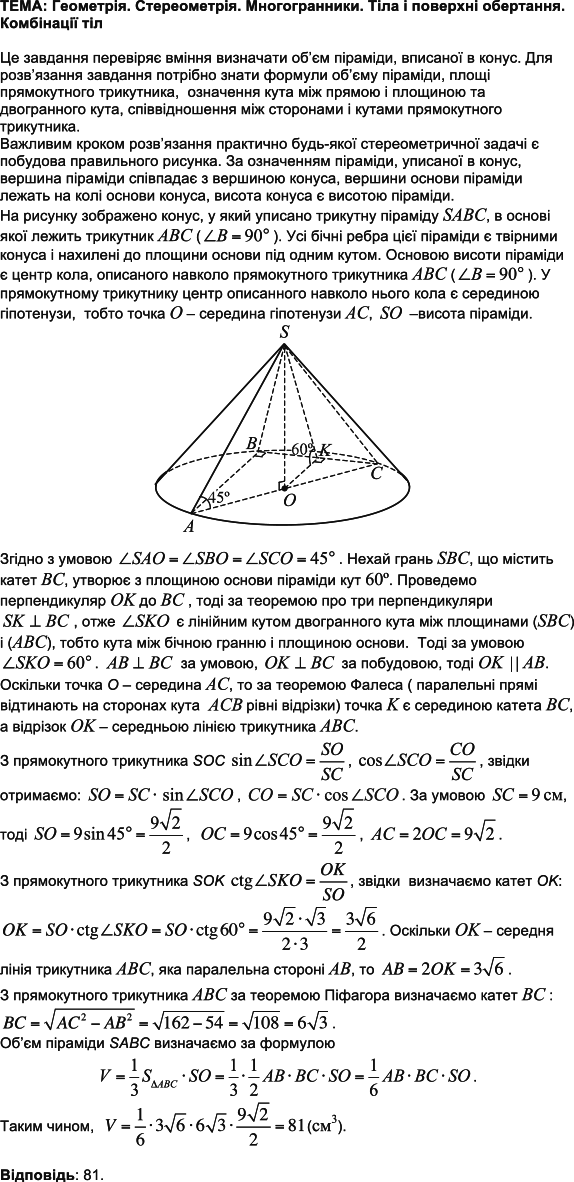
ТЕМА: Тіла обертання. Многогранники.
Завдання скеровано на перевірку знання властивостей призми й циліндра, формул для обчислення площі поверхні циліндра й об’єму призми.
Пряма призма, в основі – ромб.
Радіус основи ціліндра
У ромбі діагоналі
У
Площа бічної поверхні циліндра
Об'єм призми визначмо за формулою:
Відповідь:
ТЕМА: Тіла обертання.
Завдання скеровано на перевірку знання основних властивостей конуса, вміння розв’язувати задачі на обчислення площі поверхні конуса.
Задано конус із бічною поверхнею
Площа бічної поверхні конуса
У прямокутному
За властивістю медіани, проведеної до гіпотенузи:
Об'єм конуса
Відповідь:
ТЕМА: Тіла обертання.
Завдання скеровано на перевірку знання властивостей конуса та сфери, формул для обчислення площі поверхні сфери й об’єму конуса.
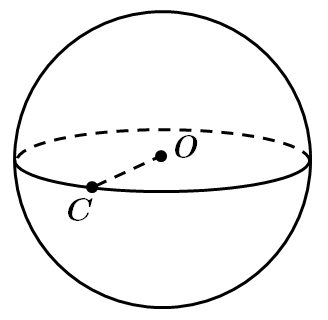
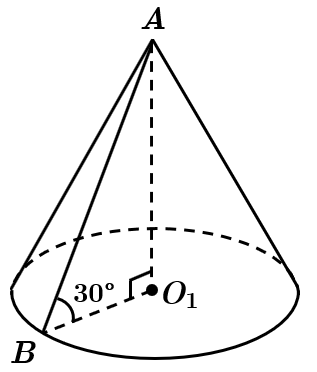
Радіус основи конуса
У
Об'єм конуса визначмо за формулою
Відповідь:
ТЕМА: Тіла обертання. Многогранники.
Завдання скеровано на перевірку знання властивостей піраміди та сфери, формул для обчислення площі поверхні сфери й об’єму піраміди.
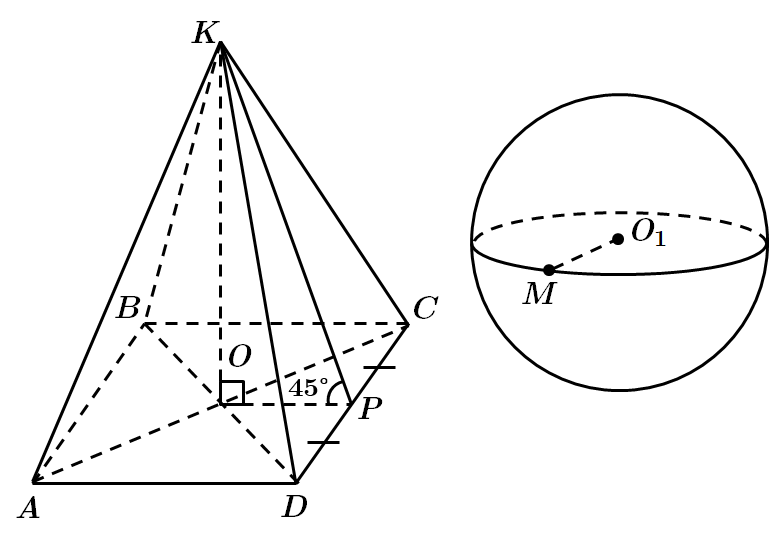
За умовою, радіус кола, описаного навколо квадрата
Об'єм піраміди
У
Відповідь:
ТЕМА: Тіла обертання. Многогранники.
Завдання скеровано на перевірку знання властивостей основних видів многогранників, зокрема піраміди, та властивостей циліндра, формул для обчислення площі поверхні циліндра й об’єму піраміди.
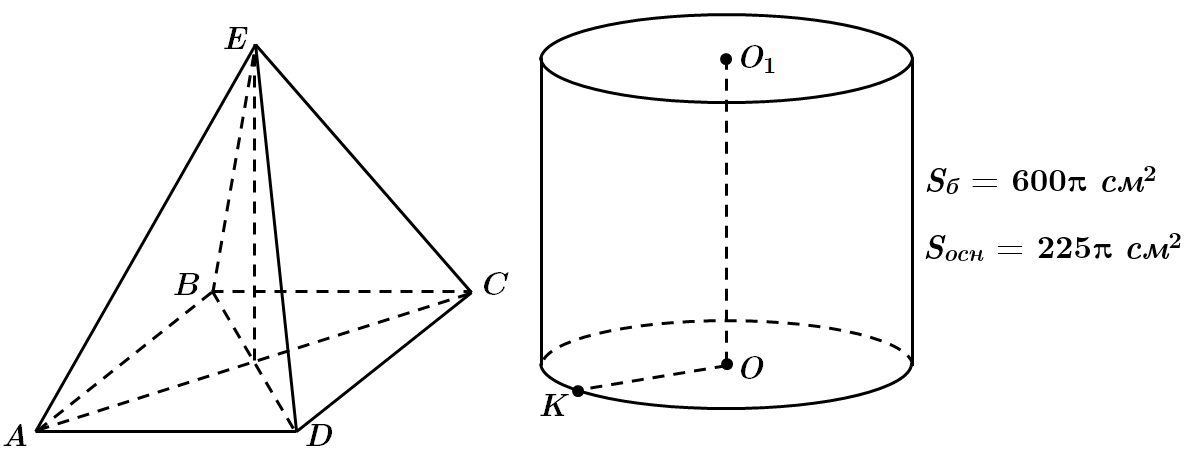
Площа основи циліндра
Площа бічної поверхні ціліндра
За умовою радіус кола, описаного навколо квадрата
Діагональ
Об'єм піраміди
Відповідь:
ТЕМА: Тіла обертання. Многогранники.
Завдання скеровано на перевірку знання основних видів многогранників, зокрема призми, властивості сфери, уміння застосовувати формули для обчислення площі поверхні сфери й об’єму призми.
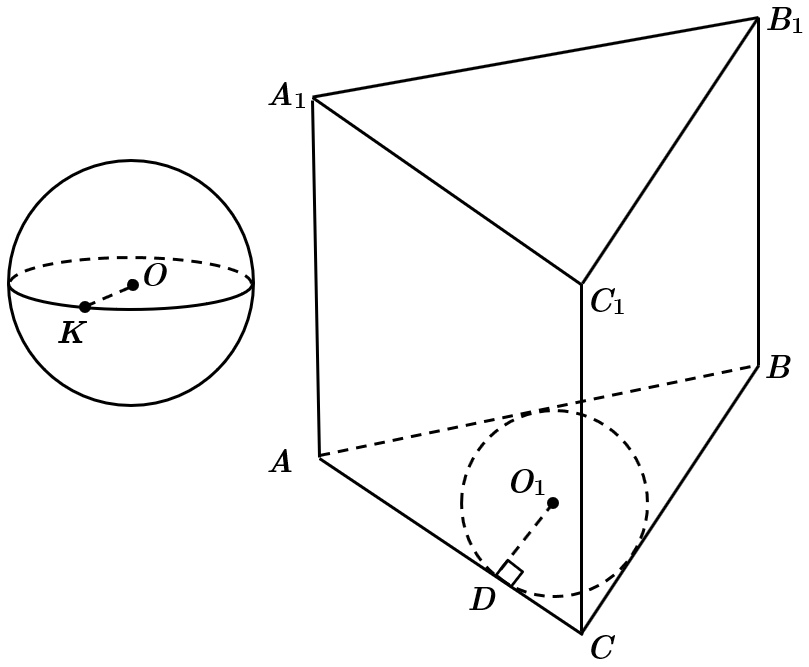
Площа поверхні сфери
За умовою задачі радіус сфери дорівнює радіусу кола, вписаного в основу призми. Отже,
Призма – правильна, отже
Площу правильного трикутника обчислiмо за формулою:
Об'єм призми
Відповідь:
ТЕМА: Тіла обертання.
Завдання скеровано на перевірку вміння розв’язувати задачі, зокрема практичного змісту, знання видів тіл обертання, як-от конуса.
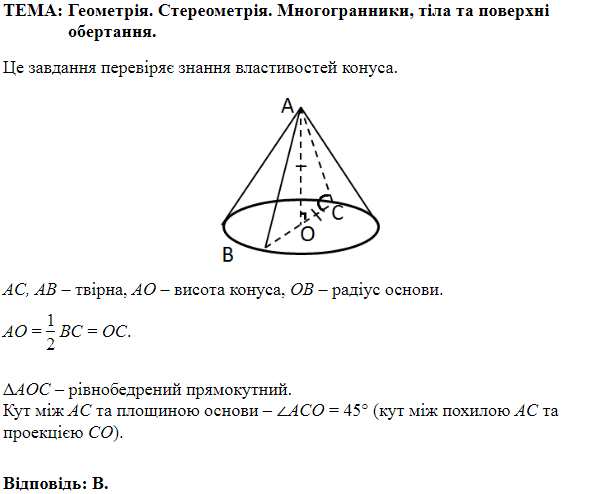
На рисунку зображено частину поверхні конуса.

Відповідь: В.
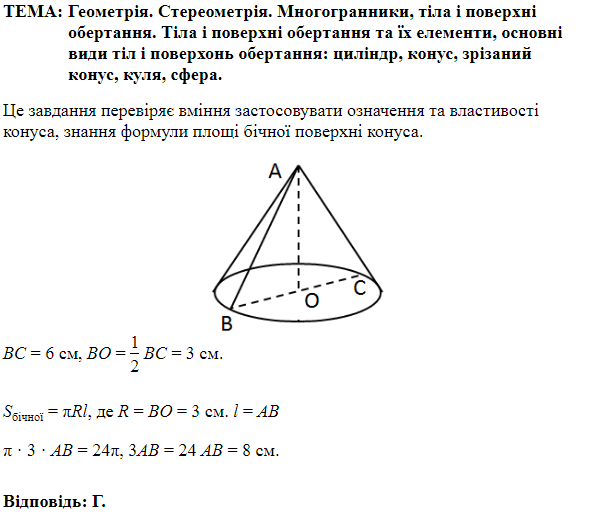
ТЕМА: Геометрія. Стереометрія. Многогранники, тіла обертання.
Завдання скеровано на перевірку знань властивостей піраміди та конуса, вміння розв’язувати задачі на обчислення площ поверхонь геометричних тіл.
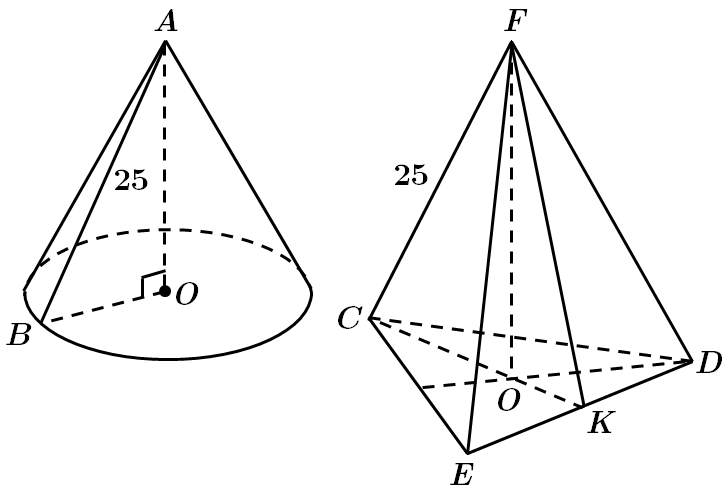
Твірна консуса
Площа бічної поверхні конуса
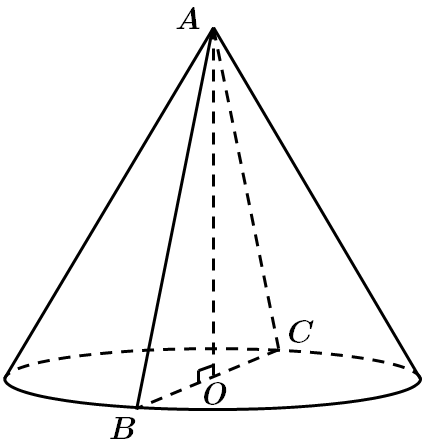
У піраміді
Площа бічної поверхні піраміди
Відповідь:
ТЕМА: Геометрія. Стереометрія. Тіла обертання. Координати у просторі.
Завдання скеровано на перевірку знань формули відстані між точками у просторі, властивостей кулі.

Знаходимо відстань між точками
Якщо б кулі були однакового радіусу, то дорівнювали б
З наведених значень – це
Відповідь: Д.
ТЕМА: Геометрія. Стереометрія. Многогранники, тіла обертання.
Завдання скеровано на перевірку знань властивостей призми та циліндра, вміння розв’язувати задачі на обчислення об’ємів і площ поверхонь геометричних тіл.
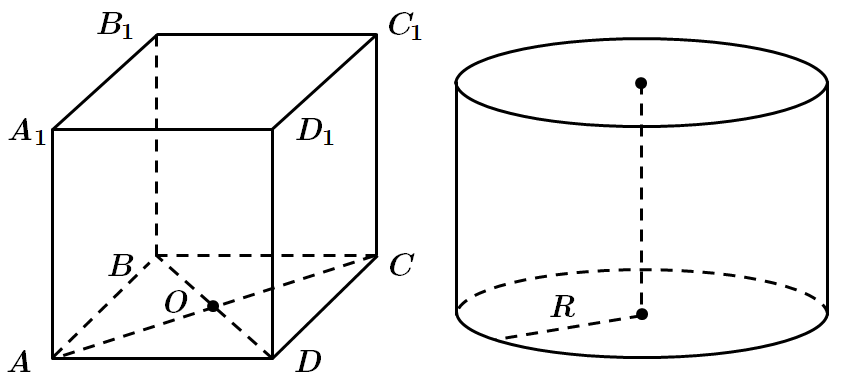
1. В основі призми – ромб з діагоналями
2. Радіус основи циліндра
3. Площа поверхні циліндра
4. Висота призми дорівнює висоті циліндра
5. Об'єм призми
Площу ромбу можна знайти за формулою:
Відповідь: 1920.
ТЕМА: Геометрія. Стереометрія. Тіла обертання. Координати на площині.
Завдання скеровано на перевірку знання про конус та його елементи, формули площ поверхонь конуса, формул для обчислення відстані між двома точками.
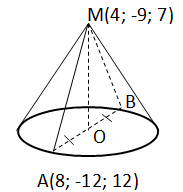
Знайдемо довжину
Відповідь:
Відповідь: 37,5.
ТЕМА: Геометрія Стереометрія. Тіла обертання.
Завдання скеровано на перевірку знання основних елементів циліндра.
Твірна циліндра – відрізок, який сполучає відповідні точки кіл кругів, які є основами циліндра.
З-поміж наведених – це
Отже, правильна відповідь – Д.
Відповідь: Д.
ТЕМА: Геометрія. Стереометрія. Тіла обертання.
Завдання перевіряє знання про циліндр та його елементи.
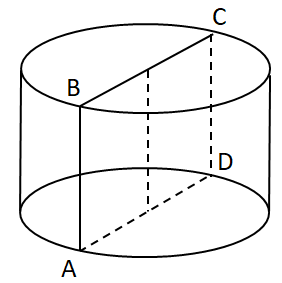
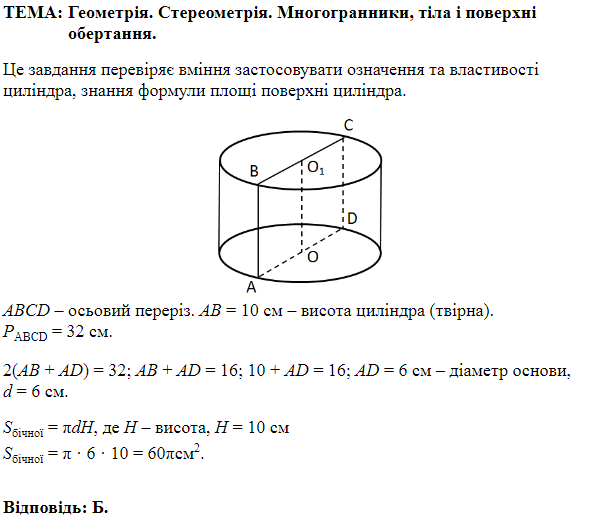
Осьовим перерізом циліндра
Відповідь: 64.
ТЕМА: Геометрія Стереометрія. Тіла обертання.
Завдання перевіряє знання властивостей геометричних тіл, зокрема циліндра.
Циліндр утворений обертанням квадрата навколо його сторони:
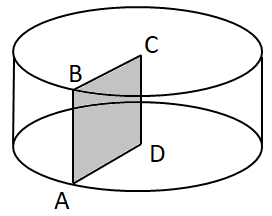
Відповідь: А.
ТЕМА: Геометрія. Стереометрія. Тіла обертання.
Завдання перевіряє знання про конус та його елементи, властивості подібних фігур.
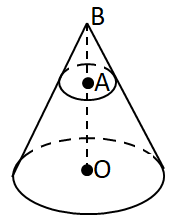
Площина, паралельна основі, відтинає подібний конус.
Коефіцієнт подібності
Отже, об'єм меншого конуса
Відповідь: 8.
ТЕМА: Геометрія Стереометрія. Тіла обертання.
Перевіряє знання формул для обчислення об'єму циліндра.
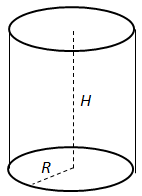
Об'єм циліндра
Відповідь: Г.
ТЕМА: Геометрія Стереометрія. Тіла обертання.
Завдання перевіряє вміння обчислення об’єму циліндра.
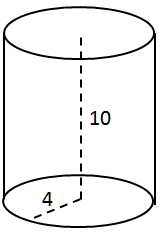
Об'єм циліндра знаходимо за формулою:
Відповідь: Д.
ТЕМА: Геометрія. Стереометрія. Тіла обертання. Прямі та площини у просторі.
Завдання скеровано на перевірку вміння знаходити кути у просторі, знання про двогранний кут, лінійний кут двогранного кута.
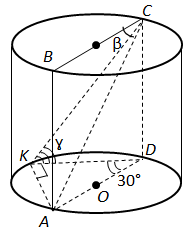
1. Вписаний кут
2. У
Відповідь: 2.
ТЕМА: Геометрія. Стереометрія. Тіла обертання.
Завдання скеровано на перевірку вміння знаходити кути у просторі, побудову осьового перерізу циліндру, знаходження об’єму.
1.
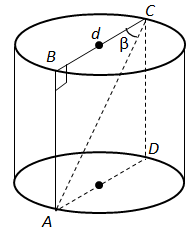
2. Твірна
3. Об'єм циліндра знаходимо за формулою:
Відповідь:
ТЕМА: Геометрія. Стереометрія. Тіла обертання.
Завдання скеровано на перевірку знання про сферу та її основні елементи, вміння розв’язувати стереометричні задачі.
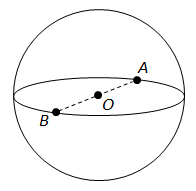
Відстань між точками на сфері – це хорда.
Найбільша відстань між двома точками на сфері – найбільша за довжиною хорда – діаметр
Відповідь: A.
ТЕМА: Геометрія. Стереометрія. Тіла обертання. Прямі та площини у просторі.
Завдання скеровано на перевірку вміння знаходити кути у просторі, знання про двогранний кут, лінійний кут двогранного кута.
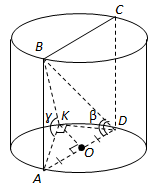
1. Прямокутник
Пряма
Таким чином,
2.
Отже,
Відповідь: 2.
ТЕМА: Геометрія. Стереометрія. Тіла обертання.
Завдання скеровано на перевірку вміння знаходити кути у просторі, побудову осьового перерізу циліндру.
1. Осьовий переріз циліндра (прямокутник
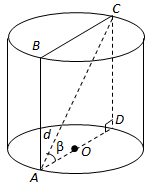
2. Твірна
3. Об'єм циліндра знаходимо за формулою:
Отже,
Відповідь:
ТЕМА: Геометрія. Стереометрія. Многогранники.
Завдання скеровано на перевірку знання про многогранники та їх основні елементи, вміння розв’язування задач, зокрема практичного змісту.
Якщо радіус кульки 6 см, то діаметр – 12 см.
Для того, щоб кульки помістилися у шухлядці, її висота може бути 13 см.
Відповідь: Г.
ТЕМА: Геометрія. Стереометрія. Тіла обертання.
Завдання скеровано на перевірку вміння розрізняти на розгортках елементи тіл обертання, знаходити їх основні елементи.
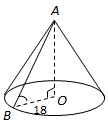
1.
2.
отже 2 - А.
3. Радіусом сектора, що є розготкою бічної поверхні конуса, є твірна
отже 3 - В.
Відповідь: 1Б, 2А, 3В.
ТЕМА: Геометрія. Стереометрія. Многогранники. Тіла обертання.
Завдання скеровано на перевірку вміння розв’язувати задачі, зокрема практичного змісту на обчислення площ поверхонь геометричних тіл.
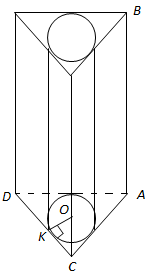
Бічні грані правильної трикутної призми виготовлені з паперу.
Площу паперу, витраченого на виготовлення коробки, визначимо за формулою площі бічної поверхні призми.
Радіус основи вписаного циліндра - це радіус кола, вписаного в правильний трикутник,
Сторону трикутника знайдемо за формулою:
Відповідь, найближча до точної, –
Відповідь: B.
ТЕМА: Геометрія. Стереометрія. Тіла обертання.
Завдання перевіряє знання формул для обчислення площ поверхонь та об'єму конуса.
1.
2.
3.
Відповідь: 1 – Б, 2 – A, 3 – Г.
ТЕМА: Геометрія Стереометрія. Тіла обертання.
Завдання перевіряє знання формул для обчислення площі поверхні кулі.
Площа сфери знаходиться за формулою:
Відповідь: Г.
ТЕМА: Геометрія Стереометрія. Тіла обертання.
Завдання перевіряє знання формул для обчислення площ поверхонь циліндра.
Отже,
Відповідь: Б.
ТЕМА: Геометрія Стереометрія. Тіла обертання.
Завдання перевіряє знання формул для обчислення площі поверхні та об’єму циліндра, циліндра та його елементів.
1. Твірна дорівнює
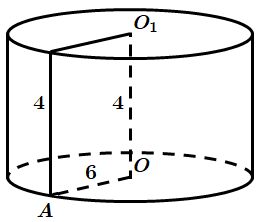
Отже, 1 – В.
2.
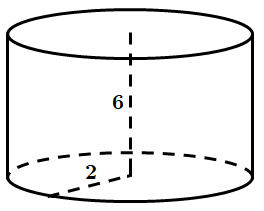
Отже, 2 – Г.
3.
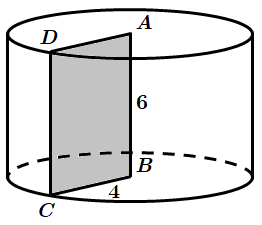
Отже, 3 – A.
Відповідь: 1 – В, 2 – Г, 3 – А.
ТЕМА: Геометрія. Планіметрія. Стереометрія. Трикутники. Тіла обертання.
Завдання перевіряє знання про конус та його елементи, співвідношення між сторонами і кутами прямокутного трикутника.
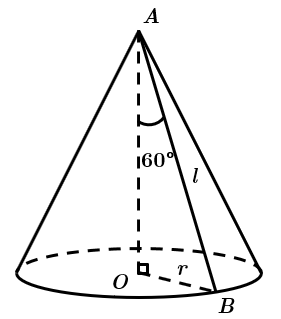
У
Відповідь: A.
ТЕМА: Геометрія. Стереометрія. Тіла обертання.
Завдання перевіряє вміння розв'язувати задачі на обчислення площі поверхні циліндра.
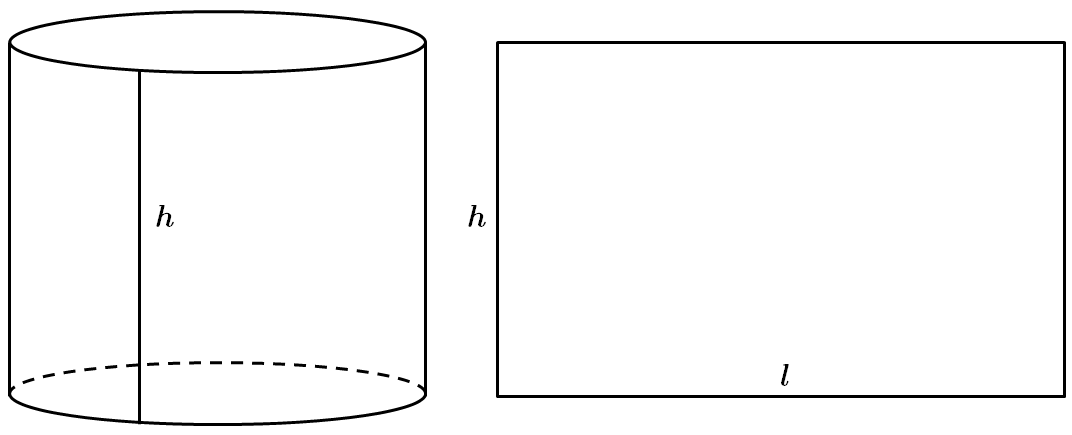
Розгорткою бічної поверхні циліндра є прямокутник.
Площа бічної поверхні
Відповідь: Г.
ТЕМА: Геометрія. Стереометрія. Тіла обертання.
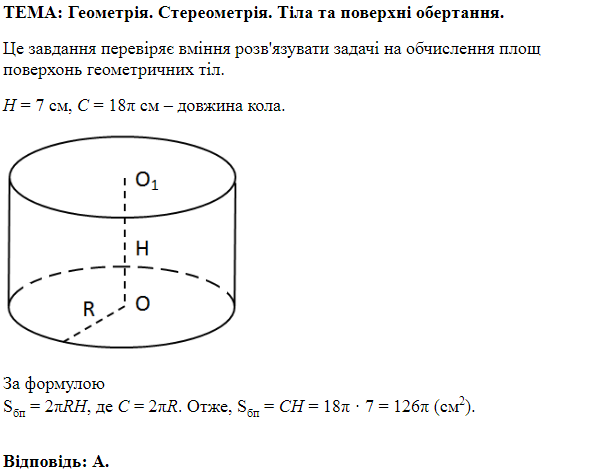
Це завдання перевіряє знання властивостей, формули площі поверхні циліндра.
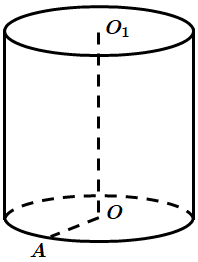
Площа бічної поверхні
Відповідь: Г.
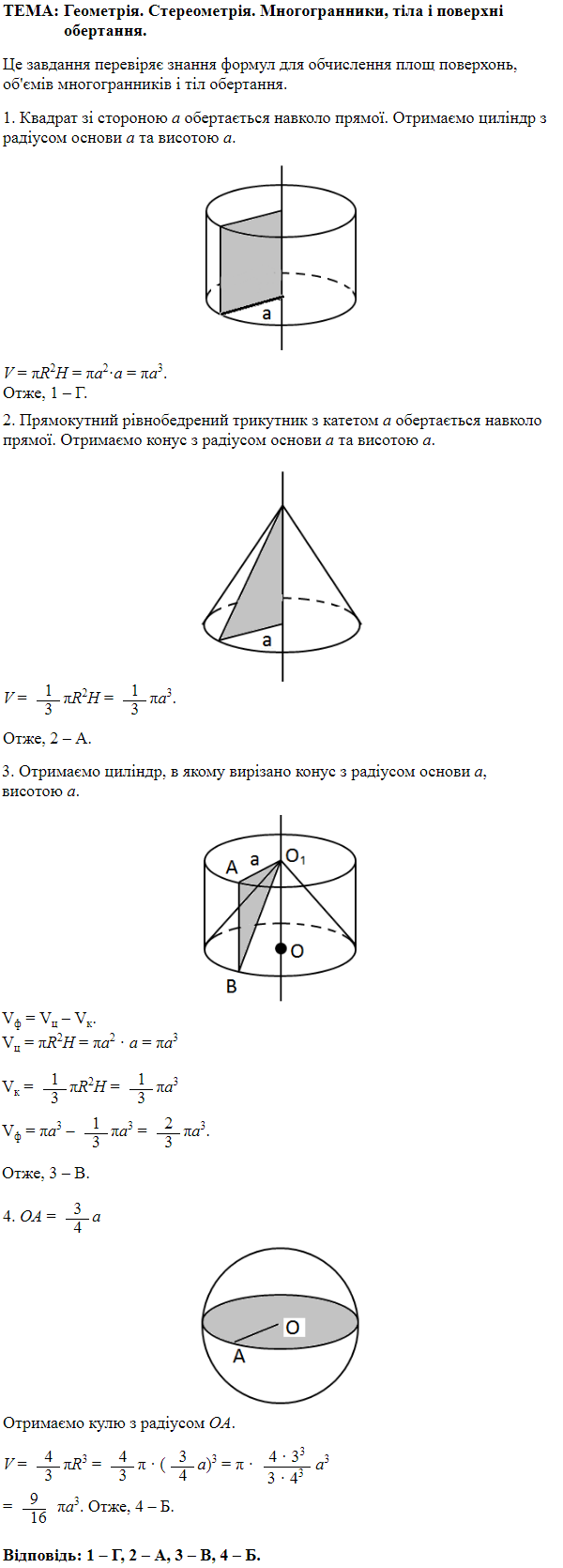
ТЕМА: Геометрія. Стереометрія. Многогранники, тіла і поверхні обертання. Тіла і поверхні обертання та їх елементи, основні види тіл і поверхонь обертання: циліндр, конус, зрізаний конус, куля, сфера.
Це завдання перевіряє знання формули об'єму циліндра.
Об'єм циліндра обчислюємо за формулою
Відповідь: Б.
ТЕМА: Геометрія. Стереометрія. Тіла обертання.
Це завдання перевіряє знання формули об'єму конуса.
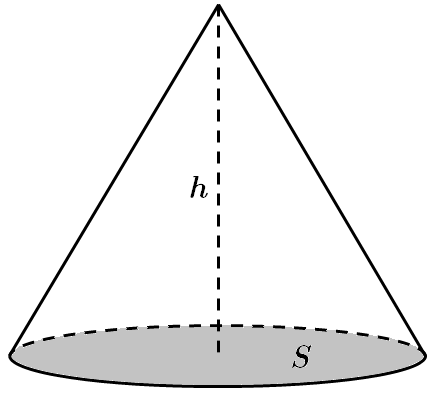
Об'єм конуса дорівнює третині добутку площі основи на висоту:
Відповідь: Д.
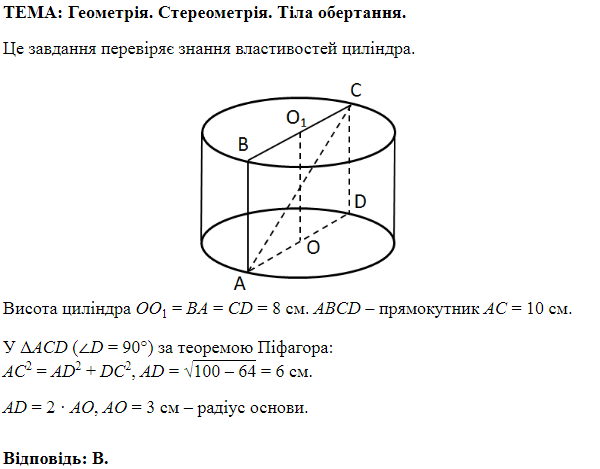
ТЕМА: Геометрія. Стереометрія. Многогранники, тіла й поверхні обертання.
Це завдання перевіряє вміння застосовувати властивості конуса до розв'язування стереометричних задач.
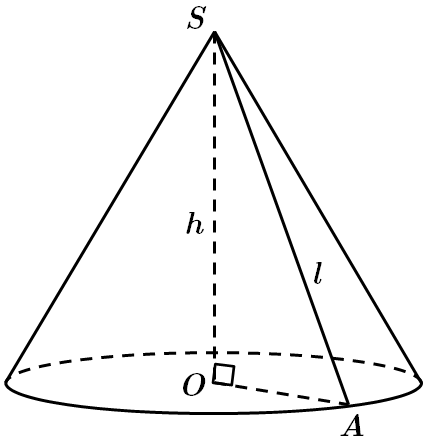
У
Отже, правильна відповідь А.
Відповідь: A.
ТЕМА: Геометрія. Стереометрія. Тіла обертання.
Це завдання перевіряє вміння розв'язувати задачі на обчислення площ поверхонь геометричних тіл, знання формул для обчислення площ поверхонь конуса та циліндра.
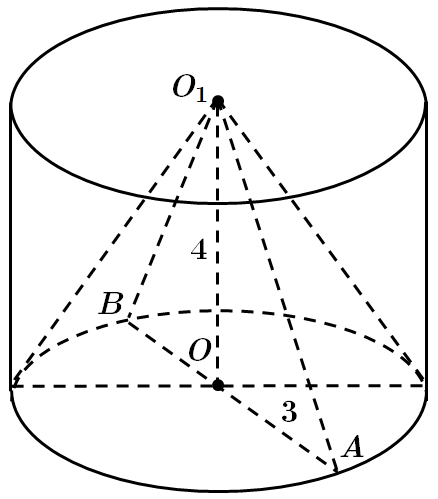
Нехай
1.
Отже, 1 – Г.
2.
Отже, 2 – Д.
3. Площа основи конуса дорівнює площі основи циліндра.
Отже,
Отже, 3 – A.
4. Площа бічної поверхні конуса
У
Отже, 4 – B.
Відповідь: 1 – Г, 2 – Д, 3 – А, 4 – В.
ТЕМА: Стереометрія. Поверхні обертання.
Це завдання перевіряє знання властивостей кулі та сфери та вміння розв'язувати стереометричні задачі.
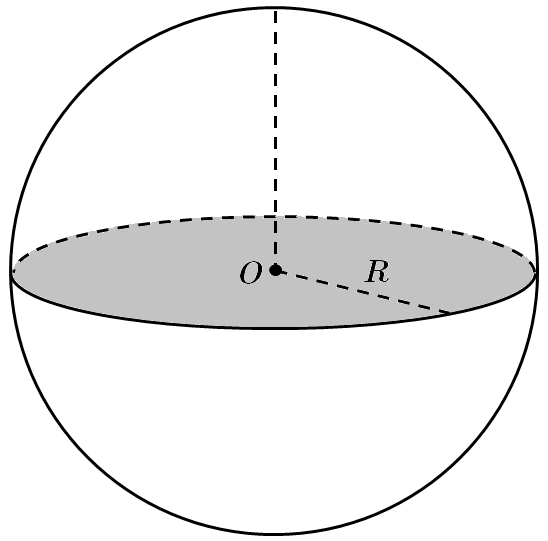
Площа великого круга дорівнює
Площа сфери визначається за формулою:
Отримаємо:
Відповідь: A.
ТЕМА: Стереометрія. Многогранники, тіла й поверхні обертання.
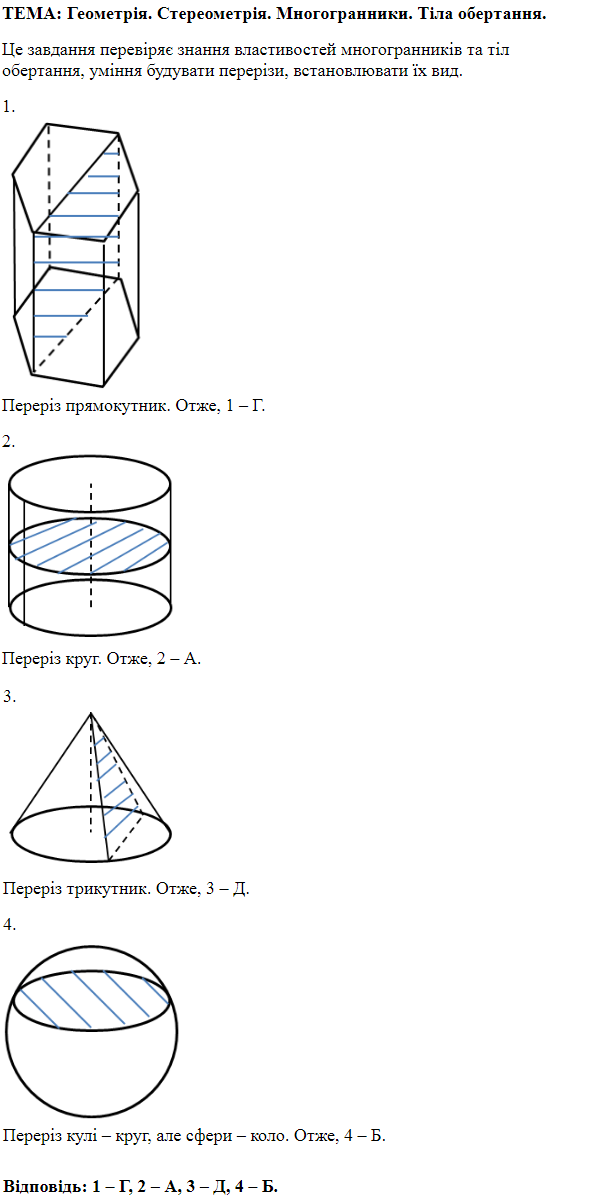
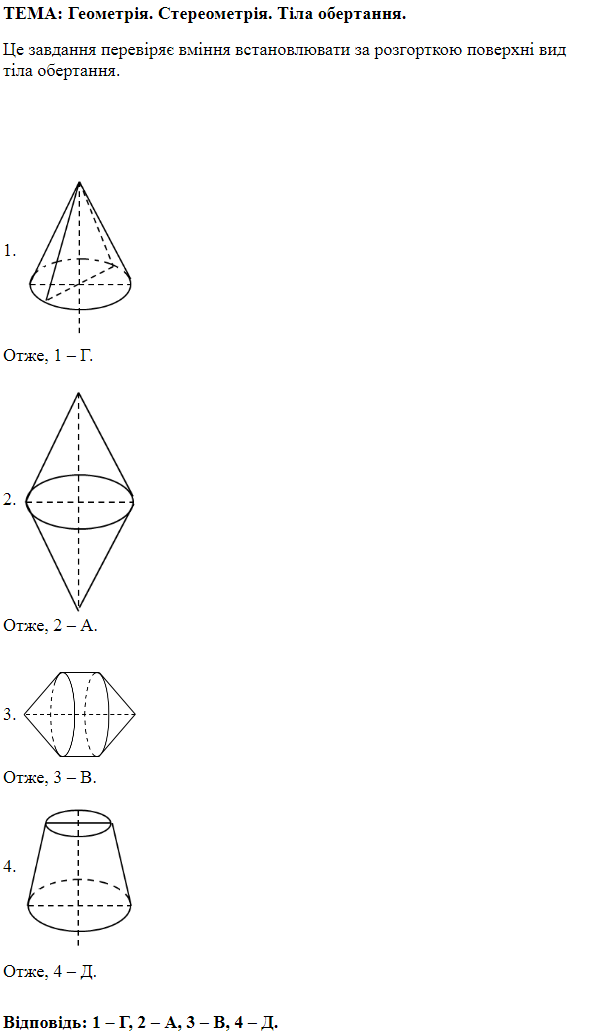
Це завдання перевіряє знання властивостей тіл і поверхонь обертання та їхніх елементів, уміння розв'язувати задачі на обчислення об'ємів геометричних тіл.
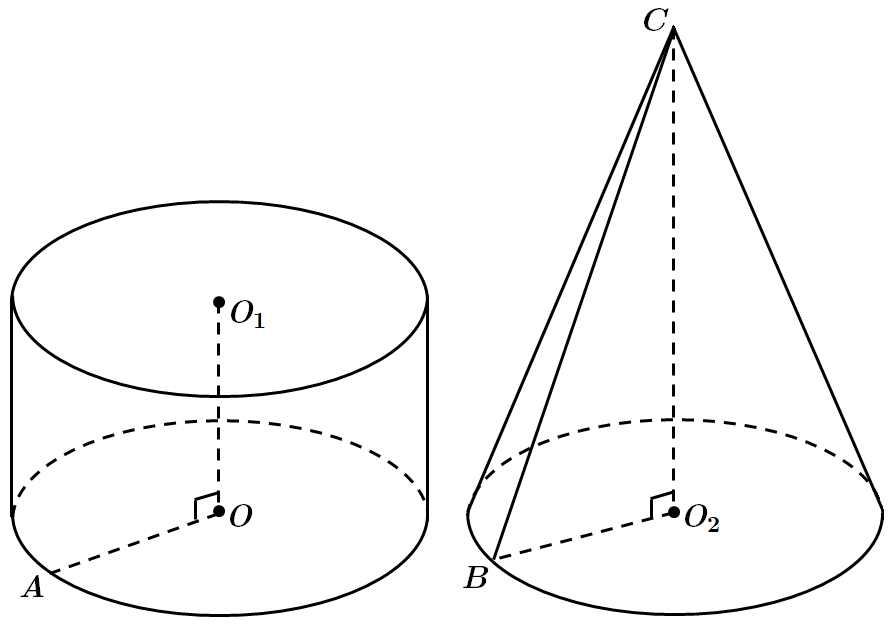
1.
Отже, правильна відповідь – A.
2.
Отже, правильна відповідь – Г.
3.
Отже, правильна відповідь – Б.
4.
Отже, правильна відповідь – Д.
Відповідь: 1 – A, 2 – Г, 3 – Б, 4 – Д.
ТЕМА: Стереометрія. Многогранники, тіла й поверхні обертання.
Це завдання перевіряє вміння розв'язувати задачі на обчислення об'єму геометричних тіл.
Об'єм кулі знаходиться за формулою
Відповідь: Б.


ТЕМА: Геометрія. Стереометрія. Многогранники, тіла й поверхні обертання. Планіметрія. Трикутники.
Це завдання перевіряє вміння розв'язувати задачі на обчислення площ поверхонь, знання формул для обчислення площ поверхонь тіл обертання, знання теореми Піфагора, співвідношення між сторонами та кутами прямокутного трикутника.
Доберемо до кожного із запитань 1 – 4 правильну відповідь.
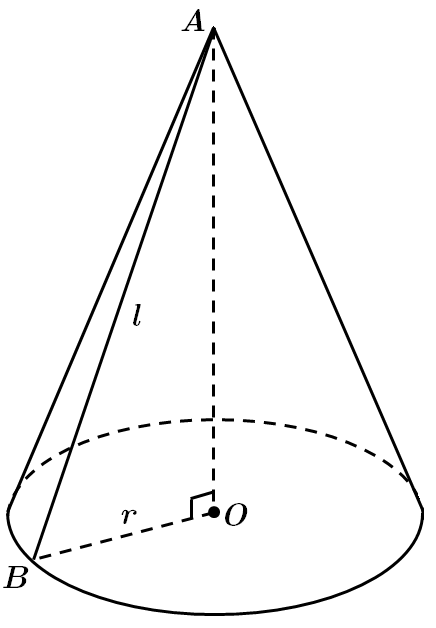
1. Якщо
2. Якщо висота конуса дорівнює радіусу основи, то
3. Якщо проекція твірної на площину основи конуса удвічі менша за твірну, то
4. Якщо площа повної поверхні конуса дорівнює
Отже, 4 – Г.
Відповідь: 1 – В, 2 – Б, 3 – А, 4 – Г.
ТЕМА: Геометрія. Стереометрія. Многогранники, тіла й поверхні обертання.
Це завдання перевіряє вміння застосовувати означення та властивості тіл і поверхонь обертання до розв'язування стереометричних задач; знання формул для обчислення площ поверхонь та об'ємів тіл обертання.
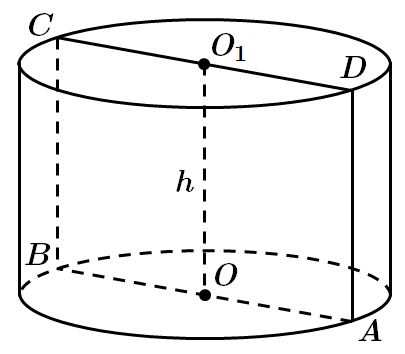
1.
Отже, 1 – Д.
2.
Отже, 2 – Б.
3.
Отже, 3 – A.
4.
Отже, 4 – B.
Відповідь: 1 – Д, 2 – Б, 3 – А, 4 – В.
ТЕМА: Геометрія. Стереометрія. Многогранники, тіла й поверхні обертання (куб, куля, циліндр, конус). Формули для обчислень площ поверхонь многогранників і тіл обертання.
Це завдання перевіряє вміння визначати площу повної поверхні куба, кулі, циліндра та конуса.
Обчислимо площу повної поверхні кожного геометричного тіла (1 – 4).
1. Площа повної поверхні циліндра, радіус основи якого дорівнює
За умовою
Отже, 1 – Г.
2. Щоб визначити площу повної поверхні конуса, потрібно знати радіус його основи
Оскільки
Отже, 2 – Б.
3. Площу повної поверхні куба із ребром
Отже, 3 – А.
4. Площа поверхні кулі радіуса
Отже, 4 – Д.
Відповідь: 1 – Г, 2 – Б, 3 – А, 4 – Д.