Розділ: Планіметрія
Тема: Трикутники
Кількість завдань: 78
ТЕМА: Трикутники. Чотирикутники.
Завдання скеровано на перевірку знання властивостей трапеції, рівнобедреного трикутника.
1. Відстань від
За теоремою Піфагора в
Правильна відповідь – Г.
2. Побудуємо
3.
Правильна відповідь – Б.
Відповідь: 1 – Г, 2 – А, 3 – Б.
ТЕМА: Трикутники.
Завдання скеровано на перевірку знання видів трикутників і їхніх основних властивостей, нерівності трикутника, суми кутів трикутника.
I. Твердження неправильне. Сума будь-яких двох сторін більша за третю. Це нерівність трикутника.
II. Твердження неправильне. Сума двох кутів трикутника може бути меншою або дорівювати
III. Твердження правильне. За наслідком із теореми синусів навпроти найбільшої сторони лежить найбільший кут, навпроти найменшої сторони – найменший кут.
Відповідь: В.
ТЕМА: Трикутники.
Завдання скеровано на перевірку знання видів трикутників та їхніх основних властивостей, властивостей медіани, висоти та бісектриси трикутника.
I. Твердження неправильне. Медіана збігається з бісектрисою, яку проведено до основи, тільки в рівнобедреному трикутнику. В умові трикутник довільний.
II. Твердження неправильне. Бісектриса довільного трикутника не збігається з медіаною.
III. Твердження правильне. Центр описаного кола – точка перетину бісектрис у будь-якому трикутнику.
Відповідь: Г.
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивостей трапеції, трикутників, уміння застосовувати теорему косинусів.
1. Оскільки точка
Отже, 1 – А.
2. Розгляньмо прямокутний трикутник
Отже, 2 – Д.
3.
Нехай
Оскільки
Проведімо висоту з точки
Оскільки
У прямокутному трикутнику
Отже, 3 – B.
Відповідь: 1 – A, 2 – Д, 3 – В.
ТЕМА: Трикутники.
Завдання скеровано на перевірку вміння застосовувати означення, ознаки та властивості трикутників різних видів, знання властивостей медіани й бісектриси трикутника.
I. За означенням, медіана – це відрізок, що сполучає вершину трикутника із серединою протилежної сторони.
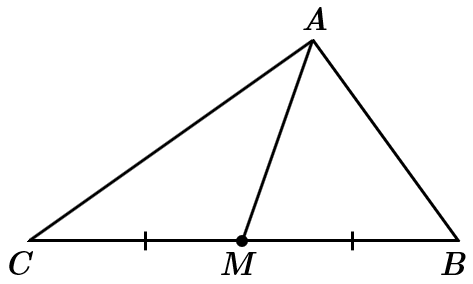
Оскільки
II. Промінь, що ділить кут навпіл, називають бісектрисою.
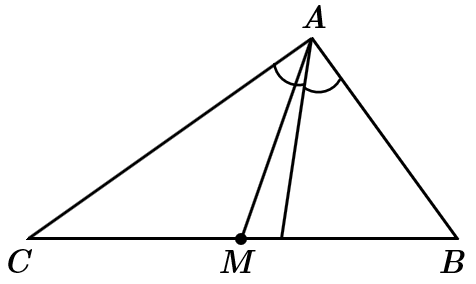
У довільному трикутнику (як зазначено в умові) медіана не збігається з бісектрисою. Твердження неправильне.
III. Медіана поділяє трикутник на два трикутники з рівними площами (рівновеликі). Площі трикутників
Площу трикутника можна обчислити за формулою:
У трикутників
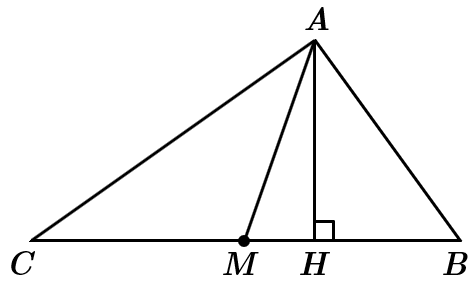
Отже,
Відповідь: B.
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивостей трапеції, її середньої лінії, співвідношення між сторонами й кутами прямокутного трикутника.
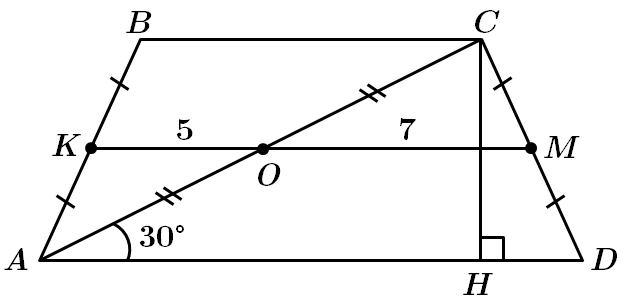
За властивістю середньої лінії трапеції:
У
У
Побудуймо
У
Площа трапеції
Відповідь: Г.
ТЕМА: Трикутники.
Завдання скеровано на перевірку вміння застосовувати означення, ознаки та властивості трикутників різних видів, знання властивостей медіани й висоти трикутника.
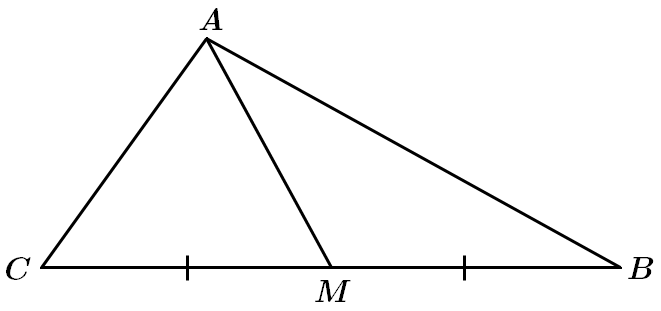
I.
II. Відстанню від точки
У довільному трикутнику медіана не є висотою, а тому твердження неправильне. Таку властивість має медіана рівнобедреного трикутника, яку проведено до основи.
III. Точка
Відповідь: B.
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знань властивостей ромба та рівнобедреного трикутника.
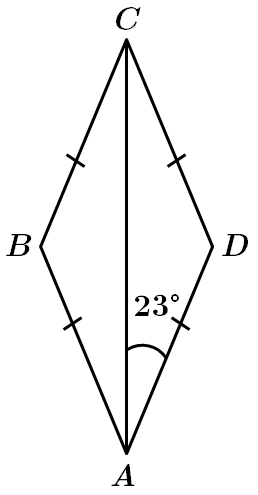
Отже,
Або можна обчислити більший кут ромба іншим способом. За властивістю ромба,
Сума сусідніх кутів будь-якого паралелограма (ромб – паралелограм) дорівнює
Відповідь: B.
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивостей прямокутника, властивості середньої лінії трикутника, уміння обчислювати площі трикутників, многокутників.
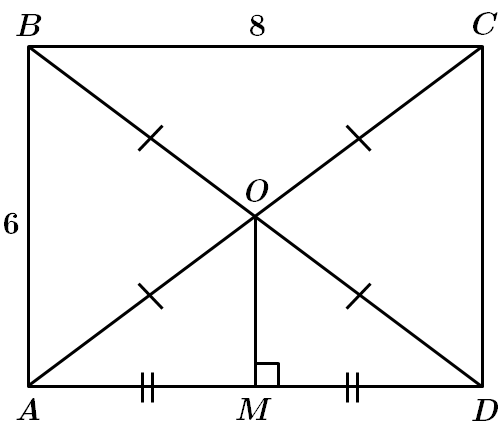
1.
Правильна відповідь – B.
2.
У
Правильна відповідь – A.
3.
Правильна відповідь – Г.
Відповідь: 1 – B, 2 – A, 3 – Г.
ТЕМА: Трикутники.
Завдання скеровано на перевірку знання видів і основних властивостей трикутників, властивостей та означення медіани трикутника.
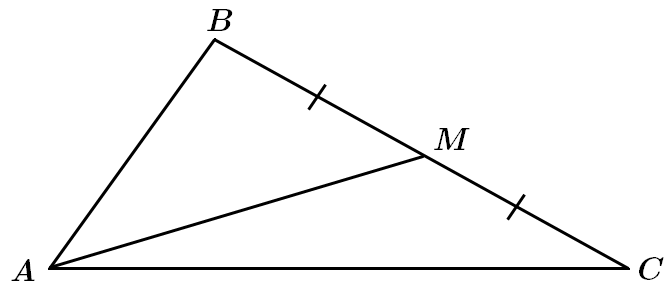
I. Твердження правильне. За означенням, медіана – відрізок, що сполучає вершину трикутника із серединою протилежної сторони.
Отже,
II. Твердження неправильне.
III. Твердження правильне.
Відповідь: В.
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знань властивостей паралелограмів, теореми косинусів, уміння розв’язувати трикутники.
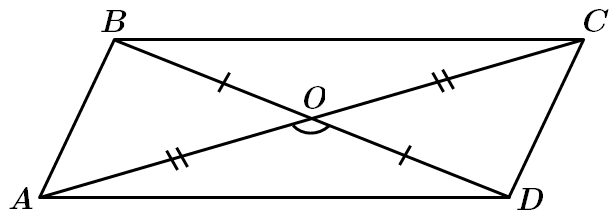
За властивістю паралелограма
У
Відповідь: A.
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивостей трапеції, її середньої лінії, трикутників, уміння застосовувати теорему синусів.
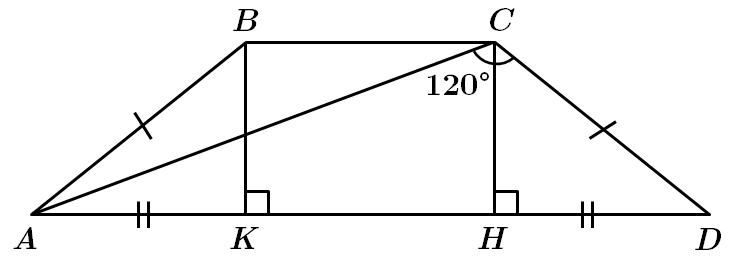
1. Середню лінію трапеції визначають за формулою
Правильна відповідь – В.
2.
Рівні похилі
Правильна відповідь – А.
3. Коло, описане навколо трапеції
За наслідком з теореми синусів:
Правильна відповідь – Г.
Відповідь: 1 – В, 2 – А, 3 – Г.
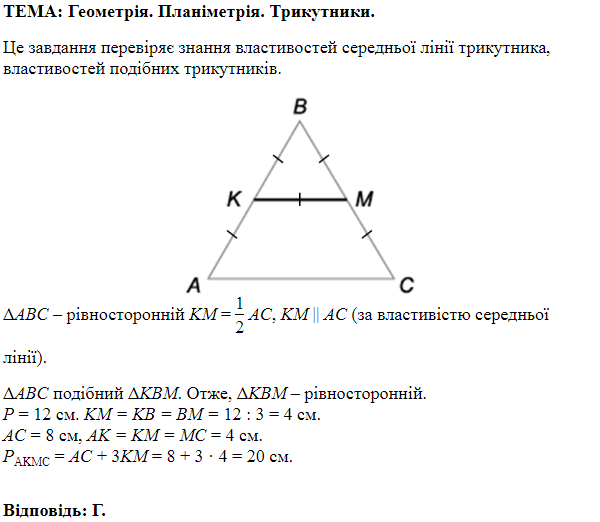
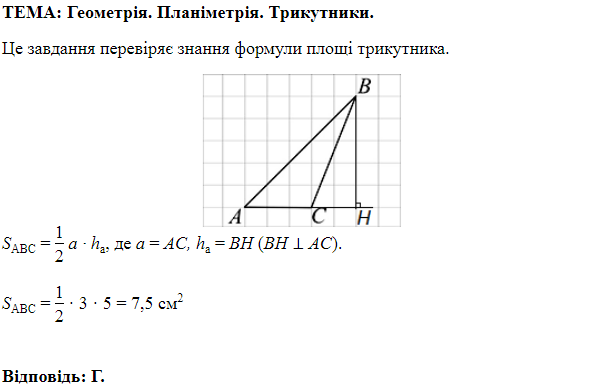
ТЕМА: Геометрія. Планіметрія. Трикутники.
Завдання скеровано на перевірку знань основних властивостей трикутника, нерівності трикутника.
I. Твердження неправильне. За нерівністю трикутника, сума довжин двох сторін трикутника більша за довжину третьої.
II. Твердження неправильне. Сума двох кутів трикутника не завжди більша за
III. Твердження правильне. За властивістю трикутника, навпроти більшої строни лежить більший кут, навпроти меншої сторони – менший кут, навпроти рівних сторін – рівні кути.
Відповідь: В.
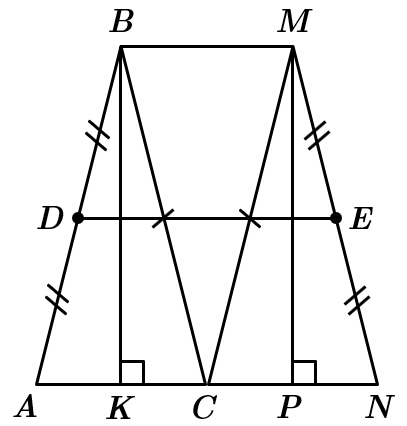
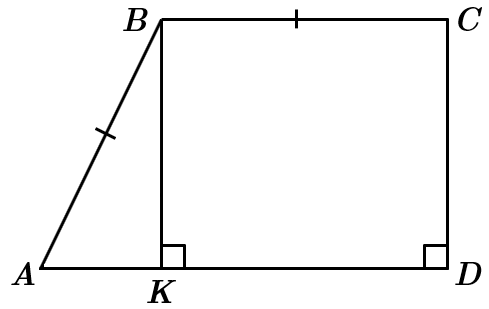
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Завдання скеровано на перевірку вміння застосовувати властивості трикутників до розв’язування планіметричних задач, знаходити довжину середньої лінії трапеції.
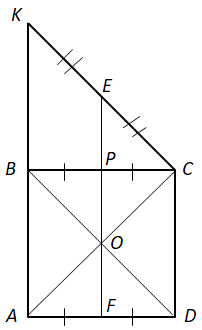
1 – A.
2 – Г.
3 – Б. Центр кола, описаного навколо квадрата, – це точка перетину діагоналей – точка
Центр кола, описаного навколо прямокутного трикутника, – середина гіпотенузи – точка
Відповідь: 1A, 2Г, 3Б.
ТЕМА: Геометрія. Планіметрія.
Завдання скеровано на перевірку знання властивості медіани трикутника, центра описаного кола трикутника.
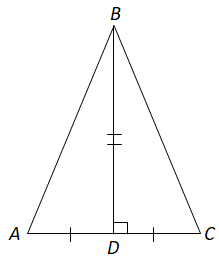
I. Серединний перпендикуляр до сторони рівностороннього трикутника ділить його на два рівних трикутники.
II. Точка перетину серединних перпендикулярів трикутника є центром описаного кола. У прямокутному трикутнику центр описаного кола – середина гіпотенузи. Отже, твердження є правильним.
III. У тупокутному трикутнику центр описаного кола знаходиться поза трикутником. Отже, твердження є неправильним.
Відповідь: Б.
ТЕМА: Геометрія. Планіметрія.
Завдання скеровано на перевірку знання властивості зовнішнього кута трикутника.
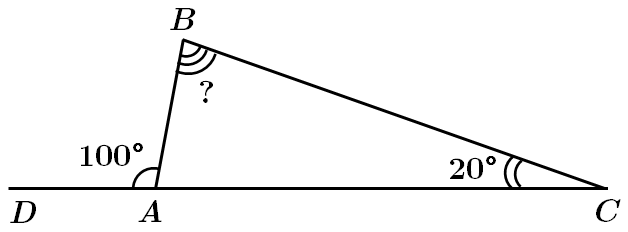
За властивістю зовнішнього кута трикутника:
Отже,
Відповідь: Г.
ТЕМА: Геометрія. Планіметрія. Трикутники.
Завдання скеровано на перевірку знання властивостей трикутника.
I.
IІ. За нерівністю трикутника
IІІ. У тупокутному трикутнику центр описаного кола лежить поза межами трикутника. Твердження правильне.
Отже, привильні твердження І та ІІІ.
Відповідь: Д.
ТЕМА: Геометрія. Планіметрія. Трикутники.
Завдання перевіряє вміння застосовувати властивості трикутників до розв’язування планіметричних задач, знання теореми Піфагора, наслідків з теореми синусів.
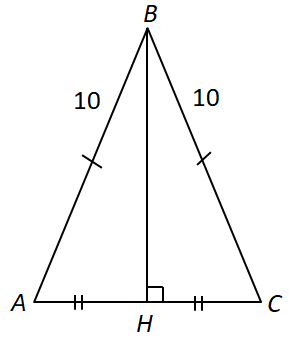
1 – Г.
2 – B. Висота
3 – A.
Відповідь: 1Г, 2В, 3А.
ТЕМА: Геометрія. Планіметрія. Трикутники.
Завдання перевіряє вміння застосовувати означення та властивості різних видів трикутників до розв'язування планіметричних задач.
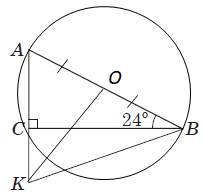
1 – Г. У
2 – B.
3 – A.
Відповідь: 1Г, 2В, 3А.
ТЕМА: Геометрія. Планіметрія.
Завдання перевіряє знання властивості трикутника про суму кутів.
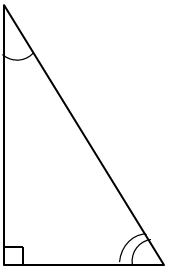
Сума кутів трикутника –
Отже,
Гострі кути
Найменший кут цього трикутника
Відповідь: B.
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.
Завдання скеровано на перевірку знання властивостей трикутника, трапеції; вміння розв’язувати задачі практичного змісту.
Побудуємо математичну модель задачі:

Відстань між паралельними сторонами
У
Уздовж сторін
Всього стовпчиків має бути
Відповідь: Б.
ТЕМА: Геометрія. Планіметрія. Трикутники.
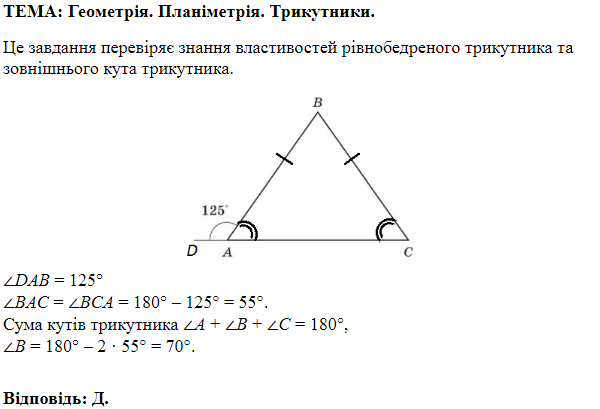
Завдання скеровано на перевірку знання теореми про суму кутів трикутника.
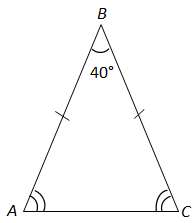
Сума кутів трикутника
За властивістю рівнобедреного трикутника
Відповідь: Б.
ТЕМА: Геометрія. Планіметрія. Трикутники.
Завдання скеровано на перевірку знання властивостей трикутника, вміння розв’язувати задачі практичного змісту.
Побудуємо математичну модель задачі:
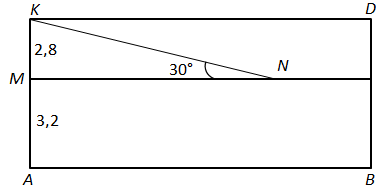
Катет
Відповідь: Г.
ТЕМА: Геометрія. Планіметрія. Трикутники.
Завдання скеровано на перевірку знання видів трикутників та їх основних властивостей, кола, описаного навколо трикутника, теореми синусів.
1. Рис. 1 – рівносторонній трикутник, отже, центри вписаного та описаного кіл збігаються, 1 - А.
2. Рис. 3 – оскільки катет прямокутного трикутника в 2 рази менше гіпотенузи, то він лежить напроти кута 30°. Отже, 2 - В.
3. Рис. 5 – за теоремою синусів:
Відповідь: 1A, 2В, 3Д.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивостей ромба, подібних трикутників, теореми Піфагора.
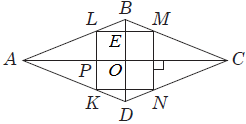
1. За теоремою Піфагора,
2.
Відповідь: 1. 12. 2. 21.
ТЕМА: Геометрія. Планіметрія. Трикутники. Координати та вектори на площині.
Завдання перевіряє вміння застосовувати властивості рівнобедреного трикутника, знаходити площу трикутника.
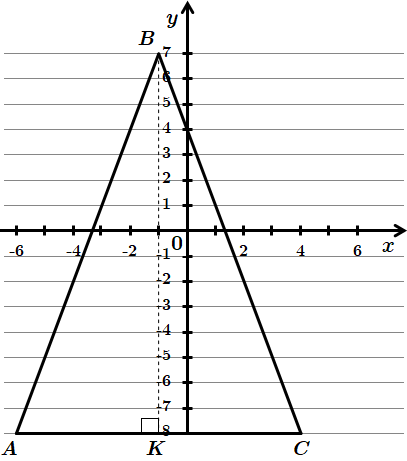
Накреслимо трикутник
Точка
Відповідь:
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.
Завдання перевіряє знання про подібні трикутники, властивість середньої лінії трапеції, властивості паралелограма.
1.
Отже, 1 – Б.
2.
Отже, 2 – B.
3.
Середня лінія трапеції дорівнює
Відповідь: 1 – Б, 2 – B, 3 – Г.
ТЕМА: Геометрія. Стереометрія. Многогранники.
Завдання перевіряє знання формул для обчислення площ поверхонь призми, площі трикутника.
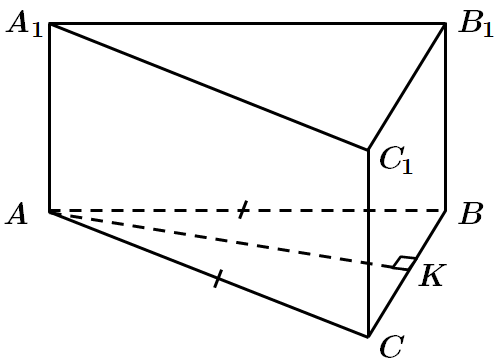
Бічні грані – прямокутники. Найбільша за площею бічна грань
У
У
Відповідь: Г.
ТЕМА: Геометрія. Планіметрія. Стереометрія. Трикутники. Многогранники.
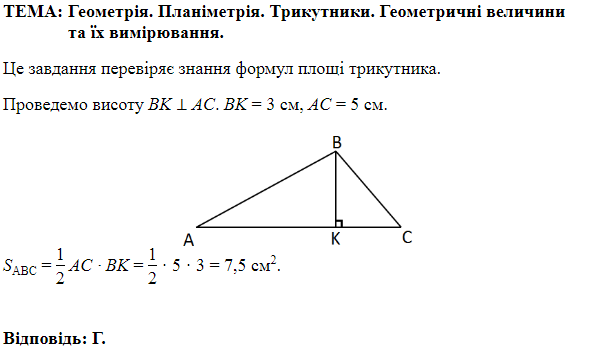
Завдання перевіряє знання про призму та її елементи, вміння знаходити площу трикутника.
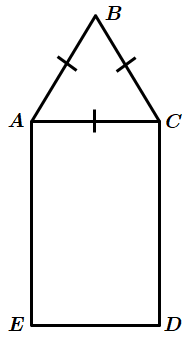
Площа основи призми – площа
За формулою
Відповідь: A.
ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури на площині та їхні властивості.
Завдання перевіряє знання властивостей суміжних та вертикальних кутів, теореми про суму кутів трикутника.
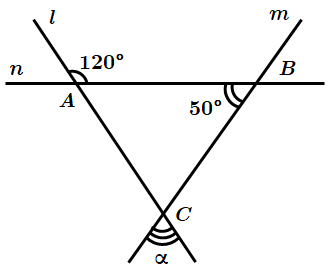
Сума кутів
Відповідь: Г.
ТЕМА: Геометрія. Планіметрія. Коло та круг. Трикутники. Координати та вектори на площині.
Завдання перевіряє вміння знаходити координати середини відрізка, складати рівняння кола, застосовувати властивості прямокутного трикутника, використовувати формули площі трикутника.
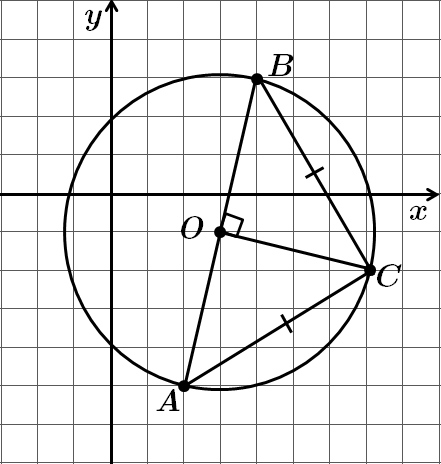
Коло задане рівнянням
Запишемо у стандартному вигляді
Точка
Отже,
Висота, проведена до гіпотенузи, – медіана та радіус описаного кола.
Отже,
Відповідь:
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання перевіряє знання властивостей ромба.
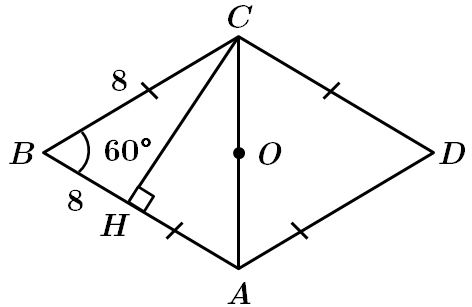
1.
2.
3. Центр кола, вписаного в ромб – точка перетину діагоналей точка
За властивістю ромба
Відповідь: 1 – B, 2 – Б, 3 – A.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Це завдання перевіряє знання властивостей паралелограмів, нерівності трикутника.
I. Протилежні сторони будь-якого паралелограма рівні (властивість параллелограма).
II. Довжина сторони будь-якого трикутника менша за суму довжин двох інших сторін (нерівність трикутника).
III. Твердження неправильне.
Відповідь: B.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
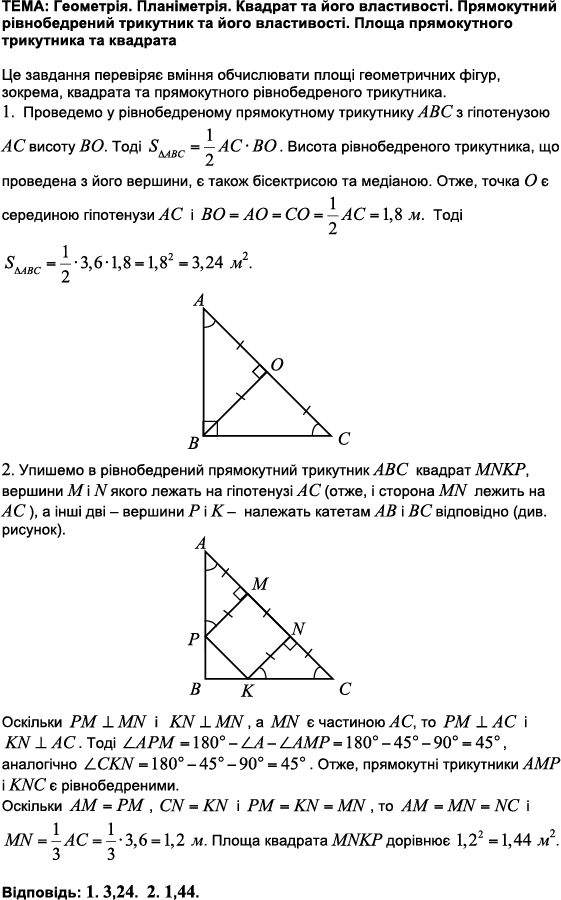
Це завдання перевіряє знання теореми Піфагора, співвідношення між сторонами і кутами прямокутного трикутника, формули площі прямокутного трикутника.
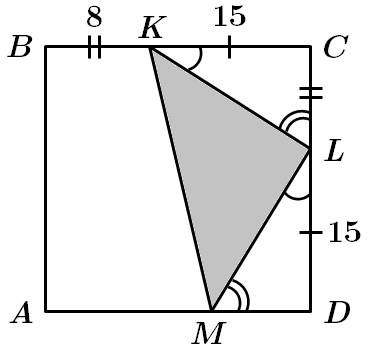
1.
У
2. Нехай
Отже,
Відповідь: 1.
2.
ТЕМА: Геометрія. Стереометрія. Многогранники, тіла і поверхні обертання. Тіла і поверхні обертання та їх елементи, основні види тіл і поверхонь обертання: циліндр, конус, зрізаний конус, куля, сфера.
Це завдання перевіряє вміння застосовувати означення та властивості призми, знання формули площі бічної поверхні призми.
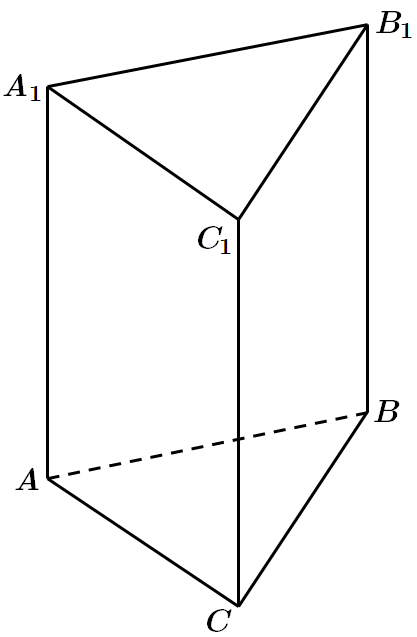
Відповідь: B.
ТЕМА: Геометрія. Планіметрія. Трикутники.
Це завдання перевіряє вміння класифікувати трикутники за сторонами та кутами, знання теореми про суму кутів трикутника, кола, описаного навколо трикутника.
Якщо
За нерівністю трикутника
Центр кола, описаного навколо тупокутного трикутника
Отже, правильна відповідь – Д.
Відповідь: Д.
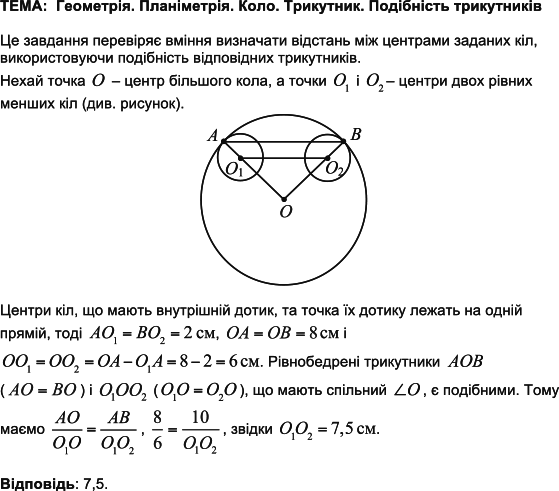
ТЕМА: Геометрія. Планіметрія. Трикутники. Коло. Круг. Координати та вектори на площині.
Це завдання перевіряє знання кола, круга та їхніх елементів; теореми синусів, рівняння кола.
Запишемо рівняння кола в канонічному вигляді
Центр кола
За наслідком з теореми синусів
Відповідь:
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.
Це завдання перевіряє знання співвідношення між сторонами і кутами прямокутного трикутника, теореми косинусів; уміння застосовувати властивості різних видів чотирикутників до розв'язування планіметричних задач.
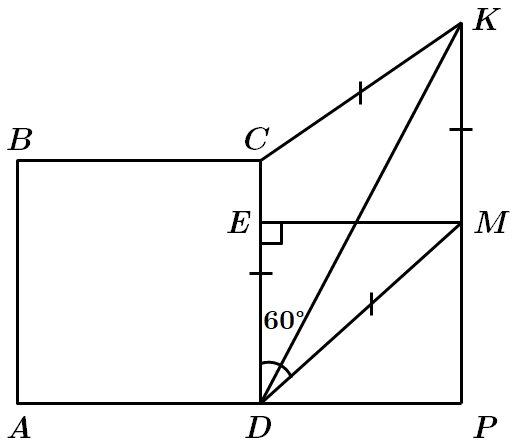
1. Периметр ромба
Отже, 1 – В.
2. Більша діагональ ромба лежить напроти більшого кута ромба.
У
Отже, 2 – Г.
3.Відстань від точки
У
Отже, 3 – Б.
4.
Отже, 4 – Д.
Відповідь: 1 – В, 2 – Г, 3 – Б, 4 – Д.
ТЕМА: Стереометрія. Многограники.
Це завдання перевіряє вміння розв'язувати задачі на обчислення об'ємів геометричних тіл, знання формул для обчислення площ трикутників.
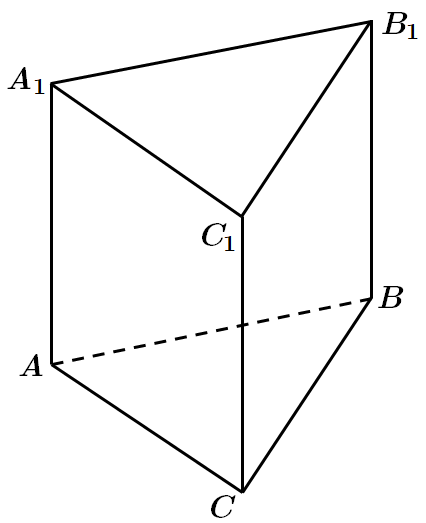
Дана трикутна призма
Усі бічні грані – квадрати, тому основа призми – рівносторонній трикутник. Площу рівностороннього трикутника можна знайти за формулою
За умовою
Об'єм призми
Відповідь: A.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Геометричні перетворення.
Це завдання перевіряє вміння застосовувати означення паралелограма, ознак подібності трикутників до розв'язування планіметричних задач.
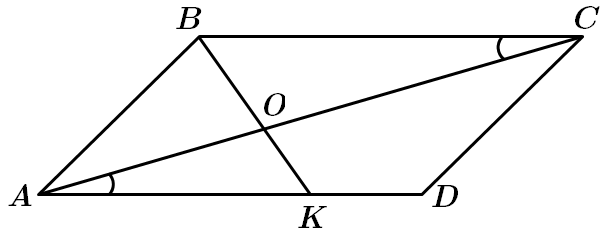
Розглянемо
Отже,
Відповідь: Б.
ТЕМА: Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості. Трикутники. Суміжні та вертикальні кути, паралельні та перпендикулярні прямі. Геометричні перетворення.
Це завдання перевіряє вміння застосовувати властивості паралельних прямих, ознаки подібності трикутників до розв'язування планіметричних задач.
Зробимо додаткову побудову і терез точку
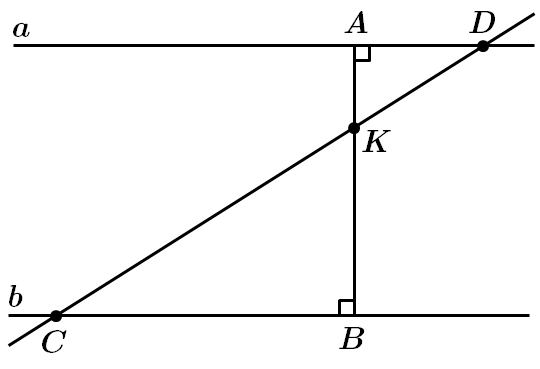
Розглянемо трикутники
У подібних трикутниках відповідні сторони пропорційні, отже
Відстань від точки
Відстань між прямими
Відповідь: B.

ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники. Геометричні перетворення.
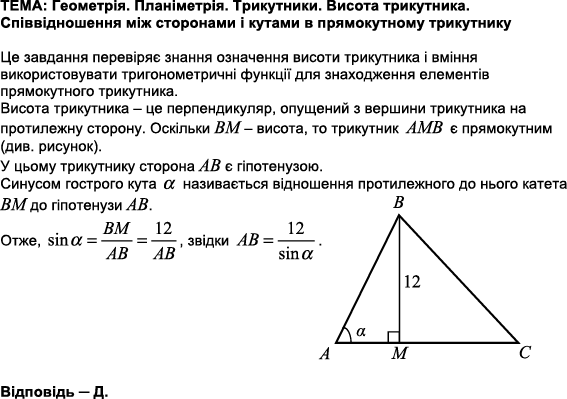
Це завдання перевіряє знання співвідношення між сторонами і кутами прямокутного трикутника, ознаки та властивості подібних фігур; уміння застосовувати властивості трикутників та чотирикутників до розв'язування планіметричних задач.
1.
За властивостю катета, який лежить напроти кута
2.
Відповідь: 1.
2.
ТЕМА: Геометрія. Планіметрія. Коло та круг. Трикутники.
Це завдання перевіряє знання властивостей дотичної до кола, центральних та вписаних кутів, видів трикутників та їхніх основних властивостей.
1. За властивістю дотичної до кола
Отже, 1 – В.
2.
Отже, 2 – A.
3. Градусна міра дуги
У
Градусна міра дуги
Отже, 3 – Г.
4. За властивістю вписаного кута:
Отже, 4 – Б.
Відповідь: 1 – В, 2 – A, 3 – Г, 4 – Б.
ТЕМА: Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості. Трикутники.
Це завдання перевіряє вміння застосовувати властивості найпростіших геометричних фігур, різних видів трикутників до розв'язування планіметричних задач.
Отже,
Відповідь: Б.
ТЕМА: Геометрія. Планіметрія. Трикутники.
Це завдання перевіряє вміння застосовувати означення та властивості різних видів трикутників до розв'язування планіметричних задач.
1.
2.
Отже, 2 – Д.
3.
Кутом між прямими, що перетинаються, називають менший із кутів, що утворився при перетині цих прямих. Кут між прямими
4.
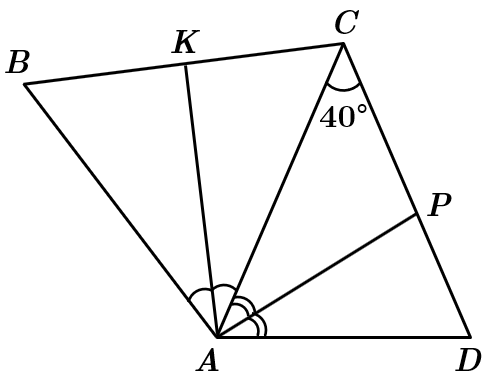
Отже, 4 – Г.
Відповідь: 1 – В, 2 – Д, 3 – Б, 4 – Г.
ТЕМА: Геометрія. Стереометрія. Многогранники, тіла й поверхні обертання. Планіметрія. Трикутники.
Це завдання перевіряє вміння розв'язувати задачі на обчислення площ поверхонь, знання формул для обчислення площ поверхонь тіл обертання, знання теореми Піфагора, співвідношення між сторонами та кутами прямокутного трикутника.
Доберемо до кожного із запитань 1 – 4 правильну відповідь.
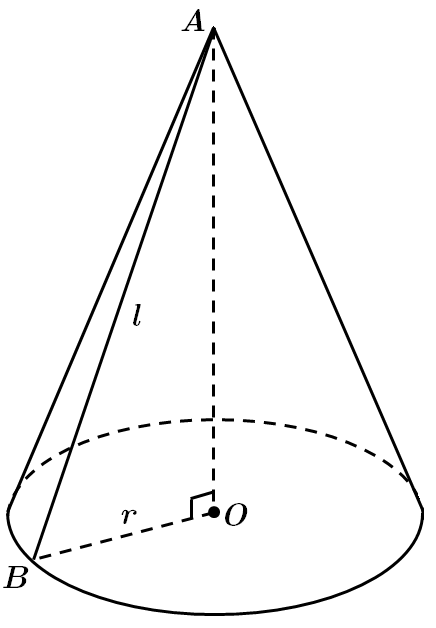
1. Якщо
2. Якщо висота конуса дорівнює радіусу основи, то
3. Якщо проекція твірної на площину основи конуса удвічі менша за твірну, то
4. Якщо площа повної поверхні конуса дорівнює
Отже, 4 – Г.
Відповідь: 1 – В, 2 – Б, 3 – А, 4 – Г.
ТЕМА: Геометрія. Планіметрія. Трикутники.
Це завдання перевіряє знання теореми косинусів, уміння застосовувати означення та властивості різних видів трикутників до розв'язування планіметричних задач, співвідношення між сторонами та кутами прямокутного трикутника.
Доберемо до кожного із запитань 1 – 4 правильну відповідь.
1. Якщо
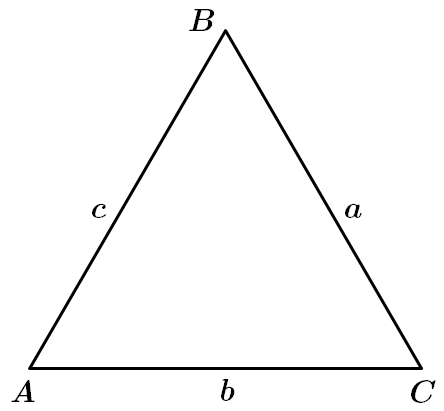
Усі кути рівностороннього трикутника дорівнюють
Отже, правильна відповідь – B.
2. Якщо
Отже, правильна відповідь – Г.
3. Якщо
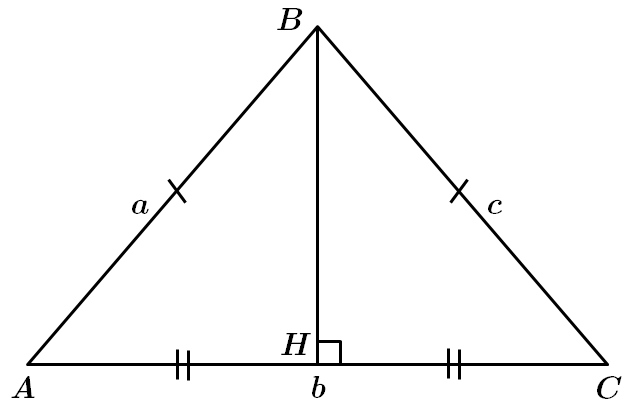
У
Отже, правильна відповідь – Б.
4. Якщо
Отже, правильна відповідь – Д.
Відповідь: 1 – B, 2 – Г, 3 – Б, 4 – Д.
ТЕМА: Геометрія. Планіметрія. Трикутники.
Це завдання перевіряє знання теореми про суму кутів трикутника.
Сума кутів трикутника дорівнює
Якщо
Отже, правильна відповідь – B.
Відповідь: B.
ТЕМА: Геометрія. Планіметрія. Описане коло, дотична до кола та її властивості. Трикутники (рівносторонній та прямокутний трикутники). Тригонометричні співвідношення в прямокутному трикутнику.
Це завдання перевіряє вміння визначати довжини відрізків, використовуючи властивості дотичної до кола, елементів кола, вписаних у коло кутів та співвідношень у прямокутному трикутнику.
Обчислимо довжини відрізків (1 – 4).
1. Оскільки діаметр кола вдвічі більший за його радіус, то згідно умови
2. Розглянемо трикутник
Такий же результат отримаємо, якщо скористаємось тим фактом, що у прямокутному трикутнику
Отже, 2 – Б.
3. Відрізок
Отже, 3 – A.
4. Розглянмо вписаний у коло трикутник
Або за теоремою Піфагора отримуємо:
Отже, 4 – Г.
Відповідь: 1 – B, 2 – Б, 3 – A, 4 – Г.
ТЕМА: Геометрія. Планіметрія. Трикутники. Нерівність трикутника.
Це завдання перевіряє вміння визначати можливе значення невідомої сторони трикутника.
Використаємо нерівність трикутника: будь-яка сторона довільного трикутника менша за суму двох інших його сторін та більша за їх різницю. Оскільки сторони трикутника
Цю умову задовольняє лише варіант Г –
Відповідь: Г.