Завдання за темами в мультитестах

ТЕМА: Механіка. Основи динаміки. Невагомість.

Завдання скеровано на перевірку знання і розуміння поняття невагомості.

Стан тіла, за якого вага тіла дорівнює нулю, називають станом невагомості.

У стані невагомості на тіло діє лише сила тяжіння (тіло вільно падає), і навпаки: якщо тіло рухається тільки під дією сили тяжіння, воно перебуває у стані невагомості.

У стані невагомості не тільки тіло не тисне на опору, а й частини тіла не тиснуть одна на одну.

Отже, з усіх умов, зазначених у варіантах відповіді, однозначно правильним є варіант А.

Відповідь: A.

ТЕМА: Механіка. Елементи механіки рідин і газів. Тиск нерухомої рідини на дно й стінки посудини.

Завдання скеровано на перевірку знання і розуміння закону Паскаля і формули гідростатичного тиску.

Із закону Паскаля (тиск, створюваний на нерухому рідину, передається рідиною однаково в усіх напрямках) і формули гідростатичного тиску \(p\ (p=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}gh,\) де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\) ‒ густина рідини, \(g\) ‒ прискорення вільного падіння, \(h\) ‒ висота стовпчика рідини) випливає, що тиск усередині нерухомої однорідної рідини на одному рівні є однаковим.

Отже, робимо висновок, що тиск усередині нерухомої однорідної рідини ‒ у воді (див. рисунок) ‒ у точках \(E\) і \(F\) є однаковим: $$ p_E=p_F. $$

На рівні точок \(C\) і \(D\) тиск стовпчиків рідин ‒ гасу й води ‒ у посудинах також є однаковим:

Це одна з властивостей сполучених посудин (у завданні ‒ \(U\text{-подібна}\) трубка): у відкритих сполучених посудинах стовпчик нерухомої рідини з меншою густиною (а густина гасу менша за густину води) буде вищим, ніж стовпчик нерухомої рідини з більшою густиною.

Тиск у точках \(A\) і \(B\) буде різний, тому що хоча вони й розташовані на одному рівні, але в різних рідинах (точка \(A\) ‒ у гасі, а точка \(B\) ‒ у воді).

На рівні точки \(B\) діє лише атмосферний тиск.

А на рівні точки \(A\) крім атмосферного діє ще тиск стовпчика гасу над точкою \(A.\)

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Основні положення молекулярно-кінетичної теорії. Маса і розмір молекул.

Завдання скеровано на перевірку знання і розуміння основних положень молекулярно-кінетичної теорії.

Скраплення газу ‒ це перетворення газу на рідину, тобто зміна агрегатного стану.

Отже, під час скраплення хімічний склад газу не змінюється, тому молекули не можуть об’єднуватися, утворюючи молекули іншої речовини.

Також молекули не можуть ні зменшуватися, ні збільшуватися, оскільки за одним із основних положень молекулярно-кінетичної теорії частинки речовини взаємодіють одна з одною. Основна причина міжмолекулярної взаємодії ‒ електричне притягання і відштовхування заряджених частинок, що утворюють атом.

На відстанях, які більші за розміри молекул, молекули притягуються одна до одної; на відстанях, які трохи менші за розміри молекул, ‒ відштовхуються. Ці сили не впливають на розміри молекул, змінюються лише проміжки між молекулами.

Отже, під час скраплення молекули газової суміші не змінюються.

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів.

Завдання скеровано на перевірку вміння застосовувати перший закон термодинаміки до ізопроцесів.

Перший закон (начало) термодинаміки можна сформулювати так:
кількість теплоти \(Q,\) передана системі, йде на зміну внутрішньої енергії системи \(\Delta U\) та на виконання системою роботи \(A\) проти зовнішніх сил: $$ Q=\Delta U+A. $$

У першому прикладі газ нагрівають за незмінного тиску \((p=\mathrm{const})\) ‒ це ізобарне нагрівання. У ході цього процесу виконується робота і змінюється внутрішня енергія газу, тому рівняння першого закону термодинаміки має незмінний вигляд: $$ Q_{(p=\mathrm{const})}=\Delta U+A. $$

Під час ізобарного процесу передана газу кількість теплоти йде і на збільшення внутрішньої енергії газу, і на виконання механічної роботи.

За умовою газ ідеальний сталої маси, тому робота газу дорівнює $$ A=p\Delta V, $$ а зміна його внутрішньої енергії $$ \Delta U=\frac 32p\Delta V. $$

Кількість теплоти, передана газу, дорівнює:

У другому прикладі газ нагрівають за незмінного об’єму \((V=\mathrm{const}),\) це ізохорне нагрівання. У ході цього процесу об’єм газу не змінюється \((\Delta V=0)\) і газ роботу не виконує \((A=0).\) Під час ізохорного процесу вся передана газу кількість теплоти витрачається на збільшення внутрішньої енергії газу, тому рівняння першого закону термодинаміки має вигляд: \begin{gather*} Q_{(V=\mathrm{const})}=\Delta U,\\[6pt] Q_{(V=\mathrm{const})}=\frac 32p\Delta V. \end{gather*}

Якщо порівняти вирази для визначення кількості теплоти в обох прикладах, то отримана газом кількість теплоти буде більшою за незмінного тиску: \begin{gather*} Q_{(p=\mathrm{const})}\gt Q_{(V=\mathrm{const})},\\[6pt] \frac 52p\Delta V\gt \frac 32p\Delta V. \end{gather*}

Відповідь: A.

ТЕМА: Електродинаміка. Основи електростатики. Принцип суперпозиції полів.

Завдання скеровано на перевірку розуміння напруженості електричного поля і вміння застосовувати принцип суперпозиції полів.

Якщо електричне поле утворене кількома зарядами, то результувальна сила \(\overrightarrow{F},\) яка діє на пробний заряд із боку системи зарядів, визначається геометричною сумою сил, з якими діють ці заряди на даний пробний заряд: $$ \overrightarrow{F}=\overrightarrow{F}_1+\overrightarrow{F}_2+\dots +\overrightarrow{F}_n. $$

Звідси випливає принцип суперпозиції (накладання) електричних полів: напруженість \(\overrightarrow{E}\) електричного поля системи зарядів у певній точці простору дорівнює векторній сумі напруженостей полів, створених цими зарядами в цій точці:

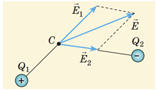
Модуль напруженості \(\overrightarrow{E}\) електричного поля, створеного точковим зарядом \(q\) на відстані \(r\) від цього заряду, обчислюють за формулою (\(k\) ‒ коефіцієнт пропорційності): $$ E=k\frac{|q|}{r^2}. $$

Визначімо модулі напруженості, які створюють заряди в точках \(1\) і \(2.\)

Той заряд, що ліворуч від точки \(1,\) створює модуль напруженості: $$ E_{11}=k\frac{|q|}{r^2_{11}}=\frac{k|q|}{1^2}=k|q|, $$ \(r_{11}\) ‒ відстань від заряду ліворуч до точки \(1,\) дорівнює \(1\) клітинці.

Заряд, що праворуч від точки \(1,\) створює модуль напруженості: $$ E_{12}=k\frac{|q|}{r^2_{12}}=\frac{k|q|}{2^2}=\frac{k|q|}{4}, $$ \(r_{12}\) ‒ відстань від заряду праворуч до точки \(1,\) дорівнює \(2\) клітинкам.

Однакові заряди розташовані по різні боки від точки \(1\) на одній прямій. Тож за принципом суперпозиції полів визначімо модуль напруженості \(E_1\) в точці \(1:\) $$ E_{1}=k|q|-\frac{k|q|}{4}=\frac 34k|q|. $$

Відносно точки \(2\) обидва однакові заряди розташовані ліворуч на відстанях трьох і шести клітинок:

Визначімо правильне співвідношення між модулями напруженості \(E_1\) і \(E_2:\)

Відповідь: A.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Електричний струм у напівпровідниках.

Завдання скеровано на перевірку знання і розуміння будови й принципу дії напівпровідникового діода.

У ході вивчення залежності провідності напівпровідників від зовнішніх чинників виявили:

1) на відміну від металевих провідників питомий опір напівпровідників зазвичай зменшується з підвищенням температури (варіант Г неправильний);

2) питомий опір більшості напівпровідників зменшується зі збільшенням освітленості.

Але основна властивість напівпровідникового діода ‒ пропускати електричний струм переважно в одному напрямку.

Якщо напівпровідник містить дві дотичні ділянки з різними типами провідності, то на межі дотику утворюється \(p\text{-}n\text{-}\textbf{перехід},\) який має однобічну провідність.

Напівпровідниковий пристрій, у внутрішній будові якого сформований один \(p\text{-}n\text{-перехід},\) називають напівпровідниковим діодом.

Відповідь: B.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Правило Ленца.

Завдання скеровано на перевірку знання і розуміння природи індукційного струму, а також вміння застосовувати правило Ленца для визначення напрямку індукційного струму.

Правило для визначення напрямку індукційного струму (правило Ленца): індукційний струм, який виникає в замкненому провідному контурі, має такий напрямок, що створений цим струмом магнітний потік перешкоджає зміні магнітного потоку, який спричинив появу індукційного струму.

Щоб з’ясувати, у якому з прикладів А ‒ Г правильно показано напрямок індукційного струму \(i\) в мідному кільці, користуємося алгоритмом:

1. Визначаємо напрямок ліній магнітної індукції \(\overrightarrow{B}\) зовнішнього магнітного поля.

2. З’ясовуємо, посилюється чи послаблюється зовнішнє магнітне поле (тобто збільшується чи зменшується кількість ліній магнітної індукції, що пронизують контур).

3. Визначаємо напрямок магнітної індукції магнітного поля, створеного індукційним струмом \(\overrightarrow{B}_i.\)

4. Визначаємо напрямок індукційного струму.

Розгляньмо рисунок А.

1. Магніт повернутий до кільця північним полюсом. А магнітні лінії поза магнітом виходять із північного полюса \(N\) магніту і входять у південний \(S.\) Отже, лінії магнітної індукції \(\overrightarrow{B}\) зовнішнього магнітного поля у цьому разі напрямлені до кільця.

2. Вертикальна стрілка на рисунку вказує, що магніт рухається до кільця, наближається, тобто зовнішнє магнітне поле посилюється (збільшується кількість ліній магнітної індукції, що пронизують кільце).

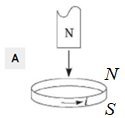
3. Це означає, що в кільці виникає індукційний струм такого напрямку, що кільце буде обернене до магніту однойменним полюсом (кільце відштовхуватиметься від магніту), тобто північним \(N,\) що запобігає наростанню зовнішнього магнітного поля: \(\overrightarrow{B}\downarrow\uparrow\overrightarrow{B}_i\) (вертикальні стрілочки вказують на напрямок ліній магнітної індукції).

4. За правилом правої руки визначаємо напрямок індукційного струму в кільці:
орієнтуємо праву руку так, що відігнутий на \(90^\circ\) великий палець вказує на північний полюс кільця, тобто вертикально вгору, тоді чотири зігнуті пальці, які наче обіймають кільце по периметру, укажуть напрямок індукційного струму в кільці. У цьому разі напрямок індукційного струму вказано правильно ‒ проти годинникової стрілки. Отже, варіант А ‒ це правильна відповідь.

Проаналізуймо інші варіанти відповіді, з’ясуймо помилки на рисунках.

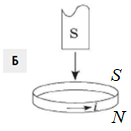
Рисунок Б. Магніт наближається до кільця південним полюсом \(S\) ‒ магнітний потік крізь кільце збільшується, отже, магнітне поле, створене індукційним струмом, протидіятиме зовнішньому полю магніту. Кільце буде обернене до магніту однойменним полюсом (кільце відштовхуватиметься від магніту), тобто південним \(S:\) $$ \overrightarrow{B}\uparrow\downarrow\overrightarrow{B}_i. $$

За правилом правої руки визначімо напрямок індукційного струму в кільці:
орієнтуємо праву руку так, що відігнутий на \(90^\circ\) великий палець вказує на північний полюс кільця, тобто вертикально вниз, тоді чотири зігнуті пальці вказують, що напрямок індукційного струму в кільці повинен бути за годинниковою стрілкою, а на рисунку ‒ проти. Отже, варіант Б ‒ неправильний.

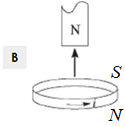
Рисунок В. Магніт віддаляється від кільця північним полюсом \(N\) ‒ магнітний потік крізь кільце зменшується, отже, магнітне поле, створене індукційним струмом, підтримуватиме зовнішнє поле, створене магнітом. Кільце буде обернене до магніту протилежним полюсом (кільце притягуватиметься до магніту), тобто південним \(S:\) $$ \overrightarrow{B}\downarrow\downarrow\overrightarrow{B}_i. $$

За правилом правої руки визначаємо напрямок індукційного струму в кільці:
орієнтуємо праву руку так, що відігнутий на \(90^\circ\) великий палець вказує на північний полюс кільця, тобто вертикально вниз, тоді чотири зігнуті пальці вказують, що напрямок індукційного струму в кільці повинен бути за годинниковою стрілкою, а на рисунку ‒ проти. Отже, варіант В ‒ неправильний.

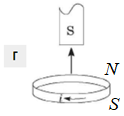
Рисунок Г. Магніт віддаляється від кільця південним полюсом \(S\) ‒ магнітний потік крізь кільце зменшується, отже, магнітне поле, створене індукційним струмом підтримуватиме зовнішнє поле, створене магнітом. Кільце буде обернене до магніту протилежним полюсом (кільце притягуватиметься до магніту), тобто північним \(N:\) $$ \overrightarrow{B}\uparrow\uparrow\overrightarrow{B}_i. $$

За правилом правої руки визначаємо напрямок індукційного струму в кільці:
орієнтуємо праву руку так, що відігнутий на \(90^\circ\) великий палець вказує на північний полюс кільця, тобто вертикально вгору, тоді чотири зігнуті пальці вказують, що напрямок індукційного струму в кільці повинен бути проти годинникової стрілки, а на рисунку ‒ за. Отже, варіант Г ‒ неправильний.

Відповідь: A.

ТЕМА: Коливання і хвилі. Механічні коливання і хвилі. Коливання вантажу на пружині.

Завдання скеровано на перевірку знання і розуміння процесу коливань тіла на пружині й характеру зміни фізичних величин, які описують ці коливання.

Розгляньмо ту частину періоду незатухаючих горизонтальних коливань тіла (наприклад, візка) на пружині, коли пружина починає стискатися.

У момент, коли візок доходить до положення рівноваги, сила пружності й прискорення дорівнюють нулю, а швидкість руху візка сягає максимального значення.

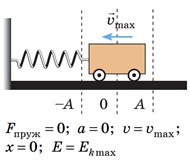
Потенціальна енергія пружини дорівнює нулю: $$ E_p=0. $$

Кінетична енергія візка максимальна й дорівнює повній енергії системи: $$ E_k=\frac{mv^2_{max}}{2}. $$

Досягнувши положення рівноваги, візок не зупиняється, а внаслідок інертності продовжує рух ліворуч. Пружина починає стискатися, і щораз більша сила пружності гальмує рух візка. Видовження \(x\) пружини збільшується, тому більшатиме й сила пружності, а отже, і прискорення руху візка (за другим законом Ньютона).

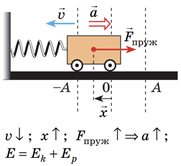
Кінетична енергія візка зменшується: $$ E_k=\frac{mv^2}{2}. $$

Потенціальна енергія пружини зростає: $$ E_p=\frac{kx^2}{2}. $$

Повна енергія системи дорівнює сумі кінетичної і потенціальної енергій.

Отже, з усіх наведених у варіантах відповіді фізичних величин меншатиме кінетична енергія тіла ‒ варіант відповіді А.

Відповідь: A.

ТЕМА: Коливання і хвилі. Оптика. Прямолінійність поширення світла в однорідному середовищі.

Завдання скеровано на перевірку знання і розуміння закону прямолінійного поширення світла, а також понять повної тіні і півтіні.

Джерело світла, яке випромінює світло однаково в усіх напрямках і розмірами якого, зважаючи на відстань до місця спостереження, можна знехтувати, називають точковим джерелом світла.

Найкращим прикладом точкових джерел світла є зорі, адже ми спостерігаємо їх із Землі, тобто з відстані, що в мільйони разів перевищує розміри самих зір.

Джерела світла, що не є точковими, називають протяжними джерелами світла.

Повна тінь ‒ це область простору, в яку не потрапляє світло від джерела.

Якщо джерело світла є точковим, тінь від предмета буде чіткою. У цьому разі утворюється тільки повна тінь.

Якщо тіло освітлене протяжним джерелом світла, то утворюється тінь із нечіткими контурами, тобто утворюється не тільки повна тінь, а ще й півтінь.

Півтінь ‒ це область простору, освітлена деякими з наявних точкових джерел світла або частиною протяжного джерела.

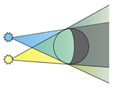
Повну тінь і півтінь пояснюють відповідно до закону прямолінійного поширення світла.

Отже, правильна відповідь ‒ Б.

Відповідь: Б.

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Квантові постулати Бора.

Завдання скеровано на перевірку знання і розуміння постулатів Бора.

Модифікацію планетарної моделі запропонував у 1913 р. данський фізик Нільс Бор (1885–1962), який був упевнений, що моделювати будову атома слід із погляду квантових уявлень. Бор припустив існування особливих станів атомів і сформулював два постулати.

Перший постулат Н. Бора (про стаціонарні стани):
атомна система може перебувати тільки в особливих стаціонарних (квантових) енергетичних станах, кожному з яких відповідає певне значення енергії; перебуваючи в стаціонарному стані, атом не випромінює енергію.

Другий постулат Н. Бора (про квантові стрибки):

Під час переходу з одного стаціонарного енергетичного стану в інший атом випромінює або поглинає квант електромагнітної енергії.

Відповідно до постулатів Бора атоми газуватих речовин в атомарному стані за підвищених температур випромінюють електромагнітні хвилі чітко визначених частот ‒ їм властивий лінійчастий спектр випромінювання. Лінійчастий спектр кожного елемента характеризується індивідуальним для цього елемента набором частот.

Відповідь: Б.

ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Гіпотеза Планка. Стала Планка. Кванти світла (фотони).

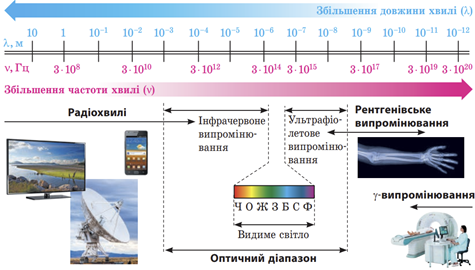
Завдання скеровано на перевірку знання і розуміння шкали електромагнітних хвиль.

Гіпотеза Планка: випромінювання електромагнітних хвиль атомами і молекулами речовини відбувається не безперервно, а дискретно, тобто окремими порціями, енергія \(E\) кожної з яких прямо пропорційна частоті \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}\) випромінювання: \begin{gather*} E=h\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}, \end{gather*} де \(h\) ‒ стала Планка.

Визначімо, до якого діапазону електромагнітної шкали належить це випромінювання, обчисливши його довжину хвилі \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}:\) $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=\frac{c}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}}, $$ де \(c\) ‒ швидкість світла у вакуумі.

Отримаємо формулу для обчислення довжини хвилі світла:

\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=600\ \text{нм}\) ‒ це довжина електромагнітних хвиль оптичного діапазону, а саме видиме світло (довжина хвилі ‒ \(400–780\) нм) електромагнітної шкали:

Відповідь: B.

ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.

Завдання скеровано на перевірку вміння і розуміння, як знаходити напрямок швидкості руху тіла і напрямок прискорення тіл під час різних видів руху.

Напрямок руху тіла визначений напрямком швидкості руху тіла. А напрямок прискорення збігається з напрямком рівнодійної всіх сил, що діють на тіло.

1) Розгляньмо рух снаряда перед падінням на землю. На рисунку зображена відповідна частина траєкторії. Як бачимо, вектор швидкості \(\overrightarrow{v}\) напрямлений по дотичній до вітки параболи. А прискорення \(\overrightarrow{g}\) вільного падіння під час руху снаряда по параболі буде напрямлене завжди вертикально вниз.

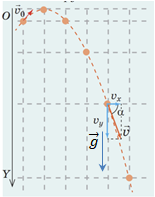
Отже, прискорення напрямлене під гострим кутом до напрямку швидкості руху (див. рисунок) ‒ варіант відповіді Г.

2) Кінець годинникової стрілки рухається по колу. Швидкість \(\overrightarrow{v}\) його руху в кожній точці кола напрямлена по дотичній до кола. А доцентрове прискорення \(\overrightarrow{a}_\text{д}\) спрямоване до центра кола (див. рисунок).

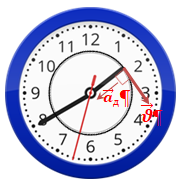
Отже, у цьому разі доцентрове прискорення буде напрямлене під прямим кутом до напрямку швидкості руху ‒ варіант відповіді Д.

3) Напрямок рівнодійної \(\overrightarrow{F}\) усіх сил, що діють на снаряд, який рухається всередині ствола гармати під час пострілу, а отже й напрямок прискорення \(\overrightarrow{a},\) збігається з напрямком швидкості \(\overrightarrow{v}\) руху снаряда. Отже, кут між напрямком руху снаряда й напрямком прискорення становитиме нуль, тобто прискорення напрямлене в напрямку швидкості руху ‒ варіант відповіді В.

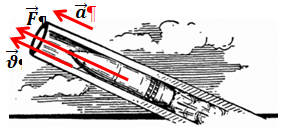
4) Після вимикання двигуна катер продовжить рухатися в попередньому напрямку і так само буде напрямлений вектор швидкості \(\overrightarrow{v}\) руху катера. Але рівнодійна всіх сил, що діють на катер, діятиме протилежно до напрямку руху катера. Відповідно й прискорення \(\overrightarrow{a}\) матиме такий самий напрямок, як і рівнодійна сил. Рух катера сповільнюватиметься.

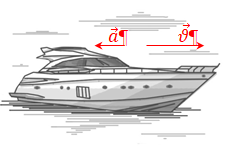
Отже, прискорення буде напрямлене протилежно до напрямку швидкості руху – варіант відповіді А.

Відповідь: 1Г, 2Д, 3В, 4А.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах.

Завдання скеровано на перевірку знання і розуміння особливостей протікання електричного струму в різних середовищах.

1. Електричний струм у розчинах і розплавах електролітів є напрямленим рухом вільних йонів.

Під час проходження електричного струму через електроліт відбувається перенесення хімічних складників електроліту, вони виділяються на електродах − осідають твердим шаром або виділяються в газуватому стані – відбувається електроліз (1 − В).

2. Напівпровідники за своєю провідністю посідають проміжне місце між провідниками і діелектриками.

Якщо напівпровідник нагріти або опромінити світлом, кількість вільних електронів і дірок збільшиться, відповідно збільшиться і провідність напівпровідника, а питомий опір більшості напівпровідників зменшиться зі збільшенням освітленості (2 − А).

3. Опір металевого провідника залежить не тільки від його геометричних розмірів і речовини, з якої він виготовлений, а й від температури.

Зі зниженням температури хаотичність теплового руху електронів зменшується, амплітуда коливань йонів у вузлах кристалічної ґратки, з якими зіштовхувалися електрони, теж зменшується, а отже, зростає провідність, а опір зменшується.

За температур, близьких до абсолютного нуля, питомий опір стрибком падає до нуля. Це явище назвали надпровідністю (3 ‒ Б).

4. Гази складаються з електрично нейтральних атомів і молекул і за звичайних умов майже не містять вільних носіїв струму, тобто є діелектриками.

А от якщо якось змусити електрон залишити атом, то в газі утворяться позитивні йони й вільні електрони; деякі електрони також можуть приєднатися до нейтральних молекул і атомів ‒ утворяться негативні йони. Цей процес утворення йонів і вільних електронів називають йонізацією. Зокрема, є термічна йонізація, коли енергія, необхідна для йонізації, виділяється під час непружного зіткнення молекул, які за високої температури газу мають велику швидкість (4 ‒ Г)

Відповідь: 1В, 2А, 3Б, 4Г.

ТЕМА: Механіка. Основи динаміки. Рух тіла під дією кількох сил.

Завдання скеровано на перевірку вміння визначати рівнодійну всіх сил, що діють на тіло під час руху.

На аеростат і під час опускання, і під час підйому діятимуть дві сили ‒ сила тяжіння і сила Архімеда (за умовою опором повітря можна знехтувати). Зобразимо ці сили на рисунках ‒ спочатку опускання, а потім, після скидання баласту, підйому.

Запишімо другий закон Ньютона у векторній формі і в проєкціях на вісь \(Oy\) для опускання:

\begin{gather*} M\overrightarrow{a}=\overrightarrow{F}_\text{т опускання}+\overrightarrow{F}_A,\\[7pt] Ma=Mg-F_A, \end{gather*} де \(M\) ‒ маса аеростата, \(a\) ‒ прискорення, з яким опускається аеростат, \(g\) ‒ прискорення вільного падіння, \(F_A\) ‒ сила Архімеда.

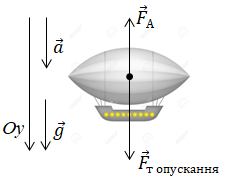
Запишімо другий закон Ньютона у векторній формі і в проєкціях на вісь \(Oy\) для піднімання:

\begin{gather*} (M-m)\overrightarrow{a}=\overrightarrow{F}_\text{т опускання}+\overrightarrow{F}_A,\\[7pt] (M-m)a=-(M-m)g+F_A, \end{gather*} де \(m\) ‒ маса баласту.

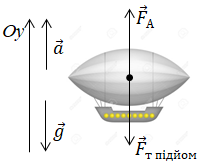
Модуль сили Архімеда залишиться сталим після скидання баласту, тому що об᾽єм \(V\) аеростата під час цього не змінюється: $$ F_a=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{повітря}gV=\mathrm{const}. $$

Тож виразімо силу Архімеда в обох ситуаціях і прирівняємо її, так зможемо визначити масу баласту:

розкриємо дужки й виразімо \(m:\)

\begin{gather*} Mg-Ma=Ma+Mg-ma-mg,\\[7pt] m(g+a)=2Ma,\\[6pt] m=\frac{2Ma}{g+a},\\[6pt] m=\frac{2\cdot 250\ \text{кг}\cdot 0,2\ \text{м/с}^2}{9,8\ \text{м/с}^2+0,2\ \text{м/с}^2}=10\ \text{кг}. \end{gather*}

Відповідь: 10.

ТЕМА: Механіка. Закони збереження в механіці. Закон збереження енергії в механічних процесах.

Завдання скеровано на перевірку вміння застосовувати знання з різних розділів механіки ‒ руху тіла по колу, другого закону Ньютона й закону збереження механічної енергії.

У нижній точці в положенні рівноваги кульці надають мінімально необхідну швидкість (тобто кулька має кінетичну енергію \(E_{k min}\)), щоб кулька змогла зробити повний оберт у вертикальній площині. Це означає, що кулька підніметься на висоту двох радіусів \(2R\) від початкового положення (тобто володітиме потенціальною енергією \(E_p\)). А також коли вона підніметься у верхню точку, у неї повинна бути певна швидкість, необхідна їй для того, щоб не впасти вертикально вниз, а зробити оберт (тобто у верхній точці у кульки також буде певна кінетична енергія \(E_k\)).

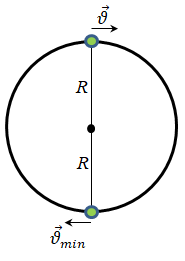
Запишімо закон збереження механічної енергії для кульки на нитці:

\begin{gather*} E_{k min}=E_p+E_k,\\[6pt] \frac{mv^2_{min}}{2}=mg2R+\frac{mv^2}{2},\\[6pt] \frac{mv^2_{min}}{2}=g2R+\frac{v^2}{2},\\[6pt] v^2_{min}=4gR+v^2. \end{gather*}

Оскільки кулька рухається по колу, то модуль швидкості руху кульки у верхній точці можна визначити за формулою $$ a_\text{д}=\frac{v^2}{R}, $$ де \(a_\text{д}\) ‒ модуль доцентрового прискорення.

Отже,

\begin{gather*} v^2=a_\text{д}R. \end{gather*}

За другим законом Ньютона $$ mg=ma_\text{д}\Rightarrow g=a_\text{д}. $$ Тоді \begin{gather*} v^2=a_\text{д}R=gR. \end{gather*}

Визначимо мінімально необхідну швидкість руху кульки:

\begin{gather*} v^2_{min}=4gR+v^2=4gR+gR=5gR,\\[7pt] v_{min}=\sqrt{5gR},\\[7pt] v_{min}=\sqrt{5\cdot 10\ \text{м/с}^2\cdot 0,5\ \text{м}}=5\ \text{м/с}. \end{gather*}

Відповідь: 5.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Відносна вологість повітря і її вимірювання.

Завдання скеровано на перевірку знання і розуміння понять абсолютної і відносної вологості.

Відносна вологість \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}\) ‒ фізична величина, яка показує, наскільки водяна пара близька до насичення, і дорівнює поданому у відсотках відношенню абсолютної вологості \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{а}\) до густини \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{н.п}\) насиченої водяної пари за цієї температури: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{а}}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{н.п}}\cdot 100\ \text{%}. $$

За умовою густина насиченої пари становить \(20\ \text{г/м}^3.\) Це означає, що за цієї незмінної температури в \(1\ \text{м}^3\) може міститися водяна пара масою \(20\ \text{г}.\) Закритий балон має об’єм \(0,5\ \text{м}^3,\) тож у ньому у вигляді пари може міститися водяна пара масою \(10\ \text{г}.\)

Отже, якщо в балоні залишили відкриту посудину з водою і з неї випарувалася вода лише масою \(6\ \text{г}\) (до насичення пари), то в балоні вже була водяна пара масою \(4\ \text{г}:\) \begin{gather*} 10\ \text{г}-6\ \text{г}=4\ \text{г}. \end{gather*}

Тоді можемо сказати, що початкова абсолютна вологість у балоні становила \(8\ \text{г/м}^3,\) адже абсолютна вологість \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{а}\) ‒ це фізична величина, яка характеризує вміст водяної пари в повітрі й чисельно дорівнює масі водяної пари, що міститься в повітрі об’ємом \(1\ \text{м}^3.\)

Обчислимо початкову відносну вологість повітря в балоні:

Відповідь: 40.

ТЕМА: Електродинаміка. Закони постійного струму. Опір провідників.

Завдання скеровано на перевірку знання і розуміння поняття електричний опір провідника.

Опір провідника \(R,\) який має незмінний поперечний переріз, дорівнює: $$ R=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac lS, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\) ‒ питомий опір речовини, з якої виготовлений провідник; \(l\) ‒ довжина провідника; \(S\) ‒ площа поперечного перерізу провідника.

Запишімо, яким був опір мідного дроту до шліфування і після нього (зауважимо, що питомий опір матеріалу, з якого виготовлений дріт, і його довжина під час цього процесу не змінилися): \begin{gather*} R_1=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac{l}{S_1}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac{l}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\left(\frac{d_1}{2}\right)^2},\\[6pt] R_2=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac{l}{S_2}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac{l}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\left(\frac{d_2}{2}\right)^2}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac{l}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\left(\frac{d_1}{4}\right)^2}, \end{gather*} де \(d_1\) ‒ діаметр дроту до шліфування, \(d_2\) ‒ діаметр дроту після шліфування, а \(S_1=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\left(\frac{d_1}{2}\right)^2\) і \(S_2=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\left(\frac{d_2}{2}\right)^2\) ‒ формули для визначення площі поперечного перерізу дроту.

Обчислімо опір дроту після шліфування:

Відповідь: 4.

ТЕМА: Коливання і хвилі. Електромагнітні коливання і хвилі. Формула Томсона.

Завдання скеровано на перевірку розуміння і вміння застосувати формулу Томсона до різних електричних схем з різними з’єднаннями пристроїв.

Період \(T\) вільних електромагнітних коливань у коливальному контурі визначаємо за формулою Томсона: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}, $$ де \(L\) ‒ індуктивність котушки, \(C\) ‒ електроємність конденсатора (батареї конденсаторів).

Запишімо формулу для обчислення періоду коливань, коли ключ \(K\) розімкнутий, і коли його замкнули.

Коли ключ розімкнутий, то струм проходитиме лише через конденсатор з електроємністю \(C_1\) і котушку: $$ T_1=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC_1}. $$

Коли ж ключ замкнути, то струм піде і через конденсатор з електроємністю \(C_2,\) і через конденсатор з електроємністю \(C_3.\) У цьому разі треба визначити загальну електроємність \(C_\text{заг}\) батареї конденсаторів, що з’єднані на поданій в умові схемі паралельно:

Формула для періоду коливань матиме вигляд: $$ T_2=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC_\text{заг}}. $$

Запишімо відношення періодів коливань для визначення, у скільки разів збільшився період коливань після того, як ключ замкнули:

\(T_2=3T_1\) ‒ після замикання ключа період коливань збільшився в \(3\) рази.

Відповідь: 3.

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Період піврозпаду.

Завдання скеровано на перевірку знання і розуміння закону піврозпаду.

Основний закон радіоактивного розпаду: $$ N=N_0\cdot 2^{-\frac tT}, $$ де \(N\) ‒ кількість ядер радіонукліда, що залишились у зразку через час \(t;\) \(N_0\) ‒ початкова кількість ядер; \(T\) ‒ період піврозпаду.

Визначімо, скільки ядер ізотопу залишилося: \begin{gather*} N=8\cdot 10^{10}\cdot 2^{-\frac{3\ \text{год}}{1\ \text{год}}},\\[6pt] N=8\cdot 10^{10}\cdot \frac 18=1\cdot 10^{10}. \end{gather*}

Можемо визначити, скільки ядер розпалося:

За умовою під час розпаду кожного з цих ядер вивільнилася енергія \(W_1=5\ \text{МеВ},\) отже, можна визначити загальну енергію \(W,\) яка виділилася протягом \(3\ \text{год}:\)

Відповідь: 56.