Розділ: Мультитести
Тест: Тренувальний мультитест (10 варіант)
Блок: Фізика
Кількість завдань: 20
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу.
Завдання скеровано на перевірку вміння визначати доцентрове прискорення на криволінійній траєкторії.
Криволінійна траєкторія утворена елементами двох кіл із різними радіусами (рис. 1).
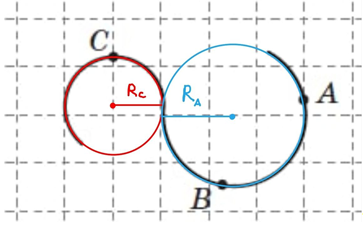
Рис. 1. Радіуси криволінійної траєкторії
Точки А і В лежать на більшому колі, а точка С – на меншому, тож
Доцентрове прискорення можна обчислити з виразу:
Оскільки модуль лінійної швидкості не змінюється, то можна записати прискорення в кожній із точок:
Оскільки
Цей вираз можна записати в іншому вигляді:
Відповідь: B.
ТЕМА: Механіка. Основи динаміки. Закони Ньютона. Закон всесвітнього тяжіння.
Завдання скеровано на перевірку розуміння закону всесвітнього тяжіння і його застосування для описування реальних ситуацій.
Закон всесвітнього тяжіння – будь-які два тіла притягуються одне до одного із силою, яка прямо пропорційна добутку мас цих тіл й обернено пропорційна квадрату відстані між ними:
Відстань між двома сусідніми цеглинами дорівнює
Відповідь: B.
ТЕМА: Механіка. Елементи динаміки рідин і газів. Умова плавання тіл.
Завдання скеровано на оцінювання розуміння поняття «густина» і вміння застосовувати закон Архімеда.
Густина речовини
Для правильного розв’язання завдання потрібно пригадати умови плавання тіл:
Густину зубної пасти, укинутої в посудину з водою, обчислюють за формулою:
Відповідь: A.
ТЕМА: Молекулярна фізика й термодинаміка. Рівняння стану ідеального газу. Ізопроцеси в газах.
Завдання скеровано на оцінювання розуміння закономірностей зміни тиску, об’єму й температури на основі аналізу результатів експерименту, зображених на рисунку.
За рисунком легко визначити, що об’єм кульки збільшився після того, як вона опинилася під ковпаком, до якого підключено насос. Ні охолоджувальних, ні нагрівальних пристроїв немає, тому температура газу всередині кульки залишається сталою. До того ж, оскільки кулька зав’язана, можна вважати, що кількість речовини всередині неї стала. За законом Бойля – Маріотта добуток тиску на об’єм до поміщення кульки під ковпак і після має бути однаковим:
Оболонка кульки еластична, тож унаслідок наповнювання повітрям вона змінюватиме свій об’єм доти, доки тиск усередині кульки не дорівнюватиме тиску ззовні.
Тому, якщо об’єм кульки збільшився, то тиск усередині – зменшився, а отже зменшився і тиск навколо (під ковпаком).
Відповідь: A.
ТЕМА: Молекулярна фізика і термодинаміка. Рівняння теплового балансу.
Завдання скеровано на перевірку вміння аналізувати графічні залежності температури тіла від кількості наданої йому теплоти.
Кількість наданої теплоти, температура тіла та його питома теплоємність пов’язані виразом
Графік у завданні – це графік залежності абсолютної температури тіла
Для цього необхідно змінити вигляд залежності:
Залежність має вигляд лінійної функції
Оскільки маси всіх трьох тіл однакові, то на нахил прямої, що відповідає лінійній функції, впливає лише питома теплоємність.
Що більший кутовий коефіцієнт, то крутішою є пряма, а кутовий коефіцієнт є тим більшим, що меншою є питома теплоємність.
Тож найпологіша пряма (для тіла 1) має найбільшу питому теплоємність, а найкрутіша (для тіла 2) – найменшу.
Відповідь: Г.
ТЕМА: Електродинаміка. Основи електростатики. Електричний заряд.
Завдання скеровано на оцінювання розуміння поняття електричного заряду, вільних носіїв заряду і їхнього передавання під час електричної взаємодії.
Позитивно заряджені частинки всередині ядра атома – це протони, а негативно заряджені частинки, що рухаються навколо ядра, – електрони. Відокремити протон від ядра дуже складно, тому під час таких електричних явищ, як, наприклад, зарядження шерсті внаслідок тертя, зміни кількості протонів у ядрах не відбувається.
Атоми зберігають свою нейтральність за рахунок однакової кількості протонів й електронів. Відповідно, щоби зарядитися позитивно, атоми речовини повинні віддати частину своїх електронів, а щоби зарядитись негативно – захопити додаткові електрони.
Оскільки за умовою завдання шерсть набуває позитивного заряду, то саме вона віддає паличці свої електрони.
Відповідь: B.
ТЕМА: Електродинаміка. Електричний струм у різних середовищах.
Завдання скеровано на перевірку розуміння поняття термоелектронної емісії.
Нитка розжарення нагріває катод, у результаті чого деякі його електрони отримують кінетичну енергію, більшу за роботу виходу матеріалу, і покидають катод.
Якщо катод підключений до негативного полюсу джерела, а анод до позитивного, то електрони, що утворилися внаслідок термоелектронної емісії, починають рухатися до анода, тобто через діод тече струм. Якщо полюси джерела підключити навпаки, то поле на катоді затримуватиме електрони.
Відповідь: Г.
ТЕМА: Електродинаміка. Магнітне поле і явище магнітної індукції. Сила Ампера.
Завдання скеровано на оцінювання вміння розраховувати модуль сили Ампера для провідників зі струмом під дією магнітного поля.
Сила Ампера – це сила, що діє на провідник зі струмом в магнітному полі. Її напрямок визначають за правилом лівої руки, а модуль – за формулою
Оскільки сила струмі
У цьому разі напрямок сили струму й напрямок ліній магнітної індукції є або паралельними
Лінії магнітної індукції проводять від північного полюса до південного, тож у випадках A, B і Г
Відповідь: Б.
ТЕМА: Механічні коливання і хвилі. Поперечні і поздовжні хвилі.
Завдання скеровано на перевірку вміння розпізнавати напрямки векторів швидкості і прискорення під час поширення поперечних хвиль.
Хвиля поширюється вправо. Якщо дорисувати нову хвилю так, як вона виглядатиме через малий проміжок часу, то стане очевидним, що тільки точка Б рухається вгору й розганяється.
Тому вектори швидкості і прискорення направлені вгору.
Відповідь: Б.
ТЕМА: Коливання і хвилі. Електромагнітні коливання і хвилі. Вільні електромагнітні коливання в коливальному контурі.
Завдання скеровано на перевірку знання і розуміння коливального процесу в коливальному контурі, а також уміння описувати цей процес відповідним рівнянням.
Коливання в коливальному контурі відбуваються за гармонічним законом:
У даному випадку за гармонічним законом змінюється напруга
За активного опору
Однак у будь-якій реальній коливальній системі завжди є втрати енергії: під час механічних коливань енергія витрачається на долання сил тертя, деформацію; під час електромагнітних коливань – на нагрівання провідників, випромінювання електромагнітних хвиль тощо. Унаслідок цього амплітуда коливань із часом зменшується. А через певний інтервал часу, якщо немає надходжень енергії від зовнішнього джерела, коливання припиняються (згасають). Тому вільні коливання завжди є згасними.
В умові не задано амплітудне значення напруги. Тому обчислимо циклічну частоту
Отже, рівняння, що відповідає умові завдання,
Відповідь: Б.
ТЕМА: Квантова фізика. Елементи теорії відносності. Релятивістський закон додавання швидкостей.
Завдання скеровано на перевірку розуміння законів релятивістської механіки.
Відповідно до другого постулату спеціальної теорії відносності (СТВ) швидкість поширення світла у вакуумі є незмінною і не залежить від швидкості руху джерела або приймача світла. Це означає, що класичний закон додавання швидкостей у релятивістській механіці застосовувати не можна. У СТВ застосовують релятивістський закон додавання швидкостей. Запишімо цей закон для ситуації, описаній в умові завдання:
Відповідно до другого постулату СТВ швидкість поширення світла ‒ максимально можлива швидкість поширення будь-якої взаємодії. Матеріальні об’єкти не можуть мати швидкість більшу за швидкість світла. Отже, варіант відповіді Г
Підставмо у формулу вирази, що відповідають швидкостям руху космічної станції відносно Землі і ракети відносно цієї станції. Звернімо увагу, що ця формула записана для випадку додавання швидкостей, напрямлених уздовж однієї прямої
Відповідь: B.
ТЕМА: Квантова фізика. Світлові кванти. Фотоефект й експериментально встановлені його закони.
Завдання скеровано на оцінювання вміння застосовувати знання про фотоефект і його особливості під час аналізування роботи приладів, на ньому заснованих (фоторезисторів).
Фоторезистор – це прилад для вимірювання освітленості. Принцип його роботи ґрунтується на залежності провідності напівпровідників від освітленості.
Опір напівпровідників зменшується зі збільшенням освітленості, тому фоторезистор у темряві матиме більший опір, ніж освітлений.
Опір фоторезисторів а і б можна визначити за законом Ома:
Значення сили струму
й у.о.
Для зручності потрібно визначити сили струму для напруги 3 у.о.
Тоді можна розрахувати опір, одиницею якого є умовна одиниця опору (у.о.
Тому
Відповідь: Г.
ТЕМА: Молекулярна фізика і термодинаміка. Квантова фізика.
Завдання скеровано на перевірку розуміння фізичного змісту фізичних сталих.
Розв’язання завдання потребує знання визначень фізичних величин і вміння аналізувати розмірності.
Розмірність сталої Авогадро –
Стала Авогадро – це число, що відповідає кількості атомів (молекул) у будь-якій речовині кількістю
Розмірність сталої Больцмана
Сталу Больцмана використовують для встановлення зв’язку між середньою кінетичною енергією руху молекул і температурою ідеального газу:
Якщо температура змінюється, то змінюється і середня кінетична енергія молекул:
Звідси можна виразити сталу Больцмана:
Розмірність сталої Планка –
За гіпотезою Планка молекули випромінюють енергію порційно, і кількість цієї енергії пропорційна до частоти випромінювання:
Відповідно стала Планка
Гравітаційна стала фігурує в законі Всесвітнього тяжіння:
Якщо маса обох тіл становить 1 кг, відстань між ними – 1 м, то
Тож сила взаємодії таких тіл за модулем дорівнює гравітаційній сталій.
До того ж сила має розмірність
Відповідь: 1Б, 2А, 3Г, 4В.
ТЕМА: Атом і атомне ядро.
Завдання скероване на перевірку розуміння історично важливих фізичних експериментів і вміння пов’язувати їх із фізичними відкриттями.
1. Анрі Беккерель проводив дослідження із використанням солей Урану й випадково поклав породу разом із фотопластинкою в темну шухляду. Наступного разу, коли він повернувся до фотопластинок, вони виявилися засвіченими, хоча ніяких джерел світла в шухляді не було. Так у нього виникла ідея про те, що саме Уран був джерелом якогось випромінювання. Це випромінювання і було радіоактивним випромінюванням, що утворювалось під час розпаду нестабільних ядер Урану.
2. Планетарну модель атома розробив Ернест Резерфорд після того, як експеримент із перевірки пудингової моделі Томсона мав неочікувані результати. За уявленнями Томсона позитивний заряд в атомі займав увесь його об’єм, як тісто в пудингу чи кексі, а негативно заряджені електрони застрягали в цьому позитивному заряді (як родзинки). Якщо атом і справді мав таку будову, то під час зустрічі з ним інші (менші) частинки мали би пролітати наскрізь. Адже самі електрони мали би занадто малу масу, щоби викликати якусь серйозну зміну траєкторії, а хмара позитивного заряду могла спричинити відхилення лише на невеликі кути. Щоби перевірити це експериментально, Резерфорд бомбардував альфа-частинками тонку фольгу золота, товщина якої становила лише кілька атомів. Деякі альфа-частинки відбивалися від фольги майже у протилежному напрямку. Таке відбивання було можливе лише за умови, що в атомі існувала велика важка частинка. Тож Резерфорд припустив, що атом більше схожий на Сонячну систему, ніж на пудинг: у його центрі є велика позитивна частинка – ядро, навколо якого обертаються електрони, як планети навколо Сонця.
3. Фотоефект – це явище взаємодії світла з речовиною, супроводжуване випромінюванням (емісією) електронів. Закони фотоефекту були відкриті під час опромінення металів світлом.
4. α-промені – це потік позитивно заряджених частинок, що складаються із двох протонів і двох нейтронів (ядра атомів Гелію), β-промені – це потік негативно заряджених електронів, γ-промені – це електромагнітне випромінювання надзвичайно високої частоти, що утворюється під час ядерних реакцій. Ернест Резерфорд виявив, що під дією магнітного поля пучок радіоактивного випромінювання ділиться на три частини. Поділ відбувається тому, що під дією магнітного поля заряджені частинки відхиляються від своєї початкової прямолінійної траєкторії. Нейтральний γ-промінь не відхилявся під дією магнітного поля, а позитивно заряджені α-частинки й негативно заряджені β-частинки відхилялися й утворювали два пучки по обидва боки від пучка γ-променів. Адже різнойменно заряджені частинки в магнітному полі відхиляються у протилежні боки.
Відповідь: 1Г, 2А, 3В, 4Б.
ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона. Вага.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на рух тіла під дією кількох сил.
Знайти:
Розв’язання цієї задачі доцільно розпочати зі створення схеми дії сил на брусок, який тягнуть по рейці (рис. 1). На нього діють сила тяжіння
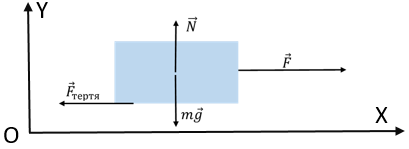
Рис. 1. Схема дії сил на брусок, що тягнуть по горизонтальній рейці
Другий закон Ньютона для бруска, що тягнуть по рейці, можна описати формулою
Оскільки брусок тягнуть рівномірно, то прискорення
Затим потрібно спроєктувати рівняння на осі
проєкція на вісь
проєкція на вісь
Тобто для осі
Величина сили тертя залежить від коефіцієнта тертя:
Тож
При цьому силу
Оскільки для тіла в стані спокою можна обчислити вагу
Тоді
Відповідь: 0,25.
ТЕМА: Рівняння теплового балансу. Потенціальна енергія.
Завдання скеровано на перевірку вміння розв’язувати комбіновані задачі на рівняння теплового балансу й потенціальну енергію тіла.
Дано:
Знайти:
Утрачену під час охолодження кульки енергію можна розрахувати за формулою
Енергію тіло втрачає, тому отримане число – від’ємне, тож знак «мінус» тут позначає лише напрямок руху енергії. У подальших розрахунках використовуватимемо значення
Коли тіло піднімається на певну висоту, то збільшується його потенціальна енергія. Її можна розрахувати за формулою:
Саме на збільшення потенціальної енергії буде витрачено
Відповідь: 0,76.
ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії (рівняння стану ідеального газу). Властивості газів, рідин і твердих тіл (теплота згоряння палива).
Завдання скеровано на перевірку вміння описувати стан газу за допомогою рівняння стану ідеального газу, визначати кількість теплоти згоряння палива.
Кількість теплоти
Визначімо масу метану в балоні. Для цього опишімо за допомогою рівняння стану ідеального газу (рівняння Менделєєва ‒ Клапейрона) стан метану в балоні:
Виразімо з рівняння стану масу:
Переведімо значення всіх величин у систему SI:
Підставимо ці значення у формулу для обчислення маси:
Підставимо значення маси у формулу для визначення кількості теплоти згоряння метану:
Відповідь: 400.
ТЕМА: Електродинаміка. Закони постійного струму. Паралельне і послідовне з’єднання провідників.
Завдання скеровано на оцінювання знання закону Ома й розуміння особливостей паралельного і послідовного з’єднання провідників.
Знайти:
Спочатку потрібно позначити напругу джерела як
Правила послідовного і паралельного підключення такі:
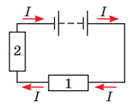
Рис. 1. Послідовне з’єднання провідників 1 і 2
Тому сила струму, яку вимірює амперметр – це сила струму на реостаті й на системі паралельно підключених провідників. За показниками на фотографії вона дорівнює 1,5 A.
Для паралельно підключених провідників правила такі:
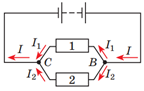
Рис. 2. Паралельне з’єднання провідників 1 і 2
Нехай
Оскільки резистор 1 і групу резисторів 2–5 підключено послідовно, можна записати:
Напруга на групі резисторів 2–5 дорівнює напрузі на кожній парі резисторів, а сила струму на групі резисторів – це сума сил струму на кожній із пар:
Усередині кожної пари з’єднання послідовне, тому для цих резисторів також можна записати відношення для напруги й сили струму:
Напруга, сила струму й опору пов’язані між собою законом Ома:
Можна обчислити загальний опір усіх резисторів:
Тоді можна записати співвідношення між силою струму в колі, напругою на обкладинках джерела й загальним опором резисторів у колі:
Можна також записати аналогічне співвідношення для п’ятого резистора:
Опір в обох парах резисторів дорівнює
Тож вираз для напруги п’ятого резистора теж спроститься:
Тоді
Відповідь: 4.
ТЕМА: Оптика. Лінза. Оптична сила лінзи.
Завдання скеровано на оцінювання вміння розв’язувати графічні задачі на зображення ходу світлових променів у системах із лінзами.
Оптична сила лінзи
Для визначення фокусної відстані лінзи потрібно проаналізувати рисунок.
Якщо вважати, що точка перетину променю з оптичною віссю зліва від лінзи – це об’єкт, а справа від лінзи – його зображення, то за формулою тонкої лінзи відстань від об’єкта до лінзи
На рисунку
Відповідь: 25.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Радіоактивність.
Завдання скеровано на перевірку розуміння поняття «доза опромінювання людини» й методів визначення її.
Фізичну величину, якою характеризують біологічний вплив поглинутої дози йонізувального випромінювання, називають еквівалентною дозою йонізувального випромінювання
Обчислімо поглинуту за добу дозу:
Урахуємо також дозу опромінювання від рентгенівського медичного обстеження організму –
А це означає, що без шкоди для здоров᾽я людина може проходити рентгенівські медичні обстеження організму лише раз на рік, оскільки за умовою річна допустима доза опромінювання становить
Відповідь: 1.




