Мультитести – Фізика

ТЕМА: Механіка. Закони збереження в механіці. Кінетична й потенціальна енергія.

Завдання скеровано на перевірку вміння обчислювати потенціальну енергію тіла, що перебуває під дією сили тяжіння.

Потенціальна енергія тіла, яке рухається під дією сили тяжіння, можна визначити за формулою $$ E_{пот}=mgh, $$ де \(m\) – маса тіла, \(g=9,8\ \text{м/с}^2\) – прискорення вільного падіння, \(h\) – висота підйому.

Прискорення вільного падіння вважаємо постійним на Землі, маса кульки під час її руху не змінюється, тому найвищу потенціальну енергію кулька матиме в найвищій точці своєї траєкторії – точці Б.

Відповідь: Б.

Механіка. Елементи динаміки рідин i газів. Умова плавання тіл.

Завдання скеровано на перевірку розуміння поняття густини та вміння застосовувати закон Архімеда.

Силу Архімеда можна визначити за формулою $$ F_\text{Арх}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{рідини}gV, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{рідини}\) − густина рідини, \(g\) – прискорення вільного падіння, \(V\) – об’єм тіла.

Силу тяжіння визначають за формулою $$ F=mg, $$ де \(m\) – маса тіла, \(g\) – прискорення вільного падіння.

Густина речовини \((\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho})\) – це фізична величина, яка характеризує речовину й дорівнює відношенню маси суцільного тіла, виготовленого із цієї речовини, до об’єму цього тіла: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}=\frac mV, $$ де \(m\) – маса тіла, а \(V\) – об’єм тіла.

Тоді масу тіла можна виразити як $$ m=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}V. $$

Тоді силу тяжіння можна записати як: $$ F_\text{тяж}=mg=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{тіла}gV, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{тіла}\) – густина тіла, \(g\) – прискорення вільного падіння, \(V\) – об’єм тіла.

Вважатимемо, що на тіло в рідині діє лише сила тяжіння, що напрямлена вниз, і виштовхувальна сила Архімеда, напрямлена вгору. За другим законом Ньютона $$ \overrightarrow{F_\text{тяж}}+\overrightarrow{F_\text{Арх}}=m\overrightarrow{a}. $$

Тіло плаває в товщі рідини, а не спливає на поверхню чи тоне, тому прискорення \(a=0\). Відповідно $$ \overrightarrow{F_\text{тяж}}+\overrightarrow{F_\text{Арх}}=0. $$

Якщо спрямувати вісь x у напрямку прискорення вільного падіння, можна спроєктувати векторне рівняння:

Відповідь: Б.

ТЕМА: Основи термодинаміки. Внутрішня енергія і способи її змінення. Способи теплопередачі.

Завдання скеровано на перевірку розуміння механізмів конвекції.

Конвекція – це вид теплопередачі, за якого тепло переносять потоки рідини або газу.

Речовини у твердому стані не мають потоків, тому конвекція в них неможлива.

Відповідь: A.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. Рівняння стану ідеального газу.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на використання рівняння стану ідеального газу.

Двоатомний газ кількістю речовини \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_0\) займає об’єм \(V\) за температури \(T_0.\) Після підвищення температури до \(T_1\), коли всі молекули розпалися на атоми, кількість речовини збільшується до \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_1\). Ці фізичні величини пов’язані між собою: \begin{gather*} T_1=3T_0;\\[7pt] \style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_1=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_0. \end{gather*}

Кількість речовини збільшилась удвічі, адже кожна молекула розпалася на два атоми.

Рівняння стану ідеального газу для обох випадків: \begin{gather*} p_0V=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_0RT_0;\\[7pt] p_1V=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_1RT_1=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_0R3T_0=6\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_0RT_0. \end{gather*}

Тоді: \begin{gather*} p_0=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_0RT_0}{V};\\[6pt] p_1=6\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_0RT_0}{V}=6p_0. \end{gather*}

Відповідь: Г.

ТЕМА: Електродинаміка. Основи електростатики. Конденсатори.

Завдання скеровано на оцінювання вміння графічно зображувати залежності між фізичними величинами.

Залежність заряду \(q\) конденсатора від напруги \(U\) описують формулою \(q=CU,\) де \(C\) – електроємність конденсатора. Ця залежність є прямо пропорційною.

Її графік – це пряма, що проходить через початок координат.

Відповідь: B.

ТЕМА: Електродинаміка. Закони постійного струму. Опір провідників.

Завдання скеровано на оцінювання вміння визначати опір провідників за їхніми геометричними характеристиками.

Опір провідника залежить від його геометричних характеристик: $$ R=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac lS, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\) – питомий опір речовини, iз якої виготовлений провідник, \(l\) – довжина провідника, \(S\) – площа поперечного перерізу провідника.

Опір провідника не зміниться, якщо не змінюється його довжина чи площа поперечного перерізу.

У варіанті відповіді А довжина провідника зменшиться вдвічі, а поперечний переріз збільшиться вдвічі, якщо розрізати його навпіл і з’єднати половинки паралельно. Тож опір провідника зменшиться: $$ R_A=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac {l/2}{2S}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac{l}{4S}=\frac 14 R. $$

У варіанті відповіді Б довжина провідника збільшиться. Під час видовження площа поперечного перерізу зменшиться. А тому опір провідника збільшиться.

У варіанті відповіді В під час нарізання різьби на провіднику зменшиться площа його поперечного перерізу, а опір, відповідно, збільшиться.

Лише у варіанті відповіді Г не змінюються геометричні характеристики провідника. Доданий зовні ізолювальний шар не впливає на його опір.

Відповідь: Г.

ТЕМА: Електродинаміка. Магнітне поле і явище магнітної індукції. Сила Ампера.

Завдання скеровано на оцінювання вміння визначати за правилом лівої руки напрямок сили Ампера.

Якщо ліву руку розташувати так, щоби лінії магнітної індукції входили в долоню, а чотири витягнуті пальці вказували напрямок струму в провіднику, то відігнутий на 90° великий палець укаже напрямок сили Ампера (рис. 1).

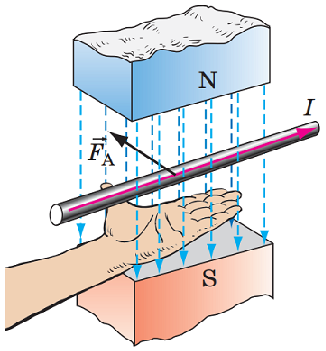
Рис. 1. Правило лівої руки

За рисунком 2 можна визначити напрямок струму I в провіднику й напрямок ліній магнітної індукції \(B\). Напрямок струму зазначено поруч із кріпленнями провідника, а напрямок ліній магнітної індукції можна визначити за таким правилом: лінії магнітної індукції беруть свій початок на північному полюсі й входять у південний. Тоді за правилом лівої руки легко визначити напрямок сили Ампера \(F_{\mathrm{A}}.\)

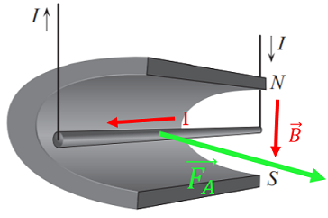
Рис. 2. Напрямок струму, ліній магнітної індукції та сили Ампера

Відповідь: A.

ТЕМА: Механічні коливання і хвилі. Частота й період коливань.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на знаходження параметрів коливань частинок хвилі.

Паперовий кораблик на гребені хвилі коливається так само, як і частинки води у хвилі.

Під час коливань за один період тіло повертається в початкове положення. Якщо вважати, що в початковий момент часу кораблик був у точці максимального відхилення рівноваги, то за чверть періоду він опиниться на рівні спокійної води, а за наступну чверть – у точці максимального відхилення від положення рівноваги з іншого боку від рівня рівноваги, тобто в найнижчому положенні.

Якщо частота коливань $$ v= 2\ \text{Гц} = 2\frac{1}{\text{c}}, $$ то період коливань $$ T=\frac 1v=\frac 12\text{c}=0,5\ \text{c}. $$

Тоді, оскільки кораблик опиниться в найнижчій точці за половину періоду, можна обчислити цей час: $$ 2)\ t=\frac T2=0,25\ \text{c}. $$

Відповідь: A.

ТЕМА: Коливання і хвилі. Власна частота й період електромагнітних коливань.

Завдання скеровано на перевірку вміння розв'язувати розрахункові задачі на залежність періоду власних коливань від параметрів системи й визначати довжину хвилі.

Дано:
\(С=50\ \text{пФ}=50\cdot 10^{-12}\ \text{Ф}\)
\(L=2\ \text{мкГн}=2\cdot 10^{-6}\ \text{Гн}\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}=3\)
\(c=3\cdot 10^8\ \text{м/с}\)

Знайти:
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}\ -\ ?\)

Відповідь: B.

ТЕМА: Елементи теорії відносності.

Завдання скеровано на перевірку розуміння постулатів спеціальної теорії відносності.

Постулати спеціальної теорії відносності:

1. В інерціальних системах відліку всі закони природи однакові.

2. Швидкість поширення світла у вакуумі однакова в усіх інерціальних системах відліку.

Відповідь: A.

ТЕМА: Квантова фізика. Світлові кванти. Фотоефект й експериментально встановлені його закони.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на знаходження затримної напруги у фотоефекті.

За законами фотоефекту енергія, отримана від фотона, має бути витрачена на те, щоби вирвати електрон із поверхні катода (цю частку енергії називають роботою виходу \(A_{\text{вих}}\)), а частина енергії, яка залишається після цього, переходить у кінетичну енергію фотоелектрона \((E_{\text{кін}})\): $$ E_{\text{ф}}=A_{\text{вих}}+E_{\text{кін}} $$

Тоді, з огляду на те, що \begin{gather*} E_{\text{ф}}=3A_{\text{вих}},\\[7pt] 3A_{\text{вих}}=A_{\text{вих}}+E_{\text{кін}},\\[7pt] 2A_{\text{вих}}=E_{\text{кін}}. \end{gather*}

Під час вимірювання швидкості фотоелектронів, анод підключають до негативного полюса джерела, а катод – до позитивного. Тоді поле затримує утворені фотоелектрони. Струм не проходитиме через фотоелемент, коли робота поля дорівнюватиме кінетичній енергії найшвидших фотоелектронів: $$ A_{\text{поля}}=\style{font-style:normal;font-size:1.1em}{e}U_{\text{зат}}=E_{\text{кін}}, $$ де \(\style{font-style:normal;font-size:1.1em}{e}\) – заряд електрона, а \(U_{\text{зат}}\) – затримна напруга.

Тоді $$ U_{\text{зат}}=\frac{E_{\text{кін}}}{\style{font-style:normal;font-size:1.1em}{e}}=\frac{2A_{\text{вих}}}{\style{font-style:normal;font-size:1.1em}{e}}. $$

Відповідь: Б.

ТЕМА: Механіка. Закони збереження в механіці. Кінетична й потенціальна енергія.

Завдання скеровано на оцінювання розуміння кінетичної і потенціальної енергії, виконання законів збереження повної механічної енергії в механіці.

Кінетична енергія \(E\) – це фізична величина, яка характеризує механічний стан рухомого тіла й дорівнює половині добутку маси \(m\) тіла на квадрат швидкості \(v\) його руху. Кінетичну енергію можна обчислити за формулою $$ E_{\text{кін}}=\frac{mv^2}{2}. $$

Потенціальна енергія \(U\) – це енергія, яку має тіло внаслідок взаємодії з іншими тілами або внаслідок взаємодії частин тіла між собою. Потенціальну енергію тіла, що перебуває на висоті від поверхні землі, можна визначити за формулою: $$ E_{\text{пот}}=mgh, $$ де \(m\) – маса тіла, \(h\) – висота, на якій перебуває тіло.

Внутрішня енергія – це сума кінетичних енергій хаотичного (теплового) руху частинок речовини (атомів, молекул, йонів), із яких складається тіло, і потенціальних енергій їхньої взаємодії.

Щодо ситуацій, описаних у завданні:

1 коли яблуко падає з гілки, висота, на якій воно перебуває, постійно зменшується, тобто зменшується його потенціальна енергія. Швидкість яблука постійно зростає. За законом збереження повної механічної енергії сума кінетичної і потенціальної енергії зберігається в системі, де діють лише консервативні сили. Тоді потенціальна енергія яблука переходить у кінетичну

2 коли м’яч летить у верхній кут воріт, його висота над землею і, відповідно, його потенціальна енергія збільшуються. Зважаючи на те, що прискорення, яке діє по вертикалі (прискорення вільного падіння), напрямлене до поверхні землі, швидкість, що напрямлена вгору, зменшується. Тому зменшується і кінетична енергія. Скориставшись законом збереження механічної енергії, можна дійти висновку, що кінетична енергія м’яча переходить у потенціальну

3 під час рівномірного падіння дощової краплі її висота, а отже й потенційна енергія, зменшується. Оскільки крапля рухається рівномірно, то її швидкість, а отже й кінетична енергія, не змінюється. Енергія не може зникнути, вона лише здатна перейти з одного виду в інший. Тож потенціальна енергія краплі переходить у її внутрішню енергію

4 під час кочення м’яча по футбольному полю висота м’яча над поверхнею землі і, відповідно, його потенціальна енергія не змінюються. Швидкість м’яча постійно зменшується внаслідок тертя. Тобто кінетична енергія м’яча переходить у внутрішню.

Відповідь: 1Г, 2В, 3А, 4Д.

ТЕМА: Механічні коливання і хвилі. Амплітуда, частота, період гармонічних коливань.

Завдання скеровано на перевірку розуміння основних величин, пов’язаних із коливаннями математичного маятника.

Тіло на довгій нитці можна вважати математичним маятником (рис. 1).

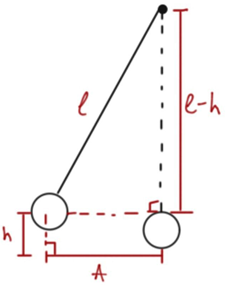
Рис. 1. Математичний маятник у положеннi максимального відхилення

1. Період коливань математичного маятника $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{\frac lg}, $$ де \(l\) – довжина маятника, \(g\) – прискорення вільного падіння. Ні від маси, ні від амплітуди ця величина не залежить.

2, 3. Енергію коливань можна визначити за формулою $$ E=E_{\text{пот}}+E_{\text{кін}}=mgh+\frac{mv^2}{2}. $$

У точці з найбільшим відхиленням потенціальна енергія тіла на підвісі максимальна, а кінетична енергія дорівнює \(0\), тож $$ E=E_{\text{пот}\ max}=mgh_{max}. $$

Максимальну висоту \(h_{max}\) можна визначити з прямокутного трикутника, зображеного на рисунку 1.

За теоремою Піфагора

Якщо коливання малі, то й висота підйому \(h\) мала порівняно з його довжиною \(l\) та амплітудою \(A\), тому доданок \(h^2\) набагато менший за інші доданки, ним можна знехтувати:

Тобто максимальна висота тягарця над нижньою точкою траєкторії залежить від \(A^2\) і не залежить від його маси.

Енергія коливань $$ E=mgh_{max}=mg\frac{A^2}{2l}. $$

Тож енергія коливань пропорційна до \(A^2\) та \(m\).

4. У найнижчій точці траєкторії потенціальна енергія тягарця дорівнює нулю, а його кінетична енергія, а отже й модуль швидкості, максимальні: $$ E=mg\frac{A^2}{2l}=\frac{mv_{max}^2}{2}. $$ Тож

Тобто максимальна швидкість пропорційна до \(A\) та не залежить від \(m\).

Відповідь: 1В, 2А, 3Д, 4Г.

ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона.

Завдання скеровано на оцінку вміння розв’язувати розрахункові задачі про рух тіла під дією кількох сил.

Дано:
\(m_1=2\ \text{кг}\)
\(m_2=3\ \text{кг}\)
\(m_3=5\ \text{кг}\)
\(T_{max}=10\ \text{Н}\)

Знайти:
\(F_{max}\ (\text{Н})\ -\ ?\)

У такій конструкції всі три бруски рухатимуться як єдине ціле з однаковим прискоренням і масою \(M\).

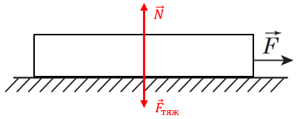
Рис. 1. Схематичне зображення дії сил на бруски як ціле

Для них можна записати 2 закон Ньютона:

Уздовж вертикальної осі бруски не рухаються, тому рівнодійна в цьому напрямку дорівнює 0. Спроєктувавши сили на цей напрямок, можна отримати вираз \begin{gather*} 0+N-F_{\text{тяж}}=0;\\[7pt] N=F_{\text{тяж}}. \end{gather*}

Спроєктувавши другий закон Ньютона на горизонтальний напрямок, можна дійти висновку, що $$ F_{max}+0+0=Ma_{max}. $$

Тож $$ F_{max}=(m_1+m_2+m_3)a_{max}. $$

Обмеження на максимальну силу, а отже й максимальне прискорення, створене міцністю ниток, якими зв’язано бруски.

Цю систему потрібно розглянути як два бруски масою \(m_3\) й \(m_1+m_2\) відповідно (рис. 2).

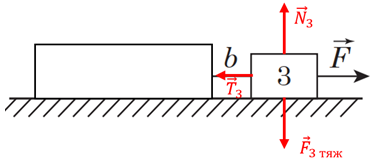
Рис. 2. Схематичне зображення сил, що діють на брусок 3

На брусок 3 діють усі зазначені вище сили й сила натягу нитки. Рухається цей брусок із тим самим прискоренням, яке використано в попередніх розрахунках. Тому можна записати рівнодійну сил, що діють на цей брусок:

Уздовж вертикальної осі брусок 3 не рухається, тому можна зробити той самий висновок, що й у попередніх розрахунках: $$ N_3=F_{3\ \text{тяж}}. $$

Проєкція другого закону Ньютона на горизонтальну вісь матиме вигляд: $$ F_{max}+0+0-T_{3\ \text{max}}=m_3a_{max}. $$

Зважаючи на те, що $$ F_{max}=(m_1+m_2+m_3)a_{max}, $$ можна зробити висновок:

Значення максимальної сили натягу відоме з умови \((10\ \text{Н})\), тому можна виразити максимальне прискорення і знайти максимальну силу:

Відповідь: 20

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Відносна вологість.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі про відносну вологість повітря.

Дано:
\(V=0,5\ \text{м}^3\)
\(\Delta m=6\ \text{г}\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{н.п.}=20\ \frac{\text{г}}{\text{м}^3}\)

Знайти:
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}_\text{до}\ (\text{%})\ -\ ?\)

Маса води в повітрі перестає змінюватися, коли рідина й пара досягають стану динамічної рівноваги – кількість випаруваної рідини дорівнює кількості сконденсованої пари. Тобто маса води в повітрі перестає змінюватися, коли пара стає насиченою.

Масу води в повітрі, якщо пара є насиченою, обчислюють за формулою \begin{gather*} m_\text{після}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{н.п.}V;\\[6pt] m_\text{після}=20\frac{\text{г}}{\text{м}^3}\cdot 0,5\ \text{м}^3;\\[6pt] m_\text{після}=10\ \text{г}. \end{gather*}

Тоді масу водяної пари в повітрі до випаровування обчислюють за формулою

Тож відносну вологість до випаровування обчислюють за формулою $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{а}}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{н.п.}}\cdot 100\ \text{%}, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}\) – відносна вологість повітря, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{н.п.}\) – густина насиченої пари, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{а}\) – густина водяної пари в повітрі. $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{а}=\frac{m_\text{до}}{V}=\frac{4\ \text{г}}{0,5\ \text{м}^3}=8\ \frac{\text{г}}{\text{м}^3}. $$

Тож

Відповідь: 40.

ТЕМА: Закони електролізу.

Завдання скеровано на перевірку вміння застосовувати закони електролізу для розв’язування розрахункових задач.

Дано:
\(S=120\ \text{см}^2\)
\(t=2\ \text{год}\)
\(I=0,3\ \text{А}\)
\(k=3\cdot 10^{-7}\ \frac{\text{кг}}{\text{Кл}}\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}=9\ \frac{\text{г}}{\text{см}^3}\)

Знайти:
\(d (\text{мкм})\ -\ ?\)

Нікелювання здійснюють електролізом. За першим законом електролізу можна визначити масу нікелю, що виділився:

За відомою масою \(m\) і густиною матеріалу \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\), то можна обчислити його об’єм: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}=\frac mV\rightarrow V=\frac{m}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}}. $$ Об’єм матеріалу можна виразити через товщину та площу його поверхні: $$ V=Sd\rightarrow d=\frac VS. $$

Тож, товщина матеріалу

Відповідь: 6.

ТЕМА: Оптика. Оптична сила лінзи. Формула тонкої лінзи.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на формулу тонкої лінзи.

Дано:
\(D=1,5\ \text{дптр}\)
\(H=3\ \text{м}\)

Знайти:
\(d\ (\text{м})-?\)

Оптичну силу лінзи і її положення відносно об’єкта і його зображення пов’язує формула тонкої лінзи: $$ d=\frac 1d+\frac 1f, $$ де \(d\) – відстань від об’єкта до лінзи, а \(f\) – відстань від лінзи до зображення (рис. 1).

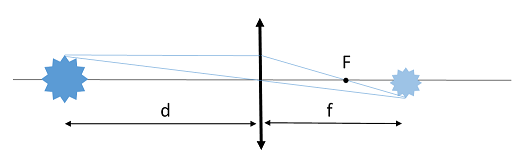
Рис. 1. Схема ходу променів крізь тонку лінзу

За умовою потрібно отримати зображення на відстані 3 м від світильника, тобто \(d+f=H,\) відповідно \(f=H\ –\ d,\) а $$ D =\frac 1d+\frac{1}{H-d}. $$

Отже \begin{gather*} \frac{H-d+d}{d(H-d)}=\frac{H}{d(H-d)}=D,\\[6pt] H=dD(H-d),\\[7pt] H=dDH-d^2 D,\\[7pt] d^2 D-dDH+H=0. \end{gather*}

Затим потрібно підставити всі відомі величини й розв’язати отримане внаслідок перетворень рівняння відносно \(d\): $$ 1,5d^2-4,5 d+3=0,\ \ d^2-3d+2=0. $$

Дискримінант \(D=(-3)^2-4\cdot 1\cdot 2=1,\) тож $$ d_1=\frac{3-\sqrt{1}}{2\cdot 1}=1\ \ \text{і}\ \ d_2=\frac{3+\sqrt{1}}{2\cdot 1}=2. $$

Умову задачі задовольняє менше значення \(d=1.\)

Відповідь: 1.

ТЕМА: Квантова фізика. Атом й атомне ядро. Випромінювання і поглинання світла атомом.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на енергію зв’язку атомних ядер.

Дано:
\(W_k=0,2\ \text{МеВ}\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=0,495\ \text{пм}\)

Знайти:
\(E_{\text{зв}}\ (\text{МеВ})\ -\ ?\)

Атом поглинає квант, отримує від нього додаткову енергію. Ця енергія витрачається на подолання енергії зв’язку й на кінетичну енергію частинок, що утворилися після розпаду: $$ E=W_k+E_{\text{зв}}. $$

Отриману від кванта випромінювання енергію можна знайти з наступного виразу, перевівши попередньо пікометри в метри:

Оскільки сумарну кінетичну енергія в завданні зазначено в МеВ, отриманий результат також потрібно перевести в МеВ:

Тоді енергія зв’язку $$ E_{\text{зв}}=2,5\ \text{МеВ}-0,2\ \text{МеВ}=2,3\ \text{МеВ}. $$

Відповідь: 2,3.