Розділ: Мультитести
Тест: Тренувальний мультитест (1 варіант)
Блок: Математика
Кількість завдань: 22
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Завдання перевіряє вміння розв’язувати тестові задачі арифметичним способом.
Столи і стільці було придбано у співвідношенні \(1:3\) відповідно. Отже, столи становлять \(\frac 14\) всіх меблів, а стільці – решту, \(\frac 34\).
Правильно відображено розподіл на рисунку Г.
Відповідь: Г.
ТЕМА: Алгебра і початки аналізу. Числа та вирази.
Завдання перевіряє вміння виконувати тотожні перетворення раціональних виразів.
Застосувавши розподільний закон множення, розкриємо дужки:
$$ 2(5x+6)=2\cdot 5x+2\cdot 6=10x+12. $$Отже, правильна відповідь – Д.
Відповідь: Д.
ТЕМА: Геометрія. Планіметрія. Коло та круг.
Завдання перевіряє знання властивостей кола та хорд.
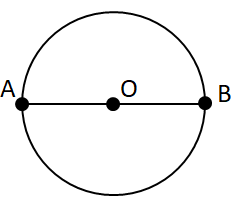
Відрізок, що сполучає дві точки кола, називається хордою. Найбільша за довжиною хорда – діаметр кола.
Отже, \(AB=32,\) тому що радіус кола дорівнює \(16\ (d=2R).\)
Відповідь: Г.
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.
Завдання перевіряє вміння розв’язувати лінійні нерівності.
Розв'яжемо лінійну нерівність: \begin{gather*} x+3\le0,\\[7pt] x\le -3. \end{gather*} Зобразимо розв'язок на координатній прямій:
$$ x\in (-\infty;\ -3]. $$
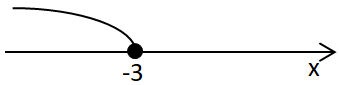
Отже, правильна відповідь – В.
Відповідь: B.
ТЕМА: Геометрія. Стереометрія. Координати та вектори у просторі.
Завдання перевіряє вміння виконувати дії з векторами.
Застосуємо правильно додавання векторів:
\begin{gather*} \overrightarrow{a}(a_1;\ a_2;\ a_3),\ \overrightarrow{b}(b_1;\ b_2;\ b_3)\\[7pt] \overrightarrow{a}+\overrightarrow{b}=\overrightarrow{c}(a_1+b_1;\ a_2+b_2;\ a_3+b_3)=\\[7pt] =\overrightarrow{c}\left(2+(-7);\ -2+(-3);\ 3+4\right)=\overrightarrow{c}(-5;\ -5;\ 7). \end{gather*}Відповідь: Б.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком та формулою.
Нулем функції називається таке значення аргумента, при якому значення функції дорівнює нулю.
На графіку функції це точка перетину з віссю \(Ox.\)
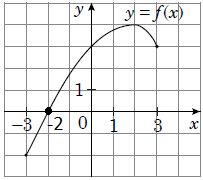
Отже, правильна відповідь – Б.
Відповідь: Б.
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Завдання перевіряє вміння розв’язувати тестові задачі арифметичним способом, розв’язувати задачі на відсоткові розрахунки.
Плата зросла на \(161-140=21\ (\text{грн}).\)
\(21\) гривня становить від \(140\) гривень: $$ \frac{21}{140}\cdot 100\text{%}=15\text{%}. $$
Відповідь: Б.
ТЕМА: Геометрія Стереометрія. Тіла обертання.
Завдання перевіряє знання властивостей геометричних тіл, зокрема циліндра.
Циліндр утворений обертанням квадрата навколо його сторони:
\(ABCD\) – квадрат.
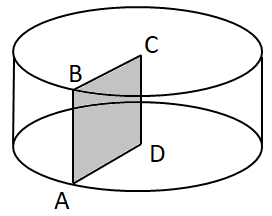
Відповідь: А.
ТЕМА: Алгебра і початки аналізу. Числа та вирази.
Завдання перевіряє вміння виконувати тотожні перетворення ірраціональних виразів.
\begin{gather*} (\frac 17\cdot \sqrt[3]{7})^3=\left(\frac 17\right)^3\cdot (\sqrt[3]{7})^3=\frac{1}{7^3}\cdot 7=\frac{1}{7^2}=\frac{1}{49}. \end{gather*}Застосували властивості:
\begin{gather*} (a\cdot b)^n=a^n\cdot b^n;\\[6pt] \left(\frac ab\right)^n=\frac{a^n}{b^n};\\[6pt] (\sqrt[n]{a})^n=a\ \text{при}\ a\ge 0. \end{gather*}Відповідь: Г.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання перевіряє знання властивостей трапеції.
Правильне лише ІІІ твердження.
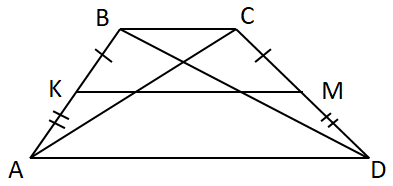
I. Середня лінія трапеції не проходить через точку перетину її діагоналей.
II. Діагональ трапеції не ділить її на два рівних трикутники \(\Delta ABC\ne \Delta ACD.\)
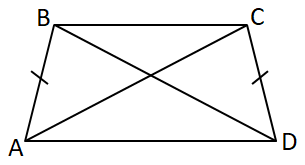
III. \(AC=BD\) (властивість рівнобічної трапеції). \(\Delta ABC=\Delta DCB\) (І ознака).
Відповідь: А.
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.
Завдання перевіряє вміння розв’язувати системи лінійних та раціональних рівнянь.
Розв'яжемо систему рівнянь:
\begin{gather*} \left\{ \begin{array}{l} \frac{1}{3y}=\frac 2x, \\ x-y=30. \end{array} \right. \end{gather*}
Застосуємо основну властивість пропорції до першого рівняння:
\begin{gather*} \left\{ \begin{array}{l} 1\cdot x=2\cdot 3y, \\ x-y=30, \end{array} \right. \ \ \ \left\{ \begin{array}{l} x=6y, \\ x-y=30. \end{array} \right. \end{gather*}Методом підстановки маємо:
\begin{gather*} \left\{ \begin{array}{l} x=6y, \\ 6y-y=30, \end{array} \right. \ \ \ \left\{ \begin{array}{l} x=6y, \\ 5y=30, \end{array} \right. \\[7pt] \left\{ \begin{array}{l} x=6y, \\ y=6, \end{array} \right. \ \ \ \left\{ \begin{array}{l} x=6\cdot 6, \\ y=6, \end{array} \right. \\[7pt] \left\{ \begin{array}{l} x=36, \\ y=6. \end{array} \right. \end{gather*}\((36;\ 6)\) – розв'язок системи, тому \(36+6=42\) – правильна відповідь.
Відповідь: Г.
ТЕМА: Алгебра і початки аналізу. Функції. Похідна.
Завдання перевіряє вміння знаходити похідну функції, знання фізичного змісту похідної.
Матеріальна точка рухається за законом \(x(t)=6t^2.\) За фізичним змістом похідної $$ v(t)=x'(t)=(6t^2)'=12t. $$
Відповідь: Б.
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.
Завдання перевіряє вміння застосовувати означення та властивості прямокутного трикутника, знаходження площі паралелограма, до розв'язування планіметричних задач.
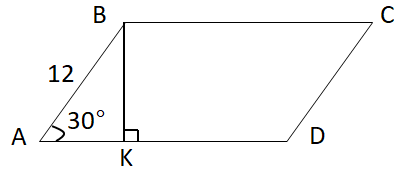
За умовою \(AD=3BK,\) де \(BK\) – висота паралелограма.
У \(\Delta ABK\ (\angle K=90^\circ)\) за властивістю катета, який лежить напроти кута \(30^\circ,\) \(AB=2BK,\) \(BK=6\ \text{см}.\) $$ AD=3BK=3\cdot 6=18\ (\text{см}). $$
Площа паралелограма \(S=ah_a,\) де \(a=AD, h_a=BK.\) $$ S=18\cdot 6=108\ (\text{см}^2). $$
Відповідь: B.
ТЕМА: Алгебра і початки аналізу. Числа та вирази.
Завдання перевіряє вміння виконувати тотожні перетворення раціональних виразів.
Спростимо вираз:
\begin{gather*} \frac{a^2+ab}{(a+b)^2}-\frac{2a+b}{a+b}=\frac{a(a+b)}{(a+b)^2}-\frac{2a+b}{a+b}=\\[6pt] =\frac{a}{a+b}-\frac{2a+b}{a+b}=\frac{a-(2a+b)}{a+b}=\frac{a-2a-b}{a+b}=\\[6pt] =\frac{-a-b}{a+b}=\frac{-(a+b)}{a+b}=-1. \end{gather*}Відповідь: Д.
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.
Завдання перевіряє вміння розв’язувати тригонометричні рівняння.
Розв'яжемо тригонометричне рівняння:
\begin{gather*} \sin 4x=-1,\\[6pt] 4x=-\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{2}+2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}n,\ n\in\mathbb{Z}\ \ |\ :4\\[6pt] x=-\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{8}+\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}n}{2},\ n\in \mathbb{Z}\\[6pt] \text{при}\ n=0\ \ x=-\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{8};\\[6pt] \text{при}\ n=1\ \ x=-\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{8}+\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{2}=\frac{-\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}+4\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{8}=\frac{3\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{8} - \text{корінь рівняння}. \end{gather*}Відповідь: А.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком та формулою.
Схематично графіки функцій виглядають таким чином:
1. \(E(y)=[0;\ +\infty)\) – B.
2. Графік симетричний відносно осі \(y\) – A.
3. Функція спадна, тому найменше значення функція набуває при найбільшому значенні аргумента – Г.
Відповідь: 1В 2А 3Г.
ТЕМА: Алгебра і початки аналізу. Числа та вирази.
Завдання перевіряє вміння виконувати тотожні перетворення раціональних, логарифмічних та степеневих виразів.
1. Якщо \(\frac na=3,\) то \(a=\frac n3\) – Д.
2. Якщо \(1+\log_3n=\log_3a,\) то \(\log_33+\log_3n=\log_3a,\) \(\log_3(3n)=\log_3a,\ 3n=a\) – A.
3. Якщо \(3^n\cdot 3=3^a,\) то \(3^{n+1}=3^a,\ n+1=a.\) – Б.
Застосували властивості логарифмів та степенів:
\begin{gather*} \log_aa=1,\ \ \log_ab+\log_ac=\log_a(b\cdot c),\\[7pt] a^n\cdot a^m=a^{n+m}. \end{gather*}Відповідь: 1Д, 2А, 3Б.
ТЕМА: Геометрія. Планіметрія. Трикутники.
Завдання перевіряє вміння застосовувати означення та властивості різних видів трикутників до розв'язування планіметричних задач.
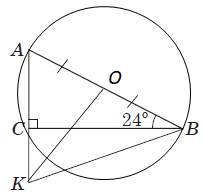
1 – Г. У \(\Delta ACB\ (\angle C=90^\circ)\) \(\angle B+\angle A=90^\circ,\) \(\angle B=24^\circ,\) тому \(\angle A=90^\circ-24^\circ=66^\circ.\) \(\angle BAC=66^\circ.\)
2 – B. \(\Delta ABK\) – рівнобедрений, \(AK=KB\) за умовою. За властивістю рівнобедреного трикутника \(\angle A=\angle B=66^\circ.\)
$$ \angle KBC=\angle KBA-\angle CBA=66^\circ-24^\circ=42^\circ. $$
3 – A. \(\Delta AKB\) – рівнобедрений, \(KO -\) медіана \(AO=OB\) (як радіуси). За властивістю рівнобедереного трикутника \(KO - \) висота, \(KO\perp AB.\) \begin{gather*} \angle OKB=90^\circ-\angle KBO=90^\circ-66^\circ=24^\circ . \end{gather*} \(\Delta ACB - \) прямокутний, тому центр кола описаного навколо нього, лежить на середині гіпотенузи \(AB.\)
Відповідь: 1Г, 2В, 3А.
ТЕМА: Алгебра і початки аналізу. Функції. Числові послідовності.
Завдання перевіряє вміння розв’язувати задачі на арифметичну прогресію, знання формули суми n-перших членів та n-го члена арифметичної прогресії.
Число \(27\) – член арифметичної прогресії, \(d=5.\)
Члени арифметичної прогресії:
Отже, числа з проміжку \(60;\ 75\) – це \(62;\ 67;\ 72.\)
Сума цих чисел: \(62+67+72=201.\)
Відповідь: 201.
ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики.
Завдання перевіряє вміння розв‘язувати задачі, використовуючи перестановки, комбінаторне правило добутку.
Розв'яжемо задачу з комбінаторики: вибираємо з \(8\) збірників \(2,\) а з \(10\) науково-популярних книг \(3.\)
Книги різні, тому застосуємо формулу сполук, щоб знайти кількість варіантів вибору книг кожного виду та правило добутку:
\begin{gather*} \mathrm{C_8^2\cdot C_{10}^3}=\frac{8!}{2!6!}\cdot \frac{10!}{3!7!}=\frac{7\cdot 8\cdot 8\cdot 9\cdot 10}{1\cdot 2\cdot 1\cdot 2\cdot 3}=\\[6pt] =4\cdot 4\cdot 3\cdot 10\cdot 7=48\cdot 70=3360. \end{gather*}Відповідь: 3360.
ТЕМА: Геометрія. Стереометрія. Многогранники.
Завдання перевіряє вміння розв’язувати стереометричні задачі, задачі на обчислення об’єму призми, побудови перерізів.
\(ABCD\) – ромб, \(AB=20,\) \(P_{AA_1C_1C}=58,\) \(AA_1=5.\) \(AA_1=CC_1=5,\) то \(A_1C_1=AC=(58-2\cdot 5):2=24.\)
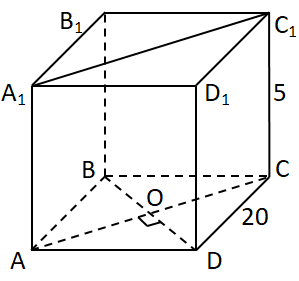
За властивістю ромба \(AC\perp BD,\ AO=OC,\ BO=OD.\) Отже, у \(\Delta COD\ (\angle O=90^\circ)\) \(CD=20,\ OC=12\) за теоремою Піфагора
\begin{gather*} OD^2+OC^2=CD^2,\\[7pt] OD=\sqrt{20^2-12^2}=\sqrt{400-144}=\sqrt{256}=16.\\[7pt] BD=2\cdot OD=32. \end{gather*}Площу ромбу можна знайти за формулою
\begin{gather*} S=\frac 12d_1d_2\ \ S=\frac 12\cdot 32\cdot 24=16\cdot 24,\\[7pt] V=S_\text{осн}\cdot H,\ \text{де}\ S_\text{осн}=16\cdot 24,\ H=AA_1=5.\\[7pt] \end{gather*}Отже,
$$ V=16\cdot 24\cdot 5=16\cdot 120=1920. $$Відповідь: 1920.
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.
Завдання перевіряє вміння розв’язувати квадратні рівняння, аналізувати та досліджувати рівняння, розв’язувати рівняння з параметром.
Дано рівняння \(x^2-4ax+4a^2-25=0.\) Корені квадратного рівняння задовольняють умову \(x_1\lt 1\lt x_2.\)
Знайдемо \(a,\) при яких
\begin{gather*} \left\{ \begin{array}{l} 2a-5\lt 1,\\ 2a+5\gt 1, \end{array} \right. \\[7pt] \left\{ \begin{array}{l} 2a\lt 6,\\ 2a\gt -4, \end{array} \right. \ \ \ \left\{ \begin{array}{l} a\lt 3,\\ a\gt -2. \end{array} \right. \end{gather*}
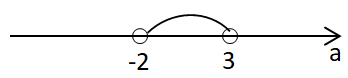
Цілі значення \(a\in (-2;\ 3)\) це \(a=-1;\ 0;\ 1;\ 2.\)
Таких значень \(4.\)
Відповідь: 4.