Мультитести – Математика

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Це завдання перевіряє вміння виконувати тотожні перетворення раціональних виразів, знання властивостей степенів.

Відповідь: A.

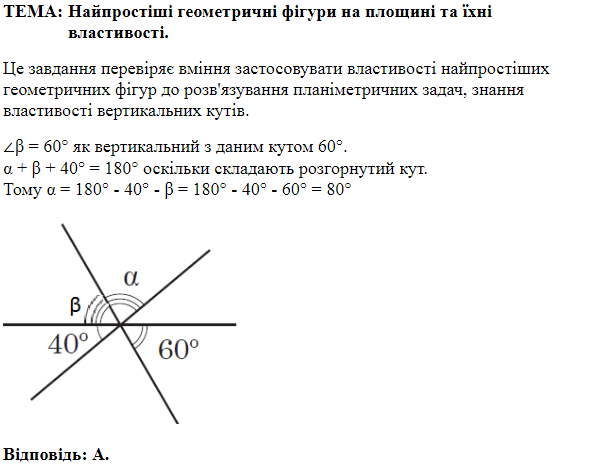
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.

Це завдання перевіряє знання властивостей паралелограмів, нерівності трикутника.

I.   Протилежні сторони будь-якого паралелограма рівні (властивість параллелограма).

II.  Довжина сторони будь-якого трикутника менша за суму довжин двох інших сторін (нерівність трикутника).

III. Твердження неправильне. \(P=4a\) – периметр квадрата, де \(a\) – сторона квадрата.

Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати логарифмічні рівняння, порівнювати дійсні числа.

За означенням логарифма $$ x=64^{\frac 12}=\sqrt{64}=8 $$ \(6\lt 8\lt 32\) – проміжок, якому належить корінь.

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Функції. Первісна.

Завдання перевіряє знання означення первісної функції.

Функція \(F(x)=5x^4-1\) є первісною функції \(f(x).\)

Формула, яка задає всі первісні функції \(f(x)\) $$ F(x)=5x^4+C, $$ де \(C\) – будь-яке число.

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв’язувати системи лінійних рівнянь.

Розв'яжемо систему лінійних рівнянь методом додавання: \begin{gather*} +\left\{\begin{array}{l} 10x-4y=26,\\ 6x+4y=6, \end{array}\right.\\[0pt] \ \ \ \ \ \ \overline{16x=32,}\\[7pt] x=32:16,\ \ x=2. \end{gather*}

Підставимо значення \(x=2\) в друге рівняння: \begin{gather*} 6\cdot 2+4y=6,\\[7pt] 12+4y=6,\\[7pt] 4y=6-12,\\[7pt] 4y=-6,\\[7pt] y=-6: 4,\\[7pt] y=-1\mathord{,}5. \end{gather*}

Розв'язок системи \((2; -1\mathord{,}5).\)
Обчислимо добуток \(x_0\cdot y_0=2\cdot (-1\mathord{,}5)=-3.\)

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання скеровано на перевірку вміння установлювати властивості числових функцій, заданих формулою або графіком, досліджувати на парність (непарність) функції.

1.

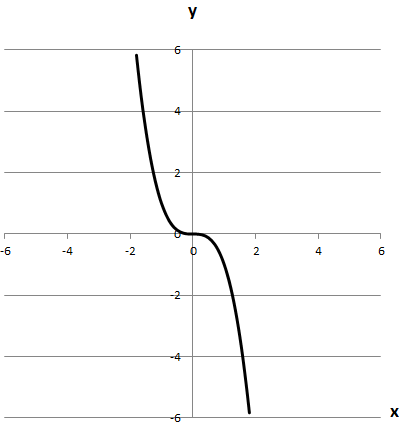
Симетричний відносно початку координат. Отже, 1 - Г.

2.

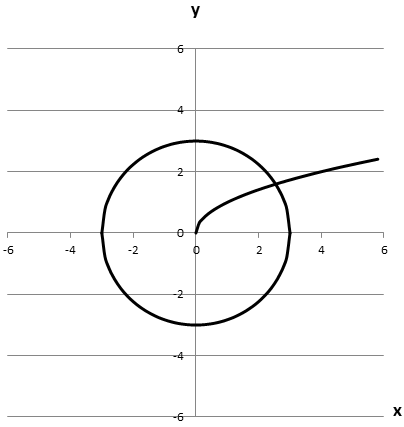
Має з графіком рівняння \(x^2+y^2=9\) лише одну спільну точку. Отже, 2 - Б.

3.

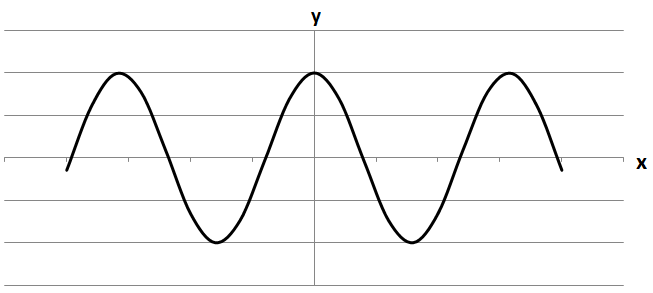
Симетричний відносно осі \(y\). Отже, 3 - В.

Відповідь: 1Г, 2Б, 3В.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Раціональні вирази, вирази з модулем та їх перетворення.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення виразів, порівнювати числа, розуміння поняття числового проміжку.

1. $$ |x-\sqrt{5}|=|\sqrt{5}-1-\sqrt{5}|=|-1|=1 $$ Oтже, 1 - Б.

2. \begin{gather*} (\sqrt{5}+1)(\sqrt{5}-1)=(\sqrt{5})^2-1^2=\\[7pt] =5-1=4 \end{gather*} використали формулу $$ a^2-b^2=(a-b)(a+b) $$ Отже, 2 - B.

3. \begin{gather*} x^2+2x+1=(x+1)^2=\\[7pt] =(\sqrt{5}-1+1)^2=(\sqrt{5})^2=5 \end{gather*} використали формулу $$ (a+b)^2=a^2+2ab+b^2 $$ Отже, 3 - Г.

Відповідь: 1Б, 2В, 3Г.

ТЕМА: Геометрія. Планіметрія. Чотирикутники.

Завдання скеровано на перевірку знання властивостей квадрата, трапеції; вміння використовувати формули площ геометричних фігур для розв’язування планіметричних задач.

\(S_{ABCD}=S_{BMNC}=36\ \text{см}^2,\ \ AM=15\ \text{см}\).

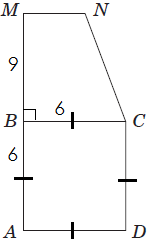
1. \(S_{ABCD}=AB^2=36\ \text{см}^2,\ AB=6\ \text{см}\) – сторона квадрата, отже, 1 - Г.

2. У прямокутній трапеції \(BM\) – висота.
\(BM=AM-AB=15-6 = 9\ \text{см}\), отже, 2 - Д.

3. \begin{gather*} S_{BMNC}=\frac{MN+BC}{2}\cdot BM,\\[6pt] 36=\frac{MN+6}{2}\cdot 9,\\[6pt] 72 = (MN+6)\cdot 9\\[7pt] MN =2\ \text{см}. \end{gather*} отже, 3 - A

Відповідь: 1Г, 2Д, 3A.

ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи статистики.

Це завдання перевіряє знання класичного означення ймовiрностi події, уміння обчислювати ймовірність випадкових подій.

У шухляді олівці та ручки.

Нехай ручок було \(x\) штук, тоді олівців: \(x-12\) шт. Всього ручок та олівців було $$ x+x-12=2x-12. $$

Відомо, що ймовірність вибрати навмання одну ручку \(P(A)=\frac 58.\) Тобто відношення кількості ручок до кількості всіх елементів дорівнює \(\frac 58.\)

\begin{gather*} \frac{x}{2x-12}=\frac 58,\ \ 5(2x-12)=x\cdot 8,\\[6pt] 10x-60=8x,\ \ 2x=60,\ \ x=30. \end{gather*}

Олівців лежить у шухляді \(30-12=18\) шт.

Відповідь: \(18.\)