Розділ: Мультитести
Тест: Тренувальний мультитест (9 варіант)
Блок: Математика
Кількість завдань: 22
ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи статистики. Графічне подання статистичної інформації.
Це завдання перевіряє вміння аналізувати статистичну інформацію, наведену у вигляді графіків або діаграм.
Щоб відповідсти на запитання, потрібно визначити на осі "роки" рік, в якому точка, що йому відповідає, віддалена від точки, що відповідає попередньому року, по вертикалі на найбільшу відстань.
З діаграми видно, що найбільші по вертикалі відстані спостерігаються між точками, що відповідають
Знайдемо різниці між річними мінімумами:
Оскільки
Відповідь: Д.
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Текстові задачі.
Це завдання перевіряє вміння розв'язувати текстові задачі арифметичним способом, виконувати тотожні перетворення раціональних виразів.
Відповідь: B.
ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості.
Це завдання перевіряє вміння застосовувати означення, ознаки та властивості найпростіших геометричних фігур до розв'язування задач практичного змісту.
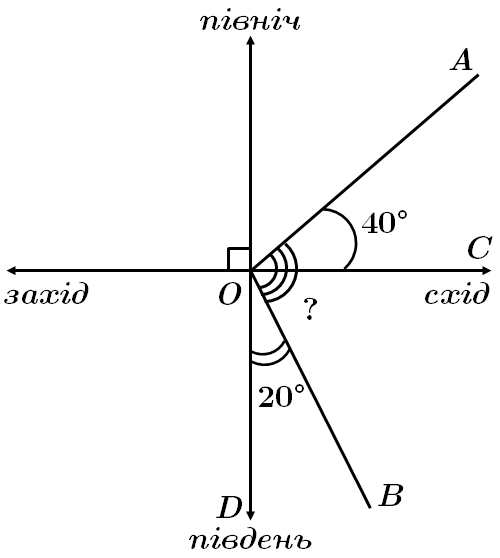
Кут
Відповідь: B.
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи. Лінійні рівняння.
Завдання перевіряє вміння розв'язувати лінійні рівняння.
Помножимо обидві частини рівняння на
Відповідь: B.
ТЕМА: Геометрія. Стереометрія. Многогранники.
Це завдання перевіряє вміння розв'язувати задачі на обчислення площ поверхонь геометричних тіл, знання многогранників та їхніх елементів.
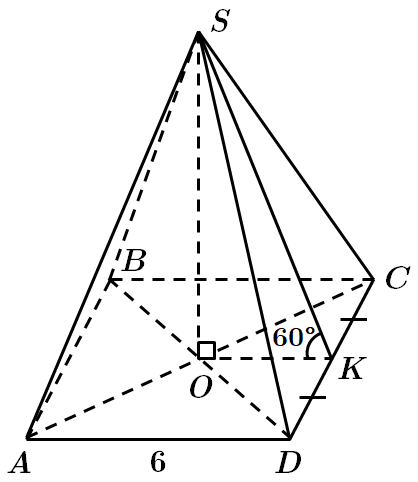
Відповідь: A.
ТЕМА: Алгебра і початки аналізу. Функції. Функціональна залежність.
Це завдання перевіряє вміння встановлювати властивості числових функцій заданих графіком.
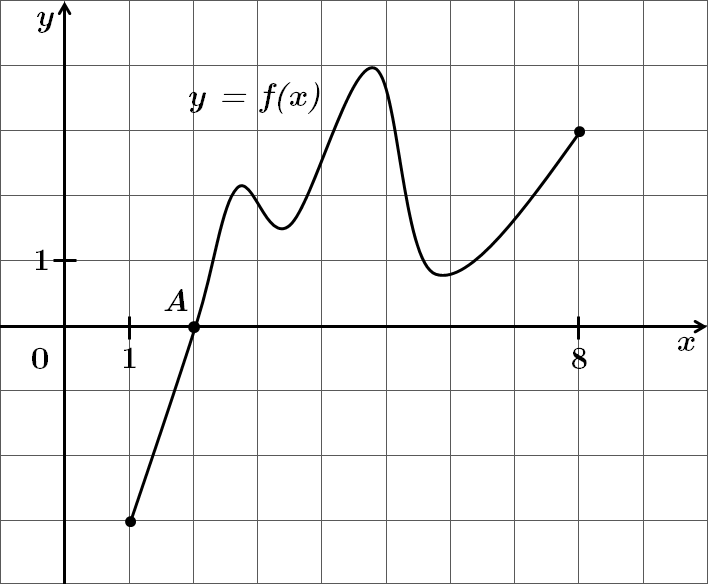
Нулі функції – точки перетину графіка функції з віссю
На рисунку бачимо лише одну точку перетину графіка функції з віссю
Відповідь: Б.

ТЕМА: Алгебра та початки аналізу. Функції. Лінійна функція.
Це завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком, використовувати перетворення графіків функцій.
Графік функції
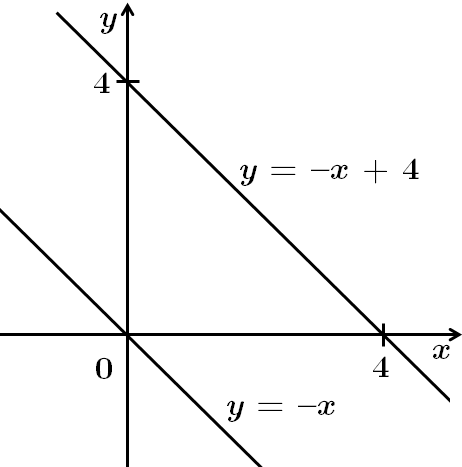
Отже, правильна відповідь Д.
Відповідь: Д.
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Завдання перевіряє вміння виконувати тотожні перетворення раціональних виразів, знання формул скороченого множення.
Спростимо вираз, використавши формулу скороченого множення
Відповідь: Б.
ТЕМА: Геометрія. Планіметрія. Трикутники.
Це завдання перевіряє вміння класифікувати трикутники за сторонами та кутами, знання теореми про суму кутів трикутника, кола, описаного навколо трикутника.
Якщо
За нерівністю трикутника
Центр кола, описаного навколо тупокутного трикутника
Отже, правильна відповідь – Д.
Відповідь: Д.
ТЕМА: Алгебра і початки аналізу. Рівняння.
Завдання перевіряє вміння розв'язувати логарифмічні рівняння, знання числових проміжків.
За означенням логарифма
Відповідь: Д.
ТЕМА: Алгебра і початки аналізу. Функції. Первісна.
Завдання перевіряє знання означення первісної.
Загальний вигляд первісної функції
Тоді,
Відповідь: A.
ТЕМА: Алгебра і початки аналізу. Рівняння та їхні системи.
Це завдання перевіряє вміння розв'язувати системи рівнянь першого степеня.
Розв'язок
Відповідь: Г.
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Логарифмічні вирази.
Це завдання перевіряє вміння виконувати тотожні перетворення логарифмічних виразів та знаходити числове значення при заданих значеннях змінних.
Якщо
Відповідь: Д.
ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Лінійні, квадратні, раціональні рівняння та їхні системи.
Це завдання перевіряє вміння розв'язувати рівняння та системи рівнянь першого та другого степеня.
Почленно віднімемо рівняння системи:
Підставимо значення
Розв'язок системи
Отже, правильна відповідь
Відповідь: A.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння установлювати властивості числових функцій, заданих формулою або графіком, досліджувати на парність (непарність) функції.
1.
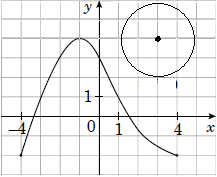
Графік функції не має спільних точок з колом. Отже, 1 - Г.
2.
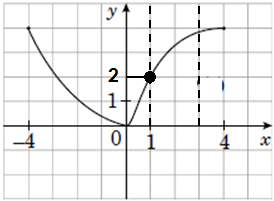
Найменше значення функції на проміжку
3. Графік функції тричі перетинає пряму
Відповідь: 1Г, 2Б, 3Д.
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа та дії над ними.
Завдання скеровано на перевірку вміння виконувати дії з дійсними числами, порівнювати числа, розуміння поняття числового проміжку.
1.
2.
3.
Відповідь: 1В, 2А, 3Б.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання скеровано на перевірку знання властивостей паралелограма, ромба; вміння використовувати формули площ геометричних фігур для розв’язування планіметричних задач.
1. На рис. 1 зображено ромб. За властивістю ромба діагоналі перетинаються під прямим кутом. Отже, 1 – A.
2.
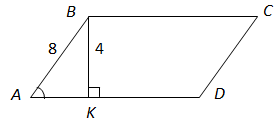
У
3.
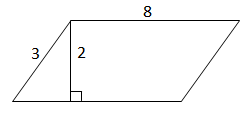
За формулою
Відповідь: 1А, 2Б, 3Д.
ТЕМА: Функції. Числові послідовності. Геометрична прогресія.
Це завдання перевіряє знання формули суми n перших членів геометричної прогресії, уміння розв'язувати задачі на геометричну прогресію..
За умовою
Знаходимо перший член цієї прогресії за формулою
Відповідь:
ТЕМА: Алгебра і початки аналізу. Елементи математичної статистики. Вибіркові характеристики.
Завдання перевіряє вміння обчислювати та аналізувати вибіркові характеристики рядів даних (середнє значення).
Знаходимо середнє арифметичне за формулою:
Відповідь:






