Розділ: Мультитести
Тест: Тренувальний мультитест (10 варіант)
Блок: Математика
Кількість завдань: 22

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Текстові задачі.
Це завдання перевіряє вміння розв'язувати текстові задачі арифметичним способом.
За
Отже,
За кожні
Отже,
Відповідь: Г.
ТЕМА: Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості. Трикутники.
Це завдання перевіряє вміння застосовувати властивості найпростіших геометричних фігур, різних видів трикутників до розв'язування планіметричних задач.
Отже,
Відповідь: Б.
ТЕМА: Рівняння, нерівності та їхні системи. Лінійні рівняння.
Це завдання перевіряє вміння розв'язувати лінійні рівняння.
Значення
Відповідь: Г.
ТЕМА: Геометрія. Стереометрія. Многогранники.
Це завдання перевіряє знання про піраміду, формулу об'єму піраміди.
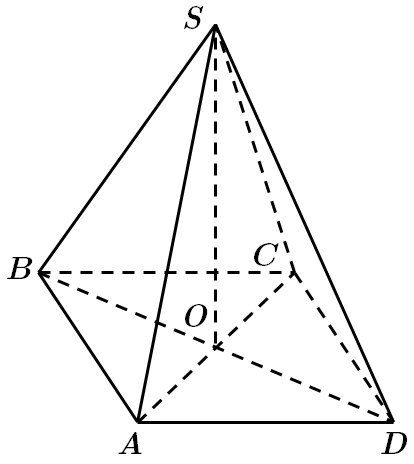
Піраміда
Відповідь: Б.
ТЕМА: Алгебра і початки аналізу. Функції. Лiнiйнi, квадратичні, степеневі, показникові, логарифмiчнi та триroнометричнi функції, їх основні властивості та графіки.
Це завдання перевіряє вміння встановлювати властивості функції, заданої графіком.
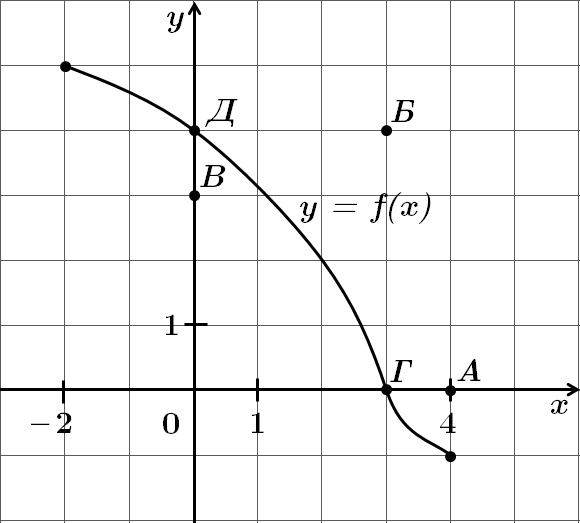
Графік функції перетинає вісь
Відповідь: Д.

ТЕМА: Функції. Функціональна залежність. Лінійна функція, її властивості.
Це завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком.
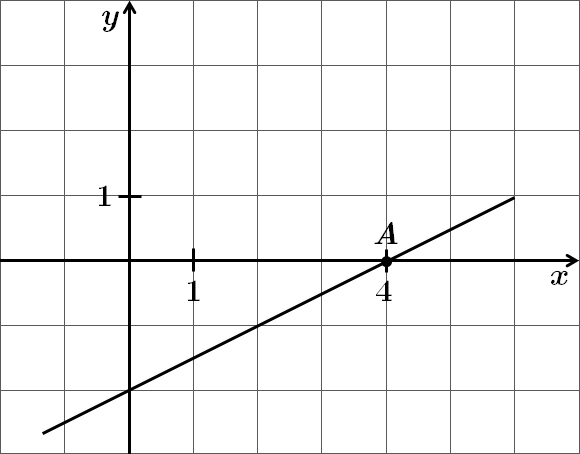
Графік функції перетинає вісь абсцис у точці
Відповідь: Д.
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Завдання перевіряє знання властивостей степенів.
Відповідь: Д.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання перевіряє знання паралелограма, ромба, квадрата та їх властивостей.
I правильне. Діагоналі ромба є бісектрисами його кутів.
II неправильне. Діагоналі точкою перетину діляться навпіл – властивість паралелограма.
III правильне. Діагоналі перпендикулярні – властивість будь-якого квадрата.
Відповідь: Д.
ТЕМА: Алгебра і початки аналізу. Рівняння і нерівності.
Завдання перевіряє вміння розв'язувати логарифмічн рівняння.
Відповідь: Д.
ТЕМА: Алгебра і початки аналізу. Функції. Похідна функції. Первісна.
Завдання перевіряє вміння знаходити похідну функції, знання означення первісної.
За означенням первісної
Отже,
Відповідь: Д.
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лiнiйнi, квaдpaтні, рацiональнi, iррацiональнi, показникові, логарифмiчнi, тригонометричні рівняння, неpiвності та їx системи.
Це завдання перевіряє вміння розв'язувати системи лінійних рівнянь.
Почленно додамо рівняння:
Розв'язок системи
Відповідь: Д.
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Логарифмічні вирази та їх перетворення.
Це завдання перевіряє знання формули суми логарифмів та вміння її застосовувати до розв'язування задач.
Оскільки
при
то
Відповідь: A.
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лiнiйнi, квaдpaтні, рацiональнi, iррацiональнi, показникові, логарифмiчнi, тригонометричні рівняння, неpiвності та їx системи.
Це завдання перевіряє знання методів розв'язування тригонометричних рівнянь.
Рівняння
Відповідь: A.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння установлювати властивості числових функцій, заданих формулою або графіком.
Побудуємо задані графіки функцій
1.
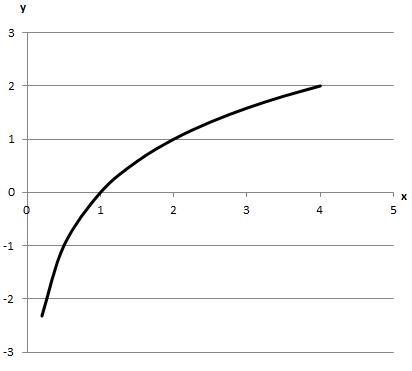
Не перетинає вісь
2.
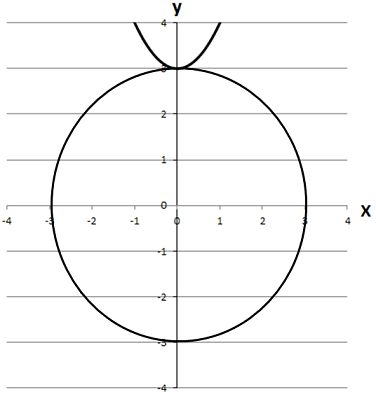
Має лише одну спільну точку з графіком рівняння
3.
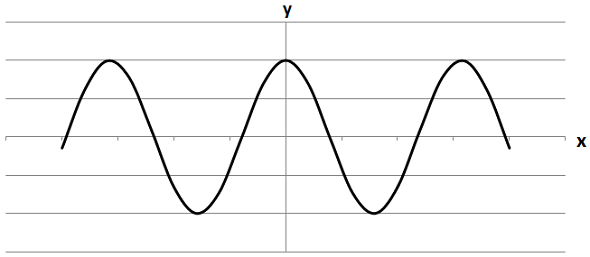
Розташований у всіх координатних чвертях. Отже, 3 - В.
Відповідь: 1А, 2Г, 3В.
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Раціональні, логарифмічні вирази та їх перетворення.
Завдання скеровано на перевірку вміння виконувати тотожні перетворення виразів, порівнювати числа, розуміння поняття числового проміжку.
1.
2.
3.
Відповідь: 1A, 2Д, 3В.
ТЕМА: Геометрія. Планіметрія. Трикутники.
Завдання скеровано на перевірку знання видів трикутників та їх основних властивостей, кола, описаного навколо трикутника, теореми синусів.
1. Рис. 1 – рівносторонній трикутник, отже, центри вписаного та описаного кіл збігаються, 1 - А.
2. Рис. 3 – оскільки катет прямокутного трикутника в 2 рази менше гіпотенузи, то він лежить напроти кута 30°. Отже, 2 - В.
3. Рис. 5 – за теоремою синусів:
Відповідь: 1A, 2В, 3Д.
ТЕМА: Алгебра і початки аналізу. Функції. Числові послідовності.
Це завдання перевіряє знання формули суми
Нехай
Різниця арифметичної прогресії
За формулою суми
За умовою,
Відповідь:
ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи математичної статистики.
Завдання скеровано на перевірку знання класичного означення ймовірності події.
Нехай імовірність того, що переможе Антон буде
Оскільки сума ймовірностей дорівнює 1, то
Відповідь: 0,25.
ТЕМА: Геометрія. Стереометрія. Планіметрія. Многогранники. Трикутники. Чотирикутники.
Завдання перевіряє вміння розв’язувати задачі на обчислення об’єму піраміди, знання теореми Піфагора та властивості квадрата.
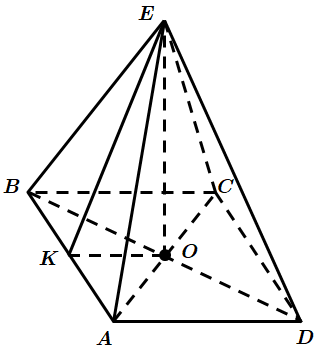
У
Відповідь:





