Розділ: Національний мультитест з математики
Тест: Тренувальні мультитести НМТ 2026
Блок: Варіант 10
Кількість завдань: 22
ТЕМА: Вибіркові характеристики.
Завдання скеровано на перевірку вміння аналізувати статистичні дані, наведені в графічній і текстовій формі.
На діаграмі наведено інформацію про кількість проданих планшетів:
січень – \(250\);
лютий – \(100\);
березень – \(200\);
квітень – \(100\);
травень – \(150\).
Місяць, у якому продано планшетів на \(100\) більше, ніж у попередньому, – березень.
Відповідь: Б.
ТЕМА: Раціональні вирази.
Завдання скеровано на перевірку вміння виконувати тотожні перетворення раціональних виразів, знання основної властивості пропорції.
Виразімо із цієї рівності \(m_1\mathord{:}\)
\begin{gather*} w=\frac{m_1}{m_2},\\[6pt] \frac w1=\frac{m_1}{m_2},\\[6pt] m_1\cdot 1=m_2\cdot w,\\[7pt] m_1=m_2\cdot w. \end{gather*}У перетворенні застосували основну властивість пропорції:
$$ \text{якщо}\ \frac ab=\frac cd,\ \text{то}\ ad=bc. $$Відповідь: А.
ТЕМА: Многогранники.
Завдання скеровано на перевірку знання про піраміду та її елементи.
У піраміді \(SABCD\mathord{:}\)
\(SA\), \(SB\), \(SC\), \(SD\) – бічні ребра;
\(AB\), \(BC\), \(CD\), \(DA\) – ребра основи. Отже, \(SA\) є бічним ребром.
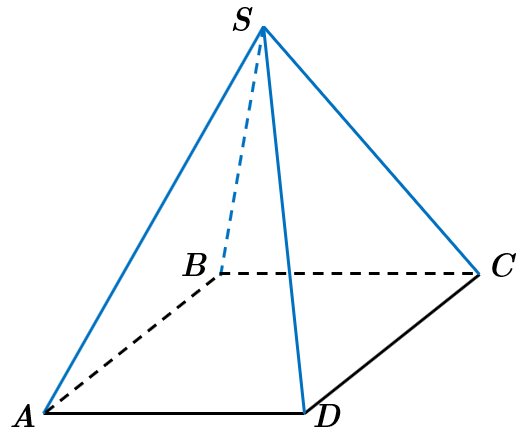
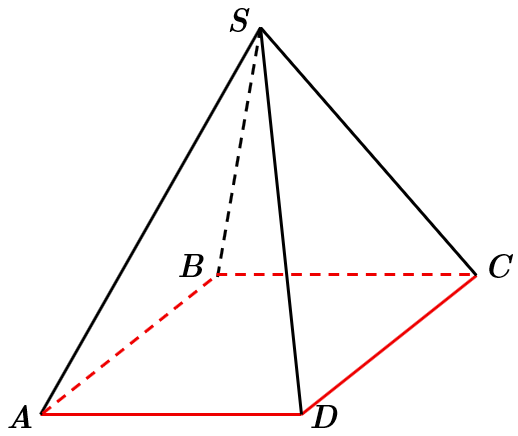
Відповідь: Г.
ТЕМА: Елементарні геометричні фігури на площині та їхні властивості.
Завдання скеровано на перевірку знання властивостей суміжних і вертикальних кутів, паралельних прямих.
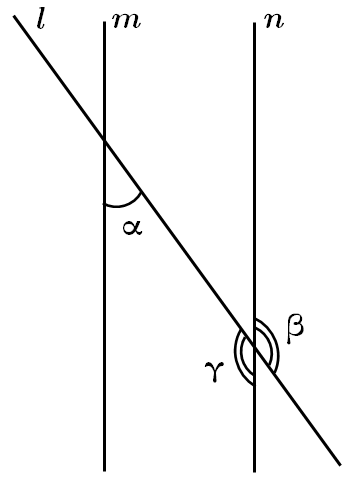
Кути \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\gamma}\) i \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\) – вертикальні. За властивістю вертикальних кутів \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta} = \style{font-style:normal;font-weight:bold;font-size:1.1em}{\gamma}.\)
Кути \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\) i \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\gamma}\) – внутрішні односторонні. За їхньою властивістю:
\begin{gather*} \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}+ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\gamma}=180^\circ,\\[7pt] \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}=35^\circ,\\[7pt] \style{font-style:normal;font-weight:bold;font-size:1.1em}{\gamma}=180^\circ - 35^\circ=145^\circ. \end{gather*}Отже, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}=145^\circ.\)
Відповідь: Д.
ТЕМА: Раціональні вирази та їх перетворення.
Завдання скеровано на перевірку знання формул скороченого множення та вмінння виконувати тотожні перетворення раціональних виразів.
Винесімо спільний множник за дужки:
Використали розподільну властивість множення: $$ a\cdot c+b\cdot c=c\cdot (a+b). $$
Відповідь: A.
ТЕМА: Функціональна залежність.
Завдання скеровано на перевірку вміння визначати властивості числових функцій, заданих графіками, використовувати елементарні перетворення графіків функцій.
Перенесення графіка функції паралельно вздовж осі \(Ox\) – це перетворення виду: $$ f(x)\rightarrow f(x+A), $$ де \(A\) – кількість одиниць, на яку перенесли графік.
Якщо \(A\gt 0\) – переносимо графік вліво, якщо \(A\lt 0\) – переносимо вправо.
Отже, графік функції \(y=x^3\) перенесли на \(4\) одиниці ліворуч й отримали графік функції \(y=(x+4)^3.\)
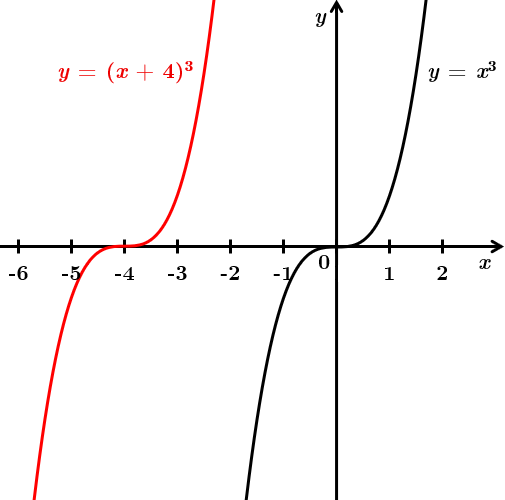
Відповідь: Г.
ТЕМА: Дійсні числа та дії з ними.
Завдання скеровано на перевірку знання властивостей коренів, уміння виконувати дії з ірраціональними числами.
Спростімо вираз:
Використали властивість кореня: \(\sqrt{a\cdot b}=\sqrt{a}\cdot \sqrt{b},\) де \(a\), \(b\gt 0.\)
Відповідь: B.
ТЕМА: Текстові задачі.
Завдання скеровано на перевірку вміння розв’язувати текстові задачі арифметичним способом.
З \(1\) га насадження ялівцю виділяється \(30\) кг фітонцидів за \(1\) день.
З \(2000\) га виділяється \(30\ \text{кг/га}\cdot 2000\ \text{га}=60000\ \text{кг}\) фітонцидів за день.
Визначмо масу фітонцидів за \(30\) днів:
Відповідь: Б.
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знань властивостей паралелограмів, теореми косинусів, уміння розв’язувати трикутники.
\(AC=8\) см, \(BD=6\) см, \(\cos \angle AOD=-\frac 14.\)
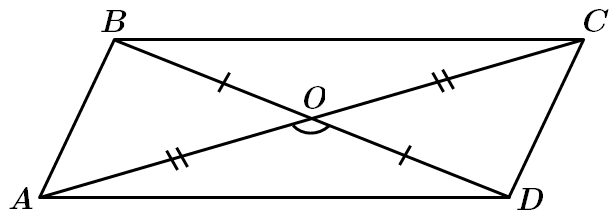
За властивістю паралелограма
\begin{gather*} AO=OC=\frac 12AC=4\ \text{см},\\[6pt] BO=OD=\frac 12BD=3\ \text{см}. \end{gather*}У \(\Delta AOD\) за теоремою косинусів:
Відповідь: A.
ТЕМА: Трикутники.
Завдання скеровано на перевірку знання видів і основних властивостей трикутників, властивостей та означення медіани трикутника.
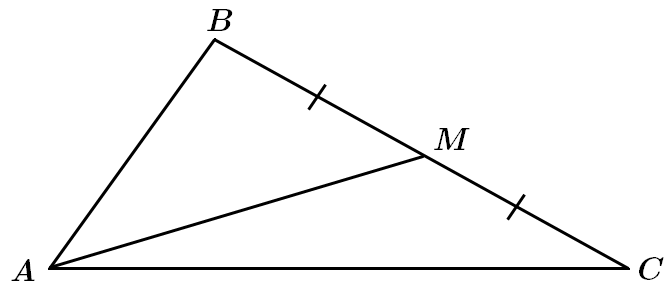
I. Твердження правильне. За означенням, медіана – відрізок, що сполучає вершину трикутника із серединою протилежної сторони.
Отже, \(M\) – середина \(BC.\)
II. Твердження неправильне. \(AM\) – медіана. Щоб медіана збіглася з бісектрисою кута, трикутник повинен бути рівнобедреним з основою \(BC.\) Але в умові \(\Delta ABC\) – довільний.
III. Твердження правильне. \(S_{ABM}=S_{AMC}.\) За властивістю медіани: будь-яка медіана трикутника ділить його на два рівновеликі (рівні за площею) трикутники.
Відповідь: В.
ТЕМА: Логарифмічні вирази та їх перетворення.
Завдання скеровано на перевірку вміння виконувати тотожні перетворення логарифмічних виразів, знання означення та властивостей логарифма.
За властивістю логарифма: $$ \log_ab^n=n\log_ab\mathord{;} $$ $$ \log_aa=1. $$
Спростімо вираз:
\begin{gather*} \log_5 5^{10}=10\log_5 5=10\cdot 1=10. \end{gather*}Відповідь: B.
ТЕМА: Числові послідовності.
Завдання скеровано на перевірку знання означення арифметичної прогресії, формули її \(n\text{-го}\) члена.
За формулою \(n\text{-го}\) члена: $$ a_n=a_1+d(n-1), $$
\begin{gather*} a_6=a_1+5d,\\[7pt] a_6-a_1=a_1+5d-a_1=5d=-30. \end{gather*}Отже, $$ d=-30:5=-6. $$
Відповідь: Д.
ТЕМА: Системи лінійних нерівностей.
Завдання скеровано на перевірку вміння розв’язувати системи лінійних нерівностей, знання властивостей нерівностей.
Розв'яжімо систему лінійних нерівностей:
За властивістю нерівностей, під час ділення нерівності на від'ємне число знак нерівності треба замінити на протилежний.
Зобразімо розв'язок на числовій прямій:
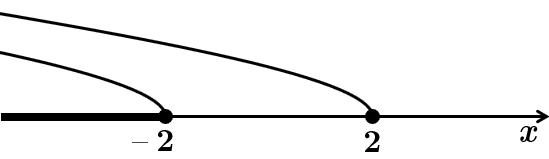
Спільний розв'язок \(x\in (-\infty; -2].\)
Відповідь: Г.
ТЕМА: Первісна й визначений інтеграл.
Завдання скеровано на перевірку вміння застосовувати формулу Ньютона – Лейбнiцa для обчислення визначеного інтеграла, обчислювати площу плоских фігур за допомогою інтеграла.
Площу заштрихованої фігури (криволінійної трапеції), обмежено лініями \(x=a\), \(x=b\), графіком функції \(y=f(x)\) і віссю \(Ox\) визначаємо за формулою:
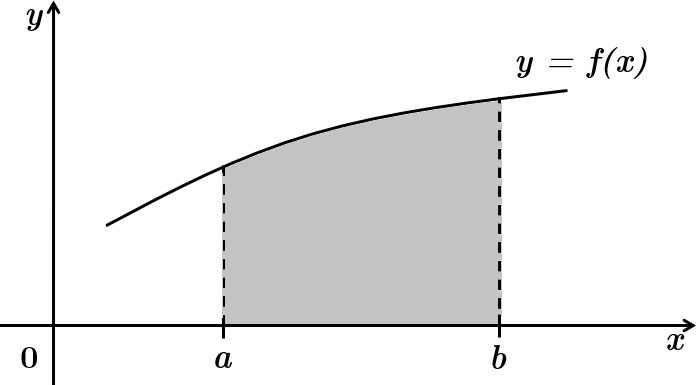
Відповідь: Д.
ТЕМА: Тригонометричні вирази.
Завдання скеровано на перевірку вміння виконувати тотожні перетворення тригонометричних виразів, уміння визначати їхні числові значення.
Функція \(y=\sin x\) періодична з найменшим додатним періодом \(T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}.\) За означенням періодичної фукнції:
Застосували формулу \(\mathrm{tg}\ (180^\circ-\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha})=-\mathrm{tg}\ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}.\)
Отже,
Відповідь: B.
ТЕМА: Функціональна залежність.
Завдання скеровано на перевірку вміння визначати властивості числових функцій, заданих формулою.
1. \(y=7x+4\) – графік функції перетинає вісь \(y\) у точці з ординатою \(4.\)
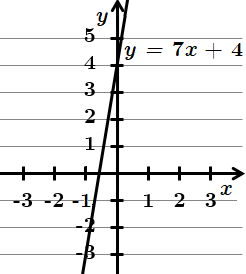
Отже, правильна відповідь – Г.
2. \(y=-\frac 7x\) – функція непарна (графік симетричний відносно початку координат).
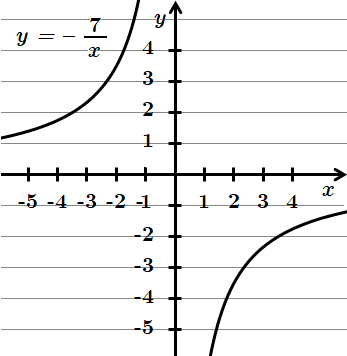
Отже, правильна відповідь – Б.
3. \(y=\log_{0\mathord{,}1}(x-4)\) – логарифмічна функція \(y=\log_a x\) спадна на всій області визначення, якщо \(a\in (0; 1).\)
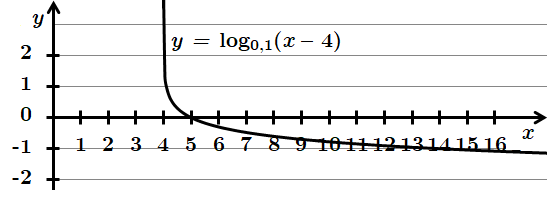
Отже, правильна відповідь – Д.
Відповідь: 1 – Г, 2 – Б, 3 – Д.
ТЕМА: Дійсні числа. Логарифмічні вирази та їх перетворення.
Завдання скеровано на перевірку знання властивостей степенів, логарифмів, уміння виконувати тотожні перетворення їх.
1. \(\frac{m}{4}=1\), \(m=4.\)
Отже, правильна відповідь – B.
2.
\begin{gather*} 4^6:4^{-m}=4^{6-(-m)}=4^{6\ +\ m}=1,\\[7pt] 4^0=1,\ \text{тому}\ 4^{6\ +\ m}=4^0,\\[7pt] 6+m=0,\\[7pt] m=-6. \end{gather*}Отже, правильна відповідь – Г.
3. \(\log_{16}2+\log_{16}m=\log_{16}(2m)=1.\)
За властивістю логарифмів: $$ \log_ab+\log_ac=\log_a(bc). $$
За означенням логарифма:
\begin{gather*} \log_{16}(2m)=1,\\[7pt] 2m=16^1,\\[7pt] 2m=16,\\[7pt] m=8. \end{gather*}Отже, правильна відповідь – Д.
Відповідь: 1 – В, 2 – Г, 3 – Д.
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивостей прямокутника, властивості середньої лінії трикутника, уміння обчислювати площі трикутників, многокутників.
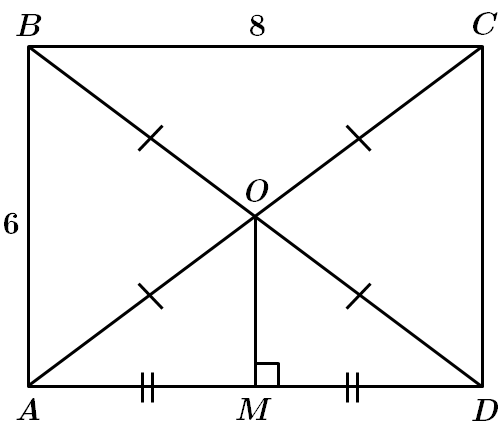
1. \(\Delta ABD\) – прямокутний із катетами \(AB=6\) см і \(AD=8\) см.
Правильна відповідь – B.
2. \(OM\ \perp\ AD.\) За властивістю прямокутника: \begin{gather*} AC=BD,\\[7pt] BO=OD=AO=OC. \end{gather*}
У \(\Delta ABD\) \(OM\) – середня лінія, тому
Правильна відповідь – A.
3.
Правильна відповідь – Г.
Відповідь: 1 – B, 2 – A, 3 – Г.
ТЕМА: Похідна функції, її геометричний зміст.
Завдання скеровано на перевірку вміння розв’язувати задачі з використанням геометричного змісту похідної, обчислювати похідні функцій.
За геометричним змістом похідної, \(f'(x_0)=k.\)
Похідна функції в точці – це кутовий коєфіцієнт дотичної до графіка в точці \(x_0.\)
За умовою, дотична до графіка функції в точці \(x_0=3\) паралельна прямій \(y=1\mathord{,}5x+5.\) Паралельні прямі мають рівні кутові коєфіцієнти. Отже, $$ f'(x_0)=f'(3)=1\mathord{,}5. $$
\begin{gather*} g(x)=\frac{18}{x}-f(x),\\[6pt] g'(x)=-\frac{18}{x^2}-f'(x). \end{gather*}Похідна
Відповідь: \(-3\mathord{,}5.\)
ТЕМА: Перестановки, комбінації, розміщення. Комбінаторні правила суми та добутку.
Завдання скеровано на перевірку вміння розв’язувати задачі, використовуючи комбінації, комбінаторні правила добутку.
Кількість варіантів вибрати з \(9\) учнів і \(12\) учениць першого класу (всього \(21\) особа) одну дитину: $$ C_{21}^1=21. $$
Кількість варіантів вибрати з \(10\) учнів одного: $$ C_{10}^1=10, $$ а з \(8\) учениць одну: $$ C_8^1=8. $$
Оскільки вибір незалежний, вибрати \(1\) учня й \(1\) ученицю з одинадцятого класу можна \begin{gather*} 10\cdot 8=80 \end{gather*} варіантами.
Вибір одного першокласника та вибір учня разом з ученицею з одинадцятого класу не впливають один на одного, тобто є незалежними подіями. Тому загальну кількість можливостей визначаємо за комбінаторним правилом добутку: \begin{gather*} 80\cdot 21=1680 \end{gather*} варіантів.
Відповідь: \(1680.\)
ТЕМА: Тіла обертання. Многогранники.
Завдання скеровано на перевірку знання властивостей піраміди та сфери, формул для обчислення площі поверхні сфери й об’єму піраміди.
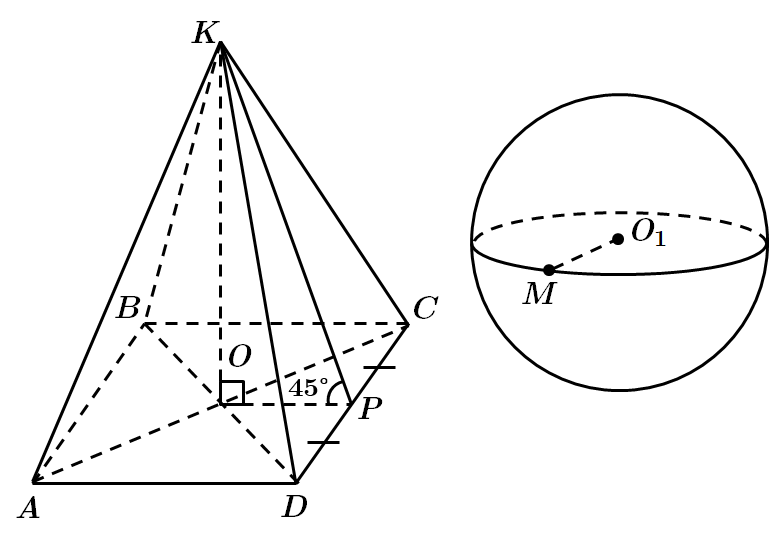
За умовою, радіус кола, описаного навколо квадрата \(ABCD\) – це $$ AO=BO=CO=DO=O_1M - $$ радіус сфери.
\begin{gather*} S_\text{сфери}=4\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}R^2=648\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi},\\[7pt] 4R^2=648,\\[7pt] R^2=162,\\[7pt] R=\sqrt{162}=\sqrt{81\cdot 2}=9\sqrt{2}\ \text{см}. \end{gather*}Об'єм піраміди $$ V=\frac 13S_\text{осн}\cdot H, $$ де
\(KP\ \perp\ DC\) – апофема піраміди (висота бічної грані). \(KO\ \perp\ (ABC)\), \(KP\) – похила на площину основи, \(OP\) – проєкція похилої \(KP.\) Звідси, \(\angle KPO=45^\circ\) – це кут між прямою \(KP\) і площиною основи.
У \(\Delta KOP\ (\angle O=90^\circ)\), \(\angle P=45^\circ\), тому трикутник рівнобедрений і $$ OP=OK=\frac 12 AD. $$
\(\Delta ADC\ (\angle D=90^\circ).\) \(AD=DC\), \(AC=18\sqrt{2}\) см. За теоремою Піфагора:
\begin{gather*} AD^2+DC^2=AC^2,\\[7pt] 2AD^2=(18\sqrt{2}\ \text{см})^2,\\[7pt] AD=18\ \text{см},\\[6pt] OK=OP=\frac 12AD=9\ \text{см},\\[6pt] V=\frac 13\cdot 324\ \text{см}^2\cdot 9\ \text{см}=972\ \text{см}^3. \end{gather*}Відповідь: \(972.\)
ТЕМА: Ірраціональні рівняння.
Завдання скеровано на перевірку вміння розв’язувати ірраціональні рівняння з параметром.
Зробімо заміну: \(\sqrt{5x-a}=t\ge 0\), тоді \(5x-a=t^2.\)
\begin{gather*} 10x-2a-7\sqrt{5x-a}+3=0,\\[7pt] 2(5x-a)-7\sqrt{5x-a}+3=0,\\[7pt] 2t^2-7t+3=0. \end{gather*}Розв'яжімо квадратне рівняння відносно \(t{:}\)
Сума коренів:
Отже, за \(a=-0\mathord{,}875\) сума коренів рівняння дорівнює \(1\mathord{,}5.\)
Відповідь: \(-0\mathord{,}875.\)