Розділ: Національний мультитест з математики
Тест: Тренувальні мультитести НМТ 2026
Блок: Варіант 11
Кількість завдань: 22
ТЕМА: Текстові задачі.
Завдання скеровано на перевірку вміння розв’язувати текстові задачі арифметичним способом.
Диню розрізали на \(6\) рівних частин. Кожна із цих частин становить \(\frac 16\) від усієї дині.
Якщо з'їли \(2\) частини, то залишилося \(4.\) Вони становлять $$ \frac 46=\frac 23 $$ від усієї дині.
Відповідь: А.
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знань властивостей ромба та рівнобедреного трикутника.
\(ABCD\) – ромб, тому \(AB=BC=CD=DA.\)
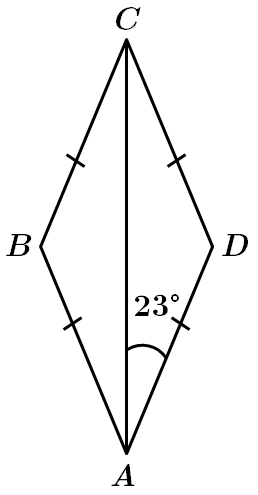
Отже, \(\Delta ADC\) – рівнобедрений з основою \(AC.\) За властивістю рівнобедреного трикутника:
Або можна обчислити більший кут ромба іншим способом. За властивістю ромба, \(AC\) – бісектриса кута \(A{:}\) $$ \angle BAD=2\cdot 23^\circ=46^\circ. $$
Сума сусідніх кутів будь-якого паралелограма (ромб – паралелограм) дорівнює \(180^\circ.\) Отже, $$ 180^\circ-46^\circ=134^\circ. $$
Відповідь: B.
ТЕМА: Текстові задачі.
Завдання скеровано на перевірку вміння визначати число за його частиною, розв’язувати текстові задачі арифметичним способом.
Клієнт банку зняв \(0\mathord{,}2\) від суми, що була на рахунку. Залишилось \(0\mathord{,}8\) від цієї суми – \(4800\) грн.
– це сума, що була на рахунку.
Отже, $$ 6000-4800=1200\ \text{грн} $$ було знято з рахунку.
Відповідь: Б.
ТЕМА: Квадратні рівняння.
Завдання скеровано на перевірку вміння розв’язувати квадратні рівняння.
А
\begin{gather*} x^2+2x+1=0,\\[7pt] (x+1)^2=0,\\[7pt] x=-1 \end{gather*}Рівняння має один корінь.
Б
\begin{gather*} x^2+2x+3=0,\\[7pt] x^2+2x+1+2=0,\\[7pt] x^2+2x+1=-2,\\[7pt] (x+1)^2=-2,\\[7pt] x\in \varnothing. \end{gather*}Рівняння коренів не має.
В
\begin{gather*} x^2+2x=0,\\[7pt] x(x+2)=0,\\[7pt] x=0\ \text{або}\ x=-2 \end{gather*}Рівняння має два різні дійсні корені.
Г
\begin{gather*} x^2+4=0,\\[7pt] x^2=-4,\\[7pt] x\in \varnothing. \end{gather*}Рівняння коренів не має.
Д
\begin{gather*} -x^2-2x-1=0,\\[7pt] x^2+2x+1=0,\\[7pt] x=1. \end{gather*}Рівняння має один корінь.
Відповідь: В.
ТЕМА: Елементарні геометричні фігури на площині та їхні властивості.
Завдання скеровано на перевірку знання властивостей і видів кутів.
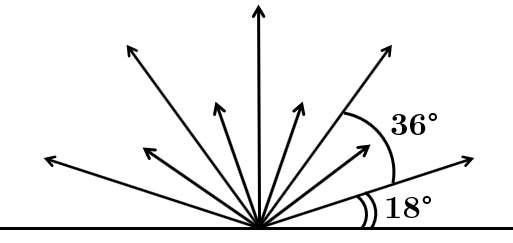
Розгорнутий кут поділено на \(10\) рівних частин. Градусна міра кожного з-поміж цих кутів $$ 180^\circ: 10=18^\circ. $$
Градусна міра кута між довгими стрілками складається з двох градусних мір кутів між довгою і короткою стрілкою.
Отже,
$$ 18^\circ\cdot 2=36^\circ. $$Відповідь: Г.
ТЕМА: Функціональна залежність.
Завдання скеровано на перевірку вміння визначати властивості числових функції.
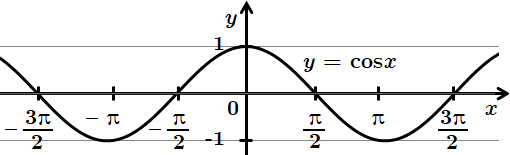
На рисунку зображено графік функції на проміжку \([-5; 4].\)
Функція набуває додатних значень там, де графік проходить вище від осі \(Ox.\) Це відповідає \(x\) із проміжку \([-5; -1).\)
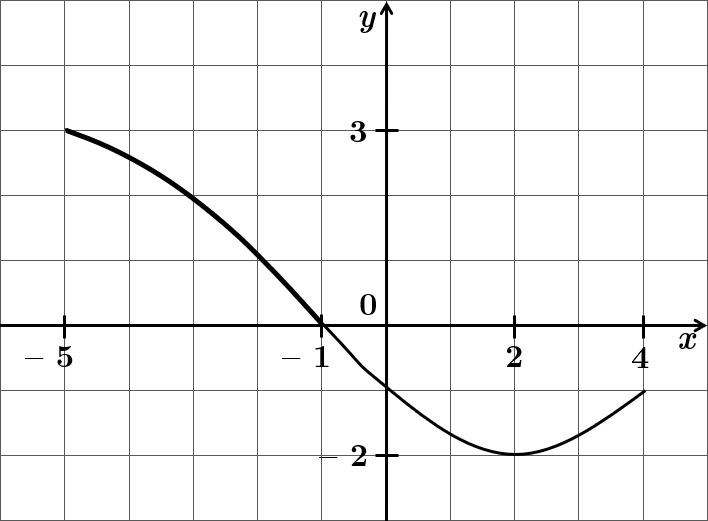
Відповідь: Б.
ТЕМА: Дійсні числа та дії з ними.
Завдання скеровано на перевірку вміння виконувати дії з раціональними числами, використовувати властивості модуля.
Спростімо вираз
за формулою різниці квадратів $$ (a-b)(a+b)=a^2-b^2. $$
Підставимо в умову:
$$ \left|\frac{-50}{3\mathord{,}5+6\mathord{,}5}\right|=\left|\frac{-50}{10}\right|=|-5|=5. $$За властивістю модуля числа:
$$ |a|=\left[\begin{array}{l} a,\ \text{якщо}\ a\ge 0, \\ -a,\ \text{якщо}\ a\lt 0. \end{array}\right. $$Відповідь: Д.
ТЕМА: Прямі та площини в просторі.
Завдання скеровано на перевірку вміння застосовувати означення, ознаки та властивості паралельних прямих.
За властивістю паралельності прямих \(AB\ ||\ CD\), \(CD\ ||\ C_1D_1\), \(AB\ ||\ C_1D_1\), \(AB\ ||\ A_1B_1\) (як протилежні сторони квадратів).
Отже, прямих, що проходять через ребра куба і є паралельними прямій \(AB\), – три \((CD\), \(\ C_1D_1\), \(\ A_1B_1).\)
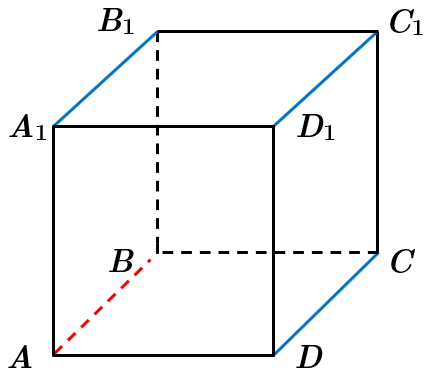
Відповідь: Г.
ТЕМА: Трикутники.
Завдання скеровано на перевірку вміння застосовувати означення, ознаки та властивості трикутників різних видів, знання властивостей медіани й висоти трикутника.
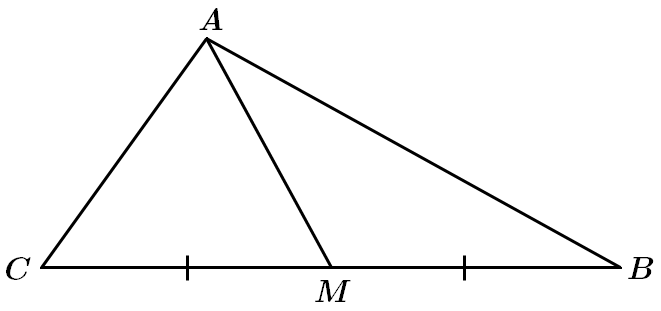
I. \(AM\) – медіана. Вона може дорівнювати довжині сторони \(BC\), але не обов'язково. Твердження неправильне.
II. Відстанню від точки \(A\) до прямої \(BC\) є довжина перпенидкуляра з точки \(A\) до \(BC.\)
У довільному трикутнику медіана не є висотою, а тому твердження неправильне. Таку властивість має медіана рівнобедреного трикутника, яку проведено до основи.
III. Точка \(M\) – середина сторони \(BC\), тож вона рівновіддалена від точок \(B\) i \(C.\) Твердження правильне.
Відповідь: B.
ТЕМА: Тригонометричні вирази.
Завдання скеровано на перевірку вміння виконувати тотожні перетворення тригонометричних виразів, обчислювати їхнє значення.
За основною тригонометричною тотожністю:
Обчислімо значення виразу:
Відповідь: A.
ТЕМА: Раціональні вирази.
Завдання скеровано на перевірку вміння виконувати тотожні перетворення раціональних виразів, застосовувати формули скороченого множення.
Щоб спростити вираз, застосуймо формулу скороченого множення \((a-b)^2=a^2-2ab+b^2{:}\)
Відповідь: B.
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивостей трапеції, її середньої лінії, співвідношення між сторонами й кутами прямокутного трикутника.
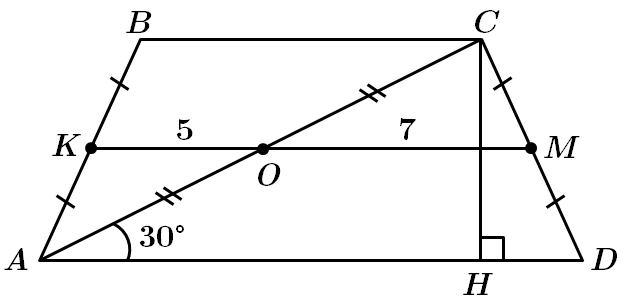
За властивістю середньої лінії трапеції: $$ KM\ ||\ BC\ ||\ AD, $$
\begin{gather*} KM=\frac 12(BC+AD). \end{gather*}У \(\Delta ABC\ KO\) – середня лінія. За властивістю середньої лінії: $$ KO=\frac 12BC. $$ Oтже, \(BC=10\) см.
У \(\Delta ACD\ OM\) – середня лінія, тому
\begin{gather*} OM=\frac 12AD,\\[6pt] AD=14\ \text{см}. \end{gather*}Побудуймо \(CH\ \perp\ AD.\)
У \(\Delta ACH\ (\angle H=90^\circ)\)
Площа трапеції
Відповідь: Г.
ТЕМА: Логарифмічні рівняння.
Завдання скеровано на перевірку вміння розв’язувати логарифмічні рівняння.
\begin{gather*} 1-\log_{0\mathord{,}5}x=3,\\[7pt] \log_{0\mathord{,}5}x=1-3,\\[7pt] \log_{0\mathord{,}5}=-2. \end{gather*}За означенням логарифма:
\begin{gather*} x=0\mathord{,}5^{-2},\\[6pt] x=\left(\frac 12\right)^{-2},\\[6pt] x=2^2,\\[7pt] x=4. \end{gather*}Корінь рівняння \(4\in [3; 10).\)
Відповідь: Г.
ТЕМА: Тригонометричні рівняння.
Завдання скеровано на перевірку вміння розв’язувати найпростіші тригонометричні рівняння.
\begin{gather*} \sin \frac{x}{2}=1,\\[6pt] \frac x2=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{2}+2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}n,\ n\in Z,\\[6pt] x=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}+4\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}n,\ n\in Z. \end{gather*}Корені рівняння:
якщо \(n=0\), $$ x=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}+4\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\cdot 0=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}, $$ якщо \(n=-1\),
Відповідь: B.
ТЕМА: Первісна та визначений інтеграл.
Завдання скеровано на перевірку вміння визначати первісну, використовуючи її основні властивості.
За таблицею первісних: функція \(f(x)=e^x\) має первсну \(F(x)=e^x + C\), функція \(f(x)=1\) має первісну \(F(x)=x+C\), де \(C\) – стала.
Визначмо загальний вигляд первісних для функції \(f(x)=2e^x+1\mathord{:}\) $$ F(x)=2e^x+x+\mathrm{C}. $$
Відповідь: Б.
ТЕМА: Функціональна залежність. Степеневі, тригонометричні функції.
Завдання скеровано на перевірку вміння встановлювати властивості числових функцій, заданих формулою.
1. \(y=-x^3\) набуває всіх значень із проміжку \((-\infty; +\infty).\)
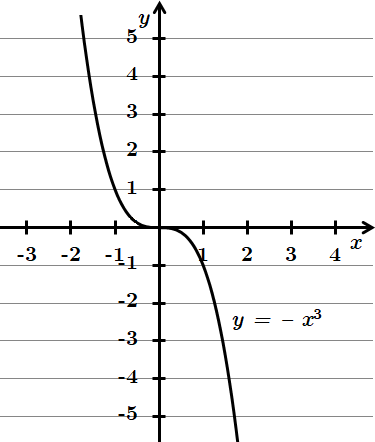
Отже, правильна відповідь – Д.
2. \(y=\sqrt{x}\) має лише одну спільну точку з колом \(x^2+y^2=9\) (центра кола \((0; 0)\) і радіус \(3\)).
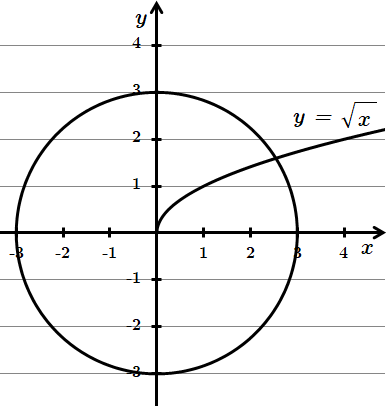
Отже, правильна відповідь – Б.
3. \(y=\cos x.\) З тригонометричних функцій \(y=\sin x\), \(y=\cos x\), \(y=\mathrm{tg}\ x\), \(y=\mathrm{ctg}\ x\) тільки одна функція парна – це \(y=\cos x\). Всі інші тригонометричні функції – непарні.
Функція \(y=\cos(x)\) є парною, бо для неї виконується рівність \(\cos(-x)=\cos(x)\), її графік є симетричним відносно осі \(Oy.\) Отже, правильна відповідь – А.
Відповідь: 1 – Д, 2 – Б, 3 – А.
ТЕМА: Дійсні числа. Раціональні, ірраціональні, тригонометричні й логарифмічні числа.
Завдання скеровано на перевірку вміння виконувати тотожні перетворення степеневих, логарифмічних і тригонометричних виразів.
1. За властивістю степенів: $$ a^n:a^m=a^{n-m}, $$
$$ \frac{3}{3^{-3}}=3\cdot 3^{3}=3^{1+3}=3^4=81. $$Отже, правильна відповідь – Д.
2. За властивістю логарифмів:
\begin{gather*} \log_{a^m}b=\frac 1m\cdot \log_ab,\\[6pt] \log_ab^n=n\cdot \log_ab. \end{gather*}Отже,
Правильна відповідь – Б.
3. Спростiмо вираз за формулою різниці квадратів: $$ (a-b)(a+b)=a^2-b^2. $$ \(\cos 30^\circ=\frac{\sqrt{3}}{2}\) – табличне значення.
Отже, правильна відповідь – A.
Відповідь: 1 – Д, 2 – Б, 3 – A.
ТЕМА: Чотирикутники. Коло та круг.
Завдання скеровано на перевірку знання властивостей кола, круга та їхніх елементів, властивостей прямокутника.
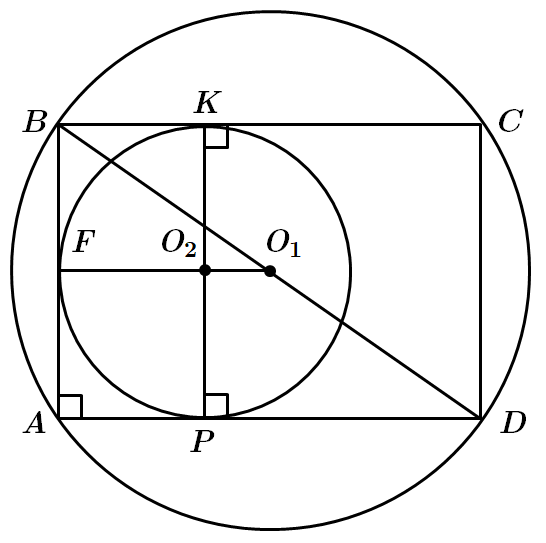
Площа круга із центром у точці \(O_1\) дорівнює \(625\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\) см\(^2.\)
1. Відстань від \(O_2\) до сторони \(BC{:}\) $$ O_2K=\frac 12BA=\frac 12\cdot 30=15\ \text{см}. $$
\(O_2K\ \perp\ BC\), а \(KP\) – діаметр кола.
Правильна відповідь – B.
2. Центр кола \(O_1\), описаного навколо прямокутника \(ABCD\), лежить на середині діагоналі \(BD.\)
\begin{gather*} O_1B=O_1D=25\ \text{см},\\[7pt] BD=50\ \text{см}. \end{gather*}У \(\Delta ABD\) \((\angle A=90^\circ)\) за теоремою Піфагора:
Правильна відповідь – Д.
3. Відстань $$ O_1O_2=FO_1-FO_2, $$ де \(FO_2\) – радіус кола із центром у точці \(O_2.\)
\begin{gather*} FO_2=15\ \text{см}.\\[7pt] OO_1=20\ \text{см}-15\ \text{см}=5\ \text{см}. \end{gather*}Правильна відповідь – A.
Відповідь: 1 – B, 2 – Д, 3 – A.
ТЕМА: Первісна й визначений інтеграл.
Завдання скеровано на перевірку вміння застосовувати формулу Ньютона – Лейбница для обчислення визначеного інтеграла, обчислювати площу плоских фігур за допомогою інтеграла.
Площу зафарбованої фігури можна обчислити за допомогою визначеного інтеграла: $$ S=\mathop{\int}\limits_a^b \left(f(x)-g(x)\right) dx, $$ де \(f(x)\) – це функція, графік якої обмежує фігуру згори, а \(g(x)\) – функція, графік якої обмежує фігуру знизу.
Відповідь: \(5\mathord{,}1.\)
ТЕМА: Перестановки, комбінації, розміщення. Комбінаторні правила суми та добутку.
Завдання скеровано на перевірку вміння розв’язувати задачі, використовуючи комбінації та комбінаторні правила добутку для розв’язку комбінаторних задач.
На ринку є \(10\) моделей кольорових принтерів. Вибрати \(2\) з них можна \(\mathrm{C}_{10}^2\) варіантами.
Вибрати \(3\) принтери з \(8\) монохромних моделей можна \(\mathrm{C}_8^3\) варіантами.
Підприємство планує купити і \(2\) кольорові, і \(3\) монохромні. Кількість варіантів такого вибору визначають за комбінаторним правилом добутку:
Відповідь: \(2520.\)
ТЕМА: Тіла обертання.
Завдання скеровано на перевірку знання властивостей конуса та сфери, формул для обчислення площі поверхні сфери й об’єму конуса.
\begin{gather*} S=4\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}R^2=300\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\ \text{см}^2,\\[7pt] 4R^2=300\ \text{см}^2,\\[7pt] R^2=75\ \text{см}^2,\\[7pt] R=OC=5\sqrt{3}\ \text{см}. \end{gather*}
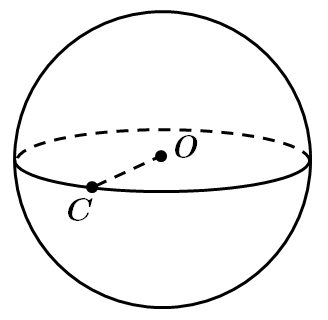
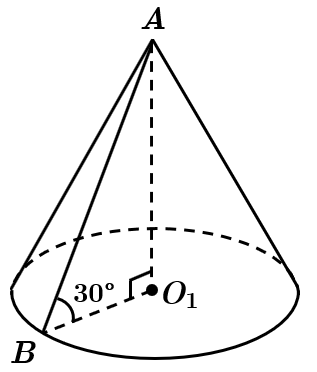
Радіус основи конуса \(O_1B=CO\) – радіусу сфери: $$ O_1B=5\sqrt{3}\ \text{см}. $$
У \(\Delta AO_1B\ (\angle O_1=90^\circ)\).
Об'єм конуса визначмо за формулою $$ V=\frac 13S_\text{осн}H=\frac 13\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}R^2H, $$ де
Відповідь: \(125.\)
ТЕМА: Лінійні рівняння.
Завдання скеровано на перевірку вміння розв’язувати лінійні рівняння з параметром.
Розв'яжімо лінійне рівняння:
\begin{gather*} ax-5=a+2x,\\[7pt] ax-2x=a+5,\\[7pt] x(a-2)=a+5. \end{gather*}Якщо \(a=2\), рівняння не має коренів \((x\cdot 0=7).\)
Якщо \(a\ne 2\), корінь є. Його визначають так: $$ x=\frac{a+5}{a-2}. $$
Корінь рівняння буде додатним, якщо $$ \frac{a+5}{a-2}\gt 0. $$
Розв'яжімо методом інтервалів:
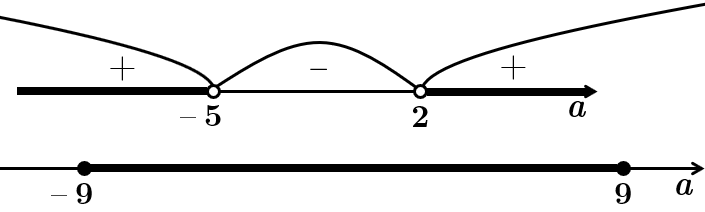
На проміжку \(a\in [-9; 9]\) рівняння має розв'язок, якщо \(a\in [-9; -5)\cup (2; 9].\)
Цілі значення \(a\) із цього проміжку: \(-9\), \(-8\), \(-7\), \(-6\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\), \(9.\) Тобто цілих значень \(a\) \(11.\)
Відповідь: \(11.\)