Розділ: Національний мультитест з математики
Тест: Тренувальні мультитести НМТ 2026
Блок: Варіант 3
Кількість завдань: 22
ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки аналізу.
Завдання перевіряє вміння обчислювати ймовірності випадкових подій, користуючись її означенням.
Монет номіналом менше \(50\) копійок – \(17\) (\(5\) монет номіналом \(10\) копійок, \(12\) монет – по
\(25\) копійок). Усього монет – \(20.\)
Отже, ймовірність того, що номінал навмання взятої монети менше \(50\) копійок становить: $$ P=\frac{17}{20}. $$
Відповідь: A.
ТЕМА: Алгебра і початки аналізу. Числа та вирази.
Завдання перевіряє вміння розв’язувати текстові задачі арифметичним способом.
\(1\) хвилина = \(60\) секунд.
За \(4\) секунди машина робить \(3\) копії.
Отже, \(60 : 4 \cdot 3 = 45\) копій.
Відповідь: A.
ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури на площині та їхні властивості.
Завдання перевіряє знання властивостей суміжних та вертикальних кутів, теореми про суму кутів трикутника.
\(\angle BAC=180^\circ-120^\circ=60^\circ\) – суміжний до кута \(120^\circ.\)
\(\angle ACB=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\) – вертикальні кути.
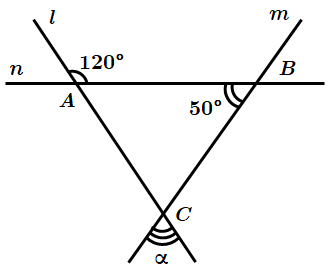
Сума кутів \(\Delta ABC\) дорівнює \(180^\circ\), тому $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}=180^\circ-(50^\circ+60^\circ)=70^\circ. $$
Відповідь: Г.
ТЕМА: Алгебра і початки аналізу. Рівняння.
Завдання перевіряє вміння розв’язувати лінійні рівняння.
Помножимо обидві частини рівняння на \(3.\)
\(5x+8=3\), \(5x=-5\), \(x=-1.\)
Відповідь: Д.
ТЕМА: Геометрія. Стереометрія. Тіла обертання.
Це завдання перевіряє знання властивостей, формули площі поверхні циліндра.
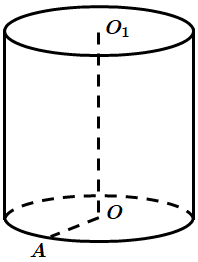
Площа бічної поверхні $$ S_\text{бічної}=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}RH=C\cdot H $$ де \(C\) – довжина кола його основи, \(H\) – висота циліндра.
$$ H=\frac{S_\text{бічної}}{C}=\frac{24\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{4\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}=6. $$
Відповідь: Г.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком.
Нуль функції – значення \(x\), при якому \(y=0.\) На рисунку – це точка перетину графіка з віссю \(x.\) Отже, \(x=1.\)
Відповідь: B.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання перевіряє знання властивостей прямокутника, вміння знаходити периметр.
$$ AB : BC = 2 : 5. $$ Нехай \begin{gather*} AB=CD=2x\ \text{см},\\[7pt] BC=AD=5x\ \text{см},\\[7pt] P_{ABCD}=2(AB+BC). \end{gather*} Отже, \begin{gather*} 2(2x+5x)=28\\[7pt] 14x=28\\[7pt] x=2. \end{gather*} Більша сторона прямокутника $$ BC=5x=5\cdot 2=10\ \text{см}. $$
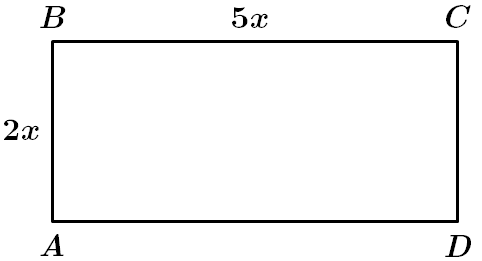
Відповідь: A.
ТЕМА: Алгебра і початки аналізу. Числа та вирази.
Це завдання перевіряє вміння виконувати тотожні перетворення раціональних виразів, знання формул скороченого множення.
Спростимо вираз за формулою "різниці квадратів":
Відповідь: Б.
ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Показникові рівняння.
Це завдання перевіряє вміння розв'язувати показникові рівняння.
\(3^{7x}=9,\) \(3^{7x}=3^2\), \(7x=2.\)
\(x=2:7\), \(x=0\mathord{,}28\text{...}\), \(x\approx 0\mathord{,}3\) якщо округлити до десятих.
Відповідь: B.
ТЕМА: Алгебра і початки аналізу. Функції. Похідні елементарних функцій.
Це завдання перевіряє вміння знаходити похідні елементарних функцій, правил знаходження похідних.
За таблицею похідних: \begin{gather*} (x^n)'=n\cdot x^{n-1},\\[6pt] (\mathrm{tg}x)'=\frac{1}{\cos^2x}. \end{gather*}
Отже,
Відповідь: Г.
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.
Завдання перевіряє вміння розв’язувати системи лінійних нерівностей.
Розв'яжемо систему нерівностей \begin{gather*} \left\{\begin{array}{l} 6\gt 2x,\\ 7x-28\le 0, \end{array}\right.\ \ \left\{\begin{array}{l} x\lt 3,\\ 7x\le 28, \end{array}\right.\ \ \left\{\begin{array}{l} x\lt 3,\\ x\le 4. \end{array}\right.\\[7pt] x\in (-\infty; 3). \end{gather*}
Відповідь: A.
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Функції. Дійсні числа. Логарифмічні вирази. Логарифмічна функція.
Це завдання перевіряє вміння порівнювати дійсні числа, виконувати тотожні перетворення логарифмічних виразів.
Функція \(y=\log_2\frac 13\) зростаюча, оскільки основа логарифмічної функції – число \(2\gt 1.\) Отже, більшому значенню аргумента відповідає більше значення функції.
\begin{gather*} \log_2\frac 14\lt \log_2\frac 13\lt \log_2\frac 12\\[6pt] \log_22^{-2}\lt \log_2\frac 13\lt \log_22^{-1}\\[6pt] -2\lt\log_2\frac 13\lt -1. \end{gather*}З наведених проміжків число належить \((-3; -1).\)
Відповідь: Б.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком.
1. Графік проходить через точку \((3; -2).\) Отже, 1 – Д.
2. Функція набуває лише додатних значень. Отже, 2 – Г.
3. Функція має лише один нуль (одна точка перетину з віссю \(Ox\)).
Отже, 3 – А.
Відповідь: 1 – Д, 2 – Г, 3 – А.
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Це завдання перевіряє вміння виконувати дії з раціональними числами, логарифмічними виразами, порівнювати числа, знання властивостей модуля числа.
1. \(a^2=(-0\mathord{,}6)^2=0\mathord{,}36\) належить проміжку \([0; 0\mathord{,}5].\) Отже, 1 – B.
2. \(|a|=|-0\mathord{,}6|=0\mathord{,}6=\frac 35.\) Отже, 2 – A.
3. \(\log_2(4+a)=\log_2(4-0\mathord{,}6)=\log_2 3\mathord{,}4\),
Відповідь: 1 – B, 2 – A, 3 – Д.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Завдання перевіряє вміння застосовувати властивості трикутників до розв’язування планіметричних задач, знаходити довжину середньої лінії трапеції, знання теореми Піфагора.
1.
\(\angle A=90^\circ\), \(AC\) бісектриса, \(\angle BAC=45^\circ.\)
\(\Delta ABC\) – рівнобедрений \((\angle B=90^\circ)\), \(AB=BC=6\) см.
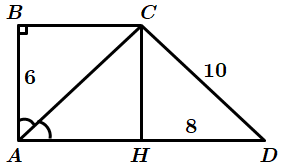
Отже, 1 – A.
2. \(CH\perp AD\), \(HD\) – проекція \(CD\) на \(AD.\)
У \(\Delta CHD\ (\angle H=90^\circ)\), \(CH=6\) см, \(HD=8\) см (єгипетський).
Отже, 2 – Б.
3. \(ABCH\) – квадрат.
\(BC=AH=6\) см, \(AD=AH+HD=14\) см.
Cередня лінія трапеції $$ \frac{BC+AD}{2}=\frac{6+14}{2}=10\ \textit{см}. $$ Отже, 3 – Г.
Відповідь: 1 – A, 2 – Б, 3 – Г.
ТЕМА: Алгебра і початки аналізу. Функції. Числові послідовності. Рівняння.
Це завдання перевіряє знання основної властивості арифметичної прогресії; уміння розв'язувати квадратні рівняння.
Задана арифметична прогресія: \begin{gather*} a_1=x^2-4,\\[7pt] a_2=3-5x,\\[7pt] a_3=2-3x. \end{gather*}
За властивістю арифметичної прогресії: \begin{gather*} a_2=\frac{a_1+a_3}{2},\\[6pt] 3-5x=\frac{x^2-4+2-3x}{2},\\[6pt] 6-10x=x^2-3x-2,\\[7pt] x^2+7x-8=0,\\[6pt] x_1=\frac{-7+9}{2}=1,\\[6pt] x_2=\frac{-7-9}{2}=-8. \end{gather*} Від'ємне значення \(x=-8.\)
Відповідь: \(-8.\)
ТЕМА: Алгебра та початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи статистики.
Це завдання перевіряє вміння обчислювати ймовірність випадкових подій.
Нехай \(P_1\) – ймовірність того, що спортсмен влучить у мішень, а \(P_2\) – ймовірність того, що не влучить.
За умовою \(P_1=7P_2\) та \(P_1+P_2=1.\)
Розв'яжемо систему рівнянь:
\begin{gather*} \left\{\begin{array}{l} P_1=7P_2,\\ P_1+P_2=1, \end{array}\right.\ \ \left\{\begin{array}{l} P_1=7(1-P_1),\\ P_2=1-P_1. \end{array}\right. \end{gather*}Розв'яжемо рівняння
\begin{gather*} P_1=7(1-P_1),\\[7pt] P_1=7-7P_1,\\[7pt] 8P_1=7,\\[6pt] P_1=\frac 78=0\mathord{,}875. \end{gather*}Відповідь: \(0\mathord{,}875.\)
