Розділ: Національний мультитест з математики
Тест: Тренувальні мультитести НМТ 2026
Блок: Варіант 8
Кількість завдань: 22
ТЕМА: Тіла обертання.
Завдання скеровано на перевірку вміння розв’язувати задачі, зокрема практичного змісту, знання видів тіл обертання, як-от конуса.
На рисунку зображено частину поверхні конуса.
Відповідь: В.
ТЕМА: Вибіркові характеристики.
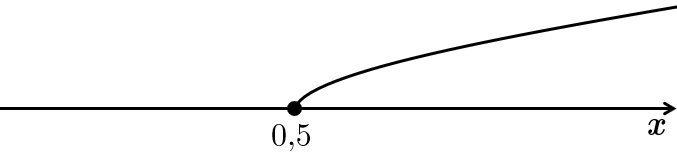
Завдання скеровано на перевірку вміння аналізувати статистичні дані в графічній і текстовій формі.
М'яч перебував на висоті не менше ніж \(3\) м з \(1\) с до \(5\) с. Тобто протягом \(4\) с.
Відповідь: В.
ТЕМА: Координати і вектори в просторі. Геометричні переміщення.
Завдання скеровано на перевірку вміння визначати координати середини відрізка, знання основних видів геометричних переміщень, зокрема симетрії відносно точки.
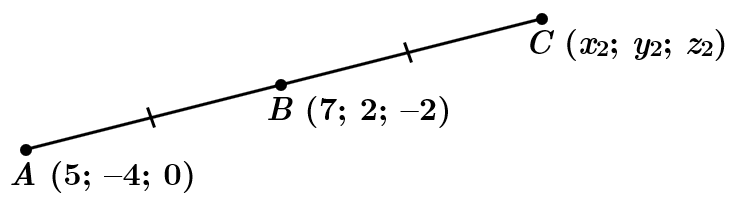
Точка \(C\) симетрична точці \(A\) відносно точки \(B\), якщо точки лежать на одній прямій і \(AB=BC.\)
Скористаймося формулою визначення координат середини відрізка:
\begin{gather*} x=\frac{x_1+x_2}{2},\\[6pt] y=\frac{y_1+y_2}{2},\\[6pt] z=\frac{z_1+z_2}{2}, \end{gather*}де кінці відрізка мають координати: \((x_1; y_1; z_1)\), \((x_2; y_2; z_2).\)
\(A(5; -4; 0)\), \(B(7; 2; -2)\), \(C(x_2; y_2; z_2).\)
Отже, правильна відповідь – \(C(9; 8; -4).\)
Відповідь: Д.
ТЕМА: Лінійні нерівності.
Завдання скеровано на перевірку вміння розв’язувати найпростіші лінійні нерівності.
\begin{gather*} 1\le 2x\\[7pt] x\ge \frac 12\\[7pt] x\ge 0\mathord{,}5. \end{gather*}
$$ x\in [0\mathord{,}5; +\infty). $$
Відповідь: Б.
ТЕМА: Похідна функції. Таблиця похідних і правила диференціювання.
Завдання скеровано на перевірку вміння визначати похідні функцій і похідну суми двох функцій.
За правилом визначення похідної суми:
$$ (f(x)+g(x))'=f'(x)+g'(x) $$і похідної степеневої функції:
$$ (x^n)'=n\cdot x^{n-1} $$визначаємо похідну функції \(y=x^3-5.\)
Похідна сталої функції \(\mathrm{c}'=0.\) Отже, \(5'=0.\)
Відповідь: Д.
ТЕМА: Коло та круг.
Завдання скеровано на перевірку вміння застосовувати властивості кола для розв’язування планіметричних задач практичного змісту.
Градусна міра повного кута дорівнює \(360^\circ.\) Якщо поділити його на \(12\) рівних частин, то кожна з них дорівнюватиме \(30^\circ.\)
Кут між хвилинною і годинниковою стрілками на циферблаті містить \(5\) таких кутів $$ 30^\circ\cdot 5=150^\circ. $$
Відповідь: Б.
ТЕМА: Прямі та площини в просторі.
Завдання скеровано на перевірку знання аксіом стереометрії, взаємного розміщення прямих у просторі.
Скористаймося аксіомою паралельності: через точку, що не лежить на прямій, можна провести лише одну пряму, паралельну даній. Отже, через точку \(S\), яка не лежить на прямій \(AB\), можна провести лише одну пряму, паралельну даній.
Відповідь: Б.
ТЕМА: Раціональні вирази та їх перетворення.
Завдання скеровано на перевірку знання формул скороченого множення, уміння розкладати багаточлен на множники й виконувати тотожні перетворення раціональних виразів.
Для скорочення дробу розкладімо чисельник і знаменник на множники:
\begin{gather*} 25-x^2=5^2-x^2=(5-x)(5+x) \end{gather*}за формулою різниці квадратів.
У виразі
$$ x^2+5x=x(x+5) $$винесімо спільний множник за дужки:
Відповідь: Д.
ТЕМА: Логарифмічні вирази та їх перетворення.
Завдання скеровано на перевірку знання означення та властивостей логарифма, модуля числа.
За означенням логарифма: $$ 2=\lg 100. $$
За властивістю логарифмів:
Відповідь: A.
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивостей чотирикутників, зокрема квадрата, прямокутного трикутника, а також теореми Піфагора.
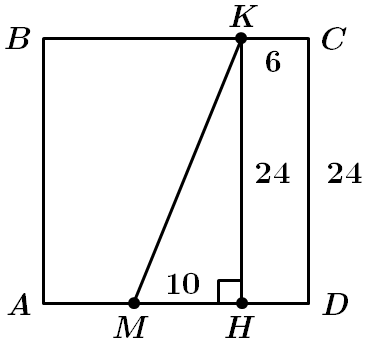
У квадраті \(ABCD\) \(AB=BC=CD=DA=24\) см.
\(AM:MD=1:2\), \(KC=6\) см.
Нехай \(AM=x\) см, \(MD=2x\) см. \(AD=AM+MD\), \(x+2x=24\) см, \(x=8\) см.
Отже, \(AM=8\) см, \(MD=16\) см.
Побудуймо \(KH\ \perp\ AD.\) \(KCDH\) – прямокутник, тому \(KC=HD=6\) см, \(CD=KH=24\) см. \(MH=MD-HD=16\ \textit{см}-6\ \textit{см}=10\) см.
Розгляньмо \(\Delta KHM\ (\angle H=90^\circ).\) Катети \(KH=24\) см і \(MH=10\) см. За теоремою Піфагора: \(a^2+b^2=c^2.\)
Визначмо довжину гіпотенузи:
Відповідь: В.
ТЕМА: Чотирикутники.
Завдання скеровано на перевірку знання властивостей чотирикутників, зокрема ромба.
I. Ромб – паралелограм, тому всі властивості паралелограма є властивостями ромба.
Отже, у будь-якому ромбі діагоналі точкою перетину діляться навпіл.
II. Периметр ромба не дорівнює сумі його діагоналей. Якби це твердження було правильним, то в \(\Delta ABC\) сума довжин двох сторін \((AB+BC)\) дорівнювала б довжині третьої сторони \(AC.\) А це суперечить нерівності трикутника.
III. Твердження правильне. Висота ромба \(BH\) удвічі більша за радіус \(OK\) вписаного кола.
Відповідь: Г.
ТЕМА: Лінійні, показникові та раціональні рівняння.
Завдання скеровано на перевірку вміння розв’язувати показникові та раціональні рівняння та їх системи.
Рівняння \(5^x=\sqrt{5}\) містить одну змінну. Розв'яжімо його, зводячи до однакової основи:
\begin{gather*} \sqrt{5}=5^{\frac 12},\\[6pt] \text{тому}\ 5^x=5^{\frac 12},\\[6pt] x=\frac 12. \end{gather*}Підставмо значення \(x\) у друге рівняння:
\begin{gather*} \frac{y+1}{2\cdot \frac 12+3}=\frac{1-4\cdot \frac 12}{2},\\[6pt] \frac{y+1}{1+3}=\frac{1-2}{2},\\[6pt] \frac{y+1}{4}=\frac{-1}{2}. \end{gather*}За основною властивістю пропорції: $$ \frac ab=\frac cd \rightarrow a\cdot d=b\cdot c. $$ Тому запишімо:
\begin{gather*} 2(y+1)=4\cdot (-1),\\[7pt] 2y+2=-4,\\[7pt] 2y=-4-2,\\[7pt] 2y=-6,\\[7pt] y=-6:2,\\[7pt] y=-3. \end{gather*}Маємо розв'язок \((x_0; y_0)\) як \(\left(\frac 12; -3\right).\)
Підставмо його у вираз:
Відповідь: А.
ТЕМА: Числові послідовності.
Завдання скеровано на перевірку розуміння геометричної прогресії, уміння застосовувати формулу \(n\text{-го}\) члена.
У геометричній прогресії \((b_n)\) за формулою \(n\text{-го}\) члена послідовності: $$ b_n=b_1\cdot q^{n-1}. $$ Спростімо вираз:
\begin{gather*} \frac{b_5}{b_7}=\frac{b_1\cdot q^4}{b_1\cdot q^6}=\frac{q^4}{q^6}=\frac{1}{q^2},\\[6pt] b_2=b_1\cdot q,\\[6pt] q=\frac{b_2}{b_1}=\frac{8}{32}=\frac 14,\\[6pt] q^2=\left(\frac 14\right)^2=\frac{1}{16}. \end{gather*}Отже,
$$ \frac{b_5}{b_7}=\frac{1}{q^2}=1:\frac{1}{16}=1\cdot \frac{16}{1}=16. $$Відповідь: Д.
ТЕМА: Первісна та визначений інтеграл.
Завдання скеровано на перевірку знання таблиці первісних, уміння застосовувати правила визначення первісних у точці.
Визначмо загальний вигляд первісної:
Первісну, яка проходить через точку \(A(0; 1)\), дізнаймося підставивши координати точки \(x=0\), \(F(0)=1\) у формулу загального вигляду первісної, щоб обчислити значення сталої \(C\mathord{:}\)
$$ 2\cdot 0^2-3\cdot 0 + C=1, $$$$ C=1. $$ Отже, \begin{gather*} F(x)=2x^2-3x+1. \end{gather*}
Відповідь: Б.
ТЕМА: Тригонометричні рівняння.
Завдання скеровано на перевірку вміння розв’язувати найпростіші тригонометричні рівняння.
Щоб визначити корінь рівняння, треба підставити значення \(x\) у рівняння. Після цього з'ясувати, за якого значення \(x\) рівняння стає правильною рівністю.
Якщо \(x=-\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{6}\mathord{:}\)
\begin{gather*} 2\sin\left(2\cdot \left(-\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{6}\right)\right)=-1,\\[6pt] 2\cdot \sin \left(-\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{3}\right)=-1,\\[6pt] 2\cdot \left(-\frac{\sqrt{3}}{2}\right)=-1,\\[6pt] \sqrt{3}\ne -1. \end{gather*}Отже, \(x=-\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{6}\) не є коренем рівняння.
Якщо \(x=-\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{3}\mathord{:}\)
\begin{gather*} 2\sin\left(2\cdot \left(-\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{3}\right)\right)=-1,\\[6pt] -2\cdot \sin \frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{2\pi}}{3}=-1,\\[6pt] \sin{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{3}=\frac 12,\\[6pt] \frac{\sqrt{3}}{2}\ne \frac 12. \end{gather*}Отже, \(x=-\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{3}\) не є коренем рівняння.
Якщо \(x=-\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{12}\mathord{:}\)
\begin{gather*} 2\sin\left(2\cdot \left(-\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{12}\right)\right)=-1,\\[6pt] -2\cdot \sin \frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{6}=-1,\\[6pt] -2\cdot \frac 12=-1. \end{gather*}Отже, \(x=-\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{12}\) – корінь рівняння.
Другий спосіб:
Якщо \(k=0\mathord{:}\)
$$ x=(-1)^{0+1}\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{12}+\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\cdot 0}{2}=-\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{12}. $$Це – корінь рівняння.
Відповідь: Д.
ТЕМА: Лінійні, квадратичні та логарифмічні функції.
Завдання скеровано на перевірку знання властивостей лінійної, квадратичної та логарифмічної функцій, уміння визначати область визначення, області значень, властивості числових функцій, заданих формулою.
1. \(y=2x-5\) – лінійна функція, її графік – пряма.
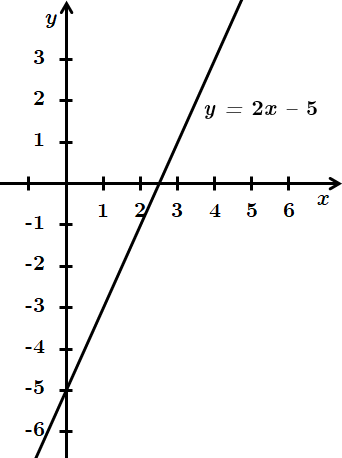
Графік функції має лише дві точки перетину з осями координат. Отже, правильна відповідь – А.
2. \(y=\log_3(x-5)\) – логарифмічна функція. Графік функції \(y=\log_3x\) перенесено паралельно вздовж осі \(Ox\) на \(5\) одиниць управо.
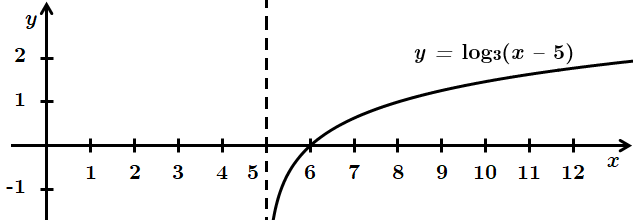
Областю визначення функції є проміжок \((5; +\infty).\) Отже, правильна відповідь – Г.
3. \(y=x^2-5\) – квадратична функція. Графік функції \(y=x^2\) перенесено вздовж осі \(Oy\) на \(5\) одиниць униз.
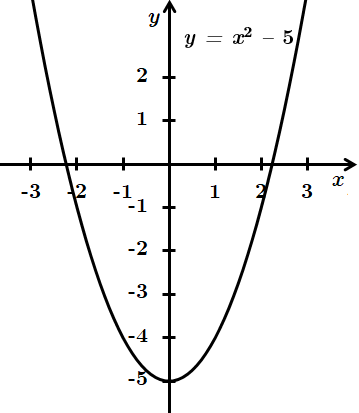
Областю значень функції є проміжок \([-5; +\infty).\) Отже, правильна відповідь – Б.
Відповідь: 1 – A, 2 – Г, 3 – Б.
ТЕМА: Дійсні числа та дії з ними.
Завдання скеровано на перевірку вміння виконувати дії з дійсними числами.
1. \(\sin\left(-\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{6}\right)=-\sin\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{6}=-\frac 12.\)
Функція \(y=\sin x\) – непарна, тому \(\sin (-x)=-\sin (x).\) Отже, правильна відповідь – А.
2. \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}-|\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}+2|=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}-(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}+2)=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}-\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}-2=-2.\)
За властивістю модуля числа: $$ |a|=\left\{\begin{array}{l} a,\ \text{якщо}\ a\ge 0,\\ -a,\ \text{якщо}\ a\lt 0. \end{array}\right. $$ \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}+2\gt 0\), тому \(|\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}+2|=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}+2.\)
Отже, правильна відповідь – Г.
3. \(\left(-\frac{1}{\sqrt{2}}\right)^2=\left(\frac{1}{\sqrt{2}}\right)^2=\frac{1^2}{(\sqrt{2})^2}=\frac 12.\) Отже, правильна відповідь – Б.
Відповідь: 1 – A, 2 – Г, 3 – Б.
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивостей трапеції, її середньої лінії, трикутників, уміння застосовувати теорему синусів.
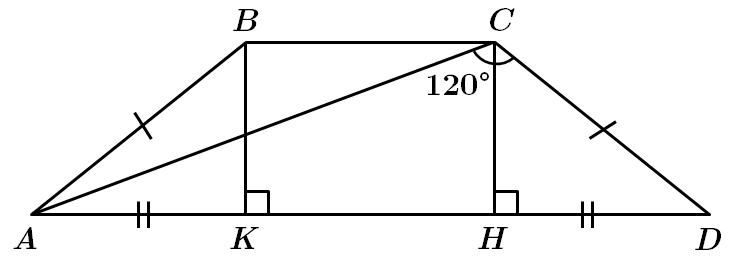
1. Середню лінію трапеції визначають за формулою $$ \frac{a+b}{2}, $$ де \(a\), \(b\) – основи. Отже, $$ \frac{BC+AD}{2}=\frac{12\ \textit{см}+30\ \textit{см}}{2}=21\ \textit{см}. $$
Правильна відповідь – В.
2. \(BK\ \perp\ AD.\) Проєкція \(AB\) на пряму \(AD\) – відрізок \(AK.\) \(ABCD\) – рівнобічна трапеція, тому \(AB=CD.\)
Рівні похилі \(BA\) i \(CD\) мають рівні проєкції \(AK=HD.\)
Правильна відповідь – А.
3. Коло, описане навколо трапеції \(ABCD\), це коло описане навколо \(\Delta ACD.\)
За наслідком з теореми синусів:
Правильна відповідь – Г.
Відповідь: 1 – В, 2 – А, 3 – Г.
ТЕМА: Функціональна залежність.
Завдання скеровано на перевірку вміння визначати властивості числових функцій, заданих формулою.
Функція \(y=f(x)\) є прямою пропорційністю, це означає, що вона має вигляд \(f(x)=kx\), де \(k\) – коефіцієнт пропорційності.
Графік функції проходить через точку \((2; 7)\). Підставимо ці координати в рівняння функції, щоб визначити \(k\mathord{:}\) \begin{gather*} 7=k\cdot 2,\\[6pt] k=\frac 72. \end{gather*}
Отже, функція \(f(x)\) має вигляд: \begin{gather*} f(x)=\frac 72x,\\[6pt] g(x)=3f(x)+\frac{|x|}{8}. \end{gather*}
Підставимо \(f(x)\) у вираз для \(g(x)\mathord{:}\)
\begin{gather*} g(x)=3\cdot \left(\frac 72x\right)+\frac{|x|}{8},\\[6pt] g(x)=\frac{21}{2}x+\frac{|x|}{8},\\[6pt] g(x)=10\mathord{,}5x+\frac{|x|}{8}. \end{gather*}Треба обчислити значення функції \(g(x)\) у точці з абсцисою \(x_0=-2.\)
\begin{gather*} g(-2)=10\mathord{,}5\cdot (-2)+\frac{|-2|}{8},\\[6pt] g(-2)=-21+\frac 28,\\[6pt] g(-2)=-21+\frac 14,\\[6pt] g(-2)=-21+0\mathord{,}25,\\[7pt] g(-2)=-20\mathord{,}75. \end{gather*}Відповідь: \(-20\mathord{,}75.\)
ТЕМА: Вибіркові характеристики.
Завдання скеровано на перевірку вміння аналізувати статистичні дані, наведені в графічній формі.
На діаграмі відображено відповіді учнів про те скільки вони витрачають годин на підготовку до контрольної роботи.
Не менш як дві години витратили:
\(2\) години – \(5\) учнів;
\(2\mathord{,}5\) години – \(4\) учні;
\(3\) години – \(2\) учні;
\(3\mathord{,}5\) та \(4\) години – по \(1\) учню.
Всього таких учнів – \(13.\)
Імовірність події \(A\) того, що навмання вибраний учень із цієї групи витратив не менш як дві години, визначмо за формулою: $$ P(A)=\frac kn, $$ де \(k\) – кількість сприятливих подій \((k=13)\), а \(n\) – кількість усіх рівноможливих подій \((n=20).\)
Отже, $$ P(A)=\frac{13}{20}=0\mathord{,}65. $$
Відповідь: \(0\mathord{,}65.\)
ТЕМА: Тіла обертання. Многогранники.
Завдання скеровано на перевірку знання основних видів многогранників, зокрема призми, властивості сфери, уміння застосовувати формули для обчислення площі поверхні сфери й об’єму призми.
\(S=64\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\) см\(^2\), \(AA_1=AC\), \(OK=O_1D.\)
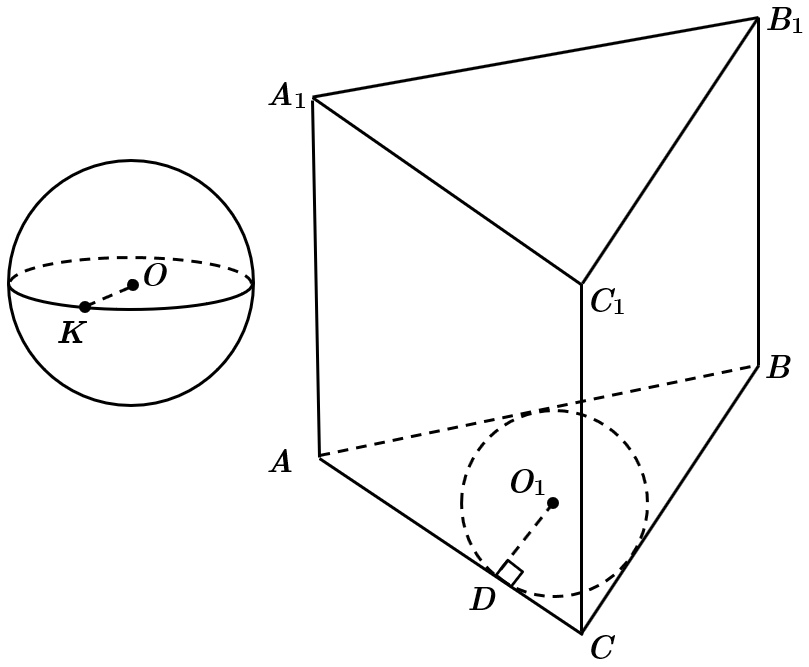
Площа поверхні сфери \(S=4\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}R^2=64\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\), \(R^2=16\ \textit{см}^2,\) \(R=4\) см.
За умовою задачі радіус сфери дорівнює радіусу кола, вписаного в основу призми. Отже, \(OK=O_1D=4\) см.
Призма – правильна, отже \(\Delta ABC\) – рівносторонній, a $$ r=O_1D=\frac{a}{2\sqrt{3}}, $$ де \(a\) – сторона трикутника. Тобто \begin{gather*} 4=\frac{AC}{2\sqrt{3}},\\[6pt] AC=8\sqrt{3}\ \textit{см}. \end{gather*}
Площу правильного трикутника обчислiмо за формулою:
Об'єм призми
\begin{gather*} S_\text{осн}=48\sqrt{3}\ \textit{см}^2,\\[6pt] H=AC=8\sqrt{3}\ \textit{см},\\[6pt] V=48\sqrt{3}\ \textit{см}^2\cdot 8\sqrt{3}\ \textit{см}=1152\ \textit{см}^3. \end{gather*}Відповідь: \(1152.\)
ТЕМА: Координати і вектори на площині.
Завдання скеровано на перевірку знання рівняння кола, властивостей прямокутної системи координат на площині, уміння застосовувати координати для розв’язання планіметричних задач.
За умовою:
Рівняння кола: \((x-x_0)^2+(y-y_0)^2=R^2.\)
Дано коло із центром у точці \((11+3a; -2)\) i радіусом \(7.\)
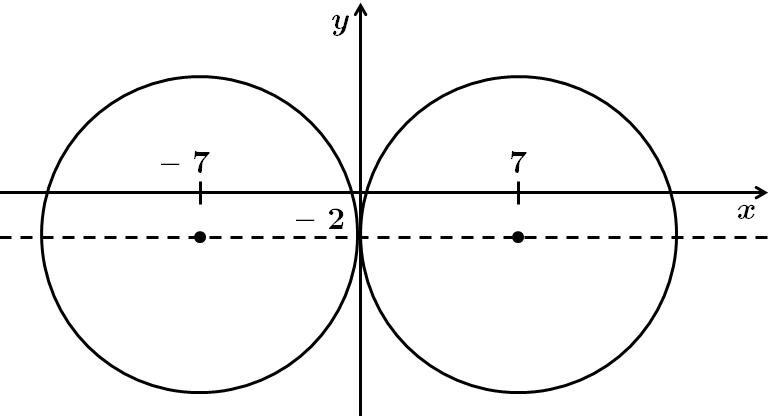
Унаслідок зміни параметра \(a\) коло переміщується вздовж прямої \(y=-2.\)
Для того, щоб коло дотикалося до осі \(Oy\), центр кола повинен бути в точці \((7; -2)\) або \((-7; -2).\)
Щоб коло перетинало двічі вісь ординат, абсциса \(a\) центра кола повинна бути цілим числом – розв'язком нерівності:
\begin{gather*} -7\lt 11+3a\lt 7,\\[7pt] -7-11\lt 3a\lt 7-11,\\[7pt] -18\lt 3a\lt -4,\\[6pt] -6\lt a\lt -1\frac 13. \end{gather*}Найменше ціле значення \(a=-5.\)
Відповідь: \(-5.\)