Розділ: Національний мультитест з математики
Тест: Тренувальні мультитести НМТ 2026
Блок: Варіант 9
Кількість завдань: 22
ТЕМА: Текстові задачі.
Завдання скеровано на перевірку вміння розв’язувати текстові задачі арифметичним способом.
Марко купив \(4\) набори з \(2\) ручок по \(25\) грн кожний і \(3\) набори з \(5\) ручок по \(40\) грн кожний.
За покупку Марко заплатив:
Відповідь: В.
ТЕМА: Дійсні числа та дії з ними.
Завдання скеровано на перевірку вміння виконувати дії з дійсними числами, знання властивостей модуля числа.
За властивістю модуля числа
\begin{gather*} |a|=\left\{\begin{array}{l} a,\ \text{якщо}\ a\ge 0,\\ -a,\ \text{якщо}\ a\lt 0. \end{array}\right.\\[7pt] 2\sqrt{2}\lt 3,\ \text{бо}\ \sqrt{2}\approx 1\mathord{,}41\\[7pt] 2\cdot 1\mathord{,}41 \lt 2\cdot 1\mathord{,}5. \end{gather*}Отже, \(|2\sqrt{2}-3|=-(2\sqrt{2}-3)=3-2\sqrt{2}.\)
Відповідь: A.
ТЕМА: Прямі та площини у просторі.
Завдання скеровано на перевірку знання аксіом стереометрії, взаємного розміщення прямих у просторі.
Застосуймо аксіому стереометрії: якщо дві прямі мають спільну точку, то через них можна провести лише одну площину.
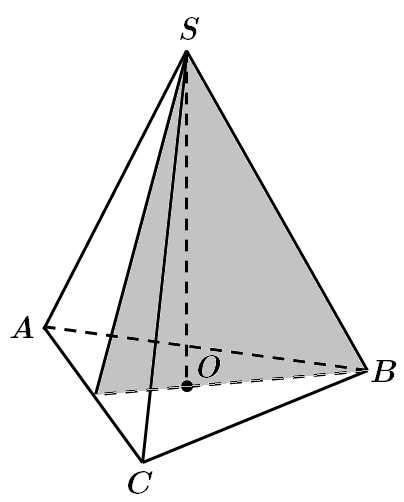
Отже, прямі \(SO\) i \(SB\) лежать в одній площині, бо мають спільну точку \(S.\)
За аксіомою стереометрії якщо дві прямі мають спільну точку, то через них можна провести площину, і до того ж, тільки одну.
Відповідь: Д.
ТЕМА: Відношення та пропорції. Відсотки. Основні задачі на відсотки. Текстові задачі.
Завдання скеровано на перевірку вміння розв’язувати основні задачі на відсотки, уміння визначати число за розміром його відсотка.
Ціна акції зросла на \(10\ \text{%}\) від початкової ціни.
Ціна тепер становить \(990\) грн і це \(110\ \text{%}\) від початкової ціни.
Визначмо \(x\) – початкову ціну акцій, яка становить \(100\ \text{%}.\) Складімо пропорцію:
\begin{gather*} x\ \textit{грн} - 100\ \ \text{%},\\[7pt] 990\ \textit{грн} - 110\ \ \text{%},\\[6pt] x=\frac{990\ \textit{грн}\cdot 100\ \text{%}}{110\ \text{%}}=900\ \textit{грн}. \end{gather*}Відповідь: A.
ТЕМА: Елементарні геометричні фігури на площині та їхні властивості.
Завдання скеровано на перевірку знання властивостей суміжних і вертикальних кутів.
Кути \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\) i \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}\) – вертикальні. За їхньою властивістю \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}.\)
За умовою \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}+\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}=70^\circ\), тому $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}=70^\circ:2=35^\circ. $$
Кути \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\) i \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\) – суміжні. За властивістю суміжних кутів:
\begin{gather*} \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}+\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}=180^\circ,\\[7pt] \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}=180^\circ - \style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}=180^\circ-35^\circ=145^\circ. \end{gather*}Відповідь: A.
ТЕМА: Показникова функція.
Завдання скеровано на перевірку вміння застосовувати властивості перетворення графіків функцій, знання властивостей показникової функції.
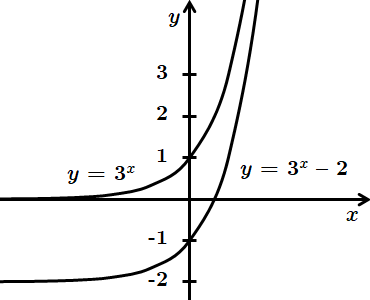
Графік функції \(y=3^x\) перенесли на \(2\) одиниці вниз уздовж осі \(y.\)
За властивістю елементарних перетворень переміщення вздовж осі \(y\) $$ f(x)\rightarrow f(x)+A, $$ де \(A\) – кількість одиниць, на які переміщують графік. Якщо \(A\gt 0\), то графік переміщують угору, а якщо \(A\lt 0\) – униз.
Запис \(y=3^x \rightarrow y=3^x-2\) означає, що графік функції перемістили вниз на \(2\) одиниці, бо \(A=-2.\)
Відповідь: А.
ТЕМА: Раціональні вирази та їх перетворення.
Завдання скеровано на перевірку вміння виконувати тотожні перетворення раціональних виразів.
\(12a\) i \(5a\) – подібні доданки. Щоб звести подібні доданки, треба додати їхні коефіцієнти й результат помножити на буквену частину.
Аналогічно спрощують \((1a-17a).\)
Відповідь: Д.
ТЕМА: Координати і вектори в просторі.
Завдання скеровано на перевірку вміння додавати і віднімати вектори, визначати модуль вектора.
Визначмо різницю векторів за формулами:
Визначимо модуль вектора \(\overrightarrow{c}\) за формулою:
Відповідь: Б.
ТЕМА: Показникові нерівності.
Завдання скеровано на перевірку вміння розв'язувати показникові нерівності, знання властивостей показникової функції.
\begin{gather*} \left(\frac 14\right)^{2x-6}\gt\frac{1}{16},\\[6pt] \left(\frac 14\right)^{2x-6}\gt\left(\frac{1}{4}\right)^2. \end{gather*}Функція \(y=\left(\frac 14\right)^x\) – спадна, тому більшому значенню функції відповідає менше значення аргументу:
\begin{gather*} a^{f(x)}\gt a^{g(x)},\\[7pt] 0\gt a\gt 1\Leftrightarrow f(x)\lt g(x),\\[7pt] 2x-6\lt 2,\\[7pt] 2x\lt 2+6,\\[7pt] 2x\lt 8,\\[7pt] x\lt 4. \end{gather*}
$$ x\in (-\infty; 4). $$
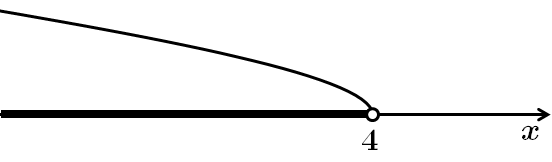
Відповідь: Д.
ТЕМА: Чотирикутники.
Завдання скеровано на перевірку знань властивостей паралелограмів, зокрема прямокутника.
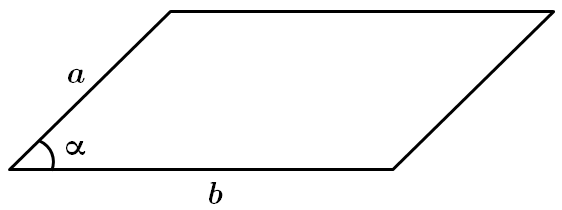
I. Периметром паралелограма називають суму довжин всіх його сторін. $$ P=2(a+b). $$ Якщо паралелограми мають рівні сторони, то вони мають рівні периметри.
Отже, твердження правильне.
II. Площу паралелограма визначають за формулою: $$ S=ab\cdot \sin \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}. $$ Отже, якщо паралелограми мають рівні сторони, але різні кути між ними, то й площі будуть різні. Тому, твердження про рівність площ паралелограмів із однаковими сторонами в разі різних кутів між ними неправильне.
III. Рівні діагоналі прямокутника не означають рівності сторін. Тільки за умови, що протилежні сторони також рівні, інші сторони прямокутників також будуть рівними між собою.
Отже, твердження неправильне.
Відповідь: А.
ТЕМА: Логарифмічні рівняння.
Завдання скеровано на перевірку вміння розв’язувати логарифмічні рівняння.
\begin{gather*} \log_5x+1=\log_5 12,\\[7pt] \log_5x=\log_5 12-1,\\[7pt] \log_5x=\log_5 12-\log_5 5,\\[6pt] \log_5x=\log_5\left(\frac{12}{5}\right). \end{gather*}Застосуймо властивості алгоритмів:
\begin{gather*} \log_a=1,\\[6pt] \log_ab-\log_ac=\log_a\left(\frac{b}{c}\right). \end{gather*}Зведімо обидві сторони рівняння до логарифмів з однаковою основою:
\begin{gather*} x=\frac{12}{5},\\[6pt] x=2\frac 25\in [2; 4). \end{gather*}Відповідь: Б.
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивостей трапеції, прямокутного трикутника, уміння визначати площу трапеції.
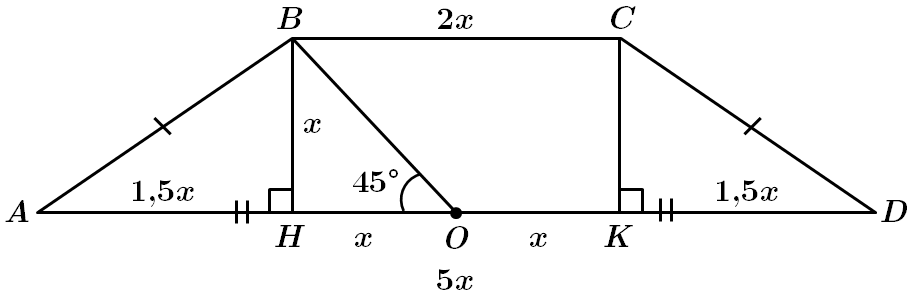
Нехай \(x\) – коефіцієнт пропорційності.
\(BC=2x\), \(AD=5x=b\), \(x=\frac b5.\)
Побудуймо висоти \(BH\) i \(CK.\) \(HBCK\) – прямокутник, тому
\begin{gather*} BC=HK=2x,\\[7pt] AH=KD=(5x-2x):2=1\mathord{,}5x. \end{gather*}Точка \(O\) – середина \(AD\), а тому \(HO=OK=x.\)
У \(\Delta BHO\ (\angle H=90^\circ)\), \(O=45^\circ.\) Отже, \(\Delta BHO\) – рівнобедрений. \(HO=BH=x.\)
Площу трапеції визначмо за формулою: $$ S=\frac{a+b}{2}\cdot h, $$ де \(a\), \(b\) – основи, \(h\) – висота
Якщо $$ x=\frac b5, $$ то
$$ S=\frac 72\cdot \left(\frac b5\right)^2=\frac{7b^2}{2\cdot 25}=\frac{7b^2}{50}. $$Відповідь: Г.
ТЕМА: Тригонометричні вирази та їх перетворення.
Завдання скеровано на перевірку вміння виконувати тотожні перетворення тригонометричних виразів, обчислення їхнього значення за заданих значень змінних.
Застосуймо формулу подвійного аргумента $$ \sin 2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}=2\sin \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\cos \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha} $$ для спрощення виразу:
Значення виразу належить проміжку \([1; 2).\)
Відповідь: Б.
ТЕМА: Похідна функції. Таблиця похідних і правила диференціювання.
Завдання скеровано на перевірку вміння визначати похідні функцій, похідну суми двох функцій.
Перетворення виразу \(\frac 3x\) за властивістю степенів \(a^{-n}=\frac{1}{a^n}\mathord{:}\) $$ \frac 3x=3\cdot \frac 1x=3x^{-1}. $$
За правилом визначення похідних \((u+v)'=u'+v'\) визначимо похідну функції:
За таблицею похідних
$$ (x^{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}})'=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}x^{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}-1}. $$Відповідь: A.
ТЕМА: Лінійні і раціональні рівняння та їх системи.
Завдання скеровано на перевірку вміння розв’язувати лінійні і раціональні рівняння.
Розв'яжімо систему рівнянь методом додавання:
\begin{gather*} \left\{\begin{array}{l} x-\frac 3y=3\ |\cdot (-1),\\ x+\frac 1y=11. \end{array}\right.\\[7pt] + \left\{\begin{array}{l} -x+\frac 3y=-3,\\ \underline{x+\frac 1y=11,} \end{array}\right.\\[6pt] \frac 3y+\frac 1y=8,\\[6pt] \frac 4y=8,\\[6pt] y=\frac 12. \end{gather*}Підставмо значення \(y=0\mathord{,}5\) у перше рівняння:
\begin{gather*} x-\frac{3}{0\mathord{,}5}=3,\\[6pt] x-6=3,\\[7pt] x=9. \end{gather*}Розв'язком системи є пара чисел \((9; 0\mathord{,}5)\mathord{:}\)
$$ x_0+y_0=9+0\mathord{,}5=9\mathord{,}5. $$Відповідь: Г.
ТЕМА: Дійсні числа та дії з ними.
Завдання скеровано на перевірку вміння виконувати дії з дійсними числами, тотожні перетворення ірраціональних і логарифмічних виразів.
1. \(\ln\frac 1e=\ln e^{-1}=-1\cdot \ln e=-1\) є від'ємним цілим числом.
Застосували формули:
\begin{gather*} \log_a b^n=n\cdot \log_a b,\\[7pt] \log_a a=1. \end{gather*}Отже, правильна відповідь – Б.
2. \(e+1\approx 2\mathord{,}7+1\approx 3\mathord{,}7\) є ірраціональним числом. Отже, правильна відповідь – Д.
3. \((e-1)^2-e^2+2e=e^2-2e+1-e^2+2e=1\) є натуральним числом. Отже, правильна відповідь – А.
Вираз \((e-1)^2\) спростили за формулою квадрата різниці: \((a-b)^2=a^2-2ab+b^2.\)
Відповідь: 1 – Б, 2 – Д, 3 – А.
ТЕМА: Функціональна залежність.
Завдання скеровано на перевірку вміння визначати властивості числових функцій, заданих графіками, використовувати перетворення графіків функцій.
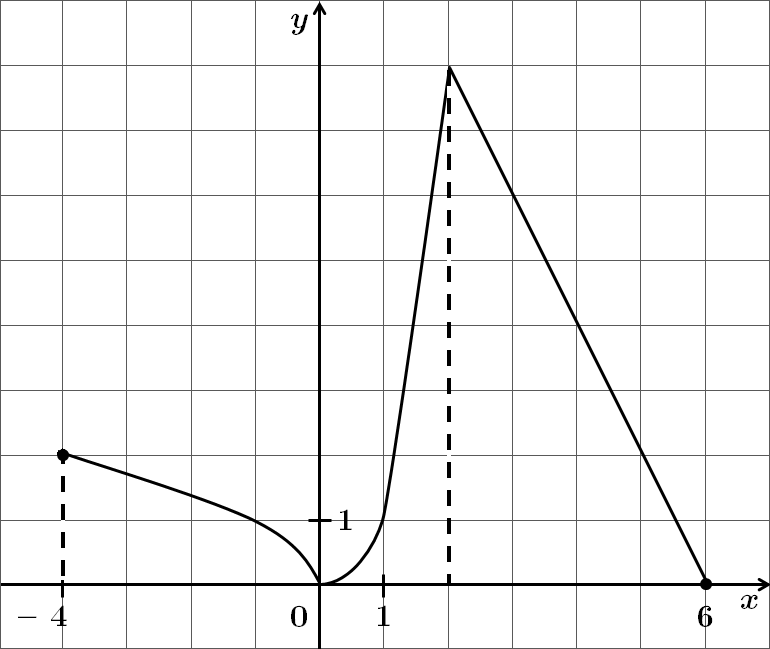
1. На проміжку \([-4; 0]\) зображено графік функції \(y=\sqrt{-x}.\)
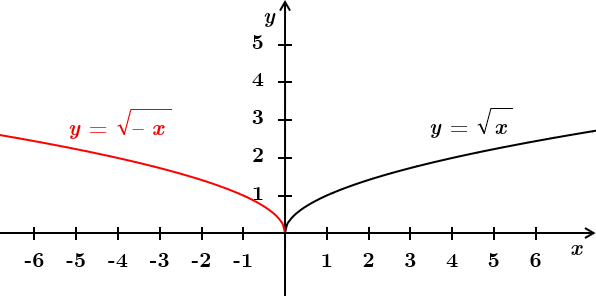
Елементарним перетворенням \(f(x)\rightarrow f(-x)\) графік відображено симетрично відносно осі \(Oy.\) Отже, правильна відповідь – Д.
2. На проміжку \((0; 2]\) зображено графік функції \(y=x^3.\) Отже, правильна відповідь – A.
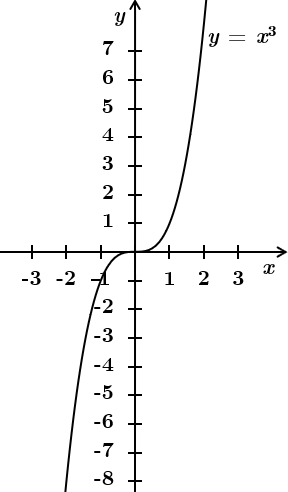
3. На проміжку \((2; 6)\) зображено графік лінійної функції \(y=12-2x.\) Отже, правильна відповідь – Б.
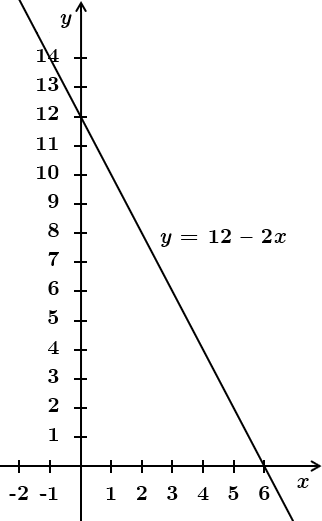
Відповідь: 1 – Д, 2 – А, 3 – Б.
ТЕМА: Коло та круг. Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивостей чотирикутників, зокрема прямокутника, кола, прямокутного трикутника, уміння застосовувати теорему Піфагора для розв’язування прямокутного трикутника.
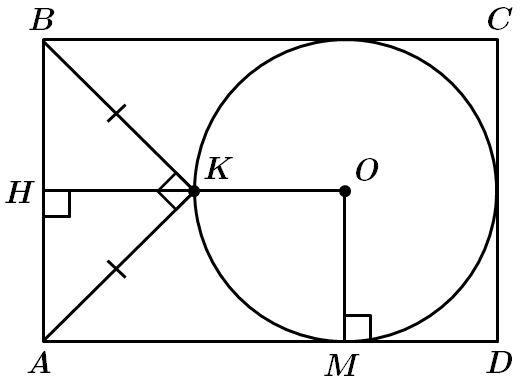
1. Коло дотикається до сторін \(BC\) i \(AD\), тому діаметр кола дорівнює стороні \(AB.\) Отже, довжина радіуса \(OK=\frac 12AB=6\) см.
Правильна відповідь – А.
2. У \(\Delta ABK\ (\angle K=90^\circ)\), \(BK=AK.\) За теоремою Піфагора:
\begin{gather*} AB^2=BK^2+KA^2=2BK^2,\\[7pt] 2BK^2=12^2\ \textit{см},\\[7pt] BK^2=144\ \textit{см}:2=72\ \textit{см},\\[7pt] BK=\sqrt{72}\ \textit{см}=\sqrt{2\cdot 36}\ \textit{см}=6\sqrt{2}\ \textit{см}. \end{gather*}Правильна відповідь – B.
3. У \(\Delta ABK\ KH\ \perp\ AB\) і є медіаною. За властивістю медіани проведеної до гіпотенузи:
\begin{gather*} KH=\frac 12AB=6\ \textit{см},\\[7pt] OH=OK+KH=6\ \textit{см}+6\ \textit{см}=12\ \textit{см}. \end{gather*}У \(\Delta AOM\ (\angle M=90^\circ)\), \(OM=6\) см, \(AM=OH=12\) см. За теоремою Піфагора:
Правильна відповідь – Г.
Відповідь: 1 – A, 2 – B, 3 – Г.
ТЕМА: Функціональна залежність. Похідна функції.
Завдання скеровано на перевірку вміння визначати властивості числових функцій, заданих формулою, похідну функції, числове значення похідної функції в точці для заданого значення аргумента.
$$ f(x)=\left\{\begin{array}{l} 10,\ \text{якщо}\ x\lt-2,\\ 4x^2+3x,\ \text{якщо}\ x\ge-2. \end{array}\right. $$Якщо \(x\lt -2\ f(x)=10.\) Отже, \(f(-4)=10.\)
Якщо \(x\ge -2\), \(f(x)=4x^2+3x.\)
\begin{gather*} f'(x)=4\cdot 2x+3\cdot 1=8x+3,\\[7pt] f'(2)=8\cdot 2+3=16+3=19. \end{gather*}Обчислімо
$$ f(-4)-f'(2)=10-19=-9. $$Відповідь: \(-9.\)
ТЕМА: Імовірність випадкової події.
Завдання скеровано на перевірку вміння обчислювати ймовірність випадкових подій.
Всього в салоні літака \(n\) рядів по \(6\) місць у кожному. Отже, всього в літаку \(6n\) місць.
Місць біля проходу в першому або останньому ряду \(4.\) Імовірність того, що пасажиру дістанеться таке місце – \(\frac{1}{45}.\)
За означенням імовірність – це відношення кількості результатів, що сприяють цій події (\(4\) місця біля проходу), до загальної кількості всіх можливих рівноймовірних результатів (\(6n\) – загальна кількість місць). Тому
\begin{gather*} \frac{1}{45}=\frac{4}{6n},\\[6pt] 6n=4\cdot 45,\\[7pt] n=30. \end{gather*}Відповідь: \(30.\)
ТЕМА: Тіла обертання. Многогранники.
Завдання скеровано на перевірку знання властивостей основних видів многогранників, зокрема піраміди, та властивостей циліндра, формул для обчислення площі поверхні циліндра й об’єму піраміди.
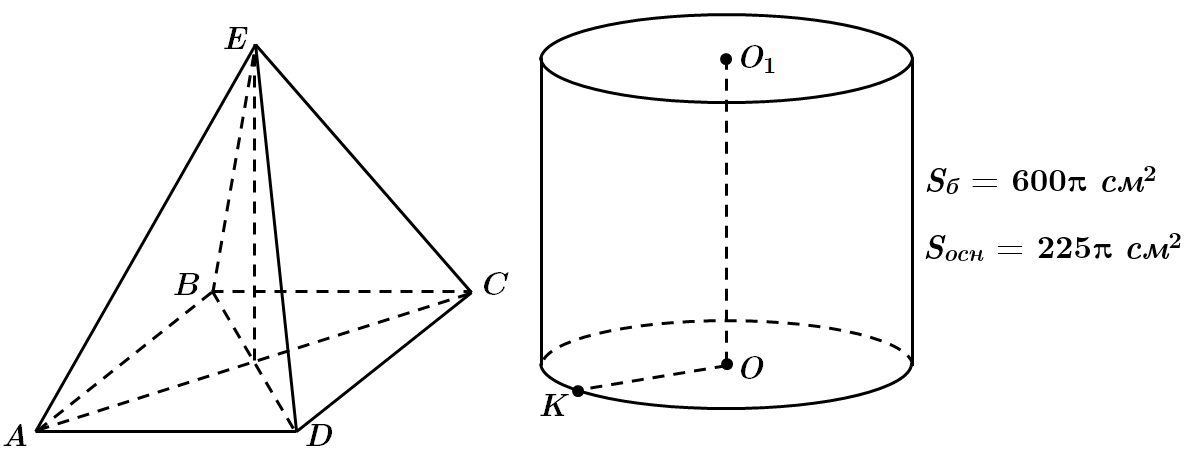
Площа основи циліндра
\begin{gather*} S=225\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}R^2,\\[7pt] R^2=225\ \textit{см}^2,\\[7pt] R=15\ \textit{см}. \end{gather*}Площа бічної поверхні ціліндра
\begin{gather*} S_\text{б}=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}RH=600\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\ \textit{см}^2,\\[7pt] 2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\cdot 15H=600\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\ \textit{см}^2,\\[7pt] H=20\ \textit{см}. \end{gather*}За умовою радіус кола, описаного навколо квадрата \(ABCD\), дорівнює радіусу основи циліндра. Отже, $$ AO=OK=15\ \textit{см}. $$
Діагональ \(AC=30\) см. Площу квадрата можна обчислити за формулою:
\begin{gather*} S=\frac 12 d^2=\frac 12\cdot (30\ \textit{см})^2=450\ \textit{см}^2. \end{gather*}Об'єм піраміди
Відповідь: \(3000.\)
ТЕМА: Показникові. Раціональні рівняння.
Завдання скеровано на перевірку вміння розв’язувати показникові та раціональні рівняння, рівняння з параметром.
Область допустимих значень:
\begin{gather*} 2-x\gt 0,\\[7pt] x\lt 2,\\[7pt] x\in (-\infty; 2). \end{gather*}Дріб дорівнює нулю за умови, що чисельник дорівнює нулю, а знаменник – ні.
\begin{gather*} 2^{4x+2a-15}-2\sqrt{2}=0\\[7pt] 2^{4x+2a-15}=2\sqrt{2}\\[7pt] 2^{4x+2a-15}=2^{1\mathord{,}5}\\[7pt] 4x+2a-15=1\mathord{,}5\\[7pt] 4x=1\mathord{,}5+15-2a\\[7pt] 4x=16\mathord{,}5-2a\\[6pt] x=\frac{33}{8}-\frac a2. \end{gather*}За умовою корінь \(x\) має бути додатним і задовольняти ОДЗ. Тобто \(x\gt 0\) та \(x\lt 2.\) Отже, \(0\lt x\lt 2.\)
Підставмо \(x\) у нерівність:
\begin{gather*} 0\lt \frac{33}{8}-\frac a2\lt 2,\ |\cdot 8\\[6pt] 0\lt 33-4a\lt 16,\\[7pt] -33\lt -4a\lt 17,\ |:(-4)\\[6pt] \frac{17}{4}\lt a\lt \frac{33}{4},\\[6pt] 4\frac 14\lt a\lt 8\frac 14. \end{gather*}Оскільки \(a\) – ціле число, то \(a=5\mathord{,}\ 6\mathord{,}\ 7\mathord{,}\ 8.\)
Сума значень \(a:\) $$ 5+6+7+8=26. $$
Відповідь: \(26.\)