Молекулярна фізика і термодинаміка – Основи молекулярно-кінетичної теорії

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Основні положення молекулярно-кінетичної теорії. Маса і розмір молекул.

Завдання скеровано на перевірку знання і розуміння основних положень молекулярно-кінетичної теорії.

Скраплення газу ‒ це перетворення газу на рідину, тобто зміна агрегатного стану.

Отже, під час скраплення хімічний склад газу не змінюється, тому молекули не можуть об’єднуватися, утворюючи молекули іншої речовини.

Також молекули не можуть ні зменшуватися, ні збільшуватися, оскільки за одним із основних положень молекулярно-кінетичної теорії частинки речовини взаємодіють одна з одною. Основна причина міжмолекулярної взаємодії ‒ електричне притягання і відштовхування заряджених частинок, що утворюють атом.

На відстанях, які більші за розміри молекул, молекули притягуються одна до одної; на відстанях, які трохи менші за розміри молекул, ‒ відштовхуються. Ці сили не впливають на розміри молекул, змінюються лише проміжки між молекулами.

Отже, під час скраплення молекули газової суміші не змінюються.

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Температура. Рівняння стану ідеального газу. Ізопроцеси.

Завдання скеровано на перевірку розуміння поняття середньої кінетичної енергії хаотичного руху молекул, а також розуміння процесів, що відбуваються з газом.

Середня кінетична енергія \(\overline{E}_k\) поступального руху молекул ідеального газу (кінетична енергія поступального руху, що в середньому припадає на одну молекулу масою \(m_0\)) дорівнює: $$ \overline{E}_k=\frac{m_0\overline{v^2}}{2}, $$ де \(\overline{v^2}\) ‒ середній квадрат швидкості.

Також середня кінетична енергія поступального руху молекул ідеального газу прямо пропорційна абсолютній температурі \(T:\) $$ \overline{E}_k=\frac 32kT, $$ де \(k\) ‒ стала Больцмана.

Під час ізохорного охолодження температура зменшуватиметься, відповідно середня кінетична енергія хаотичного руху молекул газу теж зменшуватиметься.

Ізотермічне стискання відбувається за сталої температури. Отже, середня кінетична енергія хаотичного руху молекул газу не зростатиме.

У ході адіабатного розширення, відповідно до першого закону термодинаміки, газ виконує додатну роботу внаслідок зменшення внутрішньої енергії, а температура газу зменшується. Тобто середня кінетична енергія хаотичного руху молекул газу зменшуватиметься.

Під час ізобарного розширення передана газу кількість теплоти витрачається і на збільшення внутрішньої енергії газу, і на виконання механічної роботи. Якщо збільшується внутрішня енергія, то й температура збільшуватиметься. Тому середня кінетична енергія хаотичного руху молекул газу зростатиме.

Відповідь: Г.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Основні положення молекулярно-кінетичної теорії та дослідне обґрунтування їх.

Завдання скеровано на перевірку знання і розуміння означення теплового руху.

Будь-яке тіло складається зі структурних одиниць (атомів, молекул, йонів), які невпинно хаотично (безладно) рухаються. Цей рух називають тепловим.

А Зміна із часом положення тіла в просторі відносно інших тіл ‒ це механічний рух.

Б Рух, який виникає внаслідок зміни температури тіла ‒ це може бути зміна об’єму тіла внаслідок нагрівання чи охолодження (як наприклад, рух рідини у довгій тонкій трубці термометра чи секції мосту змикаються під час спеки й розходяться під час морозів).

В Безперервний, хаотичний рух частинок, із яких складається тіло ‒ тепловий рух.

Г Упорядкований рух частинок, з яких складається тіло ‒ це може бути частково правильне визначення електричного струму, якщо частинки будуть зарядженими й будуть упорядковано рухатися під дією електричного поля.

Отже, правильна відповідь ‒ В.

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Ізопроцеси в газах.

Завдання скеровано на перевірку розуміння макроскопічних параметрів, якими описують стан ідеального газу, і вміння інтерпретувати їх графічно.

Зміну станів газу описують рівнянням Клапейрона: $$ \frac{pV}{T}=const, $$ де \(p\) ‒ тиск, \(V\) ‒ об’єм, \(T\) ‒ абсолютна температура.

Графік 1 відповідає ізохорному охолодженню (\(V=const\) ‒ графік паралельний осі абсолютної температури, температура \(T\) під час цього знижується).

Графік 3 відповідає ізотермічному стисканню (\(T=const\) ‒ графік паралельний осі об’єму, під час цього об’єм зменшується).

Під час процесів 2 і 4 змінюються і об’єм, і температура. Під час процесу 4 хоча температура й знижується, але об’єм збільшується, тому тиск також знижуватиметься. Отже, цей процес не може бути ізобарним.

Графік 2 відповідає ізобарному охолодженню (об’єм зменшується пропорційно до зниження температури, отже, \(p=const).\)

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Квантова фізика.

Завдання скеровано на перевірку розуміння фізичного змісту фізичних сталих.

Розв’язання завдання потребує знання визначень фізичних величин і вміння аналізувати розмірності.

Розмірність сталої Авогадро – \(\frac{1}{\text{моль}}\), що відповідає діленню кількості молекул на кількість речовини.

Стала Авогадро – це число, що відповідає кількості атомів (молекул) у будь-якій речовині кількістю \(1\ \text{моль}\).

Розмірність сталої Больцмана \(\frac{\text{Дж}}{\text{К}}\), що відповідає діленню енергії на температуру.

Сталу Больцмана використовують для встановлення зв’язку між середньою кінетичною енергією руху молекул і температурою ідеального газу: $$ \overline{E_k}=\frac 32 kT. $$

Якщо температура змінюється, то змінюється і середня кінетична енергія молекул: $$ \Delta\overline{E_k}=\frac 32 k\Delta T. $$

Звідси можна виразити сталу Больцмана: $$ k=\frac 23 \frac{\Delta \overline{E_k}}{\Delta T}. $$ Експериментально сталу Больцмана визначають саме за цією формулою.

Розмірність сталої Планка – \(\text{Дж}\cdot \text{с}\), що відповідає енергії, поділеній на частоту.

За гіпотезою Планка молекули випромінюють енергію порційно, і кількість цієї енергії пропорційна до частоти випромінювання: $$ E=hv. $$

Відповідно стала Планка $$ h=\frac Ev. $$

Гравітаційна стала фігурує в законі Всесвітнього тяжіння: $$ F=G\frac{m_1m_2}{r_2}. $$

Якщо маса обох тіл становить 1 кг, відстань між ними – 1 м, то $$ F_0=G\frac{1\ \text{кг}\cdot 1\ \text{кг}}{1\ \text{м}^2}=G\frac{\text{кг}^2}{\text{м}^2}. $$

Тож сила взаємодії таких тіл за модулем дорівнює гравітаційній сталій.

До того ж сила має розмірність \(H\), і єдина величина з невідомою розмірністю – це \(G\), тобто: $$ [G]=\frac{1\ \text{Н}}{\frac{1\ \text{кг}\ \cdot\ 1\ \text{кг}}{1\ \text{м}^2}}=\frac{1\ \text{Н}\cdot 1\ \text{м}^2}{1\ \text{кг}\cdot 1\ \text{кг}}=1\frac{\text{Н}\cdot \text{м}^2}{\text{кг}^2}. $$

Відповідь: 1Б, 2А, 3Г, 4В.

ТЕМА: Молекулярна фізика і термодинаміка. Ізопроцеси.

Завдання скеровано на перевірку розуміння зв’язку між макроскопічними й мікроскопічними параметрами ідеального газу.

Концентрацію визначають за формулою $$ n=\frac NV, $$ де \(N\) – кількість молекул у певному об’ємі \(V\).

Тоді, якщо за сталої маси концентрація залишається незмінною, то й об’єм у такому процесі не змінюється.

Середню кінетичну енергію молекул можна визначити за формулою $$ \overline{E_\text{кін}}=\frac{m_0\overline{v^2}}{2}, $$ де \(m_0\) – маса одної молекули, \(\overline{v^2}\) – середній квадрат швидкості молекул.

Що вища температура, то вищий середній квадрат швидкості молекул. Тож, щоб у газі певної маси концентрація молекул залишалася сталою, а їхня середня кінетична енергія зростала, газ потрібно ізохорно нагрівати.

Відповідь: A.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Рівняння стану ідеального газу.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з використання рівняння стану ідеального газу.

Об’єм, температура й тиск газу пов’язані між собою рівнянням стану ідеального газу: $$ pV=nRT=\frac mM RT, $$ де \(p\) – тиск, \(V\) – об’єм, \(n\) – кількість речовини, \(R\) – універсальна газова стала, \(T\) – температура, \(m\) – маса газу, \(M\) – молярна маса речовини.

З рівняння стану ідеального газу можна виразити тиск \(p\): $$ p=\frac mM \frac{RT}{V}. $$

За графіком (рис. 1) можна визначити тиск та об’єм у точках 1 і 2. На графіку не вказано одиниці вимірювання, тож вважатимемо, що 1 клітинка вздовж осі \(T\) відповідає 1 умовній одиниці температури (у. о. т.), а 1 клітинка вздовж осі \(V\) відповідає 1 умовній одиниці об’єму (у. о. о.).

Тоді для точок 1 і 2 об’єм і температура дорівнюють:

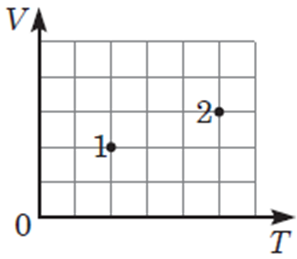
Рис. 1. Графік у координатах \(Vt\)

Можна визначити тиск у точках 1 і 2 в умовних одиницях тиску (у. о. тиску):

Відповідь: B.

ТЕМА: Основи термодинаміки. Тепловий рух.

Завдання скеровано на перевірку розуміння поняття броунівського руху.

Броунівський рух – хаотичний рух видимих у мікроскоп малих макрочастинок, завислих у рідині або газі, який відбувається під дією ударів молекул рідини або газу.

Тобто рух броунівської частинки (як наприклад частинка пилу чи квіткового пилку) залежить від руху молекул рідини чи газу, у яких вони перебувають. Молекули зіштовхуються з броунівською частинкою під час теплового руху і передають їй частину свого імпульсу.

Імпульс визначають за формулою $$ p=mv, $$ де \(m\) – маса тіла, \(v\) – його швидкість.

Тоді швидкість частинки можна визначити за формулою $$ v=\frac \pm . $$

Що швидше рухаються молекули, то частіше вони зіштовхуються з броунівською частинкою, і тим більший імпульс вона отримує, а отже більшою буде її швидкість.

Окрім того, що менша маса частинка, то більшою буде її швидкість за однакового переданого імпульсу.

Відповідь: A.

ТЕМА: Молекулярна фізика і термодинаміка. Ізопроцеси.

Завдання скеровано на перевірку вміння застосовувати закон Бойля – Маріотта.

Дано:
\(T_1=T_2\)
\(V_1=8\ \text{л}\)
\(V_2=6\ \text{л}\)
\(p_2=p_1+4\ \text{кПа}\)

Знайти:
\(p_1\ (\text{кПа})\ -\ ?\)

Для того, щоби правильно аналізувати зміни всіх фізичних величин, потрібно використати рівняння Клапейрона: $$ \frac{p_1V_1}{T_1}=\frac{p_2V_2}{T_2}. $$

Згідно нього добуток тиску на об’єм, поділений на температуру, залишається сталим під час переходу зі стану 1 у стан 2.

Для ізотермічного процесу рівняння Клапейрона спрощують і перетворюють на рівняння, яким описують закон Бойля – Маріотта: $$ p_1V_1=p_2V_2. $$

Якщо \(p_1=x\), рівняння набуває вигляду $$ x\ \text{кПа}\cdot 8\ \text{л}=(x+4)\ \text{кПа}\cdot 6\ \text{л}. $$

Після переведення всіх одиниць в одиниці системи СІ:

Відповідно \(p_1=12\ \text{кПа}\).

Відповідь: 12.

ТЕМА: Молекулярна фізика і термодинаміка. Рівняння стану ідеального газу.

Завдання скеровано на перевірку вміння застосовувати рівняння стану ідеального газу.

1. Дано:
\(V=0,83\ \text{м}^3\)
\(T_1=250\ \text{К}\)
\(p_1=100\ \text{кПа}\)
\(T_2=300\ \text{К}\)
\(p_2=195\ \text{кПа}\)
\(M=32\ \frac{\text{г}}{\text{моль}}\)
\(R=8,3\ \frac{\text{Дж}}{\text{моль}\cdot\text{К}}\)

1. Знайти:
\(n_1\ (\text{моль})\ -\ ?\)

Температура \(T\), тиск \(p\) й об’єм \(V\) пов’язані рівнянням стану ідеального газу $$ pV=nRT, $$ де \(p\) – тиск, \(V\) – об’єм, \(R\) – універсальна газова стала, \(T\) – температура, \(n\) – кількість речовини.

Для початкового стану можна записати рівняння $$ p_1V=n_1RT_1. $$

Тобто

2. Знайти:
\(\triangle m\ (\text{кг})\ -\ ?\)

Кількість речовини пов’язана з її масою формулою $$ n=\frac mM, $$ де \(m\) – маса речовини, \(M\) – її молярна маса.

Після обчислення різниці в кількості речовини у двох станах можна обчислити й різницю мас газу. Аналогічно до \(n_1\) можна обчислити \(n_2\):

Тоді

Відповідь: 1. 40. 2. 0,8.

ТЕМА: Властивості газів, рідин і твердих тіл. Насичена й ненасичена пара.

Завдання скеровано на перевірку розуміння механізмів переходу від ненасиченої до насиченої пари.

Насичена пара – це пара, яка перебуває в динамічній рівновазі зі своєю рідиною.

Тобто об’єм випаруваної за певний проміжок часу рідини дорівнюватиме об’єму сконденсованої пари. У насиченій парі найвища можлива за певної температури концентрація молекул.

Що вища температура, то вища й концентрація молекул рідини в повітрі, за якої пара є насиченою.

Щоби перетворити водяну пару в повітрі під поршнем на насичену, потрібно або збільшити концентрацію молекул води в повітрі, або знизити температуру.

Концентрацію визначають за формулою $$ n=\frac NV, $$ де \(N\) – кількість молекул у певному об’ємі \(V\).

Якщо не додавати нової води в повітря, концентрацію можна збільшити лише якщо зменшити об’єм посудини.

А під час ізотермічного розширення температура повітря залишається сталою, а його об’єм збільшується, отже концентрація молекул води в повітрі зменшується – пара не може стати насиченою

Б під час ізохорного охолодження об’єм повітря залишається незмінним, а температура знижується. У такому разі концентрація молекул у повітрі не змінюється, але концентрація молекул, що відповідає насиченій парі – зменшується, отже за достатнього охолодження пара може стати насиченою

В під час ізобарного нагрівання і об’єм повітря, і температура збільшуються, отже концентрація молекул зменшується і збільшується концентрація, необхідна для того, щоби пара стала насиченою. За таких умов пара не може стати насиченою

Г під час ізохорного нагрівання об’єм повітря, а отже й концентрація молекул залишається сталою, а температура знижується. У такому разі концентрація молекул, що відповідає насиченій парі, збільшується, тож пара насиченою стати не може

Відповідь: Б.

ТЕМА: Основи термодинаміки. Внутрішня енергія і способи її змінення. Способи теплопередачі.

Завдання скеровано на перевірку розуміння механізмів конвекції.

Конвекція – це вид теплопередачі, за якого тепло переносять потоки рідини або газу.

Речовини у твердому стані не мають потоків, тому конвекція в них неможлива.

Відповідь: A.

ТЕМА: Молекулярна фізика і термодинаміка. Рівняння стану ідеального газу.

Завдання скеровано на перевірку вміння використовувати рівняння стану ідеального газу в розрахункових задачах.

Дано:
\(V=5,5\ \text{л}\)
\(p_1=100\ \text{кПа}\)
\(V_{\text{н}}=0,1\ \text{л}\)
\(N=11\)
\(T=const\)

Знайти:
\(p_2\ (\text{кПа})\ -\ ?\)

Якщо вважати повітря ідеальним газом, то тиск, температуру й об’єм повітря пов’язує рівняння стану ідеального газу \begin{gather*} pV=nRT=\frac mM RT, \end{gather*} де \(p\) – тиск, \(V\) – об’єм, \(n\) – кількість речовини, \(R\) – універсальна газова стала, \(T\) – температура, \(m\) – маса газу, \(M\) – молярна маса речовини.

Об’єм м’яча і його температура залишаються незмінними, але змінюються тиск і маса газу всередині: \begin{gather*} p_1V=\frac mM RT;\\[6pt] p_2V=\frac{m+\triangle m}{M}RT. \end{gather*}

Тоді можна визначити відношення кінцевого й початкового тисків: $$ \frac{p_2}{p_1}=\frac{m+\triangle m}{m}=1+\frac{\triangle m}{m}. $$

Масу й об’єм пов’язує густина \(\mathbf{\rho}\) речовини: $$ m=\mathbf{\rho}V. $$

За 11 циклів накачування всередину потрапило \(NV_{\text{н}}\) літрів повітря, тому: $$ \triangle m=\mathbf{\rho}NV_{\text{н}}. $$

Тоді

Відповідь: 120

ТЕМА: Молекулярна фізика і термодинаміка. Рівняння стану ідеального газу.

Завдання скеровано на перевірку вміння користуватися графіками для визначення макроскопічних параметрів газу й використовувати це для розв’язування розрахункових задач.

Температура \(T\), тиск \(p\) й об’єм \(V\) пов’язані рівнянням стану ідеального газу $$ pV=nRT, $$ де \(R\) – газова стала, \(T\) – температура, \(n\) – кількість речовини.

Тож тиск можна визначити за значеннями об’єму й температури. Оскільки кількість речовини \(n=1\ \text{моль}\), то тиск для ідеального газу $$ p=\frac{RT}{V}. $$

Масштаб на графіках невідомий, тому точно тиск визначити неможливо, але можна порівняти його в різних варіантах, прийнявши, що клітинка вздовж осі \(T\) дорівнює умовній одиниці температури (у. о. т.), а вздовж осі \(V\) – умовній одиниці об’єму (у. о. о.). Тиск у такому разі вимірюють в умовних одиницях тиску (у. о.).

Можна визначити об’єм і температуру для варіантів відповіді, поданих у завданні:

Після цього можна розрахувати тиск:

Тож найвищий тиск у точці B.

Відповідь: B.

ТЕМА: Основи молекулярно-кінетичної теорії. Маса й розмір молекул.

Завдання скеровано на оцінку розуміння відмінності між фізичними й хімічними явищами в молекулярній фізиці.

Під час зміни макроскопічних параметрів (температури, об’єму чи тиску) хімічний склад речовини не змінюється. Молекули – це найменші частинки речовини, носії її хімічних властивостей.

Тому, якщо хімічний склад речовини не змінюється, то й самі молекули також не змінюються.

Відповідь: Б.

ТЕМА: Молекулярна фізика й термодинаміка. Ізопроцеси

Завдання скеровано на оцінювання вміння аналізувати графіки ізопроцесів і будувати їх у різних системах координат.

Процес 1–2 є ізохорним (тиск \(p\) й температура \(T\) зростають за сталого
об’єму \(V\)).

Процес 2–3 – ізобарним (температура \(T\) зростає, об’єм \(V\) за сталого тиску \(p\)).

Відповідно в координатах \(pV\) процес 1–2 відображено перпендикулярною до осі \(V\) прямою, напрямленою вгору, бо тиск зростає, а процес 2–3 – перпендикулярною до осі \(p\) прямою, напрямленою вправо, бо об’єм збільшується.

Відповідь: A.

ТЕМА: Молекулярна фізика і термодинаміка. Ізопроцеси в газах. Робота в термодинаміці.

Завдання скеровано на оцінювання вміння аналізувати графіки ізопроцесів.

1. Знайти:
\(A_{2-3}-?\)

За графіком на рисунку можна визначити типи процесів:

1–2 – ізобарне охолодження;

2–3 – ізохорне нагрівання.

Робота у довільному термодинамічному процесі можна обчислити як площу криволінійної трапеції під графіком залежності \(p(V).\)

Оскільки процес 2–3 – ізохорний, то \(A_{2-3}=0.\)

2. Дано:
\(V_3=12\ \text{л}\)

Знайти:
\(V_1 - ?\)

Оскільки процес 2–3 ізохорний, то \(V_3=V_2=12\ \text{л}.\)

Для процесу 1–2 за законом Гей-Люссака \(\frac{V_1}{T_1} =\frac{V_2}{T_2}\) (1), тоді \(V_1=\frac{T_1 V_2}{T_2}\) (2).

За графіком можна визначити, що \(T_1\) відповідає восьми поділкам, а \(T_2\) – двом.

Тоді \(\frac{T_1}{T_2} =\frac82=4,\) а \(V_1=4V_2=4\cdot 12\ \text{л}=48\ \text{л}.\)

Відповідь: 1. 0. 2. 48.

ТЕМА: Вимірювальні пристрої.

Завдання скеровано на оцінювання вміння добирати вимірювальні прилади для проведення експериментів.

A. Оскільки період – це час, за який тіло робить одне повне коливання, то для його вимірювання використовують секундомір.

Б. Для визначення електрорушійної сили (ЕРС) і внутрішнього опору джерела потрібно скористатися законом Ома для повного кола. ЕРС в цьому разі є еквівалентом напруги в законі Ома для ділянки кола, тому її також вимірюють вольтметром.

В. Для визначення фокусної відстані й оптичної сили лінзи потрібно виміряти відстань від предмета до лінзи й від лінзи до зображення. Для цього використовують лінійку.

Г. Для визначення коефіцієнта корисної дії (ККД) похилої площини необхідно обчислити корисну роботу, яку розраховують як зміну потенціальної енергії початкового й кінцевого стану й витрачену роботу, що робчислюють за формулою \(A = Fl\), де \(F\) – сила, прикладена до вантажу, а \(l\) – довжина похилої площини. Силу \(F\) у цьому досліді вимірюють динамометром.

Д. Для вивчення теплового балансу під час змішування води різної температури потрібно зафіксувати початкові й кінцеву температури. Для цього використовують термометр.

Відповідь: 1Г, 2Б, 3А, 4Д.

ТЕМА: Молекулярна фізика й термодинаміка. Ізопроцеси.

Завдання скеровано на оцінювання вміння аналізувати графіки ізопроцесів і будувати їх у різних системах координат.

Рівняння стану ідеального газу \(pV=nRT,\) де \(p\) – тиск, \(V\) – об’єм, \(R\) – універсальна газова стала, \(T\) – температура, \(n\) – кількість речовини.

З огляду на це рівняння за результатами аналізування графіків, поданих у завданні, можна дійти висновків, що процес 1–2 є ізобарним (сталий тиск, температура підвищується), 2–3 є ізохорним (сталий об’єм, температура знижується), 3–4 є ізобарним (сталий тиск, температура знижується), 4–1 є ізотермічним (стала температура).

Наступним кроком є аналіз процесів, зображених у координатах \(pT.\)

Найбільших змін зазнав графік процесу 4–1, адже в координатах \(pV\) ізотерма має форму параболи, а в координатах \(pT\) – прямої, перпендикулярної до осі \(T.\)

Такому опису відповідає лише графік на рисунку A.

Відповідь: A.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. Рівняння стану ідеального газу.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на використання рівняння стану ідеального газу.

Дано:
\(t_1=18\ ^{\circ}\text{С}\)
\(t_2=27\ ^{\circ}\text{С}\)
\(p_1=p_2\)

Знайти:
\(\left(1-\frac{N_2}{N_1}\right)\ -\ ?\)

Температура, тиск і об’єм газу пов’язані між собою рівнянням стану ідеального газу: $$ pV=vRT, $$ де \(T\) – це температура в Кельвінах, а \(v\) – це кількість речовини, яку можна обчислити за формулою: $$ v=\frac{N}{N_A}, $$ де \(N\) – кількість молекул, \(N_A\) – число Авогадро.

Об’єм кімнати не змінився після підключення опалення, тож можна записати рівняння стану ідеального газу для стану до нагрівання і після: \begin{gather*} p_1V_1=v_1RT_1;\\[7pt] p_2V_2=v_2RT_2. \end{gather*}

Зважаючи на те, що \begin{gather*} p_1V_1=p_2V_2, \end{gather*} можна записати: \begin{gather*} v_1RT_1=v_2RT_2;\\[6pt] \frac{N_1}{N_A}RT_1=\frac{N_2}{N_A}RT_2;\\[6pt] N_1T_1=N_2T_2. \end{gather*}

Тоді $$ \frac{N_2}{N_1}=\frac{T_1}{T_2}. $$

Після цього можна обчислити, на скільки змінилася кількість молекул: $$ \left(1-\frac{N_2}{N_1}\right)\cdot 100\ \text{%}=\left(1-\frac{T_1}{T_2}\right)\cdot 100\ \text{%}=\left(1-\frac{(18+273)\ \text{К}}{(27+273)\ \text{К}}\right)\cdot 100\ \text{%}=3\ \text{%}. $$

Відповідь: 3.

ТЕМА: Молекулярна фізика й термодинаміка. Ізопроцеси.

Завдання скеровано на оцінювання вміння розв’язувати задачі на аналіз графіків ізопроцесів і побудову їх у різних системах координат.

Для правильного розв’язання задачі передовсім потрібно пригадати графіки ізопроцесів (рис. 1):

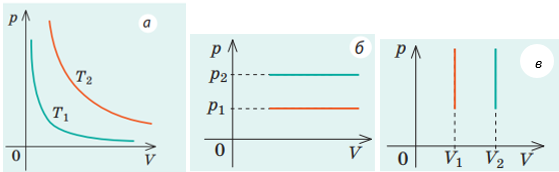
Рис. 1. Графіки ізопроцесів у координатах \((p, V)\): а) ізотермічний, б) ізобарний, в) ізохорний процеси

Важливо пам’ятати, що ізотерма може мати лише таку орієнтацію! Далі потрібно розглянути кожну послідовність із завдання і нарисувати графіки процесів.

Для правильного аналізування змін усіх фізичних величин потрібно пригадати рівняння Клапейрона: $$ \frac{p_1V_1}{T_1}=\frac{p_2V_2}{T_2}. $$

Із цього випливає, що добуток тиску на об’єм, поділений на температуру залишається сталим під час переходу зі стану 1 у стан 2.

Під час ізохорного нагрівання за рівнянням Клапейрона $$ \frac{p_1}{T_1}=\frac{p_2}{T_2}. $$

За умовою \(T_2 \gt T_1\), а отже, щоби рівність зберігалась, \(p_2\) також має бути більшим за \(p_1\), що можна зобразити прямою 1 на рисунку 2.

Ізобарне стискання можна зобразити прямою 2 на рисунку 2

З останньої точки попереднього процесу до початкової точки можна провести ізотерму (крива 3), отже газ можна повернути в початковий стан такою послідовністю процесів.

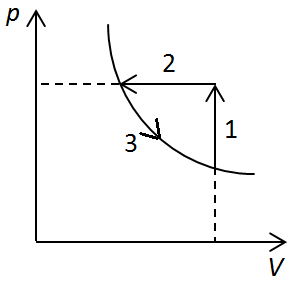
Рис. 2. Графік процесів із перебігу 1

Під час ізохорного нагрівання за рівнянням Клапейрона $$ \frac{p_1}{T_1}=\frac{p_2}{T_2}. $$

За умовою \(T_2 \gt T_1\), тому для збереження рівності \(p_2\) також має бути більшим за \(p_1\), що можна зобразити прямою 1 на рисунку 3.

Ізобарне збільшення об’єму можемо зобразити прямою 2 на рисунку 3.

З останньої точки попереднього процесу до початкової точки не можна провести ізотерму (крива 3 не перетинає початкову точку), отже газ не можна повернути в початковий стан такою послідовністю процесів.

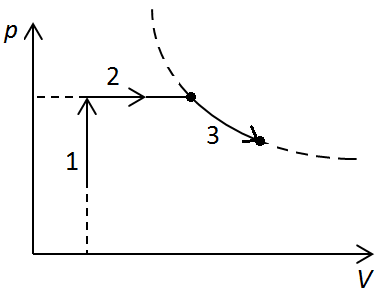
Рис. 3. Графік процесів із перебігу 2

Ізобарне стискання можна зобразити прямою 1 на рисунку 4.

Під час ізохорного охолодження за рівнянням Клапейрона $$ \frac{p_1}{T_1}=\frac{p_2}{T_2}. $$

За умовою \(T_2 \lt T_1\), тому для збереження рівності \(p_2\) також має бути меншим ніж \(p_1\), що можна зобразити прямою 2 на рисунку 4.

З останньої точки попереднього процесу до початкової точки не можна провести ізотерму (крива 3 не перетинає початкову точку), отже газ не можна повернути в початковий стан такою послідовністю процесів.

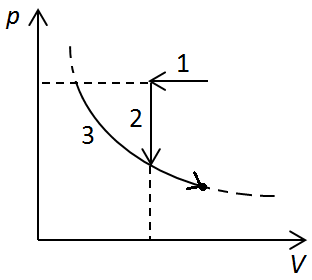
Рис. 4. Графік процесів із перебігу 3

Ізобарне збільшення об’єму можемо зобразити прямою 1 на рисунку 5.

Під час ізохорного охолодження за рівнянням Клапейрона: $$ \frac{p_1}{T_1}=\frac{p_2}{T_2}. $$

За умовою \(T_2 \lt T_1\), тому для збереження рівності \(p_2\) також має бути меншим за \(p_1\), що можна зобразити прямою 2 на рисунку 5.

З останньої точки попереднього процесу до початкової точки можна провести ізотерму (крива 3), отже газ можна повернути в початковий стан такою послідовністю процесів.

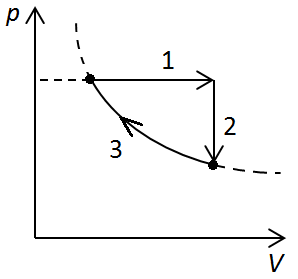
Рис. 5. Графік процесів із перебігу 4

Відповідь: B.

ТЕМА: Молекулярна фізика й термодинаміка. Рівняння стану ідеального газу. Ізопроцеси в газах.

Завдання скеровано на оцінювання розуміння закономірностей зміни тиску, об’єму й температури на основі аналізу результатів експерименту, зображених на рисунку.

За рисунком легко визначити, що об’єм кульки збільшився після того, як вона опинилася під ковпаком, до якого підключено насос. Ні охолоджувальних, ні нагрівальних пристроїв немає, тому температура газу всередині кульки залишається сталою. До того ж, оскільки кулька зав’язана, можна вважати, що кількість речовини всередині неї стала. За законом Бойля – Маріотта добуток тиску на об’єм до поміщення кульки під ковпак і після має бути однаковим: $$ p_{\text{до}}V_{\text{до}}=p_{\text{після}}V_{\text{після}}. $$

Оболонка кульки еластична, тож унаслідок наповнювання повітрям вона змінюватиме свій об’єм доти, доки тиск усередині кульки не дорівнюватиме тиску ззовні.

Тому, якщо об’єм кульки збільшився, то тиск усередині – зменшився, а отже зменшився і тиск навколо (під ковпаком).

Відповідь: A.

ТЕМА: Вимірювальні пристрої.

Завдання скеровано на оцінювання розуміння фізичних принципів роботи вимірювальних пристроїв.

Термометр – це прилад для вимірювання температури. Він працює завдяки тому, що деякі речовини за сталого тиску суттєво змінюють свій об’єм за зміни температури (ртуть чи спирт розширюються за збільшення температури і звужуються за її зменшення).

Психрометр – це прилад для вимірювання відносної вологості. Принцип його роботи такий: у корпусі приладу є два термометри. Кінець одного з них зазвичай обгорнутий вологою тканиною. Вода з тканини завжди випаровується, і швидкість випаровування залежить від вологості повітря навколо. Відповідно, для вимірювання відносної вологості фіксують покази сухого й вологого термометрів і за допомогою спеціальних таблиць виконують необхідні розрахунки.

Барометр – це прилад для вимірювання атмосферного тиску. У завданні зображено безводний барометр (анероїд). На рисунку 1 зображено конструкцію такого приладу. Усередині анероїда є камера з гофрованою поверхнею (1), із якої відкачано повітря. За високого атмосферного тиску кришка коробки сильно опускається, а за низького – піднімається. До кришки за допомогою пружини кріпиться стрілка (2). Тому, коли кришка камери піднімається чи опускається, пружина деформується, і стрілка починає рухатись по шкалі (3).

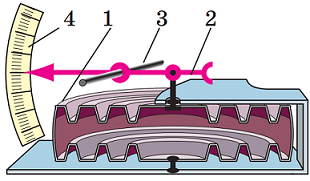
Рис. 1. Конструкція барометра-анероїда

Динамометр – це прилад для вимірювання сили. Зазвичай динамометр складається із пружини і шкали. Коли на кінець пружини діє сила, то за законом Гука пружина розтягується: $$ F=kx. $$

Тому, якщо відомий коефіцієнт жорсткості k пружини, то за значенням її видовження x можна визначити й силу, що його спричиняє.

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Основи МКТ. Ідеальний газ. Ізопроцеси в газах.

Завдання скеровано на перевірку вміння розв'язувати задачі на аналіз графіків ізопроцесів і побудову їх у різних системах координат.

Графік на рисунку відповідає ізобарному процесу бо тиск \(p=const\), тому з усіх 4-х варіантів відповіді можливий тільки B.

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Основні положення МКТ.

Завдання скеровано на перевірку вміння розрізняти різні агрегатні стани речовини й робити узагальнення щодо властивостей речовин у різних агрегатних станах.

Швидкість дифузії залежить тільки від агрегатного стану за інших однакових умов, тому найбільша швидкість дифузії в газах між парою ефіру й повітрям.

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи МКТ. Основне рівняння МКТ.

Завдання скеровано на перевірку вміння розв'язувати розрахункові задачі, застосовуючи функціональні залежності між основними фізичними величинами.

У герметично закритому балоні \(V=const\). Це ізохорний процес.

За законом Шарля: \begin{gather*} \frac{p_1}{T_1}=\frac{p_2}{T_2};\ p_2=4p_1\\[6pt] \frac{p_1}{T_1}=\frac{4p_1}{T_2} =\gt T_2=4T_1\\[6pt] v_1=\sqrt{\frac{3kT_1}{m_0}}\\[6pt] v_2=\sqrt{\frac{3k4T_1}{m_0}}\\[6pt] \frac{v_2}{v_1}=\sqrt{4}=2. \end{gather*}

Відповідь: B.

ТЕМА: Молекулярна фізика та термодинаміка. Основи термодинаміки. Рівняння стану ідеального газу.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з використанням рівняння стану ідеального газу.

Дано:
\(T=7\ ^{\circ}\text{С}\)
\(p=166\ \text{кПа}\)
\(V=70\ \text{л}\)
\(R=8,3\ \frac{\text{Дж}}{\text{моль}\ \cdot\ \text{К}}\)

Знайти:
\(\mathbf{\nu}\ (\text{моль})\ -\ ?\)

Рівняння стану ідеального газу таке: $$ pV=\mathbf{\nu}RT, $$ де \(p\) – тиск газу, \(V\) – об’єм газу, \(T\) – температура газу, \(\mathbf{\nu}\) – кількість речовини, \(R\) – універсальна газова стала.

Тоді, після переведення всіх фізичних величин в одиниці СІ,

Відповідь: 5.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки.

Завдання скеровано на розуміння суті адіабатного процесу.

Оскільки зміна внутрішньої енергії відбувається без передавання теплоти ззовні, то описаний процес – адіабатний.

Відповідь: Г.

ТЕМА: Вимірювальні пристрої.

Завдання скеровано на оцінювання розуміння фізичних принципів роботи вимірювальних пристроїв.

Термометр – це прилад для вимірювання температури. Він працює завдяки тому, що деякі речовини за сталого тиску суттєво змінюють свій об’єм за зміни температури (ртуть чи спирт розширюються за підвищення температури та звужуються за її зниження).

Динамометр – це прилад для вимірювання сили. Зазвичай складники динамометра – пружина та шкала. Коли на кінець пружини діє сила, то, за законом Гука, пружина розтягується.

Барометр – це прилад для вимірювання атмосферного тиску. У завданні зображено безводний барометр (анероїд), усередині якого є вакуумна камера з гофрованою поверхнею. За високого атмосферного тиску кришка коробки сильно опускається, а за низького – піднімається. До кришки за допомогою пружини прикріплена стрілка. Тому, коли кришка камери піднімається чи опускається, пружина деформується і стрілка починає рухатися по шкалі.

Електрометр – це прилад для виявлення та вимірювання заряду. Його складники – металева куля, стержень і стрілки. Під дією електричного поля в стержні, стрілці й кулі відбувається перерозподіл зарядів. Оскільки вони з’єднані, то заряджаються однаково. Однойменно заряджені стрілка та стержень відштовхуються, тому рухома стрілка відхиляється.

Відповідь: A.

ТЕМА: Кількість речовини.

Завдання скеровано на перевірку розуміння поняття кількості речовини.

Кількість речовини можна визначити за формулою $$ v=\frac{N}{N_A}, $$ де \(N\) – кількість молекул, \(N_A\) – число Авогадро.

Нехай кількість речовини озону становить \(v\). Кожна молекула озону утворена трьома атомами Оксигену. Тоді для утворення нових молекул доступно \(3v\) атомів. Кожна молекула кисню утворена двома атомами Оксигену, тож всього їх можна буде утворити \(3v:2=1,5v\).

Відповідь: B.

ТЕМА: Молекулярна фізика й термодинаміка. Ізопроцеси.

Завдання скеровано на оцінювання вміння аналізувати графіки ізопроцесів і будувати їх у різних системах координат.

Ізотермічний процес – процес змінювання за незмінної температури стану газу деякої маси.

На графіках у завданні процеси зображено в координатах \(V\) і \(T\). У такому вигляді ізотермічний процес – це пряма, перпендикулярна до осі \(T.\)

Відповідь: A.

ТЕМА: Молекулярна фізика й термодинаміка. Середня квадратична швидкість теплового руху молекул.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі, пов’язані із середньою квадратичною швидкістю молекул.

Кількість зіткнень залежить від середньоквадратичної швидкості руху молекул: що більша швидкість їхнього руху, то частіше вони стикаються одні з одними й зі стінками.

За основним рівнянням молекулярно-кінетичної теорії існує зв’язок між макроскопічними параметри (тиском, об’ємом і температурами) і середньою швидкістю руху молекул у квадраті: $$ p=\frac 13 m_0n\overrightarrow{v^2}, $$ де \(p\) – тиск, \(m_0\) – маса однієї молекули, \(\overrightarrow{v^2}\) – середня швидкість молекул у квадраті, \(n\) – концентрація молекул. $$ n=\frac NV. $$ де \(N\) – кількість молекул, \(V\) – об’єм.

Тоді основне рівняння молекулярно-кінетичної можна переписати: $$ pV=\frac 13 m_0N\overrightarrow{v^2}. $$

З огляду на рівняння стану $$ pV=vRT. $$

Тому $$ vRT=\frac 13 m_0N\overrightarrow{v^2}. $$

Середньоквадратичну швидкість можна обчислити з виразу $$ v_{\text{кв}}=\sqrt{\overrightarrow{v^2}}. $$

Кількість речовини $$ v=\frac mM, $$ де \(M\) – молярна маса речовини, а \(m\) – маса тіла.

Зважаючи на те, що добуток маси однієї молекули на їхню кількість становить масу всього тіла, $$ m_0N=m. $$

Тому $$ \frac mM RT=\frac 13m\overrightarrow{v^2}. $$

Тобто $$ v_{\text{кв}}=\sqrt{\overrightarrow{v^2}}=\sqrt{\frac{3RT}{M}}. $$

Аби дізнатися, у скільки разів збільшиться кількість зіткнень зі стінкою за 1 с, необхідно обчислити, чому дорівнює відношення середньоквадратичної швидкості молекул за температури 1 000 К до середньоквадратичної швидкості молекул за температури 250 К: $$ \frac{v_{\text{кв 1000 К}}}{v_{\text{кв 2500 К}}}=\frac{\sqrt{\frac{3R\cdot 1000\ \text{К}}{M}}}{\sqrt{\frac{3R\cdot 250\ \text{К}}{M}}}=\sqrt{\frac{1000\ \text{К}}{250\ \text{К}}}=2. $$

Відповідь: A.

ТЕМА: Молекулярна фізика та термодинаміка. Рівняння стану ідеального газу. Відносна вологість.

Завдання скеровано на оцінювання вміння розв’язувати комбіновані задачі з використанням рівняння стану ідеального газу й формул, що стосуються вологості повітря.

Дано:
\(V=0,83\ \text{м}^3\)
\(t=100\ ^\circ\text{С}\)
\(p=10^5\ \text{Па}\)
\(M=18\cdot 10^{-3}\ \frac{\text{кг}}{\text{моль}}\)

1. Знайти:
\(m\ -\ ?\)

$$ pV=\frac mM RT, $$ де \(p\) – тиск, \(V\) – об’єм, \(R\) – універсальна газова стала, \(T\) – температура, \(m\) – маса газу, \(M\) – молярна маса речовини.

У рівняння стану ідеального газу треба підставити температуру в кельвінах (К): \begin{gather*} T=t+273=100+273=373\ (\text{К}). \end{gather*}

Тоді з рівняння стану ідеального газу можна виразити масу газу:

2. Знайти:
\(\mathbf{\varphi}\ -\ ?\)

Відносну вологість повітря можна визначити за формулою: $$ \mathbf{\varphi}=\frac{p_{\text{а}}}{p_{\text{н. п.}}}\cdot 100\ \text{%}, $$ де \(\mathbf{\varphi}\) – відносна вологість повітря, \(p_{\text{н. п.}}\) – тиск насиченої пари, \(p_{\text{а}}\) – парціальний тиск водяної пари.

За умовою тиск насиченої пари води \(p_{\text{н. п.}}=100\ \text{кПа}\), а тиск водяної пари, що утворилась під час нагрівання, \(p_{\text{а}}=10^5\ \text{Па}\).

Тож

Відповідь: 1. 0,48. 2. 100.

ТЕМА: Основи молекулярно-кінетичної теорії.

Завдання скеровано на перевірку розуміння формул, що стосуються молекулярно-кінетичної теорії (МКТ).

A \(p=\frac 13nm_0v^2\), де \(n\) – концентрація молекул газу, \(m_0\) – маса молекули, \(\underline{v}\) – середня швидкість молекули, \(p\) – тиск ідеального газу. Рівняння визначає зв’язок мікроскопічного параметра (середньої швидкості молекули) і макроскопічного параметра (тиск). Воно є основним рівнянням МКТ.

Б \(E=\frac 32 kT\), де \(k\) – стала Больцмана, \(T\) – температура. Рівняння визначає зв’язок середньої кінетичної енергії одноатомного газу та його температури.

B \(pV=\frac mM RT\), де \(p\) – тиск, \(V\) – об’єм, \(R\) – універсальна газова стала, \(T\) – температура, \(m\) – маса газу, \(M\) – молярна маса речовини. Рівняння визначає зв’язок між трьома макроскопічними параметрами газу – температурою, тиском та об’ємом і є рівнянням стану ідеального газу.

Г \(\Delta U=cm\Delta T\), де \(U\) – внутрішня енергія, \(c\) – питома теплоємність, \(m\) – маса газу, \(T\) – температура. Рівняння описує зміну внутрішньої енергії зі зміною температури.

Д \(Q=\Delta U+A\), де \(Q\) – кількість теплоти, \(U\) – внутрішня енергія, \(A\) – робота. Рівняння описує перший закон термодинаміки: кількість теплоти \(Q\), передана системі, іде на зміну внутрішньої енергії системи \((\Delta U)\) та на виконання системою роботи \(A\) проти зовнішніх сил..

Відповідь: 1А, 2Д, 3В, 4Б.

ТЕМА: Молекулярна фізика й термодинаміка. Рівняння стану ідеального газу.

Завдання скеровано на перевірку розуміння особливостей ізопроцесів.

За графіком, наведеним в умові завдання, можна зробити висновок, що процес переводить газ зі стану з низьким тиском і малим об’ємом у стан із більшими тиском й об’ємом.

Тиск \(p\), об’єм \(V\) й температура газу \(T\) пов’язані між собою рівнянням стану $$ pV=nRT, $$ де \(p\) – тиск, \(V\) – об’єм, \(R\) – газова стала, \(T\) – температура, \(n\) – кількість речовини.

Тож температуру можна виразити з рівняння стану: $$ T=\frac{pV}{nR}. $$

Тобто внаслідок підвищення тиску й об’єму температура підвищується.

Відповідь: A.

ТЕМА: Молекулярна фізика й термодинаміка. Ізопроцеси.

Завдання скеровано на перевірку розуміння особливостей ізопроцесів.

Тиск \(p\), об’єм \(V\) й температура газу \(T\) пов’язані між собою рівнянням стану $$ pV=nRT, $$ де \(p\) – тиск, \(V\) – об’єм, \(R\) – газова стала, \(T\) – температура, \(n\) – кількість речовини.

У герметично закритій кімнаті кількість речовини й об’єм сталі.

Унаслідок роботи обігрівача температура повітря в кімнаті зростатиме.

Із рівняння стану можна виразити тиск: $$ p=\frac{nRT}{V}. $$

Тож, якщо температура зростає, а об’єм залишається незмінним, то тиск також зростатиме.

Тобто йдеться про ізохорний процес.

Відповідь: B.

ТЕМА: Молекулярна фізика й термодинаміка. Ізопроцеси.

Завдання скеровано на перевірку вміння аналізувати графіки ізопроцесів.

Тиск \(p\), об’єм \(V\) й температура газу \(T\) пов’язані між собою рівнянням стану $$ pV=nRT, $$ де \(p\) – тиск, \(V\) – об’єм, \(R\) – газова стала, \(T\) – температура, \(n\) – кількість речовини.

Зміну температури можна визначити з рівняння стану: $$ T=\frac{pV}{nR}. $$

На графіку, наведеному в умові, зображено цикл у координатах \(p - V\), складений із кількох ізопроцесів:

1–2: ізобарне розширення (\(p – const\), \(V\) збільшується).

Тож, якщо об’єм збільшується, а тиск залишається незмінним, то й температура збільшується.

2–3: ізотермічне стискання зі збільшенням тиску (\(T\ –\ const\), \(p\) зростає, \(V\) зменшується).

3–4: ізохорний процес зі зменшенням тиску (\(p\) зменшується, \(V\ –\ const\)).

Тож, якщо тиск зменшується, а об’єм залишається постійним, то й температура зменшується.

4–1: ізотермічне стискання зі збільшенням тиску (\(T\ –\ const\), \(p\) зростає, \(V\) зменшується).

А У процесі 2–3 температура зменшується, а повинна зростати.

Б У процесі 4–1 тиск зменшується, а має зростати.

В Цей графік є зображенням циклу в координатах \(p - T\).

Г Процес 1–2 є ізотермічним, а повинен бути ізобарним.

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Основні положення молекулярно-кінетичної теорії та експериментальне обґрунтування їх.

Завдання скеровано на перевірку розуміння будови речовини в різних фазових (агрегатних) станах.

Кристал солі – це тверда йонна речовина. У ній йони розташовані в певному порядку (утворюють кристалічні ґратки) на відстанях, порівнюваних із розмірами йонів. Тому електростатичні сили втримують йони, що здійснюють малі коливання навколо положень рівноваги.

Вода в басейні – рідина. Молекули рідини розташовані хаотично. Середня відстань між молекулами порівняна з їхніми розмірами. Тому міжмолекулярні сили втримують молекули біля положення рівноваги. Кожна молекула рідини певний час (бл. 10–11 с) здійснює рух, подібний до коливального, потім перескакує в інше місце та знову коливається біля нового положення рівноваги. Час «осідлого життя» молекули в сотні разів більший за час «переходу».

Атмосферний кисень – газ. Молекули газів розташовані безладно й на відстанях, які в десятки разів більші за розміри самих молекул. На таких відстанях молекули майже не взаємодіють одна з одною. Тому, безперервно зіштовхуючись, молекули газів розлітаються на всі боки доти, доки не зустрінуть якусь перешкоду, наприклад, стінки посудини.

Йонізований газ – це плазма, так званий четвертий агрегатний стан речовини. Слово «йонізований» означає, що від значної частини атомів або молекул відокремлений принаймні один електрон. Плазма має властивості, схожі на газоподібний стан речовини (частинки рухаються вільно й відстань між частинками значно більша за розмір частинок). На відміну від газу в плазмі є далекосяжна кулонівська взаємодія між частинками, тобто вони взаємодіють навіть на великих відстанях.

Відповідь: 1В, 2Б, 3А, 4Д.

ТЕМА: Властивості газів, рідин і твердих тіл. Насичена й ненасичена пара.

Завдання скеровано на перевірку розуміння особливостей температурних залежностей насиченої пари.

Тиск, об’єм і температура газу, який можна вважати ідеальним, пов’язані формулою $$pV=nRT,$$ де \(p\) – тиск, \(V\) – об’єм, \(n\) – кількість речовини, \(R\) – універсальна газова стала, \(T\) – температура.

Формула залежності тиску \(p\) від температури \(T\) така: $$p=\frac{nR}{V}T.$$

Оскільки об’єм посудини незмінний, то ця формула описує пряму. Графік залежності в початковому стані не є графіком прямої, тож в посудині не може бути просто газ.

Насичена пара – це пара, яка перебуває в стані динамічної рівноваги зі своєю рідиною. Тож насичена пара не може існувати без рідини в тій самій посудині.

Під час підвищення температури посудини, у якій перебуває рідина й насичена пара, підвищується інтенсивність випаровування. Відповідно концентрація молекул рідини в повітрі збільшується. Тиск насиченої пари в такому разі зростає і внаслідок підвищення температури (за тим же принципом, що й тиск ідеального газу), і завдяки збільшенню концентрації молекул. Тобто тиск зростає швидше, ніж для ідеального газу. Коли рідина повністю випаровується, концентрація молекул рідини в повітрі не може збільшуватися, далі тиск зростає з тою самою залежністю, що й для ідеального газу.

Відповідь: В.

ТЕМА: Молекулярна фізика і термодинаміка.

Завдання скеровано на перевірку розуміння поняття теплової рівноваги.

Стан теплової рівноваги – це такий стан макроскопічної системи, коли всі її макроскопічні параметри залишаються незмінними як завгодно довго.

Відповідь: Б.

ТЕМА: Молекулярна фізика та термодинаміка. Основи термодинаміки. Рівняння стану ідеального газу.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з використанням рівняння стану ідеального газу.

Тиск, об’єм і температура ідеального газу пов’язані рівнянням стану ідеального газу $$ pV=nRT=\frac mM RT, $$ де \(p\) – тиск, \(V\) – об’єм, \(n\) – кількість речовини, \(R\) – універсальна газова стала, \(T\) – температура, \(m\) – маса газу, \(M\) – молярна маса речовини.

Температуру газу можна визначити за формулою $$ T=pV=\frac{M}{mR}. $$

Значення тиску й об’єму для всіх станів, зображених на графіку такі (в умовних одиницях):

Тоді температури в кожному стані в умовних одиницях дорівнюватимуть:

З-поміж них вибираємо \(T_2=T_5\).

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Ізопроцеси.

Завдання скеровано на перевірку розуміння ізопроцесів та їхньої графічної інтерпретації.

Розгляньмо ізохорний процес 1–2 \((V=const),\) за якого тиск \(p\) зростає (див. рисунок). Отже, відповідно до рівняння Клапейрона температура \(T\) теж зростатиме (стрілочка, напрямлена вгору, означає зростання значення величини): $$ \frac pT=const\Rightarrow \frac{p\uparrow}{T\uparrow}=const. $$ Отже, процес 1–2 ‒ це ізохорне нагрівання (Б).

Розгляньмо ізобарний процес 2‒3 \((p=const),\) за якого об’єм \(V\) збільшується (див. рисунок). Отже, відповідно до рівняння Клапейрона, температура \(T\) теж зростатиме: $$ \frac VT=const\Rightarrow\frac{V\uparrow}{T\uparrow}=const. $$ Отже, процес 2‒3 ‒ це ізобарне нагрівання (А).

Розгляньмо ізотермічний процес 3‒4 \((T=const),\) за якого тиск \(p\) падає, а об’єм \(V\) збільшується (див. рисунок). Відповідно до рівняння Клапейрона: $$ pV=const\Rightarrow p\downarrow V\uparrow = const. $$ Отже, процес 3‒4 ‒ це ізотермічне розширення (Г).

Розгляньмо ізобарний процес 4‒1 \((p=const),\) за якого об’єм \(V\) зменшується (див. рисунок). Отже, відповідно до рівняння Клапейрона температура \(T\) теж зменшуватиметься (стрілочка, напрямлена вниз, означає зменшення значення величини): $$ \frac VT=const\Rightarrow\frac{V\downarrow}{T\downarrow}=const. $$ Отже, процес 4‒1 ‒ це ізобарне охолодження (Д).

Відповідь: 1Б, 2А, 3Г, 4Д.

ТЕМА: Молекулярна фізика та термодинаміка. Основи молекулярно-кінетичної теорії.

Завдання скеровано на перевірку розуміння макроскопічних параметрів, якими описують стан ідеального газу, і вміння інтерпретувати їх графічно.

Зміну станів газу описують рівнянням Клапейрона: $$ \frac{pV}{T}=\mathrm{const}, $$ із якого випливає, що абсолютна температура \(T\) прямо пропорційна добутку тиску \(p\) й об’єму \(V.\)

Розгляньмо кожен зі станів 1‒4 ідеального газу. Одну клітинку вважатимемо одиничним відрізком для обох величин: \begin{gather*} \boldsymbol с\boldsymbol т\boldsymbol а\boldsymbol н\boldsymbol\;\mathbf1\\[7pt] T_1\sim 5p\cdot 1V\sim 5pV;\\[7pt] \boldsymbol с\boldsymbol т\boldsymbol а\boldsymbol н\boldsymbol\;\mathbf2\\[7pt] T_2\sim 4p\cdot 2V\sim 8pV;\\[7pt] \boldsymbol с\boldsymbol т\boldsymbol а\boldsymbol н\boldsymbol\;\mathbf3\\[7pt] T_3\sim 3p\cdot 3V\sim 9pV;\\[7pt] \boldsymbol с\boldsymbol т\boldsymbol а\boldsymbol н\boldsymbol\;\mathbf4\\[7pt] T_4\sim 1p\cdot 6V\sim 6pV. \end{gather*}

Отже, найменшим є числовий коефіцієнт у стані \(1,\) температура газу буде найменшою у стані \(1.\)

Відповідь: A.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Властивості газів, рідин і твердих тіл.

Завдання скеровано на знання і розуміння явищ молекулярної фізики і термодинаміки.

Молекули рідини безперервно рухаються (коливаються біля положень рівноваги, час від часу перестрибують із місця на місце), але сили притягання не дають їм розлетітися.

Проте в рідині завжди є молекули, кінетична енергія яких у кілька разів перевищує її середнє значення. Коли ці швидкі молекули опиняються на поверхні рідини, їхньої енергії вистачає для того, щоб, подолавши притягання сусідніх молекул, залишити рідину.

З погляду молекулярно-кінетичної теорії (МКТ) під час пароутворення з поверхні рідини вилітають найшвидші молекули. І саме пароутворення з поверхні рідини називають випаровуванням.

Отже, явищу 1 відповідає опис Д.

Середня кінетична енергія \(\overline{E}_k\) поступального руху молекул ідеального газу із середнім квадратом швидкості \(\overline{v^2}\) (кінетична енергія поступального руху, що в середньому припадає на одну молекулу масою \(m_0\)) дорівнює: $$ \overline{E}_k=\frac{m_0\overline{v^2}}{2}. $$

Також середня кінетична енергія поступального руху молекул ідеального газу прямо пропорційна абсолютній температурі \(T:\) $$ \overline{E}_k=\frac 32 kT, $$ де \(k\) ‒ стала Больцмана.

Отже, середня швидкість хаотичного руху молекул (середня квадратична швидкість руху молекул \(\overline{v}_\text{кв}=\sqrt{\overline{v^2}}\)) прямо пропорційна абсолютній температурі: $$ \overline{v}_\text{кв}\sim T. $$

Отже, під час охолодження (зниження температури) газу (2) середня швидкість хаотичного руху молекул також зменшується (Г).

Відповідно під час нагрівання (підвищення температури) газу (4) середня швидкість хаотичного руху молекул збільшуватиметься (А).

Плавлення ‒ це процес переходу речовини з твердого стану в рідкий.

Після досягнення температури плавлення тверде кристалічне тіло починає плавитися, а його температура не змінюється незважаючи на те, що нагрівник продовжує працювати й передавати тілу певну кількість теплоти. Уся енергія, що надходить від нагрівника, іде на руйнування кристалічної ґратки тіла. У цей інтервал часу внутрішня енергія твердого тіла продовжує збільшуватися. Отже, процесу 3 відповідає опис B.

Відповідь: 1Д, 2Г, 3В, 4А.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Ізопроцеси в газах.

Завдання скеровано на перевірку розуміння макроскопічних параметрів, якими описують стан ідеального газу, і вміння інтерпретувати їх графічно.

Зміну станів газу описують рівнянням Клапейрона: $$ \frac{pV}{T}=const, $$ де \(p\) ‒ тиск, \(V\) ‒ об’єм, \(T\) ‒ абсолютна температура.

Графік 1 відповідає ізохорному охолодженню (\(V=const\) ‒ графік паралельний осі абсолютної температури, температура \(T\) під час цього знижується).

Графік 3 відповідає ізотермічному стисканню (\(T=const\) ‒ графік паралельний осі об’єму, під час цього об’єм зменшується).

Під час процесів 2 і 4 змінюються і об’єм, і температура. Під час процесу 4 хоча температура й знижується, але об’єм збільшується, тому тиск також знижуватиметься. Отже, цей процес не може бути ізобарним.

Графік 2 відповідає ізобарному охолодженню (об’єм зменшується пропорційно до зниження температури, отже, \(p=const\)).

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Рівняння стану ідеального газу.

Завдання скеровано на перевірку вміння описати стан газів рівнянням Менделєєва ‒ Клапейрона й обчислити необхідну величину.

Запишімо рівняння стану для гелію \((\mathrm{He})\) і для азоту \((\mathrm{N}_2):\) \begin{gather*} p(\mathrm{He})V(\mathrm{He})=\frac{m(\mathrm{He})}{M(\mathrm{He})}RT(\mathrm{He}),\\[6pt] p(\mathrm{N}_2)V(\mathrm{N}_2)=\frac{m(\mathrm{N}_2)}{M(\mathrm{N}_2)}RT(\mathrm{N}_2), \end{gather*} де \(p\) ‒ тиск газу, \(V\) ‒ об’єм газу, \(m\) ‒ маса газу, \(M\) ‒ молярна маса газу, \(R\) ‒ універсальна газова стала, \(T\) ‒ температура газу.

Поршень встановиться нерухомо на певній висоті за однакового тиску на поршень зверху й знизу: $$ p(\mathrm{He})=p(\mathrm{N}_2). $$

За умовою і температура, і маса газів однакові в обох частинах посудини. Поділімо ліві і праві частини рівнянь, щоб скоротити однакові величини:

Відношення висот тих частин циліндричної посудини, які займає кожен газ, становить \(7\) до \(1.\) Одну частину висоти посудини позначмо \(x.\) Тоді \begin{gather*} h(\mathrm{He})=7x,\\[7pt] h(\mathrm{N}_2)=x;\\[7pt] h(\mathrm{He})+h(\mathrm{N}_2)=1,2\ \text{м},\\[7pt] 7x+x=1,2\ \text{м},\\[7pt] 8x=1,2\ \text{м},\\[6pt] x=\frac{1,2\ \text{м}}{8}=0,15\ \text{м}. \end{gather*}

За умовою в нижній частині посудини міститься азот, \begin{gather*} h(\mathrm{N}_2)=x=0,15\ \text{м}, \end{gather*} тож поршень встановиться на висоті \(0,15\ \text{м}.\)

Відповідь: 0,15.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Кількість речовини.

Завдання скеровано на перевірку розуміння основних понять молекулярно-кінетичної теорії (кількість речовини, стала Авогадро, а також на перевірку вміння обчислювати кількість молекул газу).

Кількість структурних частинок у макроскопічних тілах величезна. Структурними частинками можуть бути атоми, молекули, йони, електрони або інші частинки чи певні групи частинок.

Для зручності обчислень використовують одиницю кількості речовини – моль. Будь-яка речовина кількістю \(1\ \text{моль}\) містить \(6\cdot 10^{23}\) (число Авогадро) структурних частинок.

Стала Авогадро \(N_A\approx 6\cdot 10^{23}\ \text{моль}^{‒1}\) – кількість структурних частинок \(N\) у речовині кількістю \(1\ \text{моль}.\) Кількість речовини позначають буквою \(\mathbf{\nu}\) грецької абетки й обчислюють за формулою: $$ \mathbf{\nu}=\frac{N}{N_A}. $$

Відповідно

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії (рівняння стану ідеального газу). Властивості газів, рідин і твердих тіл (теплота згоряння палива).

Завдання скеровано на перевірку вміння описувати стан газу за допомогою рівняння стану ідеального газу, визначати кількість теплоти згоряння палива.

Кількість теплоти \(Q,\) що виділиться внаслідок згоряння всього метану, який міститься в автомобільному газовому балоні, можна обчислити за формулою $$ Q=\mathbf{\lambda}m, $$ де \(\mathbf{\lambda}\) ‒ питома теплота згоряння палива, \(m\) ‒ маса метану.

Визначімо масу метану в балоні. Для цього опишімо за допомогою рівняння стану ідеального газу (рівняння Менделєєва ‒ Клапейрона) стан метану в балоні: $$ pV=\frac mMRT, $$ де \(p\) ‒ тиск газу в балоні, \(V\) ‒ об’єм метану в балоні (а це і є об’єм балона), \(m\) ‒ маса метану, \(M\) ‒ молярна маса метану, \(R\) ‒ універсальна газова стала, \(T\) ‒ температура метану в балоні.

Виразімо з рівняння стану масу: $$ m=\frac{pVM}{RT}. $$

Переведімо значення всіх величин у систему SI:

Підставимо ці значення у формулу для обчислення маси:

Підставимо значення маси у формулу для визначення кількості теплоти згоряння метану:

Відповідь: 400.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Рівняння стану ідеального газу.

Завдання скеровано на перевірку знання рівняння стану ідеального газу і вміння за допомогою його описувати стан газу.

1. За умовою випарувалася половина зрідженого гелію, тобто

Відповідно можна обчислити кількість речовини \(\mathbf{\nu}\) гелію: $$ \mathbf{\nu}=\frac mM=\frac{\mathbf{\rho}V}{M}. $$

Попередньо виразімо значення густини \(\mathbf{\rho}\) гелію в одиницях SI ‒ у кілограмах на метр кубічний \((\text{кг/м}^3):\)

Обчислімо кількість речовини \(\mathbf{\nu}\) гелію, що випарувався:

Опишімо рівнянням стану ідеального газу (рівняння Менделєєва ‒ Клапейрона) стан гелію в резервуарі до того, як туди закачали гелій, що випарувався: $$ p_1V_1=\mathbf{\nu}_1RT_1, $$ де \(p_1\) ‒ початковий тиск газу в резервуарі, \(V_1\) ‒ об’єм гелію, який вже міститься в резервуарі (це і є об’єм резервуара), \(\mathbf{\nu}_1\) ‒ кількість речовини в резервуарі, \(R\) ‒ універсальна газова стала, \(T_1\) ‒ температура гелію в резервуарі.

Знайдімо із цього рівняння, початкову кількість речовини \(\mathbf{\nu}\) гелію в резервуарі:

Тепер можна визначити кількість речовини газу в резервуарі після того, як у нього закачали гелій, зібраний після випаровування:

Відповідь: 1062,5.

2. Опишімо стан газу в резервуарі після закачування гелію ‒ зміниться кількість речовини \(\mathbf{\nu}_2\) (збільшиться), отже, збільшиться тиск \(p_2,\) абсолютна температура гелію в резервуарі залишиться сталою \((T_2=T_1=const),\) об’єм, який займатиме гелій, теж не зміниться \((V_2=V_1):\) $$ p_2V_2=\mathbf{\nu}_2RT_2. $$

Обчислімо тиск, який установиться в резервуарі:

Щоб визначити зміну тиску в резервуарі у відсотках, складімо пропорцію:

Отже, \(\Delta p\ (\text{%})=106,25\ \text{%}-100\ \text{%}=6,25\ \text{%}.\)

Відповідь: 6,25.

Відповідь: 1. 1062,5. 2. 6,25.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Рівняння стану ідеального газу.

Завдання скеровано на перевірку розуміння і вміння застосовувати рівняння стану газу.

Запишімо рівняння стану газу до накачування і після: \begin{gather*} p_1V=\frac{m_1}{M}RT,\\[6pt] p_2V=\frac{m_2}{M}RT, \end{gather*} де \(p_1\) і \(p_2\) ‒ початковий тиск і тиск повітря після накачування відповідно, \(m_1\) і \(m_2\) ‒ маса повітря в м’ячі до і після накачування. Середня молярна маса повітря \(M,\) універсальна газова стала \(R,\) абсолютна температура повітря \(T\) й об’єм \(V,\) який займає повітря в м’ячі, ‒ ці величини залишаються незмінними для обох станів повітря в м’ячі.

Запишімо формули для маси повітря як добуток густини \(\mathbf{\rho}\) і відповідного об’єму повітря в м’ячі \(V_1\) або \(V_2,\) зважаючи на кількість накачувань \(N\) (\(V_0\) ‒ об’єм повітря за одне накачування): \begin{gather*} m_1=\mathbf{\rho}\cdot V_1,\\[7pt] m_2=\mathbf{\rho}\cdot V_2=\mathbf{\rho}\cdot (V_1+N\cdot V_0). \end{gather*}

Підставімо в рівняння стану газу замість мас відповідні вирази й поділімо ліві і праві частини цих рівнянь:

Обчислімо шукану величину ‒ кількість накачувань:

Відповідь: 10.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Середня квадратична швидкість теплового руху молекул.

Завдання скеровано на перевірку знання і розуміння поняття середньої квадратичної швидкості руху молекул.

Запишімо основне рівняння молекулярно-кінетичної теорії, яке показує залежність тиску \(p\) ідеального газу від маси \(m_0\) його молекул і середнього квадрата швидкості \(\overline{v^2}\) їхнього руху: $$ p=\frac 13m_0n\overline{v^2}. $$

Зауважмо, що \(m_0\) ‒ це маса однієї молекули, а \(n\) ‒ це концентрація молекул газу, що дорівнює кількості \(N\) молекул в одиниці об’єму \(V:\) $$ n=\frac NV. $$

Отже, \begin{gather*} p=\frac 13m_0\cdot \frac NV\cdot \overline{v^2}=\frac{m\cdot \overline{v^2}}{3V}, \end{gather*} де \(m=m_0\cdot N\) ‒ маса газу.

Середня квадратична швидкість пов’язана із середнім квадратом швидкості таким співвідношенням: \begin{gather*} \overline{v}_\text{кв}=\sqrt{\overline{v^2}}. \end{gather*}

Звідси \begin{gather*} \overline{v^2}=(\overline{v}_\text{кв})^2. \end{gather*}

Підставімо цей вираз для середнього квадрату швидкості в основне рівняння молекулярно-кінетичної теорії і визначімо середню квадратичну швидкість:

Відповідь: Г.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Ізопроцеси в газах.

Завдання скеровано на перевірку вміння описати стан газу за допомогою рівняння стану газу (Менделєєва ‒ Клапейрона).

Запишімо рівняння Менделєєва ‒ Клапейрона для стану \(1\) і \(2\) ідеального газу (\(p\) ‒ тиск, \(V\) ‒ об’єм, \(T\) ‒ абсолютна температура): \begin{gather*} \frac{p_1V_1}{T_1}=\frac mMR,\\[6pt] \frac{p_2V_2}{T_2}=\frac mMR. \end{gather*}

Права частина однакова, оскільки записуємо рівняння для того самого ідеального газу масою \(m,\) молярна маса якого \(M,\) універсальна газова стала \(R.\)

Уважатимемо сторону клітинки за одиничний відрізок: \begin{gather*} p_1=2p,\ \ T_1=3T,\\[7pt] p_2=4p,\ \ T_2=6T. \end{gather*}

Запишімо рівняння Клапейрона: \begin{gather*} \frac{2pV_1}{3T}=\frac{4pV_2}{6T}. \end{gather*}

Рівність виконуватиметься, якщо \begin{gather*} V_1=V_2. \end{gather*} (тобто об’єм залишається сталим: \(V=\mathrm{const}\)).

Процес змінювання стану даного газу деякої маси, що відбувається за незмінного об’єму, називають ізохорним процесом: $$ \frac pT=\mathrm{const}=\frac mM\cdot \frac RV. $$

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Основні положення молекулярно-кінетичної теорії. Основи термодинаміки. Внутрішня енергія.

Завдання скеровано на перевірку знання і розуміння основних понять молекулярно-кінетичної теорії та їхнього зв’язку між собою.

1. Гелій – одноатомний газ. Атоми такого газу рухаються лише поступально, тому, щоб визначити його внутрішню енергію \(U,\) треба середню кінетичну енергію \(\overline{E}_k\) поступального руху атомів $$ \overline{E}_k=\frac{m_0\overline{v}^2_\text{кв}}{2} $$ помножити на кількість атомів \(N:\) $$ N=\frac mM N_A. $$

Тобто \begin{gather*} U=\overline{E}_k\cdot N,\\[6pt] U=\frac{m_0\overline{v}^2_\text{кв}}{2}\cdot \frac mM N_A,\\[6pt] U=M\cdot\frac{\overline{v}^2_\text{кв}}{2}\mathbf{\nu}, \end{gather*} де \(M=m_0\cdot N_А\) (\(M\) – молярна маса, \(m_0\) – маса молекули (атома) цієї речовини, \(N_А\) – стала Авогадро), \(\mathbf{\nu}=\frac mM\) (\(\mathbf{\nu}\) – кількість речовини, \(m\) – маса речовини).

Відповідь: 18.

2. Середню кінетичну енергію поступального руху молекул ідеального газу (кінетична енергія поступального руху, що в середньому припадає на одну молекулу) обчислюють за формулою $$ \overline{E}_k=\frac{m_0\overline{v}^2_\text{кв}}{2}. $$

З іншого боку середня кінетична енергія поступального руху молекул ідеального газу прямо пропорційна абсолютній температурі \(T:\) $$ \overline{E}_k=\frac 32 kT, $$ де \(k\) – стала Больцмана.

Прирівняймо праві частини цих формул: $$ \frac{m_0\overline{v}^2_\text{кв}}{2}=\frac 32 kT. $$

Перетворімо отриману рівність так, щоб можна було визначити температуру газу, використовуючи фізичні величини з умови завдання: \begin{gather*} m_0=\frac{M}{N_A},\\[6pt] \frac{M}{N_A}\cdot \frac{\overline{v}^2_\text{кв}}{2}=\frac 32 kT,\\[6pt] \frac{M\overline{v}^2_\text{кв}}{2}=\frac 32 kN_AT, \end{gather*} де добуток сталої Больцмана і сталої Авогадро дорівнює універсальній газовій сталій \(R:\)

Відповідь: 1500.

Відповідь: 1. 18. 2. 1500.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Рівняння стану ідеального газу.

Завдання скеровано на перевірку знання і застосування рівняння стану ідеального газу.

Запишімо рівняння стану ідеального газу (рівняння Менделєєва – Клапейрона): $$ pV=\frac mM RT, $$ де \(p\) – тиск, \(V\) − обʼєм, \(m\) – маса газу, \(M\) – молярна маса газу, \(R\) – універсальна газова стала, \(T\) – абсолютна температура.

Перетворімо це рівняння, щоб можна було визначити густину \(\mathbf{\rho}\) газу в балоні: \begin{gather*} \mathbf{\rho}=\frac mV,\\[6pt] \mathbf{\rho}=\frac mV=\frac{pM}{RT}. \end{gather*}

Запишімо температуру в градусах Кельвіна й обчислімо густину газу:

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Стала Авогадро.

Завдання скеровано на перевірку знання і розуміння кількості речовини й числа Авогадро.

У будь-якій речовині кількістю один моль міститься та сама кількість \((6,02\cdot 10^{23})\) її структурних частинок – атомів, йонів або молекул. Кількість речовини не залежить від її густини. Цю кількість частинок називають сталою Авогадро: $$ N_A\approx 6,02\cdot 10^{23}\ \text{моль}^{-1}. $$

За умовою завдання кількість речовини обох металів однакова – \(1\ \text{моль},\) тож і кількість атомів в металі кількістю речовини \(1\ \text{моль}\) та сама: $$ N_1=N_2. $$

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Середня квадратична швидкість теплового руху молекул.

Завдання скеровано на перевірку знання і розуміння зв’язку фізичних величин, що характеризують рух молекул ‒ середня квадратична швидкість руху молекул, середній квадрат швидкості, середня кінетична енергія поступального руху молекул ідеального газу.

Квадратний корінь із середнього квадрата швидкості називають середньою квадратичною швидкістю руху молекул \((\overrightarrow{v}_\text{кв}):\) $$ \overrightarrow{v}_\text{кв}=\sqrt{\overline{v^2}}. $$

(Середній квадрат швидкості \((\overline{v^2}):\) $$ \overline{v^2}=\frac{v_1^2+v_2^2+\text{...}+v_N^2}{N}, $$ де \(N\) ‒ кількість молекул; \(v_1, v_2, \text{...} v_N\) ‒ швидкості руху окремих молекул.)

Середній квадрат швидкості \(\overline{v^2}\) можна визначити з формули для середньої кінетичної енергії \(\overline{E}_\text{к}\) поступального руху молекул ідеального газу (кінетична енергія поступального руху, що в середньому припадає на одну молекулу масою \(m_0\)): $$ \overline{E}_\text{к}=\frac{m_0\overline{v^2}}{2}. $$

Залежність середньої кінетичної енергії поступального руху молекул ідеального газу від абсолютної температури \(T\) визначмо за формулою: $$ \overline{E}_\text{к}=\frac 32kT, $$ де \(k\) ‒ стала Больцмана.

Прирівняймо обидва вирази для визначення середньої кінетичної енергії поступального руху молекул ідеального газу: $$ \frac{m_0\overline{v^2}}{2}=\frac 32kT, $$ звідки $$ \overline{v^2}=\frac{3kT}{m_0}. $$

Отже, коли склянку заповнили снігом (див. рисунок 1), то температура становила \(t_1=-23\ ^\circ\mathrm{C}\) (абсолютна температура дорівнюватиме \(T_1=t_1+273=-23+273=250\ \text{K}\): $$ \overline{v}_\text{кв1}=\sqrt{\overline{v_1^2}}=\sqrt{\frac{3kT_1}{m_0}}. $$

Коли сніг у склянці розтанув, а вода нагрілася (див. рисунок 2), то температура \(t_2=87\ ^\circ\mathrm{C}\) (абсолютна температура дорівнюватиме \(T_2=t_2+273=87+273=360\ \text{K}\): $$ \overline{v}_\text{кв2}=\sqrt{\overline{v_2^2}}=\sqrt{\frac{3kT_2}{m_0}}. $$

Тепер визначимо, у скільки разів збільшилася середня квадратична швидкість руху молекул гелію в кульці:

Отже, середня квадратична швидкість руху молекул гелію в кульці збільшилася в \(1\mathord{,}2\) раза.

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Ізопроцеси в газах.

Завдання скеровано на перевірку знання і розуміння ізопроцесів, а саме ізохорного.

Ізохорний процес ‒ це процес змінювання стану даного газу деякої маси, що відбувається за незмінного об’єму \((V=\mathrm{const}).\) Ділянки графіка \(2\rightarrow 3\) і \(4\rightarrow 1\) є ізохорами.

Що більшим є об’єм газу \((V_2\gt V_1),\) то менші концентрація цього газу й тиск, який він чинить. Ділянка графіка \(2\rightarrow 3\) (див. рисунок) відповідатиме ізохорному нагріванню, тому що температура підвищується, а ділянка графіка \(4\rightarrow 1\) ‒ це ізохорне охолодження.

Ділянки графіка \(1\rightarrow 2\) і \(3\rightarrow 4\) (див. рисунок) є ізобарами. Що більшим є тиск газу, за якого відбувається ізобарний процес \((p_2\gt p_1),\) то менший об’єм займає газ й то нижче розташована ізобара.

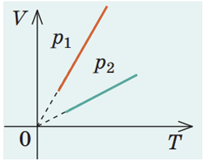
Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Стала Авогадро.

У будь-якій речовині кількістю \(1\ \text{моль}\) міститься однакова кількість атомів або молекул, ‒ стільки, скільки атомів Карбону міститься у вуглеці масою \(12\ \text{г}.\) Це стала Авогадро \(N_\mathrm{А},\) її одиниця – \(\text{моль}^{-1}.\)

Фізичну величину, яка дорівнює частці від ділення кількості структурних частинок речовини \(N\) до числа Авогадро, називають кількістю речовини \(\mathbf{\nu}:\) $$ \mathbf{\nu}=\frac{N(X)}{N_\mathrm{A}}, $$ де \(N(X)\) ‒ кількість структурних частинок речовини \(X.\)

Отже, щоб визначити кількість молекул \(N\) газу \(X\) у балоні, треба помножити одну порцію молекул \((N_\mathrm{А})\) на кількість цих порцій \((\mathbf{\nu}):\)

Відповідь: B.

Тема: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Основне рівняння молекулярно-кінетичної теорії ідеального газу. Концентрація молекул газу.

Завдання скеровано на перевірку знання і розуміння поняття концентрації молекул газу й уміння аналізувати різні практичні ситуації, пов’язані з концентрацією газу.

Концентрація \(n\) молекул газу ‒ це фізична величина, яка дорівнює кількості \(N\) молекул в одиниці об’єму \(V\) газу: $$ n=\frac NV. $$

Отже, якщо не змінюватимуться кількість молекул й об’єм, у якому ці молекули містяться, то концентрація залишиться тією самою. Проаналізуймо наведені ситуації.

Коли людина набирає повітря в легені, то об’єм легень збільшується, і кількість молекул повітря також збільшується. Тобто концентрація молекул у цьому разі змінюватиметься.

Об’єм пробитої шини, можливо, і не буде зменшуватися, а кількість молекул повітря, яке заповнювало шину, зменшуватиметься. Тому концентрація молекул у цій ситуації змінюватиметься.

Насиченою називають пару, яка перебуває в стані динамічної рівноваги зі своєю рідиною. Динамічна рівновага встановлюється між процесами конденсації і випаровування ‒ кількість молекул, які повертаються в рідину, дорівнюватиме кількості молекул, які за той самий час залишають рідину. Це можливо в закритій посудині, тобто об’єм пари між поверхнею рідини й кришкою посудини, залишатиметься сталим. Концентрація молекул насиченої пари ‒ найбільша можлива концентрація молекул пари за даної температури. Якщо ж насичену пару охолоджувати, то кількість молекул, що вилітатимуть з поверхні рідини, зменшуватиметься, а значить, концентрація вже ненасиченої пари теж стане меншою.

Говорячи про закритий балон, розуміємо, що об’єм, який займає кисень, залишається незмінним. Оскільки балон не відкривають, то кількість молекул кисню в ньому теж не змінюється, а отже, концентрація молекул не може змінитися. У результаті остигання кисню зменшиться швидкість руху молекул і, відповідно, тиск кисню в балоні.

Відповідь: Г.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Ізопроцеси в газах.

Завдання скеровано на перевірку знання і розуміння ізопроцесів в газах і вміння будувати й читати графіки відповідних ізопроцесів.

В умові завдання є графік ізобарного процесу ‒ для газу деякої маси відношення об’єму газу до температури є незмінним, якщо тиск газу не змінюється \((p=\mathrm{const}):\) \begin{gather*} \frac{V_1}{T_1}=\frac{V_2}{T_2},\\[6pt] \text{або}\ \frac VT=\mathrm{const}=\frac mM\cdot \frac Rp. \end{gather*}

Збільшуючи чисельник (об’єм), треба в стільки ж разів збільшувати знаменник (абсолютну температуру), щоб значення дробу було незмінним.

Графік ізобарного процесу називають ізобарою. Як випливає із закону Ґей-Люссака, за незмінного тиску об’єм газу даної маси прямо пропорційний його температурі: \begin{gather*} V=\mathrm{const}\cdot T,\\[6pt] \text{або}\ T=\mathrm{const}\cdot V. \end{gather*}

Графіком цієї залежності в координатах \(T,\ V\) є пряма, що проходить через початок координат (див. рисунок в умові). Аналізуючи графік, доходимо висновку, що з наближенням до абсолютного нуля об’єм ідеального газу має зменшитися до нуля. Зрозуміло, що це неможливо, оскільки реальні гази за низьких температур перетворюються на рідини.

У координатах \(p,\ V\) і \(p,\ T\) ізобари перпендикулярні до осі тиску. Єдиний рисунок із варіантів відповіді, на якому зображено графік \(p=\mathrm{const}\) ‒ варіант В:

Відповідь: B.

ТЕМА: Молекулярна фізика й термодинаміка. Основи молекулярно-кінетичної теорії. Ізопроцеси в газах.

Завдання скеровано на перевірку знання і розуміння ізопроцесів у газах і їхніх графіків.

Процес змінювання стану газу незмінної маси, що відбувається за сталого тиску \(p,\) називають ізобарним. Згідно з рівнянням Клапейрона $$ \frac{pV_1}{T_1}=\frac{pV_2}{T_2}, $$ де \(V_1\) і \(T_1\) ‒ об’єм й абсолютна температура газу в стані \(1;\) а \(V_2\) і \(T_2\) ‒ параметри газу в стані \(2.\) Після скорочення на \(p\) дістанемо: $$ \frac{V_1}{T_1}=\frac{V_2}{T_2}. $$

Графіки ізобарних процесів називають ізобарами. У координатах \(p, V\) ізобари перпендикулярні до осі тиску (див. рисунок).

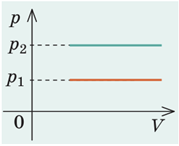
Отже, процесу за сталого тиску \((p=\mathrm{const})\) газу відповідає графік Г.

Графік А відповідає процесу за сталого об’єму \((V=\mathrm{const}):\)

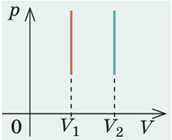
Графік Б ‒ це ізотерма, графік ізотермічного процесу \((T=\mathrm{const}):\)

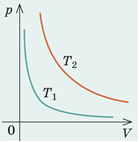
Проаналізувавши графік В, бачимо, що зростає й об’єм, і тиск, тож відповідно до рівняння Клапейрона підвищуватиметься температура: $$ \frac{pV}{T}=\mathrm{const}. $$

Відповідь: Г.

ТЕМА: Молекулярна фізика й термодинаміка. Основи молекулярно-кінетичної теорії. Рівняння стану ідеального газу.

Завдання скеровано на перевірку знання і розуміння зміни стану ідеального газу, а також вміння скласти рівність тисків.

Гелій до нагрівання мав певну температуру \(T_1\) і займав певний об’єм \(V_1.\) Цей газ створював тиск \(p\) на стінки посудини й на поршень. Зверху ж на рухомий поршень діє атмосферний тиск \(p_\text{атм},\) а також сам поршень теж діє з певним тиском \(p_\text{п}\) на гелій в посудині (див. рисунок).

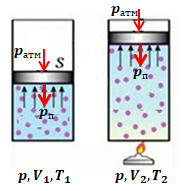
Отже, можемо прирівняти тиск, який створює гелій, і суму тисків атмосферного і поршня, оскільки поршень не рухається: $$ p=p_\text{атм}+p_\text{п}. $$

Розпишімо, чому дорівнює тиск гелію і тиск поршня. Відповідно до рівняння стану ідеального газу (рівняння Менделєєва ‒ Клапейрона) $$ pV_1=\frac mMRT_1, $$ де \(m\) ‒ маса газу, \(M\) ‒ молярна маса, \(R\) ‒ універсальна газова стала.

Тиск, який створює поршень, визначатимемо за формулою $$ p_\text{п}=\frac FS, $$ де \(S\) ‒ площа поверхні, на яку поршень створює тиск; а \(F=P=m_\text{п}g\) ‒ сила тиску, якою у цьому прикладі є вага \(P,\) що дорівнює добутку маси \(m_\text{п}\) поршня і прискорення \(g\) вільного падіння.

Потім за умовою гелій нагріли до температури \(T_2,\) відповідно збільшився об’єм до \(V_2.\) Тиск при цьому залишився сталим, оскільки маса газу не змінилася, а поршень легко рухається в посудині, тобто відбувся ізопроцес, а саме, ізобарне нагрівання: $$ pV_2=\frac mMRT_2. $$

Запишімо загальне рівняння зміни стану газу після зміни абсолютної температури на \(\Delta T\) і відповідно зміни об’єму на \(\Delta V:\) $$ p\Delta V=\frac mMR\Delta T, $$ звідки тиск дорівнюватиме $$ p=\frac{mR\Delta T}{M\Delta V}. $$

Підставімо всі вирази для відповідних величин у рівність тисків: $$ \frac{mR\Delta T}{M\Delta V}=p_\text{атм}+\frac{m_\text{п}g}{S}. $$

Обчислімо значення правої частини рівності, щоб математично легше було визначити зміну об’єму \(\Delta V:\)

Отже, визначмо, на скільки збільшиться об’єм гелію:

Відповідь: Г.

ТЕМА: Молекулярна фізика й термодинаміка. Основи молекулярно-кінетичної теорії. Маса і розмір молекул. Концентрація.

Завдання скеровано на перевірку знання і розуміння графічної інтерпретації залежності фізичних величин, а саме, концентрації молекул газу від об’єму.

Концентрація \(n\) молекул газу ‒ фізична величина, яка дорівнює числу \(N\) молекул в одиниці об’єму \(V\) газу: $$ n=\frac NV. $$

Як бачимо з формули, концентрація обернено залежить від об’єму: $$ n\sim \frac 1V. $$

За умовою газ стискають в посудині, отже, об’єм зменшується (знаменник зменшується), значить, концентрація збільшується. При цьому кількість молекул газу не змінюється ‒ газ міститься в посудині, його стискають рухомим поршнем, про витік газу мова не йде, отже, зміна концентрації залежатиме тільки від зміни об’єму.

Така обернена залежність величин відповідає математичній функції $$ y=\frac 1x, $$ графіком якої є вітки гіперболи.

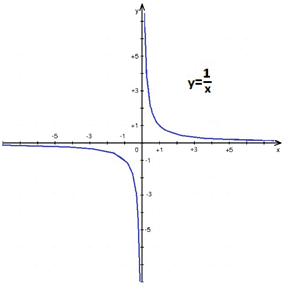
Відповідно, графіком залежності концентрації молекул газу від об’єму буде вітка гіперболи з додатними значеннями (об’єм і концентрація не можуть бути від’ємними).

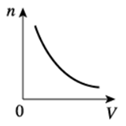
Графіки Б й В, які відображають лінійну залежність величин, не відповідають шуканій оберненій залежності. А за графіком Г зі збільшенням об’єму концентрація збільшується, що є неправильним у визначеній математичній залежності концентрації від об’єму.

Відповідь: A.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Ізопроцеси в газах.

Завдання скеровано на перевірку розуміння ізопроцесів і їхньої графічної інтерпретації.

Розгляньмо кожну ділянку графіка на рисунку з умови.

Ділянка 1‒2: тиск сталий \(p=\mathrm{const}\) (ізобарний процес), абсолютна температура \(T\) підвищується. Якщо зафіксувати тиск і нагрівати газ, то об’єм повинен збільшуватися. Отже, відповідно до рівняння Клапейрона для ізобарного процесу об’єм \(V\) теж збільшуватиметься: \begin{gather*} \frac VT=\mathrm{const}\Rightarrow \frac{V\uparrow}{T\uparrow}=\mathrm{const} \end{gather*} (стрілочка, напрямлена вгору, означає зростання значення величини; стрілочка, напрямлена вниз, означає зменшення значення величини).

Отже, ділянка 1‒2 графіка відповідає ізобарному нагріванню.

Ділянки 2‒3 й 4‒1 відповідають ізотермічному процесу, коли \(T=\mathrm{const},\) а тиск \(p\) зростає (див. рисунок). Це означає, що відповідно до рівняння Клапейрона для ізотермічного процесу об’єм зменшуватиметься: $$ pV=\mathrm{const}\Rightarrow p\uparrow V\downarrow =\mathrm{const}. $$

Отже, ділянки 2‒3 й 4‒1 графіка відповідають ізотермічному стисканню.

Ділянка 3‒4: якщо зафіксувати об’єм й охолоджувати газ, то тиск повинен зменшуватися. Отже, відповідно до рівняння Клапейрона для ізохорного процесу якщо температура \(T\) знижуватиметься, то й тиск теж зменшуватиметься: $$ \frac pT=\mathrm{const}\Rightarrow \frac{p\downarrow}{T\downarrow}=\mathrm{const}. $$

Отже, ділянка 3‒4 графіка відповідає ізохорному охолодженню.

Тепер за визначеними процесами знайдімо відповідний графік у системі координат \(V,\ T.\)

За першим процесом ‒ ізобарне нагрівання ‒ можемо виключити рисунок Г: на його ділянці 1‒2 температура знижується.

Процес 2‒3 ‒ це ізотермічне стискання. Виключаємо рисунок Б: на ньому ділянка графіка 2‒3 відповідає ізотермічному розширенню.

Процес 3‒4 (ізохорне охолодження) на рисунках А і В збігається.

А от за процесом 4‒1 ‒ ізотермічне стискання ‒ правильним буде лише рисунок А. На рисунку Б ділянка графіка 4‒1 відповідає ізотермічному розширенню.

Відповідь: A.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Основне рівняння молекулярно-кінетичної теорії.

Завдання скеровано на перевірку знання і розуміння формули-наслідку з основного рівняння молекулярно-кінетичної теорії і формули, що виражає зв’язок середньої кінетичної енергії поступального руху молекул і температури.

Тиск \(p\) газу повністю визначає його абсолютна температура \(T\) й концентрація \(n\) молекул газу: $$ p=nkT, $$ де \(k=1,38\cdot 10^{-23}\ \text{Дж/К}\) ‒ стала Больцмана.

Запишімо це рівняння до підвищення температури й після: \begin{gather*} p_1=n_1kT_1,\\[7pt] p_2=n_2kT_2. \end{gather*}

За умовою абсолютна температура підвищилася втричі: $$ T_2=3T_1. $$

Також за умовою змінилася концентрація ‒ фізична величина, яка дорівнює кількості структурних одиниць речовини \(N\) в одиниці об’єму газу \(V\) (об’єм, який займає газ у балоні, залишився незмінним, тому що балон закритий): \begin{gather*} n_1=\frac{N_1}{V},\\[6pt] n_2=\frac{N_2}{V},\\[6pt] N_2=\frac 12N_1+\frac 12N_1\cdot 2. \end{gather*}

Відповідно до умови кожна друга молекула розпалася на два атоми. Отже, $$ N_2=\frac 12N_1(1+2)=1,5N_1. $$

Тепер визначімо, у скільки разів збільшився тиск газу:

Отже, тиск газу в балоні збільшиться в 4,5 раза.

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Рівняння стану ідеального газу. Механіка. Елементи механіки рідин і газів. Тиск нерухомої рідини на дно й стінки посудини.

Завдання скеровано на перевірку знання і розуміння зв’язку між макроскопічними параметрами газу, а також на розуміння атмосферного й гідростатичного тиску.

Виразімо зв’язок між макроскопічними параметрами повітря (тиском \(p,\) об’ємом \(V\) і температурою \(T\)) в бульбашці, коли вона перебуває на глибині (положення 1), а потім спливає до поверхні озера (положення 2) за допомогою рівняння Клапейрона (маса і молярна маса повітря в бульбашці не змінюються): \begin{gather*} \frac{p_1V_1}{T_1}=\frac{p_2V_2}{T_2}. \end{gather*}

За умовою температура стала, отже, \begin{gather*} T_1=T_2,\\[7pt] p_1V_1=p_2V_2. \end{gather*}

Тиск \(p_1\) на глибині дорівнюватиме сумі атмосферного \(p_\text{атм}\) і гідростатичного \(p_\text{гідр}\) тиску: \begin{gather*} p_1=p_\text{атм}+p_\text{гідр},\\[7pt] p_1=p_\text{атм}+\mathbf{\rho}gh, \end{gather*} де \(\mathbf{\rho}\) ‒ густина рідини, \(g\) ‒ прискорення вільного падіння, \(h\) ‒ глибина.

А тиск біля поверхні дорівнює атмосферному тиску: \begin{gather*} p_2=p_\text{атм}. \end{gather*}

Запишімо відношення об’ємів, підставивши вирази для тисків:

Отже, об’єм бульбашки збільшиться у 2,5 раза.

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Ізопроцеси.

Завдання скеровано на перевірку розуміння ізопроцесів і їхньої графічної інтерпретації.

1. Розгляньмо, які з графіків відповідають ізотермічному процесу ‒ \(T=\mathrm{const}.\) Це графіки на рисунках А і Б ‒ тиск змінюється, температура залишається сталою. Процес розширення означає, що об’єм \(V\) збільшується, а тиск \(p\) падає (див. рисунок). Відповідно до рівняння Клапейрона для ізотермічного процесу: $$ pV=\mathrm{const}\Rightarrow p\downarrow V\uparrow=\mathrm{const} $$ (стрілочка, напрямлена вгору, означає зростання значення величини; стрілочка, напрямлена вниз, означає зменшення значення величини).

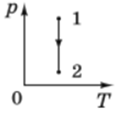
Отже, процесу ізотермічного розширення відповідає графік на рисунку А.

2. Відповідно розглянемо одразу ізотермічне стискання ‒ графік на рисунку Б.

Процес стискання означає, що об’єм \(V\) зменшується, а тиск \(p\) зростає (див. рисунок). Відповідно до рівняння Клапейрона для ізотермічного процесу: $$ pV=\mathrm{const}\Rightarrow p\uparrow V\downarrow=\mathrm{const}. $$

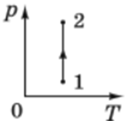
Отже, процесу ізотермічного стискання відповідає графік на рисунку Б.

3. Розгляньмо ізобарний процес ‒ \(p=\mathrm{const}.\) Можна було б припустити, що правильним буде графік, який відповідає сталому тиску, зображений на рисунку Д.

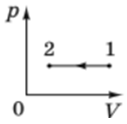
Під час цього об’єм \(V\) зменшується (див. рисунок). Але ж тоді, відповідно до рівняння Клапейрона для ізобарного процесу температура \(T\) теж буде зменшуватися: $$ \frac VT=\mathrm{const}\Rightarrow \frac{V\downarrow}{T\downarrow}=\mathrm{const}. $$

Тобто на рисунку Д зображений графік ізобарного охолодження.

На рисунку Г тиск змінюється, це не відповідає ізобарному процесу. Тоді розгляньмо рисунок В, на якому зображено графік залежності об’єму від абсолютної температури:

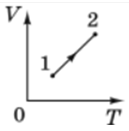
Якщо зафіксувати тиск і нагрівати газ, то об’єм повинен збільшуватися. Отже, відповідно до рівняння Клапейрона для ізобарного процесу якщо температура \(T\) підвищуватиметься, то й об’єм \(V\) теж збільшуватиметься: $$ \frac VT=\mathrm{const}\Rightarrow \frac{V\uparrow}{T\uparrow}=\mathrm{const}. $$

Отже, на рисунку В зображено графік ізобарного нагрівання.

4. І нарешті розгляньмо рисунок Г, що залишився. Як бачимо, графік на ньому відповідає сталому об’єму ‒ ізохорний процес \(V=\mathrm{const}.\)

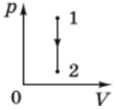
З’ясуймо, чи буде це процес охолодження. З графіка видно, що тиск \(p\) зменшується (див. рисунок). Отже, відповідно до рівняння Клапейрона для ізохорного процесу температура \(T\) теж знижуватиметься: $$ \frac pT=\mathrm{const}\Rightarrow \frac{p\downarrow}{T\downarrow}=\mathrm{const}. $$

Отже, графік на рисунку Г відповідає ізохорному охолодженню.

Відповідь: 1А, 2В, 3Г, 4Б.

Тема: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Стала Авогадро.

Завдання скеровано на перевірку знання і розуміння сталої Авогадро й кількості речовини.

У будь-якій речовині кількістю \(1\ \text{моль}\) міститься однакова кількість атомів або молекул, ‒ стільки, скільки атомів Карбону міститься у вуглеці масою \(12\ \text{г}.\) Це стала Авоґадро \(N_А,\) її одиниця – \(\text{моль}^{-1}.\)

Фізичну величину, яка дорівнює частці від ділення кількості структурних частинок речовини \(N\) на число Авогадро, називають кількістю речовини \(\mathbf{\nu}:\) $$ \mathbf{\nu}=\frac{N}{N_A}, $$ де \(N(X)\) ‒ кількість структурних частинок речовини \(X.\)