Молекулярна фізика і термодинаміка – Основи термодинаміки

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів.

Завдання скеровано на перевірку розуміння першого закону термодинаміки стосовно ізобарного процесу.

У ході ізобарного процесу виконується робота \(A\) і змінюється внутрішня енергія \(\Delta U\) газу, тому рівняння першого закону термодинаміки має вигляд $$ Q=\Delta U+A. $$

Під час ізобарного процесу передана газу кількість теплоти \(Q\) витрачається і на збільшення внутрішньої енергії газу, і на виконання механічної роботи. Якщо газ ідеальний одноатомний, то робота газу $$ A=p\Delta V, $$ де \(p\) ‒ тиск, \(\Delta V\) ‒ зміна об’єму,
а зміна його внутрішньої енергії $$ \Delta U=\frac 32p\Delta V. $$

Кількість теплоти, передана газу, така:

Або $$ Q=\frac{5\ m}{2\ M}R\Delta T=\frac 52 \style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}R\Delta T, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}\) ‒ кількість речовини, \(R\) ‒ універсальна газова стала, \(\Delta T\) ‒ зміна температури.

Виразімо з формули й обчислімо кількість речовини:

Відповідь: 6.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Кількість теплоти.

Завдання скеровано на перевірку розуміння переходу одного виду енергії в інший.

Рухоме тіло володіє кінетичною енергією \(E_k:\) $$ E_k=\frac{mv^2}{2}, $$ де \(m\) ‒ маса тіла, \(v\) ‒ швидкість руху тіла.

Оскільки, улучивши в дошку, куля втратила частину механічної енергії, то визначимо частку енергії \(Q,\) яку отримала куля:

Відповідь: 19,5.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Коефіцієнт корисної дії теплового двигуна і його максимальне значення.

Завдання скеровано на перевірку знання і розуміння формули для визначення коефіцієнта корисної дії ідеальної теплової машини.

Коефіцієнт корисної дії ідеальної теплової машини, що працює за циклом Карно з нагрівником, температура якого \(T_\text{н},\) і холодильником із температурою \(T_\text{х},\) можна визначити за формулою

За умовою абсолютна температура нагрівника у \(2,5\) раза більша за температуру холодильника: $$ T_\text{н}=2,5T_\text{х}. $$

Підставимо це співвідношення у формулу коефіцієнта корисної дії теплової машини:

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Принцип дії теплових двигунів. Коефіцієнт корисної дії і його максимальне значення.

Завдання скеровано на перевірку розуміння принципу дії теплових двигунів і вміння визначати коефіцієнт корисної дії різними способами.

Коефіцієнт корисної дії (ККД) \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}\) ‒ фізична величина, якою характеризують економічність теплового двигуна. Він дорівнює відношенню роботи \(A,\) виконуваної двигуном за цикл, до кількості теплоти \(Q,\) одержуваної від нагрівника: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}=\frac AQ. $$

Аналізуючи роботу теплових двигунів, французький інженер Саді Карно дійшов висновку, що найефективнішим \((\)із максимально можливим коефіцієнтом корисної дії \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}_{max})\) є ідеальний тепловий двигун, який працює за циклом із двох ізотермічних і двох адіабатних процесів. Карно довів, що ККД такого двигуна дорівнює: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}_{max}=\frac{T_\text{Н}-T_\text{Х}}{T_\text{Н}}, $$ де \(T_\text{Н}\) ‒ температура нагрівника; \(T_\text{Х}\) ‒ температура холодильника.

Прирівняймо ці два вирази: \begin{gather*} \frac AQ=\frac{T_\text{Н}-T_\text{Х}}{T_\text{Н}},\\[6pt] Q=\frac{A\cdot T_\text{Н}}{T_\text{Н}-T_\text{Х}}. \end{gather*}

Перш ніж виконати обчислення кількості теплоти від нагрівника, переведемо температуру в кельвіни:

Відповідь: 8.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Робота в термодинаміці. Ізопроцеси.

Завдання скеровано на перевірку вміння розв’язувати термодинамічні задачі з використанням графіка.

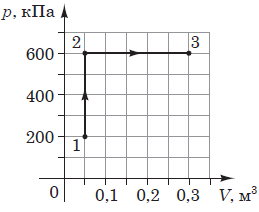
Рис. 1. Умова задачі

За рисунком можна визначити об’єм і тиск для всіх трьох точок процесу.

Дано:
\(p_1=200\ \text{кПа}\)
\(V_1=0,05\ \text{м}^3\)
\(p_2=600\ \text{кПа}\)
\(V_2=0,05\ \text{м}^3\)
\(p_3=600\ \text{кПа}\)
\(V_3=0,3\ \text{м}^3\)

Знайти:
\(A\ (\text{кДж})\ -\ ?\)

Перехід від стану 1 до стану 3 має два складники: ізохорне нагрівання, супроводжуване збільшенням тиску (1–2) та ізобарне розширення (2–3).

Робота в термодинамічному процесі виконується лише за зміни об’єму газу, тож в ізохорному процесі (1–2) робота не виконується.

Робота в ізобарному процесі (2–3) може бути обчислена за формулою $$ A=p\Delta V, $$ де \(p\) – тиск, \(\Delta V\) – зміна об’єму.

Тоді:

Відповідь: 150.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. ККД теплового двигуна.

Завдання скеровано на перевірку розуміння принципу роботи ідеальної теплової машини й знання графіків ізопроцесів.

Ідеальна теплова машина працює за циклом Карно (рис. 1). Його складниками є ізотермічне розширення (1–2), адіабатне розширення, супроводжуване охолодженням (2–3), ізотермічне зменшення об’єму (3–4) й адіабатне зменшення об’єму, супроводжуване нагріванням (4–1).

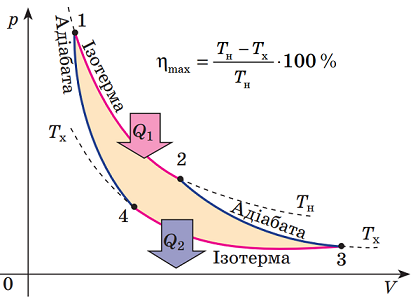
Рис. 1. Цикл Карно

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. ККД теплового двигуна.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі на обчислення коефіцієнта корисної дії теплової машини.

Дано:
\(A = 40\ \text{МДж}\)
\(Q_{\text{х}}=A\)

Знайти:
\(\text{ККД}\ (\text{%})\ -\ ?\)

ККД теплового двигуна визначається за формулою $$ \text{ККД}=\frac{A}{Q_{\text{н}}}\cdot 100\ \text{%}, $$ де \(A\) – корисна робота, виконана двигуном, \(Q_{\text{н}}\) – теплота, отримана від нагрівача.

Частина отриманої теплоти \(Q_{\text{н}}\) використовується на виконання роботи, а решта передається холодильнику. У цій задачі холодильником є середовище. Тоді можна обчислити отриману теплоту:

Після цього можна розрахувати ККД такого двигуна:

Відповідь: 50.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. Робота. Потужність. ККД теплового двигуна.

Завдання скеровано на оцінювання розуміння понять потужності й коефіцієнту корисної дії (ККД) теплової машини й уміння розв’язувати розрахункові задачі, пов’язані з цими поняттями.

Дано:
\(P_{\text{середня}}=2\ \text{кВт}\)
\(t=2\ \text{год}\)
\(Q=24\ \text{МДж}\)

Знайти:
\(\text{ККД (%)}-?\)

У цій задачі ККД можна визначити як відношення виконаної тепловою машиною роботи \(A\) до отриманої нею енергії \(Q\): $$ \text{ККД}=\frac AQ\cdot 100\ \text{%}. $$

З умови задачі відомо, яку кількість теплоти отримала машина для її функціонування, а виконану нею роботу можна визначити за її потужністю: $$ P=\frac At, $$ де \(A\) – виконувана робота, а \(t\) – час її виконання.

Тоді роботу можна обчислити за формулою \(A=Pt.\)

Після переведення кіловат у вати, годин у секунди, а мегаджоулів у джоулі можна обчислити шуканий коефіцієнт корисної дії:

Відповідь: 60.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. Рівняння стану ідеального газу. Ізопроцеси в газах. Внутрішня енергія і способи її зміни.

Завдання скеровано на оцінювання вміння визначати зміну внутрішньої енергії ідеального газу за зміною його макроскопічних параметрів, використовувати перший закон термодинаміки для ізопроцесів і розв’язувати розрахункові задачі, пов’язані із цими поняттями.

Дано:
\(A=8\ \text{кДж}\)
\(p=\mathrm{const}\)

Знайти:
\(Q\ (\text{кДж})-?\)

За першим законом термодинаміки \(Q=\triangle U+A,\) де \(Q\) – це отримана тілом кількість теплоти, \(\triangle U\) – зміна внутрішньої енергії тіла, \(A\) – робота, виконана тілом.

Зміну внутрішньої енергії одноатомного ідеального газу можна обчислити, використавши вираз $$ \triangle U=\frac 32 nR\triangle T, $$ де \(n\) – кількість речовини ідеального газу, \(R\) – універсальна газова стала,
\(\triangle T\) – зміна температури газу.

Оскільки зміна температури невідома, потрібно використати рівняння стану ідеального газу $$ pV=nRT, $$ де \(p\) – тиск, \(V\) – об’єм, \(R\) – універсальна газова стала, \(T\) – температура,
\(n\) – кількість речовини.

Процес у завданні перевів ідеальний газ зі стану 1 \((p_1,T_1,V_1)\) у стан 2 \((p_2,T_2,V_2).\)

За умовою \(p_1=p_2=p.\)

Тоді \(\triangle T=T_2-T_1,\) a $$ \triangle U=\frac 32 nR(T_2-T_1)=\frac 32(nRT_2-nRT_1). $$

За допомогою рівняння стану ідеального газу можна замінити \(nRT_2\) та \(nRT_1\):

Роботу в довільному термодинамічному процесі можна обчислити як площу криволінійної трапеції під графіком залежності \(p(V),\) а для ізобраного процесу її можна розрахувати за формулою \(A=p\triangle V=8\ \text{кДж}.\)

Після підстановки й перетворень можна обчислити шукану кількість теплоти:

Відповідь: 20.

ТЕМА: Молекулярна фізика й термодинаміка. Ізопроцеси.

Завдання скеровано на оцінювання вміння аналізувати графіки ізопроцесів і застосовувати перший закон термодинаміки для них.

1. Знайти:
\(p_2\ (\text{кПа})-?\)

За графіком процесу 1–2 (поділками на осі y) можна визначити тиск у закритій посудині у стані 2. Оскільки великі поділки підписано через одну, і перша підписана поділка – це \(2\cdot 10^5\ \text{Па},\) легко дійти висновку, що ціна великої поділки – \(1\cdot 10^5\ \text{Па}.\) Тоді ціна маленької поділки, яка ділить велику навпіл, дорівнює \(0,5\cdot 10^5\ \text{Па}.\)

З огляду на це у стані 2 тиск \(p_2=0,5\cdot 10^5\ \text{Па}=50\ \text{кПа}.\)

2. Знайти:
\(A\ (\text{кДж}) - ?\)

За першим законом термодинаміки \(Q=\triangle U+A,\) де \(Q\) – це отримана тілом кількість теплоти, \(\triangle U\) – зміна внутрішньої енергії тіла, \(A\) – робота, виконана тілом.

У координатах \(pV\) параболою зображено ізотермічний (за сталої температури) процес. У такому разі зміна внутрішньої енергії дорівнює нулю, тоді
\(Q=A=3\cdot 10^5\ \text{Дж}=300\ \text{кДж}.\)

Відповідь: 1. 50. 2. 300.

ТЕМА: Основи термодинаміки. Внутрішня енергія і способи її зміни. Способи теплопередачі.

Завдання скеровано на оцінювання розуміння різних механізмів теплопередачі.

Теплопередача (теплообмін) – процес зміни внутрішньої енергії тіла або частин тіла без виконання роботи.

Конвекція – це вид теплопередачі, за якого тепло переносять потоки рідини або газу.

Теплопровідність – це вид теплопередачі, зумовлений хаотичним рухом частинок речовини й не супроводжуваний перенесенням цієї речовини.

Випромінювання – це вид теплопередачі, за якого енергія передається за допомогою електромагнітних хвиль.

Конденсація – це процес переходу речовини з газуватого стану в рідкий

Робота \(A\) – це фізична величина, яка характеризує зміну механічного стану тіла.

Щодо ситуацій, описаних у завданні:

A Нагрівання в мікрохвильовій печі відбувається за рахунок проникнення мікрохвильового випромінювання в об’єм їжі.

Б Стіни будинку взимку нагріваються за допомогою внутрішнього опалення. Через це утворюється різниця температур між стінами й повітрям зовні. Тож аби досягти теплової рівноваги стіни віддаватимуть теплоту навколишньому середовищу без переносу речовини, із якої вони збудовані, тобто братимуть участь у теплообміні.

В Теплота передається всьому об’єму води завдяки тому, що гаряча вода має меншу густину ніж холодна, тому вона підніматиметься й обмінюватиметься теплом із холоднішою водою навколо. Тобто в окропі утворюються потоки рідини, які переносять тепло, а тому відбувається конвекція.

Г Під час тертя долонь одна об одну механічна енергія руху частково переходить у теплову за рахунок роботи сили тертя.

Відповідь: 1Б, 2Д, 3В, 4А.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. Перший закон термодинаміки.

Завдання скеровано на оцінювання розуміння першого закону термодинаміки.

За першим законом термодинаміки \(Q = \triangle U + A,\) де \(Q\) – це отримана тілом кількість теплоти, \(\triangle U\) – зміна внутрішньої енергії тіла, \(A\) – робота, виконана тілом.

Відповідно зміна внутрішньої енергії \(\triangle U = Q\ – A.\)

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Внутрішня енергія і способи її зміни. Ізопроцеси.

Завдання скеровано на оцінювання розуміння способів зміни внутрішньої енергії і вміння визначити процес, у якому відповідні зміни відбуваються.

Для правильного розв’язання завдання потрібно розглянути перетворення енергії, про які йдеться в ньому.

1. Розширення за рахунок зменшення внутрішньої енергії.

У цьому разі робота виконується за рахунок зменшення внутрішньої енергії, тобто \(A = \triangle U\).

Такий вигляд першого закону термодинаміки відповідає адіабатному процесу, адже тіло не отримує теплоти ззовні.

2. Отримана кількість теплоти витрачається на роботу і збільшення внутрішньої енергії.

Перший закон термодинаміки тоді записують як \(Q = A + \triangle U\).

Такий вигляд першого закону термодинаміки відповідає ізобарному розширенню (\(p = const,\ V\) збільшується).

3. Отримана кількість теплоти витрачається на збільшення внутрішньої енергії.

Перший закон термодинаміки записують так: \(Q = \triangle U\).

Оскільки робота не виконується, то об’єм газу не змінюється, тобто йдеться про ізохорний процес, а збільшення внутрішньої енергії передбачає нагрівання
(\(V = const,\ T\) підвищується).

4. Отримана кількість теплоти витрачається на виконання роботи.

Перший закон термодинаміки виглядає так: \(Q = A\).

Внутрішня енергія газу не змінюється, тобто процес ізотермічний. До того ж, якщо газ виконує роботу, то він розширюється (\(T = const,\ V\) збільшується).

Відповідь: 1Г, 2В, 3А, 4Д.

ТЕМА: Молекулярна фізика й термодинаміка. Внутрішня енергія і способи її зміни. Кількість теплоти.

Завдання скеровано на оцінювання розуміння понять внутрішньої енергії, кількості теплоти і їхнього взаємозв’язку.

За першим законом термодинаміки кількість теплоти \(Q\), передану системі, витрачено на зміну внутрішньої енергії системи \(\triangle U\) і на виконання системою роботи \(A\) проти зовнішніх сил: $$ Q=A+\triangle U $$ У процесах із незмінним об’ємом робота не виконується, тому \(A_{V=const}=0\).

Зміна внутрішньої енергії пов’язана зі зміною температури. Якщо однаково підвищити температуру двох газів однакової маси, то зміни їхньої внутрішньої енергії також будуть однаковими: $$ \triangle U_{V=const}=\triangle U_{p=const}=\triangle U. $$

За перший законом термодинаміки вирази для кількості теплоти такі:

Оскільки \(\triangle U \lt \triangle U+A_{p=const},\) то \(Q_{V=const}\lt Q_{p=const}.\)

Відповідь: A.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. Робота в термодинаміці. Ізопроцеси.

Завдання скеровано на оцінювання розуміння поняття ізопроцесів і вміння розраховувати роботу в термодинамічних процесах.

Ізотермічний процес – змінювання стану газу деякої маси за незмінної температури.

Ізобарний процес – змінювання стану газу деякої маси за незмінного тиску.

Ізохорний процес – змінювання стану газу деякої маси за незмінного об’єму.

Адіабатний процес відбувається без теплообміну з навколишнім середовищем.

Робота в довільному термодинамічному процесі може бути обчислена як площа криволінійної трапеції під графіком залежності \(p(V)\), що відображено на рисунку 1.

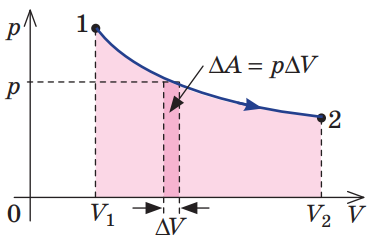
Рис. 1. Графік довільного переходу зі стану 1 у стан 2. Темнішим кольором позначено площу під криволінійною трапецією, яка дорівнює роботі

У разі ізохорного процесу об’єм не змінюється, тож площа під кривою (і робота газу) дорівнює нулю (рис. 2).

Рис. 2. Графік ізохорного процесу

Відповідь: A.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. ККД теплового двигуна.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на знаходження коефіцієнта корисної дії теплової машини.

Дано:
\(A=120\ \text{кДж}\)
\(T_{\text{н}}=500\ \text{К}\)
\(T_{\text{х}}=300\ \text{К}\)

1. Знайти:
\(\text{ККД (%)}-?\)

ККД ідеальної теплової машини залежить лише від температури нагрівача й холодильника: \begin{gather*} \text{ККД}=\frac{T_{\text{н}}-T_{\text{х}}}{T_{\text{н}}}\cdot 100\ \text{%};\\[6pt] \text{ККД}=\frac{500\ \text{К}-300\ \text{К}}{500\ \text{К}}\cdot 100\ \text{%}=40\ \text{%}. \end{gather*}

2. Знайти:
\(Q_{\text{х}}\ (\text{кДж}) - ?\)

Також ККД теплової машини можна записати як відношення виконаної роботи до отриманої енергії. У цій ситуації отримана енергія – це кількість теплоти, передана нагрівачем \(Q_{\text{н}}:\) $$ \text{ККД}=\frac{A}{Q_{\text{н}}}\cdot 100\ \text{%}. $$

Теплоту, отриману від нагрівача, теплова машина використовує на виконання роботи, а залишки теплоти передає холодильнику, тому можна записати кількість теплоти, передану нагрівачем \(Q_{\text{н}}:\) $$ Q_{\text{н}}=Q_{\text{х}}+A. $$

Тоді, після підстановок,

Відповідь: 1. 40. 2. 180.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів.

Завдання скеровано на оцінювання вміння визначати ізопроцеси за їхнім описом і застосовувати до них перший закон термодинаміки.

За першим законом термодинаміки \(Q=\triangle U+A,\) де \(Q\) – це отримана тілом кількість теплоти, \(\triangle U\) – зміна внутрішньої енергії тіла, \(А\) – робота, виконана тілом. Із цієї формули зрозуміло, що для того, щоби робота виконувалася лише за рахунок зменшення внутрішньої енергії, кількість теплоти, отриманої ззовні, має дорівнювати нулю \((Q=0).\) Такий процес є адіабатним.

Тож наступним кроком є аналізування ситуацій, описаних у завданні, для визначення адіабатного процесу.

А Оскільки повітря рухається швидко, то воно не встигає обмінятися теплом із навколишнім середовищем, тож \(Q=0\) і процес є адіабатним. Після цього газ розширюється і виконує роботу. За першим законом термодинаміки виконати цю роботу газ може лише за рахунок зменшення своєї внутрішньої енергії. Доказом цього є те, що водяна пара, яку несло повітря, сконденсувалася. Це є ознакою зменшення температури повітря і, відповідно, внутрішньої енергії.

Б У холодильнику відбувається обмін теплом із середовищем, отже процес не є адіабатним.

В Під час кипіння температура рідини залишається сталою, а отже і її внутрішня енергія не змінюється, що не відповідає умові завдання.

Г У цьому процесі внутрішня енергія повітря збільшується, що не відповідає умові завдання.

Відповідь: A.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. Внутрішня енергія і способи її зміни.

Завдання скеровано на оцінювання розуміння поняття внутрішньої енергії і способів її зміни.

Внутрішня енергія – це сума кінетичних енергій хаотичного (теплового) руху частинок речовини (атомів, молекул, йонів), із яких складається тіло, і потенціальних енергій їхніх взаємодій.

Кінетична енергія руху частинок речовини й потенціальна енергію взаємодії між ними в тілі не залежить від його положення як цілого чи його швидкості.

Швидкість руху частинок речовини збільшується з підвищенням температури, а тому змінюється і внутрішня енергія всього тіла.

Тож, якщо тіло підняти на п’ять метрів, зміниться лише його потенціальна енергія. Якщо ж надати тілу швидкості, то зміниться його кінетична енергія. Якщо нагріти тіло, то збільшиться його внутрішня енергія, а якщо помістити його в теплоізолювальну шафу, то енергія тіла не зміниться.

Відповідь: B.

ТЕМА: Молекулярна фізика й термодинаміка. Ізопроцеси.

Завдання скеровано на оцінювання вміння аналізувати графіки ізопроцесів і будувати їх у різних системах координат.

Рівняння стану ідеального газу \(pV=nRT,\) де \(p\) – тиск, \(V\) – об’єм, \(R\) – універсальна газова стала, \(T\) – температура, \(n\) – кількість речовини.

З огляду на це рівняння за результатами аналізування графіків, поданих у завданні, можна дійти висновків, що процес 1–2 є ізобарним (сталий тиск, температура підвищується), 2–3 є ізохорним (сталий об’єм, температура знижується), 3–4 є ізобарним (сталий тиск, температура знижується), 4–1 є ізотермічним (стала температура).

Наступним кроком є аналіз процесів, зображених у координатах \(pT.\)

Найбільших змін зазнав графік процесу 4–1, адже в координатах \(pV\) ізотерма має форму параболи, а в координатах \(pT\) – прямої, перпендикулярної до осі \(T.\)

Такому опису відповідає лише графік на рисунку A.

Відповідь: A.

ТЕМА: Фізичні явища й фізичні величини.

Завдання скеровано на оцінювання розуміння поняття фізичного явища й фізичної величини.

Фізичне явище – це зміни в природі, які можна описати за допомогою відповідних фізичних законів.

Фізична величина – це кількісно виражена характеристика тіла або фізичного явища.

Проаналізуймо поняття, наведені в кожному варіанті відповіді.

У варіанті А теплопровідність, остигання і горіння – це фізичні явища, а площа – це фізична величина.

У варіанті Б падіння, електроліз і нагрівання – це фізичні явища, а ньютон – це одиниця вимірювання сили.

У варіанті В гальмування – це фізичне явище, кілограм і діоптрія – це одиниці вимірювання маси й оптичної сили лінзи відповідно, а густина – це фізична величина.

У варіанті Г всі поняття є фізичними явищами.

Відповідь: Г.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. Рівняння стану ідеального газу.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на використання рівняння стану ідеального газу.

Дано:
\(t_1=18\ ^{\circ}\text{С}\)
\(t_2=27\ ^{\circ}\text{С}\)
\(p_1=p_2\)

Знайти:
\(\left(1-\frac{N_2}{N_1}\right)\ -\ ?\)

Температура, тиск і об’єм газу пов’язані між собою рівнянням стану ідеального газу: $$ pV=vRT, $$ де \(T\) – це температура в Кельвінах, а \(v\) – це кількість речовини, яку можна обчислити за формулою: $$ v=\frac{N}{N_A}, $$ де \(N\) – кількість молекул, \(N_A\) – число Авогадро.

Об’єм кімнати не змінився після підключення опалення, тож можна записати рівняння стану ідеального газу для стану до нагрівання і після: \begin{gather*} p_1V_1=v_1RT_1;\\[7pt] p_2V_2=v_2RT_2. \end{gather*}

Зважаючи на те, що \begin{gather*} p_1V_1=p_2V_2, \end{gather*} можна записати: \begin{gather*} v_1RT_1=v_2RT_2;\\[6pt] \frac{N_1}{N_A}RT_1=\frac{N_2}{N_A}RT_2;\\[6pt] N_1T_1=N_2T_2. \end{gather*}

Тоді $$ \frac{N_2}{N_1}=\frac{T_1}{T_2}. $$

Після цього можна обчислити, на скільки змінилася кількість молекул: $$ \left(1-\frac{N_2}{N_1}\right)\cdot 100\ \text{%}=\left(1-\frac{T_1}{T_2}\right)\cdot 100\ \text{%}=\left(1-\frac{(18+273)\ \text{К}}{(27+273)\ \text{К}}\right)\cdot 100\ \text{%}=3\ \text{%}. $$

Відповідь: 3.

ТЕМА: Молекулярна фізика й термодинаміка. Ізопроцеси.

Завдання скеровано на оцінювання вміння розв’язувати задачі на аналіз графіків ізопроцесів і побудову їх у різних системах координат.

Для правильного розв’язання задачі передовсім потрібно пригадати графіки ізопроцесів (рис. 1):

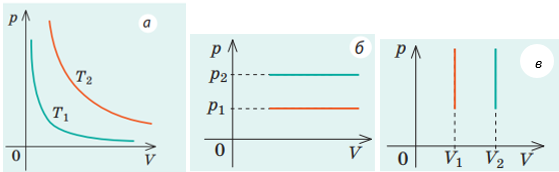
Рис. 1. Графіки ізопроцесів у координатах \((p, V)\): а) ізотермічний, б) ізобарний, в) ізохорний процеси

Важливо пам’ятати, що ізотерма може мати лише таку орієнтацію! Далі потрібно розглянути кожну послідовність із завдання і нарисувати графіки процесів.

Для правильного аналізування змін усіх фізичних величин потрібно пригадати рівняння Клапейрона: $$ \frac{p_1V_1}{T_1}=\frac{p_2V_2}{T_2}. $$

Із цього випливає, що добуток тиску на об’єм, поділений на температуру залишається сталим під час переходу зі стану 1 у стан 2.

Під час ізохорного нагрівання за рівнянням Клапейрона $$ \frac{p_1}{T_1}=\frac{p_2}{T_2}. $$

За умовою \(T_2 \gt T_1\), а отже, щоби рівність зберігалась, \(p_2\) також має бути більшим за \(p_1\), що можна зобразити прямою 1 на рисунку 2.

Ізобарне стискання можна зобразити прямою 2 на рисунку 2

З останньої точки попереднього процесу до початкової точки можна провести ізотерму (крива 3), отже газ можна повернути в початковий стан такою послідовністю процесів.

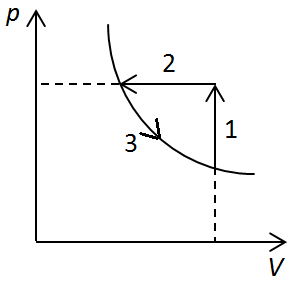
Рис. 2. Графік процесів із перебігу 1

Під час ізохорного нагрівання за рівнянням Клапейрона $$ \frac{p_1}{T_1}=\frac{p_2}{T_2}. $$

За умовою \(T_2 \gt T_1\), тому для збереження рівності \(p_2\) також має бути більшим за \(p_1\), що можна зобразити прямою 1 на рисунку 3.

Ізобарне збільшення об’єму можемо зобразити прямою 2 на рисунку 3.

З останньої точки попереднього процесу до початкової точки не можна провести ізотерму (крива 3 не перетинає початкову точку), отже газ не можна повернути в початковий стан такою послідовністю процесів.

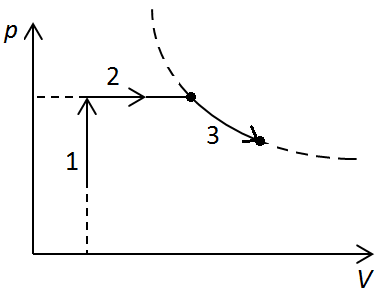
Рис. 3. Графік процесів із перебігу 2

Ізобарне стискання можна зобразити прямою 1 на рисунку 4.

Під час ізохорного охолодження за рівнянням Клапейрона $$ \frac{p_1}{T_1}=\frac{p_2}{T_2}. $$

За умовою \(T_2 \lt T_1\), тому для збереження рівності \(p_2\) також має бути меншим ніж \(p_1\), що можна зобразити прямою 2 на рисунку 4.

З останньої точки попереднього процесу до початкової точки не можна провести ізотерму (крива 3 не перетинає початкову точку), отже газ не можна повернути в початковий стан такою послідовністю процесів.

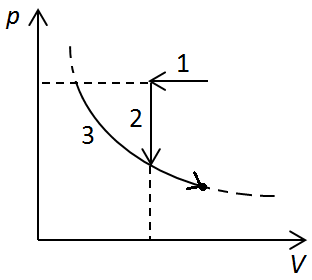
Рис. 4. Графік процесів із перебігу 3

Ізобарне збільшення об’єму можемо зобразити прямою 1 на рисунку 5.

Під час ізохорного охолодження за рівнянням Клапейрона: $$ \frac{p_1}{T_1}=\frac{p_2}{T_2}. $$

За умовою \(T_2 \lt T_1\), тому для збереження рівності \(p_2\) також має бути меншим за \(p_1\), що можна зобразити прямою 2 на рисунку 5.

З останньої точки попереднього процесу до початкової точки можна провести ізотерму (крива 3), отже газ можна повернути в початковий стан такою послідовністю процесів.

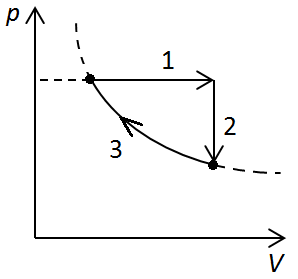
Рис. 5. Графік процесів із перебігу 4

Відповідь: B.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. Рівняння стану ідеального газу.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на використання рівняння стану ідеального газу.

Двоатомний газ кількістю речовини \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_0\) займає об’єм \(V\) за температури \(T_0.\) Після підвищення температури до \(T_1\), коли всі молекули розпалися на атоми, кількість речовини збільшується до \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_1\). Ці фізичні величини пов’язані між собою: \begin{gather*} T_1=3T_0;\\[7pt] \style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_1=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_0. \end{gather*}

Кількість речовини збільшилась удвічі, адже кожна молекула розпалася на два атоми.

Рівняння стану ідеального газу для обох випадків: \begin{gather*} p_0V=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_0RT_0;\\[7pt] p_1V=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_1RT_1=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_0R3T_0=6\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_0RT_0. \end{gather*}

Тоді: \begin{gather*} p_0=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_0RT_0}{V};\\[6pt] p_1=6\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_0RT_0}{V}=6p_0. \end{gather*}

Відповідь: Г.

ТЕМА: Основи термодинаміки. Тепловий рух. Дифузія.

Завдання скеровано на оцінювання знання практичного застосування дифузії в техніці.

Дифузія – процес взаємного проникнення молекул однієї речовини між молекулами іншої внаслідок теплового руху.

Згоряння палива, плавлення льоду, тверднення рідини пов’язані з реакцією речовини на отримання або втрату теплоти, і лише під час зварювання металів вони взаємодіють.

Під час зварювання двох металів їх нагрівають на межі контактування. Тому в місці контактування метали переходять у рідкий стан. За високої температури в рідинах дифузія відбувається набагато активніше, ніж у твердих тілах за кімнатної температури. Тому атоми металів набагато легше проникають у сусідній метал, а після охолодження між ними утворюється міцний зв’язок.

Відповідь: A.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. Перший закон термодинаміки. Потужність.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на використання першого закону термодинаміки.

Дано:
\(P=2,5\ \text{кВт}\)
\(t=1\ \text{хв}\)
\(\triangle U=80\ \text{кДж}\)

Знайти:
\(\triangle E\ -\ ?\)

Теплову енергію середовища можна розрахувати за першим законом термодинаміки: $$ Q=\triangle U+A, $$ де \(\triangle U\) – зміна внутрішньої енергії середовища, \(A\) – виконана робота.

Під час роботи кондиціонера внутрішні приміщення охолоджуються тому, що тепло виводиться в середовище зовні. Тому зниження внутрішньої енергії в кімнаті на \(\triangle U\) приводить до збільшення енергії середовища на те саме \(\triangle U\).

Виконану роботу можемо обчислити, знаючи потужність кондиціонера, за формулою: \begin{gather*} P=\frac At.\\[6pt] A=Pt=2,5\ \text{кВт}\cdot 1\ \text{хв}=2500\ \text{Вт}\cdot 60\ \text{с}=150000\ \text{Дж}=150\ \text{кДж}. \end{gather*}

Тоді $$ Q=\triangle U+A=80\ \text{кДж}+150\ \text{кДж}=230\ \text{кДж}. $$

Відповідь: 230.

ТЕМА: Молекулярна фізика й термодинаміка. Рівняння теплового балансу. Робота. Потужність. Коефіцієнт корисної дії (ККД).

Завдання скеровано на оцінювання вміння розв’язувати комплексні розрахункові задачі, що поєднують у собі використання понять роботи, потужності й рівняння теплового балансу.

Дано:
\(P=4,6\ \text{кВт}\)
\(\triangle t=10\ ^\circ\text{С}\)
\(\triangle \tau=10\ \text{хв}\)
\(m=6\ \text{кг}\)
\(c=460\ \text{Дж}/(\text{кг}\cdot \text{К})\)

1. Знайти:
\(Q(\text{кДж})\ -\ ?\)

Виділена під час тертя теплота витрачається на нагрівання верстата, тому можна скористатися рівнянням теплового балансу для її визначення: $$ Q=cm\triangle t=460\frac{\text{Дж}}{\text{кг}\cdot \text{К}}\cdot 6\ \text{кг}\cdot 10\ ^\circ\text{С}=27600\ \text{Дж}=27,6\ \text{кДж}. $$

2. Знайти:
\(\text{ККД}_{max}(\text{%})\ -\ ?\)

ККД можна визначити як відношення виконаної тепловою машиною роботи \(A\) до отриманої нею енергії \(Q\): $$ \text{ККД}=\frac{A}{Q}\cdot 100\ \text{%}. $$

Кількість енергії, що отримує верстат від двигуна, можна обчислити за його потужністю: $$ P=\frac{Q_{\text{вит}}}{\tau}, $$ де \(Q_{\text{вит}}\) – витрачена верстатом енергія, а \(\tau\) – час роботи верстата.

\begin{gather*} Q_{\text{вит}}=P\tau=4,6\ \text{кВт}\cdot 10\ \text{хв}=4600\ \text{Вт}\cdot 600\ \text{с}=\\[7pt] =2760000\ \text{Дж}=2760\ \text{кДж}. \end{gather*}

На виконання корисної роботи \(A\) піде вся енергія, передана верстату двигуном крім тої, що буде витрачена на нагрівання від тертя, тому: $$ A=Q_{\text{вит}}-Q=2760\ \text{кДж}-27,6\ \text{кДж}=2732,4\ \text{кДж}. $$

Тоді ККД дорівнюватиме: $$ \text{ККД}=\frac{A}{Q_{\text{вит}}}\cdot 100\ \text{%}=\frac{2732,4\ \text{кДж}}{2760\ \text{кДж}}\cdot 100\ \text{%}\approx 99\ \text{%}. $$

Відповідь: 1. 27,6. 2. 99.

ТЕМА: Основи термодинаміки. Внутрішня енергія і способи її зміни. Способи теплопередачі.

Завдання скеровано на оцінювання розуміння різних механізмів теплопередачі й уміння виявляти необхідний механізм теплопередачі в щоденних ситуаціях.

1 Конвекція – це вид теплопередачі, за якого тепло переносять потоки рідини або газу. Прикладом застосування конвекції є принцип обігрівання приміщень радіаторами. Радіатори передають тепло найближчим шарам повітря. Густина теплих шарів повітря зменшується, і вони починають підніматися вгору, витісняючи холодніші шари повітря вниз, де вони починають нагріватися. Під час підйому теплі шари повітря також передають тепло холоднішим. Коли ж вони досягають верху приміщення, стають суттєво холоднішими за шари повітря, тільки-но нагріті радіаторами. Тож конвекція триває.

2 Теплопровідність – це вид теплопередачі, зумовлений хаотичним рухом частинок речовини й не супроводжуваний перенесенням цієї речовини. Теплопровідність – це один із основних способів утрати теплоти в організмів. Саме тому організми, особливо морські тварини, часто мають прошарок жиру під шкірою. Адже питома теплоємність води майже вчетверо більша, ніж питома теплоємність повітря, а отже змушуватиме тіла віддавати більше енергії.

3 Механічна робота – це фізична величина, яка характеризує зміну механічного стану тіла. Одним із найпоширеніших прикладів зміни внутрішньої енергії в результаті виконання роботи є нагрівання під час тертя.

4 Випромінювання – це вид теплопередачі, за якого енергія передається за допомогою електромагнітних хвиль. Сонячні промені – це сукупність електромагнітних хвиль різної частоти. Коли вони досягають поверхні, то вона поглинає їх. Унаслідок цього збільшується її внутрішня енергія і температура.

Відповідь: 1В, 2Б, 3А, 4Г.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів.

Завдання скеровано на оцінювання вміння застосовувати перший закон термодинаміки до ізопроцесів.

За першим законом термодинаміки $$ Q=\triangle U+A, $$ де \(Q\) – отримане системою тепло, \(\triangle U\) – зміна внутрішньої енергії, \(A\) – виконана системою робота.

Ізотермічний процес – процес змінювання стану газу деякої маси, що відбувається за незмінної температури. Тобто $$ \triangle U=0, $$ і перший закон термодинаміки має: $$ Q=A. $$

Ізобарний процес – процес змінювання стану газу деякої маси, що відбувається за незмінного тиску. Тоді перший закон термодинаміки має вигляд: $$ Q=\triangle U+A. $$

Ізохорний процес – процес змінювання стану газу деякої маси, що відбувається за незмінного об’єму. Робота в такому процесі не виконується, тому перший закон термодинаміки має вигляд: $$ Q=\triangle U. $$

Адіабатний процес – це процес, який відбувається без теплообміну з навколишнім середовищем. Тобто \(Q = 0\) і перший закон термодинаміки має вигляд: $$ \triangle U+A=0. $$

А отже $$ A=-\triangle U. $$

Цей вираз описує роботу, що відбувається за рахунок зміни внутрішньої енергії.

Відповідь: A.

ТЕМА: Термодинаміка. Коефіцієнт корисної дії теплового двигуна і його максимальне значення.

Завдання скеровано на перевірку вміння розв'язувати розрахункові задачі, застосовуючи функціональні залежності між основними фізичними величинами.

Дано:
\(T_{\text{Н}}=373\ \text{К}\)
\(T_{\text{Х}}=273\ \text{К}\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=330\ \text{кДж/кг}\)
\(A_{\text{кор}}=110\ \text{кДж}\)

Знайти:
\(m(\text{г})\ -\ ?\)
\(\text{ККД}\ (\text{%})\ -\ ?\)

ККД ідеальної теплової машини можна записати у двох формах: \begin{gather*} \text{ККД}=\frac{T_{\text{Н}}-T_{\text{Х}}}{T_{\text{Н}}}\cdot 100\ \text{%}\\[6pt] \text{і}\\[6pt] \text{ККД}=\frac{A_{\text{кор}}}{A_{\text{повна}}}\cdot 100\ \text{%}. \end{gather*} Корисна робота \(A_{\text{кор}}\) передається робочому тілу, а різниця між корисною і повною роботою – холодильнику. Тобто енергію \(Qx\), отриману холодильником, визначають за формулою \begin{gather*} Qx=A_{\text{кор}}\left(\frac{T_{\text{Н}}}{T_{\text{Н}}-T_{\text{Х}}}-1\right);\\[6pt] A_{\text{кор}}\left(\frac{T_{\text{Х}}}{T_{\text{Н}}-T_{\text{Х}}}\right);\\[6pt] Qx=A_{\text{повна}}-A_{\text{кор}};\\[6pt] Qx=\frac{A_{\text{кор}}\cdot 100\ \text{%}}{\text{ККД}}-A_{\text{кор}};\\[6pt] Qx=A_{\text{кор}}\left(\frac{100\ \text{%}}{\text{ККД}}-1\right);\\[6pt] Qx=A_{\text{кор}}\left(\frac{T_{\text{Н}}}{T_{\text{Н}}-T_{\text{Х}}}-1\right);\\[6pt] Qx=110\ \frac{\text{кДж}}{\text{кг}}\cdot \left(\frac{273\ \text{К}}{373\ \text{К}-273\ \text{К}}\right);\\[6pt] Qx=110\ \cdot 10^3\ \frac{\text{Дж}}{\text{кг}}\cdot \left(\frac{273\ \text{К}}{100\ \text{К}}\right);\\[6pt] Qx=300,3\cdot 10^3\ \text{Дж}. \end{gather*} Рівняння теплового балансу для речовини під час плавлення: $$ Qx=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}m. $$ Тож

Обчислення ККД ідеальної теплової машини:

Відповідь: 1. 910. 2. 27

ТЕМА: Термодинаміка. Застосування першого закону термодинаміки до ізопроцесів.

Завдання скеровано на перевірку вміння роз'язувати розрахункові задачі на газові закони, роботу термодинамічного процесу, перший закон термодинаміки.

Перший закон термодинаміки: кількість теплоти \(Q\), надана системі, використовується на зміну її внутрішньої енергії \(\triangle U\) й на роботу системи \(A\): $$ Q=\triangle U+A\ \ (1) $$

Робота в термодинаміці визначається зміною об'єму \(\triangle V\): $$ A=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}\triangle V\ \ (2) $$

Внутрішня енергія $$ \triangle U=\frac i2 R\triangle T\ \ (3) $$ змінюється прямопропорційно до зміни термператури.

1. Ізотермічне \(T=const;\ \triangle T=0\rightarrow\ \text{з}\ (3)\ \triangle U=0\).
Розширення \(V_2\gt V_1;\ \triangle V=V_2-V_1\gt 0\rightarrow\ (2)\ A\gt 0\).
З першого закону термодинаміки (1) \(Q\gt 0\).
\(Q\gt 0,\ A\gt 0\), отже, 1 – B.

2. Адіабатне \(Q=0\).
Стискання \(V_2\lt V_1,\ \triangle V\lt 0\), тому з (2) \(A\lt 0\).
\(Q=0,\ A\gt 0\), отже, 2 – Д.

3. Ізохорне \(V=const,\ \triangle V=0,\ A=0\).
Охолодження \(T_2\lt T_1,\ \triangle U\lt 0\), тому з (1) \(Q\lt 0\).
\(Q\lt 0,\ A=0\), отже, 3 – A.

4. Ізобарне \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}=const,\ \triangle V=0,\ A=0\).
Стискання \(V_2\lt V_1,\ \triangle V\lt 0\rightarrow A\lt 0\)з (2).
За законом Гей-Люссака залежність між об'ємом i температурою прямо пропорційна, тобто \(T_2\lt T_2,\ \triangle T\lt 0\) з (3) \(\triangle U\lt 0\), тому з (1) \(Q\lt 0\).
\(Q\lt 0,\ A\lt 0\), отже, 4 – Б.

Відповідь: 1B, 2Д, 3A, 4Б.

ТЕМА: Молекулярна фізика і термодинаміка. Рівняння теплового балансу. Робота. Потужність. Коефіцієнт корисної дії (ККД).

Завдання скеровано на перевірку вміння розв’язувати комбіновані задачі, пов’язані з електричною потужністю і рівнянням теплового балансу.

Дано:
\(R=20\ \text{Ом}\)
\(U=200\ \text{В}\)
\(m=1\ \text{кг}\)
\(t_1=20\ ^\circ\text{С}\)
\(t_2=100\ ^\circ\text{С}\)
\(t=200\ \text{с}\)
\(c=4200\ \frac{\text{Дж}}{\text{кг}\ \cdot\ \text{К}}\)

1. Знайти:
\(A\ (\text{кДж})\ -\ ?\)

Потужність пов’язана з роботою формулою $$ P=\frac At, $$ де \(A\) – виконувана робота, а \(t\) – час виконання роботи.

Потужність електричного нагрівача можна визначити за формулою $$ P=UI=\frac{U^2}{R}, $$ де \(U\) – напруга, \(I\) – сила струму.

Тож

2. Знайти:
\(\text{ККД}\ (\text{%})\ -\ ?\)

ККД нагрівача визначають як відношення корисної роботи, виконаної ним, до повної роботи: \begin{gather*} \text{ККД}=\frac{Q}{A_\text{пов}}\cdot 100\ \text{%}, \end{gather*} де \(Q\) – це енергія, що необхідна для нагрівання води.

Необхідну для нагрівання води кількість енергії можна визначити за формулою $$ Q=cm(t_2-t_1), $$ де \(c\) – питома теплоємність тіла, \(m\) – маса тіла, \(t_1\) – початкова температура тіла, \(t_2\) – кінцева температура тіла.

Повна робота – це робота струму в електричному нагрівачі, тож

Відповідь: 1. 400. 2. 84.

ТЕМА: Молекулярна фізика і термодинаміка. Рівняння теплового балансу.

Завдання скеровано на перевірку вміння аналізувати графічні залежності температури тіла від кількості наданої йому теплоти.

Кількість наданої теплоти, температура тіла та його питома теплоємність пов’язані виразом $$ Q=cm\Delta T=cm(T-T_0), $$ де \(c\) – питома теплоємність речовини, що віддає тепло, \(m\) – маса, \(\Delta T\) – зміна температури під час охолодження, \(T_0\) – початкова температура, \(T\) – температура тіла.

Графік у завданні – це графік залежності абсолютної температури тіла \(T\) від часу його нагрівання \(t\). Оскільки щосекунди тіло отримує однакову кількість теплоти \(Q\), залежність абсолютної температури \(T\) від кількості теплоти \(Q\) має схожий вигляд. Тому надалі достатньо аналізувати залежність \(T(Q)\).

Для цього необхідно змінити вигляд залежності:

Залежність має вигляд лінійної функції \(y=kx+b\), де \(b\) відповідає за перетин із віссю \(oy\), а \(k\) – кутовий коефіцієнт, що впливає на нахил прямої: $$ b=T_0,\ \ k=\frac{1}{cm}. $$

Оскільки маси всіх трьох тіл однакові, то на нахил прямої, що відповідає лінійній функції, впливає лише питома теплоємність.

Що більший кутовий коефіцієнт, то крутішою є пряма, а кутовий коефіцієнт є тим більшим, що меншою є питома теплоємність.

Тож найпологіша пряма (для тіла 1) має найбільшу питому теплоємність, а найкрутіша (для тіла 2) – найменшу.

Відповідь: Г.

ТЕМА: Молекулярна фізика і термодинаміка. Рівняння теплового балансу. Робота. Потужність. ККД.

Завдання скеровано на оцінювання вміння розв’язувати комплексні розрахункові задачі, що поєднують у собі використання понять роботи, потужності й рівняння теплового балансу.

Дано:
\(V=10\ \text{л}\)
\(\triangle t=45\ ^\circ\text{С}\)
\(P=35\ \text{кВт}\)
\(c=4\ 200\ \text{Дж}/(\text{кг}\cdot \text{К})\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}=1\ 000\ \text{кг/м}^3\)

1. Знайти:
\(Q\ -\ ?\)

Кількість теплоти, що необхідна для нагрівання цієї порції води, можна обчислити з виразу: $$ Q=cm\triangle t. $$

Масу води можна обчислити за виразом:

Тоді можна обчислити кількість теплоти:

2. Знайти:
\(\text{ККД}\ (\text{%})\ -\ ?\)

Коефіцієнт корисної дії (ККД) можна визначити як відношення корисної роботи \(A\) до загальної енергії \(Q\), виробленої газовим котлом: $$ \text{ККД}=\frac{A}{Q}\cdot 100\ \text{%}. $$

Корисна робота газового котла в цьому разі – це кількість теплоти, витрачена на нагрівання води.

Загальну енергію, вироблену газовим котлом, можна обчислити з виразу для його потужності: $$ P=\frac{Q}{t}, $$ де \(Q\) - вироблена газовим котлом енергія, а \(t\) – час роботи газового котла. \begin{gather*} Q=Pt=35\ \text{кВт}\cdot 1\ \text{хв}=35\ 000\ \text{Вт}\cdot 60\ \text{с}=\\[7pt] =2\ 100\ 000\ \text{Дж}=2\ 100\ \text{кДж}. \end{gather*}

Тоді можна визначити ККД газового котла:

Відповідь: 1. 1890. 2. 90.

ТЕМА: Вимірювальні пристрої.

Завдання скеровано на оцінювання розуміння фізичних принципів роботи вимірювальних пристроїв.

Термометр – це прилад для вимірювання температури. Він працює завдяки тому, що деякі речовини за сталого тиску суттєво змінюють свій об’єм за зміни температури (ртуть чи спирт розширюються за збільшення температури і звужуються за її зменшення).

Психрометр – це прилад для вимірювання відносної вологості. Принцип його роботи такий: у корпусі приладу є два термометри. Кінець одного з них зазвичай обгорнутий у вологу тканину. Вода з тканини завжди випаровується, і швидкість випаровування залежить від того, яка вологість повітря навколо. Для вимірювання відносної вологості фіксують покази сухого й вологого термометрів і за допомогою спеціальних таблиць виконують необхідні розрахунки.

Барометр – це прилад для вимірювання атмосферного тиску. У завданні зображено безводний барометр (анероїд), усередині якого є вакуумна камера з гофрованою поверхнею. За високого атмосферного тиску кришка коробки сильно опускається, а за низького – піднімається. До кришки за допомогою пружини прикріплено стрілку. Тому, коли кришка камери піднімається чи опускається, пружина деформується, а стрілка починає рухатися по шкалі.

Динамометр – це прилад для вимірювання сили. Зазвичай динамометр складається із пружини і шкали. Коли на кінець пружини діє сила, то за законом Гука пружина розтягується: $$ F=kx. $$

Тому, якщо відомий коефіцієнт жорсткості пружини, то за значенням її видовження можна визначити й силу, що його зумовлює.

Відповідь: Б.

ТЕМА: Молекулярна фізика та термодинаміка. Рівняння теплового балансу.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з використанням рівняння теплового балансу.

Дано:
\(h=14\ \text{МДж}\)
\(Q=U\ \frac{60\ \text{%}}{100\ \text{%}}\)
\(c=4200\ \frac{\text{Дж}}{\text{кг}\ \cdot\ \text{К}}\)

Знайти:
\(\Delta t\ -\ ?\)

Потенціальну енергію води на вершині водоспаду можна розрахувати за формулою $$ U=mgh, $$ де \(m\) – маса води, \(g\) – прискорення вільного падіння, \(h\) – висота водоспаду.

Під час падіння потенціальна енергія води зменшується і біля підніжжя дорівнює нулю. Тож кількість теплоти, витрачена на нагрівання води під час падіння дорівнює 60 % від потенціальної енергії на вершині: $$ Q=\frac{60\ \text{%}}{100\ \text{%}}U=0,6U=0,6mgh. $$

Кількість витраченої на нагрівання теплоти пов’язана зі зміною температури формулою $$ Q=cm\Delta t, $$ де \(c\) – питома теплоємність, \(m\) – маса води, \(\Delta t\) – різниця температур.

Тоді можна скласти рівняння:

Відповідь: 0,02.

ТЕМА: Основи молекулярно-кінетичної теорії.

Завдання скеровано на перевірку розуміння формул, що стосуються молекулярно-кінетичної теорії (МКТ).

A \(p=\frac 13nm_0v^2\), де \(n\) – концентрація молекул газу, \(m_0\) – маса молекули, \(\underline{v}\) – середня швидкість молекули, \(p\) – тиск ідеального газу. Рівняння визначає зв’язок мікроскопічного параметра (середньої швидкості молекули) і макроскопічного параметра (тиск). Воно є основним рівнянням МКТ.

Б \(E=\frac 32 kT\), де \(k\) – стала Больцмана, \(T\) – температура. Рівняння визначає зв’язок середньої кінетичної енергії одноатомного газу та його температури.

B \(pV=\frac mM RT\), де \(p\) – тиск, \(V\) – об’єм, \(R\) – універсальна газова стала, \(T\) – температура, \(m\) – маса газу, \(M\) – молярна маса речовини. Рівняння визначає зв’язок між трьома макроскопічними параметрами газу – температурою, тиском та об’ємом і є рівнянням стану ідеального газу.

Г \(\Delta U=cm\Delta T\), де \(U\) – внутрішня енергія, \(c\) – питома теплоємність, \(m\) – маса газу, \(T\) – температура. Рівняння описує зміну внутрішньої енергії зі зміною температури.

Д \(Q=\Delta U+A\), де \(Q\) – кількість теплоти, \(U\) – внутрішня енергія, \(A\) – робота. Рівняння описує перший закон термодинаміки: кількість теплоти \(Q\), передана системі, іде на зміну внутрішньої енергії системи \((\Delta U)\) та на виконання системою роботи \(A\) проти зовнішніх сил..

Відповідь: 1А, 2Д, 3В, 4Б.

ТЕМА: Молекулярна фізика й термодинаміка. Ізопроцеси.

Завдання скеровано на перевірку розуміння особливостей ізопроцесів.

Тиск \(p\), об’єм \(V\) й температура газу \(T\) пов’язані між собою рівнянням стану $$ pV=nRT, $$ де \(p\) – тиск, \(V\) – об’єм, \(R\) – газова стала, \(T\) – температура, \(n\) – кількість речовини.

У герметично закритій кімнаті кількість речовини й об’єм сталі.

Унаслідок роботи обігрівача температура повітря в кімнаті зростатиме.

Із рівняння стану можна виразити тиск: $$ p=\frac{nRT}{V}. $$

Тож, якщо температура зростає, а об’єм залишається незмінним, то тиск також зростатиме.

Тобто йдеться про ізохорний процес.

Відповідь: B.

ТЕМА: Молекулярна фізика й термодинаміка. Ізопроцеси.

Завдання скеровано на перевірку вміння аналізувати графіки ізопроцесів.

Тиск \(p\), об’єм \(V\) й температура газу \(T\) пов’язані між собою рівнянням стану $$ pV=nRT, $$ де \(p\) – тиск, \(V\) – об’єм, \(R\) – газова стала, \(T\) – температура, \(n\) – кількість речовини.

Зміну температури можна визначити з рівняння стану: $$ T=\frac{pV}{nR}. $$

На графіку, наведеному в умові, зображено цикл у координатах \(p - V\), складений із кількох ізопроцесів:

1–2: ізобарне розширення (\(p – const\), \(V\) збільшується).

Тож, якщо об’єм збільшується, а тиск залишається незмінним, то й температура збільшується.

2–3: ізотермічне стискання зі збільшенням тиску (\(T\ –\ const\), \(p\) зростає, \(V\) зменшується).

3–4: ізохорний процес зі зменшенням тиску (\(p\) зменшується, \(V\ –\ const\)).

Тож, якщо тиск зменшується, а об’єм залишається постійним, то й температура зменшується.

4–1: ізотермічне стискання зі збільшенням тиску (\(T\ –\ const\), \(p\) зростає, \(V\) зменшується).

А У процесі 2–3 температура зменшується, а повинна зростати.

Б У процесі 4–1 тиск зменшується, а має зростати.

В Цей графік є зображенням циклу в координатах \(p - T\).

Г Процес 1–2 є ізотермічним, а повинен бути ізобарним.

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Питома теплоємність речовини.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі про фазові переходи.

Розгляньмо наведений в умові графік. Ділянка, на якій протягом двох хвилин (від 1‑ої до 3‑ої) температура речовини не змінювалася, відповідає плавленню, під час якого вся кількість теплоти \(Q_1\) витрачається на руйнування кристалічних ґраток, тобто на зміну агрегатного стану, а не на нагрівання: $$ Q_1=\lambda m, $$ де \(\lambda\) ‒ питома теплота плавлення речовини масою \(m\).

Потужність \(P,\) яку споживає під час плавлення речовина протягом часу \(\tau_1=2\ \text{хв}=120\ \text{с},\) обчислюють за формулою $$ P=\frac{Q_1}{\tau_1}. $$

Тепер розгляньмо ділянку графіка від 3‑ої до 4‑ої хвилини. Речовина розплавилася і почала нагріватися. Під час цього вона отримає кількість теплоти \(Q_2,\) яка витратиться на підвищення температури від \(0\) до \(40\ ^\circ \mathrm{C}\) протягом часу \(\tau_2=1\ \text{хв}=60\ \text{с}:\) $$ Q_2=cm\Delta t, $$ де \(c\) ‒ питома теплоємність речовини в рідкому стані. Під час цього процесу потужність \(P\) залишатиметься сталою, її обчислюють за формулою $$ P=\frac{Q_2}{\tau_2}. $$

Прирівняймо ці два вирази для потужності: \begin{gather*} \frac{Q_1}{\tau_1}=\frac{Q_2}{\tau_2},\\[6pt] \frac{\lambda m}{\tau_1}=\frac{cm\Delta t}{\tau_2}. \end{gather*}

Масу можна скоротити й дістати вираз шуканої величини ‒ питомої теплоємності: \begin{gather*} c=\frac{\lambda\cdot \tau_2}{\tau_1\cdot \Delta t}=\frac{200\cdot 10^3\ \text{Дж/кг}\cdot 60\ \text{с}}{120\ \text{с}\cdot 40\ \text{К}}=\\[6pt] =\frac{20\ 000}{8}\ \frac{\ \text{Дж}}{\ \text{кг}\cdot \ \text{К}}=2500\ \frac{\text{Дж}}{\text{кг}\cdot\text{К}}=2,5\ \frac{\text{кДж}}{\text{кг}\cdot\text{К}}. \end{gather*}

Відповідь: 2,5.

ТЕМА: Механіка. Елементи механіки рідин і газів. Тиск. Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Рівняння стану ідеального газу.

Завдання скеровано на перевірку вміння розв’язувати розрахункові комбіновані задачі з визначення сили тиску (механіка), описавши стан газу рівнянням Клапейрона (молекулярна фізика).

Опишімо стан газу в циліндрі за початкових умов (див. рис. 1). Легкий поршень ділить циліндр на дві рівні частини. Позначмо тиск, що однаково діє на поршень з обох боків \(p_0\). Об’єм газу в рівних частинах циліндра дорівнює \(V\). Температура газу не змінюється.

Коли з певною силою поршень змістили, то стан газу в обох частинах циліндра змінився. Запишімо рівняння Клапейрона для обох частин циліндра:

Із цих рівностей визначмо тиски \(p_1\) і \(p_2:\) \begin{gather*} p_1=2p_0,\\[6pt] p_2=\frac{2p_0}{3}. \end{gather*}

Щоб утримувати поршень у положенні як на рисунку 2, треба прикласти до поршня силу, щоб компенсувати різницю цих тисків: \begin{gather*} \Delta p=\frac FS,\\[6pt] \Delta=p_1-p_2=2p_0-\frac{2p_0}{3}=\frac{4p_0}{3}. \end{gather*}

Обчислімо шукану силу за формулою: \begin{gather*} F=\Delta p\cdot S=\frac{4p_0}{3}\cdot S=\\[6pt] =\frac{4\cdot 10^5\ \text{Па}\cdot 120\cdot 10^{-4}\ \text{м}^2}{3}=1600\ \text{Н}=1,6\ \text{кН}. \end{gather*}

Відповідь: 1,6.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Кількість теплоти. Коефіцієнт корисної дії.

Завдання скеровано на перевірку розуміння процесу згоряння палива й уміння обчислити коефіцієнт корисної дії.

1. Піч виконала корисну роботу – вода закипіла. Запишімо формулу для визначення кількості теплоти, яку отримала вода для того, щоб закипіти. Оскільки початкова температура води за умовою була \(10\ ^\circ \mathrm{C},\) то воді треба було надати порцію теплоти \(Q,\) щоб вона нагрілася до температури кипіння \(100\ ^\circ \mathrm{C}:\) $$ Q=cm\cdot \Delta t=c\cdot \rho V\cdot \Delta t, $$ де \(c\) ‒ питома теплоємність води, \(\rho\) – густина води, \(V\) – об'єм води, \(\Delta t\) – зміна температури.

Значення об’єму переведімо в одиниці системи СІ: \(10\ \text{л}=0,01\ \text{м}^3.\)

2. Запишімо формулу для визначення коефіцієнта корисної дії \(\eta :\) $$ \eta=\frac{Q_\text{корисна}}{Q_\text{повна}}\cdot 100\ \text{%}. $$

Корисно спожиту водою кількість теплоти \(Q_\text{корисна}\) для нагрівання води до температури кипіння вже обчислено в першій частині завдання. Обчислімо теплоту, яка виділиться внаслідок повного згоряння дров: $$ Q_\text{повна}=qm, $$ де \(q\) – питома теплота згоряння дров, \(m\) – маса дров.

Обчислімо значення кількості теплоти, що виділилася: $$ Q_\text{повна}=18,9\ \text{МДж/кг}\cdot 2\ \text{кг}=37,8\ \text{МДж}. $$

Обчислімо коефіцієнт корисної дії печі: $$ \eta=\frac{3,78\ \text{МДж}}{37,8\ \text{МДж}}\cdot 100\ \text{%}=10\ \text{%}. $$

Можна зробити висновок, що коефіцієнт корисної дії печі дуже низький, багато втрат – нагрівається сама піч, навколишнє повітря і предмети.
Відповідь: 10.

Відповідь: 1. 3,78. 2. 10.

ТЕМА: Механіка. Молекулярна фізика і термодинаміка. Електродинаміка.

Завдання скеровано на перевірку знань і розуміння принципів дії пристроїв і механізмів із різних розділів фізики.

Гальмівні механізми (дискові або барабанні) не дають обертатися колесам, унаслідок чого автомобіль зменшує швидкість. Принцип дії гальмівного механізму заснований на використанні сили тертя. Під час гальмування кінетична енергія переходить у внутрішню.

Тепловий двигун – це машина, яка працює циклічно й перетворює енергію палива на механічну роботу. Робоче тіло (газ, який виконує роботу під час свого розширення) отримує певну кількість теплоти від нагрівника. Ця теплота частково перетворюється на механічну енергію (робоче тіло виконує роботу), а частково передається холодильнику.

Індукційні генератори струму перетворюють механічну енергію на електричний струм. Складені з металевого осердя, у пази якого поміщено обмотку. Кінці обмотки з’єднані з кільцями, до кожного з яких притиснуто щітку для відведення напруги до споживача. Осердя з обмоткою (ротор) обертається в магнітному полі нерухомого постійного магніту або електромагніту.

Електричний двигун є пристроєм для перетворення електричної енергії на механічну та приведення до руху машин і механізмів. Робота електродвигуна основана на втягуванні або виштовхуванні провідника з електричним струмом у магнітному полі й дії на провідник зі струмом сили Ампера. Під час роботи двигуна рух ротора (рухомої частини двигуна) передається валу, а з нього – безпосередньо до споживача.

Відповідь: 1А, 2Б, 3В, 4Г.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Робота в термодинаміці.

Завдання скеровано на перевірку розуміння умов виконання роботи в термодинаміці, залежності її від деяких фізичних величин, а також вміння тлумачити графіки й брати з них числові дані для розв’язування задачі.

З формули для визначення роботи \(A\) газу в термодинаміці $$ A=p\Delta V=p(V_2-V_1), $$ де \(p\) – тиск, \(\Delta V\) – зміна об’єму газу,
зрозуміло: якщо об’єм газу не зазнає змін, то робота не буде виконана, тобто дорівнюватиме нулю.

На графіку ділянка 12 відповідає ізохорному охолодженню (знижуються температура й тиск, відповідно третій макроскопічний параметр газу – об᾽єм – залишатиметься сталим), ділянка 23 – ізобарному нагріванню (тиск залишається сталим, температура підвищується, відповідно об’єм збільшуватиметься).

Цих висновків можна дійти з огляду на рівняння Клапейрона: $$ \frac{p_1V_1}{T_1}=\frac{p_2V_2}{T_2},\ \text{тобто}\ \frac{pV}{T}=const. $$

Якщо під час процесу 12 об’єм не змінюється, то газ не виконує роботу, робота газу на цій ділянці дорівнює нулю. Тоді робота газу під час переходу зі стану 1 у стан 3 складатиметься лише з роботи на ділянці 23.

Об᾽єм унаслідок ізобарного нагрівання зміниться так: \begin{gather*} \frac{V_2}{T_2}=\frac{V_3}{T_3},\\[6pt] p=const,\\[6pt] V_1=V_2=0,1\ \text{м}^3. \end{gather*}

Звідси $$ V_3=\frac{V_2T_3}{T_2}=\frac{0,1\ \text{м}^3\cdot 800\ \text{К}}{200\ \text{К}}=0,4\ \text{м}^3. $$

Відповідно робота \begin{gather*} A=A_{23}=p(V_3-V_2)=\\[7pt] =1000\ \text{Па}\cdot(0,4\ \text{м}^3-0,1\ \text{м}^3)=300\ \text{Дж}. \end{gather*}

Відповідь: Г.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Ізопроцеси в газах.

Завдання скеровано на перевірку розуміння процесів, що відбуваються з газом сталої маси, тобто ізопроцесів.

За першим законом термодинаміки передана системі кількість теплоти \(Q\) витрачається на зміну внутрішньої енергії \(\Delta U\) та на виконання системою роботи \(A\) проти зовнішніх сил: $$ Q=\Delta U + A. $$

Під час ізотермічного \((T = const)\) процесу температура, а отже, і внутрішня енергія газу, не змінюються, тобто вся передана теплота витрачається на виконання роботи: $$ Q=A. $$

Під час ізобарного \((p = const)\) процесу і внутрішня енергія газу змінюється, і робота виконується: $$ Q=\Delta U + A. $$

Під час адіабатного (без обміну теплом із навколишнім середовищем) процесу теплота системі не передається, тобто газ може виконати роботу за рахунок зменшення внутрішньої енергії, при цьому температура газу зменшиться: $$ A=-\Delta U. $$

За ізохорного \((V = const)\) процесу об᾽єм газу не змінюється, тобто газ роботу не виконує \((A = 0)\), а рівняння першого закону термодинаміки таке: $$ Q=\Delta U. $$

Тож саме під час ізохорного процесу всю передану газу кількість теплоти буде витрачено на зміну його внутрішньої енергії.

Відповідь: Б.

ТЕМА: Механіка. Основи динаміки. Сили. Тиск рідин та газів.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі, пов’язані з використанням сили тиску.

Дано:
\(h=50\ \text{см}\)
\(S=40\ \text{см}^2\)
\(p=6\ 500\ \text{Па}\)

Знайти:
\(A\ (\text{Дж})\ -\ ?\)

Роботу можна визначити за формулою $$ A=Fh\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}, $$ де \(F\) – сила, що діє на тіло, \(h\) – переміщення тіла, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\) – кут між напрямками векторів сили й переміщення.

На поршень діє сила тиску газу, яку можна визначити за формулою $$ F=pS, $$ де \(p\) – тиск, \(S\) – площа поверхні, на яку відбувається тиск.

Напрямок дії сили тиску завжди перпендикулярний до поверхні, що обмежує газ, тому кут між переміщенням поршня і напрямком дії сили тиску дорівнює нулю. Тож \begin{gather*} A=Fh;\\[7pt] A=pSh;\\[7pt] A=6\ 500\ \text{Па}\cdot 40\ \text{см}^2\cdot 50\ \text{см};\\[7pt] A=6\ 500\ \text{Па}\cdot 0,004\ \text{м}^2\cdot 0,5\ \text{м};\\[7pt] A=13\ \text{Дж}. \end{gather*}

Відповідь: 13.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів.

Завдання скеровано на перевірку вміння застосовувати перший закон термодинаміки до ізопроцесів.

За першим законом термодинаміки $$ Q=\Delta U+A, $$ де \(Q\) – отримане системою тепло, \(\Delta U\) – зміна внутрішньої енергії, \(A\) – виконана системою робота.

1 Ізотермічний процес – процес змінювання стану газу деякої маси, що відбувається за незмінної температури. Тобто \(\Delta U=0\) і перший закон термодинаміки є вигляд $$ Q=A. $$ Тобто вся теплота, отримана тілом, витрачається на виконання ним роботи.

2 Адіабатний процес – це процес, який відбувається без теплообміну з навколишнім середовищем. Тобто \(Q=0\) і перший закон термодинаміки має вигляд: $$ \Delta U+A=0. $$ А отже $$ A=- \Delta U. $$ Цим виразом описано роботу, що відбувається за рахунок зміни внутрішньої енергії, а отже – охолодження.

3 Ізохорний процес – процес змінювання стану газу деякої маси, що відбувається за незмінного об’єму. Робота в такому процесі не виконується, тому перший закон термодинаміки має вигляд $$ Q=\Delta U. $$ Отже, уся теплота, отримана тілом, витрачається на збільшення його внутрішньої енергії.

4 Ізобарний процес – процес змінювання стану даного газу деякої маси, що відбувається за незмінного тиску. Тоді перший закон термодинаміки має вигляд $$ Q=\Delta U+A. $$ Тож теплота, отримана тілом, витрачається на зміну внутрішньої енергії та роботу тіла.

Відповідь: 1Г, 2В, 3А, 4Б.

ТЕМА: Молекулярна фізика і термодинаміка.

Завдання скеровано на перевірку розуміння поняття теплової рівноваги.

Стан теплової рівноваги – це такий стан макроскопічної системи, коли всі її макроскопічні параметри залишаються незмінними як завгодно довго.

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл.

Завдання скеровано на перевірку розуміння принципів теплообміну.

За першим законом термодинаміки кількість теплоти \(Q\), передана системі, іде на зміну внутрішньої енергії системи \((\Delta U)\) та на виконання системою роботи \(A\) проти зовнішніх сил: $$ Q=A+\Delta U. $$

Зміна внутрішньої енергії пов’язана зі зміною температури речовини, що не змінює свого агрегатного стану: що вища температура речовини, то вища її внутрішня енергія. Тож, якщо температура речовини не змінюється, то і внутрішня енергія тіл також не змінюється: $$ Q=A. $$

Проте під час зміни агрегатного стану (фазового переходу) температура речовини не змінюється, а внутрішня енергія – змінюється. Наприклад, під час плавлення льоду він поглинає тепло, проте його температура не почне зростати доти, доки триває плавлення (фазовий перехід).

Відповідь: Г.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Принцип дії теплових двигунів. Коефіцієнт корисної дії теплового двигуна та його максимальне значення.

Завдання скеровано на перевірку вміння розв’язувати задачі щодо принципу роботи і коефіцієнта корисної дії теплового двигуна.

Принцип роботи теплових двигунів такий: робоче тіло, одержуючи певну кількість теплоти \(Q_1\) від нагрівача, виконує механічну роботу \(A\) і передає деяку кількість теплоти \(Q_2\) холодильнику.

З одного боку, коефіцієнт корисної дії \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}\) двигуна дорівнює відношенню роботи \(A,\) виконуваної двигуном за цикл, до кількості теплоти \(Q_1,\) одержуваної від нагрівача: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}=\frac{A}{Q_1}. $$

З іншого боку, коефіцієнт корисної дії \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}\) ідеальної теплової машини дорівнює: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}=\frac{T_\text{Н}-T_\text{Х}}{T_\text{Н}}, $$ де \(T_\text{Н}\) ‒ температура нагрівача; \(T_\text{Х}\) ‒ температура холодильника.

Прирівняємо праві частини обох формул: $$ \frac{A}{Q_1}=\frac{T_\text{Н}-T_\text{Х}}{T_\text{Н}}, $$ звідки $$ Q_1=\frac{A\cdot T_\text{Н}}{T_\text{Н}-T_\text{Х}}. $$

Перед тим, як обчислити шукану кількість теплоти, визначмо температуру в кельвінах (K):

Відповідь: A.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів.

Завдання скеровано на перевірку вміння застосовувати перший закон термодинаміки до ізопроцесів.

Кількість теплоти \(Q,\) передана системі, забезпечує зміну внутрішньої енергії системи \(\Delta U\) та виконання системою роботи \(A\) проти зовнішніх сил: $$ Q=\Delta U+A. $$

Під час ізохорного нагрівання об’єм газу не змінюється \(\Delta V=0,\) газ роботу не виконує \((A=0),\) тому рівняння першого закону термодинаміки таке: $$ Q=\Delta U. $$

В ізохорному процесі вся передана газу кількість теплоти витрачається на збільшення внутрішньої енергії газу. Тож внутрішня енергія газу збільшилася на \(12\ \text{кДж.}\)

Під час ізотермічного розширення температура, а отже, і внутрішня енергія газу не змінюються \((\Delta U=0),\) тому рівняння першого закону термодинаміки таке: $$ Q=A. $$

В ізотермічному процесі вся передана газу кількість теплоти витрачається на виконання механічної роботи. Тому внутрішня енергія не змінилася на цьому етапі перетворень із газом.

Отже, за результатами двох процесів, що відбулися з газом, його внутрішня енергія змінилася лише на \(12\ \text{кДж.}\)

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Коефіцієнт корисної дії теплового двигуна і його максимальне значення.

Завдання скеровано на перевірку розуміння принципу дії теплових двигунів і вміння визначати різними способами коефіцієнт корисної дії та фізичні величини, які на нього впливають.

Коефіцієнт корисної дії (ККД) \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}\) ‒ фізична величина, якою характеризують економічність теплового двигуна. Він дорівнює відношенню корисної роботи \(A,\) виконуваної двигуном за цикл, до кількості теплоти \(Q,\) одержуваної від нагрівника: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}=\frac AQ. $$

Корисна робота двигуна полягає в подоланні сили опору руху візка \(F:\) $$ A=F\cdot s=F\cdot vt, $$ де \(s\) ‒ шлях, який долає візок, за час \(t,\ v\) ‒ швидкість руху візка.

Також коефіцієнт корисної дії такого двигуна можна визначити за формулою $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}=\frac{T_\text{Н}-T_\text{Х}}{T_\text{Н}}, $$ де \(T_\text{Н}\) ‒ температура нагрівника; \(T_\text{Х}\) ‒ температура холодильника.

Прирівняймо ці два вирази для обчислення коефіцієнта корисної дії: \begin{gather*} \frac AQ=\frac{T_\text{Н}-T_\text{Х}}{T_\text{Н}},\\[6pt] \frac{F\cdot vt}{Q}=\frac{T_\text{Н}-T_\text{Х}}{T_\text{Н}}. \end{gather*}

Виразімо звідси модуль швидкості руху візка й обчислімо його:

Відповідь: 2.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Робота в термодинаміці.

Завдання скеровано на перевірку розуміння роботи в термодинаміці.

Робота газу виконуватиметься, якщо змінюватиметься його об᾽єм. Якщо об’єм газу збільшується, то газ виконує додатну роботу. Якщо об’єм газу зменшується, то робота газу від’ємна.

Під час ізобарного процесу роботу \(A\) газу можна визначити за формулою $$ A=p\Delta V, $$ де \(p\) ‒ тиск, \(\Delta V\) ‒ зміна об᾽єму.

З іншого боку скористаємося рівнянням стану ідеального газу (рівнянням Менделєєва ‒ Клапейрона): $$ p\Delta V=\frac mM R\Delta T, $$ де \(m\) ‒ маса газу, \(M\) ‒ молярна маса газу, \(R\) ‒ універсальна газова стала, \(\Delta T\) ‒ зміна абсолютної температури.

Отже, роботу, яку виконує розріджений азот, можна визначити за формулою

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Основні положення молекулярно-кінетичної теорії та дослідне обґрунтування їх.

Завдання скеровано на перевірку знання базових понять молекулярної фізики й розуміння процесів, описаних за допомогою цих понять.

Теплопровідність ‒ це вид теплопередачі, зумовлений хаотичним рухом і взаємодією частинок речовини без перенесення її.

Хімічна реакція ‒ це перетворення речовин, під час якого з одних речовин утворюються інші.

Конвекція ‒ це вид теплопередачі, під час якого теплоту переносять потоки рідини або газу.

Дифузія ‒ це взаємне проникнення структурних частинок (молекул, атомів, йонів) однієї речовини між структурними частинками іншої внаслідок їхнього теплового руху.

Помідор у солоній воді не нагріється і нові речовини не утворяться. А от солоним він стане, тобто йони солі проникнуть у помідор унаслідок безперервного теплового руху, отже, відбудеться дифузія.

Відповідь: Г.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Коефіцієнт корисної дії теплового двигуна та його максимальне значення.

Завдання скеровано на перевірку розуміння коефіцієнта корисної дії (ККД) й уміння обчислити температуру нагрівача.

Аналізуючи роботу теплових двигунів, французький інженер Саді Карно (1796–1832) 1824 р. дійшов висновку, що найефективнішим (із максимально можливим ККД \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}_{\mathrm{max}}\) є так званий ідеальний тепловий двигун, який працює за циклом із двох ізотермічних і двох адіабатних процесів. Карно довів, що ККД такого двигуна можна обчислити за формулою $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}=\frac{T_\text{н}-T_\text{х}}{T_\text{н}}\cdot 100\ \text{%}=\left(1-\frac{T_\text{х}}{T_\text{н}}\right)\cdot 100\ \text{%}, $$ де \(T_\text{н}\) ‒ температура нагрівника; \(T_\text{х}\) ‒ температура холодильника.

Переведімо температуру холодильника в кельвіни: $$ T_\text{х}=(21+273)\ \text{К}=294\ \text{К}. $$

Обчислімо температуру нагрівача:

\begin{gather*} 30\ \text{%}=\left(1-\frac{294\ \text{К}}{T_\text{н}}\right)\cdot 100\ \text{%},\\[6pt] \frac{294\ \text{К}}{T_\text{н}}=1-0,3,\\[6pt] T_\text{н}=\frac{294\ \text{К}}{0,7}=420\ \text{К}. \end{gather*}

Відповідь: 420.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Робота в термодинаміці.

Завдання скеровано на перевірку вміння обчислювати термодинамічну роботу.

За ізобарного процесу передана газу кількість теплоти йде як на збільшення внутрішньої енергії газу, так і на виконання механічної роботи. За умовою азот розріджений, тобто відстань між молекулами набагато більша за розміри самих молекул, тому ці молекули можна вважати матеріальними точками, а їхньою взаємодією, окрім моментів зіткнення, можна знехтувати. Тобто азот можна вважати ідеальним газом, а роботу газу \(A\) визначити за формулою $$ A=p\Delta V, $$ де \(p\) ‒ тиск газу, \(\Delta V\) ‒ зміна об’єму газу.

Для визначення виконаної азотом роботи скористаймося рівнянням стану ідеального газу (рівнянням Менделєєва – Клапейрона): \begin{gather*} p\Delta V=\frac mM R\Delta T,\\[6pt] A=\frac mM R\Delta T, \end{gather*} де \(m\) ‒ маса газу, \(M\) ‒ молярна маса газу, \(R\) ‒ універсальна газова стала, \(\Delta T\) ‒ зміна температури газу.

Обчислімо шукану величину:

Відповідь: В.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів. Адіабатний процес.

Завдання скеровано на перевірку розуміння змін макроскопічних фізичних параметрів газу під час адіабатного процесу.

Адіабатний процес відбувається без теплообміну з навколишнім середовищем. За адіабатного процесу кількість теплоти, передана системі, дорівнює нулю. Тож умову завдання не задовольняють варіанти відповіді, у яких зазначено, що газ отримує тепло.

Перший закон термодинаміки для адіабатного процесу запишімо так: \begin{gather*} \Delta U+A=0,\\[7pt] A=-\Delta U. \end{gather*}

Це означає, що під час адіабатного розширення газ виконує додатну роботу \(A\) за рахунок зменшення внутрішньої енергії \(\Delta U,\) одночасно температура й тиск газу зменшуються, а об’єм збільшується.

Тобто за адіабатного розширення газ не отримує тепла, а його внутрішня енергія зменшується.

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів. Адіабатний процес.

Завдання скеровано на перевірку розуміння і застосування першого закону термодинаміки до ізопроцесів і адіабатного процесу.

Перший закон (начало) термодинаміки: кількість теплоти \(Q,\) передана системі, йде на зміну внутрішньої енергії системи \(\Delta U\) та на виконання системою роботи \(A\) проти зовнішніх сил: $$ Q=\Delta U+A. $$

Запишімо перший закон термодинаміки для ізопроцесів й адіабатного процесу.

Адіабатний процес ‒ це процес, який відбувається без теплообміну з навколишнім середовищем. Під час адіабатного процесу кількість теплоти \(Q,\) передана системі, дорівнює нулю, тому запис першого закону термодинаміки такий: $$ \Delta U+A=0\ \text{або}\ A=-\Delta U. $$

Під час адіабатного розширення газ виконує додатну роботу за рахунок зменшення внутрішньої енергії, а температура газу зменшується. Тому під опис адіабатного розширення підходять числові значення фізичних величин, зазначених у варіанті A: \(Q=0,\ A=12\ \text{кДж},\ \Delta U=-12\ \text{кДж}.\)

Ізохорне охолодження. Під час цього процесу об’єм газу не змінюється \((\Delta V = 0)\) і газ роботу не виконує \((A=0),\) тому рівняння першого закону термодинаміки має вигляд: $$ Q=\Delta U. $$

Газ під час ізохорного охолодження віддасть певну кількість теплоти, на стільки само зменшиться його внутрішня енергія. Тому ізохорному охолодженню відповідають числові значення фізичних величин, зазначені у варіанті Г: \(Q=-18\ \text{кДж},\ A=0,\ \Delta U=-18\ \text{кДж}.\)

Ізотермічне розширення. Під час цього процесу температура, а отже, і внутрішня енергія газу не змінюються \((\Delta U=0),\) тому рівняння першого закону термодинаміки таке: $$ Q=A. $$

Під час ізотермічного розширення вся передана газу кількість теплоти йде на виконання механічної роботи. Тому процесу ізотермічного розширення ставімо у відповідність варіант В: \(Q=24\ \text{кДж},\ A=24\ \text{кДж},\ \Delta U=0.\)

Ізобарне нагрівання. Під час цього процесу виконується робота й змінюється внутрішня енергія газу, тому рівняння першого закону термодинаміки таке: $$ Q=\Delta U+A. $$

Під час ізобарного нагрівання передана газу кількість теплоти йде і на збільшення внутрішньої енергії газу, і на виконання механічної роботи. Отже, підійде той варіант, у якому сума значень внутрішньої енергії і роботи дорівнюватиме значенню отриманої кількості теплоти ‒ це варіант Б: \(Q=5\ \text{кДж},\ A=2\ \text{кДж},\ \Delta U=3\ \text{кДж}.\)

У варіанті Д сума значень внутрішньої енергії і роботи також дорівнює значенню отриманої кількості теплоти, але значення кількості теплоти від’ємне, як і значення внутрішньої енергії і роботи. Це означає, що газ не нагрівається, не отримує кількість теплоти, а навпаки віддає її.

Відповідь: 1А, 2Г, 3В, 4Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Внутрішня енергія і способи зміни її.

Завдання скеровано на перевірку розуміння поняття внутрішньої енергії і знання чинників, від яких вона залежить.

Внутрішню енергію в термодинаміці визначають як суму кінетичних енергій хаотичного (теплового) руху частинок речовини (атомів, молекул, йонів), із яких складається тіло, і потенціальних енергій їхньої взаємодії.

Отже, внутрішня енергія \(U\) тіла змінюється зі зміною його температури \(T\) і під час зміни агрегатного стану речовини, з якої це тіло складається: $$ U\sim T. $$

Якщо підняти тіло на певну висоту, то зміниться його механічна енергія, зокрема потенціальна.

Якщо надати тілу швидкості, то теж зміниться його механічна енергія, зокрема кінетична.

Якщо сховати тіло до теплоізолювальної шафи, то тіло не отримуватиме або не віддаватиме тепло, не змінюватиметься його температура, а отже, не змінюватиметься його внутрішня енергія.

А от якщо нагріти тіло, то його внутрішня енергія збільшиться. Отже, правильна відповідь ‒ В.

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Адіабатний процес.

Завдання скеровано на перевірку розуміння адіабатного процесу й уміння обчислювати роботу під час цього процесу.

Без теплообміну з навколишнім середовищем відбувається адіабатний процес. Під час адіабатного процесу кількість теплоти \(Q,\) передана системі, дорівнює нулю, тому перший закон термодинаміки має вигляд: $$ \Delta U+A=0\ \text{або}\ A=-\Delta U. $$

Під час адіабатного розширення газ виконує додатну роботу \(A\) за рахунок зменшення внутрішньої енергії \(\Delta U,\) а температура газу зменшується.

Якщо газ ідеальний одноатомний, то робота газу дорівнює добутку тиску \(p\) і зміни об’єму \(\Delta V\) газу: $$ A=p\Delta V, $$ а зміна його внутрішньої енергії $$ \Delta U=\frac 32p\Delta V. $$

Використаймо рівняння Менделєєва ‒ Клапейрона $$ p\Delta V=\frac mM R\Delta T=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}R\Delta T, $$ де \(\frac mM=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}:\ m\) ‒ маса газу, \(M\) ‒ молярна маса газу, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}\) ‒ кількість речовини, \(R\) ‒ універсальна газова стала, \(\Delta T\) ‒ зміна абсолютної температури.

Отже, внутрішню енергію ідеального одноатомного газу можна обчислити за формулою $$ \Delta U=\frac 32p\Delta V=\frac 32\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}R\Delta T. $$

Пам’ятаймо, що зміна температури за шкалою Кельвіна дорівнює зміні температури за шкалою Цельсія: \begin{gather*} \Delta T=\Delta t, \end{gather*} де \(T\) ‒ абсолютна температура за шкалою Кельвіна, тобто ціна поділки шкали Кельвіна дорівнює ціні поділки шкали Цельсія:

Відповідь: A.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Закон збереження енергії в теплових процесах (перший закон термодинаміки).

Завдання скеровано на перевірку знання і розуміння першого закону термодинаміки й уміння застосовувати його в конкретних ситуаціях.

У термодинаміці розглядають системи, механічна енергія яких під час переходу з одного термодинамічного стану в інший не змінюється. У такому разі, якщо зовнішні сили виконали роботу \(A'\) й водночас системі передано певну кількість теплоти \(Q,\) то вся енергія йде на зміну внутрішньої енергії системи \(\Delta U.\)

Закон збереження та перетворення енергії в такому разі називають першим законом (началом) термодинаміки.

На практиці частіше розглядають не роботу зовнішніх сил \(A',\) а роботу \(A,\) яку виконує дана система проти зовнішніх сил.

З огляду на те, що $$ A'=-A, $$ перший закон (начало) термодинаміки можна сформулювати так:
кількість теплоти \(Q,\) передана системі, йде на зміну внутрішньої енергії системи \(\Delta U\) та на виконання системою роботи \(A\) проти зовнішніх сил: $$ Q=\Delta U+A. $$

Якщо система одержує певну кількість теплоти, то в наведеній формулі \(Q\) беремо зі знаком + (плюс), якщо внутрішня енергія системи зменшилася, то записуємо \(\Delta U\) зі знаком – (мінус): $$ Q=-\Delta U+A. $$

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Кількість теплоти. Закон збереження енергії в теплових процесах (перший закон термодинаміки).

Завдання скеровано на перевірку знання і розуміння першого закону термодинаміки і вміння його застосовувати до різних процесів.

Загальна кількість теплоти \(Q,\) отримана газом у процесах \(1‒2‒3,\) дорівнюватиме: $$ Q=Q_{1-2}+Q_{2-3}. $$

Визначимо кількість теплоти окремо для кожного процесу.

Згідно з першим законом термодинаміки кількість теплоти \(Q,\) передана системі, йде на зміну внутрішньої енергії системи \(\Delta U\) та на виконання системою роботи \(A\) проти зовнішніх сил: \begin{gather*} Q=\Delta U + A. \end{gather*}

Розгляньмо процес 1‒2. Графік цього процесу не відповідає жодному з графіків ізопроцесів, які можуть відбуватися з ідеальним газом. Під час цього процесу зростають об’єм, тиск і температура. Запишімо перший закон термодинаміки для процесу 1‒2:

відповідно до рівняння стану газу Менделєєва – Клапейрона \(pV=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}RT,\) де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}\) - кількість речовини, \(R\) ‒ універсальна газова стала, \(T\) ‒ абсолютна температура, \(p\) ‒ тиск, \(V\) ‒ об’єм.

Робота \(A_{1-2}\) дорівнює площі фігури під графіком залежності \(p(V),\)тобто площі прямокутної трапеції з основами \(p_0\) і \(4p_0,\) висотою \(2V_0:\) $$ A_{1-2}=\frac{p_0+4p_0}{2}\cdot 2V_0=5p_0V_0. $$

Визначмо \(Q_{1‒2}:\)

Розгляньмо процес 2‒3. З рисунка видно, що об’єм залишається сталим \((V_0).\) Цей графік відповідає ізохорному процесу.

Під час цього процесу об’єм газу не змінюється: $$ \Delta V=0, $$ газ роботу не виконує: $$ A_{2-3}=0, $$ тому рівняння першого закону термодинаміки має вигляд $$ Q_{2-3}=\Delta U_{2-3}. $$

Під час ізохорного процесу вся передана газу кількість теплоти витрачається на збільшення внутрішньої енергії газу. Якщо газ ідеальний одноатомний як в умові, то кількість теплоти, передана газу, дорівнює:

Значення кількості теплоти в процесі 2‒3 від’ємне. Це означає, що газ під час цього процесу віддав певну кількість теплоти.

Визначмо, на скільки збільшиться кількість теплоти \(Q\) газу внаслідок обох процесів:

Але в завданні питають, яку кількість теплоти газ отримав. Отримання відбувалося лише під час процесу 1‒2:

У цьому завданні обидві відповіді зараховані як правильні.

Відповідь: 1,6 і 4,3.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів. Адіабатний процес.

Завдання скеровано на перевірку знання і розуміння першого закону термодинаміки і вміння застосовувати його до адіабатного та ізопроцесів.

Перший закон (начало) термодинаміки: кількість теплоти \(Q,\) передана системі, йде на зміну внутрішньої енергії системи \(\Delta U\) та на виконання системою роботи \(A\) проти зовнішніх сил: $$ Q=\Delta U+A. $$

1. Ізотермічний процес. Під час цього процесу температура, а отже, і внутрішня енергія газу не змінюються \((\Delta U=0),\) тому рівняння першого закону термодинаміки має вигляд: $$ Q=A. $$

Під час ізотермічного процесу вся передана газу кількість теплоти йде на виконання механічної роботи.

Відповідний варіант відповіді – В.

2. Ізобарний процес. Під час цього процесу виконується робота і змінюється внутрішня енергія газу, тому рівняння першого закону термодинаміки має вигляд: $$ Q=\Delta U+A. $$

Під час ізобарного процесу передана газу кількість теплоти йде і на збільшення внутрішньої енергії газу, і на виконання механічної роботи.

Відповідний варіант відповіді – А.

3. Ізохорний процес. Під час цього процесу об’єм газу не змінюється \((\Delta V=0)\) і газ роботу не виконує \((A=0),\) тому рівняння першого закону термодинаміки має вигляд $$ Q=\Delta U. $$

Під час ізохорного процесу вся передана газу кількість теплоти витрачається на збільшення внутрішньої енергії газу.

Відповідний варіант відповіді – Д.

4. Адіабатний процес. Це процес, який відбувається без теплообміну з навколишнім середовищем. Під час адіабатного процесу кількість теплоти \(Q,\) передана системі, дорівнює нулю, тому запис першого закону термодинаміки має вигляд: $$ \Delta U+A=0,\ \text{або}\ A=-\Delta U. $$

Під час адіабатного розширення газ виконує додатну роботу за рахунок зменшення внутрішньої енергії, а температура газу зменшується.

Відповідний варіант відповіді – Г.

Відповідь: 1В, 2А, 3Д, 4Г.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Робота в термодинаміці

Завдання скеровано на перевірку розуміння роботи в термодинаміці і вміння визначати її під час різних ізопроцесів.

Розгляньмо окремо кожну ділянку графіка. З’ясуємо, чому дорівнюватиме загальна робота \(A,\) яку виконуватиме ідеальний газ під час процесів \(1‒2‒3:\) $$ A=A_{1-2}+A_{2-3}. $$

Процес \(1‒2:\) тиск \(p\) збільшується, об’єм \(V\) залишається сталим (див. ділянку графіка \(1‒2\)) ‒ процес ізохорний. Під час цього процесу газ роботу \(A_{1-2}\) не виконує: \begin{gather*} A_{1-2}=p\Delta V,\\[7pt] \Delta V=0\Rightarrow A_{1-2}=0. \end{gather*}

Під час ізохорного процесу вся передана газу кількість теплоти витрачається на збільшення внутрішньої енергії газу.

Процес \(2‒3:\) тиск \(p\) залишається сталим, об’єм \(V\) збільшується (див. ділянку графіка \(2‒3\)) ‒ процес ізобарний. У ході ізобарного процесу виконується робота і змінюється внутрішня енергія газу:

Отже, робота виконуватиметься лише під час ізобарного процесу:

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів.

Завдання скеровано на перевірку знання і розуміння першого закону термодинаміки і вміння застосовувати його до ізопроцесів.

Під час ізобарного процесу виконується робота і змінюється внутрішня енергія газу, тому рівняння першого закону термодинаміки має вигляд: $$ Q=\Delta U+A. $$

Під час ізобарного процесу передана газу кількість теплоти \(Q\) йде і на збільшення внутрішньої енергії газу \(\Delta U,\) і на виконання механічної роботи \(A.\)

Визначімо зміну внутрішньої енергії: $$ \Delta U=Q-A. $$

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів.

Завдання скеровано на перевірку вміння застосовувати перший закон термодинаміки до ізопроцесів, зокрема до ізобарного.

За умовою ідеальному одноатомному газу передали енергію кількістю \(Q\) за сталого тиску – процес ізобарний. У ході цього процесу виконується робота \(A\) і змінюється внутрішня енергія \(\Delta U\) газу, тому рівняння першого закону термодинаміки має вигляд: $$ Q=\Delta U + A. $$

За умовою газ ідеальний одноатомний, то робота газу дорівнює $$ A=p\Delta V, $$ де \(p\) – тиск, \(\Delta V\) – зміна об’єму.

А зміна його внутрішньої енергії $$ \Delta U=\frac 32p\Delta V. $$

Тоді кількість енергії, передана газу, дорівнює: $$ Q=\frac 32p\Delta V+p\Delta V=\frac 52p\Delta V. $$

Використавши рівняння Менделєєва – Клапейрона $$ p\Delta V=\frac mM R\Delta T=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}R\Delta T, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}=\frac mM\) – кількість речовини, що дорівнює відношенню маси газу до його молярної маси, \(R\) – універсальна газова стала, \(\Delta T\) – зміна температури, вираз для переданої ідеальному одноатомному газу енергії можна подати так: $$ Q=\frac 52p\Delta V=\frac{5}{2}\frac mM R\Delta T=\frac 52\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}R\Delta T. $$

Виразімо і обчислімо зміну температури газу:

(Зміна температури за шкалою Кельвіна дорівнює зміні температури за шкалою Цельсія: \(\Delta T=\Delta t,\) тобто ціна поділки шкали Кельвіна дорівнює ціні поділки шкали Цельсія: \(1\ ^\circ\mathrm{C}=1\ \text{K}.\))

Відповідь: 40.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Основні положення молекулярно-кінетичної теорії. Основи термодинаміки. Внутрішня енергія.

Завдання скеровано на перевірку знання і розуміння основних понять молекулярно-кінетичної теорії та їхнього зв’язку між собою.

1. Гелій – одноатомний газ. Атоми такого газу рухаються лише поступально, тому, щоб визначити його внутрішню енергію \(U,\) треба середню кінетичну енергію \(\overline{E}_k\) поступального руху атомів $$ \overline{E}_k=\frac{m_0\overline{v}^2_\text{кв}}{2} $$ помножити на кількість атомів \(N:\) $$ N=\frac mM N_A. $$

Тобто \begin{gather*} U=\overline{E}_k\cdot N,\\[6pt] U=\frac{m_0\overline{v}^2_\text{кв}}{2}\cdot \frac mM N_A,\\[6pt] U=M\cdot\frac{\overline{v}^2_\text{кв}}{2}\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}, \end{gather*} де \(M=m_0\cdot N_А\) (\(M\) – молярна маса, \(m_0\) – маса молекули (атома) цієї речовини, \(N_А\) – стала Авогадро), \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}=\frac mM\) (\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}\) – кількість речовини, \(m\) – маса речовини).

Відповідь: 18.

2. Середню кінетичну енергію поступального руху молекул ідеального газу (кінетична енергія поступального руху, що в середньому припадає на одну молекулу) обчислюють за формулою $$ \overline{E}_k=\frac{m_0\overline{v}^2_\text{кв}}{2}. $$

З іншого боку середня кінетична енергія поступального руху молекул ідеального газу прямо пропорційна абсолютній температурі \(T:\) $$ \overline{E}_k=\frac 32 kT, $$ де \(k\) – стала Больцмана.

Прирівняймо праві частини цих формул: $$ \frac{m_0\overline{v}^2_\text{кв}}{2}=\frac 32 kT. $$

Перетворімо отриману рівність так, щоб можна було визначити температуру газу, використовуючи фізичні величини з умови завдання: \begin{gather*} m_0=\frac{M}{N_A},\\[6pt] \frac{M}{N_A}\cdot \frac{\overline{v}^2_\text{кв}}{2}=\frac 32 kT,\\[6pt] \frac{M\overline{v}^2_\text{кв}}{2}=\frac 32 kN_AT, \end{gather*} де добуток сталої Больцмана і сталої Авогадро дорівнює універсальній газовій сталій \(R:\)

Відповідь: 1500.

Відповідь: 1. 18. 2. 1500.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Рівняння стану ідеального газу.

Завдання скеровано на перевірку розуміння рівняння стану ідеального газу та вміння за його допомогою визначати макроскопічні параметри газу.

За допомогою рівняння стану ідеального газу (рівняння Менделєєва – Клапейрона) $$ pV=\frac mM RT $$ можна встановити зв’язок між макроскопічними параметрами газу (\(p\) – тиск, \(V\) − обʼєм, \(T\) – абсолютна температура) у разі його переходу з одного стану в інший. Тобто якщо газ тієї ж маси \(m\) і молярної маси \(M,\) то можемо скористатися рівнянням Клапейрона: $$ \frac{p_1V_1}{T_1}=\frac{p_2V_2}{T_2}, $$ тобто для газу деякої маси відношення добутку тиску на об’єм до температури газу є незмінним: $$ \frac{pV}{T}=\text{const.} $$

Запишімо рівняння Клапейрона для кожної ділянки циклу.

Процес \(1−2\) відбувається за незмінного об’єму (відповідно до графіка), тобто \begin{gather*} V=\text{const},\\[6pt] \frac{p_1}{T_1}=\frac{p_2}{T_2},\\[6pt] \frac{p}{T_1}=\frac{2p}{T_2}, \end{gather*} \(T_2=2T_1\) – температура під час процесу \(1−2\) підвищилася в \(2\) рази порівняно з початковою температурою \(T_1.\)

Процес \(2−3\) відбувається за незмінного тиску (див. графік), тобто \begin{gather*} p=\text{const},\\[6pt] \frac{V_2}{T_2}=\frac{V_3}{T_3},\\[6pt] \frac{V}{T_2}=\frac{2V}{T_3}, \end{gather*} \(T_3=2T_2=4T_1\) – температура під час процесу \(2−3\) підвищилася в \(4\) рази порівняно з початковою температурою \(T_1.\)

Процес \(3−4\) відбувається за незмінного об’єму (відповідно до графіка), тобто \begin{gather*} V=\text{const},\\[6pt] \frac{p_3}{T_3}=\frac{p_4}{T_4},\\[6pt] \frac{2p}{T_3}=\frac{p}{T_4}, \end{gather*} \(T_4=\frac 12 T_3=\frac 12\cdot 4T_1=2T_1\) – температура під час процесу \(3−4\) підвищилася в \(2\) рази порівняно з початковою температурою \(T_1.\)

Процес \(4−1\) відбувається за незмінного тиску (відповідно до графіка), тобто \begin{gather*} p=\text{const},\\[6pt] \frac{V_4}{T_4}=\frac{V_1}{T_1},\\[6pt] \frac{2V}{T_4}=\frac{V}{T_1}, \end{gather*} \(T_4=2T_1\) – температура під час процесу \(4−1\) дійсно підвищилася в \(2\) рази порівняно з початковою температурою \(T_1,\) що вже було математично доведено на ділянці циклу \(3−4.\)

Отже, температура підвищилася найбільше під час процесу \(2−3\) – у \(4\) рази.

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Коефіцієнт корисної дії теплового двигуна та його максимальне значення.

Завдання скеровано на перевірку знання і розуміння формул для визначення коефіцієнта корисної дії теплового двигуна.

Коефіцієнт корисної дії \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}\) теплового двигуна (теплової машини) можна визначити за формулою \begin{gather*} \style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}=\frac{T_\text{н}-T_\text{х}}{T_\text{н}}\cdot 100\ \text{%}, \end{gather*} де \(T_\text{н}\) - температура нагрівника; \(T_\text{х}\) ‒ температура холодильника.

За умовою нагрівником є резервуар із водою, яка кипить. Температура кипіння дорівнює \(100\ ^\circ\mathrm{C},\) тобто $$ T_\text{н}=100\ ^\circ\mathrm{C}=373\ \text{К}. $$

Холодильником є ємність із льодом, який тане. Температура танення льоду \(0\ ^\circ\mathrm{C},\) тобто \begin{gather*} T_\text{х}=0\ ^\circ\mathrm{C}=273\ \text{К}. \end{gather*}

З іншого боку коефіцієнт корисної дії теплової машини дорівнює відношенню корисної роботи \(A,\) виконуваної машиною, до кількості теплоти \(Q_\text{н},\) одержуваної від нагрівника: \begin{gather*} \style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}=\frac{A}{Q_\text{н}}\cdot 100\ \text{%}. \end{gather*}

Частина теплоти \(Q_\text{н}\) від нагрівника піде на виконання корисної роботи \(A,\) а залишок буде переданий холодильнику \(Q_\text{х},\) унаслідок чого розтане лід: $$ Q_\text{н}=A+Q_\text{х}. $$

Прирівняймо ці два вирази для визначення коефіцієнта корисної дії:

Порція теплоти, яка буде передана холодильнику, може розплавити лід масою \(m_\text{л}:\) $$ Q_\text{х}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}m_\text{л}, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}\) ‒ питома теплота плавлення льоду.

Тобто \begin{gather*} \frac{T_\text{н}-T_\text{х}}{T_\text{н}}=\frac{A}{A+\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}m_\text{л}}. \end{gather*}

Підставимо числові значення величин з умови завдання і визначимо масу льоду:

Відповідь: 910.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Кількість теплоти. Коефіцієнт корисної дії нагрівника.

Завдання скеровано на перевірку розуміння того, що є корисною, а що – повною кількістю теплоти, уміння застосовувати формули для обчислення кількості теплоти під час нагрівання речовини і коефіцієнта корисної дії нагрівника.

1. Кількість теплоти \(Q,\) яка поглинається під час нагрівання речовини (або виділяється внаслідок її охолодження), обчислюють за формулою $$ Q=cm(t_2-t_1), $$ де \(c\) ‒ питома теплоємність речовини; \(m\) ‒ маса речовини; \(t_2\) і \(t_1\) ‒ кінцева і початкова температури.

Обчислимо кількість теплоти, необхідної для нагрівання порції води до кипіння відповідно до умови завдання:

Відповідь: 672.

2. Коефіцієнт корисної дії \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}\) нагрівника ‒ це фізична величина, яка характеризує ефективність нагрівника й дорівнює відношенню корисно спожитої теплоти \(Q_\text{кор}\) до всієї теплоти \(Q_\text{повна},\) яка може бути виділена під час повного згоряння палива (або це може бути кількість теплоти, яка виділяється в провіднику зі струмом): $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}=\frac{Q_\text{кор}}{Q_\text{повна}}\cdot 100\ \text{%}. $$

Відповідно до умови завдання корисно спожита кількість теплоти ‒ це та кількість теплоти, яку поглинула вода під час нагрівання її до кипіння: $$ Q_\text{кор}=Q=672\ \text{кДж}. $$

Під час проходження струму в електричному чайнику протягом \(10\ \text{хв}\) виділиться повна кількість теплоти, частина якої піде безпосередньо на нагрівання води до кипіння ‒ \(Q_\text{кор},\) а частина буде витрачена на нагрівання самого чайника і навколишнього середовища: $$ Q_\text{повна}=Pt, $$ де \(P\) ‒ потужність нагрівника (чайника), \(t\) ‒ час нагрівання.

Обчислімо коефіцієнт корисної дії чайника:

Відповідь: 1. 672. 2. 56.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Внутрішня енергія та способи її зміни.

Завдання скеровано на перевірку знання і розуміння, що таке внутрішня енергія газу і які параметри впливають на її зміну.

Запишемо формулу для визначення внутрішньої енергії \(U\) для одноатомного ідеального газу: $$ U=\frac 32\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}Rt, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}\) ‒ кількість речовини, \(R\) ‒ універсальна газова стала, \(T\) ‒ абсолютна температура газу.

Зміна внутрішньої енергії дорівнюватиме: \begin{gather*} \Delta U=U_2-U_1=\frac 32\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}RT_2-\frac 32\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}RT_1. \end{gather*}

Використавши рівняння Менделєєва ‒ Клапейрона, матимемо: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}RT=pV, $$ де \(p\) ‒ тиск газу, \(V\) ‒ об’єм газу.

Тоді за незмінного об’єму \((V_1=V_2=V)\) матимемо: \begin{gather*} \style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}RT_1=p_1V,\\[7pt] \style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}RT_2=p_2V. \end{gather*}

Підставмо ці вирази у формули для визначення зміни внутрішньої енергії:

Отже, зміна внутрішньої енергії дорівнюватиме добутку зміни тиску і об’єму.

Обчислімо шукану величину:

Відповідь: \(4\mathord{,}5.\)

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів.

Завдання скеровано на перевірку знання, розуміння і застосування першого закону термодинаміки до ізопроцесів, а саме до ізобарного.

Під час ізобарного нагрівання передана газу кількість теплоти витрачається і на виконання механічної роботи, і на збільшення внутрішньої енергії газу. Якщо газ ідеальний одноатомний (гелій ‒ це одноатомний газ без запаху, кольору та смаку), то робота \(A\) газу дорівнює $$ A=p\Delta V, $$ а зміна його внутрішньої енергії $$ \Delta U=\frac 32p\Delta V, $$ де \(p\) ‒ тиск, \(\Delta V\) ‒ зміна об’єму.

Отже, зміну внутрішньої енергії можна визначити за формулою:

Відповідь: 45.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Робота в термодинаміці.

Завдання скеровано на перевірку розуміння, за яких умов виконується робота в термодинаміці, від яких фізичних величин вона залежить, а також на вміння читати графіки та брати з них необхідні для розв’язування задачі числові дані.

Повна робота за цикл дорівнює сумі робіт, виконаних під час кожного процесу циклу:

Запишімо формулу для визначення роботи газу в термодинаміці: $$ A=p\Delta V=p(V_2-V_1). $$

З формули бачимо: якщо не буде зміни об’єму, то робота не буде виконана й дорівнюватиме нулю.

Проаналізуймо кожну ділянку графіка.

Ділянка графіка 1‒2: з рівняння Клапейрона

робимо висновок, що збільшуються всі три параметри газу ‒ й абсолютна температура \(T,\) і тиск \(p,\) й об’єм \(V\) (довільний процес). Відповідно до першого закону термодинаміки (\(Q=\Delta U+A\) ‒ кількість теплоти \(Q,\) передана системі, йде на зміну внутрішньої енергії системи \(\Delta U\) й на виконання системою роботи \(A\) проти зовнішніх сил) у нас недостатньо даних із графіка, щоб визначити роботу, яку виконає газ на цій ділянці.

Ділянка графіка 2‒3 – ізохорне охолодження: \(V=const,\) тиск \(p\) зменшується. Отже, відповідно до рівняння Клапейрона для ізохорного процесу, температура \(T\) теж знижуватиметься: $$ \frac pT=\mathrm{const}\Rightarrow \frac{p\downarrow}{T\downarrow}=\mathrm{const}. $$

Отже, під час цього процесу зміни об’єму не було \((\Delta V=0),\) отже, роботу газ не виконував: $$ A_{2-3}=0. $$

Ділянка графіка 3‒1 – ізобарне охолодження: \(p=const.\) Під час цього процесу об’єм \(V\) зменшується (див. рисунок). Відповідно до рівняння Клапейрона для ізобарного процесу температура \(T\) теж буде зменшуватися: $$ \frac VT=\mathrm{const}\Rightarrow \frac{V\downarrow}{T\downarrow}=\mathrm{const}. $$

У цьому процесі можна визначити роботу на ділянці 3‒1:

Значення роботи на цій ділянці від’ємне, оскільки об’єм газу зменшується.

Зважаючи на те, що на ділянці 1‒2 неможливо визначити роботу через нестачу даних, не можна визначити й повну роботу, скористаймося графічним способом розв’язання. Геометричний зміст роботи під час довільного процесу: робота газу чисельно дорівнює площі криволінійної трапеції під графіком залежності \(p(V).\)

Згідно з її геометричним змістом робота газу в процесі 1–2 чисельно дорівнює площі прямокутної трапеції (добуток є половиною суми основ трапеції і її висоти), основи якої дорівнюють \(p_1\) і \(p_2,\) а висота ‒ \((V_2-V_1 ):\) $$ A_{1-2}=\frac{p_1+p_2}{2}\cdot (V_2-V_1). $$

Об’єм газу збільшується, тому ця робота додатна.

Робота газу в процесі 2–3 дорівнює нулю, оскільки цей процес ізохорний (див. пояснення вище).

Робота газу в процесі 3–1 \((V_3=V_2)\) чисельно дорівнює площі прямокутника зі сторонами \(p_1\) і \((V_2-V_1):\) $$ A_{3-1}=p_1\cdot (V_2-V_1). $$

Об’єм газу зменшується, тому ця робота від’ємна (див. розрахунок вище).

Отже, для визначення роботи за весь цикл потрібно від площі трапеції відняти площу прямокутника. Тобто, як видно з рисунка, робота за цикл чисельно дорівнює площі прямокутного трикутника \(1–2–3\) (половина добутку катетів): $$ A=\frac 12\cdot (p_2-p_1)\cdot (V_2-V_1). $$

Необхідні значення величин знайдімо з графіка:

Відповідь: A.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Температура та її вимірювання.

Завдання скеровано на перевірку знання і розуміння поняття теплової рівноваги.

Досліди показують: коли більш нагріте тіло контактує з менш нагрітим, то більш нагріте тіло завжди охолоджується, а менш нагріте ‒ нагрівається. До того ж можуть змінюватися й інші властивості тіл: вони стають більшими або меншими за розмірами, можуть перейти в інший агрегатний стан, почати краще чи гірше проводити електричний струм, можуть почати випромінювати світло іншого кольору тощо. Натомість однаково нагріті тіла, контактуючи одне з одним, не змінюють своїх властивостей, і тоді кажуть, що ці тіла перебувають у стані теплової рівноваги.

Отже, стан теплової рівноваги ‒ це такий стан макроскопічної системи, коли всі макроскопічні параметри системи залишаються незмінними як завгодно довго.

Відповідь: Б.

Тема: Молекулярна фізика і термодинаміка. Основи термодинаміки. Коефіцієнт корисної дії теплової машини.

Завдання скеровано на перевірку знання і розуміння поняття коефіцієнта корисної дії.

З одного боку коефіцієнт корисної дії \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}\) теплової машини − фізична величина, яка характеризує економічність теплової машини й дорівнює відношенню роботи \(A,\) що виконує машина за цикл (корисної роботи), до кількості теплоти \(Q,\) одержуваної від нагрівача: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}=\frac AQ\cdot 100\ \text{%}. $$

З іншого боку коефіцієнт корисної дії ідеальної теплової машини $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}=\frac{T_\text{Н}-T_\text{Х}}{T_\text{Н}}\cdot 100\ \text{%}, $$ де \(T_\text{Н}\) − температура нагрівача; \(T_\text{Х}\) − температура холодильника.

Прирівняймо ці два вирази для коефіцієнта корисної дії: \begin{gather*} \frac AQ\cdot 100\ \text{%}=\frac{T_\text{Н}-T_\text{Х}}{T_\text{Н}}\cdot 100\ \text{%},\\[6pt] \frac AQ=1-\frac{T_\text{Х}}{T_\text{Н}}. \end{gather*}

Визначімо із цієї рівності температуру нагрівника: $$ T_\text{Н}=\frac{T_\text{Х}}{1-\frac AQ}. $$

Візьмемо до уваги, що \(A\) ‒ це корисна робота, яка дорівнюватиме різниці кількості теплоти, отриманої від нагрівника, і кількості теплоти, яка була передана холодильнику:

Тепер можна обчислити температуру нагрівача:

Відповідь: Г.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Коефіцієнт корисної дії теплової машини.

Завдання скеровано на перевірку знання і розуміння поняття коефіцієнта корисної дії.

З одного боку коефіцієнт корисної дії \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}\) теплової машини − фізична величина, яка характеризує економічність теплової машини і дорівнює відношенню роботи \(A,\) виконуваної машиною за цикл, до кількості теплоти \(Q,\) одержуваної від нагрівника: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}=\frac AQ\cdot 100\ \text{%}. $$

З іншого боку коефіцієнт корисної дії ідеальної теплової машини дорівнює: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}=\frac{T_\text{н}-T_\text{х}}{T_\text{н}}\cdot 100\ \text{%}, $$ де \(T_\text{н}\)− температура нагрівника; \(T_\text{х}\) − температура холодильника

Прирівняємо ці два вирази для коефіцієнта корисної дії: \begin{gather*} \frac AQ\cdot 100\ \text{%}=\frac{T_\text{н}-T_\text{х}}{T_\text{н}}\cdot 100\ \text{%}. \end{gather*}

Визначімо із цієї рівності кількість теплоти \(Q,\) яку має передати нагрівник робочому тілу \((T_\text{н}=527\ ^\circ\mathrm{C}+273=800\ \text{К},\) \(T_\text{х}=7\ ^\circ\mathrm{C}+273=280\ \text{К}):\)

Відповідь: 8.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів. Адіабатний процес.

Завдання скеровано на перевірку знання і розуміння першого закону термодинаміки й уміння застосовувати його до адіабатного та ізопроцесів.

Перший закон (начало) термодинаміки: кількість теплоти \(Q,\) передана системі, йде на зміну внутрішньої енергії системи \(\Delta U\) та на виконання системою роботи \(A\) проти зовнішніх сил: $$ Q=\Delta U+A. $$

1. Ізотермічний процес. Під час цього процесу температура, а отже, і внутрішня енергія газу не змінюються \((\Delta U=0),\) тому рівняння першого закону термодинаміки має вигляд $$ Q=A. $$

Під час ізотермічного процесу вся передана газу кількість теплоти йде на виконання механічної роботи.

Варіант відповіді – Г.

2. Адіабатний процес. Це процес, який відбувається без теплообміну з навколишнім середовищем. Під час адіабатного процесу кількість теплоти \(Q,\) передана системі, дорівнює нулю, тому перший закон термодинаміки має вигляд $$ \Delta U+A=0,\ \text{або}\ A=-\Delta U. $$

Під час адіабатного розширення газ виконує додатну роботу за рахунок зменшення внутрішньої енергії, а температура газу зменшується.

Відповідний варіант відповіді – В.

3. Ізохорний процес. Під час цього процесу об’єм газу не змінюється \((\Delta V=0)\) і газ роботу не виконує \((A=0),\) тому рівняння першого закону термодинаміки має вигляд \begin{gather*} Q=\Delta U. \end{gather*}

Під час ізохорного процесу вся передана газу кількість теплоти витрачається на збільшення внутрішньої енергії газу.

Варіант відповіді – А.

4. Ізобарний процес. Під час цього процесу виконується робота і змінюється внутрішня енергія газу, тому рівняння першого закону термодинаміки має вигляд $$ Q=\Delta U+A. $$

Під час ізобарного процесу передана газу кількість теплоти йде і на збільшення внутрішньої енергії газу, і на виконання механічної роботи.

Варіант відповіді – Б.

Відповідь: 1Г, 2В, 3А, 4Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Кількість теплоти.

Завдання скеровано на перевірку знання і розуміння перетворення кількості теплоти в інший вид енергії.

Унаслідок утраченої мідною кулькою внутрішньої енергії виділилася певна кількість теплоти \(Q:\) \begin{gather*} Q=cm\Delta t, \end{gather*} де \(c\) ‒ питома теплоємність міді, з якої зроблена кулька, \(m\) ‒ маса кульки, \(\Delta t\) ‒ зміна температури.

Під час підняття кульки на певну висоту \(h\) збільшиться її потенціальна енергія \(E_p\) від нуля до якогось значення: $$ E_p=mgh, $$ де \(g\) ‒ прискорення вільного падіння.

За умовою на підняття кульки витратиться \(1\ \text{%}\) від кількості теплоти, що виділиться: \begin{gather*} 0,01\cdot Q=E_p,\\[7pt] 0,01\cdot cm\Delta t=mgh,\\[7pt] 0,01\cdot c\Delta t=gh. \end{gather*}

Виразімо звідси \(h\) й обчислімо її:

Відповідь: A.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Плавлення і тверднення тіл.

Завдання скеровано на перевірку знання і розуміння зміни внутрішньої енергії речовини під час переходу з одного агрегатного стану в інший.

Після досягнення температури \(0\ ^\circ\mathrm{C}\) лід починає плавитися (танути), а його температура не змінюється попри те, що нагрівач продовжує працювати й передавати льоду певну кількість теплоти. Уся енергія, що надходить від нагрівача, витрачається на руйнування кристалічної ґратки льоду. У цей інтервал часу внутрішня енергія \(\Delta U\) льоду продовжує збільшуватися. І збільшиться вона на ту кількість теплоти \(Q,\) яка необхідна для плавлення льоду масою \(m=3\ \text{кг}:\) $$ \Delta U=Q=qm, $$ де \(q\) ‒ питома теплота плавлення;

Отже, внутрішня енергія льоду, що розтанув, збільшилася на \(9,9\cdot 10^5\ \text{Дж}.\)

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Робота в термодинаміці.

Завдання скеровано на перевірку розуміння роботи в термодинаміці.

Роботу газ виконуватиме, якщо змінюватиметься його об’єм. Якщо об’єм газу збільшується, то газ виконує додатну роботу. Якщо об’єм газу зменшується, то робота газу від’ємна.

Під час ізобарного процесу роботу \(A\) газу можна визначити за формулою \begin{gather*} A=p\Delta V, \end{gather*} де \(p\) ‒ тиск, \(\Delta V\) ‒ зміна об’єму.

Скористаймося рівнянням стану ідеального газу (рівнянням Менделєєва ‒ Клапейрона): $$ p\Delta V=\frac mMR\Delta T, $$ де \(m\) ‒ маса газу, \(M\) ‒ молярна маса газу, \(R\) ‒ універсальна газова стала, \(\Delta T\) ‒ зміна абсолютної температури.

Отже, роботу, яку виконує розріджений азот, можна визначити за формулою

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів. Адіабатний процес.

Завдання скеровано на перевірку розуміння суті адіабатного процесу і закономірностей змін макроскопічних фізичних параметрів газу під час цього процесу.

Адіабатний процес ‒ це процес, який відбувається без теплообміну з навколишнім середовищем. Під час адіабатного процесу кількість теплоти, передана системі, дорівнює нулю. Отже, варіанти відповіді, у яких зазначено, що газ отримує тепло, можна відкинути.

Перший закон термодинаміки для адіабатного процесу має вигляд: $$ \Delta U+A=0,\ \text{або}\ A=-\Delta U. $$

Це означає, що в ході адіабатного розширення газ виконує додатну роботу \(A\) за рахунок зменшення внутрішньої енергії \(\Delta U,\) температура газу знижується, тиск також знижується, а об’єм збільшується.

Отже, правильною буде відповідь, що газ не отримує тепла, а його внутрішня енергія зменшується.

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Робота в термодинаміці. Застосування першого закону термодинаміки до ізопроцесів.

Завдання скеровано на перевірку вміння визначати тип ізопроцесу й роботу газу відповідно до першого закону термодинаміки.

Роботу \(A\) газу в термодинаміці визначають за формулою \begin{gather*} A=p\Delta V, \end{gather*} де \(p\) ‒ тиск газу, \(\Delta V\) ‒ зміна об’єму газу.

Для того, щоб знати, що відбувається з тиском й об’ємом, необхідно розібратися, який процес відбувається з газом під час кожного етапу циклу.

Розгляньмо ділянку \(1‒2.\) Це ізобарний процес ‒ \(p=\mathrm{const}.\) Під час цього процесу, як видно з графіка, абсолютна температура \(T\) газу підвищується. Відповідно до рівняння Клапейрона для ізобарного процесу об’єм \(V\) газу теж буде збільшуватися:

Отже, процес \(1‒2\) ‒ це процес ізобарного нагрівання.

Оскільки температура підвищилася на дві позиції, то й об’єм збільшився на \(2\ \text{позиції},\) а тиск залишився тим самим: $$ A_{1-2}=p\cdot 2V. $$

Розгляньмо ділянку \(3‒4.\) Це теж ізобарний процес ‒ \(p=\mathrm{const}.\) Під час цього процесу, як видно з графіка, абсолютна температура \(T\) газу знижується. Відповідно до рівняння Клапейрона для ізобарного процесу об’єм \(V\) газу теж зменшуватиметься: \begin{gather*} \frac VT=\mathrm{const}\Rightarrow \frac{V\downarrow}{T\downarrow}=\mathrm{const}. \end{gather*}

Отже, процес \(3-4\) ‒ це процес ізобарного охолодження.

Оскільки температура знизилася на дві позиції, то і об’єм теж зменшився на \(2\ \text{позиції},\) а тиск залишився тим самим: $$ A_{3-4}=p\cdot 2V. $$

Визначімо відношення абсолютних (за модулем) значень робіт газу на ділянках \(1‒2\) і \(3‒4:\) $$ \frac{A_{1-2}}{A_{3-4}}=\frac{p\cdot 2V}{p\cdot 2V}=1. $$

Отже, газ виконав однакові роботи, тільки під час процесу \(1‒2\) газ розширювався, а під час процесу \(3‒4\) стискався.

Відповідь: 1.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Робота в термодинаміці.

Завдання скеровано на перевірку знання і розуміння поняття роботи в термодинаміці та його геометричного змісту.

Робота газу чисельно дорівнює площі фігури під графіком залежності \(p(V).\)

Під час ізобарного процесу роботу газу можна визначити за формулою $$ A=p\Delta V. $$

Геометричний зміст роботи під час ізобарного процесу відображено на графіках:

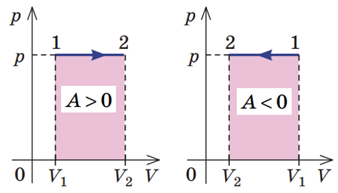
Геометричний зміст роботи під час довільного процесу: робота газу чисельно дорівнює площі криволінійної трапеції під графіком залежності \(p(V):\)

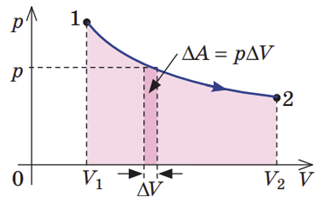
Проаналізувавши циклічні процеси, робимо висновок, що найбільшу роботу газ виконав під час циклу В.

Відповідь: B.