Геометрія – Елементарні геометричні фігури на площині. Геометричні величини

ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури на площині та їх властивості.

Завдання перевіряє знання аксіом планіметрії.

\(\angle KOB=\angle KOM+\angle MOB.\)

Підставмо відомі значення:

\begin{gather*} 115^\circ=\angle KOM+35^\circ;\\[7pt] \angle KOM=115^\circ-35^\circ;\\[7pt] \angle KOM=80^\circ. \end{gather*}

Відповідь: Д.

ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості.

Завдання перевіряє знання аксіом планіметрії, уміння застосовувати властивості найпростіших геометричних фігур у розв'язуванні планіметричних задач.

Оскільки точка \(M\) лежить на відрізку \(AB\), загальна довжина складається з двох частин:

Нехай точка \(K\) – середина відрізка \(AM.\) Тоді відстань від \(K\) до \(M\) дорівнює половині довжини \(AM{:}\)

Відстань від середини відрізка \(AM\) (точки \(K\)) до точки \(B\) складається з відрізків \(KM\) та \(MB{:}\)

Відповідь: Б.

ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури на площині та їхні властивості.

Завдання перевіряє знання аксіом планіметрії.

\(\angle KOB=\angle KOM+\angle MOB.\)

Підставмо відомі значення:

Відповідь: Б.

ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості.

Завдання перевіряє знання аксіом планіметрії, уміння застосовувати властивості найпростіших геометричних фігур у розв'язуванні планіметричних задач.

За умовою \(MB=2AM\), отже \(MB=2\cdot 12=24\) см.

Нехай точка \(K\) – середина \(AM\), а точка \(C\) – середина \(MB.\)

Відповідь: Г.

ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їх властивості. Аксіоми планіметрії.

Це завдання перевіряє вміння застосовувати властивості найпростіших геометричних фігур до розв’язування планіметричних задач.

Відрізок \(AC\) складається з \(2\) частин, отже: \(AC=2x.\)

Відрізок \(CB\) складається з \(3\) частин, отже: \(CB=3x.\)

За умовою \(CB=12\) см. Тоді

Підставимо це значення у вираз для \(AC{:}\)

\begin{gather*} AC=2x=2\cdot 4=8\ \text{см}. \end{gather*}

Відповідь: Д.

ТЕМА: Геометрія. Планіметрія. Найпростіші фігури на площині. Суміжні кути.

Завдання перевіряє вміння визначати невідомий кут, використовуючи означення і властивість суміжних кутів.

Кути \(\alpha\) та \(\beta\) суміжні, оскільки мають спільну сторону, а інші їхні сторони є доповняльними променями. Сума суміжних кутів завжди дорівнює \(180^\circ.\) Тому

Відповідь: Б.

ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури на площині та їх властивості.

Завдання перевіряє знання аксіом планіметрії.

Отже, правильна відповідь – Г.

Відповідь: Г.

ТЕМА: Геометрія. Планіметрія. Найпростіші фігури на площині. Вертикальні кути. Суміжні кути.

Завдання спрямовано на перевірку знань про суміжні та вертикальні кути як основні геометричні фігури на площині.

Суміжними називають два кути, у яких одна сторона спільна, а інші є доповняльними променями. На рис. 1 кути \(AOC\) та \(COB\) суміжні.

Рис. 1

Сума суміжних кутів дорівнює \(180^\circ.\) Оскільки в умові міру кута наведено в радіанах, скористаймось еквівалентом: \begin{gather*} \alpha+\beta=\pi. \end{gather*}

Відомо, що кут \begin{gather*} \alpha=\frac{\pi}{5}. \end{gather*}

Щоб визначити міру кута \(\beta\), віднімімо від \(\pi\) відомий кут: \begin{gather*} \beta=\pi-\frac{\pi}{5}. \end{gather*}

Зведімо до спільного знаменника:

Відповідь: B.

ТЕМА: Геометрія. Планіметрія.

Завдання скеровано на перевірку знання властивості зовнішнього кута трикутника.

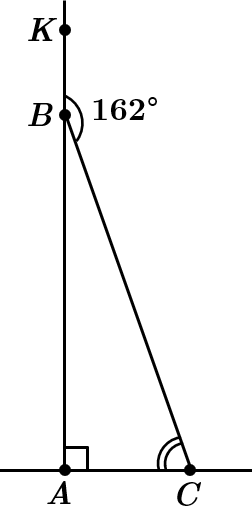
За властивістю зовнішнього кута трикутника: \begin{gather*} \angle KBC=\angle A+\angle C,\\[7pt] \angle C=\angle KBC-\angle A,\\[7pt] \angle C=162^\circ-90^\circ,\\[7pt] \angle C=72^\circ. \end{gather*}

Відповідь: B.

ТЕМА: Елементарні геометричні фігури на площині та їхні властивості.

Завдання скеровано на перевірку знання властивостей і видів кутів.

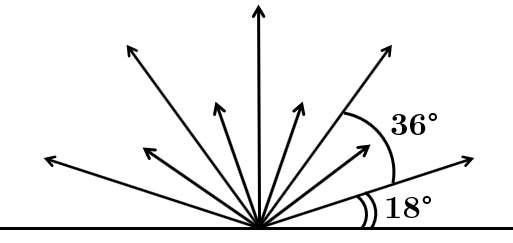
Розгорнутий кут поділено на \(10\) рівних частин. Градусна міра кожного з-поміж цих кутів $$ 180^\circ: 10=18^\circ. $$

Градусна міра кута між довгими стрілками складається з двох градусних мір кутів між довгою і короткою стрілкою.

Отже,

Відповідь: Г.

ТЕМА: Елементарні геометричні фігури на площині та їхні властивості.

Завдання скеровано на перевірку знання властивостей суміжних і вертикальних кутів, паралельних прямих.

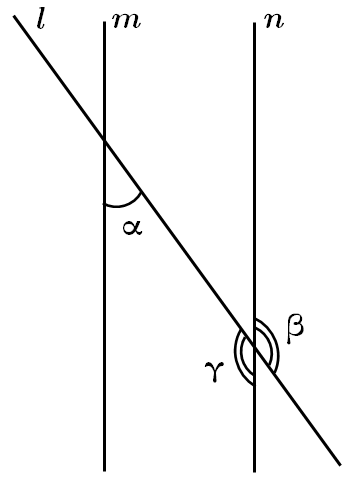
Кути \(\mathbf{\gamma}\) i \(\mathbf{\beta}\) – вертикальні. За властивістю вертикальних кутів \(\mathbf{\beta} = \mathbf{\gamma}.\)

Кути \(\mathbf{\alpha}\) i \(\mathbf{\gamma}\) – внутрішні односторонні. За їхньою властивістю:

Отже, \(\mathbf{\beta}=145^\circ.\)

Відповідь: Д.

ТЕМА: Елементарні геометричні фігури на площині та їхні властивості.

Завдання скеровано на перевірку знання властивостей суміжних і вертикальних кутів.

Кути \(\mathbf{\beta}\) i \(\mathbf{\varphi}\) – вертикальні. За їхньою властивістю \(\mathbf{\beta}=\mathbf{\varphi}.\)

За умовою \(\mathbf{\beta}+\mathbf{\varphi}=70^\circ\), тому $$ \mathbf{\beta}=\mathbf{\varphi}=70^\circ:2=35^\circ. $$

Кути \(\mathbf{\alpha}\) i \(\mathbf{\beta}\) – суміжні. За властивістю суміжних кутів:

Відповідь: A.

ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури на площині та їхні властивості.

Завдання скеровано на перевірку знання властивостей кутів, аксіом планіметрії.

\(\angle BOC=90^\circ, \angle BOA=4^\circ.\) Отже,

Відповідь: Г.

ТЕМА: Геометрія. Планіметрія.

Завдання скеровано на перевірку знання властивості зовнішнього кута трикутника.

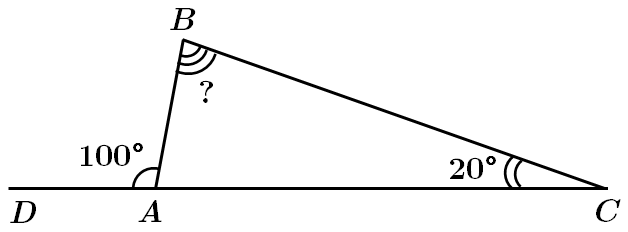
За властивістю зовнішнього кута трикутника:

\begin{gather*} \angle DAB=\angle B+\angle C. \end{gather*}

Отже, \(\angle B=100^\circ-20^\circ=80^\circ.\)

Відповідь: Г.

ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури на площині та їх властивості.

Завдання перевіряє знання аксіом планіметрії.

\(\angle AOK+\angle KOM+\angle MOB=180^\circ.\)

\(\angle AOK=180^\circ-(30^\circ+80^\circ)=70^\circ.\)

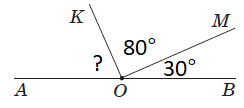
Отже, правильна відповідь – Б.

Відповідь: Б.

ТЕМА: Геометрія. Планіметрія. Геометричні перетворення.

Завдання перевіряє знання геометричних перетворень на площині: симетрії відносно прямої та точки.

1 – Б. симетрія відносно осі \(x.\)

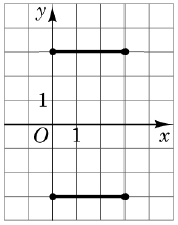
2 – Г. симетрія відносно осі \(y.\)

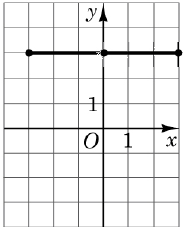
3 – Д. симетрія відносно точки \(O.\)

Відповідь: 1Б, 2Г, 3Д.

ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури та їхні властивості.

Перевіряє знання властивостей, паралельних прямих, суми кутів трикутника.

$$ \angle BAC+\angle ACK=180^\circ $$ за властивістю паралельних прямих сума внутрішніх односторонніх кутів \(180^\circ.\) $$ \angle ACK=180^\circ-52^\circ=128^\circ. $$ \(CB\) – бісектриса, тому $$ \angle ACB=\angle BCK=128^\circ:2=64^\circ. $$ Сума кутів трикутника \(180^\circ.\) Отже, \begin{gather*} \angle ABC=180^\circ-(\angle BAC +\angle ACB)=\\[7pt] =180^\circ-(52^\circ+64^\circ)=180^\circ-116^\circ=64^\circ. \end{gather*} Або в такий спосіб: \(\angle ABC=\angle BCK=64^\circ\) як внутрішні різносторонні при \(AB\ ||\ CK\) та січної \(BC.\)

Відповідь: B.

ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури на площині та їхні властивості.

Завдання перевіряє знання властивостей суміжних кутів та паралелограма.

\(\angle ABM+\angle ABC=180^\circ\) за властивістю суміжних кутів.

За властивістю паралелограма $$ \angle B=\angle D=155^\circ. $$

Відповідь: B.

ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури та їхні властивості.

Завдання перевіряє знання властивостей вертикальних i суміжних кутів, паралельних прямих.

\(\angle\mathbf{\beta}=\angle\mathbf{\gamma}\) як вертикальний. \(\mathbf{\alpha}+\mathbf{\gamma}=180^\circ.\) За властивістю паралельних прямих. \(\mathbf{\alpha}\), \(\mathbf{\gamma}\) – внутрішні односторонні. $$ \mathbf{\alpha}=180^\circ-\mathbf{\gamma}=180^\circ-125^\circ=55^\circ. $$

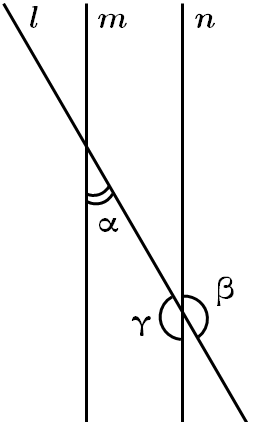
Відповідь: B.

ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури на площині та їхні властивості.

Завдання перевіряє знання властивостей суміжних та вертикальних кутів, теореми про суму кутів трикутника.

\(\angle BAC=180^\circ-120^\circ=60^\circ\) – суміжний до кута \(120^\circ.\)

\(\angle ACB=\mathbf{\alpha}\) – вертикальні кути.

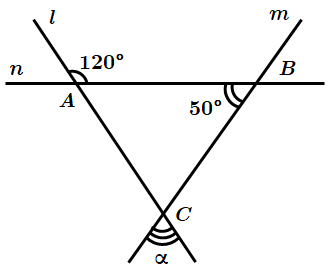
Сума кутів \(\Delta ABC\) дорівнює \(180^\circ\), тому $$ \mathbf{\alpha}=180^\circ-(50^\circ+60^\circ)=70^\circ. $$

Відповідь: Г.

ТЕМА: Геометрія. Планіметрія. Чотирикутники.

Це завдання перевіряє знання властивостей паралелограмів, суміжних кутів.

За властивістю суміжних кутів $$ \angle ABM+\angle CBA=180^\circ. $$

За властивістю паралелограма \(\angle B=\angle D=155^\circ\) як протилежні.

Відповідь: Д.

ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості.

Це завдання перевіряє вміння застосовувати означення, ознаки та властивості найпростіших геометричних фігур до розв'язування задач практичного змісту.

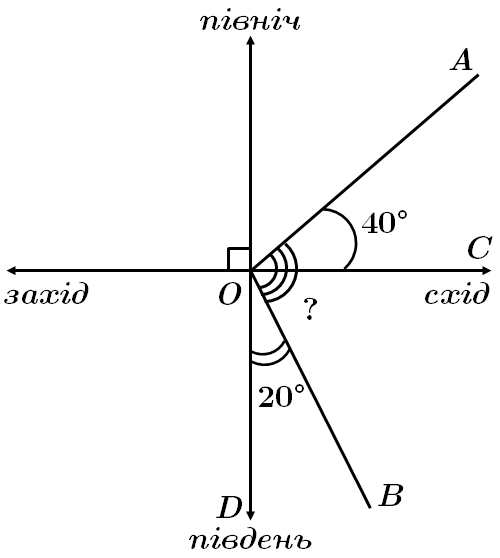
Кут \(COD\) – прямий.

Відповідь: B.

ТЕМА: Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості. Трикутники. Суміжні та вертикальні кути, паралельні та перпендикулярні прямі. Геометричні перетворення.

Це завдання перевіряє вміння застосовувати властивості паралельних прямих, ознаки подібності трикутників до розв'язування планіметричних задач.

Зробимо додаткову побудову і терез точку \(K\) проведемо пряму \(AB\), перпендикулярну до прямих \(a\) i \(b.\)

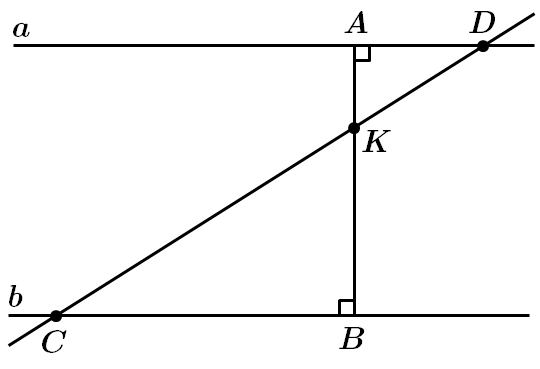
Розглянемо трикутники \(ADK\) та \(BCK.\) Вони подібні за двома кутами: \(\angle ADK=\angle BCK\) як внутрішні різносторонні при \(a\ ||\ b\) та січною \(CD.\)

\(\angle DAK=\angle KBC=90^\circ\) за побудовою.

У подібних трикутниках відповідні сторони пропорційні, отже $$ \frac{AK}{KB}=\frac{KD}{CK}. $$

Відстань від точки \(K\) до прямої \(a\) – це довжина перпенидкуляра \(KA=1\) см \begin{gather*} \frac{1}{KB}=\frac 25,\\[6pt] KB=2\mathord{,}5\ \textit{см}. \end{gather*}

Відстань між прямими \(a\) i \(b\) – це довжина спільного перпендикуляра

\(AB=AK+KB=1+2\mathord{,}5=3\mathord{,}5\) см.

Відповідь: B.

ТЕМА: Найпростіші геометричні фігури на площині та їхні властивості.

Це завдання перевіряє вміння застосовувати властивості найпростіших геометричних фігур до розв'язування планіметричних задач, знання властивості вертикальних кутів.

\(\angle \mathbf{\beta}=60^\circ\) як вертикальний з даним кутом \(60^\circ.\)

\(\mathbf{\alpha}+\mathbf{\beta}+40^\circ=180^\circ\) оскільки складають розгорнутий кут.

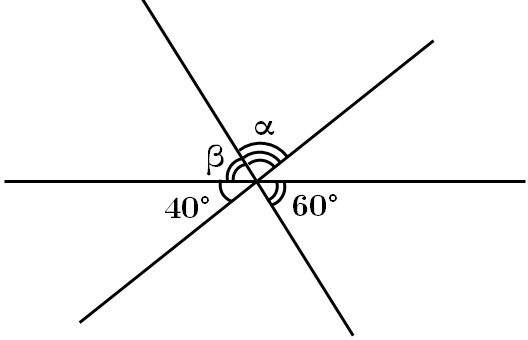
Відповідь: A.

ТЕМА: Геометрія. Планіметрія. Координати та вектори на площині. Геометричні величини та їх вимірювання.

Це завдання перевіряє знання прямокутної системи координат на площині, координати точки, формули площі трапеції.

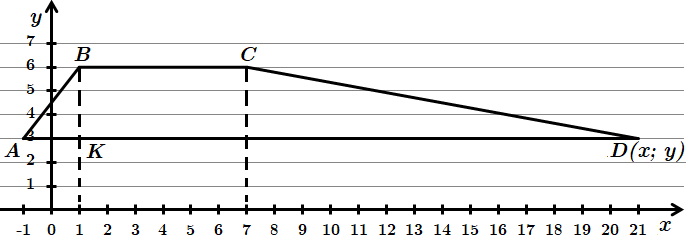
Позначимо задані точки на координатній площині.

Задано трапеція \(ABCD.\) Точки \(B\) та \(C\) мають однакову ординату, тому пряма \(BC\) паралельна осі \(Ox.\)

\(BC\ ||\ AD\), тому точка \(D\) має з точкою \(A\) однакову ординату \(y=3.\) Площа трапеції \(42\), тому $$ S=\frac{BC+AD}{2}\cdot h, $$ де \(h\) – висота трапеції, складемо рівняння.

звідси \(AD=22.\)

Так як точка \(A\) має абсцису \(-1\), то точка \(D\) буде мати абсцису \(21.\)

Відповідь: \(21.\)

ТЕМА: Геометрія. Планіметрія. Геометричні величини та їх вимірювання.

Це завдання перевіряє вміння обчислювати довжину кола та його дуг, використовувати формули знаходження довжини кола до розв'язування планіметричних задач і задач практичного змісту.

Знаходимо довжини \(6\) півкіл, які знаходяться усередині кола радіуса \(2\) м, за формулою $$ 6C_1=6\mathbf{\pi}R, $$ де \(R\) – радіус кола та \(R=1\) м.

Емблема також складається ще з одного кола, радіусом \(2\) м, тому

Довжина матеріалу складає

Вартість матеріалу

\(\mathbf{\pi}\approx 3\mathord{,}14\), тому

З-поміж наведених сум грошей найменша, якої достатньо, щоб придбати матеріал це \(7000\) грн.

Відповідь: Г.

ТЕМА: Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості. Трикутники.

Це завдання перевіряє вміння застосовувати властивості найпростіших геометричних фігур, різних видів трикутників до розв'язування планіметричних задач.

\(\Delta ABC\) – рівносторонній, тому $$ \angle A=\angle B=\angle C=60^\circ. $$

\(\angle KBM=180^\circ\) – розгорнутий. $$ \angle KBA+\angle ABC+\angle CBM=180^\circ. $$

Отже,

Відповідь: Б.

ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості.

Це завдання перевіряє знання аксіом планіметрії, уміння застосовувати властивості найпростіших геометричних фігур до розв'язування планіметричних задач.

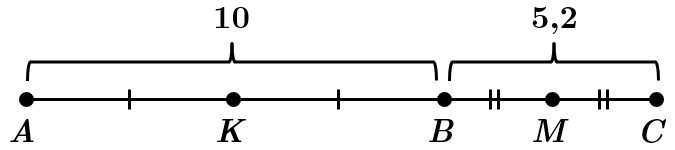
Нехай точка \(K\) – середина \(AB\), а точка \(M\) – середина \(BC.\)

\begin{gather*} KM=KB+BM=\frac 12AB+\frac 12BC=\\[6pt] =\frac 12(AB+BC)=(10+5\mathord{,}2):2=7\mathord{,6}\ \textit{см}. \end{gather*}

Відповідь: Г.

ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їх властивості.

Це завдання перевіряє знання аксіом стереометрії, властивостей паралельних прямих, уміння застосовувати властивості найпростіших геометричних фігур до розв’язування планіметричних задач.

\(\angle ABC+\angle CBD+\angle DBE=180^\circ\), \(\angle CBD=\angle BDE=70^\circ\), як внутрішні різносторонні при \(m\ ||\ n\) та січною \(BD.\) Кут \(\mathbf{\alpha}=180^\circ-60^\circ-70^\circ=50^\circ.\)

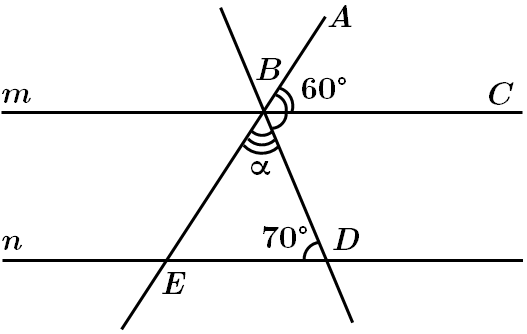
Відповідь: Б.

ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їх властивості. Аксіоми планіметрії.

Це завдання перевіряє вміння застосовувати властивості найпростіших геометричних фігур до розв’язування планіметричних задач.

Відповідь: A.

ТЕМА: Геометрія. Планіметрія. Найпростіші фігури на площині. Вертикальні та суміжні кути.

Це завдання перевіряє вміння визначати невідомий кут, використовуючи означення суміжних кутів і властивості вертикальникх кутів.

Зображені на рисунку кути \(\alpha\) i \(\beta\) є вертикальними, тому що утворені при перетині двох прямих \(m\) i \(n.\)

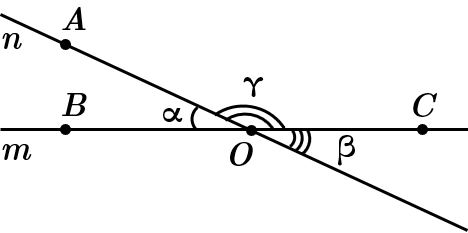
Вертикальні кути рівні, тому $$ \alpha=\beta=\frac{50^\circ}{2}=25^\circ. $$ Кути \(\alpha\) i \(\gamma\) є суміжними, оскільки промінь \(OA\), що лежить на прямій \(n\), є спільною стороною цих кутів, а сторони \(OB\) та \(OC\), що лежать на прямій \(m\), є доповняльними променями. Оскільки сума суміжних кутів дорівнює \(180^\circ\), то $$ \gamma=180^\circ-\alpha=180^\circ-25^\circ=155^\circ. $$

Відповідь: Б.

ТЕМА: Геометрія. Планіметрія. Кути при паралельних прямих. Бісектриса кута.

Це завдання перевіряє знання властивостей кутів, що утворюються при перетині двох паралельних прямих січною та означення бісектриси кута.

Кути \(\angle BAC\) та \(\angle ACK\) – внутрішні односторонні кути при паралельних прямих \(AB\) i \(CK\) та січній \(AC.\) Сума внутрішніх односторонніх кутів при паралельних прямих дорівнює \(180^\circ.\) Отже, $$ \angle BAC+\angle ACK=180^\circ, $$ звідки

Оскільки \(BC\) є бісектрисою кута \(\angle ACK\), то за означенням бісектриси, вона ділить цей кут навпіл, отже,

Кути \(\angle BCK\) i \(\angle ABC\) – внутрішні різносторонні кути при паралельних прямих \(AB\) i \(CK\) та січній \(BC\), тому вони рівні. Отже, \(\angle ABC=64^\circ.\)

Відповідь: B.

ТЕМА: Геометрія. Планіметрія. Суміжні кути. Трикутники. Зовнішній кут трикутника. Теорема про суму кутів трикутника.

Це завдання перевіряє вміння знаходити градусні міри кутів.

Для розв’язання завдання потрібно знати такі теореми.

Теорема 1. Сума внутрішніх кутів трикутника дорівнює \(180^\circ.\)

Теорема 2. Сума суміжних кутів дорівнює \(180^\circ.\)

Наведемо декілька способів розв’язання цього завдання.

Перший спосіб. Розглянемо трикутник \(ABC\) (див. рисунок), у якого \(\angle B=85^\circ\), \(\angle MAB\) – зовнішній кут трикутника, суміжний з кутом \(A\), тоді $$ \angle A=180^\circ-\angle MAB=40^\circ. $$ Знаючи два внутрішніх кути трикутника \(ABC\), можемо визначити градусну міру його третього кута: $$ \angle C=180^\circ-(40^\circ+85^\circ)=55^\circ. $$ Оскільки за умовою \(\angle ACN=90^\circ\), то $$ 55^\circ+\alpha=90^\circ, $$ звідки \(\alpha=35^\circ.\)

Другий спосіб. Опустимо з вершини \(B\) трикутника \(ABC\) на сторону \(AC\) перпендикуляр \(AD\) (див. рисунок). З паралельності прямих \(BD\) і \(CN\) випливає, що \(\angle DBC=\angle BCN\) як внутрішні різносторонні. Тому шуканий кут \(\alpha\) дорівнює куту \(DBC.\) Маємо:

Третій спосіб. Скористаємось теоремою. Зовнішній кут трикутника дорівнює сумі двох внутрішніх, не суміжних з ним. Отже, \(\angle BCP=\angle A+\angle B\) (див. рисунок). Оскільки

то

Звідки одержуємо:

Відповідь: B.

ТЕМА: Геометрія. Планіметрія. Найпростіші фігури на площині. Довжина відрізка.

Це завдання перевіряє вміння знаходити довжини відрізків, використовуючи основну властивість вимірювання відрізків.

Довжина відрізка дорівнює сумі довжин частин, на які відрізок ділиться будь-якою його точкою.

Розділимо відрізок \(AB\) точками \(K\), \(L\), \(M\) на рівні відрізки \(AK\), \(KL\), \(LM\) та \(MB\) (див. рисунок).

Тоді довжина кожного з цих відрізків дорівнює $$ \frac{1}{4} AB = \frac{1}{4} \cdot 60 = 15\ \text{см}. $$ Нехай точки \(C\) і \(D\) – середини крайніх відрізків \(AK\) і \(MB\) відповідно. Тоді

Відповідь: B.

ТЕМА: Геометрія. Планіметрія. Найпростіші фігури на площині. Вертикальні кути. Суміжні кути.

Це завдання перевіряє знання основних властивостей вертикальних та суміжних кутів, які відносяться до найпростіших геометричних фігур на площині.

Нагадаємо, що суміжними називають два кути, у яких одна сторона спільна, а інші є доповняльними променями. На рис. 1 кути \(AOC\) та \(COB\) є суміжними.

Вертикальними називаються два кути, в яких сторони одного кута є доповнювальними променями сторін другого. На рис. 2 кути \(AOB\) та \(COD\) є вертикальними. Вертикальними також є кути \(AOD\) та \(BOC.\)

Проаналізуємо наведені твердження.

I. Вертикальні кути є рівними, але їх сума дорівнює \(180^\circ\) лише тоді, коли ці кути прямі. Тому твердження I не є правильним.

II. Суміжні кути в сумі утворюють розгорнутий кут, градусна міра якого дорівнює \(180^\circ.\) Отже, твердження II є правильним.

III. Кут називається гострим, якщо його градусна міра менше \(90^\circ\), і тупим, якщо його градусна міра більше \(90^\circ\) і менше \(180^\circ.\) Їх сума не обов’язково дорівнює \(180^\circ\), а дорівнює \(180^\circ\) лише тоді, коли вони суміжні. Отже, твердження III не є правильним.

Відповідь: Б.

ТЕМА: Геометрія. Планіметрія. Трикутники. Найпростіші геометричні фігури на площині.

Це завдання перевіряє знання суміжних та вертикальних кутів, теореми про суму кутів трикутника.

Кут \(30^\circ\) та \(\angle BCA\) – вертикальні, отже, рівні. Зовнішній кут трикутника \(110^\circ\) дорівнює сумі внутрішніх кутів, не суміжних з даним.

Відповідь: Б.

ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їх властивості.

Це завдання перевіряє знання про суміжні та вертикальні кути.

Кути \(\alpha\) та \(\beta\) – вертикальні.

За властивістю вертикальних кутів \(\alpha = \beta.\)

За аксіомою вимірювання кутів:

Відповідь: Г.

ТЕМА: Геометрія. Планіметрія. Трикутники.

Це завдання перевіряє знання теореми про суму кутів трикутника, властивостей суміжних та вертикальних кутів.

\(\angle DAC + \angle CAB = 180^\circ\) як суміжні.

\(\angle DAC = 146^\circ\), \(\angle CAB = 180^\circ - 146^\circ = 34^\circ.\)

У \(\Delta ABC\) \((\angle B = 90^\circ).\) \(\angle A + \angle C = 90^\circ\), \(\angle C = 90^\circ - 34^\circ = 56^\circ.\) \(\angle ACB = \alpha = 56^\circ\) (як вертикальні).

Відповідь: Г.

ТЕМА: Геометрія. Планіметрія. Прямі на площині.

Це завдання перевіряє знання властивостей паралельних прямих.

\(a\ ||\ b\), \(c\) – січна.

За властивістю паралельних прямих:

I. \(\angle 1\) i \(\angle 3\) суміжні (за означенням суміжних кутів).

II. \(\angle 1=\angle 2\) як відповідні при паралельних прямих.

IІІ. \(\angle 1=\angle 2\), \(\angle 1+\angle 3=180^\circ\) (за властивістю суміжних кутів).

Отже, \(\angle 2+\angle 3=180^\circ\).

Усі з наведених тверджень є правильними.

Відповідь: Д.

ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їх властивості. Геометричні величини та їх вимірювання. Величини кута, вимірювання кутів.

Це завдання перевіряє вміння вимірювати кути, знання аксіом планіметрії.

Градусна міра повного кута \(360^\circ.\)

Відповідь: Б.