Розділ: Функції
Тема: Функціональна залежність
Кількість завдань: 79


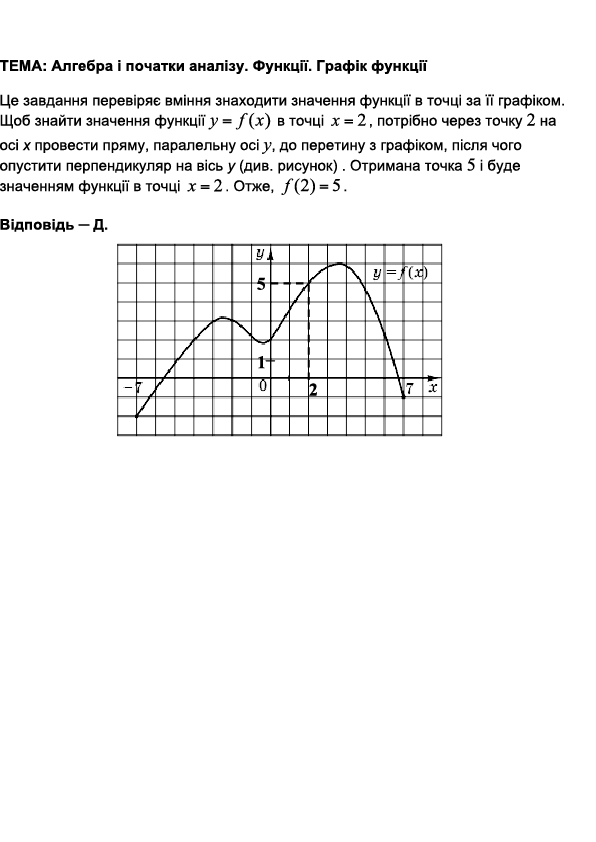
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння визначати властивості функції за її графіком, а також розуміння геометричного змісту визначеного інтеграла.
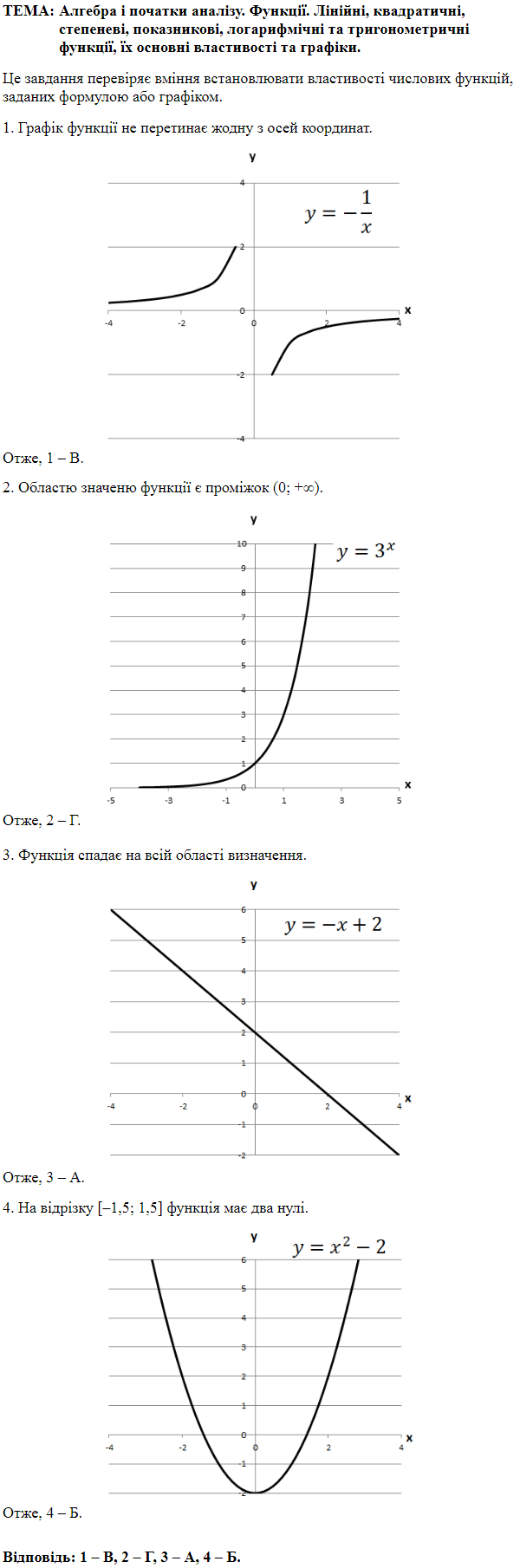
1. При \(x=8\) значення функції \(f(8)=3\mathord{,}5.\)
Число \(3\mathord{,}5\) належить проміжку \((2; 4].\)
Отже, 1 — Г.
2. Дотична до графіка функції \(f(x)\) в точці \(x=7\) паралельна осі \(Ox.\)
Тоді \(f'(7)=k=\mathrm{tg}\ 90^\circ=0.\)
Число \(0\) належить проміжку \((-0\mathord{,}5; 2].\)
Отже, 2 – B.
3. Найменше значення функції \(f(x)\) на її області визначення дорівнює \(f(0)=-3\mathord{,}5.\)
Число \(-3\mathord{,}5\) належить проміжку \((-\infty; -2].\)
Отже, 3 – A.
4. Геометричний зміст визначеного інтеграла – площа криволінійної трапеції.
З рисунку бачимо, що \(-2\lt \int_1^3f(x)dx\lt 0.\) Тобто \(\int_1^3f(x)dx \in (-2; -0\mathord{,}5].\)
Отже, 4 – Б.
Відповідь: 1 – Г, 2 – В, 3 – А, 4 – Б.































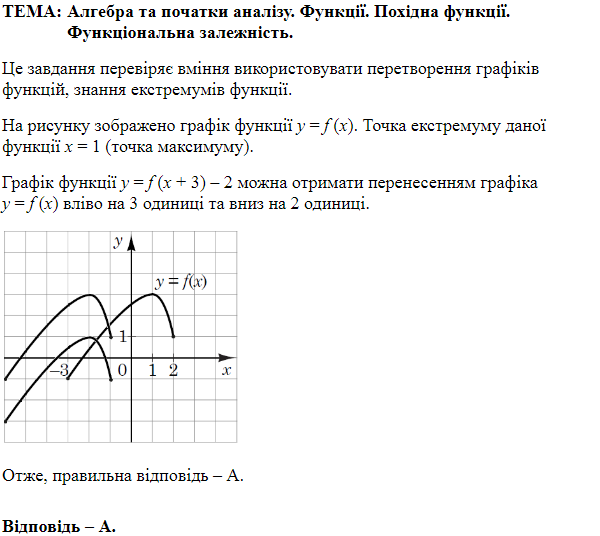




ТЕМА: Алгебра і початки аналізу. Функції.
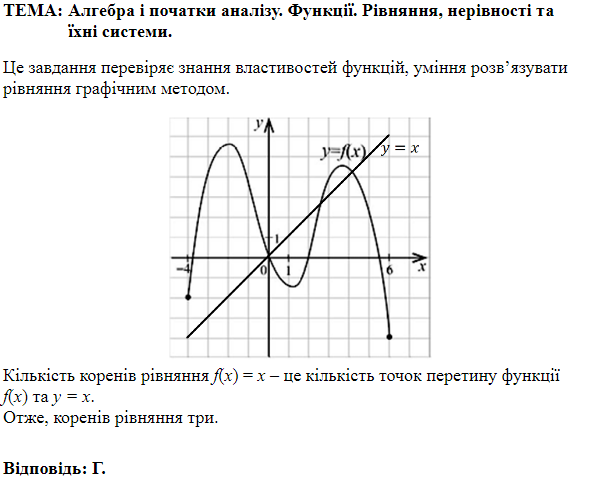
Це завдання перевіряє знання властивостей та графіків функцій.
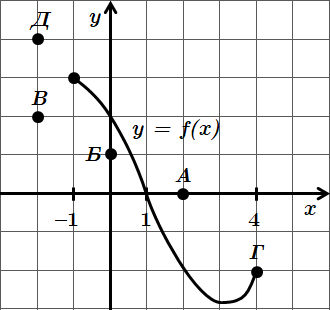
Правильна відповідь – Г\((4; -2).\)
Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком.
Нуль функції – значення \(x\), при якому \(y=0.\) На рисунку – це точка перетину графіка з віссю \(x.\) Отже, \(x=1.\)
Відповідь: B.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння виконувати перетворення графіків функцій.
Якщо графік функції \(y=f(x)\) паралельно перенесли вздовж осі \(y\) на \(3\) одиниці вниз, то отримаємо \(y=f(x)-3.\)
Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку розуміння змісту поняття екстремуму функції, знання геометричного змісту похідної.
На рисунку функція зростає при \(x \in [-2;-1]\), а спадає – при \(x\in [-1;4]\). Отже, \(x_0=-1\) – точка максимуму цієї функції (точка екстремуму).
Відповідь: Б.
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Раціональні вирази та їх перетворення.
Завдання скеровано на перевірку вміння виконувати тотожні перетворення виразів.
З формули \(T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}\) визначимо \(L\). \begin{gather*} T^2=(2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC})^2,\\[7pt] T^2=4\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}^2LC,\\[6pt] L=\frac{T^2}{4\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}^2C}. \end{gather*}
Відповідь: Д.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння знаходити область значень функції, будувати графіки квадратичних функцій, установлювати властивості числових функцій, заданих формулою, використання перетворення графіків функцій, знаходити первісну функції.
1. \begin{gather*} y(0)=2\cdot 0+8=8\\[7pt] y=0,\ \ 2x+8=0,\ \ x=-4\\[7pt] y(9)=2\cdot 9+8=26. \end{gather*}
| \(x\) | \(y\) |
| \(0\) | \(8\) |
| \(-4\) | \(0\) |
| \(9\) | \(26\) |
2. \(M(-4;\ 0)\) – точка перетину графіка функції з віссю \(x\).
3.
4. Первісна функції \(f\), яка проходить через точку \(M(-4;\ 0)\) \begin{gather*} 0=(-4)^2+8\cdot (-4)+C,\\[7pt] 0=16-32+C,\ \ C=16\\[7pt] F(x)=x^2+8x+16. \end{gather*}
5. Побудуємо графік функції \(F(x)=x^2+8x+16\), \(F(x)=(x+4)^2\).
Використаємо елементарні перетворення графіків:
\(F(x)=x^2 \rightarrow F(x)=(x+4)^2\) переносимо вліво на 4 одиниці вздовж осі \(Ox\).
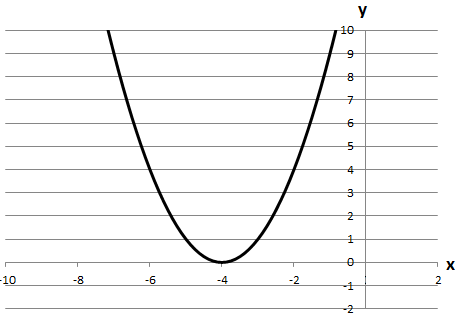
6. Область визначення функції \(F(x)\ E(y)=[0;\ +\infty)\).
Функцію \(G(x)=3F(x)+1\) отримаємо з функції \(F(x)\) стисканням в 3 рази до осі \(Oy\) та паралельним перенесенням на 1 одиницю вгору вздовж осі \(Oy\).
Отже, \(E(G)=[1;\ \infty)\).
Відповідь:
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння установлювати властивості числових функцій, заданих формулою або графіком, досліджувати на парність (непарність) функції.
1.
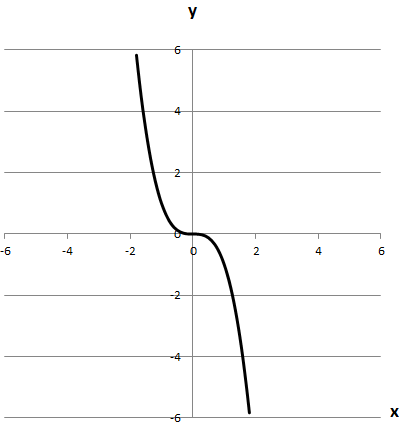
Симетричний відносно початку координат. Отже, 1 - Г.
2.
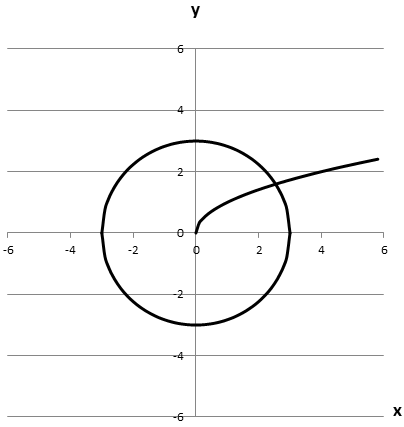
Має з графіком рівняння \(x^2+y^2=9\) лише одну спільну точку. Отже, 2 - Б.
3.
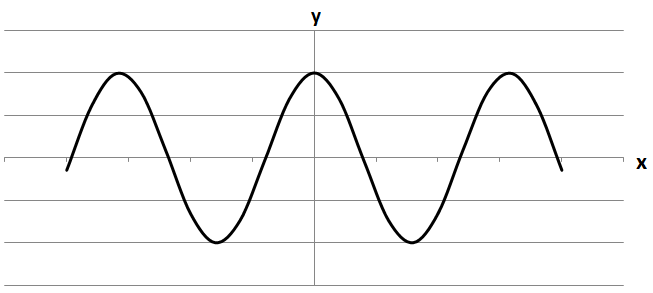
Симетричний відносно осі \(y\). Отже, 3 - В.
Відповідь: 1Г, 2Б, 3В.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння аналізувати дані, подані графіком або таблицею.
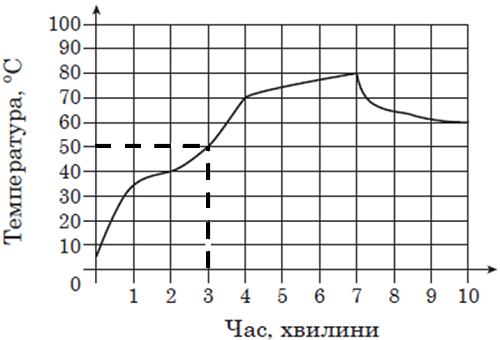
Температура двигуна була не більшою за 50 °C протягом 3 хвилин.
Відповідь: В.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння установлювати властивості числових функцій, заданих графіком.
Дано: лінійна функція \(y=-2x+3\).
\(k=-2\), отже, функція спадна
\(b=3\), отже, точка перетину графіка з віссю \(Oy\) (0; 3).
Відповідь: Б.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння установлювати властивості числових функцій, заданих формулою або графіком, досліджувати на парність (непарність) функції.
1. \((x-3)^2+(y-4)^2=4,\ \ (3;\ 4)\) – центр кола, \(R=2\).
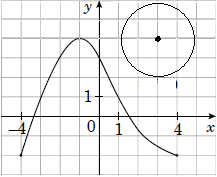
Графік функції не має спільних точок з колом. Отже, 1 - Г.
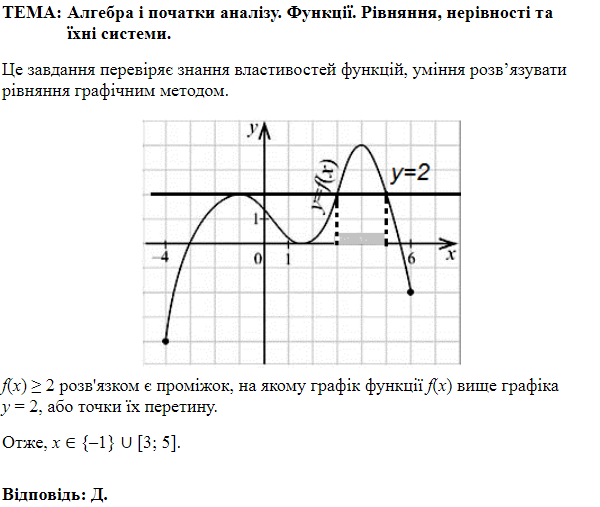
2.
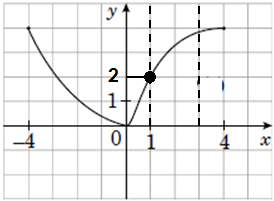
Найменше значення функції на проміжку \([1;\ 3]\) дорівнює \(2\). Отже, 2 - Б.
3. Графік функції тричі перетинає пряму \(y=1\). Отже, 3 - Д.
Відповідь: 1Г, 2Б, 3Д.
ТЕМА: Алгебра і початки аналізу. Функції. Дослідження функції за допомогою похідної. Побудова графіків функції.
Завдання скеровано на перевірку вміння знаходити похідну функції, нулів функції, екстремумів функції, будувати графіки функцій; знання достатньої умови зростання (спадання) функції.
Задано функцію \(y=x^3-3x\)
1.
| x | y |
| 0 | 0 |
| –1 | 2 |
| 2 | 2 |
2. Точки перетину графіка \(y=x^3-3x\) із віссю \(x\) знаходимо за умови \(y=0\): \begin{gather*} x^3-3x=0,\ \ x(x^2-3)=0,\\[7pt] x(x-\sqrt{3})(x+\sqrt{3})=0\\[7pt] \left [ \begin{array}{l l} x=0 & \\ x=\sqrt{3}& \\ x=-\sqrt{3}& \end{array}\right. \end{gather*} \((0;\ 0),\ (\sqrt{3};\ 0),\ (-\sqrt{3};\ 0)\) – точки перетину з віссю \(x\).
3.
4. \begin{gather*} f'(x)=0,\ \ 3x^2-3=0,\\[7pt] 3(x^2-1)=0,\ \ 3(x-1)(x+1)=0\\[7pt] \left [ \begin{array}{l l} x-1=0 & \\ x+1=0& \end{array}\right. \ \ \left [ \begin{array}{l l} x=1 & \\ x=-1& \end{array}\right. \end{gather*}
5. Визначимо проміжки зростання і спадання функції
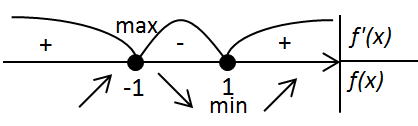
При \(f'(x)\gt 0\) функція зростає, при \(f'(x)\lt 0\) – спадає. Отже,
\(f(x)\) зростає при \(x \in (-\infty;\ -1]\) i \([1;\ +\infty)\);
\(f(x)\) спадає при \(x\in [-1;\ 1]\).
Точки екстремуму: \(x_{max}=-1;\ \ x_{min}=1\),
екстремуми функції: \(f_{max}=f(-1)=2;\ \ f_{min}=f(1)=-2\).
6.
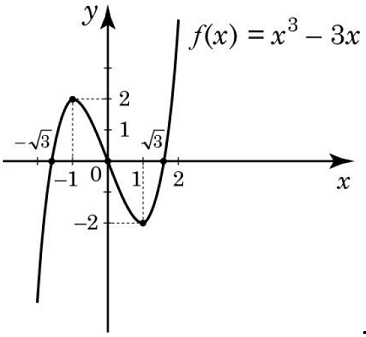
Відповідь:
1. \(x=0,\ \ y=0,\)
\(x=-1,\ \ y=2,\)
\(x=2,\ \ y=2\).
2. \((0;\ 0),\ (\sqrt{3};\ 0),\ (-\sqrt{3};\ 0)\).
3. \(f'(x)=3x^2-3\).
4. \(x=1;\ \ x=-1\).
5. Проміжки зростання: \((-\infty;\ -1],\ [1;\ +\infty)\)
проміжок спадання: \([-1;\ -1]\)
\(x_{max}=-1;\ \ x_{min}=1\).
\(f_{max}=2;\ \ f_{min}=-2\).
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння установлювати властивості числових функцій, заданих графіком.
Функція, графік якої проходить через початок координат, проходить через точку \((0;\ 0)\). З наведених функцій це \(y=x\).
Відповідь: Д.
ТЕМА: Алгебра і початки аналізу. Функції. Дослідження функції за допомогою похідної. Побудова графіків функції.
Завдання скеровано на перевірку вміння знаходити похідну функції, нулів функції, екстремумів функції, будувати графіки функцій; знання достатньої умови зростання (спадання) функції.
Задано функцію \(y=x^3-12x\)
1.
| x | y |
| –1 | 11 |
| 0 | 0 |
| 2 | –16 |
2. Точки перетину графіка \(y=x^3-12x\) із віссю \(x\):
3.
\begin{gather*} f'(x)=3x^2-12 \end{gather*}Використали правило знаходження похідної степеневої функції $$ (x^\alpha)'=\alpha x^{\alpha -1}. $$
4. Нулі функції \(f'\) \begin{gather*} f'=3x^2-12=0,\ \ 3(x^2-4)=0,\\[7pt] x^2-4=0,\ \ x_1=2\ \text{або}\ x_2=-2. \end{gather*}
5. Знайдемо знаки похідної функції.
\(f'=0\) при \(x_1=2\) та \(x_2=-2\)
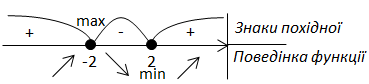
Точки екстремуму: \(x_{max}=-2\) (знак похідної змінюється з "+" на "–"),
\(x_{min}=2\) (знак похідної змінюється з "–" на "+").
\(f(x)\) зростає при \(x\in (-\infty;\ -2]\) та \([2;\ +\infty)\)
\(f(x)\) спадає при \(x\in [-2;\ 2]\).
Знайдемо екстремуми функції:
6.
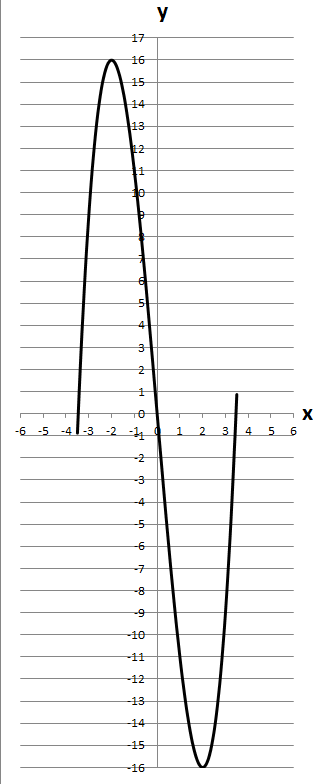
Відповідь:
1. \(x=-1,\ \ y=11,\)
\(x=0,\ \ y=0,\)
\(x=2,\ \ y=-16\).
2. \((0;\ 0),\ (-2\sqrt{3};\ 0),\ (2\sqrt{3};\ 0)\).
3. \(f'(x)=3x^2-12\).
4. \(x_1=2;\ \ x_2=-2\).
5. Проміжки зростання: \((-\infty;\ -2],\ [2;\ +\infty)\)
проміжок спадання: \([-2;\ 2]\)
точки екстремуму: \(x_{max}=-2;\ \ x_{min}=2\).
екстремуми: \(f_{max}=16;\ \ f_{min}=-16\).
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє знання властивостей квадратичної функції.
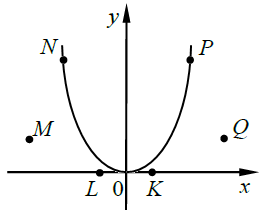
Графіком квадратичної функції \(y=x^2\) є парабола, яка симетрична осі \(Oy.\) Отже, якщо точка \(P\) належить графіку, то симетрична їй точка \(N\) може належати цьому графіку.
Відповідь: Г.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння виконувати перетворення графіків функцій.
Графік функції \(y=\sqrt{x}\) паралельно перенесли на \(2\) одиниці ліворуч уздовж осі \(x.\) Отримали функцію \(y=\sqrt{x+2}.\)
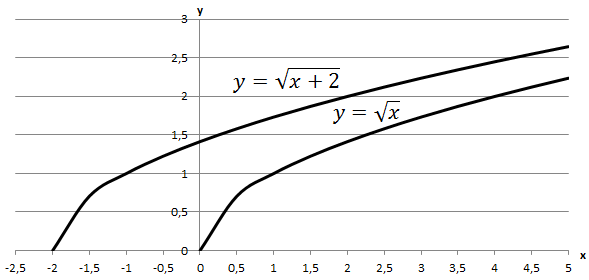
Відповідь: Г.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння встановлювати властивості числових функцій, заданих формулою.
1. \(f(x)=2^x\)
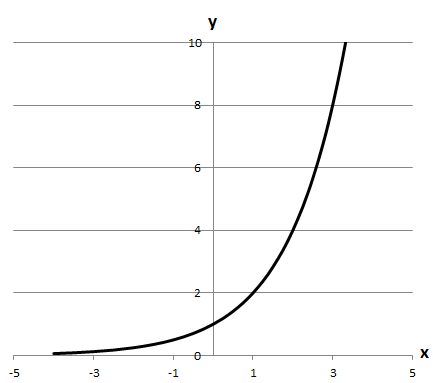
Б область значень \((0;\ +\infty).\)
2. \(f(x)=tg x\)
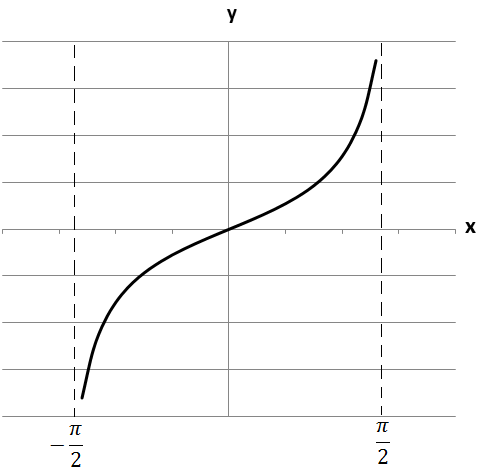
A функція непарна (графік симетричний осі \(y\)).
3. \(f(x)=2x+1\)
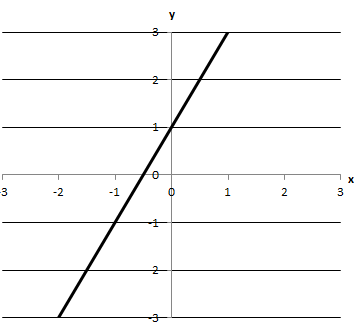
Д графік має лише дві точки перетину з осями координат.
Відповідь: 1Б, 2А, 3Д.
ТЕМА: Алгебра і початки аналізу. Функції.
Перевіряє вміння встановлювати властивості числових функцій, заданих графіком.
Графік функції проходить через точку \((-3;\ 1).\) Отже, правильна відповідь – Г.
Відповідь: Г.
ТЕМА: Алгебра і початки аналізу. Функції.
Перевіряє вміння встановлювати властивості числових функцій, заданих графіком. використовувати перетворення графіків функцій.
Якщо графік функції \(y=f(x)\) паралельно перенесли вздовж осі \(y\) вниз на \(3\) одиниці, то отримали $$ y=f(x)-3. $$
Застосували елементарне перетворення графіка функції.
Відповідь: Г.
ТЕМА: Алгебра і початки аналізу. Функції.
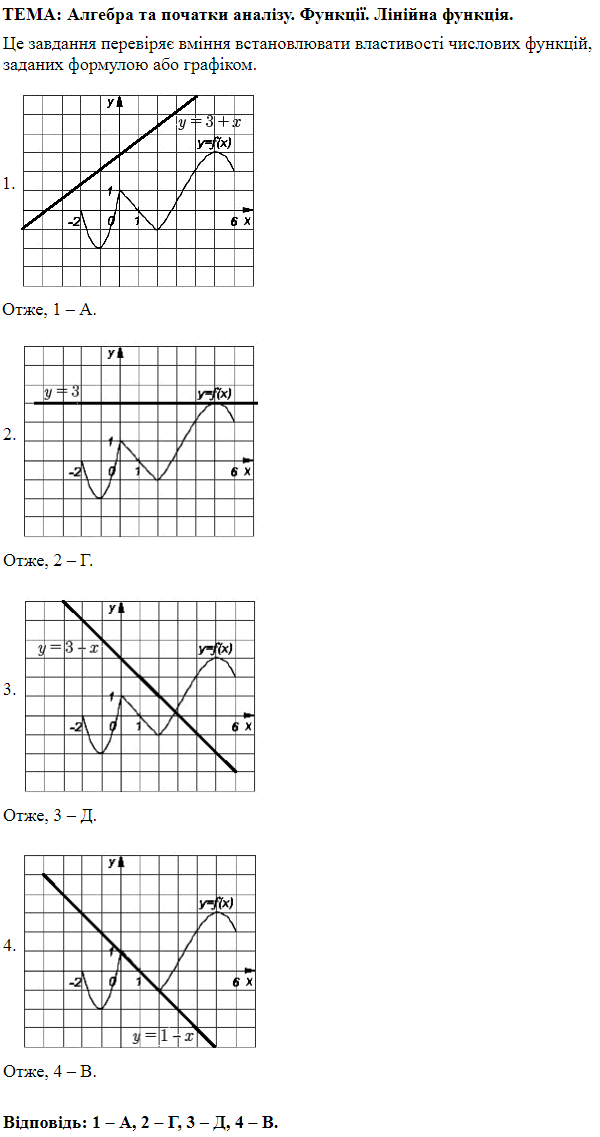
Перевіряє вміння встановлювати властивості числових функцій, заданих графіком.
1. Графік є фрагментом графіка функції \(y=1-x.\) Отже, 1 – Б.
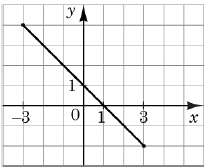
2. Графік функції двічі перетинає графік функції \(y = 2^x.\) Отже, 2 – А.
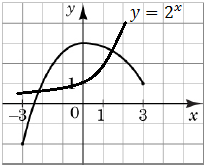
3. Функція зростає на проміжку \([0; 3].\) Отже, 3 – Д.
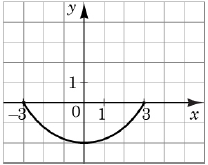
Відповідь: 1Б, 2А, 3Д.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком та формулою.
Графіком лінійної функції є пряма. Всі точки прямої, паралельної осі абсцис, мають однакові ординати.
Якщо пряма проходить через \(\text{т.}\ A(-2;\ 3),\) то функція задається формулою: \(y=3.\)
Відповідь: A.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння встановлювати властивості числових функцій, заданих формулою чи графіком.
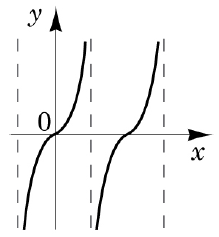
1. \(y=\mathrm{tg}x\) – Г.
2. \(y=\left(\frac 12\right)^x\) показникова функція – Д.
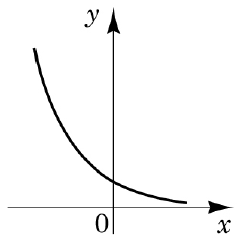
3. \(y=\frac 1x\) обернена пропорційність – А.
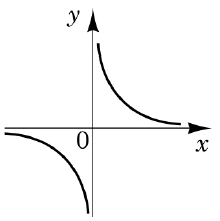
Відповідь: 1Г 2Д 3А.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком та формулою.
Нулем функції називається таке значення аргумента, при якому значення функції дорівнює нулю.
На графіку функції це точка перетину з віссю \(Ox.\)
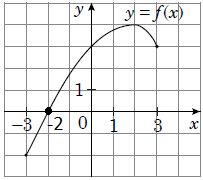
Отже, правильна відповідь – Б.
Відповідь: Б.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком та формулою.
Схематично графіки функцій виглядають таким чином:

1. \(E(y)=[0;\ +\infty)\) – B.
2. Графік симетричний відносно осі \(y\) – A.
3. Функція спадна, тому найменше значення функція набуває при найбільшому значенні аргумента – Г.
Відповідь: 1В 2А 3Г.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння встановлювати властивості числових функцій, заданих формулою чи графіком.
Точка перетину графіка функції з віссю \(x\) має координати \((3;\ 0).\)
Отже, правильна відповідь – Г.
Відповідь: Г.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком та формулою.
Графіки функцій схематично виглядають таким чином:
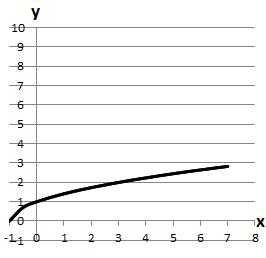
1. \(y=\sqrt{x+1}\) зростає на всій області визначення – Г.
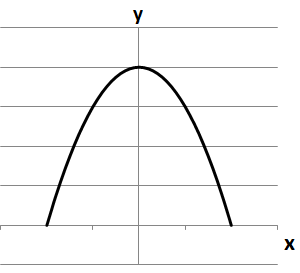
2. \(y=4-x^2\) має точку локального максимуму при \(x=0,\ f_{max}(0)=4\) – A.
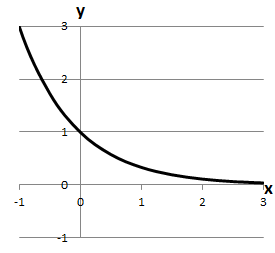
3. \(y=3^{-x}\) функція набуває лише додатних значень – Д.
Відповідь: 1Г 2А 3Д.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння встановлювати властивості числових функцій, заданих графіком.
Проміжок, упродовж якого густина пилу зменшувалась, – це проміжок спадання фукнції. Із-поміж наведених – це \([20; 24].\)
Отже, правильна відповідь – Д.
Відповідь: Д.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння виконувати перетворення графіків функцій.
Застосувавши елементарні перетворення графіків функцій, \(y=f(x)\) переміщуємо вправо вздовж осі \(Ox\) на \(4\) одиничних відрізки.
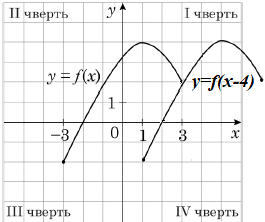
Отже, правильна відповідь – Г.
Відповідь: Г.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння встановлювати властивості числових функцій, заданих графіком.
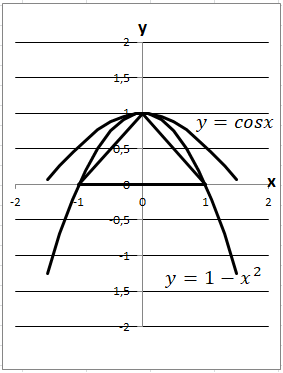
1. \(y=0\) це вісь \(Ox.\) Отже, спільних точок прямої та ламаної \(ABCA\) – безліч, правильна відповідь – Д.
2. Спільних точок параболи \((y=1-x^2)\) та ламаної \(ABCA\) – три: \((0; 1),\ (1; 0),\ (-1; 0),\) правильна відповідь – Г.
3. Спільних точок функції \(y=\cos x\) та ламаної \(ABCA\) – лише одна \((0, 1).\) Отже, правильна відповідь – Б.
Відповідь: 1Д 2Г 3Б.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння встановлювати властивості числових функцій, заданих графіком.
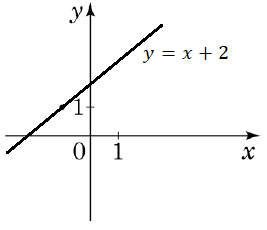
Графік лінійної функції \(y=x+2\) проходить через дану точку.
Відповідь: В.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння встановлювати властивості числових функцій, заданих графіком.
1. Найбільше значення функції \(y=f(x),\) на відрізку \([1; 9]\) дорівнює \(7.\) Правильна відповідь – Г.
2. Найменше значення функції на відрізку \([1; 3]\) дорівнює \(5.\) Правильна відповідь – Д.
3. \(f(x)\lt 0\) при \(x\in (5; 7).\) Найбільше ціле значення \(x,\) за якого справджується нерівність \(x=6.\) Правильна відповідь – В.
Відповідь: 1Г 2Д 3В.
ТЕМА: Алгебра і початки аналізу. Функції. Первісна.
Завдання скеровано на перевірку вміння находити первісну, обчислювати площу плоских фігур за допомогою інтеграла.
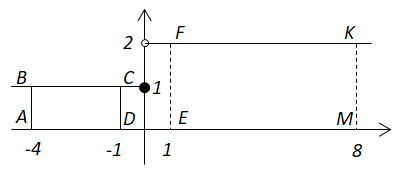
Обчислити значення виразу
$$
\int_{-4}^{-1}f(x)dx+2\int_1^8f(x)dx
$$
можна двома способами:
1) застосувати геометричний зміст визначеного інтеграла;
2) алгебраїчним.
1 спосіб:
2 спосіб:
Відповідь: 31.




