Алгебра і початки аналізу – Ірраціональні, тригонометричні рівняння та системи рівнянь

ТЕМА: Рівняння, нерівності та їхні системи. Ірраціональні рівняння.

Завдання перевіряє вміння розв’язувати ірраціональні рівняння.

Піднесімо обидві частини рівняння до квадрата й обчислімо \(x{:}\)

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Тригонометричні рівняння.

Завдання перевіряє вміння розв’язувати найпростіші тригонометричні рівняння.

Загальний розв'язок:

Поділімо обидві частини рівняння на \(\pi{:}\)

Якщо \(k=0\), то \(x=\frac 14.\)

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Тригонометричні рівняння.

Завдання скеровано на перевірку вміння розв’язувати найпростіші тригонометричні рівняння.

Корені рівняння: якщо \(k=1\), \(x=-\pi+4\pi=3\pi.\)

Серед запропонованих варіантів відповіді є цей корінь.

Відповідь: B.

ТЕМА: Ірраціональні рівняння.

Завдання скеровано на перевірку вміння розв’язувати ірраціональні рівняння.

Піднесімо обидві частини рівняння до квадрату:

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання перевіряє вміння розв’язувати найпростіші тригонометричні рівняння.

Рівняння \(\cos x=0\) має загальний розв’язок: \begin{gather*} x=\frac{\pi}{2}+\pi k,\ \text{де}\ k\in Z. \end{gather*}

Розгляньмо значення \(k\), за яких \(x\) потрапляє в проміжок \([0; 2\pi].\)

Якщо \(k=0\), то \(x=\frac{\pi}{2},\) тобто належить проміжку \([0; 2\pi].\)

Якщо \(k=1\), то \(x=\frac{\pi}{2}+\pi=\frac{3\pi}{2},\) тобто належить проміжку \([0; 2\pi].\)

Якщо \(k=2\), то \(x=\frac{\pi}{2}+2\pi=\frac{5\pi}{2},\) тобто не належить проміжку \([0; 2\pi].\)

Якщо \(k=-1\), то \(x=\frac{\pi}{2}-\pi=-\frac{\pi}{2},\) тобто не належить проміжку \([0; 2\pi].\)

Відповідь: B.

ТЕМА: Тригонометричні рівняння.

Завдання скеровано на перевірку вміння розв’язувати найпростіші тригонометричні рівняння.

Корені рівняння:

якщо \(n=0\), $$ x=\mathbf{\pi}+4\mathbf{\pi}\cdot 0=\mathbf{\pi}, $$ якщо \(n=-1\),

Відповідь: B.

ТЕМА: Ірраціональні рівняння.

Завдання скеровано на перевірку вміння розв’язувати ірраціональні рівняння з параметром.

Зробімо заміну: \(\sqrt{5x-a}=t\ge 0\), тоді \(5x-a=t^2.\)

Розв'яжімо квадратне рівняння відносно \(t{:}\)

Сума коренів:

Отже, за \(a=-0\mathord{,}875\) сума коренів рівняння дорівнює \(1\mathord{,}5.\)

Відповідь: \(-0\mathord{,}875.\)

ТЕМА: Тригонометричні рівняння.

Завдання скеровано на перевірку вміння розв’язувати найпростіші тригонометричні рівняння.

Щоб визначити корінь рівняння, треба підставити значення \(x\) у рівняння. Після цього з'ясувати, за якого значення \(x\) рівняння стає правильною рівністю.

Якщо \(x=-\frac{\mathbf{\pi}}{6}\mathord{:}\)

Отже, \(x=-\frac{\mathbf{\pi}}{6}\) не є коренем рівняння.

Якщо \(x=-\frac{\mathbf{\pi}}{3}\mathord{:}\)

Отже, \(x=-\frac{\mathbf{\pi}}{3}\) не є коренем рівняння.

Якщо \(x=-\frac{\mathbf{\pi}}{12}\mathord{:}\)

Отже, \(x=-\frac{\mathbf{\pi}}{12}\) – корінь рівняння.

Другий спосіб:

Якщо \(k=0\mathord{:}\)

Це – корінь рівняння.

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання скеровано на перевірку вміння розв’язувати тригонометричні рівняння.

При \(n=0\ \ x=-\frac{\mathbf{\pi}}{12}.\)

Відповідь: А.

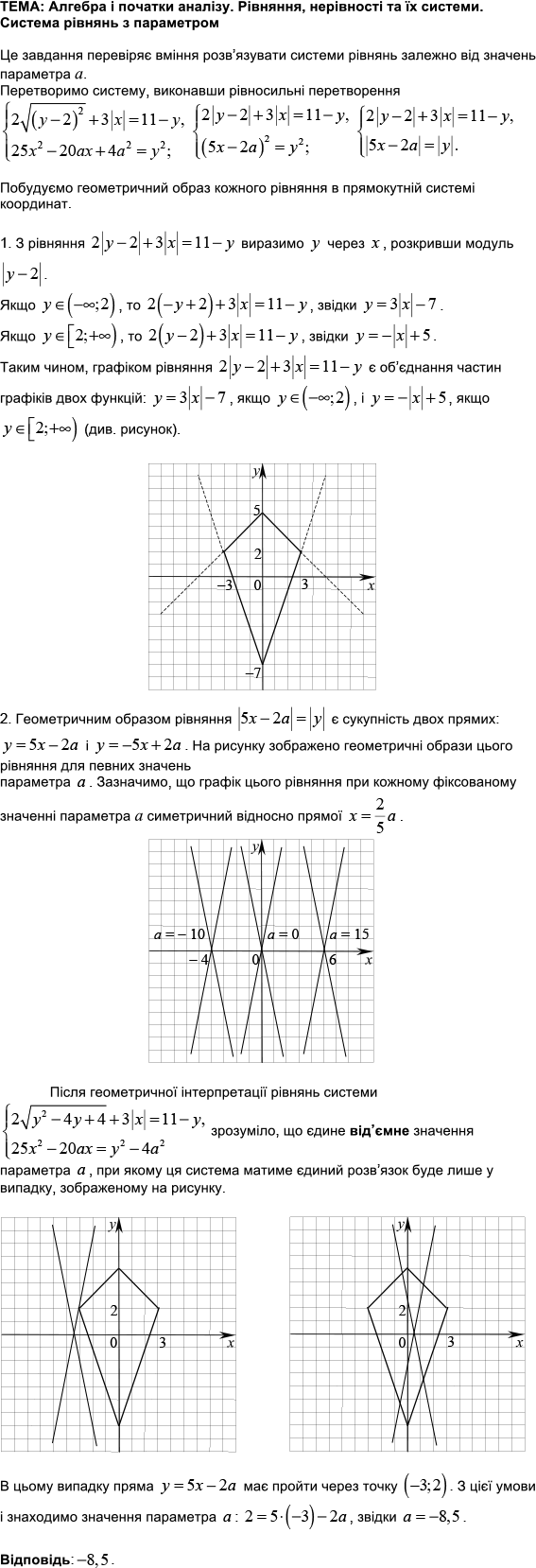
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати тригонометричні рівняння, нерівності другого степеня та їх системи з параметрами.

Тригонометричне рівняння \(\sin\left(x+\frac{\mathbf{\pi}}{3}\right)=2a^2+5a-6\) має корені при \(|2a^2+5a-6|\le 1.\)

1)

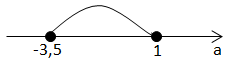
2)

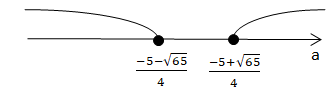
Розв'язок системи:

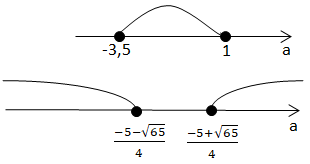
Найменше значення \(a=-3,5.\)

Відповідь: -3,5.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати тригонометричні рівняння.

Розв'яжемо тригонометричне рівняння:

Відповідь: А.

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання перевіряє вміння розв’язувати найпростіші тригонометричні рівняння.

\(\sin x=\frac{\sqrt{3}}{2}\) найпростіше тригонометричне рівняння. Корені знаходимо за формулою:

На відрізку \(x\in [0;\ 3\mathbf{\pi}]\) знаходимо корені:

Отже, правильна відповідь – Д.

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Рівняння.

Перевіряє вміння розв'язувати системи лінійних та ірраціональних рівнянь.

\((16;\ -5)\) – розв'язок системи. Отже, \begin{gather*} x_0+y_0=16+(-5)=11. \end{gather*}

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє вміння виконувати тотожні перетворення тригонометричних виразів.

За властивістю пропорції $$ \frac{\sin\mathbf{\alpha}}{\cos\mathbf{\alpha}}=\frac 25,\ \ \operatorname{tg}\ \mathbf{\alpha}=\frac{\sin\mathbf{\alpha}}{\cos\mathbf{\alpha}}. $$ Отже, \(\operatorname{tg}\ \mathbf{\alpha}=\frac 25.\)

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Рівняння і нерівності.

Завдання перевіряє вміння розв'язувати степеневі рівняння.

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лiнiйнi, квaдpaтні, рацiональнi, iррацiональнi, показникові, логарифмiчнi, тригонометричні рівняння, неpiвності та їx системи.

Це завдання перевіряє знання методів розв'язування тригонометричних рівнянь.

Рівняння \(\cos x=a\) при \(|a|\lt 1\) має розв'язок \(x\pm \mathrm{arccos}\ a+2\mathbf{\pi}n\), \(n\in Z.\)

Відповідь: A.

ТЕМА: Рівняння, нерівності та їхні системи. Ірраціональні рівняння.

Це завдання перевіряє знання методів розв'язування ірраціональних рівнянь, уміння розв'язувати ірраціональні рівняння.

Підносимо обидві частини рівняння до квадрата й знаходимо \(x.\)

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Ірраціональні рівняння. Функції.

Це завдання перевіряє вміння розв’язувати ірраціональні рівняння, знаходити область визначення функції, знання методів розв’язування ірраціональних рівнянь.

Підносимо обидві частини рівняння до квадрата. Отримали рівняння, яке є наслідком даного:

Перевірка показує, що \(x=-2\mathord{,}5\) є коренем даного рівняння:

Корінь рівняння належить проміжку \([-3; -1).\)

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Тригонометричні рівняння.

Це завдання перевіряє знання співвідношень між тригонометричними функціями одного аргумента та вміння розв'язувати тригонометричні рівняння.

Оскільки $$ \frac{\sin x}{\cos x}=\mathrm{tg}\ x, $$ то вихідне рівняння запишемо у вигляді: $$ 3\mathrm{tg}\ x=\sqrt{3}, $$ звідки $$ \mathrm{tg}\ x=\frac{\sqrt{3}}{3}. $$

Розв'язком такого рівняння є

Оскільки $$ \mathrm{arctg}\ \frac{\sqrt{3}}{3}=\frac{\pi}{6}, $$ то остаточно отримаємо

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Означення розв’язку системи рівнянь з двома змінними та методи їх розв’язування.

Це завдання перевіряє вміння розв’язувати системи рівнянь методом підстановки.

З першого рівняння маємо \(\sqrt{x} = 4.\) Піднесемо обидві частини рівняння до квадрату, отримаємо \(x_{0} = 16.\) Підставивши це значення в друге рівняння, отримаємо $$ 16 - 2y = 26, $$ звідки \(y_{0} = -5.\) Тоді $$ x_{0} + y_{0} = 16 - 5 = 11. $$

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Тригонометричні рівняння.

Це завдання перевіряє вміння досліджувати найпростіші тригонометричні рівняння \(\sin x = a\), \(\cos x = a\), \(\mathrm{tg}\ x = a\) і \(\mathrm{ctg}\ x = a.\)

Потрібно знати, що рівняння \(\sin x = a\) і \(\cos x = a\) мають безліч коренів, якщо \(a \in [-1; 1]\), і не мають коренів, якщо \(|a| \gt 1\), тобто \(a \in (-\infty; -1) \cup (1; +\infty).\) Тригонометричні рівняння \(\mathrm{tg}\ x = a\) і \(\mathrm{ctg}\ x = a\) мають безліч коренів при будь-яких значеннях \(a.\)

Отже, рівняння, наведені у варіантах Б, В і Г, мають корені.
Розглянемо А: $$ \sin x = \frac{\sqrt{3}}{2}. $$

Оскільки $$ \frac{\sqrt{3}}{2} \in [-1; 1] $$ (нагадаємо, що \(\sqrt{3} \approx 1{,}73\)), то рівняння $$ \sin x = \frac{\sqrt{3}}{2} $$ має корені.

Д: $$ \cos x = \frac{2}{\sqrt{3}}. $$ Оскільки $$ \frac{2}{\sqrt{3}} \gt 1, $$ то рівняння $$ \cos x = \frac{2}{\sqrt{3}} $$ не має коренів.

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Означення розв’язку системи рівнянь з двома змінними та методи їх розв’язування.

Це завдання перевіряє вміння розв’язувати систему рівнянь з двома змінними.

Запишемо задані рівності у вигляді системи: $$ \left\{\begin{array}{l} \sqrt{x} + y = 5,\\ 2\sqrt{x} - y = 7. \end{array}\right. $$ Ця система є лінійною відносно \(\sqrt{x}\) та \(y.\)

Перший спосіб. Додамо почленно обидва рівняння системи: $$ \sqrt{x} + y + 2\sqrt{x} - y = 5 + 7. $$ Звівши подібні доданки, отримаємо рівняння \(3\sqrt{x} = 12\), або \(\sqrt{x} = 4.\) Підставивши у перше рівняння системи замість \(\sqrt{x}\), його значення \(4\), отримаємо \(4 + y = 5\), звідки \(y = 1.\)

Другий спосіб. З першого рівняння системи виразимо \(\sqrt{x}\) через \(y\mathord{:}\) \(\sqrt{x} = 5 - y\) і підставимо в друге рівняння замість \(\sqrt{x}\) значення \(5 - y.\) Отримаємо:

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Система рівнянь з параметром.

Це завдання перевіряє вміння розв’язувати системи рівнянь залежно від значень параметра \(a.\)

Перетворимо систему, виконавши рівносильні перетворення

Побудуємо геометричний образ кожного рівняння в прямокутній системі координат.

1. З рівняння \(2|y-2|+3|x|=11-y\) виразимо \(y\) через \(x\), розкривши модуль \(|y-2|.\)

Якщо \(y\in(-\infty; 2)\), то \(2(-y+2)+3|x|=11-y\), звідки \(y=3|x|-7.\)

Якщо \(y\in[2; +\infty)\), то \(2(y-2)+3|x|=11-y\), звідки \(y=-|x|+5.\)

Таким чином, графіком рівняння \(2|y-2|+3|x|=11-y\) є об’єднання частин графіків двох функцій: \(y=3|x|-7\), якщо \(y\in(-\infty; 2)\), і \(y=-|x|+5\), якщо \(y\in[2; +\infty)\) (див. рисунок).

2. Геометричним образом рівняння \(|5x-2a|=|y|\) є сукупність двох прямих: \(y=5x-2a\) і \(y=-5x+2a.\) На рисунку зображено геометричні образи цього рівняння для певних значень параметра \(a.\) Зазначимо, що графік цього рівняння при кожному фіксованому значенні параметра \(a\) симетричний відносно прямої \(x=\frac{2}{5}a.\)

Після геометричної інтерпретації рівнянь системи $$ \left\{\begin{array}{l} 2\sqrt{y^2-4y+4}+3|x|=11-y,\\ 25x^2-20ax=y^2-4a^2, \end{array}\right. $$ зрозуміло, що єдине від’ємне значення параметра \(a\), при якому ця система матиме єдиний розв’язок буде лише у випадку, зображеному на рисунку.

В цьому випадку пряма \(y=5x-2a\) має пройти через точку \((-3; 2).\) З цієї умови і знаходимо значення параметра \(a{:}\) \(2=5\cdot(-3)-2a\), звідки \(a=-8{,}5.\)

Відповідь: \(-8{,}5.\)

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Тригонометричні рівняння.

Це завдання перевіряє вміння розв’язувати найпростіші тригонометричні рівняння.

Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи. Ірраціональні рівняння.

Це завдання перевіряє вміння розв’язувати ірраціональні рівняння.

Піднесемо обидві частини рівняння до кубу, отримаємо рівносильне рівняння: \begin{gather*} 2x=(-3)^3,\ \text{або}\\[7pt] 2x=-27,\\[6pt] x=-\frac{27}{2}=-13{,}5. \end{gather*} Отже, корінь рівняння належить проміжку \((-20; -10)\).

Відповідь: Б.

ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їх системи. Показникові рівняння.

Це завдання перевіряє вміння розв'язувати рівняння і нерівності, що містять показникові вирази, рівняння з параметрами, застосовувати властивості функцій у процесі розв'язування рівнянь.

Розглянемо ліву частину рівняння.

Оцінимо область значень функції

Розглянемо праву частину рівняння:

Отже, рівність досягається при

Корінь рівняння буде додатним при \begin{gather*} \frac{n}{2}-\frac{5}{8},\\[6pt] n\gt \frac{5}{4},\\[6pt] n\gt 1\frac{1}{4},\ n\in Z. \end{gather*}

Отже, при \(n=2\), \(3\), \(4\text{...}\)

Найменше значення параметра \(a{:}\ n=2.\)

Відповідь: \(-2{,}625.\)

ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Лінійні, ірраціональні рівняння, та їхні системи.

Це завдання перевіряє вміння розв’язувати ірраціональні, лінійні та квадратні рівняння та їхні системи.

Піднесемо до квадрату обидві частини першого рівняння.

Перевіримо, чи належить ОДЗ \((4; 11).\)

Нерівність виконується. Отже, \((4; 11)\) – розв’язок системи.

Відповідь: \(44.\)