Алгебра і початки аналізу – Лінійні, квадратні, раціональні рівняння та системи рівнянь

ТЕМА: Раціональні рівняння.

Завдання скеровано на перевірку вміння розв’язувати раціональні рівняння з параметром.

Область допустимих значень:

Прирівняймо чисельники рівних дробів:

\(x_1=6\mathord{,}5\) не буде коренем рівняння за умови:

Рівняння має один корінь \(x_2=-3.\)

\(x_2=-3\) не буде коренем рівняння за умови, що

Рівняння має один корінь \(x_1=6{,}5.\)

Отже, рівняння має один корінь за \(a=19\mathord{,}5\) або \(a=-9.\)

У відповіді запишімо їхню суму: $$ 19\mathord{,}5+(-9)=10\mathord{,}5. $$

Відповідь: \(10\mathord{,}5.\)

ТЕМА: Показникові. Раціональні рівняння.

Завдання скеровано на перевірку вміння розв’язувати показникові та квадратні рівняння, рівняння з параметром.

Замінімо змінну. Нехай \(3^x=t.\) Оскільки показникова функція завжди набуває лише додатних значень: \(t\gt 0.\) Рівняння набуває вигляду:

Помножмо все на \(t\ (t\ne 0){:}\)

Оскільки \(D\gt 0\), маємо два корені:

Щоб рівняння не мало коренів, необхідно, щоб \(t_1\le 0\) i \(t_2\le 0{:}\)

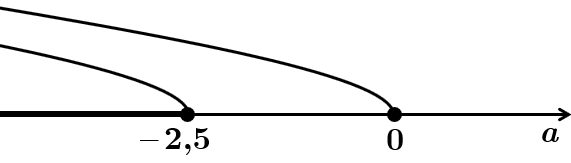
Спільна умова: \(a\le -2{,}5.\)

Найбільше значення \(a\) з проміжку \((-\infty; -2{,}5]\) це \(-2{,}5.\)

Відповідь: \(-2{,}5.\)

ТЕМА: Лінійні рівняння.

Завдання скеровано на перевірку вміння розв’язувати лінійні рівняння з параметром.

Розв'яжімо лінійне рівняння:

Якщо \(a=2\), рівняння не має коренів \((x\cdot 0=7).\)

Якщо \(a\ne 2\), корінь є. Його визначають так: $$ x=\frac{a+5}{a-2}. $$

Корінь рівняння буде додатним, якщо $$ \frac{a+5}{a-2}\gt 0. $$

Розв'яжімо методом інтервалів:

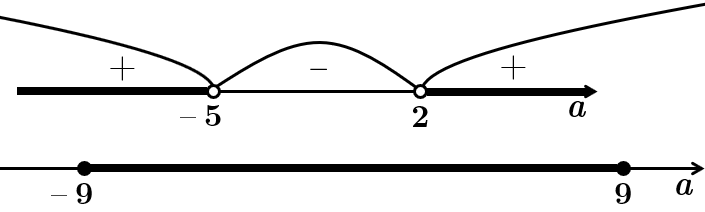
На проміжку \(a\in [-9; 9]\) рівняння має розв'язок, якщо \(a\in [-9; -5)\cup (2; 9].\)

Цілі значення \(a\) із цього проміжку: \(-9\), \(-8\), \(-7\), \(-6\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\), \(9.\) Тобто цілих значень \(a\) \(11.\)

Відповідь: \(11.\)

ТЕМА: Квадратні рівняння.

Завдання скеровано на перевірку вміння розв’язувати квадратні рівняння.

А

Рівняння має один корінь.

Б

Рівняння коренів не має.

В

Рівняння має два різні дійсні корені.

Г

Рівняння коренів не має.

Д

Рівняння має один корінь.

Відповідь: В.

ТЕМА: Лінійні і раціональні рівняння та їх системи.

Завдання скеровано на перевірку вміння розв’язувати лінійні і раціональні рівняння.

Розв'яжімо систему рівнянь методом додавання:

Підставмо значення \(y=0\mathord{,}5\) у перше рівняння:

Розв'язком системи є пара чисел \((9; 0\mathord{,}5)\mathord{:}\)

Відповідь: Г.

ТЕМА: Лінійні, квадратичні та логарифмічні функції.

Завдання скеровано на перевірку знання властивостей лінійної, квадратичної та логарифмічної функцій, уміння визначати область визначення, області значень, властивості числових функцій, заданих формулою.

1. \(y=2x-5\) – лінійна функція, її графік – пряма.

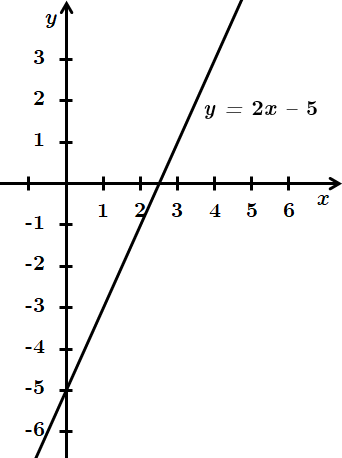
Графік функції має лише дві точки перетину з осями координат. Отже, правильна відповідь – А.

2. \(y=\log_3(x-5)\) – логарифмічна функція. Графік функції \(y=\log_3x\) перенесено паралельно вздовж осі \(Ox\) на \(5\) одиниць управо.

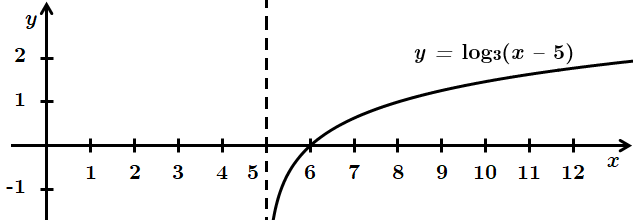
Областю визначення функції є проміжок \((5; +\infty).\) Отже, правильна відповідь – Г.

3. \(y=x^2-5\) – квадратична функція. Графік функції \(y=x^2\) перенесено вздовж осі \(Oy\) на \(5\) одиниць униз.

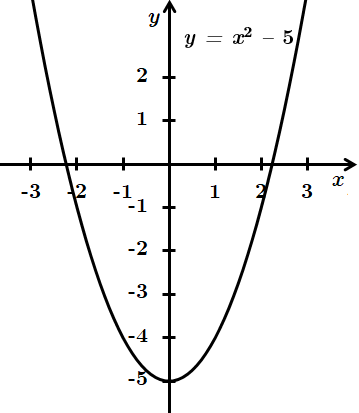
Областю значень функції є проміжок \([-5; +\infty).\) Отже, правильна відповідь – Б.

Відповідь: 1 – A, 2 – Г, 3 – Б.

ТЕМА: Лінійні, показникові та раціональні рівняння.

Завдання скеровано на перевірку вміння розв’язувати показникові та раціональні рівняння та їх системи.

Рівняння \(5^x=\sqrt{5}\) містить одну змінну. Розв'яжімо його, зводячи до однакової основи:

Підставмо значення \(x\) у друге рівняння:

За основною властивістю пропорції: $$ \frac ab=\frac cd \rightarrow a\cdot d=b\cdot c. $$ Тому запишімо:

Маємо розв'язок \((x_0; y_0)\) як \(\left(\frac 12; -3\right).\)

Підставмо його у вираз:

Відповідь: А.

ТЕМА: Алгебра і початки аналізу. Розв’язування раціональних рівнянь.

Завдання скеровано на перевірку вміння розв’язувати раціональні рівняння, та їх системи з параметрами.

Розв'яжемо систему графічним способом.

\((x-1)^2+(y+4)^2=64\) – рівняння кола з центром \((1; -4)\) і радіусом \(8.\)

\(y=-(x-1)^2+5a\) – квадратична функція з вершиною в точці \((1; 5a)\) з вітками вниз.

Для того, щоб система мала єдиний розв'язок, треба, щоб графіки мали одну спільну точку.

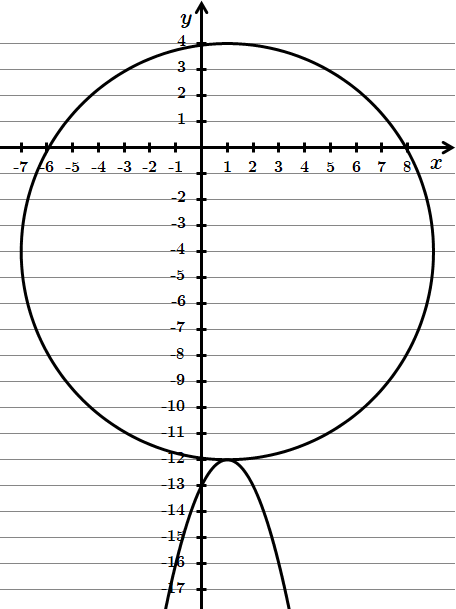
Отже,

Відповідь: \(-2\mathord{,}4.\)

ТЕМА: Алгебра. Лінійні рівняння.

Завдання скеровано на перевірку вміння розв’язувати лінійні рівняння, знання основної властивості пропорції.

Застосуємо основну властивість пропорції:

\begin{gather*} \frac ab=\frac cd,\\[6pt] a\cdot d=b\cdot c,\\[7pt] 2(2x-7)=3(5x+4),\\[7pt] 4x-14=15x+12,\\[7pt] 4x-15x=12+14,\\[7pt] -11x=26,\\[6pt] x=-\frac{26}{11},\\[6pt] x=-2\frac{4}{11}. \end{gather*}

Відповідь: B.

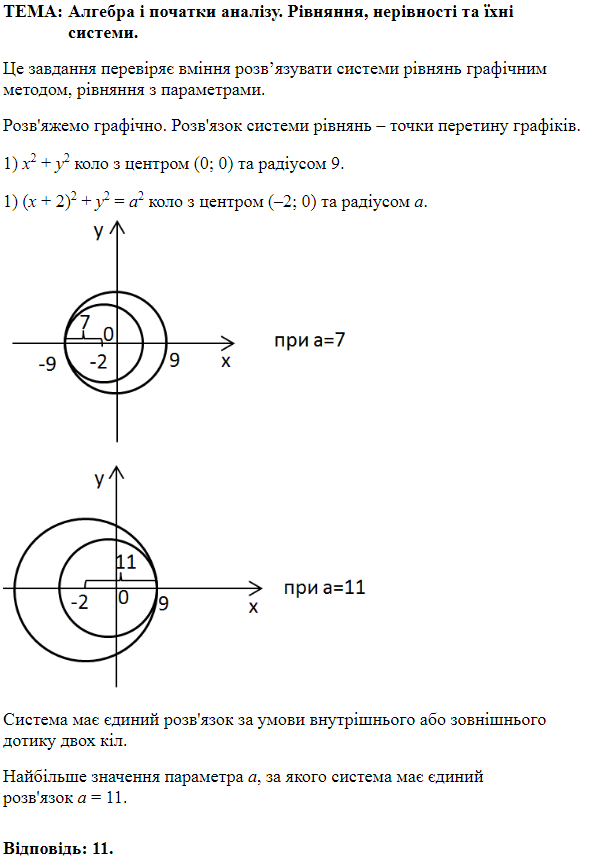
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання скеровано на перевірку вміння розв’язувати системи лінійних рівнянь.

Розв'яжемо систему: \begin{gather*} \left\{ \begin{array}{l} 2x-\frac y3=7,\\ 4x+\frac{2y}{3}=6\ | : 2, \end{array} \right. \ \ \ \ \left\{ \begin{array}{l} 2x-\frac y3=7,\\ 2x+\frac y3=3. \end{array} \right. \end{gather*}

Почленно додамо рівняння: $$ 4x=10,\ \ x=10:4,\ \ x=2,5. $$ Підставимо значення \(x\) у перше рівняння: \begin{gather*} 2\cdot 2,5-\frac y3=7,\ \ 5-\frac y3=7,\\[6pt] -\frac y3=2,\ \ y=-6. \end{gather*} \((2,5; -6)\) – розв'язок системи.

Отже, \(x_0+y_0=2,5+(-6)=-3,5.\)

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання скеровано на перевірку вміння розв’язувати раціональні рівняння, аналізувати та досліджувати рівняння, розв’язувати рівняння з параметром.

$$\frac{x^2-ax+4}{x-5}=0.$$ ОДЗ:

Рівняння буде мати один корінь за умов:
1) \(D=0\) та \(x\ne 5;\)
2) \(D\gt 0,\) але один з коренів дорівнює \(5.\)

Розглянемо обидва випадки: \begin{gather*} \text{1)}\ \ D=0,\ \ a^2-16=0,\ \ a^2=16,\\[7pt] a=4\ \text{або}\ a=-4\\[6pt] x=\frac a2=\frac 42=2\ \text{або}\ x=-2. \end{gather*} Отже, корінь один. \begin{gather*} \text{2)}\ \ D\gt 0,\ \ a^2-16=0,\\[7pt] a\in (-\infty; -4)\cup (4; +\infty) \end{gather*}

\begin{gather*} x_1=\frac{a+\sqrt{a^2-16}}{2},\\[6pt] x_2=\frac{a-\sqrt{a^2-16}}{2}. \end{gather*}

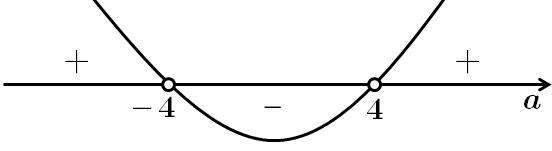
Нехай \(x_1=5,\) тоді

Нехай \(x_2=5,\) отже

Отже, рівняння має один корінь при \(a=4,\ a=-4, a=5\mathord{,}8.\) Добуток усіх значень \(a\) дорівнює: $$4\cdot (-4)\cdot 5\mathord{,}8=-92\mathord{,}8.$$

Відповідь: -92,8.

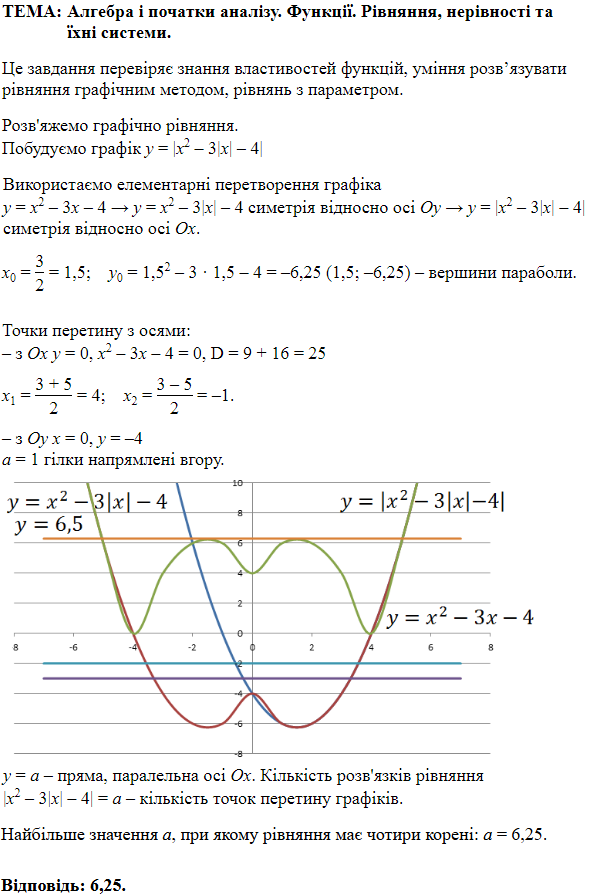
ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання скеровано на перевірку вміння розв’язувати рівняння першого степеня, використовуючи означення та властивості модуля.

\begin{gather*} |3x+2|=2\\[7pt] 3x+2=2\\[7pt] 3x=0\\[7pt] x=0\\[7pt] \text{або}\\[7pt] 3x+2=-2\\[7pt] 3x=-4\\[6pt] x=-\frac 43. \end{gather*}

З наведених чисел \(-\frac 43\) є коренем рівняння.

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати квадратні рівняння, аналізувати та досліджувати рівняння, розв’язувати рівняння з параметром.

\(x^2-(2m-4)x+16=0,\ \ x_1\gt x_2\ \text{на}\ 6.\)

Знайдемо дискримінант рівняння:

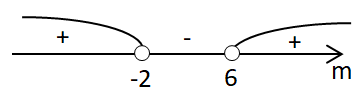
Додатнє значення \(m,\) при якому рівняння має два різних кореня \(m\gt 6.\)

За теоремою Вієта і враховуючи умову завдання:

Підставимо значення \(x_2\) у друге рівняння:

Корені рівняння:

Отже, додатнє значення \(m=7.\)

Відповідь: 7.

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання перевіряє вміння розв’язувати лінійні рівняння.

Розв'яжемо лінійне рівняння \(0,01x=-1,\) \begin{gather*} x=-1:0,01;\\[7pt] x=-100. \end{gather*}

Отже, правильна відповідь – Б.

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати квадратні рівняння, аналізувати та досліджувати рівняння, розв’язувати рівняння з параметром.

Дано рівняння \(x^2-4ax+4a^2-25=0.\) Корені квадратного рівняння задовольняють умову \(x_1\lt 1\lt x_2.\)

Знайдемо \(a,\) при яких

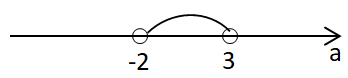
Цілі значення \(a\in (-2;\ 3)\) це \(a=-1;\ 0;\ 1;\ 2.\)

Таких значень \(4.\)

Відповідь: 4.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати системи лінійних та раціональних рівнянь.

Розв'яжемо систему рівнянь:

\begin{gather*} \left\{ \begin{array}{l} \frac{1}{3y}=\frac 2x, \\ x-y=30. \end{array} \right. \end{gather*}

Застосуємо основну властивість пропорції до першого рівняння:

Методом підстановки маємо:

\((36;\ 6)\) – розв'язок системи, тому \(36+6=42\) – правильна відповідь.

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання перевіряє вміння виконувати тотожні перетворення раціональних виразів.

Застосувавши розподільний закон множення, розкриємо дужки:

Отже, правильна відповідь – Д.

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання перевіряє вміння розв’язувати лінійні рівняння.

$$ \frac x2 +\frac x3= 2, $$ зведемо до спільного знаменника: \begin{gather*} \frac{3x+2x}{6}=2,\\[6pt] \frac{5x}{6}=2,\\[6pt] 5x=12,\\[6pt] x=2,4. \end{gather*}

Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Рівняння.

Перевіряє вміння розв'язувати квадратні рівняння, знання теореми Вієта.

Добуток коренів рівняння за теоремою Вієта для зведеного квадратного рівняння:

\begin{gather*} x^2+px+q=0\\[7pt] x_1\cdot x_2=q\\[7pt] x_1\cdot x_2=-55. \end{gather*}

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання перевіряє вміння розв’язувати лінійні рівняння.

Розв'яжемо лінійне рівняння:

\begin{gather*} 2x-3=4\\[7pt] 2x=4+3\\[7pt] 2x=7\\[7pt] x=3,5 \end{gather*}

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати раціональні рівняння.

Розв'яжемо рівняння $$ \frac{x}{9-x}=\frac 12;\ \ x\ne 9 $$

Використаємо властивість пропорції

належить проміжку \((2;\ 5]\).

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати рівняння другого степеня, знання теореми Вієта.

І спосіб: заходимо корні рівняння

ІІ спосіб: за теоремою Вієта: $$ x_1+x_2=-b=-3 $$

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати рівняння, що зводяться до квадратних.

Рівняння \(x^4-x^2-20=0\) – біквадратне. Розв'яжемо заміною:

Повернемось до заміни:

Добуток його дійсних коренів: $$ x_1\cdot x_2=\sqrt{5}\cdot (-\sqrt{5})=-5. $$

Відповідь: –5.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати рівняння першого степеню.

Розв'яжемо лінійне рівняння:

\begin{gather*} 1-5x=0\\[7pt] -5x=-1\\[6pt] x=\frac{-1}{-5}\\[6pt] x=\frac 15 \end{gather*}

Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати логарифмічні, квадратні рівняння та рівняння з параметрами.

1. Знайдемо множину допустимих значень змінної \(x\):

2. Розв'яжемо рівняння залежно від значень \(a\): \begin{gather*} \left\{ \begin{array}{ l l} \left[ \begin{array}{l l} x-2=0 & \\ x^2-3(a-1)x+2a^2-3a=0& \end{array}\right. &\\ x\in (-\infty;\ -0,5)\cup (-0,5;\ 1,5) & \end{array}\right. \end{gather*}

1) \(x-2=0,\ \ x=2\ \notin\) ОДЗ.

2) \(x^2-3(a-1)x+2a^2-3a=0\).

Розв'яжемо квадратне рівняння: \begin{gather*} D=\left(-3(a-1)\right)^2-4(2a^2-3a)=\\[7pt] =9(a^2-2a+1)-8a^2+12a=(a-3)^2\\[6pt] x_1=\frac{3(a-1)+(a-3)}{2}=2a-3;\\[6pt] x_2=\frac{3(a-1)-(a-3)}{2}=a. \end{gather*}

Знайдемо значення переметра \(a\), при яких \(x_1=2a-3\) належить ОДЗ: \begin{gather*} \left[ \begin{array}{l l} 2a-3\lt -0,5 & \\ -0,5\lt 2a-3\lt 1,5& \end{array}\right. \left[ \begin{array}{l l} a\lt 1,25 & \\ 1,25\lt a\lt 2,25& \end{array}\right. \\[7pt] a\in (-\infty;\ 1,25)\cup (1,25;\ 2,25). \end{gather*} Для кореня \(x_2=a\) \begin{gather*} \left[ \begin{array}{l l} a\lt -0,5 & \\ a\in (-0,5;\ 1,5)& \end{array}\right. \\[7pt] a\in (-\infty;\ -0,5)\cup (-0,5;\ 1,5). \end{gather*}

Відповідь:
якщо

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати рівняння, використовуючи означення та властивості модуля.

Якщо \(x\geq 0\), то \(|x|=x\). Отже, \(x+4x=3,\ 5x=3,\ x=0,6\).

Якщо \(x\lt 0\), то \(|x|=-x\). Отже, \(x-4x=3,\ -3x=3,\ x=-1\).

У відповідь запишемо їхню суму \(0,6+(-1)=-0,4\).

Відповідь: –0,4.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати системи лінійних рівнянь.

Розв'яжемо систему рівнянь методом додавання: \begin{gather*} \left\{ \begin{array}{l l} 6(x+5)+10y=3 & \\ 2x=y+4& \end{array}\right. \left\{ \begin{array}{l l} 6x+30+10y=3 & \\ 2x-y=4& \end{array}\right. \\[7pt] \left\{ \begin{array}{l l} 6x+10y=-27 & \\ 2x-y=4\ \ |\cdot (-3)& \end{array}\right. \left\{ \begin{array}{l l} 6x+10y=-27 & \\ -6x+3y=-12& \end{array}\right. \\[7pt] 13y=-39,\ \ y=-3. \end{gather*}

Підставимо значення \(y=-3\) у друге рівняння: \begin{gather*} 2x-(-3)=4;\ \ 2x+3=4; \\[6pt] 2x=1;\ \ x=\frac 12\\[6pt] x_0=\frac 12;\ \ y_0=-3. \end{gather*}

У відповідь запишемо суму $$ x_0+y_0=\frac 12+(-3)=-2,5. $$

Відповідь: А.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати рівняння першого степеня.

\begin{gather*} \frac{x}{10}=2,5;\\[6pt] x=2,5\cdot 10=25. \end{gather*}

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв'язувати квадратні рівняння.

Розв'яжемо рівняння:

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє відношення та пропорції. Перевіряє знання основної властивості пропорції.

Розв'яжемо рівняння, використавши основну властивість пропорції: \begin{gather*} \frac 8x=\frac 25,\\[6pt] 2\cdot x=8\cdot 5,\\[6pt] x=20. \end{gather*}

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання перевіряє вміння розв’язувати квадратні рівняння.

Розв'яжемо квадратне рівняння:

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання перевіряє вміння розв’язувати лінійні рівняння.

Помножимо обидві частини рівняння на \(3.\)

\(5x+8=3\), \(5x=-5\), \(x=-1.\)

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє вміння виконувати тотожні перетворення раціональних виразів, знання формул скороченого множення.

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв’язувати лінійні рівняння з модулем.

За властивістю модуля

У відповідь запишемо суму розв'язків: \(0\mathord{,}5+2=2\mathord{,}5.\)

Відповідь: \(2\mathord{,}5.\)

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв’язувати системи лінійних рівнянь.

Розв'яжемо систему лінійних рівнянь методом додавання: \begin{gather*} +\left\{\begin{array}{l} 10x-4y=26,\\ 6x+4y=6, \end{array}\right.\\[0pt] \ \ \ \ \ \ \overline{16x=32,}\\[7pt] x=32:16,\ \ x=2. \end{gather*}

Підставимо значення \(x=2\) в друге рівняння: \begin{gather*} 6\cdot 2+4y=6,\\[7pt] 12+4y=6,\\[7pt] 4y=6-12,\\[7pt] 4y=-6,\\[7pt] y=-6: 4,\\[7pt] y=-1\mathord{,}5. \end{gather*}

Розв'язок системи \((2; -1\mathord{,}5).\)
Обчислимо добуток \(x_0\cdot y_0=2\cdot (-1\mathord{,}5)=-3.\)

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв’язувати квадратні рівняння.

Розв'яжемо квадратне рівняння: \begin{gather*} x^2-8x+15=0,\\[6pt] D=(-8)^2-4\cdot 1\cdot 15=4,\\[6pt] x_1=\frac{8+2}{2\cdot 1}=5,\\[6pt] x_2=\frac{8-2}{2\cdot 1}=3. \end{gather*}

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лiнiйнi, квaдpaтні, рацiональнi, iррацiональнi, показникові, логарифмiчнi, тригонометричні рівняння, неpiвності та їx системи.

Це завдання перевіряє вміння розв'язувати системи лінійних рівнянь.

Почленно додамо рівняння: \begin{gather*} \left\{\begin{array}{l} 2x+5y=5\\ x-2y=7\ |\ \cdot (-2) \end{array}\right.\\[7pt] \ +\ \left\{\begin{array}{l} 2x+5y=5\\ \underline{-2x+4y=-14} \end{array}\right.\\[7pt] 9y=-9,\ y=-1 \end{gather*} Підставимо \(y=-1\) у друге рівняння: \begin{gather*} x-2(-1)=7,\\[7pt] x+2=7,\\[7pt] x=5. \end{gather*}

Розв'язок системи \((x_0; y_0)\) це \((5; -1).\) Сума \(x_0+y_0=5+(-1)=4.\)

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Текстові задачі. Рівняння.

Це завдання перевіряє вміння розв'язувати текстові задачі арифметичним способом, розв'язувати рівняння першого степеня.

Нехай \(x\) км/год – швидкість автобуса від \(A\) до \(B.\) Тоді:

Оскільки відстань від \(A\) до \(B\) така сама як і від \(B\) до \(A\), то складемо рівняння: \begin{gather*} 5x=4\mathord{,}5(x+8),\\[7pt] 5x=4\mathord{,}5x+36,\\[7pt] 0\mathord{,}5x=36,\\[7pt] x=72. \end{gather*}

Відповідь: \(72.\)

ТЕМА: Алгебра і початки аналізу. Рівняння та їхні системи.

Це завдання перевіряє вміння розв'язувати системи рівнянь першого степеня.

Розв'язок \((4; 10).\) Відповідь: \(4\cdot 10=40.\)

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Рівняння.

Це завдання перевіряє вміння розв'язувати рівняння з однією змінною, використовувати методи розв'язування раціональних рівнянь.

Якщо рівняння має вигляд добутку множників, що дорівнює нулю, то принаймні один з множників повинен дорівнювати нулю.

\begin{gather*} \left[\begin{array}{l} x+1=0,\\ 2x-3=0, \end{array}\right.\ \ \left[\begin{array}{l} x=-1,\\ 2x=3, \end{array}\right.\ \ \left[\begin{array}{l} x=-1,\\ x=1\mathord{,}5. \end{array}\right. \end{gather*}

Відповідь: Д.

ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Раціональні рівняння.

Це завдання перевіряє вміння розв'язувати раціональні рівняння.

зводимо до спільного знаменника:

Корінь рівняння \(x=-2\mathord{,}25\) належить проміжку \((-\infty; -2).\)

Відповідь: A.

ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Лінійні рівняння.

Це завдання перевіряє вміння розв'язувати рівняння, що містять змінну під знаком модуля.

Отже, за наведених чисел коренем рівняння є \(x=-1.\)

Відповідь: Г.

ТЕМА: Рівняння, нерівності та їхні системи. Лінійні рівняння.

Це завдання перевіряє вміння розв'язувати лінійні рівняння.

\begin{gather*} 2x-3=4,\\[7pt] 2x=4+3,\\[7pt] 2x=7,\\[7pt] x=7:2,\\[7pt] x=3\mathord{,}5. \end{gather*}

Значення \(x\) належить проміжку \([2; 4).\)

Відповідь: Г.

ТЕМА: Рівняння, нерівності та їхні системи. Лінійні, квадратні рівняння та їхні системи.

Це завдання перевіряє вміння розв'язувати системи рівнянь першого та другого степеня, застосовувати загальні методи та прийоми в процесі розв'язування систем рівнянь.

З першого рівняння добуток \(xy=-12.\)

Отримаємо:

Якщо \((x_0; y_0)\) – розв'язок системи, то \(x_0=-6.\)

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв'язувати системи рівнянь другого степеня.

Розв'яжемо способом додавання

Підставимо \(x=0\) в перше рівняння

Розв'язок системи рівнянь \((0; 2)\) та \((0; -2).\) Отже рівняння має два розв'язки.

Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Рівняння, нерівності та їхні системи.

Це завдання перевіряє знання модуля дійсного числа та його властивості; вміння розв'язувати рівняння першого ступеня.

За властивістю модуля дійсного числа, рівняння \(|x-1|=6\) рівносильне сукупності таких рівнянь:

Сума коренів рівняння дорівнює \(7+(-5)=2.\)

Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв'язувати рівняння другого степеня.

Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв’язувати рівняння першого степеня, застосовувати загальні методи та прийоми в процесі розв’язання рівнянь.

Розв’яжемо рівняння першого степеня відносно \(y:\)

Відповідь: B.

ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Лінійні, квадратні, раціональні рівняння та їхні системи.

Це завдання перевіряє вміння розв'язувати рівняння та системи рівнянь першого та другого степеня.

Почленно віднімемо рівняння системи:

Підставимо значення \(x=-3\) в перше рівняння: \begin{gather*} -3\cdot y=12,\\[6pt] y=-\frac{12}{3},\\[6pt] y=-4. \end{gather*}

Розв'язок системи \((-3; -4).\)

Отже, правильна відповідь $$ x_0+y_0=-3+(-4)=-7. $$

Відповідь: A.

ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Квадратні рівняння.

Це завдання перевіряє вміння розв'язувати неповні квадратні рівняння.

Отже, правильна відповідь – Д.

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лінійні, квадратні, раціональні, ірраціональні, показникові, логарифмічні, тригонометричні рівняння, нерівності та їх системи.

Це завдання перевіряє вміння розв'язувати раціональні рівняння з параметрами.

Рівняння буде мати один корінь у двох випадках:

1) рівняння \(x^2-x+a=0\) має один корінь \((D=0)\) та він не дорівнює \(-1{,}5.\)

2) рівняння \(x^2-x+a=0\) має два корені \((D\gt 0)\), але один з коренів дорівнює \(-1{,}5.\)

Розглянемо кожний випадок: \begin{gather*} \text{1)}\ x^2-x+a=0;\\[7pt] D=1-4a=0;\\[7pt] a=\frac 14;\\[7pt] x=\frac 12. \end{gather*}

Отже, при \(a=\frac 14\) рівняння має один корінь.

\(x_1\gt 0\), отже, не може дорівнювати \(-1{,}5.\)

Знайдемо значення \(a\), при якому \(x_2=-1{,}5.\)

Отже, при \(a=-3{,}75\) рівняння має один корінь.

У відповідь запишем найменше значення \(a.\)

Відповідь: \(-3{,}75.\)

ТЕМА: Алгебра і початки аналізу. Рівняння і нерівності. Лінійні, квадратні, раціональні, ірраціональні, показникові, логарифмічні, тригонометричні рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв'язувати лінійні рівняння.

Відповідь: Г.