Розділ: Функції
Тема: Лінійні та квадратичні функції
Кількість завдань: 38
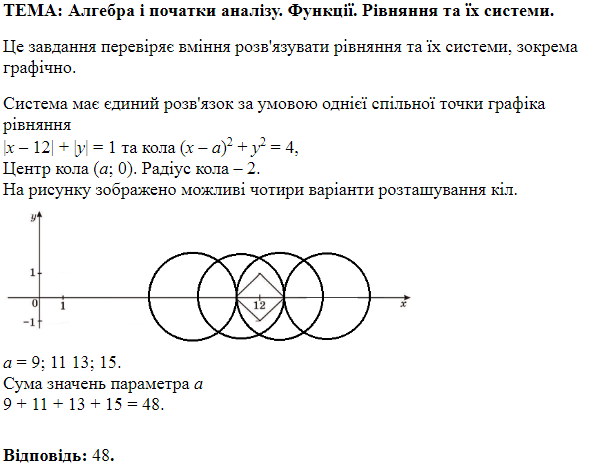
ТЕМА: Алгебра і початки аналізу. Функціональна залежність.
Завдання скеровано на перевірку вміння будувати графіки функцій, знання властивостей лінійної функцій.
1.
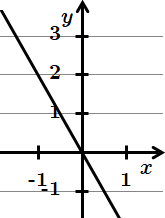
Отже, 1 – Г.
2.
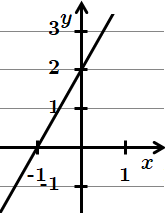
Отже, 2 – А.
3.
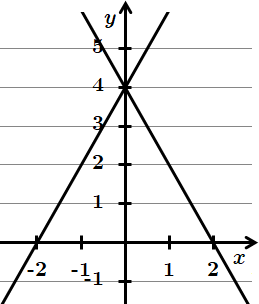
Отже, 3 – Б.
Відповідь: 1Г, 2А, 3Б.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння встановлювати властивості числових функцій, заданих графіком.
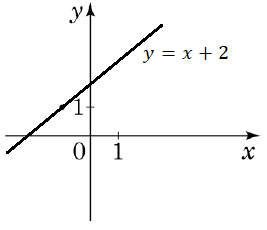
Графік лінійної функції
Відповідь: В.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння встановлювати властивості числових функцій, заданих графіком.
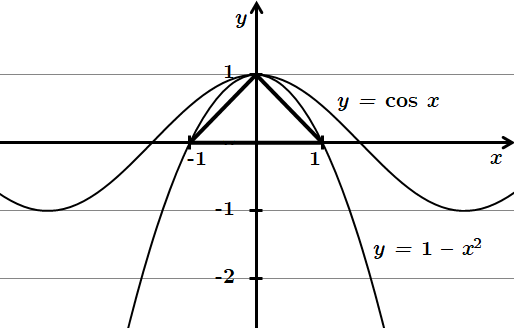
1.
2. Спільних точок параболи
3. Спільних точок функції
Відповідь: 1Д 2Г 3Б.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння установлювати властивості числових функцій, заданих формулою або графіком.
1.
2.
3.
Відповідь: 1Б 2Г 3Д.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком та формулою.
Графіком лінійної функції є пряма. Всі точки прямої, паралельної осі абсцис, мають однакові ординати.
Якщо пряма проходить через
Відповідь: A.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє знання властивостей квадратичної функції.
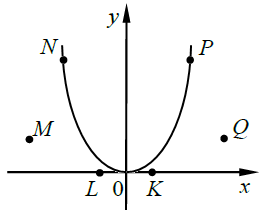
Графіком квадратичної функції
Відповідь: Г.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння установлювати властивості числових функцій, заданих графіком.
Дано: лінійна функція
Відповідь: Б.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння аналізувати дані, подані графіком або таблицею.
А неправильно, бо зупинка тривала 1 годину, а не 4.
Б неправильно, бо туристи не пройшли 20 км.
В неправильно, бо туристи пройшли до зупинки більшу відстань, ніж після зупинки.
Г правильна відповідь. Туристи зробили зупинку через 4 години.
Відповідь: Г.
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння використовувати перетворення графіків функцій.
Елементарними перетвореннями графік функції
Відповідь: Г.
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Завдання перевіряє вміння виконувати тотожні перетворення раціональних виразів.
Використаємо основну властивість пропорції:
Відповідь: A.
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Це завдання перевіряє вміння знаходити числове значення буквеного виразу.
За формулою
Відповідь: Б.
ТЕМА: Алгебра та початки аналізу. Функції. Квадратична функція.
Це завдання перевіряє вміння знаходити нулі функції.
Нулі функції знаходимо з рівняння
Відповідь: Г.
ТЕМА: Алгебра та початки аналізу. Функції. Лінійна функція.
Це завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком, використовувати перетворення графіків функцій.
Графік функції
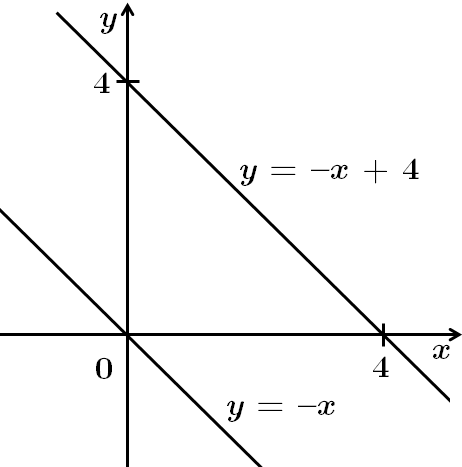
Отже, правильна відповідь Д.
Відповідь: Д.
ТЕМА: Функції. Функціональна залежність. Лінійні, квадратичні, показникові функції, їхні основні властивості.
Це завдання перевіряє вміння знаходити область значень функції, встановлювати властивості числових функцій, заданих формулою.
1. Пряма
Отже, правильна відповідь – В.
2. Пряма
Отже, правильна відповідь – Б.
3. Пряма
Отже, правильна відповідь – A.
4. Пряма
Отже, правильна відповідь – Д.
Відповідь: 1 – В, 2 – Б, 3 – А, 4 – Д.

ТЕМА: Функції. Функціональна залежність. Лінійна функція, її властивості.
Це завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком.
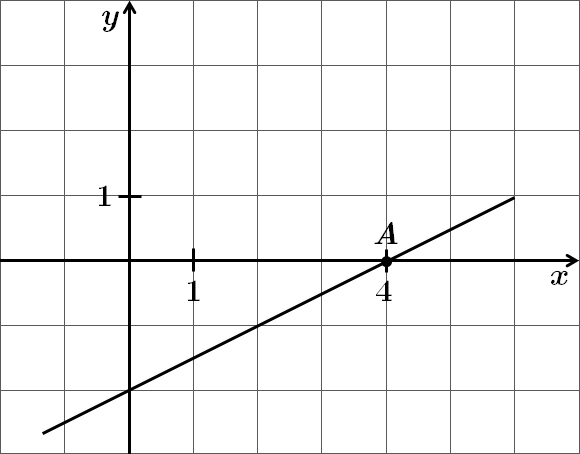
Графік функції перетинає вісь абсцис у точці
Відповідь: Д.
ТЕМА: Алгебра і початки аналізу. Функції. Числа і вирази.
Це завдання перевіряє знання основних властивостей функцій, уміння розв’язувати рівняння першого степеня.
Точка перетину графіка функції
Точка перетину графіка з віссю абсцис
Відповідь: B.
ТЕМА: Алгебра та початки аналізу. Функції. Квадратична функція.
Це завдання перевіряє вміння будувати графіки елементарних функцій, використовувати перетворення графіків функцій.
Задано функцію
Використаємо елементарні перетворення графіків функції. Вершина параболи
Отримана функція
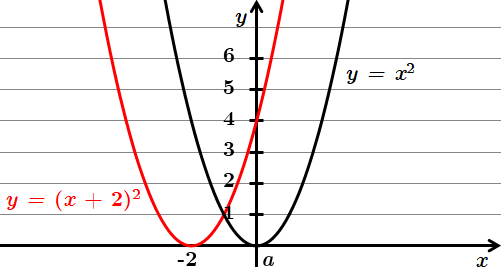
Відповідь: B.























