Первісна та визначений інтеграл – тести ЗНО/НМТ – завдання з математики

Предмет: Алгебра і початки аналізу
Розділ: Функції
Тема: Первісна та визначений інтеграл
Кількість завдань: 43

12345678910111213141516171819202122232425262728293031323334353637383940414243

Зачекайте, йде розрахунок...

Завдання 1 з 43

Обчисліть інтеграл $\mathop{\int}\limits_1^{e^3} \frac{dx}{6x}.$

Впишіть відповідь:

0.5

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра та початки аналізу. Функції. Первісна та визначений інтеграл.

Завдання перевіряє вміння обчислювати первісну, використовуючи її основні властивості, застосовувати формулу Ньютона – Лейбніца для обчислення визначеного інтеграла.

\begin{gather*} \mathop{\int}\limits_1^{e^3}\ \frac{dx}{6x}=\mathop{\int}\limits_1^{e^3}\frac{1}{6x}\ dx=\mathop{\int}\limits_1^{e^3}\frac 16\cdot \frac 1x\ dx=\frac 16\mathop{\int}\limits_1^{e^3}\frac 1x\ dx=\frac 16(\ln|x|)|_1^{e^3}=\\[6pt] =\frac 16(\ln(e^3)-\ln 1)=\frac 16(3-0)=\frac 16\cdot 3=\frac 36=\frac 12=0{,}5. \end{gather*}

Функція $f(x)$	Загальний вигляд первісних $F(x)+C$, де $C$ – довільна стала
\begin{gather}\frac 1x\end{gather}	\begin{gather}\ln\|x\|+C\end{gather}

За властивістю логарифма:

\begin{gather*} \log_a 1=0;\\[7pt] \log_a b^n=n\cdot \log_a b. \end{gather*}

Відповідь: $0{,}5.$

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 734. Завдання: 36608

Завдання 2 з 43

Визначте загальний вигляд первісних для функції \begin{gather*} f(x)=\frac{2}{\cos^2 x}+\frac 3x+\cos x+2. \end{gather*}

А$\mathrm{tg}\ x+3\ln|x|+\sin x+C$

Б$\mathrm{tg}\ x+3\ln|x|+\sin x+2x+C$

В$2\mathrm{tg}\ x+3\ln|x|+\sin x+C$

Г$2\mathrm{tg}\ x+3\ln|x|+\sin x+2x+C$

Д$\mathrm{tg}\ x+\ln|x|+\sin x+2x+C$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Первісна.

Завдання скеровано на перевірку вміння визначати загальний вигляд первісних функції.

Перепишімо перші два доданки, винісши множники з їхніх чисельників: \begin{gather*} \frac{2}{\cos^2 x}=2\cdot \frac{1}{\cos^2 x};\\[6pt] \frac 3x=3\cdot \frac 1x. \end{gather*}

Тепер функція має такий вигляд:

\begin{gather*} f(x)=2\cdot \frac{1}{\cos^2 x}+3\cdot \frac 1x+\cos x+2. \end{gather*}

Визначмо загальний вигляд первісних для цієї функції, проаналізувавши доданки:

1. Доданок $2\cdot \frac{1}{\cos^2 x}$ – множник $2$ залишмо без змін, первісна для $\frac{1}{\cos^2 x}$ за таблицею первісних дорівнює $\mathrm{tg}\ x$, тож маємо $2\mathrm{tg}\ x.$

2. Доданок $3\cdot \frac 1x$ – множник $3$ залишмо без змін, первісна для $\frac 1x$ за таблицею первісних дорівнює $\ln |x|$, тож $3\ln |x|.$

3. Доданок $\cos x$ – первісна для $\cos x$ за таблицею первісних дорівнює $\sin x$ , тож маємо $\sin x.$

4. Доданок $2$ – первісна від сталої $2$ дорівнює $2x.$

Запишімо суму всіх доданків, які визначили в пунктах 1–4, у кінці додамо константу $C$, бо за умовою треба визначити загальний вигляд первісних функції:

\begin{gather*} F(x)=2\mathrm{tg}\ x+3\ln|x|+\sin x+2x+C. \end{gather*}

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 761. Завдання: 36557

Завдання 3 з 43

На рисунку зображено графіки функцій $y=3\sqrt{x}$ i $y=\frac 32x.$ Обчисліть площу фігури, обмеженої графіками цих функцій.

Впишіть відповідь:

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Функції. Первісна та визначений інтеграл. Застосування визначеного інтеграла до обчислення площ плоских фігур.

Завдання скеровано на перевірку вміння застосовувати формулу Ньютона – Лейбніца для обчислення визначеного інтеграла, обчислювати площу плоских фігур за допомогою інтеграла.

Площу зафарбованої фігури можна обчислити за допомогою визначеного інтеграла: \begin{gather*} S=\mathop{\int}\limits_a^b (f(x)-g(x))\ dx, \end{gather*} де $f(x)$ – це функція, графік якої обмежує фігуру згори, а $g(x)$ – функція, графік якої обмежує фігуру знизу.

З рисунка видно, що графіки функцій перетинаються у двох точках: $(0; 0)$ – точка початку координат; точка $(4; 6).$

Отже, межі інтегрування – від $0$ до $4.$

Графік функції $y=3\sqrt{x}$ проходить вище за пряму $y=\frac 32x.$

Обчислімо площу зафарбованої фігури: \begin{gather*} S=\mathop{\int}\limits_0^4 \left(3\sqrt{x}-\frac 32x\right)\ dx, \end{gather*}

Первісна для кожної частини:

\begin{gather*} \mathop{\int} 3\sqrt{x}\ dx=3\mathop{\int} x^{\frac 12}\ dx=3\frac{x^{\frac 32}}{\frac 32}=3\cdot \frac 23\cdot x\sqrt{x}=2x\sqrt{x};\\[6pt] \mathop{\int} \frac 32x\ dx=\frac 32\cdot \frac{x^2}{2}=\frac 34x^2. \end{gather*}

Застосуймо формулу Ньютона -Лейбніца:

\begin{gather*} \mathop{\int}\limits_a^b f(x)\ dx=F(x)\ \left|_a^b\right.=F(b)-F(a), \end{gather*}

де $f(x)$ – це неперервна функція на проміжку $[a; b]$, а $F(x)$ – її перевісна.

\begin{gather*} S=\mathop{\int}\limits_0^4 \left(3\sqrt{x}-\frac 32x\right)\ dx=\left(2x\sqrt{x}-\frac 34x^2\right)\left|_0^4\right.=\\[6pt] =\left(2\cdot 4\cdot \sqrt{4}-\frac 34\cdot 16\right)-2\cdot 0\cdot \sqrt{0}-\frac 34\cdot 0=(16-12)-0=4. \end{gather*}

Відповідь: $4.$

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 732. Завдання: 36365

Завдання 4 з 43

Позначте формулу для обчислення площі $S$ фігури, обмеженої графіками функцій $y=2^x$, $y=2$ і $x=0$ (див. рисунок).

А$S=\mathop{\int}\limits_0^1 2^x dx$

Б$S=\mathop{\int}\limits_0^1 (2^x-2) dx$

В$S=\mathop{\int}\limits_1^2 (2-2^x) dx$

Г$S=\mathop{\int}\limits_0^1 (2-2^x) dx$

Д$S=\mathop{\int}\limits_1^2 (2^x-2) dx$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Первісна й визначений інтеграл.

Завдання скеровано на перевірку вміння застосовувати формулу Ньютона - Лейбніца для обчислення визначеного інтеграла, обчислювати площу плоских фігур за допомогою інтеграла.

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 731. Завдання: 36336

Завдання 5 з 43

Обчисліть інтеграл $\mathop{\int}\limits_1^5 3f(x)dx,$ якщо $ \mathop{\int}\limits_1^5 f(x)dx=14.$

А$11$

Б$42$

В$17$

Г$\frac{14}{3}$

Д$52$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Первісна та визначений інтеграл.

Завдання скеровано на перевірку вміння обчислювати первісну, знання її основних властивостей, правил визначення визначеного інтеграла.

За правилом інтегрування:

\begin{gather*} \mathop{\int}\limits_a^b=kf(x)dx=k\mathop{\int}\limits_a^bf(x)dx.\\[6pt] \mathop{\int}\limits_1^5 3f(x)dx=3\mathop{\int}\limits_1^5 f(x)dx=3\cdot 14=42. \end{gather*}

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 703. Завдання: 35805

Завдання 6 з 43

Позначте формулу для визначення площі $S$ фігури, обмеженої графіками функцій $y=2^x$, $y=2$ та прямою $x=0$ (див. рисунок).

А$S=\mathop{\int}\limits_0^2 2^x\ dx$

Б$S=\mathop{\int}\limits_0^1 2^x\ dx$

В$S=\mathop{\int}\limits_0^1 (2^x-2)\ dx$

Г$S=\mathop{\int}\limits_0^1 (2-2^x)\ dx$

Д$S=\mathop{\int}\limits_0^2 (2-2^x)\ dx$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Первісна й визначений інтеграл.

Завдання скеровано на перевірку вміння застосовувати формулу Ньютона – Лейбнiцa для обчислення визначеного інтеграла, обчислювати площу плоских фігур за допомогою інтеграла.

Площу зафарбованої фігури можна обчислити за допомогою визначеного інтеграла:

\begin{gather*} S=\mathop{\int}\limits_a^b (f(x)-g(x))\ dx, \end{gather*}

де $f(x)$ – це функція, графік якої обмежує фігури згори, а $g(x)$ – функція графік якої обмежує фігуру знизу.

\begin{gather*} S=\mathop{\int}\limits_0^1 (2-2^x)\ dx. \end{gather*}

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 712. Завдання: 35435

Завдання 7 з 43

Графіки функцій $y=f(x)$ й $y=x^2-2x+3$ перетинаються в точках з абсцисами $x_1=0$ й $x_2=3.$ Обчисліть площу зафарбованої фігури, якщо $$ \mathop{\int}\limits_0^3 f(x)dx=14\mathord{,}1. $$

Впишіть відповідь:

5.1

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Первісна й визначений інтеграл.

Завдання скеровано на перевірку вміння застосовувати формулу Ньютона – Лейбница для обчислення визначеного інтеграла, обчислювати площу плоских фігур за допомогою інтеграла.

Площу зафарбованої фігури можна обчислити за допомогою визначеного інтеграла: $$ S=\mathop{\int}\limits_a^b \left(f(x)-g(x)\right) dx, $$ де $f(x)$ – це функція, графік якої обмежує фігуру згори, а $g(x)$ – функція, графік якої обмежує фігуру знизу.

\begin{gather*} S=\mathop{\int}\limits_0^3 \left(f(x)-y\right) dx=\mathop{\int}\limits_0^3 f(x) dx-\mathop{\int}\limits_0^3(x^2-2x+3)dx=\\[6pt] =14\mathord{,}1-\left.\left(\frac{x^3}{3}-\frac{2x^2}{2}+3x\right)\right|_0^3=14\mathord{,}1-\left(\frac{27}{3}-\frac{2\cdot 9}{2}+3\cdot 3-0\right)=\\[6pt] =14\mathord{,}1-9+9-9=5\mathord{,}1. \end{gather*}

Відповідь: $5\mathord{,}1.$

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 701. Завдання: 35383

Завдання 8 з 43

Визначте загальний вигляд первісних для функції $f(x)=2e^x+1.$

А$F(x)=2e^x+C$

Б$F(x)=2e^x+x+C$

В$F(x)=e^{x^2}+C$

Г$F(x)=e^{x^2}+x+C$

Д $F(x)=\frac{2e^{x+1}}{x+1}+x+C$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Первісна та визначений інтеграл.

Завдання скеровано на перевірку вміння визначати первісну, використовуючи її основні властивості.

За таблицею первісних: функція $f(x)=e^x$ має первсну $F(x)=e^x + C$, функція $f(x)=1$ має первісну $F(x)=x+C$, де $C$ – стала.

Визначмо загальний вигляд первісних для функції $f(x)=2e^x+1\mathord{:}$ $$ F(x)=2e^x+x+\mathrm{C}. $$

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 701. Завдання: 35379

Завдання 9 з 43

Обчисліть площу $S$ заштрихованої фігури, обмеженої графіком функції $y=e^x$, віссю абсцис і прямою $x=1.$

А$S=e+1$

Б$S=e$

В$S=1$

Г$S=1-e$

Д$S=e-1$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Первісна й визначений інтеграл.

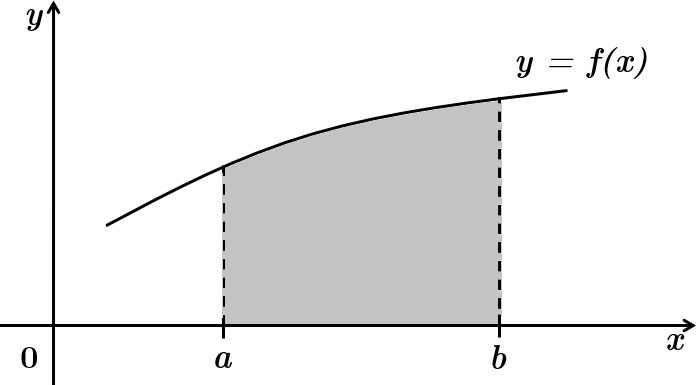
Площу заштрихованої фігури (криволінійної трапеції), обмежено лініями $x=a$, $x=b$, графіком функції $y=f(x)$ і віссю $Ox$ визначаємо за формулою:

\begin{gather*} \mathop{\int}\limits_a^b f(x)dx=F(b)-F(a),\\[6pt] S=\mathop{\int}\limits_0^1 e^x dx=\left.e^x\right|_0^1=e^1-e^0=e-1. \end{gather*}

Відповідь: Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 700. Завдання: 35356

Завдання 10 з 43

Для функції $f(x)=4x-3$ знайдіть первісну $F(x)$, графік якої проходить через точку $A(0; 1).$

А$F(x)=4$

Б$F(x)=2x^2-3x+1$

В$F(x)=4x^2-3x$

Г$F(x)=2x^2+1$

Д$F(x)=4x^2-3x+1$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Первісна та визначений інтеграл.

Завдання скеровано на перевірку знання таблиці первісних, уміння застосовувати правила визначення первісних у точці.

Визначмо загальний вигляд первісної:

$$ F(x)=4\cdot\frac{x^2}{2}-3\cdot x+C=2x^2-3x+C. $$

Первісну, яка проходить через точку $A(0; 1)$, дізнаймося підставивши координати точки $x=0$, $F(0)=1$ у формулу загального вигляду первісної, щоб обчислити значення сталої $C\mathord{:}$

$$ 2\cdot 0^2-3\cdot 0 + C=1, $$

$$ C=1. $$ Отже, \begin{gather*} F(x)=2x^2-3x+1. \end{gather*}

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 698. Завдання: 35311

Завдання 11 з 43

Обчисліть інтеграл $\int_{3}^{5}\frac{x^2+2x+1}{x+1}dx.$

Впишіть відповідь:

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Функції. Первісна.

Завдання скеровано на перевірку знання правил знаходження первісної, визначеного інтеграла.

\begin{gather*} \int_{3}^{5}\frac{x^2+2x+1}{x+1}dx=\int_{3}^{5}\frac{(x+1)^2}{x+1}dx=\\[6pt] =\int_{3}^{5}(x+1)dx=\left(\frac{x^2}{2}+x\right)\left.\right|_{3}^{5}=\\[6pt] =\left(\frac{5^2}{2}+5\right)-\left(\frac{3^2}{2}+3\right)=\frac{25}{2}+5-\frac 92-3=\\[6pt] =\frac{16}{2}+2=8+2=10. \end{gather*}

Відповідь: 10.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 585. Завдання: 28372

Завдання 12 з 43

Обчисліть $\int_{0}^{7} f(x)dx,$ використавши зображений на рисунку графік лінійної функції $y=f(x).$

Впишіть відповідь:

38.5

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Функції. Первісна.

Завдання перевіряє знання означення геометричного змісту визначеного інтеграла, вміння обчислювати площу плоских фігур.

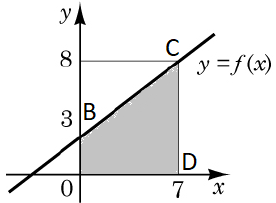
$\int_0^{7}f(x)dx.$ Геометричний зміст визначеного інтеграла – площа фігури, обмеженої лініями: графіком $f(x),$ $x=0,$ $x=7$ та віссю $x.$

\begin{gather*} \int_0^{7}f(x)dx=S_{OBCD}=\frac{OB+CD}{2}\cdot OD=\\[6pt] =\frac{3+8}{2}\cdot 7=5,5\cdot 7=38,5. \end{gather*}

Відповідь: 38,5.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 523. Завдання: 26202

Завдання 13 з 43

У прямокутній системі координат на площині зображено план паркової зони, що має форму фігури, обмеженої графіками функцій $y=f(x)$ і $y=3$ (див. рисунок). Укажіть формулу для обчислення площі $S$ цієї фігури.

А$S=\int_{-1}^{3}(f(x)-3)dx$

Б$S=\int_{-1}^{3}(3-f(x))dx$

В$S=\int_{0}^{4}(f(x)+3)dx$

Г$S=\int_{0}^{4}(f(x)-3)dx$

Д$S=\int_{0}^{4}(3-f(x))dx$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Функції. Первісна функції.

Завдання скеровано на перевірку знання геометричного змісту визначеного інтеграла.

Використаємо геометричний зміст визначеного інтеграла та формулу Ньютона-Лейбніца, знаходимо площу фігури: \begin{gather*} S=\int_{0}^{4}(3-f(x))dx \end{gather*}

Відповідь: Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 489. Завдання: 24694

Завдання 14 з 43

Яка з наведених функцій є первісною для функції $f(x)=x^{-4}$?

А$F(x)=-\frac{1}{5x^5}$

Б$F(x)=-\frac{3}{x^5}$

В$F(x)=-\frac{4}{x^5}$

Г$F(x)=-\frac{5}{x^5}$

Д$F(x)=-\frac{1}{3x^3}$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Функції. Первісна функції.

Завдання скеровано на перевірку вміння знаходження первісної степеневої функції.

Знаходимо первісну степеневої функції:

\begin{gather*} F(x)=\frac{x^{-4+1}}{-4+1}+C=\frac{x^{-3}}{-3}+C=-\frac{1}{3x^3}+C \\[6pt] \text{при}\ C=0\ \ F(x)=-\frac{1}{3x^3}. \end{gather*}

Відповідь: Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 469. Завдання: 23670

Завдання 15 з 43

Задано функцію $y=2x+8$.

1. Для наведених у таблиці значень аргументу $x$ і значень функції $y$ визначте відповідні їм значення $y$ та $x$.

$x$	$y$
$0$
	$0$
$9$

2. Запишіть координати точки $M$ перетину графіка заданої функції з віссю $x$.

3. Знайдіть загальний вигляд первісних функції $f(x)=2x+8$.

4. Знайдіть первісну $F(x)$ функції $f$, графік якої проходить через точку $M$.

5. Побудуйте графік функції $F$.

6. Визначте область значень функції $G(x)=3\cdot F(x)+1$.

Це завдання відкритого типу з розгорнутою відповіддю, воно оцінюється екзаменатором за спеціальними критеріями оцінювання. Під час розрахунку бала за це завдання, на сайті ЗНО-онлайн використовується спеціальна формула розрахунку в залежності від якості виконання інших завдань тесту. Максимальна кількість балів за це завдання: 6.

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання скеровано на перевірку вміння знаходити область значень функції, будувати графіки квадратичних функцій, установлювати властивості числових функцій, заданих формулою, використання перетворення графіків функцій, знаходити первісну функції.

1. \begin{gather*} y(0)=2\cdot 0+8=8\\[7pt] y=0,\ \ 2x+8=0,\ \ x=-4\\[7pt] y(9)=2\cdot 9+8=26. \end{gather*}

$x$	$y$
$0$	$8$
$-4$	$0$
$9$	$26$

2. $M(-4;\ 0)$ – точка перетину графіка функції з віссю $x$.

\begin{gather*} F(x)=2\cdot \frac{x^2}{2}+8x+C,\\[6pt] F(x)=x^2+8x+C\ \ \text{загальний вигляд первісних.} \end{gather*}

4. Первісна функції $f$, яка проходить через точку $M(-4;\ 0)$ \begin{gather*} 0=(-4)^2+8\cdot (-4)+C,\\[7pt] 0=16-32+C,\ \ C=16\\[7pt] F(x)=x^2+8x+16. \end{gather*}

5. Побудуємо графік функції $F(x)=x^2+8x+16$, $F(x)=(x+4)^2$.

Використаємо елементарні перетворення графіків:

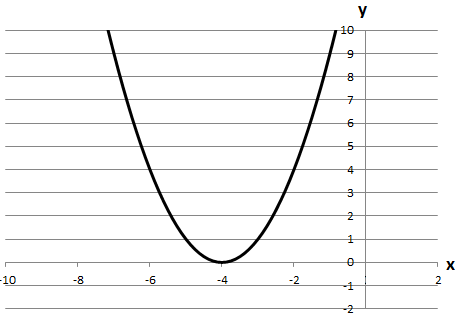
$F(x)=x^2 \rightarrow F(x)=(x+4)^2$ переносимо вліво на 4 одиниці вздовж осі $Ox$.

6. Область визначення функції $F(x)\ E(y)=[0;\ +\infty)$.

Функцію $G(x)=3F(x)+1$ отримаємо з функції $F(x)$ стисканням в 3 рази до осі $Oy$ та паралельним перенесенням на 1 одиницю вгору вздовж осі $Oy$.

Отже, $E(G)=[1;\ \infty)$.

Відповідь:

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 455. Завдання: 22929

Завдання 16 з 43

Функція $F(x)=10x^5-4$ є первісною функції $f(x).$ Укажіть функцію $G(x)$, яка також є первісною функції $f(x).$

А$G(x)=10x^5+7$

Б$G(x)=2x^6-4x$

В$G(x)=50x^6$

Г$G(x)=50x^4$

Д$G(x)=x^5-4$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Функції. Первісна.

Завдання перевіряє знання означення первісної.

Загальний вигляд первісної функції $f(x)$

$F(x)=10x^5+C$, де $C$ – довільне число.

Тоді, $G(x)=10x^5+7.$

Відповідь: A.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 425. Завдання: 21224

Завдання 17 з 43

Функція $F(x)=5x^4-1$ є первісною функції $f(x).$ Укажіть функцію $G(x)$, яка також є первісною функції $f(x).$

А$G(x)=x^5-x$

Б$G(x)=5x^4-x$

В$G(x)=20x^3$

Г$G(x)=5x^4+1$

Д$G(x)=x^4-5$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Функції. Первісна.

Завдання перевіряє знання означення первісної функції.

Функція $F(x)=5x^4-1$ є первісною функції $f(x).$

Формула, яка задає всі первісні функції $f(x)$ $$ F(x)=5x^4+C, $$ де $C$ – будь-яке число.

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 400. Завдання: 19964

Завдання 18 з 43

Функція $F(x)=2x^3-1$ є первісною функції $f(x).$ Укажіть функцію $f(x).$

А$f(x)=6x^2-1$

Б$f(x)=6x-1$

В$f(x)=4x^2$

Г$f(x)=\frac{x^4}{2}-x$

Д$f(x)=6x^2$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Функції. Похідна функції. Первісна.

Завдання перевіряє вміння знаходити похідну функції, знання означення первісної.

$F(x)=2x^3-1.$

За означенням первісної $F'(x)=f(x).$

Отже, $f(x)=F'(x)=(2x^3-1)'=(2x^3)'-1'=6x^2-0=6x^2.$

Відповідь: Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 390. Завдання: 19504

Завдання 19 з 43

На рисунку зображено графіки функцій $y=\sqrt{x}$ та $y=\frac{x}{2}.$ Укажіть формулу для обчислення площі зафарбованої фігури.

А$S=\mathop{\int}\limits_0^2\left(\sqrt{x}-\frac x2\right)dx$

Б$S=\mathop{\int}\limits_0^2\left(\frac x2-\sqrt{x}\right)dx$

В$S=\mathop{\int}\limits_0^4\left(\sqrt{x}-\frac x2\right)dx$

Г$S=\mathop{\int}\limits_0^4\left(\frac x2-\sqrt{x}\right)dx$

Д$S=\mathop{\int}\limits_0^4\left(\frac x2+\sqrt{x}\right)dx$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Це завдання перевіряє вміння обчислювати площу плоских фігур за допомогою інтеграла.

Площу зафарбованої фігури знаходимо за допомогою визначеного інтеграла. Границі інтегрування – абсциси точок перетину графіків: $x=0$, $x=4.$ $$ S=\mathop{\int}\limits_0^4\left(\sqrt{x}-\frac x2\right)dx. $$

За правилом: від "верхньої" лінії віднімаємо "нижню", знаходимо площу зафарбованої фігури.

Відповідь: B.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 357. Завдання: 17659

Завдання 20 з 43

На рисунку зображено графіки функцій $y=f(x)$ i $y=g(x).$ Укажіть формулу для обчислення площі зафарбованої фігури.

А$S=\mathop{\int}\limits_1^4(f(x)-g(x))dx$

Б$S=\mathop{\int}\limits_1^4(g(x)-f(x))dx$

В$S=\mathop{\int}\limits_2^7(f(x)+g(x))dx$

Г$S=\mathop{\int}\limits_2^7(f(x)-g(x))dx$

Д$S=\mathop{\int}\limits_2^7(g(x)-f(x))dx$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Функції. Первісна та визначений інтеграл.

Це завдання перевіряє вміння обчислювати площу плоских фігур за допомогою інтеграла.

Якщо фігура обмежена графіками двох функцій, то границі інтегрування – точки їх перетину.

Функції $f(x)$ та $g(x)$ перетинаються в точках $x=2$ та $x=7$, отже межі інтегрування від $2$ до $7.$ У межах від $2$ до $7$ функція $f(x)$ лежить вище функції $g(x)$, отже, запишемо формулу для обчислення площі зафарбованої фігури: $$ S=\mathop{\int}\limits_2^7(f(x)-g(x))dx. $$

Отже, правильна відповідь Г.

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 346. Завдання: 17078

Завдання 21 з 43

На рисунку зображено графік непарної функції $y=f(x)$, визначеної на проміжку $[–5; 5].$ Яке з наведених співвідношень є справедливим для $f(x)$?

А$\mathop{\int}\limits_{-3}^0f(x)dx\lt 0$

Б$\mathop{\int}\limits_{0}^3f(x)dx\gt 0$

В$\mathop{\int}\limits_{-3}^3f(x)dx\lt 0$

Г$\mathop{\int}\limits_{-3}^3f(x)dx\gt 0$

Д$\mathop{\int}\limits_{-3}^3f(x)dx=0$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

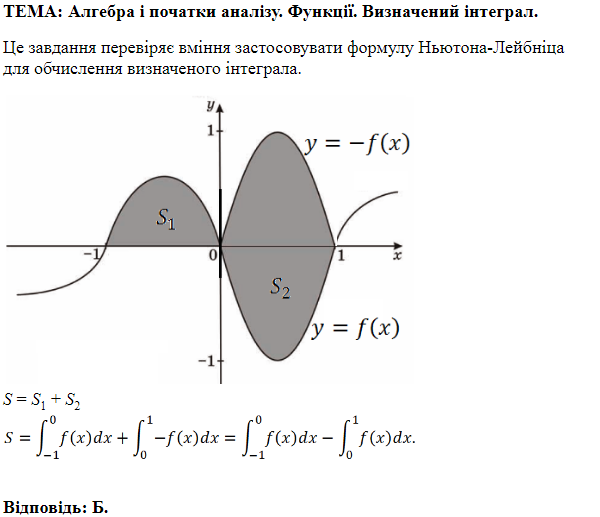
ТЕМА: Алгебра та початки аналізу. Функції. Первісна та визначений інтеграл. Застосування визначеного інтеграла до обчислення площ плоских фігур.

Це завдання перевіряє знання означення первісної функції, вміння обчислювати площу плоских фігур за допомогою інтеграла.

На рисунку зображено графік непарної функції $y=f(x).$

Функція інтегрована на симетричному проміжку $[-5; 5].$

Так як площі фігур розташованих вище та нижче осі $Ox$, рівні, то $$ \mathop{\int}\limits_{-3}^3f(x) dx=0. $$

Відповідь: Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 337. Завдання: 16617

Завдання 22 з 43

Знайдіть первісну функції $f(x)=2x+2$, графік якої проходить через точку з координатами $(1;4)$.

А$F(x)=x^2+2x$

Б$F(x)=x^2+2x+1$

В$F(x)=x^2+2x+2$

Г$F(x)=x^2+2x-4$

Д$F(x)=x^2+2x-23$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 296. Завдання: 14537

Завдання 23 з 43

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 292. Завдання: 14324

Завдання 24 з 43

Обчисліть площу зафарбованої фігури, зображеної на рисунку.

А$\frac 12$

Б$\frac{\sqrt{3}}{2}$

В$1$

Г$\sqrt{2}$

Д$\sqrt{3}$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Це завдання перевіряє вміння застосовувати формулу Ньютона-Лейбнiца для обчислення визначеного інтеграла.

$$ S_\text{ф}=\mathop{\int}\limits_0^{\frac{\mathbf{\pi}}{6}} 2\cos xdx=\left.2\sin x\right|_0^{\frac{\mathbf{\pi}}{6}}=2\sin\frac{\mathbf{\pi}}{6}-2\sin 0=2\cdot \frac 12-2\cdot 0=1. $$

Використали формулу Ньютона-Лейбніца:

$$ \mathop{\int}\limits_a^b f(x)dx=F(x)\left.\right|_a^b=F(b)-F(a). $$

Відповідь: B.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 290. Завдання: 14254

Завдання 25 з 43

Обчисліть інтеграл $ \mathop{\int}\limits_0^2(f(x)+6)dx, $ якщо $ \mathop{\int}\limits_0^2f(x)dx=8. $

А$20$

Б$14$

В$2$

Г$28$

Д$48$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Функції. Первісна та визначений інтеграл.

Це завдання перевіряє вміння застосовувати формулу Ньютона-Лейбніцa для обчислення визначеного інтеграла.

$$ \mathop{\int}\limits_{0}^2 f(x)dx=8. $$

За формулою Ньютона-Лейбніца:

\begin{gather*} \mathop{\int}\limits_{0}^2 f(x)dx=\left.F(x)\right|_0^2=F(2)-F(0)=8. \end{gather*}

Звідси,

\begin{gather*} \mathop{\int}\limits_{0}^2 (f(x)+6)dx=\left.F(x)+6x\right|_0^2=\\[6pt] =F(2)+6\cdot 2-F(0)-6\cdot 0=F(2)-F(0)+12=\\[6pt] =8+12=20. \end{gather*}

Відповідь: A.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 256. Завдання: 12519

Завдання 26 з 43

А$S=\mathop{\int}\limits_1^4 (f(x)-g(x))dx$

Б$S=\mathop{\int}\limits_1^4 (g(x)-f(x))dx$

В$S=\mathop{\int}\limits_2^7 (f(x)+g(x))dx$

Г$S=\mathop{\int}\limits_2^7 (f(x)-g(x))dx$

Д$S=\mathop{\int}\limits_2^7 (g(x)-f(x))dx$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Це завдання перевіряє вміння обчислювати площу плоских фігур за допомогою інтеграла.

Зафарбована фігура обмежена графіками функцій $y=g(x)$ та $y=f(x).$

Площу фігури знаходимо за допомогою визначеного інтегралу. Абсциси точок перетину графіків $x=2$ та $x=7$ – межі інтегрування.

Функція $y=f(x)$ приймає більші значення на заданому проміжку (обмежує фігуру згори), а $y=g(x)$ – менші значення (обмежує знизу).

Тому,

$$ S=\mathop{\int}\limits_2^7 (f(x)-g(x))dx. $$

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 221. Завдання: 10851

Завдання 27 з 43

Використовуючи формулу Ньютона - Лейбніца, обчисліть $\mathop{\int}\limits_1^2 6x^2dx.$

А$12$

Б$14$

В$18$

Г$22$

Д$42$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Функції. Первісна та визначений інтеграл. Формула Ньютона - Лейбніца.

Це завдання перевіряє знання таблиці первісних основних елементарних функцій та вміння застосовувати формулу Ньютона - Лейбніца для знаходження визначеного інтеграла.

За формулою Ньютона - Лейбніца:

$$ \mathop{\int}\limits_a^b f(x)dx=\left.F(x)\right|_a^b=F(b)-F(a), $$

де $F(x)$ – будь-яка первісна функції $f(x)$ на відрізку $[a; b].$

Нагадаємо, що функція $F(x)$ називається первісною для функції $f(x)$ на проміжку $(a; b)$, якщо для будь-якого $x\in (a; b)$ виконується рівність $F'(x)=f(x).$

Визначимо одну з первісних функції $y=6x^2.$

Правило знаходження первісних. Якщо $F_1(x)$ – первісна функції $f_1(x)$, а $\mathrm{C}$ – довільна стала, то $$ F(x)=\mathrm{C}F_1(x) $$ є первісною функції $$ f(x)=\mathrm{C}f_1(x). $$

Отже, $$ F(x)=6F_1(x) $$ є первісною функції $$ f(x)=6x^2, $$ де $F_1(x)$ – первісна функції $f_1(x)=x^2.$

Однією з первісних степеневої функції $x^n$, причому $n\ne -1$, є $$ \frac{x^{n+1}}{n+1}. $$ Тому $$ F_1(x)=\frac{x^{2+1}}{2+1}=\frac{x^3}{3}. $$ Отже, $$ F(x)=6\cdot \frac{x^3}{3}=2x^3. $$ Тоді

\begin{gather*} \mathop{\int}\limits_1^2 6x^2dx=\left.2x^3\right|_1^2=2\cdot (2^3-1^3)=14. \end{gather*}

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 191. Завдання: 9442

Завдання 28 з 43

Укажіть первісну $F(x)$ для функції $f(x)=\frac{1}{2x}.$

А$F(x)=\frac{1}{x^2}$

Б$F(x)=\frac{1}{2}\ln |x|$

В$F(x)=-\frac{1}{2x^2}$

Г$F(x)=2\ln |x|$

Д$F(x)=\ln |2x|$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Функції. Первісна.

Це завдання перевіряє вміння знаходити первісну раціональної функції.

Правило знаходження первісних. Якщо $F_1(x)$ – первісна для функції $f_1(x)$, а $C$ – довільна стала, то $F(x)=CF_1(x)$ є первісною для $Cf_1(x).$

У нашому випадку $$ f(x)=\frac{1}{2x}=\frac 12\cdot \frac 1x. $$

Оскільки функція $F_1(x)=\ln|x|$ є первісною для \begin{gather*} f_1(x)=\frac 1x,\ \text{то}\\[6pt] F(x)=\frac 12\ln|x| \end{gather*} є первісною для заданої функції $$ f(x)=\frac 12\cdot \frac 1x. $$

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 187. Завдання: 9250

Завдання 29 з 43

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 144. Завдання: 7183

Завдання 30 з 43

Визначте для функції $f(x)=2x+2$ первісну, графік якої проходить через точку $(1; 4).$

А$F(x)=2x^2+2x$

Б$F(x)=x^2+2x+1$

В$F(x)=x^2+2x+2$

Г$F(x)=x^2+2x-4$

Д$F(x)=2x^2+x+1$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Функції. Первісна.

Це завдання перевіряє вміння знаходити первісну раціональної функції, графік якої проходить через задану точку.

Нагадаємо, що функція $F(x)$ називається первісною для функції $f(x)$ на проміжку $(a; b)$, якщо для будь-якого $x \in (a; b)$ виконується рівність $F'(x) = f(x).$

Якщо $F(x)$ – первісна для функції $f(x)$, то для цієї функції існує безліч первісних і всі ці первісні мають вигляд $F(x) + C$, де $C \in R$ – довільна стала.

Правило знаходження первісних. Якщо $F_{1}(x)$ – первісна для функції $f_{1}(x)$, а $F_{2}(x)$ – первісна для функції $f_{2}(x)$, то $F_{1}(x) + F_{2}(x)$ є первісною для $f_{1}(x) + f_{2}(x).$

У нашому випадку $f_{1}(x) = 2x$, $f_{2}(x) = 2$, тоді $F_{1}(x) = x^{2}$, оскільки $(x^{2})' = 2x$, $F_{2}(x) = 2x$, оскільки $(2x)' = 2.$

Отже,

$$ F(x) = F_{1}(x) + F_{2}(x) + C = x^{2} + 2x + C $$

загальний вигляд первісної для функції $$ f(x) = 2x + 2, $$ де $C$ – довільна стала.

Якщо графік первісної $y = F(x)$ проходить через точку $(1; 4)$, то виконується умова $4 = F(1).$ Підставивши у рівняння первісної $$ F(x) = x^{2} + 2x + C $$ значення $x = 1$ і $F(1) = 4$, отримаємо: $$ 4 = 1 + 2 + C, $$ звідки $C = 1$. Отже, первісна функції $y = 2x + 2$, що проходить через точку $(1; 4)$, має вигляд $$ F(x) = x^{2} + 2x + 1. $$

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 142. Завдання: 7089

Завдання 31 з 43

На рисунку зображено ескіз графіка квадратичної функції $$ f(x)=ax^2+\frac{2b}{3}x+5. $$ Площа криволінійної трапеції, обмеженої лініями $y=f(x)$, $y=0$, $x=0$, $x=1$, дорівнює $21$ кв. од. Обчисліть суму $a+b.$

Впишіть відповідь:

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Функції. Визначений інтеграл. Площа криволінійної трапеції.

Це завдання перевіряє знання геометричного змісту визначеного інтеграла як площі криволінійної трапеції.

Площа криволінійної трапеції, обмеженої графіком функції $y=f(x)$, прямими $x=0$, $x=1$ і віссю $x$ (пряма $y=0$) (див. рисунок) дорівнює визначеному інтегралу:

$$ \mathop{\int}\limits_0^1 f(x)dx=\mathop{\int}\limits_0^1\left(ax^2+\frac{2b}{3}x+5\right)dx= \left(\frac{ax^3}{3}+\frac{bx^2}{3}+5x\right)\bigg|_0^1=\frac{a}{3}+\frac{b}{3}+5=\frac{a+b}{3}+5. $$

За умовою значення цього інтеграла дорівнює $21$ кв. од. Тоді $$ \frac{a+b}{3}+5=21, $$ звідки $a+b=48$.

Відповідь: $48.$

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 138. Завдання: 6903

Завдання 32 з 43

Впишіть відповідь:

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 131. Завдання: 6473

Завдання 33 з 43

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 129. Завдання: 6400

Завдання 34 з 43

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 127. Завдання: 6332

Завдання 35 з 43

Впишіть відповідь:

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 126. Завдання: 6311

Завдання 36 з 43

Обчисліть $$ \mathop{\int}\limits_{\frac{\pi}{6}}^{\frac{\pi}{2}} 5\mathrm{ctg}\ x\sin x\ dx. $$

Впишіть відповідь:

2.5

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра та початки аналізу. Функції. Первісна та визначений інтеграл.

Це завдання перевіряє вміння знаходити первісну, використовуючи її основні властивості, застосовувати формулу Ньютона – Лейбніца для обчислення визначеного інтеграла.

\begin{gather*} \mathop{\int}\limits_{\frac{\pi}{6}}^{\frac{\pi}{2}} 5\mathrm{ctg}\ x\cdot \sin x\ dx= \mathop{\int}\limits_{\frac{\pi}{6}}^{\frac{\pi}{2}} 5\cdot \frac{\cos x}{\sin x}\cdot \sin x\ dx=\\[6pt] =5\mathop{\int}\limits_{\frac{\pi}{6}}^{\frac{\pi}{2}} \cos x\ dx=\left. 5\sin x\right|_{\frac{\pi}{6}}^{\frac{\pi}{2}}=5\left(\sin \frac{\pi}{2}-\sin \frac{\pi}{6}\right)=\\[6pt] =5\left(1-\frac 12\right)=5\cdot \frac 12=2{,}5. \end{gather*}

Відповідь: $2{,}5.$

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 125. Завдання: 6273

Завдання 37 з 43

Впишіть відповідь:

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 124. Завдання: 6244

Завдання 38 з 43

Впишіть відповідь:

6.25

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 3. Завдання: 6207

Завдання 39 з 43

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 122. Завдання: 6145

Завдання 40 з 43

Впишіть відповідь:

38.5

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 121. Завдання: 6119

Завдання 41 з 43

Впишіть відповідь:

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 2. Завдання: 5344

Завдання 42 з 43

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 2. Завдання: 5316

Завдання 43 з 43

На рисунку зображено графік функції $y=f(x)$, визначеної на проміжку $[0; 11]$ та диференційовної на проміжку $(0; 11).$ Установіть відповідність між числом (1–4) та проміжком (А–Д), якому належить це число.

Число

1$f(8)$

2$f'(7)$

3найменше значення функції $y=f(x)$ на її області визначення

4$\int_1^3f(x)dx$

Проміжок

А$(-\infty; -2]$

Б$(-2; -0\mathord{,}5]$

В$(-0\mathord{,}5; 2]$

Г$(2; 4]$

Д$(4; +\infty]$

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3
4

Показати відповідь Читати пояснення

Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

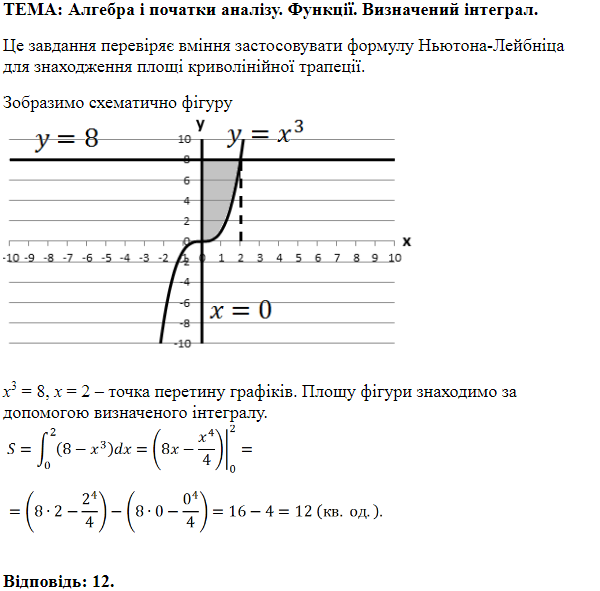
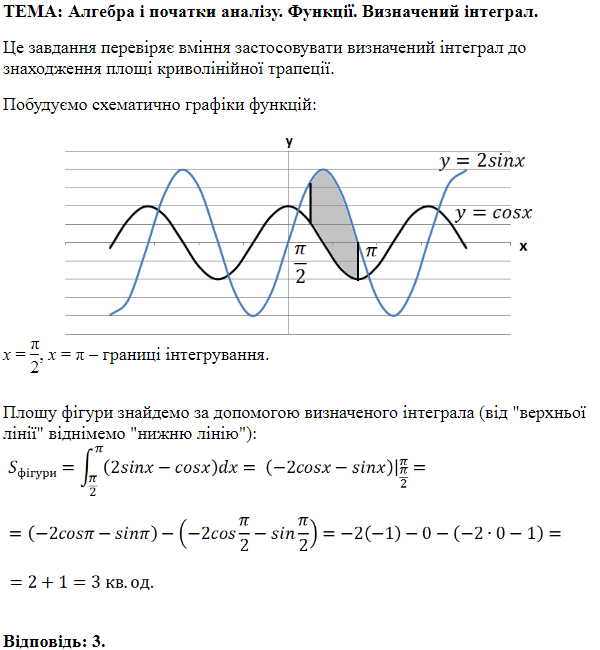
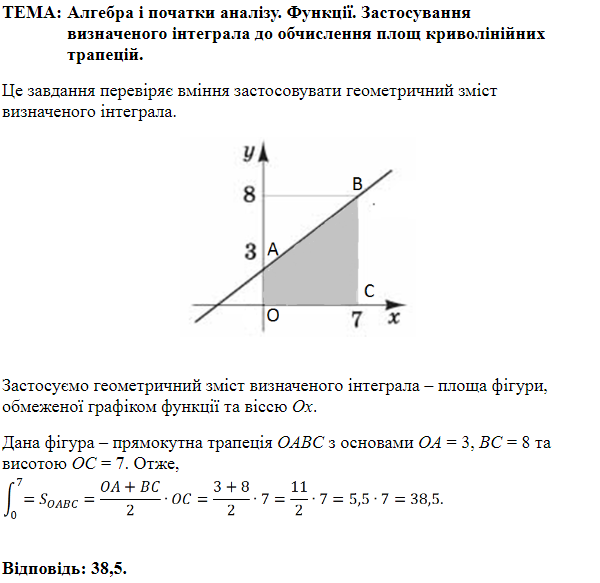
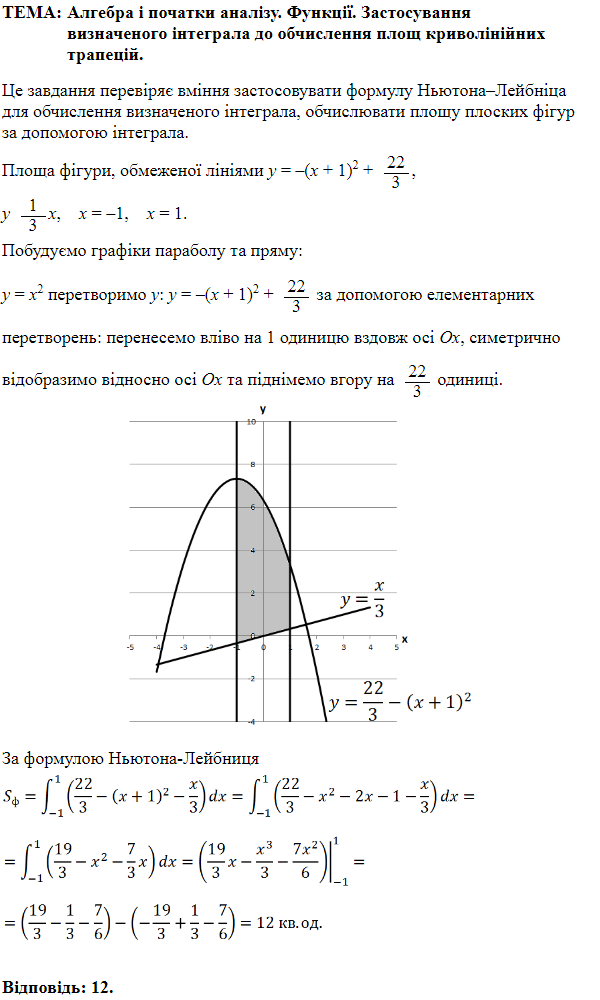
ТЕМА: Алгебра і початки аналізу. Функції.

Завдання перевіряє вміння визначати властивості функції за її графіком, а також розуміння геометричного змісту визначеного інтеграла.

1. При $x=8$ значення функції $f(8)=3\mathord{,}5.$
Число $3\mathord{,}5$ належить проміжку $(2; 4].$
Отже, 1 — Г.

2. Дотична до графіка функції $f(x)$ в точці $x=7$ паралельна осі $Ox.$
Тоді $f'(7)=k=\operatorname{tg}\ 90^\circ=0.$
Число $0$ належить проміжку $(-0\mathord{,}5; 2].$
Отже, 2 – B.

3. Найменше значення функції $f(x)$ на її області визначення дорівнює $f(0)=-3\mathord{,}5.$
Число $-3\mathord{,}5$ належить проміжку $(-\infty; -2].$
Отже, 3 – A.

4. Геометричний зміст визначеного інтеграла – площа криволінійної трапеції.
З рисунку бачимо, що $-2\lt \int_1^3f(x)dx\lt 0.$ Тобто $\int_1^3f(x)dx \in (-2; -0\mathord{,}5].$
Отже, 4 – Б.

Відповідь: 1 – Г, 2 – В, 3 – А, 4 – Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 1. Завдання: 4325

Новини

Вступ іноземців на бакалаврат в Україні
Коли та як реєструють електронний кабінет вступника у 2026 році
Як розрахувати конкурсний бал при вступі до вишу

Інформація

Усі завдання ЗНО з математики за темами
Усі тести ЗНО з математики онлайн
Завдання й відповіді ЗНО з математики минулих років
Усе про тест ЗНО з математики
Програма ЗНО з математики
Тести ЗНО онлайн з інших предметів
Дорожня карта учасника ЗНО
Дорожня карта вступника на бакалавра

Facebook

Twitter

Функція \(f(x)\)	Загальний вигляд первісних \(F(x)+C\), де \(C\) – довільна стала
\begin{gather}\frac 1x\end{gather}	\begin{gather}\ln\|x\|+C\end{gather}

\(x\)	\(y\)
\(0\)
	\(0\)
\(9\)

\(x\)	\(y\)
\(0\)	\(8\)
\(-4\)	\(0\)
\(9\)	\(26\)

Алгебра і початки аналізу – Первісна та визначений інтеграл