Показникові, логарифмічні, тригонометричні вирази та їхні перетворення – тести ЗНО/НМТ

Предмет: Алгебра і початки аналізу
Розділ: Числа і вирази
Тема: Показникові, логарифмічні, тригонометричні вирази та їхні перетворення
Кількість завдань: 113

123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113

Зачекайте, йде розрахунок...

Завдання 1 з 113

До виразу (1–3) доберіть множину (А – Д), якій належить значення цього виразу, якщо $a=5.$

Вираз

1$\log_{0{,}2} a$

2$2^{-a}$

3$\frac{10}{a}$

Множина

Амножина ірраціональних чисел

Бмножина натуральних чисел

Вмножина цілих від'ємних чисел

Гмножина раціональних нецілих чисел

Дмножина ірраціональних від'ємних чисел

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа та вирази. Дійсні числа.

Завдання скеровано на перевірку знання означення степеня з цілим показником та її властивості, тотожних перетворень раціональних та логарифмічних виразів.

1. $\log_{0{,}2} a=\log_{0{,}2} 5=\log_{\frac 15} 5=\log_{5^{-1}} 5=-1\cdot \log_5 5=-1.$

$-1$ є цілим від'ємним числом. Отже, 1 – B.

Застосували властивості логарифмів:

\begin{gather*} \log_a a=1;\\[7pt] \log_a b^n=n\log_a b;\\[6pt] \log_{a^k} b=\frac 1k\log_a b. \end{gather*}

2. $2^{-a}=2^{-5}=\dfrac{1}{2^5}=\dfrac{1}{32}.$

$\dfrac{1}{32}$ є раціональним числом, що не є цілим. Отже, 2 – Г.

Застосували властивість степенів:

\begin{gather*} a^{-n}=\frac{1}{a^n}\ \text{для}\ a\ne 0,\ n\in N. \end{gather*}

3. $\dfrac{10}{a}=\dfrac{10}{5}=2.$

$2$ є натуральним числом. Отже, 3 – Б.

Відповідь: 1 – В, 2 – Г, 3 – Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 737. Завдання: 37176

Завдання 2 з 113

$\log_3 \dfrac{1}{27}=$

А$\frac 19$

Б$\frac 13$

В$-\frac 13$

Г$-3$

Д$3$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Логарифмічні вирази.

Завдання скеровано на вміння використовувати степеневі властивості й основну логарифмічну тотожність для спрощення виразів.

Використаймо властивість степенів:

\begin{gather*} a^{-n}=\frac{1}{a^n}\ \text{для}\ a\ne 0,\ n\in N \end{gather*}

і логарифмічні тотожності:

\begin{gather*} \log_a b^n=n\cdot \log_a b;\\[7pt] \log_a a=1.\\[6pt] \log_3 \frac{1}{27}=\log_3 \frac{1}{3^3}=\log_3 3^{-3}=-3\cdot \log_3 3=-3\cdot 1=-3. \end{gather*}

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 737. Завдання: 37165

Завдання 3 з 113

Обчисліть $0{,}25^{\log_{0{,}5}4}.$

А$16$

Б$0{,}5$

В$0{,}25$

Г$4$

Д$2$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Логарифмічні вирази.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення логарифмічних виразів, знання властивостей логарифмів.

\begin{gather*} 0{,}25^{\log_{0{,}5} 4}=0{,}5^{2\log_{0{,}5} 4}=0{,}5^{\log_{0{,}5} 4^2}=0{,}5^{\log_{0{,}5} 16}=16. \end{gather*}

За властивістю логарифмів:

\begin{gather*} a^{\log_a b}=b;\\[7pt] \log_a b^n=n\cdot \log_a b. \end{gather*}

Відповідь: A.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 736. Завдання: 37111

Завдання 4 з 113

Який вираз тотожно рівний виразу $(\cos x-\sin x)^2$?

А$\cos 2x$

Б$1$

В$\cos 2x-\sin 2x$

Г$\cos 2x-1$

Д$1-\sin 2x$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Тригонометричні вирази.

Завдання перевіряє вміння виконувати тотожні перетворення тригонометричних виразів.

Спростiмо вираз за формулою квадрата різниці:

\begin{gather*} (a-b)^2=a^2-2ab+b^2;\\[7pt] (\cos x-\sin x)^2=\cos^2 x-2\sin x\cos x+\sin^2 x=\\[7pt] =(cos^2 x+\sin^2 x)-2\sin x\cos x=1-2\sin x\cos x=1-\sin 2x. \end{gather*}

Застосували основну тригонометричну тотожність $\sin^2 \alpha+\cos^2 \alpha =1$ і формулу подвійного кута $\sin 2x=2\sin x\cos x.$

Відповідь: Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 735. Завдання: 36915

Завдання 5 з 113

Доберіть на координатній прямій (див. рисунок) до виразу (1–3) точку (А – Д), координатою якої є значення цього виразу за $a=0{,}5.$

Вираз

1$|a-2{,}5|$

2$a^0$

3$\log_2 a$

Точка

А$K$

Б$L$

В$M$

Г$N$

Д$P$

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Числа і вирази. Дійсні числа. Логарифмічні та степеневі вирази.

Завдання перевіряє вміння обчислювати значення (модуль, степінь, логарифм) математичних виразів і визначати положення отриманих чисел на координатній прямій.

1. За властивістю модуля:

\begin{gather*} |a|=\left\{\begin{array}{l} a,\ \text{якщо}\ a\ge 0, \\ -a,\ \text{якщо}\ a\lt 0. \end{array}\right.\\[7pt] |0{,}5-2{,}5|=|-2|=2. \end{gather*}

Числу $2$ на прямій відповідає точка $P.$

Отже, 1 – Д.

2. $0{,}5^0=1.$ Числу $1$ на прямій відповідає точка $N.$

Отже, 2 – Г.

3. За властивістю логарифма:

\begin{gather*} \log_a a=1;\\[7pt] \log_a b^n=n\cdot \log_a b.\\[7pt] \log_2 0{,}5=\log_2 \frac 12=\log_2 2^{-1}=-1\log_2 2=-1. \end{gather*}

Числу $-1$ на прямій відповідає точка $L.$

Отже, 3 – Б.

Відповідь: 1 – Д, 2 – Г, 3 – Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 734. Завдання: 36605

Завдання 6 з 113

Визначте $\sin(180^\circ+\alpha)$, якщо $\sin \alpha=0{,}8.$

А$0{,}6$

Б$0{,}2$

В$-0{,}8$

Г$-0{,}6$

Д$0{,}8$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Тригонометричні вирази.

Завдання перевіряє вміння виконувати тотожні перетворення тригонометричних виразів і застосовувати формули зведення.

Використаймо формулу:

\begin{gather*} \sin(180^\circ+\alpha)=-\sin \alpha. \end{gather*}

Підставмо значення $\sin \alpha=0{,}8.$

Отже, $\sin(180^\circ+\alpha)=-0{,}8.$

Кут $(180^\circ+\alpha)$ розташований у III чверті тригонометричного кола.

У III чверті синус набуває від’ємного значення, тому поставлено знак мінус.

Відповідь: B.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 734. Завдання: 36596

Завдання 7 з 113

$|1-\lg 1000|=$

А$\lg 999$

Б$2$

В$4$

Г$-2$

Д$-\lg 999$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Логарифмічні вирази та перетворення їх.

Завдання скеровано на перевірку знання означення та властивостей логарифма, модуля числа.

За означенням логарифма:

\begin{gather*} \log_{10}a=\lg a;\\[7pt] 1=\lg 10. \end{gather*}

За властивістю логарифмів:

\begin{gather*} \log_a \frac bc=\log_a b-\log_a c;\\[6pt] \log_a a=1;\\[7pt] \log_a b^n=n\cdot \log_a b;\\[6pt] |1-\lg 1000|=|\lg 10-\lg 1000|=\left|\lg\frac{10}{10000}\right|=\left|\lg\frac{1}{100}\right|=\\[6pt] =|\lg 10^{-2}|=|-2\cdot \lg 10|=|-2\cdot 1|=2. \end{gather*}

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 733. Завдання: 36389

Завдання 8 з 113

До кожного початку речення (1–3) доберіть його закінчення (А – Д) так, щоб утворилося правильне твердження, якщо $m$ i $n$ – натуральні числа, $n\gt 1$, $m\gt 1.$

Початок речення

1Якщо $n\sin m\pi=a$, то

2Якщо $\frac{2^m}{2^n}=2^a$, то

3Якщо $\sqrt[n]{\sqrt[m]{2}}=\sqrt[a]{2}$, то

Закінчення речення

А$a=mn.$

Б$a=0.$

В$a=m-n.$

Г$a=n.$

Д$a=\frac mn.$

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Дійсні числа та дії з ними.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення тригонометричних, ірраціональних виразів, степеня з натуральним показником.

1. Якщо $n\sin m\pi=a$, то...

Для будь-якого цілого числа $k\ \sin k\pi=0.$ Оскільки $m$ – натуральне число, то $\sin m\pi$ завжди дорівнює нулю. Тоді $a=n\cdot 0=0.$

Отже, правильна відповідь – Б.

2. Якщо $\frac{2^m}{2^n}=2^a$, то...

Скористаймося властивістю $\frac{a^x}{a^y}=a^{x-y}{:}$

\begin{gather*} \frac{2^m}{2^n}=2^{m-n}=2^a. \end{gather*}

Звідси $a=m-n.$

Отже, правильна відповідь – B.

3. Якщо $\sqrt[n]{\sqrt[m]{2}}=\sqrt[a]{2}$, то...

Скористаймося властивістю $\sqrt[n]{\sqrt[m]{x}}=\sqrt[n\cdot m]{x}\ \ {:}$

\begin{gather*} \sqrt[n]{\sqrt[m]{2}}=\sqrt[n\cdot m]{2}\ \ ;\\[7pt] \sqrt[n\cdot m]{2}=\sqrt[a]{2}. \end{gather*}

Звідси $a=n\cdot m=mn.$

Отже, правильна відповідь – A.

Відповідь: 1 – Б, 2 – В, 3 – А.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 732. Завдання: 36362

Завдання 9 з 113

До кожного початку речення (1–3) доберіть його закінчення (А – Д) так, щоб утворилося правильне твердження.

Початок речення

1Якщо $3^m\cdot 9^n=3^a$, то

2Якщо $(m+n)^2-m^2-n^2=a$, то

3Якщо $\log_3 27^{mn}=a$, то

Закінчення речення

А$a=0.$

Б$a=27^{mn}.$

В$a=3mn.$

Г$a=2mn.$

Д$a=m+2n.$

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа.

Завдання скеровано на перевірку знання властивостей степенів із цілим показником, тотожних перетворень раціональних і логарифмічних виразів.

1. Оскільки $9=3^2$, то

\begin{gather*} 3^m\cdot 9^n=3^m\cdot (3^2)^n=3^m\cdot 3^{2n}=3^{m+2n};\\[7pt] 3^{m+2n}=3^a. \end{gather*}

Отже, $a=m+2n.$ Правильна відповідь – Д.

2. Скористаймося формулою скороченого множення:

\begin{gather*} (a+b)^2=a^2+2ab+b^2;\\[7pt] (m+n)^2-m^2-n^2=m^2+2mn+n^2-m^2-n^2=2mn. \end{gather*}

Отже, $a=2mn.$ Правильна відповідь – Г.

3. Скористаймося властивостями логарифма:

\begin{gather*} \log_a b^n=n\cdot \log_a b;\\[7pt] \log_a a=1;\\[7pt] \log_3 27^{mn}=mn\cdot \log_3 27=mn\cdot \log_3 3^3=mn\cdot 3\log_3 3=3mn. \end{gather*}

Отже, $a=3mn.$ Правильна відповідь – B.

Відповідь: 1 – Д, 2 – Г, 3 – В.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 731. Завдання: 36340

Завдання 10 з 113

$\lg 25 + \lg 40 =$

А$1$

Б$\lg 65$

В$2$

Г$3$

Д$4$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа та вирази. Логарифмічні вирази.

Завдання скеровано на перевірку знання властивостей логарифмів, уміння виконувати тотожні перетворення логарифмічних виразів.

\begin{gather*} \lg 25+\lg 40=\lg (25\cdot 40)=\lg 1000=\lg 10^3=3\lg 10=3. \end{gather*}

Застосуймо властивості логарифмів:

\begin{gather*} \log_{10} a=\lg a;\\[7pt] \log_a a=1;\\[7pt] \log_a b^n=n\log_a b;\\[7pt] \log_a (b\cdot c)=\log_a b+\log_a c. \end{gather*}

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 731. Завдання: 36327

Завдання 11 з 113

Обчисліть $$ \frac{\sin\left(\frac{3\pi}{2}-\alpha\right)}{\cos \alpha}= $$

А$1$

Б$-\mathrm{tg}\ \alpha$

В$\frac{1}{\mathrm{tg}\ \alpha}$

Г$\mathrm{tg}\ \alpha$

Д$-1$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Тригонометричні вирази.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення тригонометричних виразів.

Спростімо за формулою зведення:

\begin{gather*} \sin \left(\frac{3\pi}{2}-\alpha\right)=-\cos \alpha. \end{gather*}

Підставмо у вираз:

$$ \frac{\sin\left(\frac{3\pi}{2}-\alpha\right)}{\cos \alpha}=-\frac{\cos \alpha}{\cos \alpha}=-1. $$

Відповідь: Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 703. Завдання: 35804

Завдання 12 з 113

$\mathrm{tg}^2\ \alpha\cos^2 \alpha+\cos^2 \alpha=$

А$\sin^2 \alpha$

Б$\cos 2\alpha$

В$\cos^2 \alpha$

Г$1$

Д$\mathrm{tg}^2\ \alpha$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Тригонометричні вирази.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення тригонометричних виразів.

Спростімо за формулами:

\begin{gather*} \mathrm{tg}\ \alpha=\frac{\sin \alpha}{\cos \alpha},\\[6pt] \sin^2 \alpha+\cos^2 \alpha=1,\\[6pt] \mathrm{tg}^2\ \alpha\cdot \cos^2 \alpha+\cos^2 \alpha=\frac{\sin^2 \alpha}{\cos^2 \alpha}\cdot \cos^2 \alpha+\cos^2 \alpha=\sin^2 \alpha+\cos^2 \alpha=1. \end{gather*}

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 702. Завдання: 35783

Завдання 13 з 113

Обчисліть $0\mathord{,}25^{\log_{0\mathord{,}5}4}.$

А$16$

Б$0\mathord{,}5$

В$0\mathord{,}25$

Г$4$

Д$2$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Логарифмічні вирази.

\begin{gather*} 0\mathord{,}25^{\log_{0\mathord{,}5}4}=0\mathord{,}5^{2\log_{0\mathord{,}5}4}=0\mathord{,}5^{\log_{0\mathord{,}5}4^2}=0\mathord{,}5^{\log_{0\mathord{,}5}16}=16. \end{gather*}

За властивістю логарифмів:

\begin{gather*} a^{\log_a b}=b,\\[7pt] \log_a b^n=n\cdot \log_a b. \end{gather*}

Відповідь: A.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 702. Завдання: 35782

Завдання 14 з 113

Узгодьте вираз (1–3) із його значенням (А – Д).

1$\frac{3}{3^{-3}}$

2$\log_8\sqrt[3]{2}$

3$2(\cos 30^\circ-0\mathord{,}5)(\cos 30^\circ+0\mathord{,}5)$

А$1$

Б$\frac 19$

В$\sqrt{3}$

Г$3$

Д$81$

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Дійсні числа. Раціональні, ірраціональні, тригонометричні й логарифмічні числа.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення степеневих, логарифмічних і тригонометричних виразів.

1. За властивістю степенів: $$ a^n:a^m=a^{n-m}, $$

$$ \frac{3}{3^{-3}}=3\cdot 3^{3}=3^{1+3}=3^4=81. $$

Отже, правильна відповідь – Д.

2. За властивістю логарифмів:

\begin{gather*} \log_{a^m}b=\frac 1m\cdot \log_ab,\\[6pt] \log_ab^n=n\cdot \log_ab. \end{gather*}

Отже,

\begin{gather*} \log_8\sqrt[3]{2}=\log_{2^3}2^{\frac 13}=\frac 13\cdot \frac 13\cdot\log_2 2=\frac 19\cdot 1=\frac 19. \end{gather*}

Правильна відповідь – Б.

3. Спростiмо вираз за формулою різниці квадратів: $$ (a-b)(a+b)=a^2-b^2. $$ $\cos 30^\circ=\frac{\sqrt{3}}{2}$ – табличне значення.

\begin{gather*} 2(\cos 30^\circ-0\mathord{,}5)(\cos 30^\circ+0\mathord{,}5)=2(\cos^2 30^\circ-0\mathord{,}5^2)=\\[6pt] =2\left(\left(\frac{\sqrt{3}}{2}\right)^2-\frac 14\right)=2\left(\frac 34-\frac 14\right)=2\cdot \frac 24=1. \end{gather*}

Отже, правильна відповідь – A.

Відповідь: 1 – Д, 2 – Б, 3 – A.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 701. Завдання: 35381

Завдання 15 з 113

Обчисліть значення виразу $5(1-\cos^2 \mathbf{\beta})$, якщо $\sin \mathbf{\beta}=0\mathord{,}8.$

А$3\mathord{,}2$

Б$1$

В$2$

Г$1\mathord{,}8$

Д$4$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Тригонометричні вирази.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення тригонометричних виразів, обчислювати їхнє значення.

За основною тригонометричною тотожністю:

\begin{gather*} \sin^2 \mathbf{\beta}+\cos^2 \mathbf{\beta}=1,\\[7pt] 1-\cos^2 \mathbf{\beta}=\sin^2 \mathbf{\beta}=0\mathord{,}8^2=0\mathord{,}64. \end{gather*}

Обчислімо значення виразу:

\begin{gather*} 5(1-\cos^2 \mathbf{\beta})=5\cdot 0\mathord{,}64=3\mathord{,}2. \end{gather*}

Відповідь: A.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 701. Завдання: 35374

Завдання 16 з 113

$4\sin 450^\circ+\operatorname{tg} 135^\circ=$

А$-3$

Б$-5$

В$3$

Г$-1$

Д$5$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Тригонометричні вирази.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення тригонометричних виразів, уміння визначати їхні числові значення.

Функція $y=\sin x$ періодична з найменшим додатним періодом $T=2\mathbf{\pi}.$ За означенням періодичної фукнції:

\begin{gather*} f(x)=f(x\pm T),\\[7pt] 2\mathbf{\pi}=360^\circ,\\[7pt] \sin 450^\circ=\sin(360^\circ+90^\circ)=\sin 90^\circ=1,\\[7pt] \operatorname{tg}\ 135^\circ=\operatorname{tg} (180^\circ-45^\circ)=-\operatorname{tg} 45^\circ=-1. \end{gather*}

Застосували формулу $\operatorname{tg}\ (180^\circ-\mathbf{\alpha})=-\operatorname{tg}\ \mathbf{\alpha}.$

Отже,

$$ 4\sin 450^\circ+\operatorname{tg}\ 135^\circ=4\cdot 1+(-1)=4-1=3. $$

Відповідь: B.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 700. Завдання: 35357

Завдання 17 з 113

$\log_55^{10}=$

А$1$

Б$2$

В$10$

Г$50$

Д$5$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Логарифмічні вирази та їх перетворення.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення логарифмічних виразів, знання означення та властивостей логарифма.

За властивістю логарифма: $$ \log_ab^n=n\log_ab\mathord{;} $$ $$ \log_aa=1. $$

Спростімо вираз:

\begin{gather*} \log_5 5^{10}=10\log_5 5=10\cdot 1=10. \end{gather*}

Відповідь: B.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 700. Завдання: 35353

Завдання 18 з 113

Якому проміжку належить значення виразу $6\sin 15^\circ\cos 15^\circ$?

А$[0; 1)$

Б$[1; 2)$

В$[2; 3)$

Г$[3; 5)$

Д$[5; 6]$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Тригонометричні вирази та їх перетворення.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення тригонометричних виразів, обчислення їхнього значення за заданих значень змінних.

Застосуймо формулу подвійного аргумента $$ \sin 2\mathbf{\alpha}=2\sin \mathbf{\alpha}\cos \mathbf{\alpha} $$ для спрощення виразу:

\begin{gather*} 6\sin 15^\circ\cos 15^\circ=3\cdot (2\sin 15^\circ\cos 15^\circ)=\\[6pt] =3\sin 30^\circ=3\cdot \frac 12=1\mathord{,}5. \end{gather*}

Значення виразу належить проміжку $[1; 2).$

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 699. Завдання: 35333

Завдання 19 з 113

$|\lg 50-2|=$

А$\lg 2$

Б$\lg 0\mathord{,}5$

В$\lg 48$

Г$\lg 25$

Д$\lg 5$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Логарифмічні вирази та їх перетворення.

Завдання скеровано на перевірку знання означення та властивостей логарифма, модуля числа.

За означенням логарифма: $$ 2=\lg 100. $$

За властивістю логарифмів:

\begin{gather*} \log_a\frac bc=\log_ab-\log_ac\\[6pt] |\lg50-\lg100|=|\lg\frac{50}{100}|=|\lg\frac 12|=|\lg 0\mathord{,}5|=-\lg 0\mathord{,}5=-\lg \frac 12=-\lg 2^{-1}=\lg 2. \end{gather*}

Відповідь: A.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 698. Завдання: 35306

Завдання 20 з 113

Узгодьте вираз (1-3) та проміжок (А – Д), якому належить його значення, де $\mathbf{\varphi}=\frac{\sqrt{5}+1}{2}$ – відома математична величина, яку називають золотим числом.

Вираз

1$\mathbf{\varphi}^0$

2$(\sqrt{5}-1)\cdot \mathbf{\varphi}$

3$\log_{\frac 15}(2\mathbf{\varphi}-1)$

Проміжок

А$(-\infty; -1]$

Б$(-1; 0]$

В$(0; 1]$

Г$(1; 2]$

Д$(2; +\infty)$

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Дійсні числа та дії з ними.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення ірраціональних, логарифмічних та степеневих виразів.

1. $\mathbf{\varphi}^0=\left(\frac{\sqrt{5}+1}{2}\right)^0=1\in (0; 1].$

Отже, правильна відповідь – B.

2. $(\sqrt{5}-1)\cdot \frac{\sqrt{5}+1}{2}=\frac{(\sqrt{5}-1)(\sqrt{5}+1)}{2}=\frac{5-1}{2}=2\in (1; 2].$

Отже, правильна відповідь – Г.

\begin{gather*} \log_{\frac 15}(2\mathbf{\varphi}-1)=\log_{\frac 15}\left(2\cdot \frac{\sqrt{5}+1}{2}-1\right)=\\[6pt] =\log_{\frac 15}(\sqrt{5}+1-1)=\log_{\frac 15}\sqrt{5}=\log_{5^{-1}}5^{\frac 12}=\\[6pt] =-1\cdot \frac 12\cdot \log_55=-\frac 12\cdot 1=-0\mathord{,}5\in (-1; 0]. \end{gather*}

Отже, правильна відповідь – Б.

При спрощенні виразу застосовували формули:

\begin{gather*} \log_ab^n=n\cdot \log_ab,\\[6pt] \log_{a^k}b=\frac 1k\log_ab,\\[6pt] \log_aa=1. \end{gather*}

Відповідь: 1В, 2Г, 3Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 672. Завдання: 34411

Завдання 21 з 113

Визначте найбільше значення $a$, за якого рівняння $$ \frac{3^{2a-5x+2}-\sqrt{27}}{\sqrt{x}+\sqrt{3-x}}=0 $$ має корінь.

Впишіть відповідь:

7.25

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Розв’язування показникових, раціональних рівнянь.

Завдання скеровано на перевірку вміння розв’язувати показникові, раціональні і ірраціональні рівняння й нерівності та їх системи з параметрами.

1. Область допустимих значень

\begin{gather*} \left\{ \begin{array}{l} x\ge 0,\\ 3-x\ge 0,\\ \sqrt{x}+\sqrt{3-x}\ne 0, \end{array} \right.\\[7pt] \left\{ \begin{array}{l} x\ge 0,\\ x\le 3. \end{array} \right.\\[7pt] x\in [0; 3]. \end{gather*}

2. Розв'яжемо рівняння:

\begin{gather*} 3^{2a-5x+2}-\sqrt{27}=0,\\[7pt] 3^{2a-5x+2}=3\sqrt{3},\\[7pt] 3^{2a-5x+2}=3^{1\mathord{,}5},\\[7pt] 2a-5x+2=1\mathord{,}5,\\[7pt] 5x=2a+0\mathord{,}5,\\[7pt] x=0\mathord{,}4a+0\mathord{,}1. \end{gather*}

Для того, щоб рівняння мало корінь

\begin{gather*} 0\le 0\mathord{,}4a+0\mathord{,}1\le 3,\\[7pt] -0\mathord{,}1\le 0\mathord{,}4a\le 2\mathord{,}9,\\[6pt] -\frac 14\le a\le \frac{29}{4},\\[6pt] -\frac 14\le a\le 7\frac 14. \end{gather*}

Найбільше значення $a=7\frac 14=7\mathord{,}25.$

Відповідь: $7\mathord{,}25.$

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 671. Завдання: 34394

Завдання 22 з 113

Доберіть до числового виразу (1-3) його значення (А – Д).

Числовий вираз

1$\sin\left(-\frac{\mathbf{\pi}}{6}\right)$

2$\mathbf{\pi}-|\mathbf{\pi}+2|$

3$\left(-\frac{1}{\sqrt{2}}\right)^2$

Значення виразу

А$\frac 12$

Б$-2$

В$2$

Г$-\frac 12$

Д$\sqrt{2}$

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Дійсні числа та дії з ними.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення тригонометричних, ірраціональних виразів, знання модуля числа та його властивостей.

1. $\sin \left(-\frac{\mathbf{\pi}}{6}\right)=-\sin\frac{\mathbf{\pi}}{6}=-\frac 12.$

$y=\sin x$ – непарна, тому

$\sin(x)=-\sin x.$

Отже, правильна відповідь – Г.

2. $\mathbf{\pi}-|\mathbf{\pi}+2|=\mathbf{\pi}-(\mathbf{\pi}+2)=\mathbf{\pi}-\mathbf{\pi}-2=-2.$

Отже, правильна відповідь – Б.

3. $\left(-\frac{1}{\sqrt{2}}\right)^2=\left(\frac{1}{\sqrt{2}}\right)^2=\frac 12.$

Отже, правильна відповідь – A.

Відповідь: 1Г, 2Б, 3A.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 671. Завдання: 34389

Завдання 23 з 113

$\log_55^{10}=$

А$5$

Б$10$

В$50$

Г$5^{10}$

Д$10^{5}$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Логарифмічні вирази.

Завдання скеровано на перевірку знання означення та властивостей логарифмів.

$$ \log_55^{10}=10\cdot \log_55=10\cdot 1=10. $$

Застосували властивості логарифмів:

\begin{gather*} \log_ab^n=n\log_ab,\\[7pt] \log_aa=1. \end{gather*}

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 671. Завдання: 34381

Завдання 24 з 113

$2\log_63+\log_64=$

А$\log_610$

Б$\log_624$

В$\log_613$

Г$2$

Д$6$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення логарифмічних виразів.

\begin{gather*} 2\log_6 3+\log_6 4=\log_6 3^2+\log_6 4=\\[7pt] =\log_6 9+\log_6 4=\log_6(9\cdot 4)=\log_6 36=2. \end{gather*}

Застосували властивості логарифмів: \begin{gather*} \log_a b^n=n\log_a b,\\[7pt] \log_{a}(b\cdot c)=\log_a b+\log_a c. \end{gather*}

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 606. Завдання: 28388

Завдання 25 з 113

Узгодьте вираз (1–3) з твердженням (А – Д) про його значення, якщо $a=3.$

Вираз

1$a^{-1}$

2$a^0$

3$\sin(\mathbf{\pi}a)$

Твердження про значення виразу

Ає раціональним числом, що не є цілим

Бє натуральним числом

Вє цілим від’ємним числом

Гє ірраціональним числом

Ддорівнює $0$

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання скеровано на перевірку знання означення степеня з цілим показником та її властивості, означення синуса.

1. $a^{-1}=\frac 1a=\frac 13$ є раціональним числом, що не є цілим. Отже, правильна відповіль – А.

2. $a^0=1$ є натуральним числом. Отже, правильна відповіль – Б.

3. $\sin(\mathbf{\pi}a)=\sin(3\mathbf{\pi})=\sin(2\mathbf{\pi}+\mathbf{\pi})=\sin\mathbf{\pi}=0.$

$y=\sin x$ – періодична функція з найменшим додатним періодом $2\mathbf{\pi}.$ Отже, правильна відповіль – Д.

Відповідь: 1А, 2Б, 3Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 585. Завдання: 28370

Завдання 26 з 113

Укажіть проміжок, якому належить значення виразу $\log_{0,2}125.$

А$(-\infty;\ -3)$

Б$[-3;\ 0)$

В$[0;\ 3)$

Г$[3;\ 25)$

Д$[25;\ +\infty)$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення логарифмічних виразів.

\begin{gather*} \log_{0,2}125=\log_{\frac 15}5^3=\log_{5^{-1}}5^3=\\[6pt] =-1\cdot 3\log_5 5=-3\in [-3; 0). \end{gather*}

Застосували властивості логарифмів: $$ \log_a b^n=n\log_a b,\ \ \log_{a^k}b=\frac 1k\log_ab. $$

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 585. Завдання: 28366

Завдання 27 з 113

Розкладіть вираз $4x^2-144$ на множники.

А$(2x-12)(2x+12)$

Б$(2x-72)(2x+72)$

В$(2x-12)^2$

Г$(2x-72)^2$

Д$2(x-6)(x+6)$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання скеровано на перевірку знання формул скороченого множення, вміння виконувати тотожні перетворення раціональних виразів.

За формулою скороченого множення $a^2-b^2=(a-b)(a+b)$ розкладемо на множники:

$$ 4x^2-144=(2x)^2-12^2=(2x-12)(2x+12). $$

Отже, правильна відповідь – A.

Відповідь: A.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 585. Завдання: 28356

Завдання 28 з 113

Установіть відповідність між виразом (1–3) і тотожно рівним йому виразом (А – Д), якщо $a$ – довільне додатне число, $a\ne 1.$

Вираз

1$a^4 : a^3$

2$\frac{a^2-a}{1-a}$

3$7^{-\log_7 a}$

Тотожно рівний вираз

А$a^2$

Б$a^7$

В$\frac 1a$

Г$-a$

Д$a$

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа.

Завдання скеровано на перевірку знання властивостей степенів з цілим показником, тотожних перетворень раціональних та логарифмічних виразів.

1. $a^4:a^3=a^{4-3}=a^1=a.$ Отже, правильна відповіль – Д.

2. $$ \frac{a^2-a}{1-a}=\frac{a(a-1)}{-(a-1)}=\frac{a}{-1}=-a. $$ Отже, правильна відповідь – Г.

3. $$ 7^{-\log_7 a}=7^{\log_7 a^{-1}}=a^{-1}=\frac 1a. $$ Застосували правила \begin{gather*} a^{-n}=\frac{1}{a^n},\\[6pt] \log_a b^n=n\cdot \log_a b,\\[7pt] a^{\log_a b}=b. \end{gather*} Отже, правильна відповідь – B.

Відповідь: 1Д, 2Г, 3B.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 570. Завдання: 27701

Завдання 29 з 113

Доберіть до числового виразу (1–3) рівний йому за значенням вираз (А – Д).

Вираз

1$\frac{1}{\sqrt{10}-3}$

2$|3-\sqrt{10}|$

3$\log_5{125}$

Вираз

А$\sqrt{10}-3$

Б$3-\sqrt{10}$

В$\sqrt{10}+3$

Г$3$

Д$25$

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Дійсні числа та дії з ними.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення ірраціональних, логарифмічних виразів, уміння використовувати властивості модуля числа.

Спростімо вирази:

1. – В. $\frac{1}{\sqrt{10}-3}=\frac{\sqrt{10}+3}{(\sqrt{10}-3)(\sqrt{10}+3)}=\frac{\sqrt{10}+3}{10-9}=\sqrt{10}+3.$

2. – A. $|3-\sqrt{10}|=\sqrt{10}-3.$ Вираз $3-\sqrt{10}\lt 0,$ тому $|3-\sqrt{10}|=-(3-\sqrt{10})=-3+\sqrt{10}.$

3. – Г. $\log_5125=\log_55^3=3\log_55=3.$

Відповідь: 1В, 2А, 3Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 547. Завдання: 26840

Завдання 30 з 113

Укажіть вираз, тотожно рівний виразу $(\cos x-\sin x)^2.$

А$\cos 2x$

Б$\cos 2x-\sin 2x$

В$\cos 2x-1$

Г$1-\sin 2x$

Д$1$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання перевіряє вміння виконувати тотожні перетворення тригонометричних виразів.

\begin{gather*} (\cos x-\sin x)^2=\cos^2x-2\cos x\cdot \sin x+\sin^2 x=\\[7pt] =1-2\sin x\cos x=1-\sin 2x. \end{gather*}

Застосували формули скороченого множення $$ (a-b)^2=a^2-2ab+b^2 $$ та тригонометрії

\begin{gather*} \sin^2\mathbf{\alpha}+\cos^2\mathbf{\alpha}=1\\[7pt] \sin 2\mathbf{\alpha}=2\sin\mathbf{\alpha}\cos\mathbf{\alpha}. \end{gather*}

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 547. Завдання: 26837

Завдання 31 з 113

До початку речення (1–3) доберіть закінчення (А – Д) так, щоб утворилося правильне твердження, якщо $n$ – натуральне число.

Початок речення

1Якщо $\frac na = 3,$ то

2Якщо $1 + \log_3n = \log_3a,$ то

3Якщо $3^n\cdot 3 = 3^a,$ то

Закінчення речення

А$a=3n.$

Б$a=n+1.$

В$a=n+3.$

Г$a=\frac 3n$

Д$a=\frac n3$

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання перевіряє вміння виконувати тотожні перетворення раціональних, логарифмічних та степеневих виразів.

1. Якщо $\frac na=3,$ то $a=\frac n3$ – Д.

2. Якщо $1+\log_3n=\log_3a,$ то $\log_33+\log_3n=\log_3a,$ $\log_3(3n)=\log_3a,\ 3n=a$ – A.

3. Якщо $3^n\cdot 3=3^a,$ то $3^{n+1}=3^a,\ n+1=a.$ – Б.

Застосували властивості логарифмів та степенів:

\begin{gather*} \log_aa=1,\ \ \log_ab+\log_ac=\log_a(b\cdot c),\\[7pt] a^n\cdot a^m=a^{n+m}. \end{gather*}

Відповідь: 1Д, 2А, 3Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 546. Завдання: 26815

Завдання 32 з 113

Обчисліть значення виразу $\log_2{(8a)},$ якщо $\log_2{a}=4.$

А6

Б7

В5

Г8

Д12

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання перевіряє вміння виконувати тотожні перетворення логарифмічних виразів.

$$ \log_2(8a)=\log_28+\log_2a=3+4=7. $$

Застосували властивість логарифма $$ \log_a(b\cdot c)=\log_ab+\log_ac. $$

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 523. Завдання: 26191

Завдання 33 з 113

Обчисліть значення виразу $4\sin^2\alpha,$ якщо $4\cos^2\alpha = 1.$

А$0$

Б$\frac 14$

В$\frac 34$

Г$3$

Д$4$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Перевіряє вміння виконувати тотожні перетворення тригонометричних виразів.

$$ 4\cos^2 \alpha=1,\ \ \cos^2\alpha=\frac 14. $$

За основною тригонометричною тотожністю: \begin{gather*} \sin^2\alpha+\cos^2\alpha=1,\\[7pt] \sin^2\alpha=1-\cos^2\alpha=1-\frac 14=\frac 34. \end{gather*} Отже, $$ 4\sin^2\alpha = 4\cdot \frac 34 = 3. $$

Відповідь: Г

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 521. Завдання: 26127

Завдання 34 з 113

$\log_5 49+2\log_5\frac 57=$

А$25$

Б$\log_5 70$

В$\log_5 49\frac 57$

Г$\log_5 35$

Д$2$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Перевіряє вміння виконувати тотожні перетворення логарифмічних виразів.

\begin{gather*} \log_5 49+2\log_5\frac 57=\\[6pt] =\log_5 49+\log_5\left(\frac 57\right)^2=\\[6pt] =\log_5 49+\log_5\frac{25}{49}=\\[6pt] =\log_5\left(49\cdot \frac{25}{49}\right)=\log_5 25=2. \end{gather*}

При розв'язанні застосували властивості логарифмів:

\begin{gather*} \log_a b^n=n\log_a b\ (b\gt 0)\\[7pt] \log_a b+\log_a c=\log_a(b\cdot c). \end{gather*}

Відповідь: Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 521. Завдання: 26122

Завдання 35 з 113

Скоротіть дріб $\frac{10ab^3}{5a^2b}.$

А$\frac{2b^2}{a}$

Б$\frac{b^4}{2a^3}$

В$50a^3b^4$

Г$\frac{2b^4}{a^3}$

Д$\frac{b^2}{a^2}$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Перевіряє вміння виконувати тотожні перетворення раціональних виразів, властивості степенів.

$$ \frac{10ab^3}{5a^2b}=\frac{2b^2}{a} $$

Скоротили дріб використовуючи властивість степенів: \begin{gather*} a^n:a^m=a^{n-m}. \end{gather*}

Відповідь: A.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 521. Завдання: 26120

Завдання 36 з 113

У якому рядку числа $\log_2{64},\ \log_{64}{2},\ 11$ розташовано за зростанням?

А$\log_{64}{2},\ \log_2{64},\ 11$

Б$\log_2{64},\ 11,\ \log_{64}{2}$

В$\log_2{64},\ \log_{64}{2},\ 11$

Г$11,\ \log_{64}{2},\ \log_2{64}$

Д$\log_{64}{2},\ 11,\ \log_2{64}$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє вміння виконувати тотожні перетворення логарифмічних виразів.

За властивістю логарифма числа

\begin{gather*} \log_a{b^n}=n\cdot \log_a{b},\\[7pt] \log_{a^k}{b}=\frac 1k\log_a{b},\\[7pt] \log_2{64}=\log_2{2^6}=6\cdot \log_2{2}=6,\\[7pt] \log_{64}{2}=\log_{2^6}{2}=\frac 16\log_2{2}=\frac 16. \end{gather*}

Отже, у порядку зростання числа $$ \log_{64}{2},\ \ \log_{2}{64},\ \ 11 $$

Відповідь: A.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 516. Завдання: 26007

Завдання 37 з 113

Обчисліть $400^{1-\log_{20}4}$.

Впишіть відповідь:

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Логарифмічні вирази та їх перетворення.

Завдання скеровано на перевірку знання вміння виконувати тотожні перетворення логарифмічних виразів.

Використаємо властивості степені та логарифмів

\begin{gather*} 400^{1-\log_{20}4}=400^1:400^{\log_{20}4}=\\[7pt] =400: 20^{2\log_{20}4}=400:\left(20^{\log_{20}4}\right)^2=\\[7pt] =400:16=25. \end{gather*}

Відповідь: 25.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 489. Завдання: 24708

Завдання 38 з 113

Укажіть правильну подвійну нерівність, якщо $a=0,5^{-1},\ b=0,2,\ c=\log_{0,2}5$.

А$c\lt b\lt a$

Б$b\lt c\lt a$

В$a\lt c\lt b$

Г$c\lt a\lt b$

Д$b\lt a\lt c$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа.

Завдання скеровано на перевірку знання властивостей степенів з цілим показником, логарифмічних виразів.

Запишемо числа $a,\ b$ i $c$ в іншому вигляді:

\begin{gather*} a=0,5^{-1}=\left(\frac 12\right)^{-1}=\left(\frac 21\right)^1=2;\\[6pt] b=0,2\\[7pt] c=\log_{0,2}5=\log_{\frac 15}5=\log_{5^{-1}}5=-1 \end{gather*}

Правильна подвійна нерівність \begin{gather*} -1\lt 0,2\lt 2,\ \text{отже},\\[7pt] c\lt b\lt a \end{gather*}

Відповідь: A.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 489. Завдання: 24693

Завдання 39 з 113

$\frac{7-(\sin ^2\mathbf{\beta}+\cos^2 \mathbf{\beta})}{3\sin^2\mathbf{\beta}+3\cos^2\mathbf{\beta}}=$

А$\frac 76$

Б$\frac 73$

В$\frac 83$

Г$12$

Д$2$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення тригонометричних виразів.

Використаємо основну тригонометричну тотожність $\sin^2\mathbf{\alpha}+\cos^2\mathbf{\beta}=1$ та спростимо вираз:

\begin{gather*} \frac{7-(\sin^2\mathbf{\beta}+\cos^2\mathbf{\beta})}{3\sin^2\mathbf{\beta}+3\cos^2\mathbf{\beta}}=\\[6pt] =\frac{7-1}{3(\sin^2\mathbf{\beta}+\cos^2\mathbf{\beta})} =\frac{6}{3\cdot 1}=2. \end{gather*}

Відповідь: Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 489. Завдання: 24691

Завдання 40 з 113

Установіть відповідність між виразом (1-3) і твердженням про його значення (А – Д), яке є правильним, якщо $a=-2\frac 13$.

Вираз

1$a^2$

2$a+|a|$

3$\log_5 5^a$

Твердження про значення виразу

Абільше від $5$

Бналежить проміжку $(0; 1)$

Вє від'ємним числом

Гналежить проміжку $[1; 5)$

Ддорівнює $0$

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Раціональні, логарифмічні вирази та їх перетворення.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення виразів, порівнювати числа, розуміння поняття числового проміжку.

1. $$ a^2=\left(-2\frac 13\right)^2=\left(-\frac 73\right)^2=\frac{49}{9}=5\frac 49 $$ число більше від 5, отже, 1 - А.

2. \begin{gather*} a+|a|=a+(-a)=0,\ \text{оскільки}\ a\lt 0.\\[6pt] |a|= \left\{ \begin{array}{l l} a,\ \text{якщо}\ a\geq 0, & \\ -a,\ \text{якщо}\ a\lt 0,& \end{array}\right. \end{gather*} Отже, 2 - Д.

3. \begin{gather*} \log_5 5^a=a\log_5 5=a\cdot 1=a=-2\frac 13, \end{gather*} є від'ємним числом, отже, 3 - В.

Відповідь: 1A, 2Д, 3В.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 469. Завдання: 23677

Завдання 41 з 113

$\sin^2 2x=$

А$2\sin^2 x$

Б$4\sin^2 x$

В$4\sin^2 x\cos^2 x$

Г$2\sin^2 x\cos^2 x$

Д$\sin 4x^2$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Тригонометричні вирази та їх перетворення.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення тригонометричних виразів.

$$ \sin^2 2x=(\sin 2x)^2=(2\sin x\cos x)^2=4\sin^2 x\cos^2 x. $$

Формула синуса подвійного кута $\sin 2x=2\sin x\cos x$ є в довідкових матеріалах.

Відповідь: В.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 469. Завдання: 23673

Завдання 42 з 113

Установіть відповідність між виразом (1–3) і проміжком (А – Д), якому належить значення цього виразу, якщо $a=4,5$.

Вираз

1$a-2,7$

2$\sqrt[3]{3,5-a}$

3$\log_5 a$

Проміжок

А$(-2; 0)$

Б$(0; 1)$

В$(1; 2)$

Г$(2; 3)$

Д$(3; 5)$

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа та дії над ними.

Завдання скеровано на перевірку вміння виконувати дії з дійсними числами, порівнювати числа, розуміння поняття числового проміжку.

1. $(a-2,7)=4,5-2,7=1,8\in\ (1;\ 2)$, отже 1 - В.

2. $\sqrt[3]{3,5-4,5}=\sqrt[3]{-1}=-1\in\ (-2;\ 0)$, отже 2 - A.

3. \begin{gather*} \log_5 a=\log_5 4,5;\\[7pt] \log_5 1\lt\log_5 4,5\lt \log_5 5.\\[7pt] y=\log_5 x\ \text{зростаюча функція}\\[7pt] 0\lt\log_5 4,5\lt 1, \end{gather*} отже, 3 - Б

Відповідь: 1В, 2А, 3Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 455. Завдання: 22995

Завдання 43 з 113

Спростіть вираз $2\cos(450^\circ + \mathbf{\alpha})-\sin \mathbf{\alpha}$.

А$\sin\mathbf{\alpha}$

Б$-3\sin\mathbf{\alpha}$

В$-2\cos\mathbf{\alpha}-\sin\mathbf{\alpha}$

Г$2\cos\mathbf{\alpha}-\sin\mathbf{\alpha}$

Д$3\sin\mathbf{\alpha}$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Функції. Тригонометричні вирази та їх перетворення.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення тригонометричних виразів, знання властивостей періодичних функцій.

Спростимо вираз: $2\cos (450^\circ+\mathbf{\alpha})-\sin\mathbf{\alpha}$.

Функція $y=\cos x$ періодична з періодом $T=2\mathbf{\pi}$, отже $\cos(x+T)=\cos x$.

\begin{gather*} 2\cos(360^\circ+90^\circ+\mathbf{\alpha})-\sin\mathbf{\alpha}=2\cos(90^\circ+\mathbf{\alpha})-\sin\mathbf{\alpha}=\\[7pt] =-2\sin\mathbf{\alpha}-\sin\mathbf{\alpha}=-3\sin\mathbf{\alpha},\\[7pt] \end{gather*}

оскільки $$ \cos(90^\circ+\mathbf{\alpha})=-\sin\mathbf{\alpha}. $$

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 455. Завдання: 22913

Завдання 44 з 113

Установіть відповідність між виразом (1–3) i тотожно рівним йому виразом (А – Д), якщо $a$ – довільне додатне число, $a\neq 1.$

Вираз

1$a^4:a^3$

2$\frac{a^2-a}{1-a}$

3$7^{-\log_7a}$

Тотожно рівний вираз

А$a^2$

Б$a^7$

В$\frac 1a$

Г$a$

Д$-a$

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє знання властивостей степенів, вміння виконувати тотожні перетворення раціональних, степеневих виразів.

1. $a^4:a^3=a^{4-3}=a^1=a.$ Отже, 1 – Г.

2. $\frac{a^2-a}{1-a}=\frac{a(a-1)}{-(a-1)}=-a.$ Отже, 2 – Д.

3. $7^{-\log_7a}=7^{\log_7a^{-1}}=a^{-1}=\frac 1a.$ Отже, 3 – B.

Відповідь: 1 – Г, 2 – Д, 3 – B.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 425. Завдання: 21228

Завдання 45 з 113

$ \frac{\cos\mathbf{\alpha}\operatorname{tg}\ \mathbf{\alpha}}{\sin^2\mathbf{\alpha}}= $

А$\sin\mathbf{\alpha}$

Б$\frac{1}{\sin^2\mathbf{\alpha}}$

В$\frac{1}{\sin\mathbf{\alpha}}$

Г$\cos\mathbf{\alpha}$

Д$1$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє вміння виконувати тотожні перетворення тригонометричних виразів.

За формулою $$ \operatorname{tg}\ \mathbf{\alpha}=\frac{\sin\mathbf{\alpha}}{\cos\mathbf{\alpha}} $$ спростимо: $$ \frac{\cos\mathbf{\alpha}\cdot\operatorname{tg}\ \mathbf{\alpha}}{\sin^2\mathbf{\alpha}}=\frac{\frac{\cos\mathbf{\alpha}\cdot\sin\mathbf{\alpha}}{\cos\mathbf{\alpha}}}{\sin^2\mathbf{\alpha}}=\frac{\sin\mathbf{\alpha}}{\sin^2\mathbf{\alpha}}=\frac{1}{\sin\mathbf{\alpha}}. $$

Відповідь: B.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 425. Завдання: 21219

Завдання 46 з 113

Установіть відповідність між виразом (1–3) та тотожно рівним йому виразом (А – Д), якщо $a$ – довільне від'ємне число.

Вираз

1$a^0$

2$|a|+a$

3$a\log_22^a$

Тотожно рівний вираз

А$0$

Б$2a$

В$a^2$

Г$1$

Д$-2a$

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє вміння використовувати властивості модуля до розв’язування задач, виконувати тотожні перетворення раціональних, логарифмічних виразів.

1. $a^0=1.$
Отже, 1 – Г.

2. $|a|+a=-a+a=0.$

За означенням модуля $$ |a|=\left\{\begin{array}{l} a,\ \ \text{якщо}\ \ a\gt 0\\ 0,\ \ \text{якщо}\ \ a=0\\ -a,\ \ \text{якщо}\ \ a\lt 0 \end{array}\right. $$ Отже, 2 – A.

3. $a\log_22^a=a^2\log_22=a^2.$
Отже, 3 – B.

Відповідь: 1 – Г, 2 – A, 3 – B.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 400. Завдання: 19966

Завдання 47 з 113

Спростіть вираз $(1+\operatorname{tg}^2\mathbf{\alpha})\sin^2\mathbf{\alpha}.$

А$\frac{1}{\operatorname{tg}^2\mathbf{\alpha}}$

Б$1$

В$\cos^2\mathbf{\alpha}\sin^2\mathbf{\alpha}$

Г$\cos^2\mathbf{\alpha}$

Д$\operatorname{tg}^2\mathbf{\alpha}$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання перевіряє вміння виконувати тотожні перетворення тригонометричних виразів, знання основних співвідношень між тригонометричними функціями одного аргументу.

Спростимо вираз

$$ (1+\operatorname{tg}^2\mathbf{\alpha})\cdot \sin^2\mathbf{\alpha}=\frac{1}{\cos^2\mathbf{\alpha}}\cdot \sin^2\mathbf{\alpha}=\frac{\sin^2\mathbf{\alpha}}{\cos^2\mathbf{\alpha}}=\operatorname{tg}2\mathbf{\alpha}. $$

Відповідь: Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 400. Завдання: 19958

Завдання 48 з 113

Якщо $2\cos\mathbf{\alpha}-5\sin\mathbf{\alpha}=0$, то $\operatorname{tg}\ \mathbf{\alpha}=$

А$\frac 25$

Б$-\frac 25$

В$-3$

Г$-\frac 52$

Д$\frac 52$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє вміння виконувати тотожні перетворення тригонометричних виразів.

\begin{gather*} 2\cos\mathbf{\alpha}-5\sin\mathbf{\alpha}=0,\ \ 2\cos\mathbf{\alpha}=5\sin\mathbf{\alpha}. \end{gather*}

За властивістю пропорції $$ \frac{\sin\mathbf{\alpha}}{\cos\mathbf{\alpha}}=\frac 25,\ \ \operatorname{tg}\ \mathbf{\alpha}=\frac{\sin\mathbf{\alpha}}{\cos\mathbf{\alpha}}. $$ Отже, $\operatorname{tg}\ \mathbf{\alpha}=\frac 25.$

Відповідь: A.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 390. Завдання: 19500

Завдання 49 з 113

Обчислить значення виразу $$ \frac{\log_527}{\log_52-\log_5162}. $$

Впишіть відповідь:

-0.75

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Логарифмічні вирази.

Це завдання перевіряє вміння виконувати тотожні перетворення логарифмічних виразів.

$$ \frac{\log_5 27}{\log_52-\log_5 162}=\frac{\log_5 27}{\log_5(2:162)}=\frac{\log_5 3^3}{\log_5 3^{-4}}=\frac{3\log_5 3}{-4\log_5 3}=-\frac 34=-0\mathord{,}75. $$

Відповідь: $-0\mathord{,}75.$

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 384. Завдання: 19001

Завдання 50 з 113

Установіть відповідність між виразом (1–3) та твердженням про його значення (А – Д), яке є правильним, якщо $a=-0\mathord{,}6.$

Вираз

1$a^2$

2$|a|$

3$\log_2(4+a)$

Твердження про значення виразу

Адорівнює дробу $\frac 35$

Бє від'ємним не цілим числом

Вналежить проміжку $[0; 0\mathord{,}5]$

Гє цілим числом

Дбільше за $1$

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Це завдання перевіряє вміння виконувати дії з раціональними числами, логарифмічними виразами, порівнювати числа, знання властивостей модуля числа.

1. $a^2=(-0\mathord{,}6)^2=0\mathord{,}36$ належить проміжку $[0; 0\mathord{,}5].$ Отже, 1 – B.

2. $|a|=|-0\mathord{,}6|=0\mathord{,}6=\frac 35.$ Отже, 2 – A.

3. $\log_2(4+a)=\log_2(4-0\mathord{,}6)=\log_2 3\mathord{,}4$,

$\log_22\lt \log_2 3\mathord{,}4$, $1\lt \log_2 3\mathord{,}4.$ Отже, 3 – Д.

Відповідь: 1 – B, 2 – A, 3 – Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 384. Завдання: 18992

Завдання 51 з 113

Обчисліть $\cos 210^\circ.$

А$\frac 12$

Б$-\frac 12$

В$\frac{\sqrt{3}}{2}$

Г$-\frac{\sqrt{3}}{2}$

Д$-\frac{\sqrt{2}}{2}$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Це завдання перевіряє вміння виконувати тотожні перетворення тригонометричних виразів.

$$ \cos(210^\circ)=\cos(180^\circ+30^\circ)=-\cos 30^\circ=-\frac{\sqrt{3}}{2}. $$

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 384. Завдання: 18988

Завдання 52 з 113

Спростіть вираз $2\sin^2\mathbf{\alpha}\cdot \operatorname{ctg}\ \mathbf{\alpha}.$

А$\cos 2\mathbf{\alpha}$

Б$2\cos 2\mathbf{\alpha}$

В$\frac{2\sin^3 \mathbf{\alpha}}{\cos \mathbf{\alpha}}$

Г$2\sin 2\mathbf{\alpha}$

Д$\sin 2\mathbf{\alpha}$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Рацiональнi, iррацiональнi, степеневі, показникові, логарифмiчнi, тригонометричні вирази та їхні перетворення.

Це завдання перевіряє вміння виконувати тотожні перетворення тригонометричних виразів.

Спростимо вираз:

$$ 2\sin^2\mathbf{\alpha}\cdot \operatorname{ctg}\ \mathbf{\alpha}=2\sin^2\mathbf{\alpha}\cdot \frac{\cos\mathbf{\alpha}}{\sin\mathbf{\alpha}}=\frac{2\sin^2\mathbf{\alpha}\cdot \cos \mathbf{\alpha}}{\sin\mathbf{\alpha}}= 2\sin\mathbf{\alpha}\cdot \cos \mathbf{\alpha}=\sin 2\mathbf{\alpha}. $$

Відповідь: Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 357. Завдання: 17654

Завдання 53 з 113

Якому з наведених проміжків належить число $\log_2\frac 13$?

А$(-\infty; -3)$

Б$(-3; -1)$

В$(-1; 1)$

Г$(1; 3)$

Д$(3; +\infty)$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Функції. Дійсні числа. Логарифмічні вирази. Логарифмічна функція.

Це завдання перевіряє вміння порівнювати дійсні числа, виконувати тотожні перетворення логарифмічних виразів.

Функція $y=\log_2\frac 13$ зростаюча, оскільки основа логарифмічної функції – число $2\gt 1.$ Отже, більшому значенню аргумента відповідає більше значення функції.

\begin{gather*} \log_2\frac 14\lt \log_2\frac 13\lt \log_2\frac 12\\[6pt] \log_22^{-2}\lt \log_2\frac 13\lt \log_22^{-1}\\[6pt] -2\lt\log_2\frac 13\lt -1. \end{gather*}

З наведених проміжків число належить $(-3; -1).$

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 346. Завдання: 17074

Завдання 54 з 113

Спростіть вираз $(1-\sin^2\mathbf{\alpha})\cdot\operatorname{tg}^2\ \mathbf{\alpha}.$

А$\sin 2\mathbf{\alpha}$

Б$\cos 2\mathbf{\alpha}$

В$\frac{\cos^4 \mathbf{\alpha}}{\sin^2 \mathbf{\alpha}}$

Г$\sin^2 \mathbf{\alpha}$

Д$\operatorname{ctg}^2\ \mathbf{\alpha}$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Тригонометричні вирази.

Це завдання перевіряє вміння виконувати тотожні перетворення тригонометричних виразів.

$$ (1-\sin^2\mathbf{\alpha})\cdot \operatorname{tg}^2\ \mathbf{\alpha}= \cos^2\mathbf{\alpha}\cdot \operatorname{tg}^2\ \mathbf{\alpha}= \frac{\cos^2 \mathbf{\alpha}\cdot \sin^2\mathbf{\alpha}}{\cos^2\mathbf{\alpha}}=\sin^2\mathbf{\alpha}. $$

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 346. Завдання: 17070

Завдання 55 з 113

Якому проміжку належить значення виразу $\sin\frac{7\mathbf{\pi}}{6}-1$?

А$(-\infty; -2)$

Б$[-2; -1)$

В$[-1; 0)$

Г$[0; 1)$

Д$[1; +\infty)$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра та початки аналізу. Числа і вирази. Тригонометричні вирази та їхні перетворення.

Це завдання перевіряє вміння виконувати тотожні перетворення тригонометричних виразів та знаходити їхнє числове значення при заданих значеннях змінних, знання формул зведення.

$$ \sin\frac{7\mathbf{\pi}}{6}-1=\sin\left(\mathbf{\pi}+\frac{\mathbf{\pi}}{6}\right)-1=-\sin\frac{\mathbf{\pi}}{6}-1=-\frac 12-1=-1\frac 12. $$

Отже, значення виразу належить проміжку $[-2; -1).$

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 337. Завдання: 16612

Завдання 56 з 113

$\frac{\cos(90^\circ+\mathbf{\alpha})}{\sin \mathbf{\alpha}}=$

А$-1$

Б$\operatorname{ctg}\ \mathbf{\alpha}$

В$\operatorname{tg}\ \mathbf{\alpha}$

Г$-\operatorname{ctg}\ \mathbf{\alpha}$

Д$1$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Числа і вирази. Тригонометричні вирази та їхні перетворення.

Це завдання перевіряє знання формул зведення, означення котангенса числового аргументу.

За формулою зведення $$ \cos(90^\circ+\mathbf{\alpha})=-\sin \mathbf{\alpha}. $$

Отримаємо,

\begin{gather*} \frac{\cos(90^\circ+\mathbf{\alpha})}{\sin \mathbf{\alpha}}=\frac{-\sin \mathbf{\alpha}}{\sin \mathbf{\alpha}}=-1. \end{gather*}

Відповідь: A.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 310. Завдання: 15244

Завдання 57 з 113

Обчисліть значення виразу $\log_345+\log_3900-\log_3500.$

А$\frac 14$

Б$4$

В$3$

Г$27$

Д$\log_34445$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Числа і вирази. Логарифмічні вирази та їхні перетворення.

Це завдання перевіряє вміння виконувати тотожні перетворення логарифмічних виразів, знання властивостей логарифма.

Використаємо властивості логарифму

\begin{gather*} \log_ab+\log_ac=\log_a(b\cdot c),\\[6pt] \log_ab-\log_ac=\log_a\left(\frac bc\right)\ \text{для}\ b,\ c\gt 0,\\[6pt] \log_345+\log_3900-\log_3500=\log_3\left(\frac{45\cdot 900}{500}\right)=\log_381=4. \end{gather*}

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 298. Завдання: 14611

Завдання 58 з 113

$1-\sin \mathbf{\alpha}\operatorname{ctg}\ \mathbf{\alpha}\cos \mathbf{\alpha}=$

А$\cos 2\mathbf{\alpha}$

Б$1-\sin 2\mathbf{\alpha}$

В$0$

Г$\cos^2 \mathbf{\alpha}$

Д$\sin^2 \mathbf{\alpha}$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Числа і вирази. Тригонометричні вирази та їхні перетворення.

Це завдання перевіряє вміння виконувати тотожні перетворення тригонометричних виразів.

\begin{gather*} 1-\sin\mathbf{\alpha}\operatorname{ctg}\mathbf{\alpha}\cos\mathbf{\alpha}=\\[6pt] =1-\sin\mathbf{\alpha}\cdot \frac{\cos\mathbf{\alpha}}{\sin\mathbf{\alpha}}\cdot \cos\mathbf{\alpha}=\\[6pt] =1-\cos^2\mathbf{\alpha}=\sin^2\mathbf{\alpha}. \end{gather*}

Відповідь: Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 298. Завдання: 14608

Завдання 59 з 113

Обчисліть $\log_34\cdot\log_45\cdot\log_57\cdot\log_781$.

Впишіть відповідь:

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 296. Завдання: 14551

Завдання 60 з 113

Обчисліть $2\sin15^\circ\cos15^\circ\operatorname{tg}30^\circ\operatorname{ctg}30^\circ$.

Впишіть відповідь:

0.5

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 296. Завдання: 14547

Завдання 61 з 113

Обчисліть $\log_\frac{1}{25} \sqrt5$.

А$-\frac{1}{4}$

Б$-\frac{1}{2}$

В$-2$

Г$\frac{1}{2}$

Д$\frac{1}{4}$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 296. Завдання: 14533

Завдання 62 з 113

Обчисліть $\sqrt{(2\sin 45^\circ + 1)^2} - \sqrt{(1 - 2\cos 45^\circ)^2}$.

А$1$

Б$\frac {\sqrt 2}{2}$

В$\frac {1}{2}$

Г$\sqrt 2$

Д$2$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 296. Завдання: 14529

Завдання 63 з 113

Обчисліть $\log_a\sqrt{ab}$, якщо $\log_a b=7$.

А$\frac{2}{3}$

Б$2$

В$3$

Г$\frac{7}{2}$

Д$4$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 292. Завдання: 14317

Завдання 64 з 113

Укажіть найменший додатний період функції $y=2\operatorname{ctg}(3x)$.

А$2\pi$

Б$\pi$

В$\frac{\pi}{3}$

Г$\frac{2\pi}{3}$

Д$\frac{\pi}{2}$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 292. Завдання: 14314

Завдання 65 з 113

Обчисліть $\cos^4\dfrac{\pi}{12}-\sin^4\dfrac{\pi}{12}$.

А$1$

Б$\frac{\sqrt3}{2}$

В$\frac{1}{2}$

Г$\frac{\sqrt2}{2}$

Дінша відповідь

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 292. Завдання: 14313

Завдання 66 з 113

Укажіть правильну нерівність, якщо $a=\sin 120^\circ$, $b=\cos 120^\circ.$

А$0\lt b\lt a$

Б$a\lt 0\lt b$

В$a\lt b\lt 0$

Г$0\lt a\lt b$

Д$b\lt 0\lt a$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Тригонометричні вирази та їхні перетворення.

Це завдання перевіряє вміння знаходити числове значення тригонометричних виразів, порівнювати числові вирази.

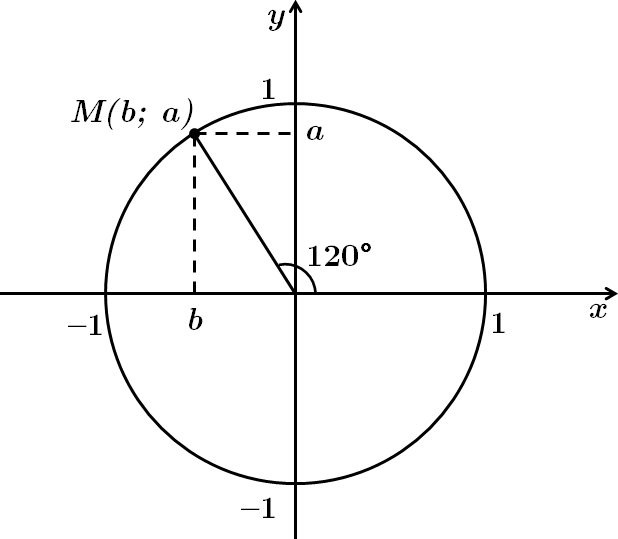
$a=\sin 120^\circ\gt 0$, $b=\cos 120^\circ\lt 0$ тому, що кут $120^\circ$ лежить у ІІ координатній чверті.

Враховуючи знаки тригонометричних функцій $b\lt 0\lt a.$

Відповідь: Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 290. Завдання: 14250

Завдання 67 з 113

Якщо $\log_43=a$, то $\log_{16}9=$

А$4a$

Б$a^2$

В$2a$

Г$\frac a2$

Д$a$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Логарифмічні вирази.

Це завдання перевіряє вміння виконувати тотожні перетворення логарифмічних виразів та знаходити числове значення при заданих значеннях змінних.

Якщо $\log_43=a$, то за властивостями логарифма

\begin{gather*} \log_{a^n}b^m=\frac mn\log_ab,\\[6pt] \log_{16}9=\log_{4^2}3^2=\frac 22\log_43=1\cdot a=a. \end{gather*}

Відповідь: Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 290. Завдання: 14246

Завдання 68 з 113

Якщо $2\sin \mathbf{\alpha}=\cos \mathbf{\alpha}$, то $\operatorname{tg}\ \mathbf{\alpha}=$

А$-2$

Б$-0\mathord{,}5$

В$0\mathord{,}2$

Г$0\mathord{,}5$

Д$2$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Тригонометричні вирази та їх перетворення.

Це завдання перевіряє вміння виконувати тотожні перетворення тригонометричних виразів та знаходити їхнє числове значення при заданих значеннях змінних.

$2\sin \mathbf{\alpha}=\cos \mathbf{\alpha}.$ Поділимо обидві частини рівності на вираз $\cos \mathbf{\alpha}\ne 0.$

\begin{gather*} \frac{2\sin \mathbf{\alpha}}{\cos \mathbf{\alpha}}=\frac{\cos \mathbf{\alpha}}{\cos \mathbf{\alpha}},\\[6pt] 2\operatorname{tg}\ \mathbf{\alpha}=1,\\[6pt] \operatorname{tg}\ \mathbf{\alpha}=\frac 12=0\mathord{,}5. \end{gather*}

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 256. Завдання: 12516

Завдання 69 з 113

Укажіть проміжок, якому належить число $\log_29.$

А$(0; 1)$

Б$(1; 2)$

В$(2; 3)$

Г$(3; 4)$

Д$(4; 5)$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра та початки аналізу. Числа та вирази. Логарифмічні вирази та їх перетворення. Функції. Основні властивості логарифмічної функції.

Це завдання перевіряє вміння виконувати перетворення логарифмічних виразів, знання властивостей логарифмічної функції.

Функція $y=\log_2x$ зростаюча, тому

\begin{gather*} \log_28\lt\log_29\lt\log_216,\\[7pt] 3\lt \log_29\lt 4. \end{gather*}

Тому $x\in (3; 4).$

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 247. Завдання: 12078

Завдання 70 з 113

$1-\sin^2 \mathbf{\alpha}-\cos^2 \mathbf{\alpha}=$

А$-2$

Б$0$

В$1$

Г$2\cos^2 \mathbf{\alpha}$

Д$1+\cos 2\mathbf{\alpha}$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа та вирази. Тригонометричні вирази та їхні перетворення.

Це завдання перевіряє знання основних тригонометричних тотожностей та вміння виконувати тотожні перетворення тригонометричних виразів.

$$ 1-\sin^2 \mathbf{\alpha}-\cos^2 \mathbf{\alpha}=1-(\sin^2 \mathbf{\alpha}+\cos^2 \mathbf{\alpha})=1-1=0. $$

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 247. Завдання: 12076

Завдання 71 з 113

Обчисліть значення виразу $ \frac{2\mathrm{ctg}\ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}}{\mathrm{tg}\ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}}, $ якщо $ \mathrm{tg}\ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}=\frac 15. $

А$50$

Б$5$

В$2$

Г$1$

Д$\frac{1}{50}$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра та початки аналізу. Числа і вирази. Тригонометричні вирази та їхні перетворення.

Це завдання перевіряє вміння виконувати тотожні перетворення тригонометричних виразів і знаходити їхне числове значення при заданих значеннях виразу.

Використаємо тотожність:

\begin{gather*} \mathrm{ctg}\ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}=\frac{1}{\mathrm{tg}\ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}}=1:\frac 15=5,\\[6pt] \frac{2\mathrm{ctg}\ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}}{\mathrm{tg}\ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}}=\frac{2\cdot 5}{\frac 15}=2\cdot 25=50. \end{gather*}

Відповідь: A.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 221. Завдання: 10847

Завдання 72 з 113

$\log_3 54-\log_3 2=$

А$\log_3 52$

Б$3$

В$9$

Г$24$

Д$27$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра та початки аналізу. Числа і вирази. Логарифмічні вирази та їхні перетворення.

Це завдання перевіряє вміння виконувати тотожні перетворення логарифмічних виразів.

Використаємо властивості логарифмів:

\begin{gather*} \log_a a=1,\\[7pt] \log_a b^n=n\cdot \log_a b,\\[6pt] \log_ab-\log_ac=\log_a\left(\frac bc\right)\ (\text{при}\ a\gt 0,\ a\ne 1,\ b\gt 0,\ c\gt 0),\\[6pt] \log_3{54}-\log_32=\log_3\left(\frac{54}{2}\right)=\log_327=\log_3 3^3=3\log_33=3. \end{gather*}

Отже, правильна відповідь – Б.

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 221. Завдання: 10837

Завдання 73 з 113

Обчисліть значення виразу $4\sin^2 \alpha$, якщо $4\cos^2 \alpha=1.$

А$3$

Б$\frac 34$

В$\frac 14$

Г$4$

Д$0$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і почати аналізу. Числа і вирази. Тригонометричні вирази та їх перетворення.

Це завдання перевіряє знання основної тригонометричної тотожності та вміння її застосовувати до перетворення тригонометричних виразів.

Для будь-якого кута $\alpha$ виконується рівність: $$ \sin^2 \alpha+\cos^2 \alpha=1. $$

I спосіб. Домножимо обідві частини цієї рівності на $4\mathord{:}$

$$ 4\sin^2 \alpha+4\cos^2 \alpha=4, $$

звідси

$$ 4\sin^2 \alpha=4-4\cos^2 \alpha. $$

Оскільки за умовою

$$ 4\cos^2 \alpha=1, $$

то отримаємо:

$$ 4\sin^2 \alpha=4-4\cos^2 \alpha=4-1=3. $$

II спосіб. Виразимо з основної тригонометричної тотожності $\sin^2 \alpha\mathord{:}$ $$ \sin^2 \alpha=1-\cos^2 \alpha. $$ Оскільки за умовою $$ 4\cos^2 \alpha=1, $$ то $$ \cos^2 \alpha=\frac 14, $$ тоді $$ \sin^2 \alpha=1-\cos^2 \alpha=1-\frac 14=\frac 34. $$ Звідки $$ 4\sin^2 \alpha=4\cdot\frac 34=3. $$

Зауваження. Правильну відповідь до завдання можна отримати, якщо навіть не знати (чи не пам'ятати) основної тригонометричної тотожності. Якщо знати, що $$ \cos 60^\circ=\frac 12, $$ тобто $\alpha=60^\circ$ задовольняє умову $$ 4\cos^2 \alpha=1, $$ а $$ \sin 60^\circ=\frac{\sqrt{3}}{2}, $$ тоді $$ 4\sin^2 \alpha=4\cdot\left(\frac{\sqrt{3}}{2}\right)^2=3. $$

Відповідь: A.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 191. Завдання: 9441

Завдання 74 з 113

$\log_2 5+\log_2 1\mathord{,}6=$

А$3$

Б$3\mathord{,}3$

В$0\mathord{,}25$

Г$4$

Д$\log_2 6\mathord{,}6$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Логарифмічні вирази та їх перетворення.

Це завдання перевіряє знання формули суми логарифмів та вміння її застосовувати до розв'язування задач.

Оскільки

\begin{gather*} \log_a b+\log_a c=\log_a (bc) \end{gather*}

при

\begin{gather*} a\gt 0, \ \ a\ne 0,\\[7pt] b\gt 0,\\[7pt] c\gt 0, \end{gather*}

то

\begin{gather*} \log_2 5+\log_2 1\mathord{,}6=\log_2(5\cdot 1\mathord{,}6)=\log_2 8=\log_2 2^3=3. \end{gather*}

Відповідь: A.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 191. Завдання: 9439

Завдання 75 з 113

Якщо $2^a=\frac 15$, то $2^{6-a}=$

А$12\mathord{,}8$

Б$59$

В$69$

Г$240$

Д$320$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Степеневі вирази та їхні перетворення.

Це завдання перевіряє вміння знаходити значення степеневого виразу.

Щоб розв'язати це завдання, достатньо скористатися формулами: $$ a^{x-y}=\frac{a^x}{a^y}, $$ або \begin{gather*} a^{x+y}=a^x\cdot a^y,\\[6pt] a^{-x}=\frac{1}{a^x}. \end{gather*}

Перший спосіб. Оскільки

\begin{gather*} 2^{6-a}=\frac{2^6}{2^a}=\frac{64}{2^a}\ \text{і}\ 2^a=\frac 15,\ \text{то}\\[6pt] 2^{6-a}=\frac{64}{\frac 15}=64\cdot 5=320. \end{gather*}

Другий спосіб. Оскільки

\begin{gather*} 2^{6-a}=2^6\cdot 2^{-a}\ \text{і}\ 2^{-a}=\left(\frac 15\right)^{-1}=5,\ \text{то}\\[6pt] 2^{6-a}=2^6\cdot 2^{-a}=64\cdot 5=320. \end{gather*}

Відповідь: Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 187. Завдання: 9249

Завдання 76 з 113

Обчисліть $\mathrm{tg}\ \alpha$, якщо $4\sin \alpha-\cos \alpha=2\cos \alpha-\sin \alpha.$

А$\frac 35$

Б$\frac 13$

В$\frac 15$

Г$3$

Д$\frac 53$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Тригонометричні вирази та їх перетворення.

Це завдання перевіряє знання основних тригонометричних формул та вміння виконувати тотожні перетворення тригонометричних виразів.

Зберемо в лівій частині заданої рівності доданки, що містять $\sin \alpha$, а в правій частині – доданки, що містять $\cos \alpha.$ Отримаємо: $$ 4\sin \alpha+\sin \alpha=2\cos \alpha+\cos \alpha, $$ звідки $$ 5\sin \alpha=3\cos \alpha. $$

Виразимо з отриманої рівності $\sin \alpha$ через $\cos \alpha\mathord{:}$ $$ \sin \alpha=\frac 35\cos \alpha. $$ За означенням $$ \mathrm{tg} \alpha=\frac{\sin \alpha}{\cos \alpha}=\frac{\frac 35\cos \alpha}{\cos \alpha}=\frac 35. $$

Відповідь: A.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 187. Завдання: 9243

Завдання 77 з 113

$\log_{5^{-2}}5^{\frac 12}=$

А$0{,}25$

Б$-1$

В$0{,}5$

Г$-2$

Д$-0{,}25$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Логарифмічні вирази та їх перетворення.

Це завдання перевіряє знання формул перетворень логарифмічних виразів: \begin{gather*} \log_{a} b^{k} = k \cdot \log_{a} b,\\[6pt] \log_{a^{k}} b = \frac{1}{k} \cdot \log_{a} b \end{gather*} та вміння їх використовувати для перетворення логарифмічного виразу.

Застосуємо ці формули:

$$ \log_{5^{-2}} 5^{\frac{1}{2}} = \frac{1}{2} \cdot \log_{5^{-2}} 5 = \frac{1}{2} \cdot \frac{1}{-2} \cdot \log_{5} 5 = -\frac{1}{4} \cdot \log_{5} 5. $$

Оскільки $\log_{5} 5 = 1$, остаточно отримуємо: $$ \log_{5^{-2}} 5^{\frac{1}{2}} = -\frac{1}{4}\cdot 1 = -0{,}25. $$

Відповідь: Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 166. Завдання: 8183

Завдання 78 з 113

Якому проміжку належить значення виразу $\sin 415^\circ$?

А$\left(-1; -\frac 12\right)$

Б$\left(-\frac 12; \frac 12\right)$

В$\left(\frac 12; \frac{\sqrt{2}}{2}\right)$

Г$\left(\frac{\sqrt{2}}{2}; \frac{\sqrt{3}}{2}\right)$

Д$\left(\frac{\sqrt{3}}{2}; 1\right)$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Тригонометричні вирази та їх перетворення.

Це завдання перевіряє знання формул зведення та властивостей функції $y = \sin x$.

Спочатку спростимо заданий вираз. Оскільки $$ 415^\circ = 360^\circ + 55^\circ, $$ а $360^\circ$ є періодом функції $y = \sin x$, то $$ \sin 415^\circ = \sin(360^\circ + 55^\circ) = \sin 55^\circ. $$

Оцінимо значення виразу $\sin 55^\circ.$ Оскільки функція $y = \sin x$ зростає на проміжку $(-90^\circ; 90^\circ)$, то $$ \sin 45^\circ \lt \sin 55^\circ \lt \sin 60^\circ, $$ тобто $$ \frac{\sqrt{2}}{2} \lt \sin 55^\circ \lt \frac{\sqrt{3}}{2}. $$

Отже, значення виразу $\sin 415^\circ$ належить проміжку $\left( \frac{\sqrt{2}}{2}; \frac{\sqrt{3}}{2} \right).$

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 166. Завдання: 8174

Завдання 79 з 113

Укажіть проміжок, якому належить число $\log_5 4.$

А$(0; 1)$

Б$(1; 2)$

В$(2; 3)$

Г$(3; 4)$

Д$(4; 5)$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Логарифмічні вирази та їх перетворення.

Це завдання перевіряє вміння оцінювати значення логарифмічного виразу.

Оцінимо значення заданого логарифмічного виразу: $$ 0 = \log_{5} 1 \lt \log_{5} 4 \lt \log_{5} 5 =1. $$ Отже, значення виразу $\log_{5} 4$ належить проміжку $(0; 1).$

Відповідь: A.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 154. Завдання: 7639

Завдання 80 з 113

Спростіть вираз $$ \frac{1}{1+\mathrm{tg}^2 \alpha}. $$

А$\cos^2 \alpha$

Б$\sin^2 \alpha$

В$\mathrm{tg}^2\ \alpha$

Г$\mathrm{ctg}^2\ \alpha$

Д$1$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Тригонометричні вирази та їх перетворення.

Це завдання перевіряє знання основних формул тригонометрії, а саме співвідношень між тригонометричними функціями одного кута.

Скористаємося формулою $$ 1 + \mathrm{tg}^{2}\ \alpha = \frac{1}{\cos^{2} \alpha}. $$ Тоді $$ \frac{1}{1 + \mathrm{tg}^{2}\ \alpha} = \frac{1}{\frac{1}{\cos^{2}\alpha}} = \cos^{2}\alpha. $$

Можна також розв’язувати це завдання наступним чином:

$$ \frac{1}{1 + \mathrm{tg}^{2}\ \alpha} = \frac{1}{1 + \frac{\sin^{2} \alpha}{\cos^{2} \alpha}} = \frac{1}{\frac{\cos^{2} \alpha + \sin^{2} \alpha}{\cos^{2} \alpha}} = \frac{1}{\frac{1}{\cos^{2} \alpha}} = \cos^{2} \alpha. $$

Відповідь: A.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 154. Завдання: 7631

Завдання 81 з 113

Обчисліть $\cos \alpha$, якщо $\sin \alpha=0,8$ i $\dfrac{\pi}{2}\lt \alpha \lt \pi$.

Впишіть відповідь:

-0.6

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 151. Завдання: 7528

Завдання 82 з 113

Впишіть відповідь:

0.44

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 144. Завдання: 7193

Завдання 83 з 113

Впишіть відповіді:

1.			2.
	1.25			-2

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 144. Завдання: 7190

Завдання 84 з 113

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3
4

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 144. Завдання: 7185

Завдання 85 з 113

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 144. Завдання: 7180

Завдання 86 з 113

Установіть відповідність між виразом (1–4) та тотожно рівним йому виразом (А – Д).

1$1-\cos^2 \alpha$

2$2\sin \alpha\cos \alpha$

3$\cos^2 \alpha-\sin^2 \alpha$

4$\cos^4 \alpha+\sin^2\alpha\cos^2 \alpha$

А$\cos^2 \alpha$

Б$\cos 2\alpha$

В$\sin 2\alpha$

Г$-\cos 2\alpha$

Д$\sin^2 \alpha$

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3
4

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Тригонометричні вирази та їхні перетворення.

Це завдання перевіряє вміння перетворювати вирази, що містять тригонометричні функції.

Для розв’язання завдання потрібно знати основну тригонометричну тотожність: $$ \sin^{2}\alpha + \cos^{2}\alpha = 1 $$ та формули синуса та косинуса подвійного кута: \begin{gather*} \sin 2\alpha = 2\sin\alpha \cos\alpha, \\[7pt] \cos 2\alpha = \cos^{2}\alpha - \sin^{2}\alpha. \end{gather*}

Тоді $$ 1 - \cos^{2}\alpha = \sin^{2}\alpha. $$ Отже, 1 – Д.

$$ 2\sin\alpha \cos\alpha= \sin 2\alpha. $$ Отже, 2 – В.

$$ \cos^{2}\alpha - \sin^{2}\alpha = \cos 2\alpha. $$ Отже, 3 – Б.

Перетворимо вираз 4:

$$ \cos^{4}\alpha + \cos^{2}\alpha \sin^{2}\alpha = \cos^{2}\alpha(\cos^{2}\alpha + \sin^{2}\alpha) = \cos^{2}\alpha \cdot 1 = \cos^{2}\alpha. $$

Отже, 4 – А.

Відповідь: 1 – Д, 2 – В, 3 – Б, 4 – А.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 142. Завдання: 7148

Завдання 87 з 113

Обчисліть $36^{\log_6 5}.$

А$5$

Б$6$

В$10$

Г$25$

Д$36$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Логарифмічні вирази та їхні перетворення.

Це завдання перевіряє знання основної логарифмічної тотожності та вміння використовувати її та властивості степенів для перетворення логарифмічних виразів.

Подамо $36$ у вигляді степеня з основою $6\mathord{:}$ $36 = 6^{2}.$ Підставимо в заданий вираз: $$ 36^{\log_{6} 5} = \left(6^{2}\right)^{\log_{6} 5}. $$ Використовуючи властивість степеня: $$ (a^{x})^{y} = a^{xy} = (a^{y})^{x}, $$ одержимо: $$ \left(6^{2}\right)^{\log_{6} 5} = \left(6^{\log_{6} 5}\right)^{2}. $$

Врахувавши основну логарифмічну тотожність $$ a^{\log_{a} b} = b, $$ отримуємо: $$ 6^{\log_{6} 5} = 5. $$ Отже, $$ 36^{\log_{6} 5} = \left(6^{\log_{6} 5}\right)^{2} = 5^{2} = 25. $$

Такий же результат отримаємо, якщо виконаємо такі перетворення:

$$ 36^{\log_{6} 5} = \left(6^{2}\right)^{\log_{6} 5} = 6^{2 \log_{6} 5} = 6^{\log_{6} 5^{2}} = 6^{\log_{6} 25} = 25. $$

Використавши логарифмічну тотожність: \begin{gather*} \log_a b^n=n\cdot \log_a b. \end{gather*}

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 142. Завдання: 7084

Завдання 88 з 113

До кожного виразу (1–4) доберіть тотожно йому рівний (А – Д), якщо $m\gt 2$, $m$ – натуральне число.

1$(m+1)^2-m^2-1$

2$m\cos^2 \alpha+m\sin^2 \alpha$

3$100^{\lg m}$

4$\log_2\sqrt[m]{2}$

А$0$

Б$m$

В$2m$

Г$m^2$

Д$\frac 1m$

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3
4

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Раціональні, тригонометричні, логарифмічні вирази та їхні перетворення.

Це завдання перевіряє знання формул скороченого множення, основних тригонометричних та логарифмічних співвідношень.

Перетворимо кожен з наведених виразів:

1. $(m+1)^2-m^2-1=m^2+2m+1-m^2-1=2m.$ Отже, 1 – В.

2. $m\cos^2\alpha+m\sin^2\alpha=m(\cos^2\alpha+\sin^2\alpha)=m\cdot 1=m.$ Отже, 2 – Б.

3. $100^{\lg m}=10^{2\lg m}=10^{\lg m^2}=m^2.$ Отже, 3 – Г.

4. $\log_2\sqrt[m]{2}=\log_2 2^{\frac{1}{m}}=\frac{1}{m}\log_2 2=\frac{1}{m}\cdot 1=\frac{1}{m}.$ Отже, 4 – Д.

Відповідь: 1 – B, 2 – Б, 3 – Г, 4 – Д.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 138. Завдання: 6892

Завдання 89 з 113

Відомо, що $\mathrm{ctg}\ \alpha\lt 0$, $\cos \alpha\gt 0.$ Якого значення може набувати $\sin \alpha$?

А$-1$

Б$-\frac 12$

В$0$

Г$\frac 12$

Д$1$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Тригонометричні вирази.

Це завдання перевіряє вміння визначати координатну чверть, в якій тригонометричні функції набувають певних знаків, та можливе значення іншої тригонометричної функції для кута, що належить цій чверті.

Якщо $\mathrm{ctg}\alpha\lt 0$, то кут $\alpha$ належить першій або третій координатній чверті (див. рисунок); $\cos\alpha\gt 0$ для кутів першої та четвертої чверті (див. рисунок). Отже, якщо одночасно $\mathrm{ctg}\alpha\lt 0$ і $\cos\alpha\gt 0$, то кут $\alpha$ знаходиться у IV координатній чверті. Для кутів $\alpha$ цієї чверті виконується нерівність $\sin\alpha\lt 0$ (див. рисунок), причому $\sin\alpha \ne -1.$ Якщо припустити, що $\sin\alpha=-1$, то $\mathrm{ctg}\alpha=\cos\alpha=0$, що суперечить умові завдання. Тому

$\sin\alpha$ серед наведених значень може приймати лише значення $-\frac{1}{2}.$

Або можна міркувати наступним чином: оскільки $$ \mathrm{ctg}\alpha=\frac{\cos\alpha}{\sin\alpha}\lt 0 $$ і $\cos\alpha\gt 0$, то $\sin\alpha\lt 0$, причому $\sin\alpha\ne -1$, тому що тоді $\mathrm{ctg}\alpha=\cos\alpha=0$, що суперечить умові завдання.

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 138. Завдання: 6885

Завдання 90 з 113

Впишіть відповідь:

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 131. Завдання: 6469

Завдання 91 з 113

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 131. Завдання: 6452

Завдання 92 з 113

Впишіть відповідь:

-48.4

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 129. Завдання: 6412

Завдання 93 з 113

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 129. Завдання: 6394

Завдання 94 з 113

Впишіть відповідь:

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 128. Завдання: 6377

Завдання 95 з 113

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 128. Завдання: 6368

Завдання 96 з 113

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 128. Завдання: 6360

Завдання 97 з 113

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 128. Завдання: 6358

Завдання 98 з 113

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3
4

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 127. Завдання: 6334

Завдання 99 з 113

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 127. Завдання: 6326

Завдання 100 з 113

Впишіть відповідь:

1.6

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 126. Завдання: 6308

Завдання 101 з 113

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 126. Завдання: 6297

Завдання 102 з 113

Укажіть правильну нерівність, якщо $a=\sin 120^\circ$, $b=\cos 120^\circ.$

А$0\lt a\lt b$

Б$a\lt 0\lt b$

В$a\lt b\lt 0$

Г$b\lt 0\lt a$

Д$0\lt b\lt a$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра та початки аналізу. Числа та вирази. Тригонометричні вирази та їхні перетворення.

Це завдання перевіряє вміння знаходити числове значення тригонометричних виразів.

$a=\sin 120^\circ\gt 0$,
$b=\cos 120^\circ\lt 0$, отже $b\lt 0\lt a.$

Кут $120^\circ$ належить II координатній чверті. У даній координатній чверті функція $y=\sin x$ має додатний знак, а $y=\cos x$ – від’ємний.

Отже, правильна відповідь – Г.

Відповідь: Г.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 125. Завдання: 6257

Завдання 103 з 113

Впишіть відповідь:

20.25

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 124. Завдання: 6239

Завдання 104 з 113

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 124. Завдання: 6217

Завдання 105 з 113

Впишіть відповідь:

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 3. Завдання: 6205

Завдання 106 з 113

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 123. Завдання: 6169

Завдання 107 з 113

Обчисліть $\log_3 18-\log_3 2.$

А$2$

Б$3$

В$\log_3 16$

Г$6$

Д$9$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Це завдання перевіряє знання властивостей логарифма та вміння виконувати тотожні перетворення логарифмічних виразів.

\begin{gather*} \log_3 18-\log_3 2=\log_3\left(\frac{18}{2}\right)=\log_3 9=\log_3 3^2=2\log_3 3=2. \end{gather*}

Використали властивість логарифма:

\begin{gather*} \log_a a=1;\\[7pt] \log_a b^p=p\cdot \log_a b. \end{gather*}

Відповідь: A.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 123. Завдання: 6165

Завдання 108 з 113

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 122. Завдання: 6130

Завдання 109 з 113

Обчисліть $\log_2\frac 18+\log_5 25.$

А$-2$

Б$-1$

В$5$

Г$\lg \frac{25}{8}$

Д$\lg_7 25\frac 18$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Раціональні, ірраціональні, степеневі, показникові, логарифмічні, тригонометричні вирази та їх тотожні перетворення.

Це завдання перевіряє вміння виконувати тотожні перетворення логарифмічних виразів.

\begin{gather*} \log_2\frac 18+\log_5 25=\log_2 2^{-3}+\log_5 5^2=-3\cdot \log_2 2+2\cdot \log_5 5=-3+2=-1. \end{gather*}

Використали властивість логарифма:

\begin{gather*} \log_a a=1;\\[7pt] \log_a b^p=p\cdot \log_a b. \end{gather*}

Відповідь: Б.

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 122. Завдання: 6127

Завдання 110 з 113

Впишіть відповідь:

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 121. Завдання: 6118

Завдання 111 з 113

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 121. Завдання: 6104

Завдання 112 з 113

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Продовжити пізніше

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 3. Завдання: 6086

Завдання 113 з 113

Позначте відповіді:

А	Б	В	Г	Д

Показати відповідь Читати пояснення

Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

Побажання та зауваження щодо роботи розділу пишіть, будь ласка, на адресу

Тест 2. Завдання: 5331

Новини

Вступ на підставі індивідуальної співбесіди у 2026 році
Ваговий, регіональний, галузевий коефіцієнти для вступу: що має знати вступник
Правила вступу на контракт у 2026 році

Інформація

Усі завдання ЗНО з математики за темами
Усі тести ЗНО з математики онлайн
Завдання й відповіді ЗНО з математики минулих років
Усе про тест ЗНО з математики
Програма ЗНО з математики
Тести ЗНО онлайн з інших предметів
Дорожня карта учасника ЗНО
Дорожня карта вступника на бакалавра

Facebook

Twitter

Алгебра і початки аналізу – Показникові, логарифмічні, тригонометричні вирази та їхні перетворення