Розділ: Планіметрія
Тема: Прямокутні трикутники
Кількість завдань: 57
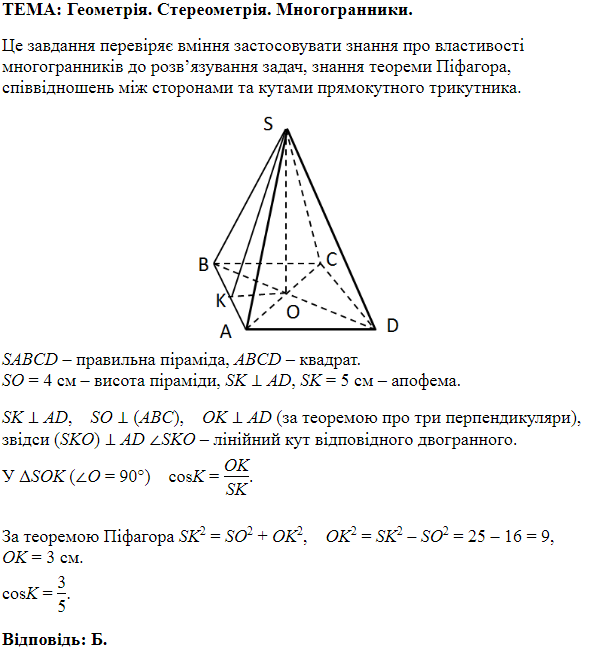
ТЕМА: Геометрія. Планіметрія. Трикутники.
Завдання перевіряє вміння застосовувати означення та властивості різних видів трикутників до розв'язування планіметричних задач.
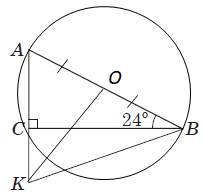
1 – Г. У \(\Delta ACB\ (\angle C=90^\circ)\) \(\angle B+\angle A=90^\circ,\) \(\angle B=24^\circ,\) тому \(\angle A=90^\circ-24^\circ=66^\circ.\) \(\angle BAC=66^\circ.\)
2 – B. \(\Delta ABK\) – рівнобедрений, \(AK=KB\) за умовою. За властивістю рівнобедреного трикутника \(\angle A=\angle B=66^\circ.\)
$$ \angle KBC=\angle KBA-\angle CBA=66^\circ-24^\circ=42^\circ. $$
3 – A. \(\Delta AKB\) – рівнобедрений, \(KO -\) медіана \(AO=OB\) (як радіуси). За властивістю рівнобедереного трикутника \(KO - \) висота, \(KO\perp AB.\) \begin{gather*} \angle OKB=90^\circ-\angle KBO=90^\circ-66^\circ=24^\circ . \end{gather*} \(\Delta ACB - \) прямокутний, тому центр кола описаного навколо нього, лежить на середині гіпотенузи \(AB.\)
Відповідь: 1Г, 2В, 3А.
ТЕМА: Геометрія. Планіметрія.
Завдання перевіряє знання властивості трикутника про суму кутів.
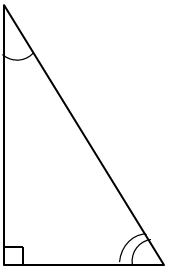
Сума кутів трикутника – \(180^\circ .\) Сума гострих кутів – \(90^\circ .\)
Отже, \(115^\circ \) – це сума прямого та гострого кута. Тоді гострий кут \(115^\circ -90^\circ =25^\circ .\) Другий гострий кут трикутника.
Гострі кути \(65^\circ\) та \(25^\circ .\)
Найменший кут цього трикутника \(25^\circ .\)
Відповідь: B.
ТЕМА: Геометрія. Планіметрія. Трикутники.
Завдання перевіряє вміння застосовувати означення та властивості різних видів трикутників до розв'язування планіметричних задач.
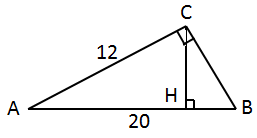
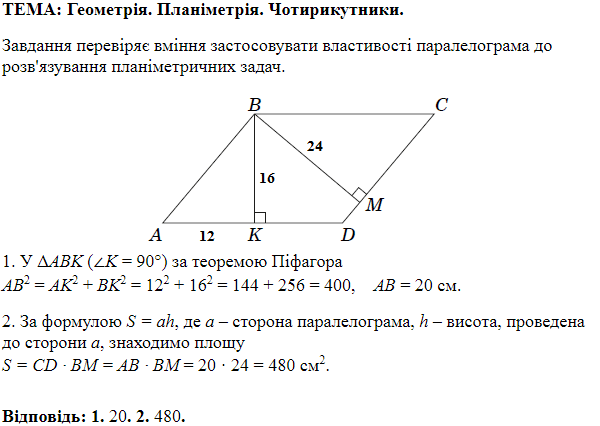
1. За теоремою Піфагора: \begin{gather*} AB^2=AC^2+BC^2\\[7pt] BC^2=20^2-12^2=400-144=256.\\[7pt] BC=16\ \text{см}. \end{gather*} Отже, правильна відповідь – Д.
2. Радіус кола, описаного навколо прямокутного трикутника, дорівнює половині гіпотенузи. Отже, \(R=\frac 12 AB=10\ \text{см}.\) Отже, правильна відповідь – B.
3. \(CH\perp AB\)
Висоту \(CH\) можна знайти, прирівнявши площу трикутника
\begin{gather*} S=\frac 12 a\cdot b\ \text{та}\ S=\frac 12 ch_c, \end{gather*} де \(a,\ b\) – катети, \(c\) – гіпотенуза.
Або знайти висоту за допомогою метричних співвідношень у прямокутному трикутнику:
\begin{gather*} AC^2=AH\cdot AB,\ \ 144=AH\cdot 20,\\[7pt] AH=144:20=7,2\ (\text{см}) \end{gather*}\(\Delta ACH\ (\angle H=90^\circ)\) за теоремою Піфагора:
Отже, правильна відповідь – Б.
Відповідь: 1Д, 2В, 3Б.
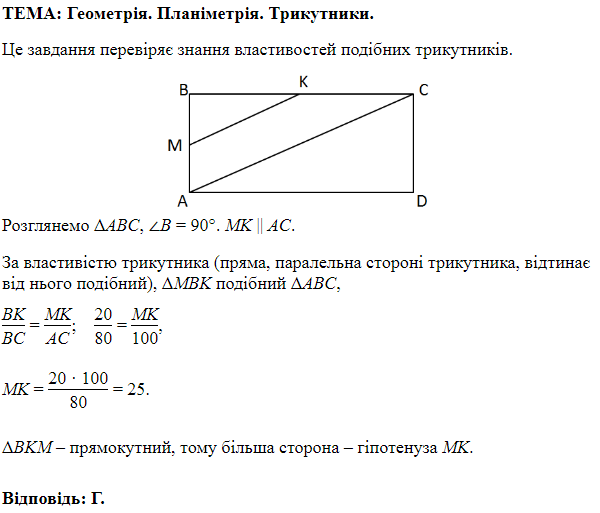
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.
Завдання скеровано на перевірку знання властивостей трикутників та їх основних властивостей.
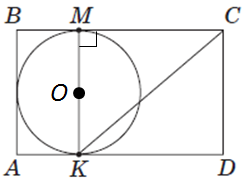
\(P_{ABMK}=24\ \text{см}\ \ KC=17\ \text{см}.\)
1.
2. \(2OM=MK=8\ \text{см}, \triangle MKC\ (\angle M=90^\circ)\) - за теоремою Піфагора
Відповідь: 1. 4. 2. 152.
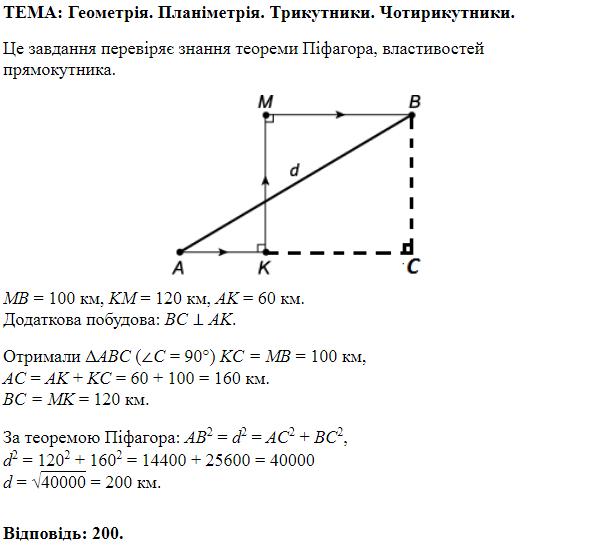
ТЕМА: Геометрія. Планіметрія. Трикутники.
Завдання скеровано на перевірку знання властивостей трикутника, вміння розв’язувати задачі практичного змісту.
Побудуємо математичну модель задачі:
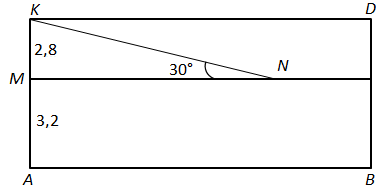
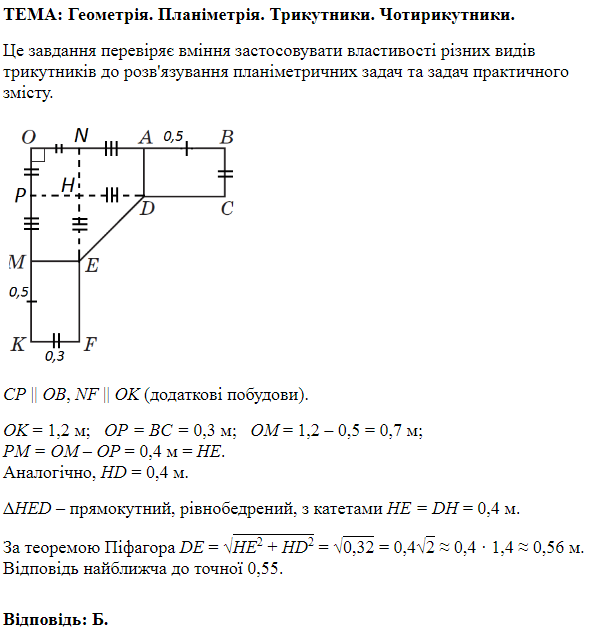
$$ DB=6\ \text{м},\ AM=3,2\ \text{м}\ KM=AK-AM=6-3,2=2,8\ \text{м}. $$
$$ \triangle KMN (\angle M=90^\circ) \ \ KN=2KM=2,8\cdot 2=5,6\ \text{м}. $$
Катет \(KM\) протилеглий куту \(30^\circ\) дорівнює половині гіпотенузи \(KN\). $$ 5,5 \leq 5,6\lt 6 $$
Відповідь: Г.
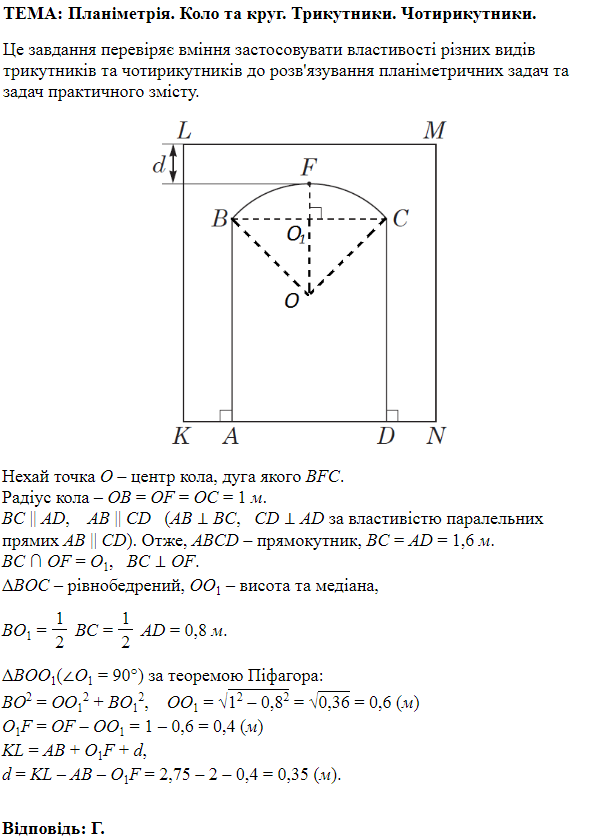
ТЕМА: Геометрія. Стереометрія. Многогранники.
Завдання перевіряє вміння розв’язувати задачі на обчислення об’ємів піраміди.
\(KABCD\) – правильна піраміда. \(ABCD\) – квадрат, \(AB=9\sqrt{2}\) см, \(BK=15\) см.
У квадраті \(BD=AB\cdot\sqrt{2}=9\sqrt{2}\cdot \sqrt{2}=18\) см.
$$ BO=\frac 12BD=9\ \textit{см}. $$У \(\Delta KOB\ (\angle O=90^\circ)\) за теоремою Піфагора \(BK^2=BO^2+KO^2\),
\(KO=\sqrt{15^2-9^2}=\sqrt{6\cdot 24}=\sqrt{6\cdot 6\cdot 4}=6\cdot 2=12\) см – висота піраміди.
\(S_{ABCD}=AB^2=(9\sqrt{2})^2=81\cdot 2=162\) см\(^2.\)
Об'єм піраміди знаходимо за формулою:
\begin{gather*} V=\frac 13S_\text{основи}\cdot H,\\[6pt] \text{де}\ S_\text{основи}=S_{ABCD}=162\ \textit{см}^2,\\[7pt] H=KO=12\ \textit{см},\\[6pt] V=\frac 13\cdot 162\cdot 12=54\cdot 12=648\ \textit{см}^3. \end{gather*}Відповідь: \(648.\)
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Коло та круг.
Завдання перевіряє вміння застосовувати властивості різних видів трикутників до розв'язування планіметричних задач.
\(BK=8\) см, \(KM=10\) см – діаметр.
1. \(BK=MD=8\) см, \(KM=10\) см.
За властивістю прямокутника, діагоналі рівні. \begin{gather*} AC=BD=BK+KM+MD=8+10+8=26\ \textit{см}. \end{gather*}
2. \(P_{ABCD}=2(AB+BC)\), \(AB=KM=10\) см.
\(\Delta ABD (\angle A=90^\circ)\) за теоремою Піфагора
\begin{gather*} BD^2=AB^2+AD^2,\\[7pt] AD^2=BD^2-AB^2=26^2-10^2,\\[7pt] AD=\sqrt{(26-10)(26+10)}=\sqrt{16\cdot 36}=4\cdot 6=24\ \textit{см},\\[7pt] P_{ABCD}=2(10+24)=68\ \textit{см}. \end{gather*}Відповідь: 1. \(26.\)
2. \(68.\)
ТЕМА: Геометрія. Планіметрія.
Завдання перевіряє вміння застосовувати означення та властивості різних видів трикутників до розв'язування планіметричних задач практичного змісту.
Відповідь: Г.
ТЕМА: Геометрія. Планіметрія. Коло і круг. Чотирикутники. Трикутники.
Завдання перевіряє знання про коло та його елементи, теореми Піфагора, знання формули для обчислення площі трикутника.
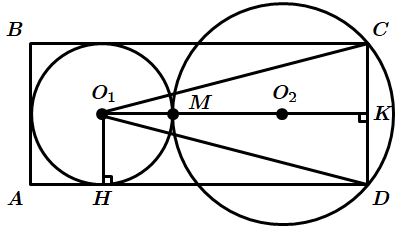
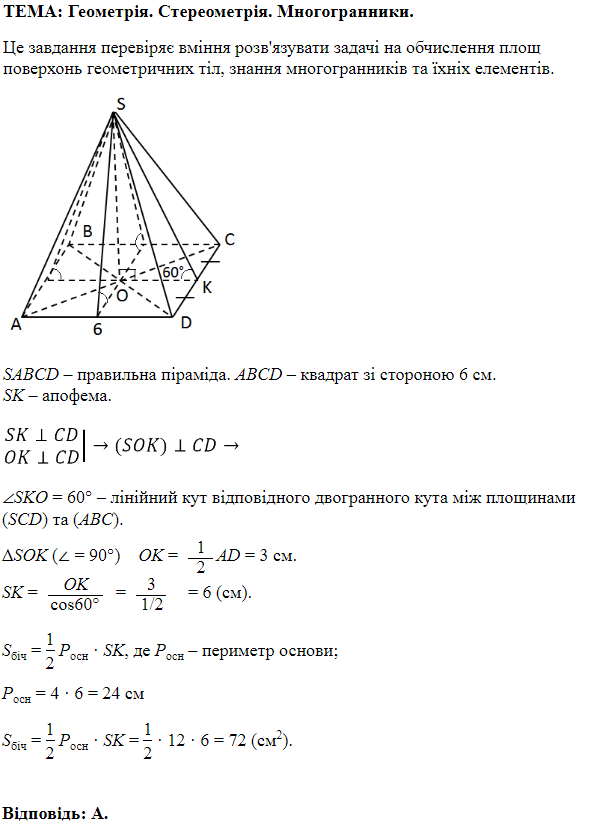
1. \(O_2C=20\) см, \(O_2K\perp CD\), \(O_2K=12\) см.
За теоремою Піфагора \begin{gather*} \Delta O_2KC\ (\angle K=90^\circ),\\[7pt] O_2C^2=O_2K^2+CK^2,\\[7pt] CK=\sqrt{400-144}=\sqrt{256}=16\ \textit{см},\\[7pt] O_1H=CK=16\ \textit{см}. \end{gather*}
2. \(S_{DO_1C}=\frac 12CD\cdot O_1K\),
\begin{gather*} O_1K=O_1O_2+O_2K=O_1M+MO_2+O_2K=16+20+12=48\ \textit{см},\\[6pt] S_{DO_1C}=\frac 12\cdot 32\cdot 48=16\cdot 48=768\ \textit{см}^2. \end{gather*}Відповідь: 1. \(16.\)
2. \(768.\)
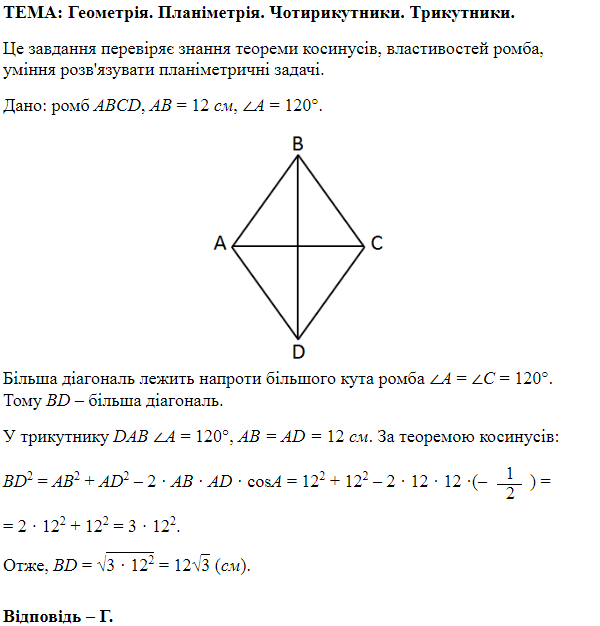
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Завдання перевіряє вміння застосовувати властивості трикутників до розв’язування планіметричних задач, знаходити довжину середньої лінії трапеції, знання теореми Піфагора.
1.
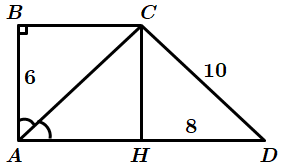
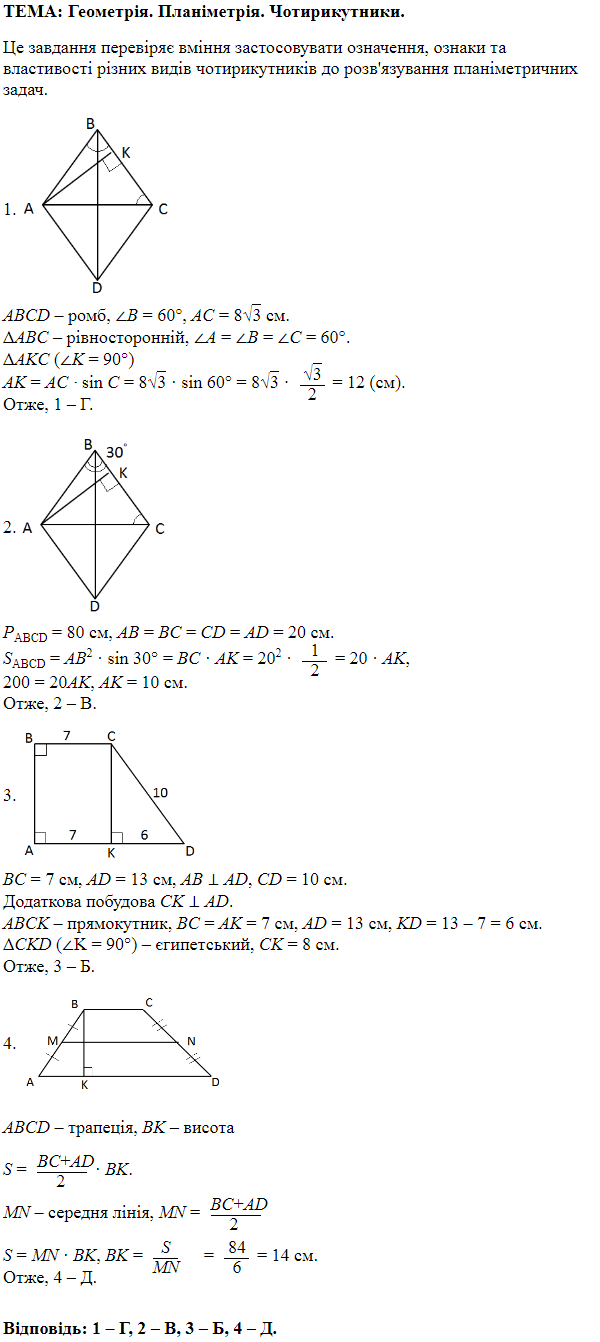
\(\angle A=90^\circ\), \(AC\) бісектриса, \(\angle BAC=45^\circ.\)
\(\Delta ABC\) – рівнобедрений \((\angle B=90^\circ)\), \(AB=BC=6\) см.
Отже, 1 – A.
2. \(CH\perp AD\), \(HD\) – проекція \(CD\) на \(AD.\)
У \(\Delta CHD\ (\angle H=90^\circ)\), \(CH=6\) см, \(HD=8\) см (єгипетський).
Отже, 2 – Б.
3. \(ABCH\) – квадрат.
\(BC=AH=6\) см, \(AD=AH+HD=14\) см.
Cередня лінія трапеції $$ \frac{BC+AD}{2}=\frac{6+14}{2}=10\ \textit{см}. $$ Отже, 3 – Г.
Відповідь: 1 – A, 2 – Б, 3 – Г.
ТЕМА: Геометрія. Стереометрія. Тіла обертання.
Завдання перевіряє вміння розв’язувати задачі на обчислення об’ємів і площ поверхонь конуса.
Площа основи конуса – \(S_\text{основи}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}R^2=100\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\) см\(^2\), \(R^2=100\), \(R=10\) см. \(OB=10\) см.
Об'єм конуса знаходимо за формулою:
\(V=\frac 13S_\text{основи}H,\) де \(S_\text{основи}=100\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\) см\(^2\), \(H=AO.\)
\(\frac 13\cdot 100\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\cdot H=800\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\), \(H=24\) см.
У \(\Delta AOB\ (\angle O=90^\circ)\) за теоремою Піфагора:
\(AB^2=AO^2+OB^2=24^2+10^2=576+100=676.\)
\(AB=26\) см – твірна конуса.
Відповідь: \(26.\)
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання перевіряє вміння застосовувати властивості паралелограма до розв'язування планіметричних задач.
1. У \(\Delta ABK\ (\angle K=90^\circ)\) за теоремою Піфагора \begin{gather*} AB^2=AK^2+BK^2=12^2+16^2=144+256=400,\\[7pt] AB=20\ \textit{см}. \end{gather*}
2. За формулою \(S=ah\), де \(a\) – сторона паралелограма, \(h\) – висота, проведена до сторони \(a\), знаходимо площу
Відповідь: 1. \(20.\)
2. \(480.\)
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання перевіряє знання властивостей ромба.
\(ABCD\) – ромб, \(\angle B=60^\circ\), \(AB=BC=CD=DA=8.\)
1. \(\Delta ABC\) – рівносторонній, \(AC=8.\) Отже, 1 – B.
2. \(\Delta BCH\ (\angle H=90^\circ)\ CH=BC\cdot\sin B=8\cdot \sin 60^\circ=8\cdot\frac{\sqrt{3}}{2}=4\sqrt{3}.\) Отже, 2 – Б.
3. Центр кола, вписаного в ромб – точка перетину діагоналей точка \(O.\)
За властивістю ромба \(AO=OC=\frac 12AC=4.\) Отже, 3 – A.
Відповідь: 1 – B, 2 – Б, 3 – A.
ТЕМА: Геометрія. Планіметрія. Геометричні величини та їх вимірювання.
Завдання перевіряє вміння знаходити довжини відрізків, розв'язувати задачі практичного змісту.
У \(\Delta BOC\ (\angle O=90^\circ)\ OB=OC\) як радіуси.
\(BC=6\) м. За теоремою Піфагора
Ширина смуги
Відповідь: Г.
ТЕМА: Геометрія. Стереометрія. Многогранники.
Завдання перевіряє знання властивостей піраміди, означення кута між прямою та площиною.
Висота піраміди \(AO=24.\) За означенням кута між прямою та площиною,
\(AO\perp (DOC)\)
\(AB\) – похила
\(OB\) – проекція похилої на площину.
Отже, \(\angle ABO=45^\circ.\) \(\Delta AOB\ (\angle O=90^\circ)\) – рівнобедрений.
\(OB=OA=24.\)
\(OB=\frac 12CE\), \(CE=48.\)
Відповідь: Г.
