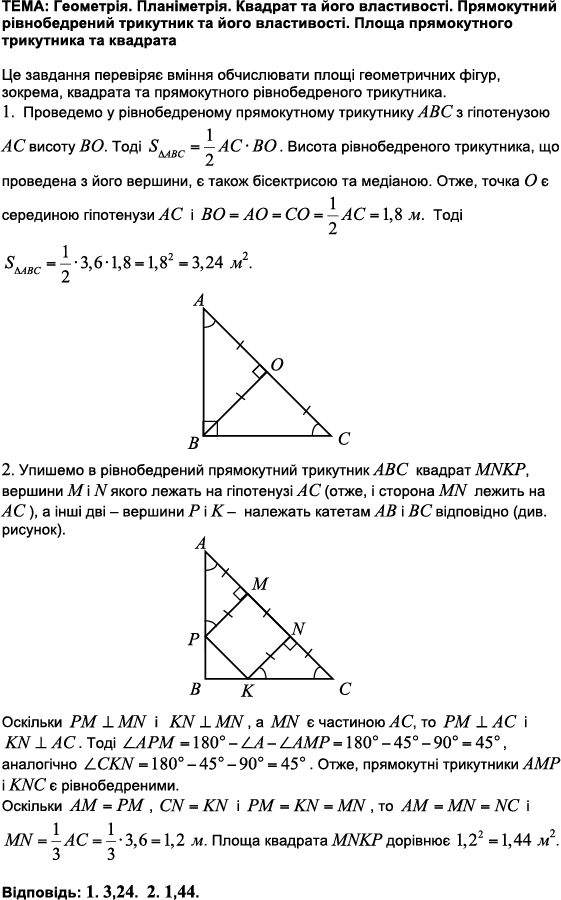
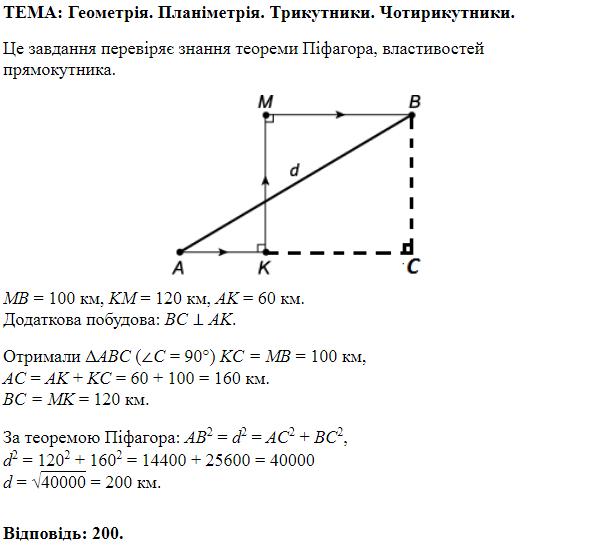
Розділ: Планіметрія
Тема: Прямокутник. Квадрат
Кількість завдань: 61
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивостей квадрата, уміння обчислювати площі трикутників.
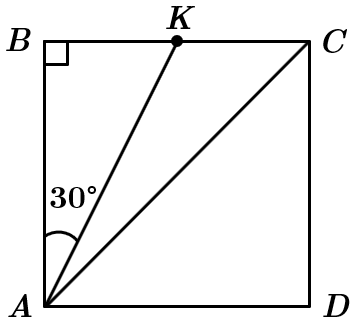
Сторону квадрата визначмо з
У
Відповідь: A.
ТЕМА: Чотирикутники. Коло та круг.
Завдання скеровано на перевірку знання властивостей кола, круга та їхніх елементів, властивостей прямокутника.
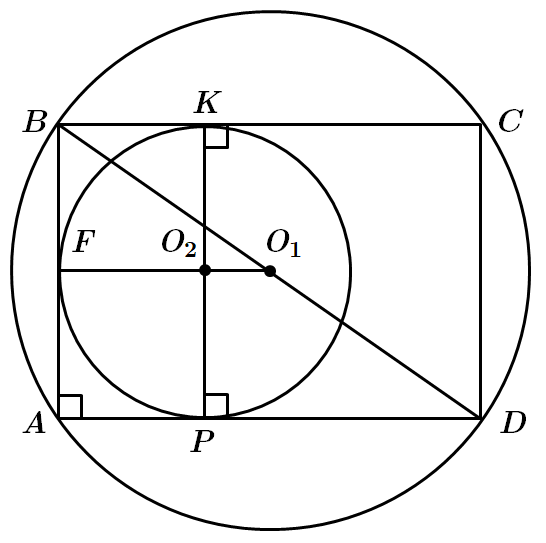
Площа круга із центром у точці
1. Відстань від
Правильна відповідь – B.
2. Центр кола
У
Правильна відповідь – Д.
3. Відстань
Правильна відповідь – A.
Відповідь: 1 – B, 2 – Д, 3 – A.
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивостей прямокутника, властивості середньої лінії трикутника, уміння обчислювати площі трикутників, многокутників.
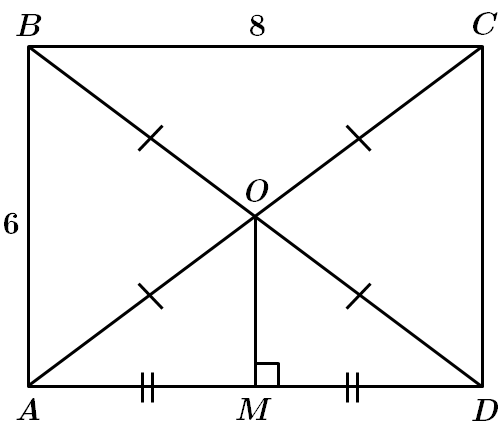
1.
Правильна відповідь – B.
2.
У
Правильна відповідь – A.
3.
Правильна відповідь – Г.
Відповідь: 1 – B, 2 – A, 3 – Г.
ТЕМА: Коло та круг. Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивостей чотирикутників, зокрема прямокутника, кола, прямокутного трикутника, уміння застосовувати теорему Піфагора для розв’язування прямокутного трикутника.
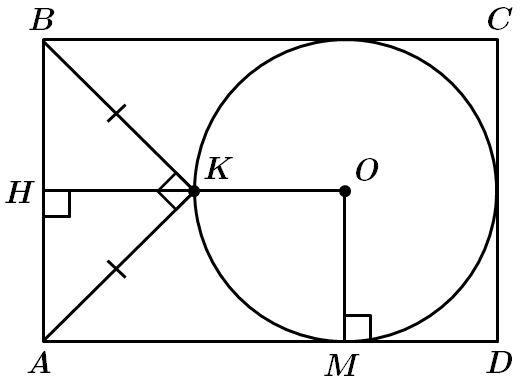
1. Коло дотикається до сторін
Правильна відповідь – А.
2. У
Правильна відповідь – B.
3. У
У
Правильна відповідь – Г.
Відповідь: 1 – A, 2 – B, 3 – Г.
ТЕМА: Чотирикутники.
Завдання скеровано на перевірку знань властивостей паралелограмів, зокрема прямокутника.
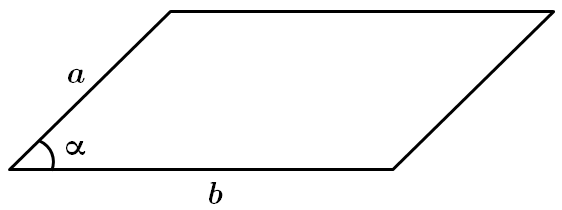
I. Периметром паралелограма називають суму довжин всіх його сторін.
Отже, твердження правильне.
II. Площу паралелограма визначають за формулою:
III. Рівні діагоналі прямокутника не означають рівності сторін. Тільки за умови, що протилежні сторони також рівні, інші сторони прямокутників також будуть рівними між собою.
Отже, твердження неправильне.
Відповідь: А.
ТЕМА: Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивостей чотирикутників, зокрема квадрата, прямокутного трикутника, а також теореми Піфагора.
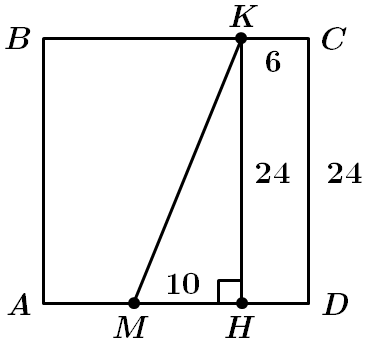
У квадраті
Нехай
Отже,
Побудуймо
Розгляньмо
Визначмо довжину гіпотенузи:
Відповідь: В.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання скеровано на перевірку вміння застосовувати властивості трапеції та квадрата, розв’язування трикутників.
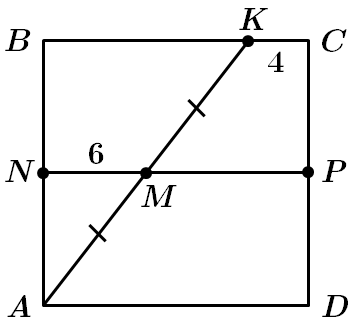
1 – В. Точка
У
2 – A.
У трапеції
За властивістю середньої лінії:
3 – Г.
За теоремою Піфагора:
Відповідь: 1В, 2А, 3Г.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Завдання скеровано на перевірку вміння застосовувати властивості прямокутника та прямокутного трикутника.
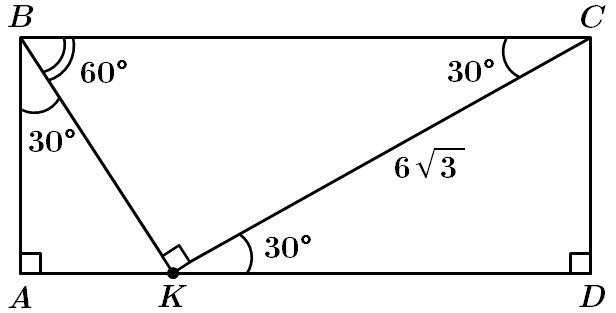
У
У прямокутнику
Відповідь: B.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання скеровано на перевірку вміння застосовувати властивості прямокутника та квадрата, розв’язування трикутників.
1.
Отже, правильна відповідь – В.
2.
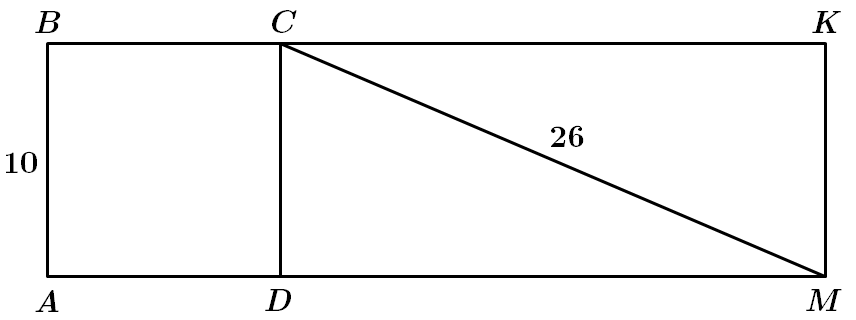
Отже, правильна відповідь – Г.
3. Відстань між точкою
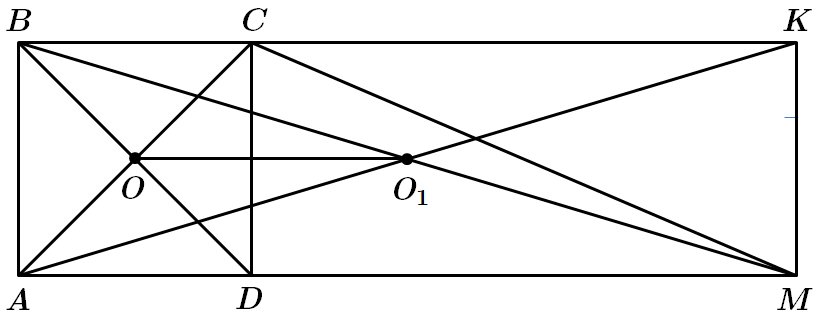
У
Отже, правильна відповідь – Б.
Відповідь: 1В, 2Г, 3Б.
ТЕМА: Геометрія. Планіметрія. Трикутники.
Завдання скеровано на перевірку знання властивостей прямокутного трикутника, співвідношення між сторонами та кутами прямокутного трикутника.
У
У
Відповідь: Б.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Завдання перевіряє знання прямокутника та трикутника, їхніх властивостей.
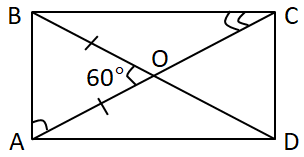
Площа прямокутника
Або іншим способом:
Відповідь: B.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Завдання перевіряє вміння застосовувати властивості трикутників, прямокутника до розв’язування планіметричних задач.
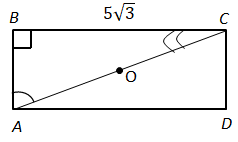
За умовою завдання більша сторона прямокутника дорівнює
У прямокутному трикутнику
У
Центр кола, описаного навколо прямокутника, є точка перетину діагоналей – середина діагоналі
Довжина кола
Відповідь: A.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Перевіряє знання властивостей прямокутника, вміння знаходити довжини відрізків, градусні міри кутів, площі геометричних фігур.
1.
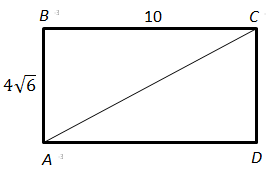
За теоремою Піфагора:
2.
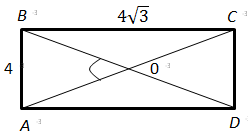
Отже, 2 – Б.
3.
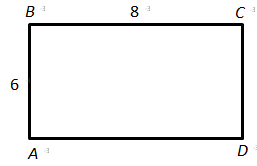
Відповідь: 1Г, 2Б, 3B.
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники. Круг.
Завдання скеровано на перевірку знання основних властивостей геометричних фігур.
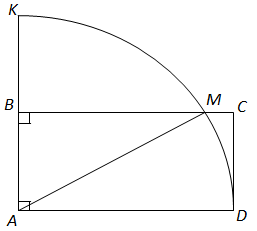
1. Площа сектора
Площа круга
2.
У
Відповідь: 1. 20. 2. 240.
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.
Завдання скеровано на перевірку знання властивостей трикутників та їх основних властивостей.
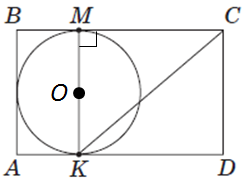
1.
2.
Відповідь: 1. 4. 2. 152.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання скеровано на перевірку знання властивостей квадрата, трапеції; вміння використовувати формули площ геометричних фігур для розв’язування планіметричних задач.
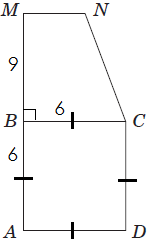
1.
2. У прямокутній трапеції
3.
Відповідь: 1Г, 2Д, 3A.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання скеровано на перевірку знання властивостей прямокутника, трапеції, вміння використовувати формули площ геометричних фігур для розв’язування планіметричних задач.
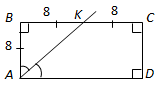
1.
2.
3.
Відповідь: B.
ТЕМА: Геометрія. Стереометрія. Многогранники.
Завдання перевіряє вміння розв’язувати задачі на обчислення об’ємів піраміди.
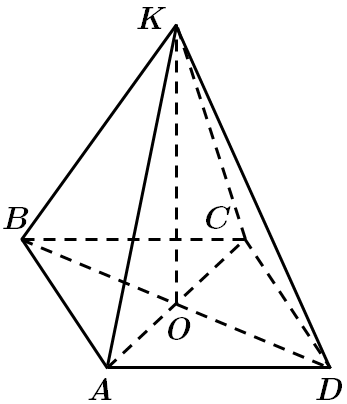
У квадраті
У
Об'єм піраміди знаходимо за формулою:
Відповідь:
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Коло та круг.
Завдання перевіряє вміння застосовувати властивості різних видів трикутників до розв'язування планіметричних задач.
1.
За властивістю прямокутника, діагоналі рівні.
2.
Відповідь: 1.
2.
ТЕМА: Геометрія. Стереометрія. Многогранники.
Завдання перевіряє знання формул для обчислення площ поверхонь призми, площі трикутника.
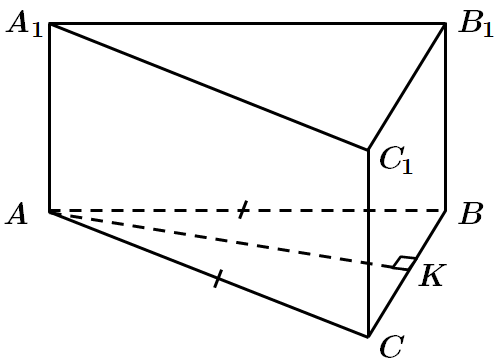
Бічні грані – прямокутники. Найбільша за площею бічна грань
У
У
Відповідь: Г.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання перевіряє знання властивостей ромба, трапеції, прямокутника, властивостей чотирикутників, вписаних в коло.
Навколо чотирикутника можна описати коло, якщо сума протилежних кутів дорівнює
Відповідь: B.
ТЕМА: Геометрія. Планіметрія. Стереометрія. Трикутники. Многогранники.
Завдання перевіряє знання про призму та її елементи, вміння знаходити площу трикутника.
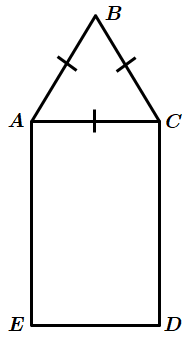
Площа основи призми – площа
За формулою
Відповідь: A.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання перевіряє знання паралелограма, ромба, квадрата та їх властивостей.
I правильне. Діагоналі ромба є бісектрисами його кутів.
II неправильне. Діагоналі точкою перетину діляться навпіл – властивість паралелограма.
III правильне. Діагоналі перпендикулярні – властивість будь-якого квадрата.
Відповідь: Д.
ТЕМА: Геометрія. Стереометрія. Многогранники.
Завдання перевіряє знання властивостей піраміди, означення кута між прямою та площиною.
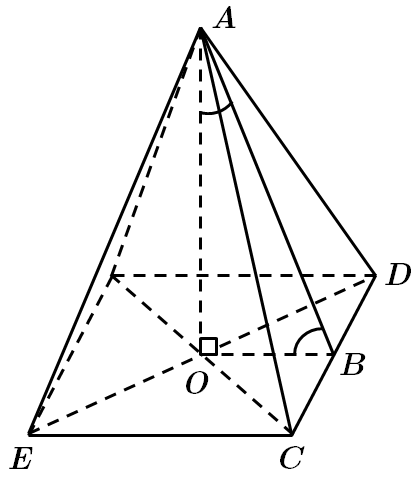
Висота піраміди
Отже,
Відповідь: Г.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання перевіряє знання властивостей прямокутника, вміння знаходити периметр.
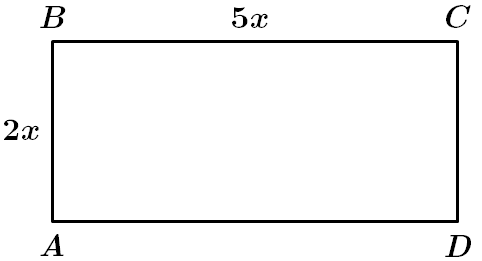
Відповідь: A.
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.
Це завдання перевіряє знання властивостей прямокутника, прямокутного та рівнобедреного трикутників, теореми Піфагора.
1. За умовою завдання у прямокутник
2. Центр кола, описаного навколо прямокутника, лежить на перетині діагоналей. Радіус кола – половина діагоналі
Отже, 2 – A.
3.
Відповідь: 1 – Б, 2 – A, 3 – В.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Це завдання перевіряє знання властивостей паралелограмів, нерівності трикутника.
I. Протилежні сторони будь-якого паралелограма рівні (властивість параллелограма).
II. Довжина сторони будь-якого трикутника менша за суму довжин двох інших сторін (нерівність трикутника).
III. Твердження неправильне.
Відповідь: B.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Це завдання перевіряє знання теореми Піфагора, співвідношення між сторонами і кутами прямокутного трикутника, формули площі прямокутного трикутника.
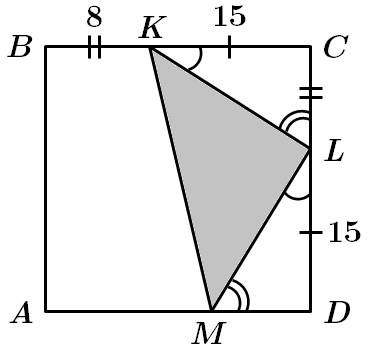
1.
У
2. Нехай
Отже,
Відповідь: 1.
2.
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.
Це завдання перевіряє знання теореми про суму кутів трикутника, властивостей суміжних та вертикальних кутів, властивості прямокутника.
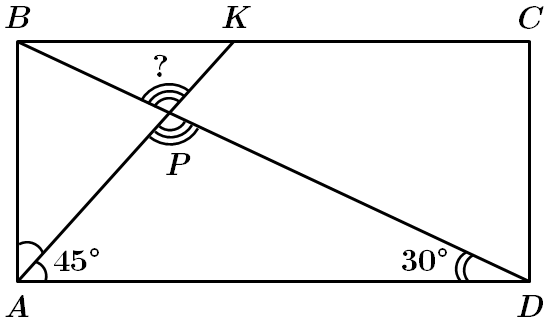
У трикутнику
Звідси
Відповідь: A.
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Це завдання перевіряє знання про трапецію та її властивості; середню лінію трапеції, вписані в коло та описані навколо кола чотирикутники, теореми Піфагора.
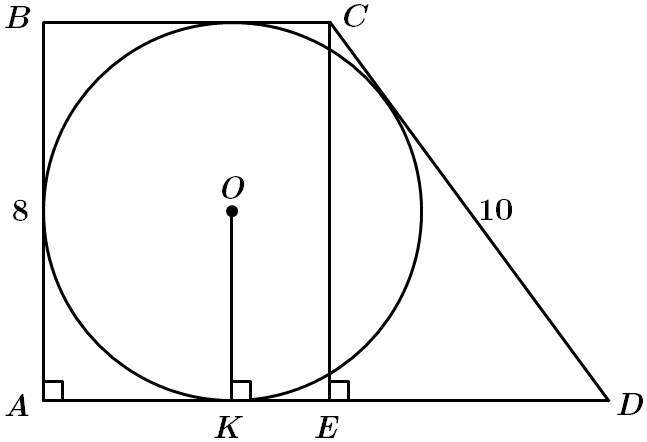
1. Висота трапеції – діаметр кола
Отже, 1 – Б.
2.
3. За властивістю чотирикутника, описаного навколо кола
4. Середня лінія трапеції дорівнює
Відповідь: 1 – Б, 2 – A, 3 – Г, 4 – B.
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.
Це завдання перевіряє вміння застосовувати властивості різних видів трикутників до розв'язування планіметричних задач та задач практичного змісту.
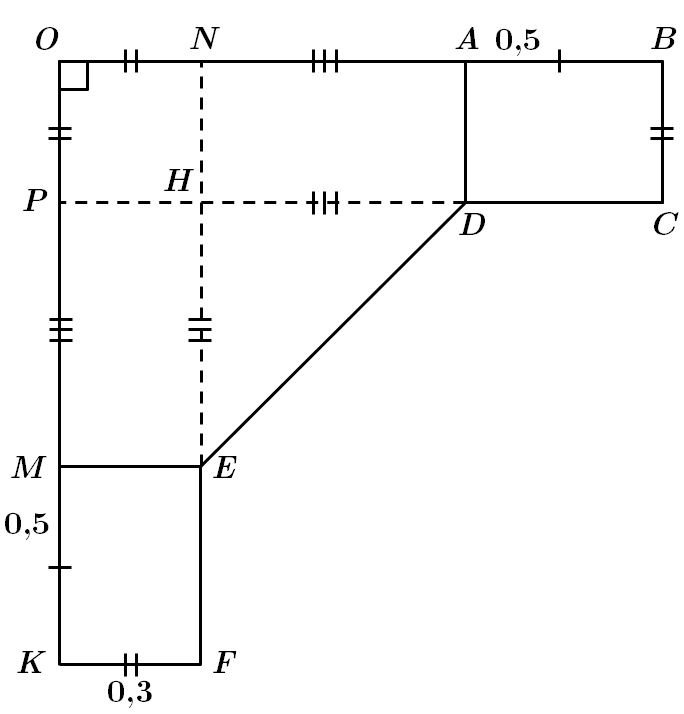
За теоремою Піфагора
Число
Серед відповідей цю нерівність задовольняє число
Відповідь: Б.
ТЕМА: Геометрія. Стереометрія. Многогранники.
Це завдання перевіряє вміння розв'язувати задачі на обчислення площ поверхонь геометричних тіл, знання многогранників та їхніх елементів.
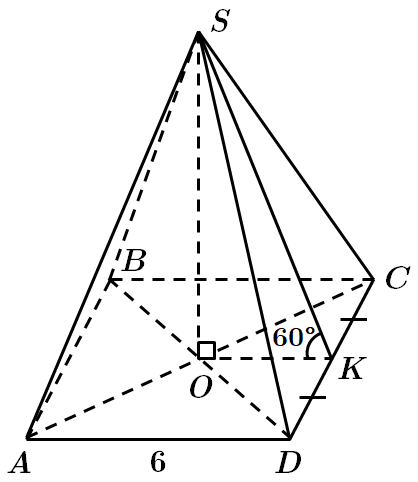
Відповідь: A.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Коло та круг.
Це завдання перевіряє знання про центральні та вписані кути, прямокутник, формули для обчислення площі трикутників.
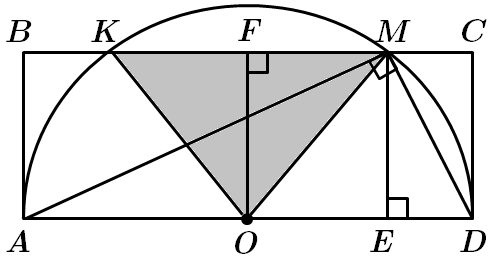
1.
За властивістю висоти до гіпотенузи:
Нехай
2.
Відповідь: 1.
2.
ТЕМА: Геометрія. Стереометрія. Многогранники.
Це завдання перевіряє вміння застосовувати означення та властивості прямокутного паралелепіпеда до розв'язування стереометричних задач і задач практичного змісту.
Площа плівки, якою обгорнута коробка – це площа поверхні прямокутного паралелепіпеда.
Основа паралелепіпеда – прямокутник зі сторонами
Відповідь: Б.
ТЕМА: Геометрія. Стереометрія. Многогранники.
Це завдання перевіряє знання про піраміду, формулу об'єму піраміди.
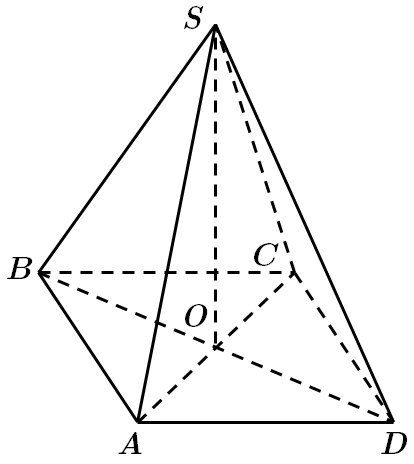
Піраміда
Відповідь: Б.
ТЕМА: Геометрія. Планіметрія. Коло та круг. Чотирикутники. Геометричні величини та їх вимірювання.
Це завдання перевіряє знання дотичної до кола та її властивості, формули довжини кола; уміння застосовувати ознаки та властивості різних видів чотирикутників до розв'язування планіметричних задач.
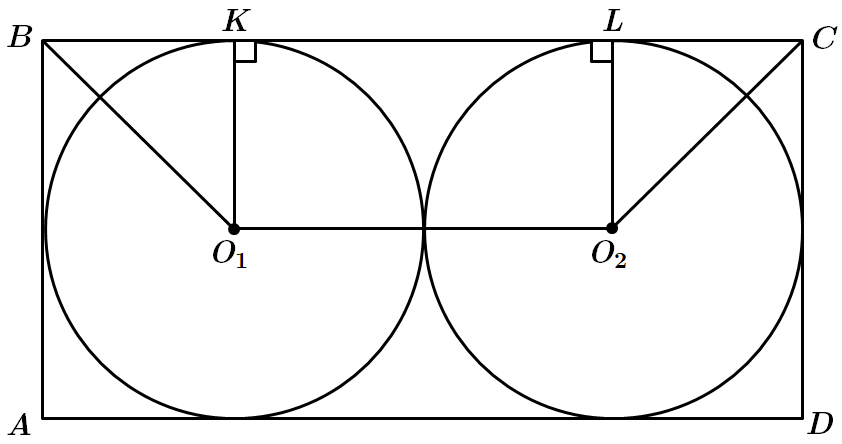
1.Довжина кола знаходиться за формулою
Отже,
2. У прямокутник
Відповідь: 1.
2.
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники. Коло та круг.
Це завдання перевіряє знання властивості дотичної до кола, вміння застосовувати набуті знання до розв'язування планіметричних задач та задач практичного змісту.
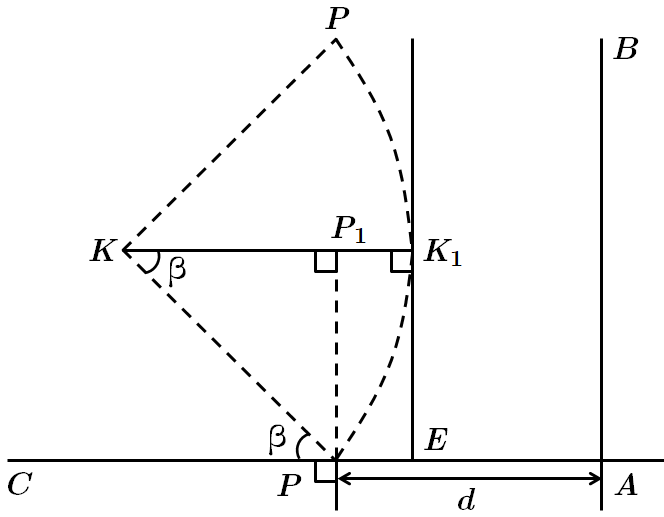
Проведемо
За властивістю дотичної до кола
У
Серед наведених відстаней найменша
Відповідь: Г.
ТЕМА: Планіметрія. Коло та круг. Трикутники. Чотирикутники.
Це завдання перевіряє вміння застосовувати властивості різних видів трикутників та чотирикутників до розв'язування планіметричних задач та задач практичного змісту.
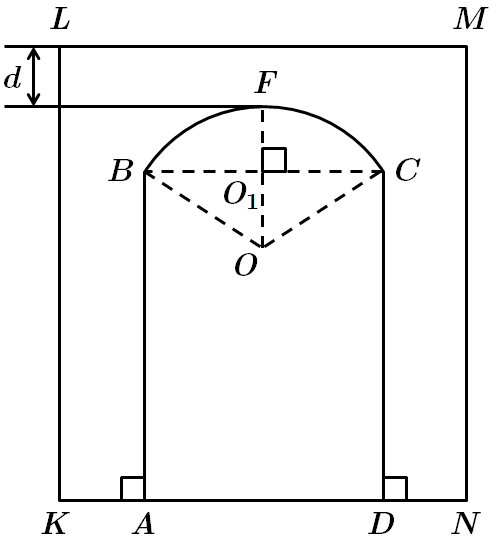
Нехай точка
Радіус кола –
Відповідь: Г.

26
ТЕМА: Геометрія. Планіметрія. Коло та круг. Чотирикутники. Геометричні величини та їхні вимірювання. Трикутники.
Це завдання перевіряє знання про коло, круг та їхні елементи, формул для обчислення площі кругового сектора, прямокутника.
1. Площу кругового сектора знаходимо за формулою
2. Нехай
У
Відповідь: 1.
2.
ТЕМА: Планіметрія. Чотирикутники.
Це завдання перевіряє знання властивостей квадрата, уміння застосовувати властивості квадрата до розв'язування планіметричних задач практичного змісту.
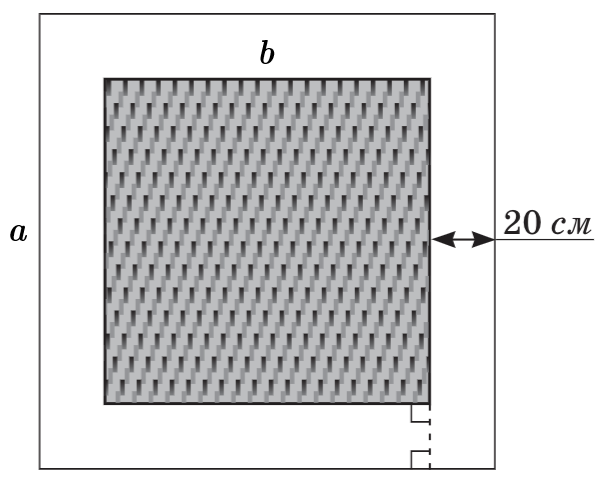
Нехай сторона квадрата (підлоги)
Сторона квадрата (килима)
Відповідь: Г.
ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості. Трикутники. Чотирикутники.
Це завдання перевіряє знання теореми Фалеса, властивостей середньої лінії трикутника, трапеції, теореми Піфагора, уміння застосовувати властивості геометричних фігур до розв'язання планіметричних задач.
1. Оскільки площа квадрата
За теоремою Фалеса
За теоремою Піфагора
2. Оскільки
Відповідь: 1.
2.
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Многогранники, тіла й поверхні обертання.
Це завдання перевіряє вміння застосовувати означення та властивості піраміди до розв’язування стереометричних задач, знаходити відстані в просторі, використовувати пряму та обернену теореми про три перпендикуляри.
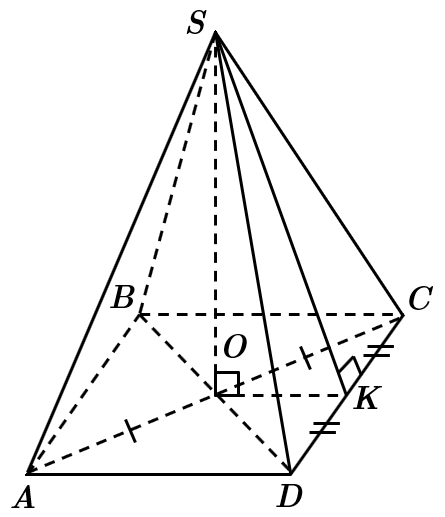
Піраміда – правильна, тому основа – квадрат, основа висоти – центр квадрата (точка перетину діагоналей).
Відповідь: Г.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
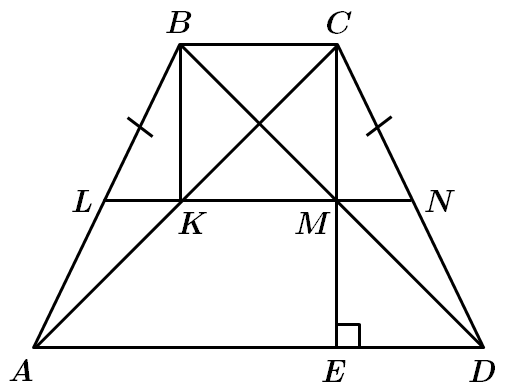
Це завдання перевіряє знання про прямокутник та його властивості, середню лінію трикутника та її властивості.
1. У
(за властивістю середньої лінії).
Отже, 1 – A.
2.
Отже, 2 – B.
3. У
Отже, 3 – Б.
4. Нехай
Отже, 4 – Г.
Відповідь: 1 – A, 2 – B, 3 – Б, 4 – Г.
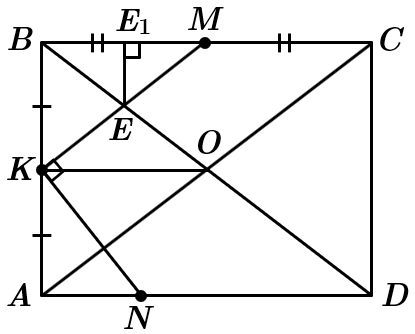
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Квадрат та його властивості. Трапеція та її властивості. Прямокутний трикутник. Теорема Піфагора.
Це завдання перевіряє вміння обчислювати довжини відрізків як елементи відповідних геометричних фігур, використовуючи властивості середньої лінії трапеції та означення квадрата.
1. Оскільки чотирикутник
тоді
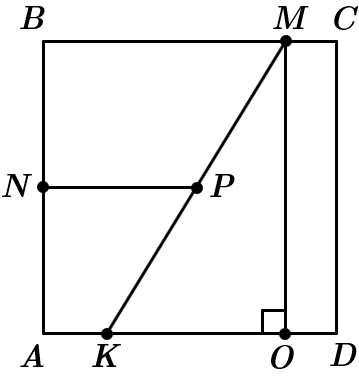
2. Опустимо з точки
За теоремою Піфагора отримуємо:
Відповідь: 1.
2.
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Подібність фігур.
Це завдання перевіряє вміння знаходити подібні фігури та використовувати пропорційність їх відповідних лінійних елементів для знаходження відношення площ цих фігур.
Подібними називаються фігури однакової форми. Коефіцієнтом подібності називається відношення відповідних лінійних елементів цих фігур. Оскільки у зображених на рисунку телевізорів екрани мають форму прямокутників, відповідні сторони яких пропорційні, то ці прямокутники подібні.
Коефіцієнт подібності дорівнює відношенню діагоналей цих прямокутників, тобто діагоналей екранів телевізорів:
Відповідь: Д.