Алгебра і початки аналізу – Розв’язування задач за допомогою рівнянь і систем рівнянь

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Рівняння, нерівності та їх системи. Відношення та пропорції.

Завдання скеровано на перевірку вміння розв’язувати текстові задачі за допомогою рівнянь на пропорційні величини та пропорційний поділ.

Нехай \(x\ \text{с}\) – тривалість жовтого сигналу, систематизуємо дані:
Зелений - \(12x\ \text{с}\)
Червоний - \((12x-15)\ \text{с}\)
Жовтий - \(x\ \text{с}\).

Тривалість зеленого сигналу відноситься до сумарної тривалості червоного та жовтого сигналів як 3 до 2.

Отже, \begin{gather*} \frac{12x}{12x-15+x}=\frac 32,\ \ \frac{12x}{13x-15}=\frac 32,\\[6pt] 3(13x-15)=2\cdot 12x,\ \ 39x-45=24x,\\[7pt] 15x=45,\ \ x=3. \end{gather*} Тривалість червоного сигналу: $$ 12x-15=12\cdot 3-15=36-15=21\ \text{с}. $$

Відповідь: 21.

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання перевіряє вміння застосовувати рівняння до розв’язування текстових задач.

Нехай власна швидкість човна \(x\) км/год.

Відстань проти течії човен подолав за час, вдвічі менший, ніж за течією. $$ \frac{48}{x+2\mathord{,}5}=\frac{18\cdot 2}{x-2\mathord{,}5}. $$ Поділимо обидві частини рівняння на \(12.\) \begin{gather*} \frac{4}{x+2\mathord{,}5}=\frac{3}{x-2\mathord{,}5}\\[6pt] 4(x-2\mathord{,}5)=3(x+2\mathord{,}5)\\[7pt] 4x-10=3x+7\mathord{,}5\\[7pt] x=17\mathord{,}5. \end{gather*}

Відповідь: \(17\mathord{,}5.\)

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання перевіряє вміння розв’язувати текстові задачі, застосовувати системи рівнянь до розв’язування текстових задач.

Нехай тривалість одного рекламного ролика \(x\) хв., а одного трейлера – \(y\) хв. Тоді,

Трейлер триває \(2\mathord{,}5\) хв \(=150\) с.

Відповідь: \(150.\)

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Текстові задачі.

Це завдання перевіряє вміння розв'язувати задачі на рух.

Нехай швидкість велосипедиста \(x\) км/год, тоді мотоцикліста \((x+48)\) км/год.

На дорогу з міста \(A\) до міста \(B\) велосипедист витратив \(2\) години. Отже, відстань з \(A\) до \(B\) становить \(2x\) км.

Мотоцикліст виїхав на \(1\mathord{,}5\) год пізніше, але прибув одночасно з велосипедистом. Отже, \(0\mathord{,}5(x+48)\) км становить відстань від \(A\) до \(B.\)

Відстань між містами \(A\) та \(B\)    \(2\cdot 16=32\) км.

Відповідь: \(32.\)

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лiнiйнi, квaдpaтні, рацiональнi, iррацiональнi, показникові, логарифмiчнi, тригонометричні рівняння, неpiвності та їx системи.

Це завдання перевіряє вміння застосовувати рівняння до розв'язування текстових задач.

\(2\) год \(15\) хв \(=2\frac 14\) год.

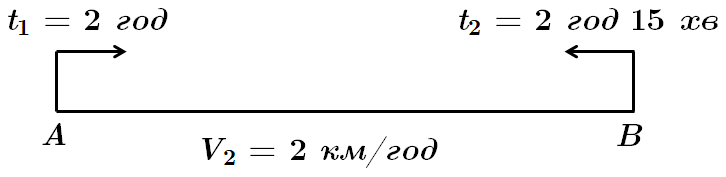
Нехай власна швидкість телохода \(x\) км/год, тоді швидкість за течією \((x+2)\) км/год, проти течії – \((x-2)\) км/год. Оскільки відстань, яку пройшов теплохід за течією та проти течії, однакова, то складемо рівняння

Отже, власна швидкість теплохода \(34\) км/год.

Відповідь: \(34.\)

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Відсотки. Основні задачі на відсоки. Текстові задачі. Квадратні рівняння.

Це завдання перевіряє вміння застосовувати рівняння до розв'язування текстових задач, розв'язувати задачі на відсотки.

1. Нехай у кожному ряду висадили \(x\) кущів, тоді кількість рядів буде \((x-20).\) Усього висадили \(125\) кущів троянд. Складемо рівняння:

Отже, в кожному ряду \(25\) кущів.

2. Усього кущів у першому рядку \(25.\) Ушкоджених кущів виявилось \(16\text{%}\), отже, неушкоджених кущів \(84\text{%}\) від кількості кущів у першому рядку.

Відповідь: 1. \(25.\)
                   2. \(21.\)

ТЕМА: Алгебра. Рівняння, нерівності та їхні системи. Раціональні рівняння. Застосування рівнянь до розв'язування текстових задач.

Це завдання перевіряє вміння розв'язувати раціональні рівняння, застосовувати рівняння до розв'язування текстових задач.

Нехай щодня планували виробляти \(\frac{240}{n}\) стільців. Оскільки завдання виконали на \(2\) дні раніше запланованого терміну, то щодня виробляли \(\frac{240}{n-2}\) стільців. Денна норма збільшилась на \(4\) стільця, тому складемо рівняння

За теоремою Вієта знаходимо корені рівняння: \(n=-10\) або \(n=12.\)

Оскільки \(n\) – кількість днів, то визначається натуральним числом, то правильна відповідь: \(12\) днів.

Відповідь: \(12.\)

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Текстові задачі. Рівняння, нерівності та їхні системи. Раціональні рівняння.

Це завдання перевіряє вміння розв'язувати рівняння, що зводиться до квадратного, розв'язувати текстові задачі.

Нехай порожній басейн заповнюється з другої труби за \(x\) хвилин, тоді з першої труби – за \((x-40)\) хвилин.

За \(1\) хвилину працюючи разом вони заповнять \(1/21\) частину басейну. Складемо рівняння:

Корені рівняння

Отже, друга труба наповнює басейн за \(70\) хвилин, а перша – за $$ 70-40=30\ \text{хв.} $$

Відповідь: \(30.\)

ТЕМА: Алгебра та початки аналізу. Числа і вирази. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв'язувати текстові задачі, застосовувати рівняння до розв'язування текстових задач, знання методів розв'язування раціональних рівнянь.

Нехай швидкість автобуса \(x\) км/год, тоді швидкість автомобіля

\(150\) км автобус проїжджає за \(\frac{150}{x}\) год, а автомобіль за \(\frac{150}{1\mathord{,}2x}\) год. Це на \(30\) хв \(\left(\frac 12\ \textit{год}\right)\) менше. Розв'яжемо рівняння

Час, за який автомобіль долає відстань між \(A\) та \(B\) $$ \frac{150}{1\mathord{,}2\cdot 50}=2\mathord{,}5\ \textit{год}. $$

Відповідь: \(2\mathord{,}5.\)

ТЕМА: Алгебра та початки аналізу. Числа і вирази. Текстові задачі. Застосування рівнянь до розв'язування задач.

Це завдання перевіряє вміння розв'язувати текстові задачі, застосовувати рівняння до розв'язування задач.

Розв'яжемо задачу складанням рівняння.

Нехай на виготовлення \(1\) стола необхідно \(x\) пластику, тоді на \(1\) диван витрачають \((x+1)\) кг, а на крісло – \((x+1-3)\) кг.

На \(10\) крісел витрачають стільки пластику, скільки на \(2\) стола та \(4\) дивана, тому

На \(1\) стiл витрачається пластику \(6\) кг, \(1\) диван – \(7\) кг, \(2\) крісла – \(2\cdot 4=8\) кг.

Отже, на виготовлення одного комплекту меблів витрачають $$ 6+7+8=21\ \text{кг} $$ пластику.

Відповідь: \(21.\)