Розділ: Мультитести
Тест: Тренувальний мультитест (11 варіант)
Блок: Фізика
Кількість завдань: 20
ТЕМА: Механіка. Основи кінематики. Додавання швидкостей.
Завдання скеровано на перевірку знання і розуміння додавання швидкостей і вміння застосовувати цей закон до будь-яких ситуацій.
Скористаймося законом додавання швидкостей:
швидкість
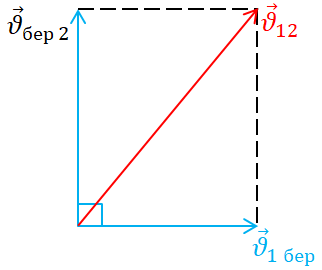
Модуль швидкості
Відповідь: Б.
ТЕМА: Механіка. Закони збереження в механіці. Прості механізми.
Завдання скеровано на перевірку знання і розуміння принципу дії простих механізмів.
Давнє золоте правило механіки стверджує: «У скільки разів ми виграємо в силі, у стільки ж разів програємо у відстані».
Важіль ‒ це тверде тіло, яке може обертатися навколо нерухомої осі ‒ осі обертання. Лом, лопата, лінійка ‒ все це приклади важелів. Найчастіше як важіль використовують довгий стержень із закріпленою віссю обертання. За допомогою важеля можна отримати виграш у силі: так, прикладаючи досить малу силу, можна підняти порівняно важке тіло. Однак виграш у силі завжди супроводжується програшем у відстані: плече меншої сили є більшим, тому, коли людина за допомогою важеля підіймає важке тіло навіть на невелику висоту, рука долає значну відстань. І навпаки, діючи на коротке плече важеля, програє в силі, проте у стільки ж разів виграє у відстані.
Похила площина ‒ це простий механізм, за допомогою якого можна піднімати важкі предмети, прикладаючи до них відносно невелику силу. Що пологіший ухил площини, то легше виконати роботу. Для втягування тіла вгору похилою площиною потрібна значно менша сила, ніж для підняття цього самого тіла вертикально. Властивість похилої площини давати виграш у силі та змінювати напрямок дії цієї сили застосовують у конструкціях сходів, ескалаторів, конвеєрів, пандусів тощо.
Блок – це простий механізм, що має форму колеса із жолобом по ободу, через який перекинуто мотузку (канат). Розрізняють рухомий і нерухомий блоки. Нерухомий блок подібний до важеля з однаковими плечима, і тому він не дає виграшу в силі, проте дає змогу змінювати напрямок дії сили.
Рухомий блок подібний до важеля, у якого відношення плечей становить
Отже, з усіх названих простих механізмів лише нерухомий блок змінює напрямок сили, не даючи виграшу в ній.
Відповідь: Г.
ТЕМА: Механіка. Основи динаміки. Взаємодія тіл. Маса. Сила. Третій закон Ньютона.
Завдання скеровано на перевірку знання і розуміння основних понять динаміки, третього закону Ньютона.
Пружним називають зіткнення, унаслідок якого сумарна кінетична енергія тіл зберігається. Отже, утрат енергії немає.
Центральним називають зіткнення, під час якого швидкості руху тіл до і після нього (пружного чи непружного) напрямлені вздовж прямої, що проходить крізь центри мас цих тіл.
Під час пружного центрального зіткнення тіла однакової маси обмінюються швидкостями.
За третім законом Ньютона кулі взаємодіятимуть із силами, що мають одну природу, напрямлені вздовж однієї прямої, рівні за модулем і протилежні за напрямком:
Різним тілам властиво по-різному реагувати на ту саму дію. Властивість тіла, яка полягає в тому, що для зміни швидкості руху тіла під дією сили потрібен деякий час, називають інертністю.
Якщо на два тіла масами
Отже, визначимо співвідношення між модулями прискорень цих куль:
Відповідь: Б.
ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл.
Завдання скеровано на перевірку знання і розуміння термодинамічних процесів і зміни внутрішньої енергії.
Внутрішня енергія тіла змінюється зі зміною його температури: зі збільшенням температури тіла його внутрішня енергія збільшується, а зі зменшенням температури ‒ зменшується. Також внутрішня енергія змінюється зі зміною агрегатного стану речовини: під час зміни агрегатного стану речовини змінюється взаємне розташування її частинок, тобто змінюється потенціальна енергія їхньої взаємодії.
Нагрівання – це природний чи штучний фізичний процес підвищення температури. Це може відбуватися за рахунок внутрішньої енергії або підведення енергії ззовні. Під час нагрівання тіла поглинають порції теплоти, внутрішня енергія збільшується.
Плавлення ‒ це процес переходу речовини з твердого стану в рідкий. Під час плавлення температура речовини не змінюється. Уся енергія, що надходить від нагрівача, витрачається на руйнування кристалічної ґратки. У цей інтервал часу триває збільшення внутрішньої енергії речовини.
Кристалізація ‒ це процес переходу речовини з рідкого стану у твердий кристалічний. За температури кристалізації швидкість руху молекул зменшується настільки, що молекули вже не перестрибують із місця на місце. Вони поступово займають фіксовані положення, а на момент завершення кристалізації вже всі молекули коливаються у вузлах кристалічної ґратки. Внутрішня енергія речовини зменшується.
Пароутворенням називають процес переходу речовини з рідкого стану в газуватий. Пароутворення відбувається за будь-якої температури, і воно то інтенсивніше, що вища температура рідини. Крім того, під час пароутворення виконується робота проти сил міжмолекулярного притягання і проти сил зовнішнього тиску, тому процес випаровування супроводжується поглинанням енергії, внутрішня енергія речовини збільшується.
Відповідь: B.
ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Питома теплоємність речовини.
Завдання скеровано на перевірку знання і розуміння фізичного змісту питомої теплоємності речовини.
Питома теплоємність речовини
Застосуймо цю формулу для ситуації, про яку йдеться в умові завдання. Дані візьмемо з графіка умови завдання:
Відповідь: Б.
ТЕМА: Електродинаміка. Основи електростатики. Закон Кулона.
Завдання скеровано на перевірку знання і розуміння закону Кулона, а також вміння шукати рівнодійну сил.
Закон Кулона: сила
Сили, з якими взаємодіють точкові заряди, називають силами Кулона. Сили Кулона напрямлені вздовж умовної прямої, яка з’єднує точкові заряди, що взаємодіють.
З боку кульки
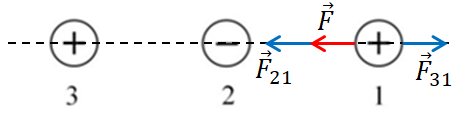
Відповідно до закону Кулона сила, що діє з боку кульки
Тож рівнодійна
Відповідь: Б.
ТЕМА: Електродинаміка. Закони постійного струму.
Завдання скеровано на перевірку знання і розуміння законів постійного струму.
Амперметр використовують для вимірювання сили струму. Його послідовно зі споживачем вмикають у коло, у якому вимірюють силу струму. Сила струму в послідовно з’єднаних провідниках однакова і дорівнює загальній силі струму в ділянці кола. Як і будь-який вимірювальний прилад, амперметр не має впливати на значення вимірюваної величини. Тому амперметр сконструйовано так, що в разі приєднання його до електричного кола значення сили струму в колі практично не змінюється. З метою уникнення змін у роботі кола внутрішній опір амперметра має бути суттєво меншим, ніж опір елементів, які послідовно з ним увімкнені.
На запропонованих схемах А, Б і В електричних кіл послідовно з амперметром підключені інші споживачі, тому напруга на ньому буде невелика і він не зіпсується.
На рисунку Г зображено схему електричного кола, де амперметр підключено паралельно до джерела струму. Опір амперметра невеликий, напруга буде така сама, яку подають на споживачі, тому сила струму буде великою, що може зіпсувати амперметр.
Відповідь: Г.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Ампера.
Завдання скеровано на перевірку знання і розуміння дії магнітного поля на провідник із струмом.
Однорідне магнітне поле з індукцією діє на провідник зі струмом (у цьому випадку на дротяну рамку) із силою Ампера
Якщо провідник (сторона рамки) розташований паралельно лініям магнітної індукції ‒ магнітне поле на провідник не діє:
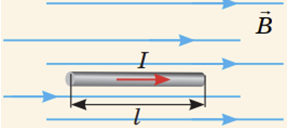
Отже, відповідно до рисунку в умові завдання, сторони рамки
Відповідь: B.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Гармонічні коливання.
Завдання скеровано на перевірку знання суті й розуміння закономірностей коливального процесу тіла на пружині, а також уміння описувати цей процес відповідним рівнянням.
Коливання, під час яких координата
В умові зазначено, що в початковий момент часу відхилення від положення рівноваги було максимальним. Це відповідає функції косинуса, тому варіанти відповіді Б і Г не підходять.
Також відомо, що максимальне відхилення від положення рівноваги ‒ амплітуда ‒ дорівнює
Упевнимося в цьому, перевіривши циклічну частоту коливань:
Отже, обчислімо циклічну частоту:
Отже, за цих умов єдиним рівнянням, що описує рух пружинного маятника, може бути рівняння
Відповідь: B.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Власна частота й період електромагнітних коливань.
Завдання скеровано на перевірку знання і розуміння формули для визначення довжини електромагнітної хвилі, її зв’язку з періодом коливань.
Довжину
Запишімо формули для визначення періоду коливань для обох випадків:
Визначімо відношення періодів, щоб дізнатися, у скільки разів змінився період коливань контуру від зміни конденсатора:
Отже, період коливань контуру збільшився втричі (в
Відповідь: B.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Радіоактивність. Альфа-, бета-, гамма-випромінювання.
Завдання скеровано на перевірку знання і розуміння видів радіоактивного випромінювання.
Дозиметр ‒ це прилад для вимірювання поглиненої дози або еквівалентної дози йонізувального випромінювання, а також їхньої потужності. Дозиметр, яким вимірюють активність радіонукліду в джерелі або зразку (в об’ємі рідини, газу, аерозолю, на забруднених поверхнях) або щільність потоку йонізувального випромінювання для перевірки на радіоактивність підозрілих предметів й оцінювання радіаційного стану в певному місці в цей час, називають радіометром.
Різні радіонукліди можуть випромінювати промені трьох видів:
1)
2)
3)
Від впливу радіації можна захиститися. Як показали експерименти, досить тонкого аркуша паперу
Найважче захиститися від
Тож якщо дозиметр помістити в металевий футляр, то прилад не фіксуватиме
Металевий футляр зі стінками завтовшки кілька міліметрів пропускатиме лише
Відповідь: Б.
Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Радіоактивність.
Завдання скеровано на перевірку знання і застосування основного закону радіоактивного розпаду.
Скористаймося основним законом радіоактивного розпаду:
Підставімо всі дані у формулу:
Відповідь: B.
ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл.
Завдання скеровано на перевірку знання і розуміння властивостей станів речовин.
1. Рідина ‒ речовина зберігає свій об’єм, не зберігає форму (Б).
Молекули рідини в цілому розташовані хаотично, однак у розташуванні найближчих молекул зберігається певний (ближній) порядок. Середня відстань між молекулами приблизно дорівнює розмірам самих молекул, тому міжмолекулярні сили втримують їх біля положення рівноваги. Кожна молекула рідини певний час (порядку
2. Насичена пара ‒ тиск речовини не збільшується під час ізотермічного стиснення (В).
Пару, яка перебуває в стані динамічної рівноваги зі своєю рідиною, називають насиченою парою. Динамічна рівновага встановлюється між процесами конденсації і випаровування, якщо кількість молекул, які повертаються в рідину, дорівнюватиме кількості молекул, які за той самий час залишають рідину. Якщо зменшити об’єм, який займає насичена пара, то на короткий проміжок часу концентрація молекул пари збільшиться, динамічна рівновага порушиться і кількість молекул, що надходять у рідину, перевищить кількість молекул, які залишають її поверхню. Конденсація переважатиме над випаровуванням доти, доки концентрація молекул пари не зменшиться до концентрації молекул насиченої пари, а тиск не стане дорівнювати тиску насиченої пари. Зі збільшенням об’єму, який займає насичена пара, навпаки, переважатиме процес випаровування, унаслідок цього знову встановиться початковий тиск. Тобто (на відміну від ідеального газу) тиск насиченої пари не залежить від її об’єму.
3. Розріджений газ ‒ потенціальною енергією взаємодії молекул речовини можна знехтувати (Г).
Потенціальна енергія ‒ це енергія, яку має тіло внаслідок взаємодії з іншими тілами або внаслідок взаємодії частин тіла між собою. Розріджений газ можна вважати ідеальним газом. У розріджених газах (такими, наприклад, є звичайні гази за нормальних умов) відстань між молекулами в багато разів перевищує розміри самих молекул, тому ці молекули можна вважати матеріальними точками, а їхньою взаємодією, за винятком моментів зіткнення, можна знехтувати.
4. Кристалічне тверде тіло ‒ речовині може бути властива анізотропія (Д).
Анізотропія ‒ це залежність фізичних властивостей кристала від вибраного в ньому напрямку. Монокристал ‒ тверде тіло, частинки якого утворюють єдину кристалічну ґратку. Упорядковане розташування частинок у монокристалі є причиною того, що монокристали мають плоскі грані й незмінні кути між гранями; фізичні властивості монокристалів залежать від вибраного в них напрямку. Механічна міцність багатьох кристалів різна в різних напрямках: шматок слюди легко розшаровується на тонкі пластинки в одному напрямку, але його набагато складніше розламати перпендикулярно до пластинок. Від напрямку, вибраного в кристалі, залежать його теплопровідність, електропровідність, заломлення, прозорість, лінійне розширення і багато інших фізичних властивостей. Анізотропія кристалів зумовлена їхніми кристалічними ґратками: у різних напрямках відстані між частинками, що утворюють кристалічну ґратку, різні.
Відповідь: 1Б, 2В, 3Г, 4Д.
ТЕМА: Коливання і хвилі. Оптика. Закони відбивання і заломлення світла.
Завдання скеровано на перевірку знання і розуміння законів відбивання і заломлення, ураховуючи геометричні побудови.
Як позначено на рисунку, кут
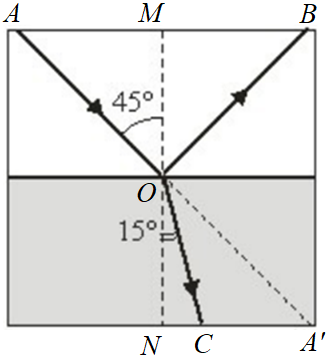
Сформулюймо закони відбивання світла:
1. Промінь
2. Кут відбивання світла дорівнює куту його падіння:
Кут
1. Кут падіння (за означенням):
2. Кут заломлення (за означенням):
3. Кут відхилення заломленого променя від початкового напрямку:
4. Кут між променем, що падає, і відбитим:
Відповідь: 1В, 2А, 3Б, 4Д.
ТЕМА: Механіка. Основи кінематики. Додавання швидкостей.
Завдання скеровано на перевірку знання і розуміння додавання швидкостей.
Визначімо довжину потяга
Якщо за умовою зустрічний потяг
Значення швидкості
Тоді обчислімо швидкість
Відповідь: 22.
ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона.
Завдання скеровано на перевірку знання і розуміння стану спокою тіла, застосування другого закону Ньютона.
Рівнодійна сил, що діють на тягарець, дорівнює нулю (тягарець просто висить на пружині, не коливається). За другим законом Ньютона сила тяжіння
Прирівняймо вирази для зазначених сил й обчислімо масу тягарця:
Відповідь: 0,3.
ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Поверхневий натяг рідин. Сила поверхневого натягу.
Завдання скеровано на перевірку знання і розуміння дії сили поверхневого натягу.
Сила тяжіння
Виведемо формулу для маси краплі і обчислимо її:
Відповідь: 12,56.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Ампера.
Завдання скеровано на перевірку знання і розуміння сили Ампера.
З боку магнітного поля на провідник зі струмом діє сила Ампера. Якщо провідник прямолінійний, а магнітне поле, в якому він перебуває, однорідне, то модуль сили Ампера визначають за формулою
Виразімо силу струму із цієї формули й обчислімо його значення:
Відповідь: 20.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Вільні електромагнітні коливання в коливальному контурі. Перетворення енергії в коливальному контурі.
Завдання скеровано на перевірку знання і розуміння перетворення енергії в коливальному контурі.
Щоб у коливальному контурі виникли вільні коливання, системі треба передати енергію, наприклад, зарядити конденсатор, як це описано в завданні. На обкладках конденсатора електроємністю
Під час коливань відбувається періодичне перетворення енергії: енергія електричного поля перетворюється на енергію магнітного поля і навпаки.
У будь-якій коливальній системі завжди є втрати енергії, тому реальні коливання є згасними. Енергія витрачається на нагрівання підвідних проводів, обмотки котушки, на поляризацію діелектрика, тощо:
Відповідь: 8.
ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Фотоефект і його експериментально встановлені закони. Рівняння Ейнштейна для фотоефекту.
Завдання скеровано на перевірку знання, розуміння і застосування фізичних характеристик фотоефекту, рівняння Ейнштейна для фотоефекту, його законів.
Унаслідок поглинання фотона матеріалом (металом) енергія фотона
Енергію фотона визначімо за формулою
Робота виходу
За умовою завдання частота випромінювання, що падало на поверхню матеріалу, змінювалася. Запишімо рівняння Ейнштейна для обох випадків:
Матеріал, який опромінювали, не змінювали, тому робота виходу в обох випадках однакова:
Виразимо з рівнянь максимальні кінетичні енергії:
Визначімо співвідношення цих енергій після зміни частоти випромінювання:
Відповідь: 2,5.




