Розділ: Мультитести
Тест: Тренувальний мультитест (1 варіант)
Блок: Фізика
Кількість завдань: 20
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Період і частота.
Завдання скеровано на перевірку розуміння рівномірного руху по колу та його характеристик.
Період
Тоді час
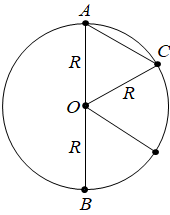
Час руху
Визначімо, у скільки разів модуль переміщення за
Відповідь: B.
ТЕМА: Механіка. Закони збереження в механіці. Механічна робота.
Завдання скеровано на перевірку розуміння поняття механічної роботи.
Механічна робота (робота сили)
Випадок, коли робота дорівнюватиме нулю, зілюстровано на рисунку: на тіло, наприклад, діє сила, напрямлена вертикально вниз – сила тяжіння, а переміщення відбувається горизонтально завдяки іншій силі – силі тяги двигуна, напрямок дії якої збігається з вектором переміщення. Між вектором сили тяжіння і вектором переміщення кут дорівнює
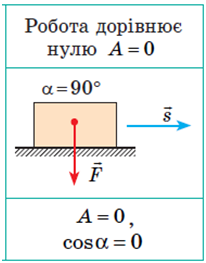
Розгляньмо випадки, наведені у варіантах відповіді завдання.
А У разі горизонтального польоту літака вектор сили тяжіння напрямлений вертикально вниз (сила тяжіння завжди напрямлена вертикально вниз), а вектор переміщення ‒ горизонтально. Отже, кут між вектором сили тяжіння і вектором переміщення дорівнює
Б і Г Коли яблуко падає вертикально з дерева, то кут між вектором сили тяжіння і вектором переміщення дорівнює
В М’яч, кинутий під кутом до горизонту, рухатиметься вздовж траєкторії, що є параболою. Якщо з’єднати початкову точку
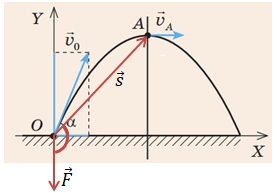
Отже, робота сили тяжіння дорівнюватиме нулю у випадку горизонтального руху літака.
Відповідь: A.
ТЕМА: Механіка. Основи динаміки. Умови рівноваги тіла.
Завдання скеровано на перевірку знання і розуміння умов рівноваги тіла.
Важіль перебуває в рівновазі, якщо сума моментів сил, що обертають його проти годинникової стрілки
У формулі
Отже, для врівноваження важеля тягарець треба підвісити у точці
Відповідь: A.
ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Основні положення молекулярно-кінетичної теорії та дослідне обґрунтування їх.
Завдання скеровано на перевірку знання і розуміння означення теплового руху.
Будь-яке тіло складається зі структурних одиниць (атомів, молекул, йонів), які невпинно хаотично (безладно) рухаються. Цей рух називають тепловим.
А Зміна із часом положення тіла в просторі відносно інших тіл ‒ це механічний рух.
Б Рух, який виникає внаслідок зміни температури тіла ‒ це може бути зміна об’єму тіла внаслідок нагрівання чи охолодження (як наприклад, рух рідини у довгій тонкій трубці термометра чи секції мосту змикаються під час спеки й розходяться під час морозів).
В Безперервний, хаотичний рух частинок, із яких складається тіло ‒ тепловий рух.
Г Упорядкований рух частинок, з яких складається тіло ‒ це може бути частково правильне визначення електричного струму, якщо частинки будуть зарядженими й будуть упорядковано рухатися під дією електричного поля.
Отже, правильна відповідь ‒ В.
Відповідь: B.
ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Коефіцієнт корисної дії теплового двигуна і його максимальне значення.
Завдання скеровано на перевірку знання і розуміння формули для визначення коефіцієнта корисної дії ідеальної теплової машини.
Коефіцієнт корисної дії ідеальної теплової машини, що працює за циклом Карно з нагрівником, температура якого
За умовою абсолютна температура нагрівника у
Підставимо це співвідношення у формулу коефіцієнта корисної дії теплової машини:
Відповідь: B.
ТЕМА: Електродинаміка. Основи електростатики. Напруженість електричного поля. Потенціал, різниця потенціалів.
Завдання скеровано на перевірку розуміння силової та енергетичної характеристик електростатичного поля.
Напруженість – це силова характеристика електричного поля. Якщо відстань між лініями напруженості в деякій області простору є однаковою, то так само однаковою є напруженість поля в цій області. Електричне поле, вектори напруженості якого однакові в усіх точках простору, називають однорідним. Оскільки з рисунка в умові випливає, що відстані між лініями напруженості електричного поля різні, то це поле неоднорідне. Напруженість поля більшає в міру наближення до заряду, силові лінії згущуються. Отже, напруженість у точці
Потенціал – це енергетична характеристика електростатичного поля. Силові лінії поля напрямлені в бік зменшення потенціалу. Що більша напруженість, то швидше зменшується потенціал під час переміщення вздовж силової лінії (напруженість характеризує швидкість зміни потенціалу). Отже, потенціал у точці
Відповідь: Б.
ТЕМА: Електродинаміка. Закони постійного струму. Послідовне і паралельне з’єднання. Закон Ома для повного кола.
Завдання скеровано на перевірку вміння застосовувати знання про співвідношення між фізичними величинами, що характеризують електричний струм, за паралельного і послідовного з’єднання.
Коли ключ не замкнений, то струм проходить через одну лампочку й амперметр. А якщо ключ замкнути, то струм проходитиме через дві лампочки, з’єднані паралельно.
За паралельного з’єднання загальний опір лампочок буде у
Сила струму
Отже, якщо опір удвічі зменшиться, то сила струму вдвічі збільшиться, тобто покази амперметра збільшаться (варіанти відповіді А і В відкидаємо).
Покази вольтметра не зміняться, тому що друга лампочка приєднана паралельно.
Відповідь: Г.
ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Електричний струм у розчинах і розплавах електролітів.
Завдання скеровано на перевірку знання різних середовищ і носіїв струму в них.
Силіцій ‒ це напівпровідник, електричні властивості якого істотно залежать від домішок, тому основними носіями заряду в ньому можуть бути і умовні частинки, що мають позитивний заряд – «дірки», і електрони.
Солона вода ‒ це розчин електроліту. Провідність такого розчину йонна, тобто носіями струму є лише позитивні і негативні йони.
Сплав міді з оловом ‒ це бронза, провідник. Носіями електричного струму в цьому сплаві є вільні електрони.
У газах, як то пара ртуті всередині лампи, носіями електричного струму є і вільні електрони, і позитивні та негативні йони.
Відповідь: Б.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Трансформатор.
Завдання скеровано на перевірку знання і розуміння співвідношень між фізичними величинами, що характеризують трансформатор.
У режимі холостого ходу трансформатора (без навантаження, тобто вторинна обмотка розімкнена, до неї не підключено споживача) справджується рівність:
Із цієї рівності визначимо напругу на вторинній обмотці:
Відповідь: Г.
ТЕМА: Коливання і хвилі. Оптика. Дисперсія світла.
Завдання скеровано на перевірку знання та розуміння хвильових явищ.
Дифракція ‒ це явище потрапляння світлових хвиль в область геометричної тіні, тобто відхилення їх від прямолінійного поширення.
Явище розкладання світла в спектр, зумовлене залежністю абсолютного показника заломлення середовища від частоти світлової хвилі, називають дисперсією світла.
Отже, різнокольоровий блиск каміння, освітленого білим світлом, пояснюють дисперсією.
Інтерференція ‒ це явище накладання когерентних хвиль, унаслідок якого спостерігають стійку в часі картину посилення їх і послаблення в різних точках простору.
Поляризація ‒ це властивість світлових і електромагнітних коливань відбуватися в одній площині. Максвелл припустив, що заряди не приходять ззовні, а утворюються завдяки поляризації всередині речовини. Поляризація світла ‒ перетворення пучків природного світла на світло з обмеженим напрямком коливань.
Отже, дисперсія є причиною утворення різних кольорів, спектру.
Відповідь: Б.
ТЕМА: Квантова фізика. Елементи теорії відносності. Релятивістський закон додавання швидкостей.
Завдання скеровано на перевірку розуміння закону додавання швидкостей у класичній і релятивістській механіці.
Швидкість світла
Також швидкість руху електрона в системі відліку, пов’язаній із космічним кораблем, що за умовою віддаляється в протилежний від електрона бік, не може бути менша за
Залишається єдина можлива із запропонованих швидкість руху електрона –
Відповідь: B.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Альфа-, бета- і гамма-випромінювання.
Завдання скеровано на перевірку знання і розуміння радіоактивних перетворень.
Запишемо рівняння ядерної реакції відповідно до умови завдання:
Порядковий номер елемента в періодичній системі хімічних елементів відповідає кількості протонів у ядрі (зарядовому або протонному числу
Пригадаємо правила зміщення:
1. Під час
2. Під час
Відповідно до цих правил і згідно з умовою обчислимо, на скільки будуть відрізнятися в періодичній системі порядкові номери цих елементів:
Відповідь: A.
ТЕМА: Механіка. Основи кінематики. Закони збереження в механіці. Потенціальна і кінетична енергія.
Завдання скеровано на перевірку розуміння характеру прямолінійного рівноприскореного руху тіла, кинутого вертикально вгору, а також під час цього руху перехід механічної енергії з одного виду в інший.
Рух тіла, кинутого вертикально вгору, − це прямолінійний рівноприскорений рух.
Прискорення, із яким рухається тіло, − це прискорення вільного падіння
Розглянемо кожний момент часу.
1)
Потенціальна енергія дорівнює нулю, оскільки тіло ще не встигло піднятися на хоч якусь висоту від нульового рівня:
Отже, моменту часу
2)
Кінетичну енергію в цей момент часу обчислюють за формулою:
Тоді потенціальна енергія тіла за законом збереження механічної енергії дорівнюватиме різниці максимальної кінетичної енергії (під час старту тіла в момент часу
Отже, моменту часу
3)
Кінетична енергія в цей момент часу дорівнює нулю:
Тоді потенціальна енергія тіла за законом збереження механічної енергії дорівнює максимальній кінетичній енергії під час старту тіла в момент часу
Отже, моменту часу
4)
Кінетична енергія в цей момент часу дорівнює:
Тоді потенціальна енергія тіла за законом збереження механічної енергії дорівнює різниці максимальної кінетичної енергії (під час старту тіла в момент часу
Отже, моменту часу
Відповідь: 1А, 2Г, 3Д, 4В.
ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Фотоефект та експериментально встановлені його закони.
Завдання скеровано на перевірку знання і розуміння рівняння Ейнштейна для зовнішнього фотоефекту та його законів.
Доберімо до початку твердження його продовження відповідно до законів зовнішнього фотоефекту.
1 Кількість електронів, що вилітають із поверхні металу під дією електромагнітного випромінювання, пропорційна інтенсивності опромінювання (В).
Більша інтенсивність світла означає більшу кількість фотонів, які падають на катод. Поглинаючись електронами речовини, фотони сприяють випромінюванню електронів.
2 Максимальна кінетична енергія фотоелектронів –залежить від частоти опромінювання і не залежить від його інтенсивності (Б).
Електрон може поглинути тільки один фотон (більше − лише за дуже великої інтенсивності світла), тому максимальна кінетична енергія електрона визначається тільки енергією фотона, а отже, частотою світла і не залежить від кількості фотонів.
3 Мінімальна частота або максимальна довжина світлової хвилі, за якої ще можливий фотоефект – визначена речовиною освітленого катода (Д).
Для кожної речовини існує максимальна довжина світлової хвилі
4 Енергія кванта світла, яка спричиняє фотоефект, − дорівнює сумі роботи виходу електрона з металу й кінетичної енергії фотоелектрона (Г).
Це вербально описане рівняння Ейнштейна для зовнішнього фотоефекту.
Відповідь: 1В, 2Б, 3Д, 4Г.
ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона.
Завдання скеровано на перевірку знання, розуміння і застосування другого закону Ньютона.
За другим законом Ньютона прискорення
Оскільки на тіло діє кілька сил, то сила
Знайдемо рівнодійну сил за допомогою додаткових побудов (див. рисунок). Побудуємо паралелограм спочатку на векторах
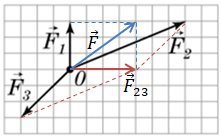
Обчислимо тепер модуль прискорення, набутого тілом під дією цих сил:
Відповідь: 2,5.
ТЕМА: Механіка. Елементи механіки рідин і газів. Архімедова сила.
Завдання скеровано на перевірку знання і застосування закону Архімеда.
Для того, щоб пліт із вантажем утримувався на плаву (пліт буде максимально навантажений так, щоб вантаж на намокав), потрібно, щоб силу тяжіння
Відповідь: 2000.
ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Кількість теплоти.
Завдання скеровано на перевірку розуміння переходу одного виду енергії в інший.
Рухоме тіло володіє кінетичною енергією
Оскільки, улучивши в дошку, куля втратила частину механічної енергії, то визначимо частку енергії
Відповідь: 19,5.
ТЕМА: Електродинаміка. Закони постійного струму. Робота і потужність електричного струму.
Завдання скеровано на перевірку знання і застосування формули для потужності електричного струму.
Потужності нагрівальних елементів однакові:
Запишемо потужності через добуток напруги
За законом Ома для ділянки кола виразимо силу струму через відношення напруги і опору і підставимо у рівність потужностей:
Визначимо опір нагрівального елемента, розрахованого на іншу напругу, але тієї ж потужності:
Відповідь: 16.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Гармонічні коливання.
Завдання скеровано на перевірку розуміння гармонічних коливань і знання базового поняття механічного руху ‒ переміщення.
Запишімо рівняння гармонічних коливань у загальному вигляді:
Модуль переміщення
На початку відліку часу, коли
Через
Відповідь: 8.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Радіоактивність.
Завдання скеровано на перевірку знання і застосування основного закону радіоактивного розпаду.
Скористаймося основним законом радіоактивного розпаду:
Виразимо кількість ядер радіонукліда, що залишились у зразку, через початкову кількість ядер відповідно до умови завдання:
Підставимо всі дані у формулу:
За радіоактивним розпадом речовини спостерігали
Відповідь: 20.




