Розділ: Мультитести
Тест: Тренувальний мультитест (4 варіант)
Блок: Фізика
Кількість завдань: 20
ТЕМА: Механіка. Закони збереження в механіці. Механічна робота.
Завдання скеровано на оцінку вміння розв’язувати розрахункові задачі з визначення роботи сил.
Якщо тіло зісковзує по площині рівномірно, то його прискорення \(\overline{a}\) дорівнює нулю. Тоді за другим законом Ньютона $$ \overline{F}=m\overline{a}=0, $$ де \(\overline{F}\) – рівнодійна, \(m\) – маса тіла, \(\overline{a}\) – прискорення тіла.
Рівнодійна сил, які діють на тіло, що рухається по похилій площині (рис. 1), дорівнює векторній сумі всіх цих сил: $$ \overline{F}=\overline{F_{\text{тяж}}} +\overline{F_{\text{тер}}}+\overline{N}=0. $$
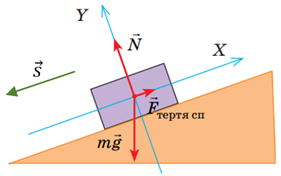
Рис. 1. Схематичне зображення сил, що діють на тіло на похилій площині
Це рівняння можна спроєктувати на осі \(OX\) і \(OY\) відповідно. Напрямок осей вибрано як на рисунку 1: \begin{gather*} F_x=-F_{\text{тяж}}\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}+F_{\text{тер}}=0;\\[7pt] F_y=-F_{\text{тяж}}\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}+N=0, \end{gather*} де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\) – кут нахилу похилої площини.
Тож \begin{gather*} F_{\text{тяж}}\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}=F_{\text{тер}};\\[7pt] F_{\text{тяж}}\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}=N. \end{gather*}
Силу тертя визначають за формулою $$ F_{\text{тер}}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\mu}N. $$
Тож \begin{gather*} F_{\text{тяж}}\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\mu}N=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\mu}F_{\text{тяж}}\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha};\\[7pt] \sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\mu}\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}. \end{gather*}
Роботу сили можна обчислити за формулою $$ A=Fs\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}, $$ де \(F\) – сила, що діє на тіло, \(s\) – переміщення тіла, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\) – кут між напрямками векторів сили й переміщення.
Тоді можна записати роботу сили тяжіння і сили тертя. Кут \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\) між напрямком сили тяжіння і переміщення \(s\) дорівнює \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}=90-\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\), тож можна скористатися тригонометричними формулами зведення: \begin{gather*} A_{\text{тяж}}=F_{\text{тяж}}s\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}=F_{\text{тяж}}s\cos(90-\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha})=\\[7pt] =F_{\text{тяж}}s\sin(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}). \end{gather*}
Кут між напрямком сили тертя і переміщенням \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}=180^\circ\), тож \begin{gather*} A_{\text{тер}}=F_{\text{тер}}s\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}=-F_{\text{тер}}s=\\[7pt] =-F_{\text{тяж}}\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}s. \end{gather*}
Оскільки модуль сили тяжіння і переміщення додатні, а \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\) – це кут, менший за \(90^\circ\), синус якого більший за нуль, можна зробити висновок: $$ A_{\text{тяж}}=-A_{\text{тер}}\gt 0. $$
Відповідь: B.
ТЕМА: Механіка. Основи кінематики. Матеріальна точка.
Завдання скеровано на перевірку розуміння поняття матеріальної точки.
Матеріальна точка – це фізична модель тіла, розмірами якого в умовах задачі можна знехтувати.
Диспетчер не може знехтувати розмірами Землі, адже літаки набагато менші за планету та рухаються близько до її поверхні. Відстані, що проходять літаки, є лише невеликими відрізками на поверхні Землі.
З тієї самої причини космонавт не може знехтувати розміром Землі під час посадки корабля.
Геолог не може знехтувати розміром планети, адже корисні копалини закладені в її корі.
Під час обчислення сили тяжіння розмірами тіла можна знехтувати.
Відповідь: B.
ТЕМА: Механіка. Основи динаміки. Закони Ньютона. Сила тертя.
Завдання скеровано на оцінювання розуміння впливу сили тертя в задачах на основі побутових прикладів.
Під час перетягування каната виграє той, хто може перетягнути стрічку посередині на свій бік. Чим більшою є сила тертя між учасником і підлогою, тим більшу силу треба прикласти, щоби зсунути його з місця. Тому для здобуття перемоги тягнути канат із більшою силою ніж опонент не достатньо, якщо сила тертя з боку підлоги в нього більша.
Сила тертя з боку каната важлива, але вона не визначає переможця, адже за дуже великої сили тертя між канатом й учасником він почне рухатися разом із канатом.
Маса учасників впливає лише на те, наскільки сила тяжіння діятиме на них. Притягування Землі може піти як на користь, так і на шкоду залежно від того в який бік нахилене тіло учасника.
Відповідь: B.
ТЕМА: Молекулярна фізика і термодинаміка. Ізопроцеси.
Завдання скеровано на перевірку розуміння зв’язку між макроскопічними й мікроскопічними параметрами ідеального газу.
Концентрацію визначають за формулою $$ n=\frac NV, $$ де \(N\) – кількість молекул у певному об’ємі \(V\).
Тоді, якщо за сталої маси концентрація залишається незмінною, то й об’єм у такому процесі не змінюється.
Середню кінетичну енергію молекул можна визначити за формулою $$ \overline{E_\text{кін}}=\frac{m_0\overline{v^2}}{2}, $$ де \(m_0\) – маса одної молекули, \(\overline{v^2}\) – середній квадрат швидкості молекул.
Що вища температура, то вищий середній квадрат швидкості молекул. Тож, щоб у газі певної маси концентрація молекул залишалася сталою, а їхня середня кінетична енергія зростала, газ потрібно ізохорно нагрівати.
Відповідь: A.
ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів.
Завдання скеровано на оцінювання вміння визначати ізопроцеси за їхнім описом і застосовувати до них перший закон термодинаміки.
За першим законом термодинаміки \(Q=\triangle U+A,\) де \(Q\) – це отримана тілом кількість теплоти, \(\triangle U\) – зміна внутрішньої енергії тіла, \(А\) – робота, виконана тілом. Із цієї формули зрозуміло, що для того, щоби робота виконувалася лише за рахунок зменшення внутрішньої енергії, кількість теплоти, отриманої ззовні, має дорівнювати нулю \((Q=0).\) Такий процес є адіабатним.
Тож наступним кроком є аналізування ситуацій, описаних у завданні, для визначення адіабатного процесу.
А Оскільки повітря рухається швидко, то воно не встигає обмінятися теплом із навколишнім середовищем, тож \(Q=0\) і процес є адіабатним. Після цього газ розширюється і виконує роботу. За першим законом термодинаміки виконати цю роботу газ може лише за рахунок зменшення своєї внутрішньої енергії. Доказом цього є те, що водяна пара, яку несло повітря, сконденсувалася. Це є ознакою зменшення температури повітря і, відповідно, внутрішньої енергії.
Б У холодильнику відбувається обмін теплом із середовищем, отже процес не є адіабатним.
В Під час кипіння температура рідини залишається сталою, а отже і її внутрішня енергія не змінюється, що не відповідає умові завдання.
Г У цьому процесі внутрішня енергія повітря збільшується, що не відповідає умові завдання.
Відповідь: A.
ТЕМА: Атом й атомне ядро. Основи електростатики. Електричний заряд.
Завдання скеровано на перевірку розуміння будови атома й уміння обчислювати електричний заряд тіл.
Атом – це нейтральна частинка, складниками якої є позитивно заряджене ядро й негативно заряджені електрони. Тому заряд увсіх електронів в атомі дорівнює заряду його ядра.
Ядро містить позитивно заряджені протони й електронейтральні нейтрони. Заряд усіх електронів в атомі дорівнює заряду всіх його протонів. Заряд електрона й заряд протона рівні за модулем, але протилежні за знаком, тому кількість електронів в атомі дорівнює кількості його протонів.
У ядерній фізиці використовують опис ядер, у якому поруч із символом хімічного елемента лівим надрядковим індексом позначають кількість нуклонів у ядрі \(n\) (сумарна кількість протонів і нейтронів), а в лівим підрядковим – кількість протонів \(p\).
В атомі \(^1_1\mathrm{H}\) міститься один протон і, відповідно, один електрон, а в атомі \(^{16}_8\mathrm{O}\) – вісім протонів і вісім електронів.
У молекулі води два атоми Гідрогену, у кожного з яких по одному електрону, й один атом Оксигену, у якому вісім електронів. Разом у молекулі води десять електронів, їхній сумарний заряд
Відповідь: B.
ТЕМА: Електродинаміка. Закони постійного струму. Закон Джоуля – Ленца.
Завдання скеровано на перевірку вміння використовувати закон Джоуля – Ленца.
Кількість теплоти, що виділяється під час проходження струму провідником, визначають за законом Джоуля – Ленца: $$ Q=I^2Rt, $$ де \(I\) – сила струму в провіднику, \(R\) – опір провідника, \(t\) – час проходження струму.
Якщо до збільшення сила струму в провіднику дорівнювала \(I\), то після збільшення вона дорівнюватиме \(I'=4I\).
Тоді:
\begin{gather*} Q=I^2Rt;\\[7pt] Q'=I'^2Rt=(4I)^2Rt=16I^2Rt=16Q. \end{gather*}Тож кількість теплоти збільшиться в 16 разів.
Відповідь: Г.
ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Електричний струм у газах.
Завдання скеровано на перевірку розуміння механізму іскрового розряду.
Іскровий розряд виникає за атмосферного тиску та великої напруги.
Іскровий розряд має вигляд яскравих зиґзаґів із багатьма розгалуженнями.
Нетривалий, супроводжуваний характерним тріском.
Прикладом іскрового розряду є блискавка.
Відповідь: Б.
ТЕМА: Механічні коливання і хвилі.
Завдання скеровано на перевірку розуміння закономірностей зміни енергії під час коливального руху.
Якщо маятник настінного годинника має частоту коливань 2 Гц, то він виконує 2 коливання за секунду. Тоді за хвилину він робить 120 коливань.
Потенціальну енергію маятника можна визначити за формулою $$ U=mgh, $$ де \(m\) – маса тіла, \(g\) – прискорення вільного падіння, \(h\) – висота підняття тіла над поверхнею.
На найбільшій висоті маятник перебуває в крайніх точках своєї траєкторії (рис. 1).
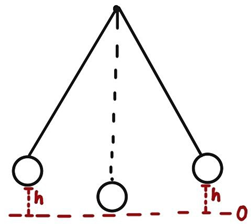
Рис. 1. Крайні положення коливання маятника
Тож за одне коливання маятник двічі опиняється в точках, де його потенціальна енергія максимальна. Тоді за 120 коливань його потенціальна енергія буде максимальною 240 разів.
Відповідь: Г.
ТЕМА: Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі.
Завдання скеровано на оцінювання вміння розраховувати енергію елементів коливального контуру і його повну енергію.
Коливальний контур – це схематично зображений на рисунку 1 фізичний пристрій із послідовно з’єднаних котушки індуктивності 1 і конденсатора 2.
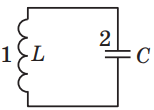
Рис. 1. Електрична схема коливального контуру
В ідеальному коливальному контурі вся енергія під час коливань перетікає від конденсатора до котушки без утрат. Якщо вважати, що в початковий момент часу конденсатор заряджений на повну, то його енергія перетікатиме в енергію котушки з максимальним струмом індукції під час коливань у такому електромагнітному контурі.
Тож можна обчислити зміну повної енергії контуру за зміною енергії зарядженого конденсатора: $$ W_{\text{конденсатора}}= \frac{q^2}{2C}, $$ де \(q\) – це максимальний заряд на обкладинці, а \(C\) – ємність конденсатора. Після збільшення максимального заряду енергія конденсатора
Відповідь: Г.
ТЕМА: Елементи теорії відносності. Принципи (постулати) теорії відносності Ейнштейна.
Завдання скеровано на оцінку розуміння постулатів спеціальної теорії відносності.
Щоби порівняти час, виміряний у рухомій і нерухомій системах, потрібно пригадати, як їх визначають.
Рухома система координат прив’язана до тіла, що рухається. У ній спостерігач рухається разом із тілом, як, наприклад, пасажир усередині ракети. Для такого спостерігача тіло і світловий годинник, який вимірює час, не рухається.
У нерухомій системі координат спостерігач стежить за рухомим тілом, як, наприклад, людина, що залишається на Землі, коли ракета пролітає в небі. У такому разі світловий годинник рухається.
За спеціальною теорією відносності швидкість світла у вакуумі має однакові значення в усіх системах відліку. Тож, щоби швидкість світла в рухомій і нерухомій системі відліку могла бути однаковою, час у них має текти по-різному. Час, виміряний у рухомій системі координат, має бути меншим, ніж виміряний у нерухомій системі: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\tau}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\tau}_0}{\sqrt{1-\frac{v^2}{c^2}}}, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\tau}_0\) – час, виміряний у рухомій системі координат, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\tau}\) – час, виміряний у нерухомій систем координат (у цій системі координат спостерігач бачить рух тіла ззовні).
Відповідь: Г.
ТЕМА: Оптика. Електромагнітні хвилі. Кванти світла.
Завдання скероване на перевірку розуміння зв’язку між характеристиками квантів світла та електромагнітних хвиль.
Енергію фотона можна обчислити за формулою: $$ E=hv, $$ де \(E\) – енергія фотона, \(v\) – частота випромінювання, \(h\approx 6,62\cdot 10^{-34}\ \text{Дж}\cdot \text{с}\) – стала Планка.
Тож, що більша частота випромінювання, то вища його енергія.
Частота видимого випромінювання збільшується від червоного \((\approx 480\ \text{ТГц})\) до фіолетового \((\approx 790\ \text{ТГц})\), тож й енергія збільшуватиметься так само.
Відповідь: Г.
ТЕМА: Енергія. Робота. Потужність. Сила.
Завдання скеровано на перевірку розуміння понять енергії, потужності, сили й прискорення.
Потужність \(P\) – це фізична величина, яка характеризує швидкість виконання роботи.
Енергія \(E\) – це фізична величина, яка характеризує здатність тіла виконати роботу.
Сила \(F\) – це векторна фізична величина, що є мірою взаємодії тіл, у результаті якої тіло набуває прискорення або деформується.
Прискорення \(a\) – це векторна фізична величина, яка характеризує зміну швидкості руху тіла.
Відповідь: 1В, 2Д, 3Б, 4А.
ТЕМА: Сила тяжіння. Сила пружності. Сила кулона. Ядерні сили.
Завдання скеровано на перевірку розуміння впливу сил різної природи на природні явища.
1 електронейтральні нейтрони й позитивно заряджені протони утримуються в ядрах (й альфа-частинках, що є ядрами атомів Гелію, зокрема) завдяки дії ядерних сил
2 куля деформує броню в момент зіткнення. Залежно від величини цієї деформації броня повертається в попередній стан (зазнає пружної деформації), зберігає деформацію після зіткнення (зазнає пластичної деформації) або руйнується. Подальший рух кулі також від цього залежить, адже завдяки силі пружності, що виникає в броні, куля може зрикошетити й змінити напрямок руху чи його швидкість
3 причиною руху Місяця навколо Землі є її сила тяжіння
4 часто рух негативно зарядженого електрона в атомі зумовлений його кулонівською взаємодією з позитивно зарядженим ядром.
Відповідь: 1Г, 2Д, 3А, 4Б.
ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.
Завдання скеровано на перевірку розуміння характеру руху тіл.
Позначимо сталу – модуль швидкості руху потягу – \(v.\) Тоді відстань \(s_\text{п},\) яку пройшов потяг за час \(t\) від моменту відчеплення до моменту зупинки вагона, можна визначити за формулою для обчислення відстані під час прямолінійного рівномірного руху: $$ s_\text{п}=v\cdot t. $$
Час руху потяга на цьому відрізку шляху такий самий, як і час руху відчепленого останнього вагона до зупинки. Вагон рівномірно сповільнюватиметься. Його початковою швидкістю \(v_0\) буде швидкість руху потягу \(v,\) а кінцева швидкість \(v_\text{к}\) дорівнюватиме нулю.
Отже, $$ s_\text{в}=\frac{v_0+v_\text{к}}{2}\cdot t=\frac v2\cdot t, $$ де \(s_\text{в}\) ‒ відстань, яку пройшов вагон до зупинки.
Виразімо із цієї формули час руху вагона \(t\) і підставімо цей вираз у формулу для відстані, яку пройшов потяг:
Відповідь: 400.
ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Поверхневий натяг.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з використанням сили поверхневого натягу.
Дано:
\(r=5\ \text{см}\)
\(m=1,2\ \text{г}\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\sigma}=70\ \text{мН/м}\)
Знайти:
\(F\ (\text{мН})\ -\ ?\)
На кільце на поверхні води діють сили поверхневого натягу, що утримують його на поверхні, і сила тяжіння. Силу тяжіння можна визначити за формулою $$ F_{\text{тяж}}=mg. $$
Окрім того, кільце обмежує на поверхні дві ділянки – усередині й зовні. Тому з обох боків на нього діятимуть сили поверхневого натягу.
Дріт, із якого зроблене кільце, – тонкий, тому можна вважати, що внутрішній радіус дорівнює зовнішньому радіусу кільця. Тож довжина кільця з боку зовнішньої і внутрішньої поверхні буде однаковою: $$ l=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}r_{\text{зовн}}=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}r_{\text{вн}}=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}r. $$
Тоді сила, що необхідна для того, щоби підняти кільце з поверхні, має подолати силу тяжіння і сили поверхневого натягу із зовнішнього і внутрішнього боку:
Відповідь: 56.
ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Абсолютна й відносна вологість. Точка роси.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі про відносну вологість і точку роси.
Дано:
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}=80\ \text{%}\)
\(t=25\ ^\circ\text{С}\)
Знайти:
\(t_{\text{туман}}\ -\ ?\)
Туман почне формуватися, коли температура повітря сягне точки роси. Точка роси – це температура, за якої водяна пара, що міститься в повітрі, стає насиченою.
Для визначення температури, що є точкою роси, потрібно визначити густину водяної пари в повітрі за початкових умов і за таблицею визначити температуру, за якої ця густина є густиною насиченої пари.
Пригадаймо, що густина водяної пари в повітрі та відносна вологість пов’язані формулою: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{a}}}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{н.п.}}}\cdot 100\ \text{%}, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}\) – відносна вологість повітря, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{н.п.}}\) – густина насиченої пари, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{a}}\) – густина водяної пари в повітрі.
Тож можна визначити густину водяної пари в повітрі: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{a}}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{н.п.}}}{100\ \text{%}} $$
Густина насиченої пари за температури \(25\ ^\circ\text{С}\) за таблицею становить \(23,0\ \text{г/см}^3\), тоді:
Найближча величина густини насиченої пари до її обчисленої густини – \(18,3\ \text{г/см}^3\), що відповідає \(21\ ^\circ\text{С}\). $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{н.п.}}=21\ \frac{\text{г}}{\text{см}^3} $$
Відповідь: 21.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція, Закон електромагнітної індукції.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на застосування закону електромагнітної індукції.
Дано:
\(\triangle\style{font-style:normal;font-weight:bold;font-size:1.1em}{\Phi}=20\ \text{мВб}\)
\(R=0,04\ \text{Ом}\)
Знайти:
\(q\ (\text{Кл})-?\)
Заряд проходить через виток під час зміни магнітного потоку, бо за законами електромагнітної індукції в такому разі утвориться струм. Цей струм сприятиме виникненню власного магнітного поля витка, що протидіятиме зміні потоку крізь нього. Такий струм називають індукційним. Силу індукційного струму визначають за формулою $$ I=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_l}{R}, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_l\) – електрорушійна сила (ЕРС) індукції.
За законом електромагнітної індукції ЕРС індукції дорівнює швидкості зміни магнітного потоку, який пронизує поверхню, обмежену контуром. Тобто $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_l=-\frac{\triangle\style{font-style:normal;font-weight:bold;font-size:1.1em}{\Phi}}{\triangle t}, $$ де \(\triangle t\) – час, за який відбуваються зміни магнітного потоку. Знак «мінус» у цьому виразі показує, що ЕРС самоіндукції утворюється, щоби протистояти (правило Ленца) зміні магнітного потоку. Тоді $$ I= \frac{\triangle\style{font-style:normal;font-weight:bold;font-size:1.1em}{\Phi}}{\triangle t\cdot R}. $$
За визначенням сила струму – це фізична величина, яка характеризує електричний струм. Її описують формулою $$ I=\frac{q}{\triangle t}, $$ де \(q\) – це заряд, що проходить через поперечний переріз провідника, а \(\triangle t\) – проміжок часу, за який це відбувається.
Тоді $$ \frac{q}{\triangle t}=\frac{\triangle\style{font-style:normal;font-weight:bold;font-size:1.1em}{\Phi}}{\triangle t\cdot R}, $$ a
Відповідь: 0,5.
ТЕМА: Оптика. Лінза. Формула тонкої лінзи.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі із застосування законів геометричної оптики й формули тонкої лінзи.
Дано:
\(F=20\ \text{см}\)
\(l=12\ \text{мм}\)
\(L=6\ \text{м}\)
Знайти:
\(D\ -\ ?\)
Фокусну відстань лінзи та її положення відносно об’єкта і його зображення пов’язує формула тонкої лінзи: $$ \frac 1F=\frac 1d+\frac 1f, $$ де \(d\) – відстань від об’єкта до лінзи, а \(f\) – відстань від лінзи до зображення, \(F\) – фокусна відстань лінзи.
Розміри зображення і предмета з їхніми відстанями від лінзи пов’язує лінійне збільшення лінзи Г: $$ \boldsymbol Г=\frac lL=\frac fd. $$
З виразу для лінійного збільшення лінзи можемо обчислити відстань \(f\) від предмета до лінзи: $$ f=\frac{ld}{L}. $$ Тоді
Відповідь: 100.
ТЕМА: Квантова фізика. Атом і атомне ядро. Радіоактивність.
Завдання скеровано на перевірку розуміння процесу радіоактивного розпаду.
Дано:
\(T_{1/2}=1\ \text{год}\)
\(E'=5\ \text{МеВ}\)
\(t=3\ \text{год}\)
\(N_0=8\cdot 10^{10}\)
Знайти:
\(E\ (\text{мДж})\ -\ ?\)
Енергію, яка виділилася під час розпадів за три години, можна обчислити як добуток кількості розпадів, що відбулися за цей час, й енергії \(N'\), що виділяється під час кожного з них \(E'\): $$ E=E'N'. $$
Період піврозпаду \((Т_{1/2})\) – це фізична величина, що характеризує радіонуклід і дорівнює часу, протягом якого розпадається половина наявної кількості ядер цього радіонукліда.
Тоді можна визначити кількість ядер, що залишилася після розпаду: $$ N=N_02^{\frac{t}{T_{1/2}}}, $$ де \(N\) – кількість ядер, що залишилася після розпаду, \(N_0\) – початкова кількість ядер, \(t\) – час розпаду.
Кількість ядер, що розпалися, дорівнює:
Тоді енергія, що виділилася під час розпаду, дорівнює:
Для того, щоби подати енергію в мДж, потрібно взяти до уваги, що \(1\ \text{еВ}\) – це енергія, необхідна для того, щоби перенести елементарний електричний заряд між точками, різниця потенціалів між якими дорівнює \(1\ \text{В}\). $$ 1\ \text{еВ}=1,6\cdot 10^{-19}\ \text{Кл}\cdot 1\ \text{В}=1,6\cdot 10^{-19}\ \text{дЖ}. $$
Тобто
Відповідь: 56.