Розділ: Мультитести
Тест: Тренувальний мультитест (6 варіант)
Блок: Фізика
Кількість завдань: 20
ТЕМА: Механіка. Основи кінематики.
Завдання скеровано на перевірку вміння аналізувати графіки, що описують рух тіла.
Прямолінійний рух – це рух, траєкторію якого є пряма.
Щодо графіків у завданні:
А Це графік залежності проєкції швидкості
Б Це графік залежності координати
В Це графік залежності координати
Г Це графік залежності проекції швидкості
Відповідь: B.
ТЕМА: Вимірювальні пристрої.
Завдання скеровано на оцінювання розуміння фізичних принципів роботи вимірювальних пристроїв.
Термометр – це прилад для вимірювання температури. Він працює завдяки тому, що деякі речовини за сталого тиску суттєво змінюють свій об’єм за зміни температури (ртуть чи спирт розширюються за збільшення температури і звужуються за її зменшення).
Психрометр – це прилад для вимірювання відносної вологості. Принцип його роботи такий: у корпусі приладу є два термометри. Кінець одного з них зазвичай обгорнутий вологою тканиною. Вода з тканини завжди випаровується, і швидкість випаровування залежить від вологості повітря навколо. Відповідно, для вимірювання відносної вологості фіксують покази сухого й вологого термометрів і за допомогою спеціальних таблиць виконують необхідні розрахунки.
Барометр – це прилад для вимірювання атмосферного тиску. У завданні зображено безводний барометр (анероїд). На рисунку 1 зображено конструкцію такого приладу. Усередині анероїда є камера з гофрованою поверхнею (1), із якої відкачано повітря. За високого атмосферного тиску кришка коробки сильно опускається, а за низького – піднімається. До кришки за допомогою пружини кріпиться стрілка (2). Тому, коли кришка камери піднімається чи опускається, пружина деформується, і стрілка починає рухатись по шкалі (3).
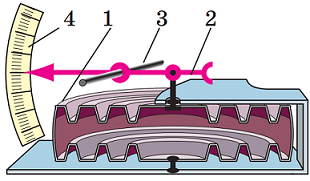
Рис. 1. Конструкція барометра-анероїда
Динамометр – це прилад для вимірювання сили. Зазвичай динамометр складається із пружини і шкали. Коли на кінець пружини діє сила, то за законом Гука пружина розтягується:
Тому, якщо відомий коефіцієнт жорсткості k пружини, то за значенням її видовження x можна визначити й силу, що його спричиняє.
Відповідь: B.
ТЕМА: Механіка. Основи динаміки. Момент сил.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з визначення моменту сил.
Момент сили
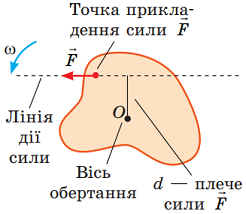
Рис. 1. Схема визначення плеча сили
Проаналізувавши рисунок 2 (його наведено в завданні), потрібно визначити плечі сил, схематично зображених на ньому.
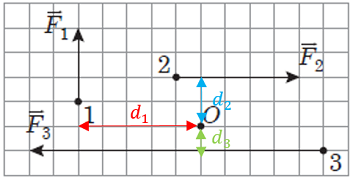
Рис. 2. Визначення плечей сил, про які йдеться в завданні
У завданні не зазначено розмір клітинок, тож можна вважати довжину сторони клітинки умовною одиницею довжини (у. о. д.).
Згідно з виразом (1):
Відповідь: A.
ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Рівняння стану ідеального газу.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з використання рівняння стану ідеального газу.
Об’єм, температура й тиск газу пов’язані між собою рівнянням стану ідеального газу:
З рівняння стану ідеального газу можна виразити тиск
За графіком (рис. 1) можна визначити тиск та об’єм у точках 1 і 2. На графіку не вказано одиниці вимірювання, тож вважатимемо, що 1 клітинка вздовж осі
Тоді для точок 1 і 2 об’єм і температура дорівнюють:
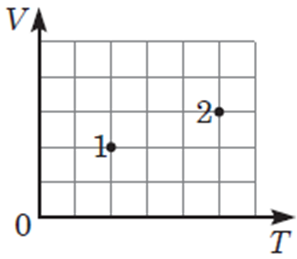
Рис. 1. Графік у координатах
Можна визначити тиск у точках 1 і 2 в умовних одиницях тиску (у. о. тиску):
Відповідь: B.
ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Абсолютна й відносна вологість. Точка роси.
Завдання скеровано на оцінювання розуміння понять динамічної рівноваги й відносної та абсолютної вологості.
Абсолютна вологість – фізична величина, якою характеризують уміст водяної пари в повітрі. Вона чисельно дорівнює масі водяної пари в повітрі об’ємом
Відносна вологість – фізична величина, яка показує, наскільки водяна пара близька до насичення. Вона дорівнює відношенню абсолютної вологості до густини насиченої водяної пари за певної температури або відношенню парціального тиску водяної пари за певної температури до тиску насиченої пари за тої самої температури (у частках від одиниці або у відсотках).
Tочка роси – це температура, за якої водяна пара, що міститься в повітрі, стає насиченою.
Питома теплоємність – кількість теплоти, яку необхідно надати одиниці маси речовини й нагріти її на
Відповідь: Б.
ТЕМА: Основи електростатики. Закон Кулона.
Завдання скеровано на оцінювання розуміння взаємодії між електричними зарядами.
Тіла з однойменними електричними зарядами відштовхуються, а з різнойменними – притягаються. За таким законом змінили своє положення лише кульки на рисунку Б.
Відповідь: Б.
ТЕМА: Електродинаміка. Електричний струм у різних середовищах.
Завдання скеровано на оцінювання знання особливостей проходження струму в різних середовищах.
За результатами аналізування ситуацій, описаних у завданні, можна дійти таких висновків:
А Вільними носіями заряду в газах є електрони, позитивні й негативні йони, а не лише електрони.
Б З підвищенням температури в напівпровідниках виникають додаткові вільні носії заряду, тому питомий опір зменшується.
В Йони в металах залишаються у вузлах кристалічної ґратки й не є вільними носіями заряду, а тому не беруть участь в електропровідності.
Г В електролітах негативні йони рухаються до анода, а позитивні – до катода, а не в один бік.
Відповідь: Б.
ТЕМА: Електродинаміка. Явище й закони електромагнітної індукції.
Завдання скеровано на оцінювання знання поняття «електромагнітна індукція» і вміння застосовувати закони електромагнітної індукції.
Гальванометр у досліді, описаному в завданні, фіксує індукційний струм у котушці.
Для правильного розв’язання завдання потрібно пригадати закони електромагнітної індукції.
1. Електричний струм у замкненому провідному контурі виникає лише тоді, коли змінюється магнітний потік через поверхню, обмежену контуром.
2. Чим швидше змінюється магнітний потік, тим більшою є сила індукційного струму в контурі.
3. Напрямок індукційного струму в контурі залежить від того, збільшується чи зменшується магнітний потік через поверхню, обмежену контуром.
За першим законом електромагнітної індукції в котушці виникає струм, бо за наближення або введення магніту змінюється магнітний потік, що через неї протікає.
Чим швидше змінюватиметься магнітний потік, тим більшою, відповідно до другого закону електромагнітної індукції, буде сила струму. Щоби швидше змінювати магнітний потік від магніту, його треба рухати швидше.
Якщо тримати магніт нерухомо, то струм індукції в котушці не виникне, бо магнітний потік, який протікає через контур котушки, не змінюватиметься. А якщо змінити напрямок руху магніту, то, за правилом Ленца, зміниться лише напрямок індукованого струму.
Відповідь: Б.
ТЕМА: Механічні коливання і хвилі. Амплітуда, частота, період гармонічних коливань.
Завдання скеровано на перевірку розуміння базових понять, що стосуються механічних коливань.
А Швидкість світла в повітрі близька до швидкості світла у вакуумі
Б Вимушені коливання – це коливання, які відбуваються в системі внаслідок дії зовнішньої сили, що періодично змінюється. Між двома торканнями на струни не діє жодна зовнішня сила, тому в цьому разі коливання є вільними.
В Звук – це поздовжня механічна хвиля. Механічні хвилі можуть поширюватися лише в середовищі. У відкритому космосі немає атмосфери, у якій би міг поширюватися звук, тому єдиний спосіб комунікації – це електромагнітні хвилі, які можуть поширюватись у вакуумі. Радіохвилі – це електромагнітні хвилі із частотою меншою, ніж
Г Збіг власної частоти коливання крил і частоти коливання повітряних потоків приведе до резонансу. Резонанс – це явище різкого збільшення амплітуди, яке виникає, якщо частота зовнішньої сили, що періодично змінюється, збігається із власною частотою коливань системи. Кріплення крил літака можуть не витримати різкого збільшення амплітуди коливань і зруйнуватися.
Тож твердження Г – правильне.
Відповідь: Г.
ТЕМА: Оптика. Закони заломлення світла.
Завдання скеровано на оцінювання розуміння законів заломлення світла.
За законом заломлення променів
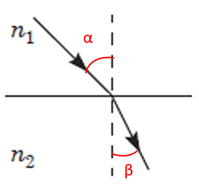
Рис. 1. Закон заломлення променів
Кут падіння і кут заломлення мають бути меншими за 90° (рис. 1).
За графіком функції
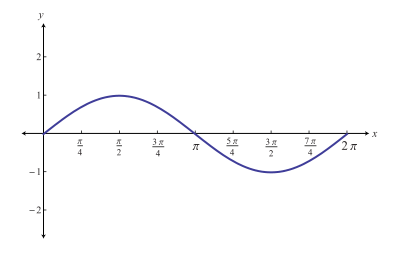
Рис. 2. Графік функції
Отже, якщо кут заломлення менший, ніж кут падіння, то і синус кута заломлення буде меншим за синус кута падіння. Тож, щоб закон заломлення виконувався, якщо кут падіння більший за кут відбивання, то показник заломлення в середовищі падаючого променю має бути меншим за показник заломлення і середовищі заломленого променю.
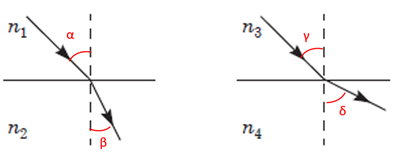
Рис. 3. Умова завдання
За умовою завдання для у першому випадку кут заломлення
У другому випадку кут падіння
Відповідь: Б.
ТЕМА: Елементи теорії відносності. Релятивістський закон додавання швидкостей.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з використанням релятивістського закону додавання швидкостей.
Обидві частинки рухаються зі швидкістю, порівнюваною зі швидкістю світла. Тому в цьому разі для додавання швидкостей необхідно використовувати релятивістський закон:
У цьому випадку нерухома система відліку К – це адронний колайдер (на рисунку 1 позначено чорним кольором). Рухому систему координат К' варто «прив’язати» до одного з ядер (на рисунку 1 позначено синім кольором). Інше ядро тоді можна вважати рухомим тілом у цих системах координат (на рисунку 1 позначено червоним кольором).
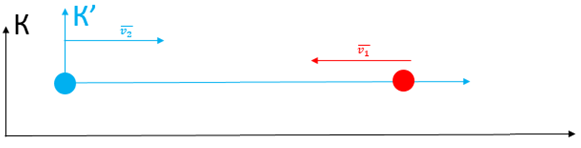
Рис. 1. Схема руху протонів в адронному колайдері
За умовою відомі швидкості руху ядер в адронному колайдері, тобто це швидкість v руху тіла відносно нерухомої системи координат і швидкість
Тоді, щоби знайти швидкість руху одного ядра відносно іншого, необхідно знайти швидкість руху тіла відносно рухомої системи координат (
Тож одне з ядер рухалось назустріч іншому зі швидкістю
Відповідь: B.
ТЕМА: Оптіка. Спектральній аналіз.
Завдання скеровано на перевірку вміння розв'язувати задачі, які передбачають оброблення й аналіз результатів експерименту, поданих на фото або схематичному рисунку.
Усі спектральні лінії
Спектральні лінії
Натомість ліній із довжинами хвиль як у
Відповідь: B.
ТЕМА: Вимірювальні пристрої.
Завдання скеровано на оцінювання знання вимірювальних пристроїв і розуміння фізичних величин, для вимірювання яких їх використовують.
1. Фізична величина, що дорівнює відношенню шляху до часу – це швидкість:
Прилад, що вимірює швидкість – це спідометр.
2. Фізична величина, що дорівнює добутку густини, прискорення вільного падіння і висоти стовпчика рідини – це гідростатичний тиск (тиск нерухомого стовпчика рідини):
Прилад, що вимірює тиск рідини чи газу – це манометр.
3. Фізична величина, що дорівнює відношенню густини водяної пари до густини насиченої пари за певної температури й виражена у відсотках – це відносна вологість:
Прилад, що вимірює відносну вологість – це гігрометр.
4. Фізична величина, що дорівнює добутку маси на прискорення вільного падіння – це сила тяжіння:
Прилад, що вимірює силу – це динамометр.
Відповідь: 1В, 2А, 3Г, 4Б.
ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Магнітне поле, електромагнітна індукція.
Завдання скеровано на перевірку вміння застосовувати теоретичні знання з електродинаміки для пояснення принципу дії відповідних технічних пристроїв.
На взаємодії магнітного поля постійних магнітів компаса з горизонтальним складником магнітного поля Землі заснований принцип дії цього приладу. Вільно обертова магнітна стрілка повертається навколо осі, розташовуючись уздовж силових ліній магнітного поля. Тож стрілка завжди вказує одним кінцем у напрямку ліній магнітної індукції, що йдуть до Південного магнітного (Північного географічного) полюса.
Посудину з високою стійкістю до впливів кислот, лугів і розчинників, у якій відбувається електроліз, називають електролітичною ванною (електролізером). Проходження електричного струму крізь розчин або розплав електроліту зумовлює хімічні реакції на поверхні поділу електрод ‒ розчин (розплав електроліту). Отже, хімічну дію електричного струму спостерігають під час проходження його крізь розчин електроліту в електролітичній ванні.
Електромагнітна індукція ‒ явище створення в просторі вихрового електричного поля змінним магнітним потоком. Один із наслідків електромагнітної індукції, практично важливий для генерації електричного струму, ‒ виникнення електрорушійної сили в провідному контурі, магнітний потік через який змінюється. Саме генератори змінного струму (ГЗС) ‒ це джерела електричної енергії, які створюють електрорушійну силу (ЕРС), що періодично змінюється.
Робота всіх електричних нагрівачів ґрунтується на тепловій дії струму: у таких пристроях енергія електричного струму перетворюється на внутрішню енергію нагрівача. Під час проходження електричного струму спіраль лампи розжарювання сильно нагрівається завдяки тепловій дії струму.
Будь-який напівпровідниковий діод складений із двох контактних напівпровідникових ділянок із різними типами провідності ‒ електронною і дірковою; до кожної ділянки приєднано виводи. Основна властивість напівпровідникового діода ‒ пропускати електричний струм переважно в одному напрямку.
Відповідь: 1Б, 2Г, 3А, 4В.
ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.
Завдання скеровано на перевірку знання і розуміння кінематичних рівнянь, що описують прямолінійний рівноприскорений рух і вміння застосовувати їх.
Обчислімо модуль переміщення
Можна також спочатку визначити проміжок часу, за який швидкість руху зміниться від
Знаючи проміжок часу, за який відбулася зазначена в умові зміна швидкості, можна визначити модуль переміщення:
Відповідь: 27.
ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Коефіцієнт корисної дії теплового двигуна і його максимальне значення.
Завдання скеровано на перевірку розуміння принципу дії теплових двигунів і вміння визначати різними способами коефіцієнт корисної дії та фізичні величини, які на нього впливають.
Коефіцієнт корисної дії (ККД)
Корисна робота двигуна полягає в подоланні сили опору руху візка
Також коефіцієнт корисної дії такого двигуна можна визначити за формулою
Прирівняймо ці два вирази для обчислення коефіцієнта корисної дії:
Виразімо звідси модуль швидкості руху візка й обчислімо його:
Відповідь: 2.
ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Робота в термодинаміці. Ізопроцеси.
Завдання скеровано на перевірку вміння розв’язувати термодинамічні задачі з використанням графіка.
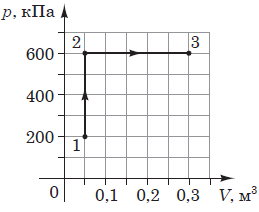
Рис. 1. Умова задачі
За рисунком можна визначити об’єм і тиск для всіх трьох точок процесу.
Дано:
Знайти:
Перехід від стану 1 до стану 3 має два складники: ізохорне нагрівання, супроводжуване збільшенням тиску (1–2) та ізобарне розширення (2–3).
Робота в термодинамічному процесі виконується лише за зміни об’єму газу, тож в ізохорному процесі (1–2) робота не виконується.
Робота в ізобарному процесі (2–3) може бути обчислена за формулою
Тоді:
Відповідь: 150.
ТЕМА: Електродинаміка. Закони постійного струму. Опір провідників.
Завдання скеровано на оцінювання вміння визначати опір провідників за їхніми геометричними характеристиками.
Дано:
Знайти:
Електричний опір
Залежність опору провідника від його геометричних характеристик описують формулою
Після переведення міліметрів квадратних у метри квадратні можна обчислити шукану довжину дроту:
Відповідь: 40.
ТЕМА: Електромагнітні коливання та хвилі. Вільні електромагнітні коливання в коливальному контурі.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з використанням формули Томсона.
Дано:
Знайти:
Якщо вважати, що швидкість електромагнітної хвилі в повітрі дорівнює швидкості світла у вакуумі, то довжина випроміненої контуром хвилі пов’язана з періодом коливань цього контуру:
Період електромагнітних коливань в електричному контурі визначають за формулою Томсона:
Тоді індуктивність котушки можна визначити за формулою:
Відповідь: 9.
ТЕМА: Квантова фізика. Світлові кванти. Рівняння теплового балансу.
Завдання скеровано на перевірку вміння розв’язувати комплексні задачі із застосуванням рівняння теплового балансу, зокрема із джерелом теплоти, що пов’язане з квантами світла.
Дано:
Знайти:
Кількість отриманої теплоти й зміна температури пов’язані формулою
Теплоту крапля отримує від поглинання енергії фотонів, яку для одного фотона визначають за формулою
Частота й довжина хвилі пов’язані виразом
Якщо за одну секунду крапля отримує
Відповідь: 20.




