Розділ: Мультитести
Тест: Тренувальний мультитест (8 варіант)
Блок: Фізика
Кількість завдань: 20
2
ТЕМА: Механіка. Динаміка. Рух під дією сили тяжіння.
Завдання скеровано на оцінювання розуміння процесу руху кинутого горизонтально тіла, на яке діє сила тяжіння.
Тіло, кинуте під кутом до горизонту, рухається під дією сили тяжіння. Сила тяжіння не змінюється протягом усього руху, й не залежить від того, у якій точці траєкторії перебуває тіло. Не залежить ця сила й від напрямку руху тіла. Тож і прискорення, якого сила тяжіння надає тілу, залишається сталим.
Це прискорення – прискорення вільного падіння
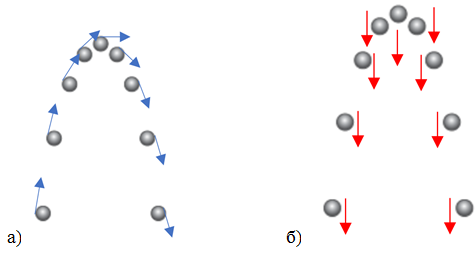
Рис. 1. Схематичне зображення напрямку в різні моменти часу
векторів: а) швидкості
Відповідь: A.
ТЕМА: Механіка. Основи кінематики. Основи динаміки. Другий закон Ньютона.
Завдання скеровано на перевірку знання законів кінематики й законів динаміки Ньютона, а також уміння розв'язувати комбіновані задачі, використовуючи поняття і закономірності з кількох розділів механіки.
Ураховуючи загальний вид рівняння руху
За II законом Ньютона
Відповідь: Б.
ТЕМА: Елементи механіки рідин і газів. Гідростатичний тиск.
Завдання скеровано на розуміння понять тиску й сили тиску та вміння визначати гідростатичний тиск.
Якщо всю воду з ширшої посудини перелили у вужчу, то об’єм води не змінився, площа дна посудини зменшилася, а рівень води збільшився, як показано на рисунку 1.
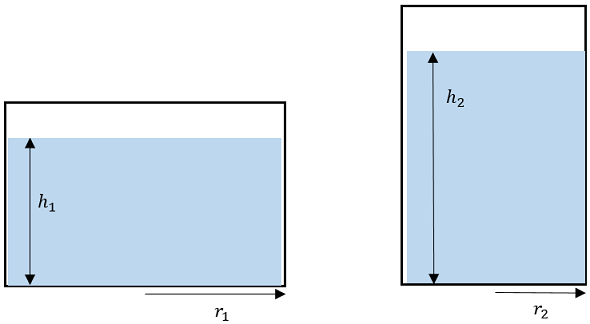
Рис. 1. Рівень води в широкій і високій посудинах
Тиск на дно в обох посудинах є сумою гідростатичного тиску стовпчика води й атмосферного тиску. Гідростатичний тиск
Тиск на дно в першій (широкій) посудині дорівнює:
Вирази для тиску відрізняються лише висотою стовпчика, тож у посудині, де вона більша, тиск на дно також буде більшим.
Сила, що діє на дно обох посудин і створює тиск, – це вага рідини в посудині:
Маса води після переливання не змінилася, посудини перебувають у стані спокою, а отже й вага не змінилася. Тож сила тиску під час такого переливання не зміниться.
Відповідь: Б.
ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл.
Завдання скеровано на перевірку розуміння принципів теплообміну.
За першим законом термодинаміки кількість теплоти
Зміна внутрішньої енергії пов’язана зі зміною температури речовини, що не змінює свого агрегатного стану: що вища температура речовини, то вища її внутрішня енергія. Тож, якщо температура речовини не змінюється, то і внутрішня енергія тіл також не змінюється:
Проте під час зміни агрегатного стану (фазового переходу) температура речовини не змінюється, а внутрішня енергія – змінюється. Наприклад, під час плавлення льоду він поглинає тепло, проте його температура не почне зростати доти, доки триває плавлення (фазовий перехід).
Відповідь: Г.
ТЕМА: Молекулярна фізика й термодинаміка. Властивості газів, рідин і твердих тіл. Капілярні явища.
Завдання скеровано на оцінювання розуміння загальних принципів капілярних явищ.
Висоту підйому або опускання води в капілярі порівняно з рівнем води в широкій посудині обчислюють за формулою:
Вода змочує скло, тому вона підніматиметься в капілярах.
Поверхневий натяг мильного розчину становить
Зі збільшенням температури поверхневий натяг зменшується, адже більше молекул пари опиняється поруч із поверхнею рідини. Що більше молекул газу опиняється поруч із поверхнею, то ближчими будуть сумарні сили взаємодії молекул рідини на поверхні з молекулами газу й молекулами рідини. А отже рівнодійна, що затягує молекули на поверхні вглиб об’єму рідини буде меншою, що й зменшує поверхневий натяг. Тож зі збільшенням температури зменшиться і висота підйому рідини в капілярі.
Ширина посудини з водою ніяк не впливає на підйом рідини всередині капіляра.
Тонший капіляр має менший радіус. Що менший радіус капіляра, то вища висота підйому рідини в ньому.
Відповідь: Г.
ТЕМА: Електродинаміка. Основи електростатики. Електростатичний потенціал.
Завдання скеровано на оцінювання розуміння понять електростатичного потенціалу, різниці потенціалів і роботи електричного поля з перенесення заряду й уміння розв’язувати розрахункові задачі, пов’язані із цими поняттями.
Потенціал
Для точкового заряду потенціал можна розрахувати за формулою
де
Різниця потенціалів – скалярна фізична величина, яка дорівнює відношенню роботи сил електростатичного поля з переміщення заряду з початкової точки в кінцеву до значення цього заряду:
Тож робота, виконувана полем під час перенесення заряду залежить від різниці потенціалів між початковою і кінцевою точкою: чим менша ця різниця, тим менша (за модулем) виконувана робота.
З огляду на те, що точки О і Г лежать на одній еквіпотенціальній поверхні, то
Інші точки лежать на інших еквіпотенціальних поверхнях, тому найменшу (за модулем) роботу
Відповідь: Г.
ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для ділянки кола.
Завдання скеровано на оцінювання розуміння схематичного зображення електричного кола й уміння використовувати закон Ома для ділянки електричного кола.
Реостат – це прилад, опір якого можна змінювати. Часто опір реостата регулюють за допомогою ковзного контакту, положення якого визначає частину провідника, уключеного в коло. На схемі електричного кола чим більша частина реостата розташована після стрілки, яка показує точку включення, тим більшим є опір цього приладу (рис. 1).
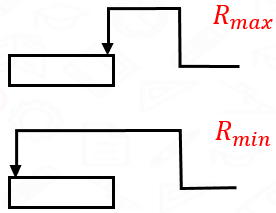
Рис. 1. Опір реостата за різних положень ковзного контакту
За умовою задачі ковзний контакт реостата перемістили в крайнє ліве положення, за рисунком це положення з мінімальним опором. Тож можна дійти висновку, що опір реостата зменшився.
Потрібно розглянути дві ситуації з відповідними показаннями амперметра, вольтметра й опором реостата – до зміни
Реостат послідовно підключено до лампи. Сила струму в послідовно з’єднаних провідниках однакова й дорівнює загальній силі струму в ділянці кола:
Загальна напруга на послідовно з’єднаних провідниках дорівнює сумі напруг на них:
Загальний опір послідовно з’єднаних провідників дорівнює сумі опорів цих провідників:
Позначивши загальну напругу в колі
Тож можна порівняти силу струму в двох випадках:
Вольтметром у схемі вимірюють напругу на лампі. Позначивши опір лампи як
Тепер можна порівняти напругу на лампі:
Відповідь: B.
ТЕМА: Електричний струм у різних середовищах. Електричний струм у напівпровідниках. Електронно-дірковий перехід.
Завдання скеровано на оцінювання розуміння принципу роботи p-n переходу й основних його особливостей.
Зменшення опору зі збільшенням температури й освітленості є важливими особливостями напівпровідників.
p-n-Перехід – це ділянка контакту двох напівпровідників із різними типами провідності. Їхньою головною особливістю є одностороння провідність. Під час прямого підключення p-напівпровідник із дірковою провідністю з’єднують із позитивним полюсом джерела, а n-напівпровідник – із негативним полюсом. У такому разі електрони з напівпровідника n-типу рухаються до позитивного полюса джерела, а дірки з напівпровідника p-типу рухаються до негативного полюса джерела. Цей рух проходить крізь p-n перехід, а отже потоку електронів у колі від одного полюса джерела до іншого нічого не заважає (рис. 1).
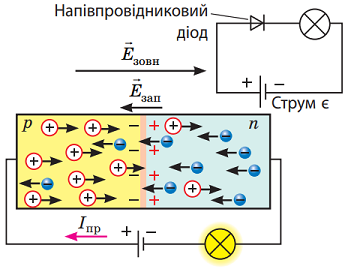
Рис. 1. Процеси в p-n переході під час прямого підключення
Якщо p-n перехід до джерела навпаки (негативний полюс до напівпровідника p-типу, а позитивний до напівпровідника n-типу), то дірки й електрони знову почнуть рухатися до протилежних полюсів джерела, але цього разу рух відбувається не крізь p-n перехід, а навпаки. Тому потік електронів між полюсами джерела в колі майже зупиняється (рис. 2).
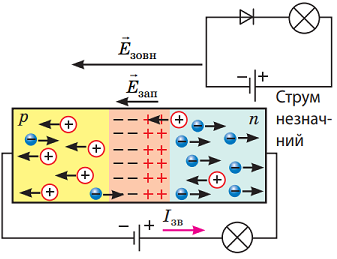
Рис. 2. Процеси в p-n переході під час зворотного підключення
Відповідь: B.
ТЕМА: Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі.
Завдання скеровано на оцінювання вміння розраховувати енергію елементів коливального контуру.
Коливальний контур – це фізичний пристрій, який складено з послідовно з’єднаних конденсатора й котушки індуктивності (рис. 1).
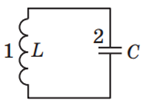
Рис. 1. Електрична схема коливального контуру: 1 – котушка індуктивності, 2 – конденсатор
В ідеальному коливальному контурі вся енергія під час коливань перетікає від конденсатора до котушки без утрат. Цей процес описують за допомогою формули
Під час коливань у контурі енергія повністю зарядженого конденсатора перетікатиме в енергію котушки, яку можна визначити за формулою
У контурі електрони, що накопичилися на одній з обкладинок конденсатора, рухатимуться в напрямку до іншої його обкладинки, утворюючи струм у колі. У результаті цього конденсатор почне розряджатися, напруга на його обкладинках зменшується, а отже зменшуватиметься і його енергія.
У котушці ж сила струму поступово збільшуватиметься, а разом із нею збільшуватиметься й енергія магнітного поля, яке вона створює. Коли конденсатор розрядиться повністю, струм у котушці стане максимальним.
Після того, як конденсатор повністю розрядиться, електрони продовжать свій рух, адже просто зупинитися вони не можуть. Тож тепер на вже нейтральну обкладинку конденсатора починають потрапляти електрони. У результаті цього вона заряджається, а струм у котушці поступово зменшується.
Унаслідок цього процесу заряд з однієї обкладинки конденсатора опиниться на іншій обкладинці. Тож тепер конденсатор заряджений протилежно до початкового стану, і напруга на ньому за модулем дорівнює початковій напрузі, але має протилежний знак.
Після цього струм почне текти в протилежному напрямку. Одне повне коливання закінчиться тоді, коли заряд повністю повернеться на першу обкладинку.
Тож за одне коливання потенціальна енергія конденсатора двічі досягає максимуму (коли весь заряд опиняється на одній з обкладинок) і двічі досягає
Відповідь: Г.
ТЕМА: Оптика. Закони відбивання світла. Закони заломлення світла. Лінза.
Завдання скеровано на перевірку розуміння принципів роботи оптичних елементів.
Промені проходять крізь склянку з водою, адже в іншому разі неможливо було би побачити Гаррі, що розташований за нею. Тому склянка з водою не виконує функцію дзеркала. З тієї самої причини склянка не змінює хід променів на зворотний.
Після наповнення склянки водою утворюється дійсне перевернуте зображення Гаррі. Розсіювальна лінза утворює лише уявне пряме зменшене зображення. Збиральна ж лінза може утворювати дійсне перевернуте зображення, що має ті самі розміри, що і предмет, якщо він перебуває на відстані від лінзи, яка дорівнює її подвійному фокусу.
Відповідь: А.
ТЕМА: Квантова фізика. Світлові кванти. Фотоефект й експериментально встановлені його закони.
Завдання скеровано на оцінювання розуміння фізичних засад фотоефекту.
Заряджена цинкова пластинка розряджається внаслідок поглинання квантів світла: електрони на її поверхні отримують достатньо енергії, щоб покинути пластинку. Тож це прояв зовнішнього фотоефекту.
Пластинка розряджатиметься швидше, якщо більше електронів вилітатиме з її поверхні за одиницю часу. Що більше квантів світла потрапляє на поверхню, то більше електронів зможуть її покинути. Тобто для того, щоби збільшити швидкість розрядження пластинки, треба збільшити світловий потік.
Світло поширюється від джерела в усіх напрямках, утворюючи сферу. Тому що ближче до джерела світла знаходиться тіло, то більше фотонів потрапляє на його поверхню. Наприклад, що ближче до стіни ліхтарик, то яскравішою виглядає його світлова пляма.
Тож унаслідок зменшення відстані між ліхтарем і пластиною вона розряджатиметься швидше.
Відповідь: B.
ТЕМА: Квантова фізика. Атом й атомне ядро. Ядерні реакції.
Завдання скеровано на оцінювання вміння аналізувати рівняння ядерних реакцій і розуміння процесу ядерного розпаду.
Під час радіоактивних розпадів масове число дорівнює кількості нуклонів у ядрі, а зарядове число – кількості протонів.
За альфа розпаду масове число нукліда зменшується на чотири, а зарядове – на два за схемою
Під час бета-розпаду зарядове число нукліда збільшується на одиницю за схемою
Послідовні розрахунки для трьох альфа-розпадів такі:
Послідовні розрахунки для двох бета-розпадів:
Відповідь: Б.
ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Абсолютна та відносна вологість. Точка роси.
Завдання скерованo на перевірку розуміння понять точки роси, випаровування, кристалізації та адіабатного процесу.
А Роса почне формуватися, коли повітря сягне точки роси. Точка роси – це температура, за якої водяна пара, що міститься в повітрі, стає насиченою.
Б Стискання повітря в насосі відбувається настільки швидко, що воно не встигає обмінятись енергією з довкіллям. У такому разі робота, виконана тілом, переходить у його внутрішню енергію.
В Замерзання водоймищ восени – це приклад кристалізації рідини.
Г Висихання білизни після прання – це приклад випаровування рідини.
Д Іній – це тонкий шар льоду на поверхнях. Він утворюється завдяки тому, що водяна пара в повітрі кристалізується.
Відповідь: 1Г, 2Б, 3А, 4Д.
ТЕМА: Коливання і хвилі. Оптика.
Завдання скеровано на перевірку знання і розуміння явищ геометричної і хвильової оптики.
Заломлення ‒ це явище зміни напрямку поширення хвилі під час її проходження через плоску межу двох однорідних середовищ.
Дифракція ‒ це явище потрапляння світлових хвиль в область геометричної тіні, тобто відхилення їх від прямолінійного поширення.
Дисперсія ‒ це явище залежності показника заломлення середовища від довжини електромагнітної хвилі.
Інтерференція ‒ це явище накладання когерентних хвиль, унаслідок якого спостерігається стійка в часі картина посилення їх та послаблення в різних точках простору.
Відповідь: 1Б, 2Д, 3А, 4Г.
ТЕМА: Механіка. Закони збереження в механіці. Механічна робота. Закон збереження енергії в механічних процесах.
Завдання скеровано на перевірку вміння застосовувати закон збереження механічної енергії під час розв’язування задач про рух тіла під дією кількох сил.
Якщо тілу надати певної швидкості, то воно матиме кінетичну енергію
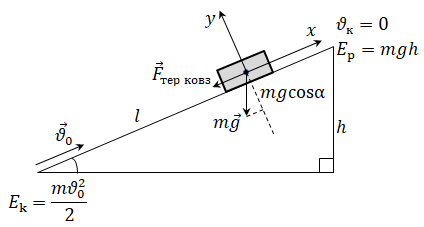
Отже,
Відповідь: 6.
ТЕМА: Механіка. Закони збереження в механіці. Імпульс тіла. Закон збереження імпульсу.
Завдання скеровано на перевірку вміння розв'язувати розрахункові задачі на закон збереження імпульсу.
Дано:
Знайти:
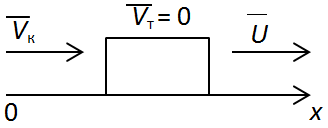
Запишемо закон збереження імпульсу:
Перейдемо до проєкцій на вісь
Відповідь: 600.
ТЕМА: Молекулярна фізика і термодинаміка. Рівняння стану ідеального газу.
Завдання скеровано на перевірку вміння використовувати рівняння стану ідеального газу в розрахункових задачах.
Дано:
Знайти:
Якщо вважати повітря ідеальним газом, то тиск, температуру й об’єм повітря пов’язує рівняння стану ідеального газу
Об’єм м’яча і його температура залишаються незмінними, але змінюються тиск і маса газу всередині:
Тоді можна визначити відношення кінцевого й початкового тисків:
Масу й об’єм пов’язує густина
За 11 циклів накачування всередину потрапило
Тоді
Відповідь: 120
ТЕМА: Магнітне поле, електромагнітна індукція. Індуктивність. Енергія магнітного поля.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі, пов’язані з енергією магнітного поля і її перетворенням на інші види енергії.
Дано:
Знайти:
Робота сторонніх сил акумулятора витрачається на збільшення енергії котушки. Максимальна енергія котушки може бути визначена за формулою
Проте коло за умовою не ідеальне – частина роботи акумулятора втрачається у вигляді виділеної теплоти. Тоді разом робота сторонніх сил акумулятора має дорівнювати сумі енергії котушки й кількості виділеної теплоти:
Відповідь: 95.
ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона. Вага. Рівномірний рух по колу.
Завдання скеровано на перевірку вміння розв’язувати комплексні задачі про рівномірний рух по колу.
Дано:
Знайти:
Гойдалка рухається за траєкторією, що є частиною кола. Тож вона матиме доцентрове прискорення, напрямлене в бік кріплення підвісу гойдалки. У найнижчій точці це прискорення буде напрямлене вертикально вгору. Вага тіл, що рухаються із прискоренням, що напрямлене вертикально вгору, може бути розрахована за формулою:
Доцентрове прискорення можна обчислити з виразу
Тоді
Відповідь: 5
ТЕМА: Квантова фізика.
Завдання скеровано на перевірку розуміння зв’язку маси та енергії.
Дано:
1. Знайти:
Енергію, спожиту родиною, необхідно перевести в Дж:
Енергія пов’язана з масою формулою
Тоді
Відповідь: 8.




