Розділ: Мультитести
Тест: Тренувальний мультитест (9 варіант)
Блок: Фізика
Кількість завдань: 20
ТЕМА: Механіка. Основи кінематики. Поступальний і обертальний рух.
Завдання скеровано на перевірку розуміння понять поступального й обертального рухів.
За визначенням поступальний рух – це такий рух тіла, за якого всі його точки рухаються однаково.
Обертальний рух – це такий рух тіла, за якого його точки рухаються по колах, центри яких лежать на одній прямій – осі обертання.
Сходи ескалатора в метро, курсор на моніторі й потяг на прямолінійній ділянці дороги рухаються поступально, тобто всі їхні точки рухаються з однаковою швидкістю і в однаковому напрямку.
Точки дзиґи під час її обертання описують кола різного радіуса навколо осі її обертання. Тобто дзиґа рухається непоступально.
Відповідь: Г.
ТЕМА: Механіка. Основа динаміки. Додавання сил.
Завдання скеровано на оцінювання розуміння поняття рівнодійної.
Якщо рівнодійна сил, що діють на тіло, дорівнює нулю, то тіло перебуває у стані спокою. Тіло у стані спокою має постійну швидкість.
Адже за другим законом Ньютона $$ \overline{F}=m\overline{a}, $$ де \(\overline{F}\) – рівнодійна, \(m\) – маса тіла, \(\overline{a}\) – прискорення тіла.
Якщо тіло не рухається, можна вважати, що його швидкість постійна й дорівнює 0 м/с.
У варіанті відповіді А віз залишається на своєму місці, а в Б вода у склянці нерухома, тож їхні швидкості дорівнюють нулю. А отже й рівнодійна сил, що діють на них, – теж.
У варіанті відповіді В парашутист рухається рівномірно вниз, тобто його швидкість постійна, а отже й рівнодійна, що діє на нього, дорівнює нулю.
У варіанті відповіді Г літак щойно відірвався від злітно-посадкової смуги. Тобто він лише почав набирати швидкість і рухався із прискоренням. Тож рівнодійна сил, що діють на нього, не дорівнює нулю.
Відповідь: Г.
ТЕМА: Механіка. Основи динаміки. Момент сил.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з визначення моменту сил.
Момент сили \(M\) – це фізична величина, що дорівнює добутку модуля сили \(F\), яка діє на тіло, на плече \(d\) цієї сили: $$ M = Fd\ \ (1) $$ Плече \(d\) сили \(F\) – це найменша відстань від осі обертання тіла до лінії, уздовж якої діє сила (рис. 1).
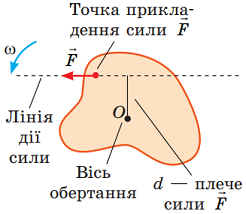
Рис. 1. Схема визначення плеча сили
Проаналізувавши рисунок 2 (його наведено в завданні), потрібно визначити плечі сил, схематично зображених на ньому.
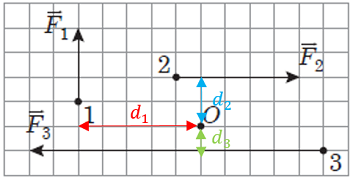
Рис. 2. Визначення плечей сил, про які йдеться в завданні
У завданні не зазначено розмір клітинок, тож можна вважати довжину сторони клітинки умовною одиницею довжини (у. о. д.).
Згідно з виразом (1): \begin{gather*} M_1=F_1 d_1=3Н\cdot\ 5\ \text{у. о. д.}=15Н \cdot\ \text{у.о.д.;}\\[7pt] M_2=F_2 d_2=5Н\cdot\ 2\ \text{у. о. д.}=10Н\cdot\ \text{у.о.д.;}\\[7pt] M_3=F_3 d_3=12Н\cdot\ 1\ \text{у. о. д.}=12Н\cdot\ \text{у.о.д.} \end{gather*} Отже: $$ M_1\gt M_3\gt M_2. $$
Відповідь: A.
ТЕМА: Молекулярна фізика й термодинаміка. Ізопроцеси
Завдання скеровано на оцінювання вміння аналізувати графіки ізопроцесів і будувати їх у різних системах координат.
Процес 1–2 є ізохорним (тиск \(p\) й температура \(T\) зростають за сталого
об’єму \(V\)).
Процес 2–3 – ізобарним (температура \(T\) зростає, об’єм \(V\) за сталого тиску \(p\)).
Відповідно в координатах \(pV\) процес 1–2 відображено перпендикулярною до осі \(V\) прямою, напрямленою вгору, бо тиск зростає, а процес 2–3 – перпендикулярною до осі \(p\) прямою, напрямленою вправо, бо об’єм збільшується.
Відповідь: A.
ТЕМА: Вимірювальні пристрої.
Завдання скеровано на оцінювання розуміння фізичних принципів роботи вимірювальних пристроїв.
Термометр – це прилад для вимірювання температури. Він працює завдяки тому, що деякі речовини за сталого тиску суттєво змінюють свій об’єм за зміни температури (ртуть чи спирт розширюються за збільшення температури і звужуються за її зменшення).
Психрометр – це прилад для вимірювання відносної вологості. Принцип його роботи такий: у корпусі приладу є два термометри. Кінець одного з них зазвичай обгорнутий у вологу тканину. Вода з тканини завжди випаровується, і швидкість випаровування залежить від того, яка вологість повітря навколо. Для вимірювання відносної вологості фіксують покази сухого й вологого термометрів і за допомогою спеціальних таблиць виконують необхідні розрахунки.
Барометр – це прилад для вимірювання атмосферного тиску. У завданні зображено безводний барометр (анероїд), усередині якого є вакуумна камера з гофрованою поверхнею. За високого атмосферного тиску кришка коробки сильно опускається, а за низького – піднімається. До кришки за допомогою пружини прикріплено стрілку. Тому, коли кришка камери піднімається чи опускається, пружина деформується, а стрілка починає рухатися по шкалі.
Динамометр – це прилад для вимірювання сили. Зазвичай динамометр складається із пружини і шкали. Коли на кінець пружини діє сила, то за законом Гука пружина розтягується: $$ F=kx. $$
Тому, якщо відомий коефіцієнт жорсткості пружини, то за значенням її видовження можна визначити й силу, що його зумовлює.
Відповідь: Б.
ТЕМА: Електродинаміка. Закони постійного струму. Паралельне й послідовне з’єднання провідників.
Завдання скеровано на оцінювання знання закону Ома й розуміння особливостей паралельного й послідовного з’єднання провідників.
Яскравість світіння лампи залежить від її потужності, яку визначають за формулою \(P=UI\), де \(U\) – напруга, а \(I\) – сила струму в колі. Чим більша потужність лампи, тим більша яскравість її світіння. Тобто для правильного розв’язання задачі потрібно обчислити напругу й силу струму, який протікає через кожну з ламп.
Позначимо напругу в колі \(U,\) а опір лампочок – \(R'.\)
З рисунку зрозуміло, що лампа 1 послідовно з’єднана з лампами 2 і 3, які між собою з’єднані паралельно.
Правильне розв’язання завдання ґрунтується на розумінні законів паралельного й послідовного з’єднання провідників (див. рисунки 1–2).
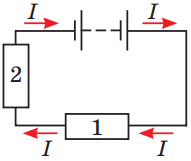
Рис. 1. Послідовне з’єднання провідників 1 і 2: \(U=U_1+U_2,\ R=R_1+R_2,\ I=I_1=I_2\)
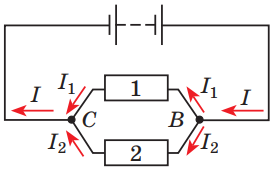
Рис. 2. Паралельне з’єднання провідників 1 і 2: \(U=U_1=U_2,\ \frac 1R=\frac{1}{R_1}+\frac{1}{R_2},\ I=I_1+I_2\)
Оскільки за умовою завдання лампи 2 і 3 з’єднані паралельно, то для цієї частини кола
Для повного кола до виходу лампи 2 з ладу
З огляду на те, що опір усіх ламп однаковий, сила струму \(I\) за законом Ома дорівнює частці від ділення напруги на опір: $$ I=\frac UR=\frac{U}{R_1+\frac{R_2 R_3}{R_2+R_3}} =\frac{2U}{3R '}. $$
Тож $$ I_1=\frac{2U}{3R '}, $$ а $$ I_3=\frac{U}{3R '}. $$ Тому на лампі 1 напруга $$ U_1=I_1 R_1=\frac{2U}{3}, $$ а на лампі 3 напруга $$ U_3=I_3 R_3=\frac U3. $$
Тобто до поломки потужність цих ламп була $$ P_{1\ до}=U_1 I_1=\frac{2U}{3}\cdot\frac{2U}{3R '} =\frac{4U^2}{9R '} $$ і $$ P_{3\ до}=U_3 I_3=\frac U3\cdot \frac{U}{3R '}=\frac{U^2}{9R '} $$ відповідно.
Після того, як лампа 2 вийшла з ладу, її опір став дуже великим, тому крізь неї струм не потече. Електричне коло після виходу з ладу лампи 2 схематично зображено на рисунку 3.
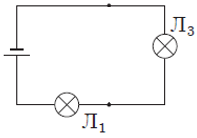
Рис. 3. Схема електричного кола після виходу з ладу лампи 2
У цьому електричному колі лампи 1 і 3 з’єднано послідовно, тому $$ U=U_1+U_3,\ R=R_1+R_3,\ I=I_1=I_3. $$
Напруга в колі не змінилася через поломку лампи, тож, за законом Ома, у цьому колі сила струму $$ I=\frac UR=\frac{U}{R_1+R_3}=\frac{U}{2R '}=I_1=I_3. $$ На кожній із ламп напруга така: $$ U_1=I_1 R_1=\frac U2,\ U_3=I_3 R_3=\frac U2. $$ Тоді після поломки їхня потужність становить
Отже, \(P_{1\ до}\gt P_{1\ після}\), а \(P_{3\ до}\lt P_{3\ після}\)
Відповідь: B.
ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Поняття про плазму.
Завдання скеровано на перевірку розуміння поняття плазми.
Пригадаймо, що плазма – це частково або повністю йонізований газ, у якому концентрації позитивних і негативних зарядів майже однакові. Під час йонізації нейтральні атоми газу втрачають електрони й перетворюються на позитивні йони. Тож вільними носіями в плазмі є як утворені вільні електрони, так і позитивні йони.
Відповідь: Г.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція.
Завдання скеровано на оцінювання розуміння природи магнітної індукції і вміння аналізувати результати експерименту за його схематичним рисунком.
Лінії індукції магнітного поля, утвореного провідником зі струмом, мають вигляд кола. Чим далі від провідника точка, тим менше в ній значення індукції магнітного поля.
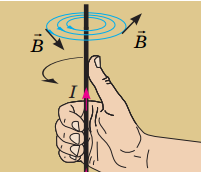
Рис. 1. Лінії магнітної індукції навколо провідника зі струмом
Коли провідник скручують у петлі, утворюється котушка. Лінії магнітної індукції всередині котушки набагато густіші (рис. 2), тож і значення індукції більше. Чим більше витків у котушці, тим більшим може бути значення індукції всередині неї.
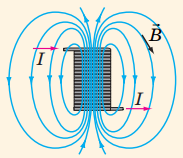
Рис. 2. Напрямок магнітної індукції в котушці
Тож, оскільки провідник поруч з усіма точками відрізняється лише тим, якої форми він набуває (петля, дві петлі чи пряма). То найбільшим буде значення індукції в центрі котушки з найбільшою кількістю петель. Тобто в точці 3.
Відповідь: B.
ТЕМА: Сила пружності. Механічні коливання. Коливання вантажу на пружині.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з виявлення зв’язку між періодом коливання і параметрами коливальної системи.
Період коливання \(T\) пружинного маятника обчислюють за формулою $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{\frac mk}, $$ де \(m\) – маса тягарця, а \(k\) – коефіцієнт жорсткості пружини.
Якщо вдвоє скласти гумову нитку, яка виконує функцію пружини, то утвориться маятник, що коливається на двох удвічі менших пружинах, з’єднаних паралельно. Тоді до складання велику пружину (гумову нитку) можемо вважати двома половинками, що з’єднані послідовно.
Якщо є дві пружини із жорсткістю \(k_1\) і \(k_2\) відповідно, то можна визначити жорсткість пружин, які відповідають паралельному й послідовному їхньому з’єднанню.
Для паралельного з’єднання пружин їхня жорсткість \(k' = k_1 + k_2.\)
Для послідовного з’єднання жорсткість $$ k=\frac{k_1 k_2}{k_1+k_2}. $$
Половинки пружини мають однакову жорсткість і \(k_1 = k_2 = k'',\) тому жорсткість $$ k= \frac{(k'')^2}{2k''}=\frac{k''}{2}. $$
Оскільки \(k'' = 2k,\) жорсткість кожної половинки вдвічі більша за жорсткість початкової пружини (гумової нитки).
Якщо з’єднати ці дві половинки паралельно, то отримана пружина матиме жорсткість \(k'= k''+ k''= 2k''.\)
Тоді період такої пружини дорівнюватиме
Порівняння його з періодом коливання \(T\) пружинного маятника \(T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{\frac mk}\) дає змогу дійти висновку, що \(T'=1/2T.\)
Відповідь: Б.
ТЕМА: Оптика. Закони відбивання і заломлення світла. Лінза. Дифракційна ґратка.
Завдання скеровано на оцінювання розуміння принципів роботи оптичних елементів.
До оптичного елемента на рисунку, наведеному в умові завдання, пучок променів розширюється, а після – перетворюється на пучок паралельних променів.
Пучок не може стати паралельним після проходження через плоске дзеркало чи дифракційну ґратку за жодних обставин.
Щодо лінз: якщо пучок виходить із фокусу лінзи, після неї промені будуть паралельними, але ця умова набирає різних форм для розсіювальних і збиральних лінз. Для розсіювальної лінзи продовження напрямку променів до лінзи мають збиратись у фокусі за лінзою (рис. 1), тобто пучок до лінзи повинен звужуватись, а для збиральної лінзи пучок має виходити із фокусу перед лінзою, тобто пучок розширюватиметься (рис. 2).
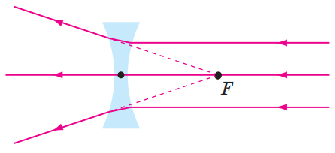
Рис. 1. Хід променів у розсіювальній лінзі
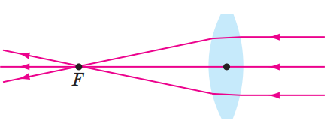
Рис. 2. Хід променів у збиральній лінзі
Відповідь: Б.
ТЕМА: Квантова фізика. Елементи теорії відносності. Взаємозв’язок маси й енергії.
Завдання скеровано на перевірку розуміння потужності й уміння визначати її.
Потужність випромінювання \(P\) – це повна енергія \(E,\) яку переносить світло за одиницю часу \(t:\) $$ P=\frac Et. $$
Виділення тілом енергії (випромінювання) супроводжується зменшенням його маси. Зміна енергії тіла прямо пропорційна зміні його маси: $$ \Delta E=\Delta mc^2, $$ де \(m\) – маса тіла, \(c\) – швидкість поширення випромінювання.
Відповідно \begin{gather*} P=\frac{\Delta E}{t}=\frac{\Delta mc^2}{t};\\[6pt] \Delta m=\frac{Pt}{c^2}. \end{gather*}
Перед обчисленням потрібно перевести значення часу в систему СІ: \(3\ \text{хв} = 180\ \text{с.}\)
Відповідь: B.
ТЕМА: Атом й атомне ядро.
Завдання скеровано на оцінювання розуміння дослідів Резерфорда та їхнього значення для розуміння будови атома.
α-частинки – позитивно заряджені важкі частинки (ядра атомів Гелію). Під час їхнього наближення до позитивно зарядженого важкого ядра Ауруму починають діяти електростатичні сили відштовхування α-частинок від ядра (рис. 1).
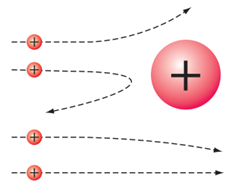
Рис. 1. Траєкторії α-частинок, що пролітають поряд із ядром
Відповідь: Б.
ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів. Адіабатний процес.
Завдання скеровано на перевірку розуміння і застосування першого закону термодинаміки до ізопроцесів і адіабатного процесу.
Перший закон (начало) термодинаміки: кількість теплоти \(Q,\) передана системі, йде на зміну внутрішньої енергії системи \(\Delta U\) та на виконання системою роботи \(A\) проти зовнішніх сил: $$ Q=\Delta U+A. $$
Запишімо перший закон термодинаміки для ізопроцесів й адіабатного процесу.
Адіабатний процес ‒ це процес, який відбувається без теплообміну з навколишнім середовищем. Під час адіабатного процесу кількість теплоти \(Q,\) передана системі, дорівнює нулю, тому запис першого закону термодинаміки такий: $$ \Delta U+A=0\ \text{або}\ A=-\Delta U. $$
Під час адіабатного розширення газ виконує додатну роботу за рахунок зменшення внутрішньої енергії, а температура газу зменшується. Тому під опис адіабатного розширення підходять числові значення фізичних величин, зазначених у варіанті A: \(Q=0,\ A=12\ \text{кДж},\ \Delta U=-12\ \text{кДж}.\)
Ізохорне охолодження. Під час цього процесу об’єм газу не змінюється \((\Delta V = 0)\) і газ роботу не виконує \((A=0),\) тому рівняння першого закону термодинаміки має вигляд: $$ Q=\Delta U. $$
Газ під час ізохорного охолодження віддасть певну кількість теплоти, на стільки само зменшиться його внутрішня енергія. Тому ізохорному охолодженню відповідають числові значення фізичних величин, зазначені у варіанті Г: \(Q=-18\ \text{кДж},\ A=0,\ \Delta U=-18\ \text{кДж}.\)
Ізотермічне розширення. Під час цього процесу температура, а отже, і внутрішня енергія газу не змінюються \((\Delta U=0),\) тому рівняння першого закону термодинаміки таке: $$ Q=A. $$
Під час ізотермічного розширення вся передана газу кількість теплоти йде на виконання механічної роботи. Тому процесу ізотермічного розширення ставімо у відповідність варіант В: \(Q=24\ \text{кДж},\ A=24\ \text{кДж},\ \Delta U=0.\)
Ізобарне нагрівання. Під час цього процесу виконується робота й змінюється внутрішня енергія газу, тому рівняння першого закону термодинаміки таке: $$ Q=\Delta U+A. $$
Під час ізобарного нагрівання передана газу кількість теплоти йде і на збільшення внутрішньої енергії газу, і на виконання механічної роботи. Отже, підійде той варіант, у якому сума значень внутрішньої енергії і роботи дорівнюватиме значенню отриманої кількості теплоти ‒ це варіант Б: \(Q=5\ \text{кДж},\ A=2\ \text{кДж},\ \Delta U=3\ \text{кДж}.\)
У варіанті Д сума значень внутрішньої енергії і роботи також дорівнює значенню отриманої кількості теплоти, але значення кількості теплоти від’ємне, як і значення внутрішньої енергії і роботи. Це означає, що газ не нагрівається, не отримує кількість теплоти, а навпаки віддає її.
Відповідь: 1А, 2Г, 3В, 4Б.
ТЕМА: Коливання і хвилі. Оптика. Шкала електромагнітних хвиль. Властивості електромагнітного випромінювання різних діапазонів.
Завдання скеровано на перевірку знань про різні види електромагнітного випромінювання і їхні джерела.
Під час розпаду радіонуклідів у ядерному реакторі виникає радіоактивне випромінювання, один із видів якого – гамма-промені.
Будь-які тіла, температура яких вища від абсолютного нуля, випромінюють інфрачервоні промені. Саме на цьому ґрунтується застосування їх у тепловізорах – приладах нічного бачення. Тому гарячий чай є джерелом інфрачервоного (теплового) випромінювання.
Радіохвилі – від наддовгих із довжиною понад \(10\ \text{км}\) до ультракоротких і мікрохвиль із довжиною менш ніж \(0,1 \ \text{мм}\) – породжує змінний електричний струм. Електромагнітні хвилі радіодіапазону породжені високочастотним змінним струмом, який створюють генератори високочастотних електромагнітних коливань. У цьому завданні джерелом радіохвиль є супутник зв’язку.
Люмінофор – речовина, яка здатна світитися за збудження, тобто люмінесціювати. Люмінофори широко використовують в електроніці, наприклад, ними вкривають екран телевізора, електропроменевої трубки, де їхнє світіння за бомбардування електронами формує зображення, у сцинтиляційних лічильниках тощо. Людське око сприймає це світіння, отже це діапазон видимого світла.
Відповідь: 1В, 2А, 3Г, 4Д.
ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона. Сила тяжіння. Рівномірний рух по колу. Кінетична енергія.
Завдання скеровано на перевірку вміння розв’язувати комплексні задачі про рівномірний рух по колу.
Дано:
\(F_{\text{тяж}}=4\ \text{кН}\)
\(R=10000\ \text{км}\)
Знайти:
\(E_{\text{кін}}\ (\text{ГДж})\ -\ ?\)
Кінетичну енергію тіла можна обчислити за формулою \begin{gather*} E_k=\frac{mv^2}{2}, \end{gather*} де \(m\) – маса тіла, а \(v\) – швидкість його руху.
Під час руху супутника навколо Землі його швидкість спрямована по дотичній до кола, а прискорення – до центру.
Доцентрове прискорення можна обчислити з виразу $$ a_{\text{доц}}=\frac{v^2}{R}, $$ де \(v\) – швидкість супутника, а \(R\) – радіус обертання.
За другим законом Ньютона рівнодійна дорівнює добутку маси тіла на прискорення, набуте під час взаємодії: $$ \overrightarrow{F}=m\overrightarrow{a}. $$
Єдиною силою, що діє на частинки в площині напрямку руху є сила тяжіння Землі: $$ \overrightarrow{F_{\text{тяж}}}=m\overrightarrow{g}. $$
Тобто $$ mg=m\frac{v^2}{R}. $$
Із цього рівняння можна виразити добуток маси й квадрату швидкості та підставити його у формулу для кінетичної енергії:
Відповідь: 20
ТЕМА: Робота. Сила Архімеда.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі про силу Архімеда.
Дано:
\(H=4\ \text{м}\)
\(m=600\ \text{кг}\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{бетону}}=2000\ \frac{\text{кг}}{\text{м}^3}\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{води}}=1000\ \frac{\text{кг}}{\text{м}^3}\)
\(g=10\ \frac{\text{м}}{\text{с}^2}\)
Знайти:
\(A_{min}\ (\text{кДж})\ -\ ?\)
Для того, щоби перевернути блок, достатньо його центр мас підняти на висоту, на якій він у вертикальному положенні. Оскільки блок циліндричний, то в обох положеннях він на половині висоти блока (рис. 1).
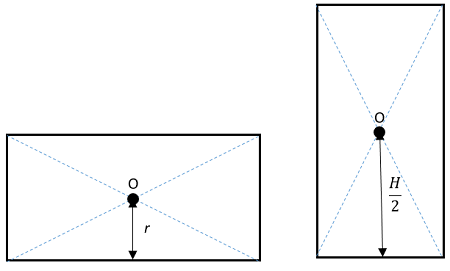
Рис. 1. Положення центра мас у вертикальному й горизонтальному положенні
Оскільки поперечні розміри стовпа за умовою враховувати не потрібно, то можна вважати, що під час перевертання центр мас піднімають на половину всієї висоти \(H\).
Рівнодійну сил, що діють на блок, можна обчислити за формулою $$ \overrightarrow{F}=\overrightarrow{F_{\text{тяж}}}+\overrightarrow{F_{\text{Арх}}}. $$
Сила тяжіння діє вертикально вниз, притягуючи блок до землі, а сила Архімеда виштовхує блок вертикально вгору, інші сили на блок не діють. Якщо вважати напрямок «вертикально вниз» додатним, \begin{gather*} F_x=0;\\[6pt] F_y=mg-\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_{\text{води}}gV_{\text{блока}}. \end{gather*}
Маса тіла пов’язана з його густиною формулою $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}=\frac mV, $$ де \(m\) – маса тіла, \(V\) – його об’єм.
Тоді
Оскільки об’єму блока невідомий, із дужок можна винести його густину:
Тоді робота, необхідна для підняття центра мас бетонного блока на половину його висоти, дорівнює
Відповідь: 6.
ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. ККД теплового двигуна.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі на обчислення коефіцієнта корисної дії теплової машини.
Дано:
\(A = 40\ \text{МДж}\)
\(Q_{\text{х}}=A\)
Знайти:
\(\text{ККД}\ (\text{%})\ -\ ?\)
ККД теплового двигуна визначається за формулою $$ \text{ККД}=\frac{A}{Q_{\text{н}}}\cdot 100\ \text{%}, $$ де \(A\) – корисна робота, виконана двигуном, \(Q_{\text{н}}\) – теплота, отримана від нагрівача.
Частина отриманої теплоти \(Q_{\text{н}}\) використовується на виконання роботи, а решта передається холодильнику. У цій задачі холодильником є середовище. Тоді можна обчислити отриману теплоту:
Після цього можна розрахувати ККД такого двигуна:
Відповідь: 50.
ТЕМА: Електродинаміка. Основи електростатики. Конденсатори.
Завдання скеровано на перевірку розуміння впливу зовнішніх чинників на електроємність конденсатора.
Знайти:
\(\frac{S_2}{S_1}\ -\ ?\)
Електроємність конденсатора залежить від його геометричних характеристик: $$ C=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_0S}{d}, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}\) – діелектрична проникність діелектрика між обкладинками, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_0\) – електрична стала, \(S\) – площа обкладинок, \(d\) – відстань між обкладинками.
Під час повороту обкладинок конденсатора змінюється площа їхнього перекриття. Нехай довжина пластини становить \(5\) клітинок, а ширина – \(3\) клітинки. Тоді можна обчислити початкову площу перекриття в умовних одиницях: $$ S_1=3\cdot 5=15\ (\text{у. о.}). $$
Після повороту область перекриття перетворилася на квадрат зі стороною 3 клітинки, площа якої дорівнює:
\begin{gather*} S_2=3\cdot 2=9\ (\text{у. о.});\\[6pt] \frac{S_2}{S_1}=\frac{9\ \text{у. о.}}{15\ \text{у. о.}}=0,6. \end{gather*}Відповідь: 0,6.
ТЕМА: Електродинаміка. Закони постійного струму. Електрорушійна сила.
Завдання скеровано на перевірку вміння аналізувати графіки тригонометричних залежностей фізичних величин.
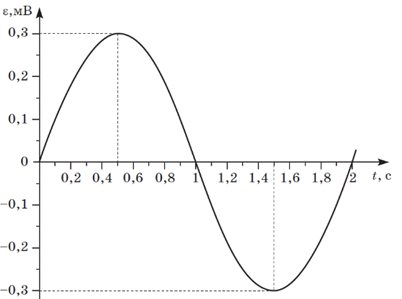
Рис. 1. Умова завдання
Знайти:
\(\text{ЕРС}\ (\text{мВ})\ -\ ?\)
Графік, зображений на рисунку 1, – це графік синусоїдальної залежності, тож електрорушійна сила (ЕРС) залежить від часу: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}=A\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}t, $$ де \(A\) – амплітуда коливань, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}\) – циклічна частота коливань, \(t\) – момент часу.
Циклічна частота пов’язана з періодом формулою $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}=\frac{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{T}. $$
За графіком можна також визначити амплітуду коливань, яка дорівнює максимальному відхиленню від положення рівноваги: $$ A=0,3\ \text{мВ}, $$ тож $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}=0,3\sin\frac{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{T}t. $$
Тоді можна обчислити ЕРС в момент часу \(t=\frac{T}{12}\):
\begin{gather*} \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}=0,3\sin\left(\frac{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{T}\ \frac{T}{12}\right);\\[6pt] \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}=0,3\sin\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{6};\\[6pt] \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}=0,3\cdot \frac 12;\\[6pt] \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}=0,15\ (\text{мВ}). \end{gather*}Відповідь: 0,15.
ТЕМА: Квантова фізика. Світлові кванти. Фотоефект й експериментально встановлені його закони.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на обчислення червоної межі фотоефекту.
Дано:
\(A_{\text{вих}}=4,5\ \text{еВ}\)
\(1\ \text{еВ}=1,6\cdot 10^{-19}\ \text{Дж}\)
\(h=6,6\cdot 10^{-34}\ \text{Дж}\cdot \text{с}\)
\(c=3\cdot 10^8\ \text{м/с}\)
Знайти:
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}_{\text{гранична}}\ (\text{м})-?\)
Фотоефект – це явище взаємодії світла з речовиною, супроводжуване випромінюванням (емісією) електронів.
Частинки світла (фотони) під час зустрічі з катодом передають енергію електронам на його поверхні. Енергію рухомого фотона визначають за формулою \(E=hv,\) де \(E\) – енергія фотона, \(v\) – частота випромінювання.
Енергію \(E\), отриману від фотона, електрон витрачає на те, щоби вирватися з поверхні металу (робота виходу \(A_{\text{вих}}\)) і на його рух після цього (кінетична енергія \(E_{\text{кін}}\): $$ E = A_{\text{вих}}+E_{\text{кін}}. $$
Мінімальна енергія, яку потрібно передати електронам, щоби фотоефект відбувався дорівнює роботі виходу: $$ E = A_{\text{вих}}+hv_{\text{гранична}}. $$
Між частотою випромінювання і довжиною хвилі випромінювання є зв’язок: $$ v=\frac{c}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}} $$
Тому
Відповідь: 275.