Мультитести – Математика

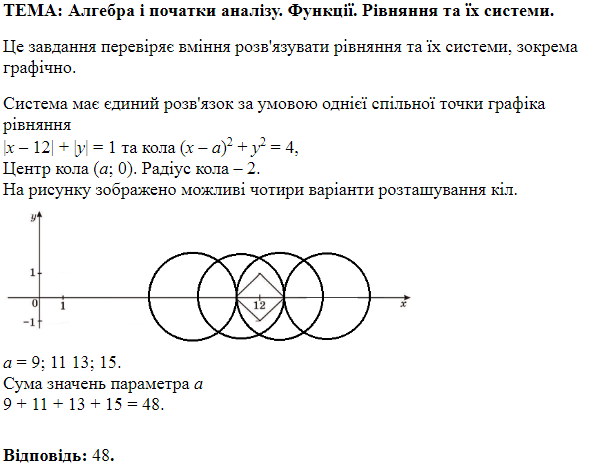
ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє вміння знаходити неповну частку, остачу від ділення одного натурального числа на інше.

\(194\) учні можна розсадити в їдальні
\(194 : 6 = 32\) (остача \(2\)).

Таким чином, учні розсядуться по \(6\) учнів за \(32\) столи та \(2\) учні сядуть за \(33\text{-й}\) стіл.

Відповідь: Г.

ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури та їхні властивості.

Завдання перевіряє знання властивостей вертикальних i суміжних кутів, паралельних прямих.

\(\angle\mathbf{\beta}=\angle\mathbf{\gamma}\) як вертикальний. \(\mathbf{\alpha}+\mathbf{\gamma}=180^\circ.\) За властивістю паралельних прямих. \(\mathbf{\alpha}\), \(\mathbf{\gamma}\) – внутрішні односторонні. $$ \mathbf{\alpha}=180^\circ-\mathbf{\gamma}=180^\circ-125^\circ=55^\circ. $$

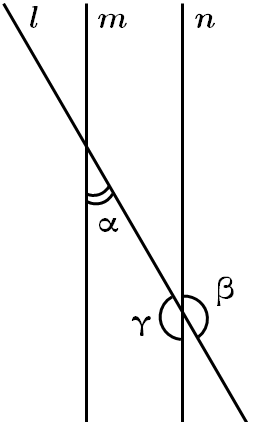
Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє відношення та пропорції. Перевіряє знання основної властивості пропорції.

Розв'яжемо рівняння, використавши основну властивість пропорції: \begin{gather*} \frac 8x=\frac 25,\\[6pt] 2\cdot x=8\cdot 5,\\[6pt] x=20. \end{gather*}

Відповідь: A.

ТЕМА: Геометрія Стереометрія. Тіла обертання.

Завдання перевіряє знання формул для обчислення площ поверхонь циліндра.

\(S_\text{бічної}=56\mathbf{\pi}\), \(S_\text{поверхні}=S_\text{бічної}+2S_\text{основи}=92\mathbf{\pi}.\)

Отже, \(92\mathbf{\pi}=56\mathbf{\pi}+2S_\text{основи}.\)

\(2S_\text{основи}=36\mathbf{\pi}\), \(S_\text{основи}=18\mathbf{\pi}.\)

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Функції. Функціональна залежність.

Це завдання перевіряє вміння будувати графіки елементарних функцій, використовувати перетворення графіків функцій.

Функції \(y=f(x)\) та \(y=-f(x)\) симетричні відносно осі \(Ox.\)

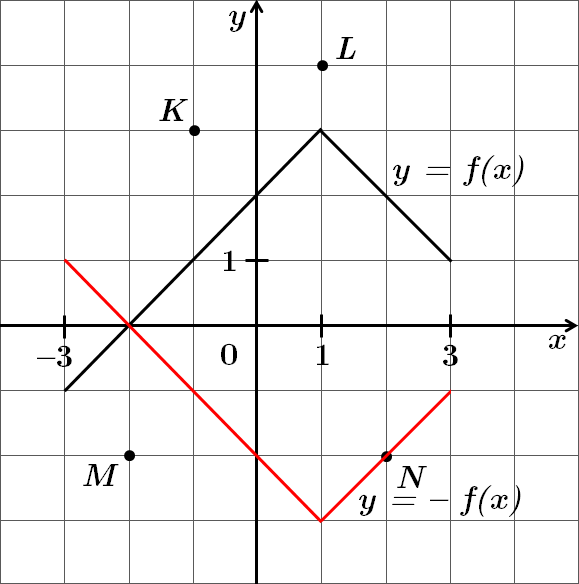
Точка \(N\) належить графіку \(y=-f(x).\)

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання перевіряє вміння використовувати перетворення графіків функцій.

Елементарними перетвореннями графік функції \(y=x^2\) перемістили на \(2\) одиниці вліво вздовж осі \(Ox\) та отримали графік фукнції \(y=(x+2)^2.\)

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє вміння виконувати тотожні перетворення числових виразів.

Розкриємо дужки та зведемо подібні доданки: $$ x+2(x-2)=x+2x-4=3x-4. $$

Відповідь: A.

ТЕМА: Рівняння, нерівності та їхні системи. Показникові рівняння.

Це завдання перевіряє вміння розв'язувати показникові рівняння.

Отже, корінь рівняння \(x=4.\)

Відповідь: Б.

ТЕМА: Функції. Похідна функції. Похідні елементарних функцій. Правила диференціювання.

Це завдання перевіряє вміння знаходити похідну елементарних функцій, знаходити суми двох функцій.

Знайдемо похідну за правилом знаходження похідної суми двох функцій та похідної степеневої функції: $$ f'(x)=4x^3+1. $$

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв'язувати систему лінійних нерівностей.

Розв'яжемо системи лінійних нерівностей:

\begin{gather*} \left\{\begin{array}{l} 4x-7\ge 2x+1,\\ x\ge -3, \end{array}\right.\ \ \left\{\begin{array}{l} 4x-2x\ge 1+7,\\ x\ge -3, \end{array}\right.\\[7pt] \left\{\begin{array}{l} 2x\ge 8,\\ x\ge -3, \end{array}\right.\ \ \left\{\begin{array}{l} x\ge 4,\\ x\ge -3. \end{array}\right. \end{gather*}

Отже, розв'язок нерівності \(x\in [4; +\infty).\)

Відповідь: Д.

ТЕМА: Числа і вирази. Логарифмічні вирази та їхні перетворення.

Це завдання перевіряє вміння виконувати тотожні перетворення логарифмічних виразів, знання властивостей логарифма.

Використаємо властивості логарифму

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання перевіряє вміння встановлювати властивості числових функцій, заданих формулою.

1. \(y=\sqrt{x-4}\) не визначена в точці \(x=1.\)

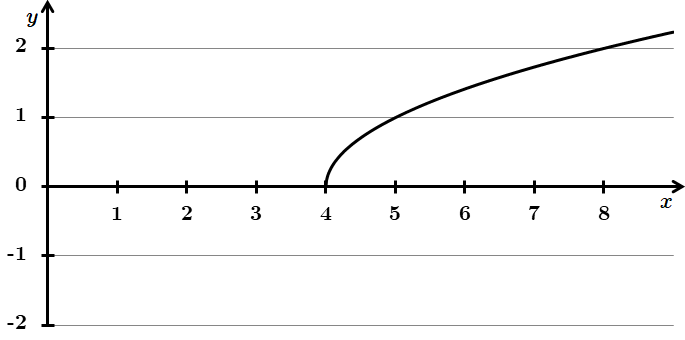
Отже, 1 – Б.

2. \(y=x+4\) набуває додатного значення при \(x=-3.\) $$y(-3)=-3+4=1.$$

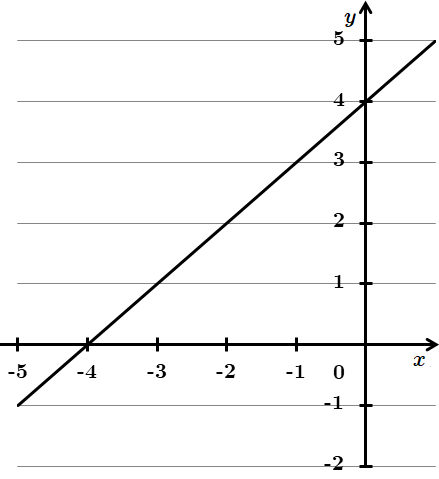
Отже, 2 – Г.

3. \(y=x^3\) – непарна (симетричний графік відносно початку координат). $$y(-x)=(-x)^3=-x^3=-y(x).$$

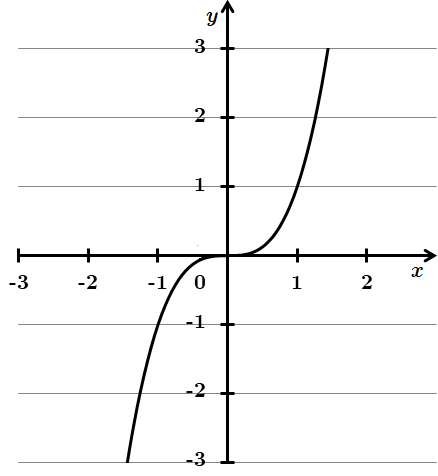
Отже, 3 – Д.

Відповідь: 1 – Б, 2 – Г, 3 – Д.

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє вміння порівнювати дійсні числа, використовувати властивості модуля до розв’язування задач.

З рисунку визначаємо, що \(a\approx 0\mathord{,}8.\)

1. \(-2a\approx -2\cdot 0\mathord{,}8=-1\mathord{,}6.\)
Значенню \(-1\mathord{,}6\) на рисунку відповідає точка \(K.\)
Отже, 1 – Г.

2. \(3^a\approx 3^{0\mathord{,}8}\),
\(3^{0\mathord{,}5}\lt 3^{0\mathord{,}8}\lt 3^1\),
\(\sqrt{3}\lt 3^{0\mathord{,}8}\lt 3\),
\(\sqrt{3}\approx 1\mathord{,}7.\)
Отже, нас цікавить точка яка належить проміжку \((1\mathord{,}7; 3.)\)
На рисунку даному проміжку належить точка \(P.\)
Отже, 2 – B.

3. \(|a-1|\approx |0\mathord{,}8-1|=|-0\mathord{,}2|=0\mathord{,}2.\)
Значенню \(0\mathord{,}2\) на рисунку відповідає точка точка \(M.\)
Отже, 3 – A.

Відповідь: 1 – Г, 2 – B, 3 – A.

ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.

Це завдання перевіряє знання властивостей прямокутника, прямокутного та рівнобедреного трикутників, теореми Піфагора.

1. За умовою завдання у прямокутник \(ABCD\) (\(AD=BC=12\) см) вписано рівнобедрений трикутник \(AKD.\) Якщо трикутник рівнобедрений, то $$ BK=KC=\frac 12BC=\frac 12\cdot 12=6\ \textit{см}. $$ \(\Delta ABK\ (\angle B=90^\circ)\) – єгипетський, \(AB=8\) см. Отже, 1 – Б.

2. Центр кола, описаного навколо прямокутника, лежить на перетині діагоналей. Радіус кола – половина діагоналі \(BD.\) У \(\Delta ABD\ (\angle A=90^\circ).\) За теоремою Піфагора:

Отже, 2 – A.

3. \(ABKD\) – трапеція. Довжина середньої лінії $$ \frac{AD+BK}{2}=\frac{12+6}{2}=9\ \textit{см}. $$ Отже, 3 – В.

Відповідь: 1 – Б, 2 – A, 3 – В.

ТЕМА: Алгебра і початки аналізу. Функції. Числові послідовності. Означення геометричної прогресії.

Це завдання перевіряє знання властивостей геометричної прогресії, уміння розв'язувати квадратні рівняння.

Якщо \(x-8\), \(3x\) та \(6x\) є послідовними членами геометричної прогресії, то \begin{gather*} b_1=x-8\\[7pt] b_2=3x\\[7pt] b_3=6x. \end{gather*}

За властивістю геометричної прогресії:

Ненульове значення \(x=-16.\)

Відповідь: \(-16.\)