Розділ: Квантова фізика. Елементи теорії відносності
Тема: Атом та атомне ядро
Кількість завдань: 84
Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Ядерні реакції.
Завдання скеровано на перевірку знання і розуміння будови атома і ядра атома.
Порядковий номер елемента в періодичній системі хімічних елементів відповідає кількості протонів у ядрі (зарядовому числу). Зарядовим (протонним) числом називають кількість протонів у ядрі й позначають символом
Запишімо рівняння ядерної реакції відповідно до умови:
Під час ядерних реакцій, як і під час будь-яких явищ, що відбуваються у Всесвіті, справджуються закони збереження: закон збереження електричного заряду, закон збереження імпульсу, закон збереження енергії-маси.
Відповідно до закону збереження електричного заряду й закону збереження енергії-маси визначімо
Отже, унаслідок такої реакції утворився нуклід
Відповідь: A.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Період піврозпаду.
Завдання скеровано на перевірку знання і розуміння закону піврозпаду.
Основний закон радіоактивного розпаду:
Визначімо, скільки ядер ізотопу залишилося:
Можемо визначити, скільки ядер розпалося:
За умовою під час розпаду кожного з цих ядер вивільнилася енергія
Відповідь: 56.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Квантові постулати Бора.
Завдання скеровано на перевірку знання і розуміння постулатів Бора.
Модифікацію планетарної моделі запропонував у 1913 р. данський фізик Нільс Бор (1885–1962), який був упевнений, що моделювати будову атома слід із погляду квантових уявлень. Бор припустив існування особливих станів атомів і сформулював два постулати.
Перший постулат Н. Бора (про стаціонарні стани):
атомна система може перебувати тільки в особливих стаціонарних (квантових) енергетичних станах, кожному з яких відповідає певне значення енергії; перебуваючи в стаціонарному стані, атом не випромінює енергію.
Другий постулат Н. Бора (про квантові стрибки):
Під час переходу з одного стаціонарного енергетичного стану в інший атом випромінює або поглинає квант електромагнітної енергії.
Відповідно до постулатів Бора атоми газуватих речовин в атомарному стані за підвищених температур випромінюють електромагнітні хвилі чітко визначених частот ‒ їм властивий лінійчастий спектр випромінювання. Лінійчастий спектр кожного елемента характеризується індивідуальним для цього елемента набором частот.
Відповідь: Б.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Радіоактивність. Період піврозпаду.
Завдання скеровано на перевірку знання і застосування основного закону радіоактивного розпаду.
Скористаймося основним законом радіоактивного розпаду:
Виразимо кількість ядер радіонукліда, що залишились у зразку, через початкову кількість ядер відповідно до умови завдання:
Підставимо всі дані у формулу:
Кількість атомів радіонукліда, що потрапили у водойму, зменшиться в
Відповідь: 150.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Ядерні реакції.
Завдання скеровано на перевірку вміння складати рівняння ядерних реакцій.
Ядерною реакцією називають взаємодію ядер або елементарних частинок із ядром, яка відбувається з утворенням частинок, відмінних від початкових.
Під час ядерних реакцій, як і під час будь-яких явищ, що відбуваються у Всесвіті, справджуються закони збереження: закон збереження електричного заряду, закон збереження імпульсу, закон збереження енергії-маси.
Запишімо рівняння ядерної реакції відповідно до умови завдання:
Порядковий номер елемента
Відповідь: B.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Радіоактивність.
Завдання скеровано на перевірку знання і застосування основного закону радіоактивного розпаду.
Скористаймося основним законом радіоактивного розпаду:
Виразимо кількість ядер радіонукліда, що залишились у зразку, через початкову кількість ядер відповідно до умови завдання:
Підставимо всі дані у формулу:
За радіоактивним розпадом речовини спостерігали
Відповідь: 20.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Альфа-, бета- і гамма-випромінювання.
Завдання скеровано на перевірку знання і розуміння радіоактивних перетворень.
Запишемо рівняння ядерної реакції відповідно до умови завдання:
Порядковий номер елемента в періодичній системі хімічних елементів відповідає кількості протонів у ядрі (зарядовому або протонному числу
Пригадаємо правила зміщення:
1. Під час
2. Під час
Відповідно до цих правил і згідно з умовою обчислимо, на скільки будуть відрізнятися в періодичній системі порядкові номери цих елементів:
Відповідь: A.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Радіоактивність.
Завдання скеровано на перевірку розуміння закону радіоактивного розпаду й уміння застосовувати формулу, якою описують цей закон.
Період піврозпаду
Основний закон радіоактивного розпаду описують формулою
Виразімо кількість
Кінцева кількість ядер
Підставмо ці вирази у формулу закону радіоактивного розпаду:
Підставмо числові дані з умови й обчислімо шуканий проміжок часу
Відповідь: 13.
ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Атом та атомне ядро.
Завдання скеровано на перевірку знання і розуміння важливих фізичних відкриттів.
1. Явище радіоактивності випадково відкрив 1896 року Анрі Антуан Беккерель. Він виявив, що сіль Урану самочинно випускає невидимі промені, які засвічують світлочутливі матеріали (фотопластинки) навіть у повній темряві. Згодом таке випромінювання назвали радіоактивним (Г).
2. У 1908–1911 рр. під керівництвом Ернеста Резерфорда науковці досліджували будову атома. Вони спрямовували на тонку золоту фольгу вузький пучок
- в атомі позитивно заряджене ядро оточене негативно зарядженими частинками ‒ електронами, які обертаються навколо ядра, як планети навколо Сонця;
- саме в ядрі зосереджена мало не вся маса атома (A).
3. Зовнішній фотоефект відкрив 1887 року німецький фізик Генріх Герц. Детальніше це явище дослідив Олександр Столєтов. У досліді він використав вакуумну камеру з двома електродами (катод і анод) усередині, на які подається напруга від джерела постійного струму. Під дією світла, яке потрапляє в камеру через спеціальне віконце, катод випромінює електрони. Рухаючись від катода до анода в електричному полі, електрони створюють фотострум. Якщо збільшувати напругу на електродах, сила фотоструму теж зросте. Змінюючи почергово інтенсивність і частоту світла, що падає на катод, а також матеріал катода, О. Столєтов сформулював три закони зовнішнього фотоефекту (В).
4. Досліди з вивчення природи радіоактивного випромінювання показали, що різні радіонукліди можуть випромінювати промені трьох видів:
1)
2)
3)
Один із таких дослідів полягає в тому, що пучок радіоактивного випромінювання потрапляє спочатку в сильне магнітне поле постійного магніту, а потім – на фотопластинку. Після проявлення фотопластинки на ній чітко видно три темні плями, які свідчать про те, що урановий зразок висилає промені трьох видів. Магнітне поле по-різному діє на частинки різних знаків, або
Відповідь: 1Г, 2А, 3В, 4Б.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Ядерна модель атома.
Завдання скеровано на перевірку вміння аналізувати склад ядра атома.
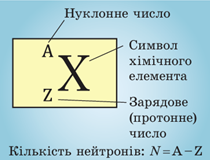
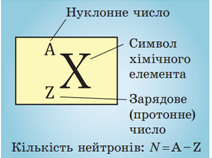
Атомне ядро утворюють нуклони: позитивно заряджені протони й електронейтральні нейтрони. Сумарну кількість протонів і нейтронів в атомі називають нуклонним або масовим числом і позначають буквою
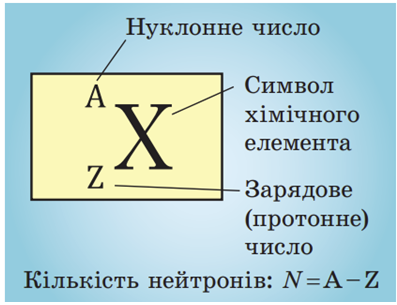
Кількість протонів у ядрі називають зарядовим або протонним числом і позначають буквою
Отже, у ядрі атома Урану
Відповідь: B.
ТЕМА: Перетворення енергії в коливальному контурі. Закон Джоуля – Ленца. Рівняння теплового балансу.
Завдання скеровано на оцінювання знання формул для визначення енергії коливального контуру, кількості теплоти, що виділяється під час згоряння палива, і закону Джоуля – Ленца.
Відповідь: 1В, 2А, 3Г, 4Д.
ТЕМА: Квантова фізика. Атом та атомне ядро. Альфа-, бета- та гамма-випромінювання.
Завдання скеровано на оцінювання розуміння принципів захисту від йонізувального випромінювання.
Для захисту від α-випромінювання досить аркуша паперу, для захисту від β-випромінювання вже потрібен шар алюмінію понад 1 мм завтовшки, для захисту від γ-випромінювання використовують товстий шар бетону чи свинцю, а від потоку нейтронів захищає шар води.
Відповідь: B.
ТЕМА: Квантова фізика. Атом та атомне ядро.
Завдання скероване на перевірку знань про нуклони.
Атомна одиниця маси дорівнює
Маса електронів набагато менша за масу нуклонів, тож нею можна знехтувати. Можна вважати, що маса нуклона дорівнює 1 а. о. м. (точніше визначена маса протона трохи відрізняється від маси нейтрона:
Протон – це позитивно заряджена частинка, за модулем її заряд дорівнює елементарному.
Відповідь: B.
ТЕМА: Квантова фізика. Атом й атомне ядро. Ядерні реакції.
Завдання скеровано на оцінювання вміння аналізувати рівняння ядерних реакцій і розуміння процесу ядерного розпаду.
Під час радіоактивних розпадів масове число дорівнює кількості нуклонів у ядрі, а зарядове число – кількості протонів.
За альфа розпаду масове число нукліда зменшується на чотири, а зарядове – на два за схемою
Під час бета-розпаду зарядове число нукліда збільшується на одиницю за схемою
Послідовні розрахунки для трьох альфа-розпадів такі:
Послідовні розрахунки для двох бета-розпадів:
Відповідь: Б.
ТЕМА: Атом й атомне ядро.
Завдання скеровано на оцінювання розуміння дослідів Резерфорда та їхнього значення для розуміння будови атома.
α-частинки – позитивно заряджені важкі частинки (ядра атомів Гелію). Під час їхнього наближення до позитивно зарядженого важкого ядра Ауруму починають діяти електростатичні сили відштовхування α-частинок від ядра (рис. 1).
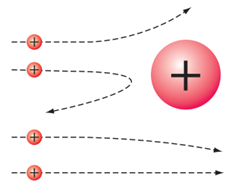
Рис. 1. Траєкторії α-частинок, що пролітають поряд із ядром
Відповідь: Б.
ТЕМА: Квантова фізика. Атом і атомне ядро. Радіоактивність.
Завдання скеровано на перевірку розуміння процесу радіоактивного розпаду.
Дано:
Знайти:
Енергію, яка виділилася під час розпадів за три години, можна обчислити як добуток кількості розпадів, що відбулися за цей час, й енергії
Період піврозпаду
Тоді можна визначити кількість ядер, що залишилася після розпаду:
Кількість ядер, що розпалися, дорівнює:
Тоді енергія, що виділилася під час розпаду, дорівнює:
Для того, щоби подати енергію в мДж, потрібно взяти до уваги, що
Тобто
Відповідь: 56.
ТЕМА: Атом і атомне ядро.
Завдання скероване на перевірку розуміння історично важливих фізичних експериментів і вміння пов’язувати їх із фізичними відкриттями.
1. Анрі Беккерель проводив дослідження із використанням солей Урану й випадково поклав породу разом із фотопластинкою в темну шухляду. Наступного разу, коли він повернувся до фотопластинок, вони виявилися засвіченими, хоча ніяких джерел світла в шухляді не було. Так у нього виникла ідея про те, що саме Уран був джерелом якогось випромінювання. Це випромінювання і було радіоактивним випромінюванням, що утворювалось під час розпаду нестабільних ядер Урану.
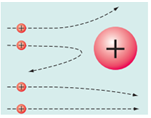
2. Планетарну модель атома розробив Ернест Резерфорд після того, як експеримент із перевірки пудингової моделі Томсона мав неочікувані результати. За уявленнями Томсона позитивний заряд в атомі займав увесь його об’єм, як тісто в пудингу чи кексі, а негативно заряджені електрони застрягали в цьому позитивному заряді (як родзинки). Якщо атом і справді мав таку будову, то під час зустрічі з ним інші (менші) частинки мали би пролітати наскрізь. Адже самі електрони мали би занадто малу масу, щоби викликати якусь серйозну зміну траєкторії, а хмара позитивного заряду могла спричинити відхилення лише на невеликі кути. Щоби перевірити це експериментально, Резерфорд бомбардував альфа-частинками тонку фольгу золота, товщина якої становила лише кілька атомів. Деякі альфа-частинки відбивалися від фольги майже у протилежному напрямку. Таке відбивання було можливе лише за умови, що в атомі існувала велика важка частинка. Тож Резерфорд припустив, що атом більше схожий на Сонячну систему, ніж на пудинг: у його центрі є велика позитивна частинка – ядро, навколо якого обертаються електрони, як планети навколо Сонця.
3. Фотоефект – це явище взаємодії світла з речовиною, супроводжуване випромінюванням (емісією) електронів. Закони фотоефекту були відкриті під час опромінення металів світлом.
4. α-промені – це потік позитивно заряджених частинок, що складаються із двох протонів і двох нейтронів (ядра атомів Гелію), β-промені – це потік негативно заряджених електронів, γ-промені – це електромагнітне випромінювання надзвичайно високої частоти, що утворюється під час ядерних реакцій. Ернест Резерфорд виявив, що під дією магнітного поля пучок радіоактивного випромінювання ділиться на три частини. Поділ відбувається тому, що під дією магнітного поля заряджені частинки відхиляються від своєї початкової прямолінійної траєкторії. Нейтральний γ-промінь не відхилявся під дією магнітного поля, а позитивно заряджені α-частинки й негативно заряджені β-частинки відхилялися й утворювали два пучки по обидва боки від пучка γ-променів. Адже різнойменно заряджені частинки в магнітному полі відхиляються у протилежні боки.
Відповідь: 1Г, 2А, 3В, 4Б.
ТЕМА: Квантова фізика. Атом і атомне ядро.
Завдання скеровано на перевірку розуміння будови атома й уміння інтерпретувати рівняння ядерних реакцій.
Атом складається із позитивно зарядженого ядра й негативно заряджених електронів. Ядро ж складається із частинок двох видів – позитивно заряджених протонів і нейтральних нейтронів. Заряди протона й електрона однакові за модулем. Атом – це нейтральна частинка, тому кількість електронів у ньому дорівнює кількості протонів. Кількість нейтронів може відрізнятися від кількості протонів чи електронів.
Для того, щоб описати нуклон, поруч із хімічним символом елемента зазначають лівий надрядковий індекс – кількість нуклонів у ядрі (сумарна кількість протонів і нейтронів) – і лівий підрядковий індекс – кількість протонів.
Оскільки в атомі зарядженими частинками є електрони й протони, кількість яких однакова, то сумарна кількість заряджених частинок дорівнює
Відповідь: Б.
ТЕМА: Квантова фізика. Атом й атомне ядро. Ядерні реакції.
Завдання скеровано на оцінювання розуміння ядерної взаємодії між частинками.
За малої кінетичної енергії в силу вступлять електричні сили, і заряджена позитивно
Ядро зрідка захоплює електрони. Коли це трапляється, то ядро захоплює ті електрони свого атома, що перебувають найближче до ядра. Це приводить до зменшення кількості протонів у ядрі на один. Зокрема, електричний струм у провідниках – це потік вільних електронів. І якби ядра захоплювали електрони під час проходження струму, будь-яке явище електрики супроводжували б активні ядерні реакції, що зазвичай не відбувається.
Відповідь: Г.
ТЕМА: Квантова фізика. Атом і атомне ядро. Ядерні реакції.
Завдання скеровано на оцінювання вміння виконувати обчислення за рівняннями ядерних реакцій.
Під час радіоактивних розпадів масове число дорівнює кількості нуклонів у ядрі, а зарядове – кількості протонів.
Схема радіоактивного розпаду така:
Після чотирьох
У цього нукліда масове число відповідає тому, що вказано в завданні, а зарядове – на три менше ніж в умові.
Для збільшення зарядового числа має пройти три
Відповідь: 3.
ТЕМА: Квантова фізика. Атом і атомне ядро. Ядерні реакції.
Завдання скеровано на оцінювання розуміння процесу ядерного розпаду й уміння інтерпретувати рівняння ядерних реакцій.
У рівняннях ядерних реакцій біля символу хімічного елемента зліва зазначають індекси: надрядковий, що показує кількість нуклонів у ядрі (сумарну кількість протонів і нейтронів), і підрядковий – кількість протонів.
За рівнянням ядерної реакції ядро атома Алюмінію з 13 протонами й 14 нейтронами
Аби визначити склад ядра нукліда
Корені рівнянь
Відповідь: Б.
ТЕМА: Квантова фізика. Атом і атомне ядро. Альфа-, бета- й гамма-випромінювання.
Завдання скеровано на оцінювання розуміння явища бета-випромінювання.
Потік
Потік
Потік ядер атомів Гелію називають
Відповідь: Б.
ТЕМА: Квантова фізика. Атом й атомне ядро. Випромінювання і поглинання світла атомом.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на енергію зв’язку атомних ядер.
Дано:
Знайти:
Атом поглинає квант, отримує від нього додаткову енергію. Ця енергія витрачається на подолання енергії зв’язку й на кінетичну енергію частинок, що утворилися після розпаду:
Отриману від кванта випромінювання енергію можна знайти з наступного виразу, перевівши попередньо пікометри в метри:
Оскільки сумарну кінетичну енергія в завданні зазначено в МеВ, отриманий результат також потрібно перевести в МеВ:
Тоді енергія зв’язку
Відповідь: 2,3.
ТЕМА: Коливання і хвилі. Оптика. Шкала електромагнітних коливань.
Завдання скеровано на оцінювання знання галузей застосування електромагнітних коливань певного типу.
За результатами аналізування описаних у завданні ситуацій можна дійти таких висновків:
1 У ядерному реакторі відбувається радіоактивний розпад, нестабільні ядра розпадаються на стабільніші, цей розпад супроводжуваний гамма-випромінюванням.
2 Тепло, яке відчуваємо від тіл навколо – це інфрачервоне випромінювання, і саме його фіксують тепловізори.
3 Супутники зв’язку використовують радіохвилі, бо земна атмосфера найпрозоріша в цьому діапазоні, а отже інформацію можна передавати на довші відстані.
4 Люмінофор – це речовина, що випромінює видиме світло за збудження.
Відповідь: 1В, 2А, 3Г, 4Д.
ТЕМА: Квантова фізика. Атом й атомне ядро. Радіоактивність.
Завдання скеровано на оцінювання розуміння поняття «період напіврозпаду».
Період напіврозпаду
Тоді кількість ядер, що залишилася після розпаду, визначають за формулою
Обчислити кількість ядер, що розпалися, можна зі співвідношення
Частку ядер, які розпалися, від початкової їхньої кількості, обчислюють за формулою
Відповідь: B.
ТЕМА: Квантова фізика. Атом й атомне ядро. Ядерні реакції.
Завдання скеровано на оцінювання розуміння процесу ядерного розпаду й уміння тлумачити рівняння ядерних реакцій.
У рівняннях ядерних реакцій поруч зі знаковим символом хімічного елементом позначають лівим надрядковим індексом
Схема альфа-розпаду:
За один альфа-розпад заряд ядра зменшуються на два елементарні заряди, а його маса зменшується на 4 а. о. м.
Схема бета-розпаду:
За 1 бета-розпад заряд ядра збільшується на 1, а маса ядра не змінюється.
Тож, щоби маса ядра зменшилась на 8 а. о. м., треба, аби пройшло 2 альфа-розпади:
Після двох альфа-розпадів заряд ядра зменшився на 4 елементарні заряди, а за умовою завдання заряд мав зменшитись на 3 елементарні заряди. Для цього повинен відбутися бета-розпад:
Відповідь: Б.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом й атомне ядро. Квантові постулати Бора.
Завдання скеровано на оцінювання розуміння практичного застосування лінійчастих спектрів у техніці.
Лінійчасті спектри утворюються тоді, коли електрони в атомах поглинають (для спектрів поглинання) або випромінюють (для спектрів випромінювання) кванти світла. Це відбувається завдяки тому, що електрони перебувають в особливих стаціонарних станах і перехід між цими станами потребує певної кількості енергії
Для кожного елемента переходи можуть відбуватися лише на певних енергетичних рівнях. У результаті цих переходів утворюється унікальний набір ліній у спектрах поглинання і випромінювання, що дає змогу використати їх для визначення хімічного складу речовин.
Відповідь:Г.
ТЕМА: Методи реєстрування йонізувального випромінювання.
Завдання скеровано на оцінювання розуміння принципу роботи бульбашкової камери.
Бульбашкову камеру використовують як прилад для реєстрування йонізувального випромінювання. Усередині камери міститься перегріта рідина, у якій йони, що опиняються на шляху частинки, стають центрами кипіння, тож траєкторію частинки можна визначити за бульбашками.
Для того, щоб утворити перегріту рідину, тиск усередині камери швидко зменшують. За нижчого тиску температура кипіння рідини також нижча. Температура рідини в камері не змінюється, тож рідина, що в камері, стає перегрітою.
Відповідь: Б.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Квантові постулати Бора.
Завдання скеровано на оцінювання розуміння постулатів Бора і їхнього застосування для опису процесів випромінювання і поглинання.
Модель атома Бора є вдосконаленням планетарної моделі. Один із головних недоліків планетарної моделі такий:
якщо описувати рух електронів навколо ядра законами класичної механіки, то вони б постійно наближались до ядра і з часом упали б на нього. Такий атом не може існувати.
Тому Бор сформулював постулати:
1) атомна система може перебувати лише в особливих стаціонарних (квантових) енергетичних станах, кожному з яких відповідає певне значення енергії; у стаціонарному стані атом не випромінює енергію;
2) під час переходу з одного стаціонарного енергетичного стану (з енергією
Квант електромагнітної хвилі має специфічну частоту, для видимого випромінювання це означає, що випромінений квант на спектрах випромінювання виглядає як вузька кольорова смужка. У спектрі поглинання поглинутий квант виглядає як вузька темна смужка (рис. 1).
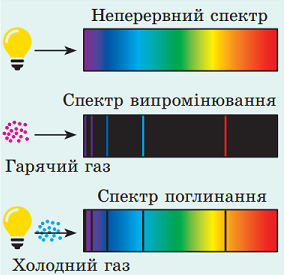
Рис. 1. Вигляд лінійчастих спектрів поглинання і випромінювання
Відповідь: Б.
ТЕМА: Методи реєстрування йонізувального випромінювання. Насичена й ненасичена пара.
Завдання скеровано на оцінювання розуміння принципу роботи камери Вільсона.
Перенасичена пара – це пара, тиск якої є вищим порівняно з тиском насиченої пари за цих самих умов.
Камеру Вільсона використовують як прилад для реєстрування йонізувального випромінювання. Усередині камери зазвичай міститься пара спирту. Коли йонізувальні частинки проходять крізь камеру, за ними утворюється ланцюжок зі сконденсованих крапель. Для того, щоб ефект був помітним, пара спирту в камері має бути перенасиченою.
Для цього поршень камери швидко опускають, тим самим збільшуючи її об’єм. Через це газ всередині не встигає обмінятися теплом із середовищем, а отже має змінити свою внутрішню енергію – охолодитися. Пара, що була всередині камери, теж охолоджується. Оскільки тиск насиченої пари за зниження температури зменшується, то тиск пари спирту, тиск якої не змінився, може перевищити його. Так і утворюється перенасичена пара в камері Вільсона.
Відповідь: B.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Квантові постулати Бора.
Завдання скерованo на перевірку розуміння природи спектрів поглинання і випромінювання.
Модель атома Бора є вдосконаленням планетарної моделі. Один із головних недоліків планетарної моделі такий: якщо описувати рух електронів навколо ядра законами класичної механіки, то електрони б постійно наближались до ядра і з часом впали б на нього. Такий атом не може існувати.
Тому Бор сформулював постулати:
1) атомна система може перебувати тільки в особливих стаціонарних (квантових) енергетичних станах, кожному з яких відповідає певне значення енергії. Перебуваючи в стаціонарному стані, атом не випромінює енергію;
2) під час переходу з одного стаціонарного енергетичного стану (з енергією
У кванта електромагнітної хвилі специфічнa частотa, для видимого випромінювання це означає, що випромінений квант на спектрах випромінювання має вигляд вузької кольорової смужки. У спектрі поглинання поглинутий квант має вигляд вузької темної смужки.
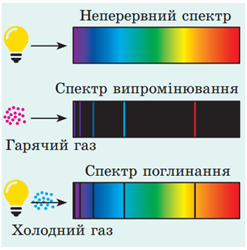
Рис. 1. Вигляд лінійчастих спектрів поглинання і випромінювання
Відповідь: Б.
ТЕМА: Квантова фізика. Атом та атомне ядро.
Завдання скеровано на оцінку розуміння досліду Резерфорда.
Під час досліду Резерфорд бомбардував позитивно зарядженими альфа-частинками тонку фольгу золота, лише кілька атомів завтовшки. Деякі альфа-частинки відбивалися від фольги майже в протилежному напрямку, що було можливо лише якщо ця частинка «відбивається» від якоїсь важкої частинки в атомі – ядра. Позитивно заряджене ядро та позитивно заряджена альфа-частинка відштовхуються завдяки електричній взаємодії (за законом Кулона).
Відповідь: Б.
ТЕМА: Квантова фізика. Атом i атомне ядро. Альфа-, бета- і гамма-випромінювання.
Завдання скеровано на оцінювання розуміння природи радіоактивного випромінювання.
1.
2.
3.
4. Світлове випромінювання – це потік фотонів із частотами
Відповідь: 1В, 2Б, 3А, 4Г.
ТЕМА: Квантова фізика. Атом і атомне ядро. Радіоактивність.
Завдання скеровано на оцінювання розуміння поняття напіврозпаду.
Період піврозпаду
Тоді кількість ядер, що залишилася після розпаду, можна визначати за формулою
Якщо за час
Тож можна використати таке відношення:
Тоді
Якщо значення чисел зі степенями рівні й основи цих чисел рівні, то й степені цих чисел теж рівні:
Тому
Відповідь: Г.
Квантова фізика. Атом та атомне ядро. Радіоактивність.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі, пов’язані з періодом піврозпаду.
Період піврозпаду
Тоді кількість ядер, що залишилася після розпаду, визначають за формулою
Після підставлення відомих з умови значень у формулу:
Відповідь: A.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Радіоактивність.
Завдання скеровано на перевірку розуміння поняття «доза опромінювання людини» й методів визначення її.
Фізичну величину, якою характеризують біологічний вплив поглинутої дози йонізувального випромінювання, називають еквівалентною дозою йонізувального випромінювання
Обчислімо поглинуту за добу дозу:
Урахуємо також дозу опромінювання від рентгенівського медичного обстеження організму –
А це означає, що без шкоди для здоров᾽я людина може проходити рентгенівські медичні обстеження організму лише раз на рік, оскільки за умовою річна допустима доза опромінювання становить
Відповідь: 1.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Методи реєстрування йонізувального випромінювання.
Завдання скеровано на перевірку знання і розуміння дії пристроїв для реєстрування йонізувального випромінювання.
Загальний принцип реєстрування йонізувального випромінювання полягає в реєстрації дії цього випромінювання.
Бульбашкова камера є трековим детектором. Робочим тілом у бульбашковій камері є перегріта рідина: йони, які утворюються вздовж траєкторії руху частинки, стають центрами кипіння. Унаслідок цього виникає ланцюжок бульбашок, за якими й фіксують випромінювану частинку (випромінювання)
Унаслідок руху швидкої зарядженої частинки в шарі фотоемульсії проступають сліди (треки) первинної частинки та всіх заряджених частинок, що виникли внаслідок ядерних взаємодій. За товщиною і довжиною треків можна визначити заряди частинок та їхню енергію.
Газорозрядний лічильник і йонізаційна камера працюють за одним принципом: робоче тіло – газ – розміщено в електричному полі з високою напругою; заряджена частинка, що пролітає крізь газ, йонізує його, і в пристрої виникає газовий розряд.
Камера Вільсона – також трековий детектор. Це контейнер, заповнений парою спирту або ефіру. Під час різкого опускання поршню пара внаслідок адіабатного розширення охолоджується і стає перенасиченою. Заряджена частинка, потрапивши в перенасичену пару, йонізує на своєму шляху молекули пари. Йони, що утворилися, стають центрами конденсації. Ланцюжок крапель cконденсованої пари вздовж траєкторії руху (треку) частинки знімають на камеру або фотографують.
Відповідь: A.
ТЕМА: Квантова фізика. Атом та атомне ядро. Радіоактивність.
Завдання скеровано на перевірку розуміння природи радіоактивного випромінювання.
Ернест Резерфорд виявив, що під дією магнітного поля пучок радіоактивного випромінювання ділиться на три частини (рис. 1).
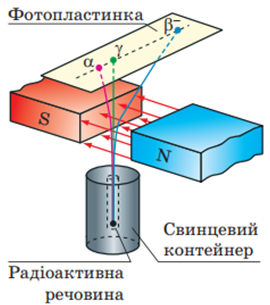
Рис. 1. Дослідження явища радіоактивності методом відхилення променів у магнітному полі
Поділ відбувається тому, що під дією магнітного поля заряджені частинки відхиляються від своєї початкової прямолінійної траєкторії завдяки дії сили Лоренца.
Нейтральний γ-промінь не відхилявся під дією магнітного поля, натомість позитивно заряджені α-частинки й негативно заряджені β-частинки відхилялися та утворювали два пучки по обидва боки обабіч пучка γ-променів. Адже різнойменно заряджені частинки в магнітному полі відхиляються в протилежні боки.
Відповідь: B.
ТЕМА: Квантова фізика. Атом та атомне ядро. Ядерні реакції.
Завдання скеровано на перевірку розуміння поняття енергетичного виходу реакції.
Енергетичним виходом ядерної реакції називають різницю енергій спокою ядер і частинок до і після реакції:
Відповідь: Б.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Утворення лінійчастого спектра.
Завдання скеровано на перевірку розуміння і застосування знань про спектральний аналіз речовин.
Кожен газ в атомарному стані дає власний набір ліній спектра (власний чітко визначений набір довжин хвиль). Ці лінії завжди розташовані в тих самих місцях спектра, незалежно від способу збудження атомів.
Лінійчастий спектр будь-якого хімічного елемента не збігається з лінійчастим спектром інших хімічних елементів, тож є своєрідною «візитівкою» атомів із тим самим зарядом ядра.
Порівняймо за рисунком, наведеним в умові завдання, лінії спектра зразка невідомої речовини зі спектрами випромінювання Стронцію і Кальцію. Усі лінії спектра Стронцію є в зразку невідомої речовини, а ліній спектра Кальцію немає. Отже, у невідомій речовині є атоми Стронцію, але немає атомів Кальцію.
Відповідь: A.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Ядерні реакції.
Завдання скеровано на перевірку вміння записувати рівняння ядерної реакції та визначати її результати.
Запишімо рівняння ядерної реакції, описаної в умові завдання:
У лівій і правій частинах рівняння реакції суми зарядів, як і суми мас, мають збігатися. Із відповідних рівнянь визначмо зарядове
Запишімо суму мас і суму зарядів для обох частин рівняння реакції:
Із цих рівнянь маємо:
Невідомий елемент
Відповідь: Б.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Поділ ядер Урану.
Завдання скеровано на перевірку розуміння поділу ядер урану.
Спочатку обчислімо кількість
Кількість структурних частинок речовини можна визначити, знаючи
Звідси виразімо масу ядер Урану й обчислімо її:
Відповідь: 1,175.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Методи реєстрації йонізувального випромінювання.
Завдання скеровано на перевірку знання і розуміння методів реєстрування йонізувального випромінювання.
Газорозрядний лічильник (лічильник Гейгера ‒ Мюллера) працює за таким принципом: робоче тіло ‒ газ ‒ розміщено в електричному полі з високою напругою; заряджена частинка, що пролітає крізь газ, йонізує його й у пристрої виникає газовий розряд: 1‒Д.
Камера Вільсона ‒ це трековий детектор. Камеру заповнено парою спирту або медичного ефіру. Коли поршень різко опускають, то внаслідок адіабатного розширення пара охолоджується і стає перенасиченою. Коли в перенасичену пару потрапляє заряджена частинка, на своєму шляху вона йонізує молекули пари. Йони, що утворилися, стають центрами конденсації. Ланцюжок крапель cконденсованої пари, який утворюється вздовж траєкторії руху частинки (трек частинки), знімають на камеру або фотографують: 3‒Г.
Бульбашкова камера також є трековим детектором. Принцип її роботи подібний до камери Вільсона, а відмінність у тому, що робочим тілом у бульбашковій камері є перегріта рідина: йони, які виникають уздовж траєкторії руху частинки, стають центрами кипіння ‒ утворюється ланцюжок бульбашок: 2‒А.
Фотоемульсійний лічильник. Швидка заряджена частинка, рухаючись у шарі фотоемульсії, що містить кристали аргентум броміду
Відповідь: 1Д, 2А, 3Г, 4В.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Альфа-, бета- і гамма-випромінювання.
Завдання скеровано на перевірку знання і застосування правил альфа- і бета-розпадів.
Запишімо реакцію розпаду ядра атома Урану:
За нуклонним (масовим) числом визначімо кількість альфа-розпадів
Перепишімо рівняння розпаду ядра атома Урану, зваживши на те, що альфа-розпадів було
Тепер за протонним (зарядовим) числом визначімо, скільки було бета-розпадів.
Відповідь: Г.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Радіоактивність.
Завдання скеровано на перевірку розуміння закону радіоактивного розпаду й уміння працювати з формулою, якою описано цей закон.
Період піврозпаду
Основний закон радіоактивного розпаду:
Виразимо кількість
Початкова кількість
Підставмо ці вирази у формулу закону радіоактивного розпаду:
Підставмо числові дані з умови й обчислімо шуканий проміжок часу
Відповідь: 13.
ТЕМА: Квантова фізика. Елементи теорії відносності.
Завдання скеровано на перевірку знання і розуміння основних фундаментальних дослідів квантової і ядерної фізики.
Золоту фольгу бомбардували альфа-частинками для дослідження внутрішньої структури атома і доведення існування ядра.
За пропускання білого світла крізь газ спостерігають темні лінії на тлі неперервного спектра. Сукупність цих ліній називають лінійчастим спектром поглинання.
Опромінювання металів світлом дало змогу відкрити й дослідити фотоефект.
Засвітивши закриту фотопластинку сіллю Урану, з’ясували, що ця сіль дійсно висилає випромінювання з великою проникною здатністю ‒ радіоактивне.
Відповідь: Г.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Ядерні реакції.
Завдання скеровано на перевірку знання і вміння складати рівняння ядерних реакцій.
Ядерною реакцією називають взаємодію ядер або елементарних частинок із ядром, яка відбувається з утворенням частинок, відмінних від початкових. Під час ядерних реакцій, як і під час будь-яких явищ, що відбуваються у Всесвіті, справджуються закони збереження: закон збереження електричного заряду, закон збереження імпульсу, закон збереження енергії-маси.
Запишімо рівняння ядерної реакції відповідно до умови завдання для кожного випадку 1‒4 і відповідно до закону збереження електричного заряду і закону збереження енергії-маси визначімо
У реакції 1 бере участь нуклід Нітрогену
У реакції 2 бере участь нуклід Нітрогену
У реакції 3 бере участь нуклід Нітрогену
У реакції 4 бере участь нуклід Нітрогену
Відповідь: 1А, 2Б, 3Д, 4Г.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Ядерні реакції.
Завдання скеровано на перевірку знання і вміння складати рівняння ядерних реакцій.
Ядерною реакцією називають взаємодію ядер або елементарних частинок із ядром, яка відбувається з утворенням частинок, відмінних від початкових. Під час ядерних реакцій, як і під час будь-яких явищ, що відбуваються у Всесвіті, справджуються закони збереження: закон збереження електричного заряду, закон збереження імпульсу, закон збереження енергії-маси.
Запишімо рівняння ядерної реакції відповідно до умови завдання:
Відповідно до закону збереження електричного заряду і закону збереження енергії-маси визначімо
Отже, частинка з таким нуклонним і протонним числами ‒ це протон
Відповідь: A.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом й атомне ядро. Період піврозпаду.
Завдання скеровано на перевірку розуміння закону радіоактивного розпаду й уміння застосовувати формулу, якою описують цей закон.
Період піврозпаду
Основний закон радіоактивного розпаду описують формулою
Визначімо, у скільки разів було більше атомів Урану, ніж їх залишилося після розпаду за зазначений період розпаду:
Отже, кількість атомів Урану зменшиться в
Відповідь: B.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Альфа-, бета- і гамма-випромінювання.
Завдання скеровано на перевірку знання і застосування правил альфа- і бета-розпадів.
Запишімо реакцію розпаду ядра атома
Унаслідок реакції отримали інше ядро атома
Під час ядерних реакцій, як і під час будь-яких явищ, що відбуваються у Всесвіті, справджуються закони збереження: закон збереження електричного заряду, закон збереження імпульсу, закон збереження енергії-маси.
Відповідно до цих законів запишімо рівності:
За умовою масове число зменшилося на
Водночас заряд ядра атома зменшився на
Підставімо ці вирази:
Отримуємо
Отже, відбулися два
Відповідь: 2.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Склад ядра атома.
Завдання скеровано на перевірку знання будови атома і його ядра.
Атомне ядро складається із частинок двох видів: протонів, які мають позитивний електричний заряд, і нейтронів, які не мають заряду.
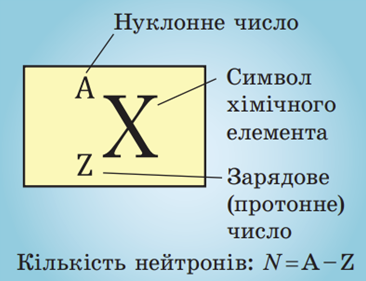
Сумарну кількість протонів і нейтронів в атомі називають нуклонним (масовим) числом і позначають символом
Атом є електрично нейтральним: сумарний заряд протонів у ядрі дорівнює сумарному заряду електронів, що розташовані навколо ядра. Оскільки заряд протона за модулем дорівнює заряду електрона, то зрозуміло, що в атомі кількість протонів дорівнює кількості електронів.
Кількість протонів у ядрі називають зарядовим (протонним) числом і позначають символом
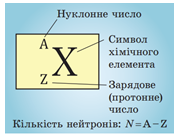
Порядковий номер хімічного елемента в періодичній системі відповідає кількості протонів у ядрі (зарядовому числу).
Отже, у ядрі атома Урану
А зарядове (протонне) число, тобто кількість протонів –
Тоді кількість нейтронів
Обчислімо, на скільки кількість нейтронів
Відповідь: B.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Ядерні реакції.
Завдання скеровано на перевірку вміння складати рівняння ядерних реакцій.
Ядерною реакцією називають взаємодію ядер або елементарних частинок із ядром, яка відбувається з утворенням частинок, відмінних від початкових.
Під час ядерних реакцій, як і під час будь-яких явищ, що відбуваються у Всесвіті, справджуються закони збереження: закон збереження електричного заряду, закон збереження імпульсу, закон збереження енергії-маси.
1. Запишімо рівняння ядерної реакції відповідно до умови завдання:
У лівій і правій частинах рівняння реакції суми зарядів, як і суми мас, мають збігатися. Із відповідних рівнянь дістанемо зарядове (протонне)
Запишімо суму мас і суму зарядів для обох частин рівняння реакції:
З одержаних рівнянь маємо:
Невідома частинка в рівнянні – позитрон
2. Наступне рівняння
Запишімо суму мас і суму зарядів для обох частин рівняння реакції:
З одержаних рівнянь маємо:
Невідома частинка в рівнянні – електрон
3. Наступне рівняння
Запишімо суму мас і суму зарядів для обох частин рівняння реакції:
З одержаних рівнянь маємо:
Невідома частинка в рівнянні – протон
4. Наступне рівняння
Запишімо суму мас і суму зарядів для обох частин рівняння реакції:
З одержаних рівнянь маємо:
Невідома частинка в рівнянні – нейтрон
Відповідь: 1Б, 2А, 3В, 4Г.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Склад ядра атома. Ізотопи.
Завдання скеровано на перевірку знання і розуміння складу ядра атома та їхніх різновидів.
Різновиди атомів того самого хімічного елемента, ядра яких містять однакову кількість протонів, але різну кількість нейтронів, називають ізотопами («однакові за місцем»). Кожний хімічний елемент має декілька ізотопів. Наприклад, ізотопи Гідрогену, які існують у природі:
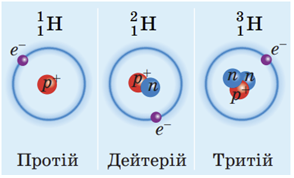
Відповідь: B.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом й атомне ядро. Ядерні реакції.
Завдання скеровано на перевірку вміння складати рівняння ядерних реакцій.
Ядерною реакцією називають взаємодію ядер або елементарних частинок із ядром, яка відбувається з утворенням частинок, відмінних від початкових.
Під час ядерних реакцій, як і під час будь-яких явищ, що відбуваються у Всесвіті, справджуються закони збереження: закон збереження електричного заряду, закон збереження імпульсу, закон збереження енергії-маси.
Запишімо рівняння ядерної реакції відповідно до умови завдання:
де
У лівій і правій частинах рівняння реакції суми зарядів, як і суми мас, мають збігатися. Із відповідних рівнянь дістанемо зарядове (протонне)
Запишімо суму мас і суму зарядів для обох частин рівняння реакції:
З одержаних рівнянь маємо:
Невідоме в рівнянні – нуклід
Відповідь: B.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Радіоактивність. Період піврозпаду.
Завдання скеровано на перевірку знання і застосування основного закону радіоактивного розпаду.
Період піврозпаду
Фізичну величину, яка чисельно дорівнює кількості розпадів, що відбуваються в певному радіоактивному джерелі за одиницю часу, називають активністю радіоактивного джерела.
Нехай
Це означає, що відбулося три піврозпади: унаслідок першого розпаду кількість ядер зменшилася у
Отже, за час
Отже, період піврозпаду радіоактивного елемента становить
Відповідь: 5.
ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл.
Завдання скеровано на перевірку знання і розуміння процесів, що відбуваються з парою і рідиною, застосування цих процесів у приладах.
1) Пару, яка перебуває зі своєю рідиною в стані динамічної рівноваги (тобто кількість молекул, які повертаються в рідину, дорівнює кількості молекул, які за той самий час залишають рідину), називають насиченою.
Перенасиченою є пара, тиск якої перевищує тиск насиченої пари за певної температури. Перенасичена пара утворюється внаслідок збільшення тиску пари в об’ємі, вільному від центрів конденсації (пилинок, йонів, краплинок рідини малих розмірів тощо). Інший спосіб отримання ‒ охолодження насиченої пари за тих же умов. Саме цей спосіб використовують у камері Вільсона.
Камера Вільсона ‒ це трековий детектор. Камеру заповнено парою спирту або медичного ефіру. Коли поршень різко опускають, то внаслідок адіабатного розширення пара охолоджується і стає перенасиченою. Коли в перенасичену пару потрапляє заряджена частинка, на своєму шляху вона йонізує молекули пари. Йони, що утворилися, стають центрами конденсації. Ланцюжок крапель cконденсованої пари, який утворюється вздовж траєкторії руху частинки (трек частинки), знімають на камеру або фотографують: 1 ‒ Г.
2) Властивість рідини розширюватися під час нагрівання використовують у медичному термометрі: 2 ‒ Д. Причина теплового розширення полягає в тому, що зі збільшенням температури збільшується швидкість руху частинок речовини (атомів, молекул, йонів), унаслідок чого збільшується середня відстань між частинками. Медичний термометр складається зі скляного резервуара, наповненого ртуттю, який переходить у капіляр, скляної шкали з поділками та скляної захисної трубки. Ртуть ‒ це єдиний метал, який за кімнатної температури є рідиною. Об’єм рідини є мірою температури: що вища температура тіла, то більшим є об’єм рідини й вищим стовпчик рідини в термометрі.
3) Якщо з рідини видалити розчинене повітря (наприклад, багатократним кип’ятінням) і можливі центри пароутворення (пилинки, йони тощо), то можна нагріти рідину до температури, дещо вищої від температури кипіння. Такий стан називають перегрітою рідиною. Стан перегрітої рідини також можна одержати й унаслідок зниження зовнішнього тиску до рівня, нижчого за тиск насиченої пари рідини за цієї температури.
Саме цей процес лежить в основі роботи бульбашкової камери. Вона також є трековим детектором, як і камера Вільсона. І принцип роботи бульбашкової камери подібний до принципу роботи камери Вільсона. А відмінність полягає в тому, що робочим тілом у бульбашковій камері є перегріта рідина: йони, які виникають уздовж траєкторії руху частинки, стають центрами кипіння ‒ утворюється ланцюжок бульбашок: 3 ‒ А.
4) У рідині завжди є молекули, які рухаються досить швидко, а тому випаровування рідин відбувається за будь-якої температури. Оскільки під час випаровування рідину залишають найшвидші молекули, то середня кінетична енергія решти молекул зменшується. Тому, якщо рідина не отримує енергії ззовні, вона охолоджується.
Саме цей принцип використовують у психрометрах (гігрометрах психрометричних ‒ приладах для прямого вимірювання вологості повітря), а ще той факт, що швидкість випаровування рідини то вища, що нижча відносна вологість повітря: 4 ‒ В.
Манометр ‒ це прилад для вимірювання тиску рідин і газів. Рідинним манометром вимірюють різницю рівнів рідини в колінах U-подібної трубки. Тобто визначають, на скільки тиск газу в груші, закріпленій на одному з отворів трубки, відрізняється від атмосферного. Є також металеві деформаційні манометри.
Відповідь: 1Г, 2Д, 3А, 4В.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Радіоактивність. Період піврозпаду.
Завдання скеровано на перевірку знання і застосування основного закону радіоактивного розпаду.
Скористаймося основним законом радіоактивного розпаду:
Тоді кількість ядер радіонукліда, що розпадеться за час, зазначений в умові, становитиме
Запишімо це відношення відповідно до умови завдання:
Отже, розпадеться
Відповідь: A.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Період піврозпаду.
Завдання скеровано на перевірку знання і розуміння закону періоду піврозпаду.Основний закон радіоактивного розпаду:
Кількість
Підставмо цей вираз у формулу для періоду піврозпаду:
Визначмо шукану величину
Відповідь:
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Склад ядра атома.
Завдання скеровано на перевірку знання і розуміння будови атома.
Атом є електрично нейтральним: сумарний заряд протонів у ядрі дорівнює сумарному заряду електронів, що розташовані навколо ядра. Оскільки заряд протона за модулем дорівнює заряду електрона, то зрозуміло, що в атомі кількість протонів
Отже,
Відповідь: Г.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Енергія зв’язку атомних ядер.
Завдання скеровано на перевірку знання і розуміння енергетичного виходу ядерних реакцій.
Енергетичний вихід ядерної реакції можна визначити як різницю енергії зв’язку ядер до реакції та енергії зв’язку ядер після реакції:
Якщо
Ця реакція екзотермічна.
Відповідь: 15.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Ядерні реакції.
Завдання скеровано на перевірку вміння складати рівняння ядерних реакцій.
Ядерною реакцією називають взаємодію ядер або елементарних частинок із ядром, яка відбувається з утворенням частинок, відмінних від початкових.
Під час ядерних реакцій, як і під час будь-яких явищ, що відбуваються у Всесвіті, справджуються закони збереження: закон збереження електричного заряду, закон збереження імпульсу, закон збереження енергії-маси.
1. Запишімо рівняння ядерної реакції відповідно до умови завдання:
У лівій і правій частинах рівняння реакції суми зарядів, як і суми мас, мають збігатися. Із відповідних рівнянь дістанемо зарядове (протонне)
Запишімо суму мас і суму зарядів для обох частин рівняння реакції:
З одержаних рівнянь маємо:
Невідомий нуклід у рівнянні – Літій
2. Наступне рівняння
Запишімо суму мас і суму зарядів для обох частин рівняння реакції:
З одержаних рівнянь маємо:
Невідомий нуклід у рівнянні – Ферум
3. Наступне рівняння
Запишімо суму мас і суму зарядів для обох частин рівняння реакції:
З одержаних рівнянь маємо:
Невідомий нуклід у рівнянні – Літій
4. Наступне рівняння
Запишімо суму мас і суму зарядів для обох частин рівняння реакції:
З одержаних рівнянь маємо:
Невідомий нуклід у рівнянні – Гелій
Відповідь: 1Д, 2В, 3Г, 4Б.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Методи реєстрації йонізувального випромінювання.
Завдання скеровано на перевірку знання і розуміння методів реєстрації йонізувального випромінювання.
Камера Вільсона ‒ це трековий детектор, ємність, заповнена парою спирту або ефіру. Коли поршень різко опускають, то внаслідок адіабатного розширення пара охолоджується і стає перенасиченою. Коли в перенасичену пару потрапляє заряджена частинка, на своєму шляху вона йонізує молекули пари ‒ отримані йони стають центрами конденсації. Ланцюжок крапель cконденсованої пари, який утворюється вздовж траєкторії руху частинки (трек частинки), знімають на камеру або фотографують (див. рисунок).

Загальний принцип реєстрації йонізувального випромінювання полягає в реєстрації дії, яку чинить це випромінювання:
‒ йонізація молекул фотоемульсії ‒ використовують шари фотоемульсій;
‒ газовий розряд унаслідок йонізації молекул газу ‒ газорозрядний лічильник;
‒ випромінювання квантів світла люмінофором, на який потрапляють частинки;
‒ сцинтиляційні лічильники.
Відповідь: B.
ТЕМА: Квантова фізика. Елементи теорії відносності.
Завдання скеровано на перевірку знання і розуміння дослідів або спостережень, що сприяли відкриттям із розділів «Елементи теорії відносності», «Світлові кванти» й «Атом та атомне ядро».
1. Явище радіоактивності – засвічення фотопластинки солями Урану (Г).
Анрі Антуан Беккерель (1852–1908) − французький фізик, знаючи, що рентгенівські промені, на відміну від світлових, проходять крізь чорний папір, узяв загорнуту в чорний папір фотопластинку, поклав на неї крупинки уранової солі й на кілька годин виніс фотопластинку на яскраве сонячне світло. Після проявлення на фотопластинці виявилися темні плями саме в тих місцях, де лежала уранова сіль. Таким чином було з’ясовано, що уранова сіль дійсно випускає випромінювання, яке має велику проникну здатність і діє на фотопластинку. Беккерель вирішив продовжити дослідження і підготував дослід, який дещо відрізнявся від попереднього. Проте науковцю завадила похмура погода, і він із жалем поклав готову до досліду фотопластинку з урановою сіллю та мідним хрестом між ними в шухляду стола. Через кілька днів, так і не дочекавшись появи сонця, Беккерель вирішив про всяк випадок проявити фотопластинку. Результат був несподіваним: на пластинці з’явився контур хреста. Тож сонячне світло тут ні до чого, і сіль Урану сама, без впливу зовнішніх чинників, випускає невидиме випромінювання, якому не є перешкодою навіть шар міді! Пізніше таке випромінювання назвали радіоактивним випромінюванням (від латин. radio − випромінюю, activus − дієвий); здатність речовин до радіоактивного випромінювання – радіоактивністю. Це був 1896 рік.
2. Планетарна модель атома − бомбардування альфа-частинками золотої фольги (А).
Вузький пучок
Ядерна (планетарна) модель атома, запропонована Резерфордом, була розвинена в роботах видатного данського фізика Нільса Бора (1885–1962). Саме на ядерній моделі ґрунтується сучасне уявлення про будову атома.
3. Закони фотоефекту – опромінювання металів світлом (В).
Розрізняють зовнішній фотоефект, за якого фотоелектрони вилітають за межі тіла, і внутрішній фотоефект, за якого електрони, «вирвані» світлом із молекул і атомів, залишаються всередині тіла.
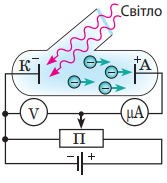
Зовнішній фотоефект відкрив німецький фізик Г. Герц 1887 р., а детально дослідив О. Столєтов (1839–1896) у 1888–1890 рр. Для вивчення фотоефекту О. Столєтов використав пристрій, сучасне зображення якого схематично наведено на рисунку. Усередині камери, з якої викачано повітря, розташовані два електроди (катод К і анод А), на які подається напруга від джерела постійного струму.
4. Три типи радіоактивних променів – дія магнітного поля на випромінювання урану (Б).
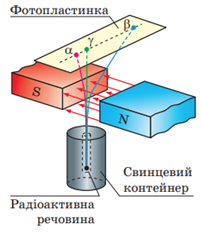
Досліди з вивчення природи радіоактивного випромінювання показали, що радіоактивні речовини можуть випромінювати промені трьох видів: позитивно заряджені частинки (
Відповідь: 1Г, 2А, 3В, 4Б.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Альфа-, бета- і гамма-випромінювання.
Завдання скеровано на перевірку знання і застосування правил альфа- і бета-розпадів.
Запишімо реакцію розпаду ядра атома Торію
Під час ядерних реакцій, як і під час будь-яких явищ, що відбуваються у Всесвіті, справджуються закони збереження: закон збереження електричного заряду, закон збереження імпульсу, закон збереження енергії-маси.
Пригадаймо також правила зміщення для
Під час
Під час
Тепер відповідно до закону збереження електричного заряду й закону збереження енергії-маси, а також правил зміщення визначімо
Отже, унаслідок такого розпаду ізотопа Торію утворився ізотоп Бісмуту
Відповідь: Б.
ТЕМА: Квантова фізика. Елементи теорії відносності. Фотоефект. Радіоактивність. Методи реєстрації йонізувального випромінювання.
Завдання скеровано на перевірку знання і розуміння відкриттів (винаходів).
Відкриття явища радіоактивності ‒ А. Беккерель (Д)
Історія відкриття радіоактивності почалася з відкриття рентгенівського випромінювання. Поштовхом до досліджень стало припущення, що рентгенівське випромінювання може виникати внаслідок флуоресценції деяких речовин, опромінених сонячним світлом. Такою речовиною і скористався французький фізик Анрі Антуан Беккерель (1852–1908) у лютому 1896 р. Для досліджень він випадково вибрав здатну до флуоресценції маловідому сіль Урану. Було з’ясовано, що уранова сіль дійсно висилає випромінювання, яке має велику проникну здатність. Сіль Урану сама, без впливу зовнішніх чинників, висилає невидиме випромінювання. Пізніше таке випромінювання назвуть радіоактивним випромінюванням; здатність речовин до радіоактивного випромінювання ‒ радіоактивністю; а нукліди, ядра яких мають таку здатність, ‒ радіонуклідами.
Відкриття трьох видів радіоактивного випромінювання ‒ Е. Резерфорд (В)
Ернест Резерфорд експериментально встановив (1899), що солі Урану випромінюють три типи променів, які по-різному відхиляються в магнітному полі:
– промені першого типу відхиляються так само, як потік додатно заряджених частинок; їх назвали альфа-променями;
– промені другого типу відхиляються в магнітному полі так само, як потік негативно заряджених частинок (у протилежну сторону); їх назвали бета-променями;
– промені третього типу, які не відхиляються магнітним полем, назвали гамма-променями.
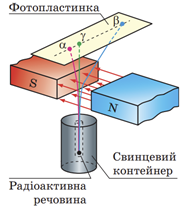
Створення приладу, за допомогою якого можна спостерігати траєкторію руху зарядженої частинки ‒ Ч. Вільсон (Г)
Загальний принцип реєстрації йонізувального випромінювання полягає в реєстрації дії, яку чинить це випромінювання.
Камера Вільсона ‒ це трековий детектор. Вона являє собою ємність, заповнену парою спирту або ефіру. Коли поршень різко опускають, то внаслідок адіабатного розширення пара охолоджується і стає перенасиченою. Коли в перенасичену пару потрапляє заряджена частинка, на своєму шляху вона йонізує молекули пари ‒ отримані йони стають центрами конденсації. Ланцюжок крапель cконденсованої пари, який утворюється вздовж траєкторії руху частинки (трек частинки), знімають на камеру або фотографують.
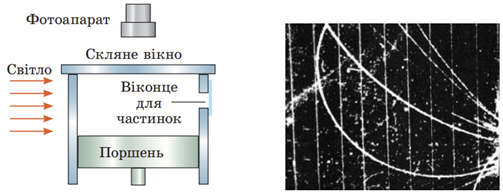
Створення теорії фотоефекту ‒ А. Ейнштейн (Б)
Зовнішній фотоефект відкрив 1887 року німецький фізик Генріх Герц. Детальніше це явище дослідив Олександр Столєтов. У досліді він використав вакуумну камеру з двома електродами (катод і анод) усередині, на які подають напругу від джерела постійного струму. Під дією світла, яке потрапляє в камеру через спеціальне віконце, катод випромінює електрони. Рухаючись від катода до анода в електричному полі, електрони створюють фотострум. Якщо збільшувати напругу на електродах, сила фотоструму теж зросте. Змінюючи почергово інтенсивність і частоту світла, що падає на катод, а також матеріал катода, О. Столєтов сформулював три закони зовнішнього фотоефекту. Але лише більш як через 20 років завдяки своєму рівнянню для зовнішнього фотоефекту А. Ейнштейн зміг пояснити всі закони фотоефекту. Саме ідею М. Планка про кванти використав Ейнштейн для пояснення законів фотоефекту. За пояснення явища фотоефекту А. Ейнштейн одержав найвищу наукову нагороду ‒ Нобелівську премію (1921 р.).
Відповідь: 1Д, 2В, 3Г, 4Б.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Альфа-, бета- і гамма-випромінювання.
Завдання скеровано на перевірку знання і розуміння радіоактивних перетворень.
Атомне ядро утворюють нуклони: позитивно заряджені протони й електронейтральні нейтрони. Сумарну кількість протонів і нейтронів в атомі називають нуклонним або масовим числом і позначають буквою
Кількість протонів у ядрі називають зарядовим або протонним числом і позначають буквою
Пригадаймо правила зміщення для
Під час
Отже, електричний заряд ядра внаслідок
Відповідь: B.
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Квантові постулати Бора.
Завдання скеровано на перевірку знання і розуміння моделі атома Бора і його постулатів.
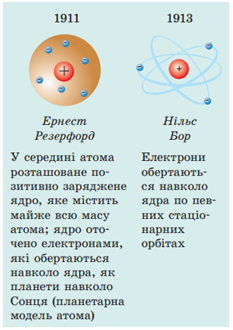
Ернест Резерфорд 1911 р. після дослідів із розсіяння α-частинок запропонував планетарну (ядерну) модель будови атома: атом складається з позитивно зарядженого ядра, у якому зосереджена мало не вся маса атома; біля ядра по певних орбітах обертаються електрони.
Модифікацію планетарної моделі запропонував 1913 р. данський фізик Нільс Бор (1885–1962), який був упевнений, що розглядати будову атома треба під кутом квантових уявлень. Бор припустив існування особливих станів атомів і сформулював два постулати.
Перший постулат Н. Бора (про стаціонарні стани): атомна система може перебувати лише в особливих стаціонарних (квантових) енергетичних станах, кожному з яких відповідає певне значення енергії; перебуваючи в стаціонарному стані атом не випромінює енергію.
Другий постулат Н. Бора (про квантові стрибки): під час переходу з одного стаціонарного енергетичного стану в інший атом випромінює або поглинає квант електромагнітної енергії.
Повертаючись в основний стан, атоми, відповідно до постулатів Бора, випромінюють електромагнітні хвилі чітко визначених частот, а отже, і довжин. Якщо газ розріджений і перебуває в атомарному (не молекулярному) стані, то на екрані спектрографа спостерігають різнокольорові лінії, розділені широкими темними смугами. Сукупність цих ліній називають лінійчастим спектром випромінювання.

Існує і зворотне явище: якщо біле світло пропускати через речовину в газуватому стані, то спостерігають темні лінії на фоні неперервного спектра. Сукупність цих ліній називають лінійчастим спектром поглинання.

Лінійчастий спектр будь-якого хімічного елемента не збігається з лінійчастими спектрами інших хімічних елементів, а отже, є своєрідною візитівкою елемента.
Відповідь: Б.
ТЕМА: Квантова фізика. Елементи теорії відносності.
Завдання скеровано на перевірку знання досягнень фізичної науки й авторів цих відкриттів.
1. Вимірювання тиску світла ‒ Лебедєв П. (А).
Тиском світла називається тиск, який чинять електромагнітні світлові хвилі, які падають на поверхню будь-якого тіла. Гіпотезу про існування тиску висунув Дж. Максвел у своїй електромагнітній теорії світла.

Експериментально існування світлового тиску вперше встановив 1900 р. фізик П.М. Лебедєв. Для вимірювання світлового тиску він спрямував інтенсивний світловий потік на легкі металеві пластинки, підвішені на тонкій нитці в балоні, з якого було викачано повітря. Пластинки лівого ряду підвісу були чорними, а пластинки правого ‒ блискучими. Тому тиск світла на пластинки лівого ряду був меншим, ніж на пластинки правого ряду. Унаслідок цього під впливом світла підвіс повертався на певний кут, за значенням якого можна було визначити силу закручування і, отже, світловий тиск.
2. Створення планетарної моделі атома ‒ Резерфорд Е. (Б).
У 1908–1911 рр. під керівництвом Ернеста Резерфорда науковці досліджували будову атома. Вони спрямовували на тонку золоту фольгу вузький пучок
- в атомі позитивно заряджене ядро оточене негативно зарядженими частинками ‒ електронами, які обертаються навколо ядра, як планети навколо Сонця;
- саме в ядрі зосереджена мало не вся маса атома.
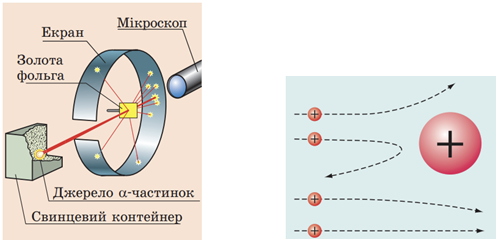
3. Створення теорії фотоефекту ‒ Ейнштейн А. (В).
Зовнішній фотоефект відкрив 1887 року німецький фізик Генріх Герц. Детальніше це явище дослідив Олександр Столєтов. У досліді він використав вакуумну камеру з двома електродами (катод і анод) усередині, на які подається напруга від джерела постійного струму. Під дією світла, яке потрапляє в камеру через спеціальне віконце, катод випромінює електрони. Рухаючись від катода до анода в електричному полі, електрони створюють фотострум. Якщо збільшувати напругу на електродах, сила фотоструму теж зросте. Змінюючи почергово інтенсивність і частоту світла, що падає на катод, а також матеріал катода, О. Столєтов сформулював три закони зовнішнього фотоефекту. Але лише більш як через
4. Створення першого ядерного реактора ‒ Фермі Е. (Г).
Фермі 1938 року одержав Нобелівську премію за «демонстрацію існування нових радіоактивних елементів, утворених під час опромінення нейтронами, і за пов’язані відкриття ядерних реакцій, викликані повільними нейтронами». До весни 1941 року розробляв теорію ланцюгової реакції в урано-графітовій системі, а вже влітку розпочав серію експериментів, головним завданням яких було вимірювання нейтронного потоку. Разом з Г. Андерсоном провів близько тридцяти дослідів. У червні 1942 року було досягнуто значення коефіцієнта розмноження нейтронів, більшого за одиницю. Це означало можливість отримання ланцюгової реакції у достатньо великій ґратці з урану й графіту й послужило початком розроблення конструкції водно-графітового реактора. Фермі також спроєктував гігантський намет із тканини для оболонок аеростатів навколо конструкції реактора. Так з’явилася можливість підтримувати відповідний склад середовища, що оточувало реактор. Будівництво реактора розпочалося в Металургійній лабораторії Чиказького університету в жовтні, а завершилося 2 грудня 1942 року. У лабораторії під стадіоном англ. Stagg Field Stadium на цьому реакторі під назвою англ. Chicago Pile-1 (CP-1) було проведено експеримент, що продемонстрував першу самопідтримну ланцюгову ядерну реакцію.
Відповідь: 1А, 2Б, 3В, 4Г.