Розділ: Механіка
Тема: Динаміка: основні сили
Кількість завдань: 61
ТЕМА: Механіка. Основи динаміки.
Завдання скеровано на перевірку знання і розуміння сил в динаміці, а також уміння визначати їхню залежність від певних параметрів у кожній конкретній ситуації.
А ‒ 2. Коли тіло перебуває в стані спокою на похилій площині, то сила тертя спокою дорівнює за модулем проєкції сили тяжіння на вісь
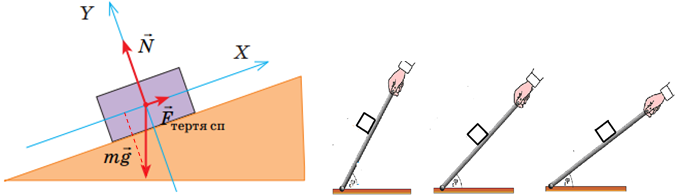
Б ‒ 1. Механічна робота (робота сили)
Оскільки вектор сили тяжіння завжди напрямлений вертикально вниз, а за умовою автомобіль рухається горизонтальною дорогою, то кут між вектором сили тяжіння і вектором переміщення дорівнює
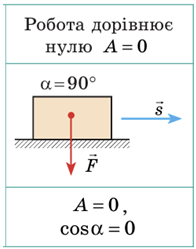
В ‒ 4. За законом всесвітнього тяжіння будь-які два тіла притягуються одне до одного із силою
Відповідно до заданої в умові ситуації сили гравітаційної взаємодії між Сонцем і Землею не змінюватимуться (але й не дорівнюватимуть нулю).
Г ‒ 3. Сила пружності
За другим законом Ньютона:
Отже, проаналізуємо цю рівність. Якщо поїзд скидає швидкість на повороті (
Під час коливань нитяного маятника сила натягу його нитки весь час змінюється, досягаючи максимуму в нижній точці (найнижчій точці траєкторії) і мінімуму на крайніх точках (коли маятник зупиняється). У найнижчій точці сила натягу дорівнює сумі сили тяжіння та сили, що створює доцентрове прискорення. Сила натягу максимальна, оскільки вона повинна протидіяти силі тяжіння та забезпечувати доцентрове прискорення, яке спрямоване до центру кола (точки підвісу). У крайніх точках сила натягу мінімальна і дорівнює проекції силі тяжіння. У ці моменти швидкість маятника дорівнює нулю, тому немає сили, що створює доцентрове прискорення.
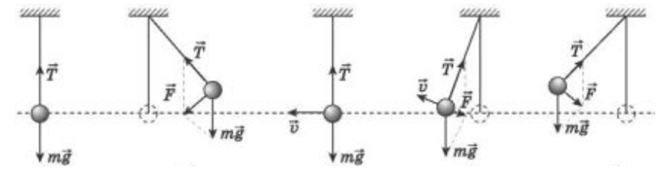
Відповідь: 1Б, 2А, 3Г, 4В.
ТЕМА: Механіка. Основи динаміки. Вага тіла. Невагомість.
Завдання скеровано на перевірку знання і розуміння стану невагомості.
Стан тіла, за якого вага тіла дорівнює нулю, називають станом невагомості.
У стані невагомості на тіло діє лише сила тяжіння (тіло вільно падає), і навпаки: якщо тіло рухається тільки під дією сили тяжіння, воно перебуває в стані невагомості.
Проаналізуймо стан запропонованих в умові рухомих об’єктів.
Якщо діти підстрибнули, відірвалися від землі, то вони не тиснуть на опору (на землю), а отже, їхня вага дорівнюватиме нулю. Цієї миті діти перебувають у стані невагомості. Також уважатимемо, що на дітей діє тільки сила тяжіння, опором повітря можна в цій ситуації знехтувати, настільки він незначний.
Підлітки у ліфті тиснуть на опору ‒ на підлогу ліфта, отже, вага не дорівнює нулю. Цей стан не є станом невагомості. Це правильна відповідь.
За умовою завдання повітря з трубки Ньютона відкачано. Падіння тіл у безповітряному просторі називають вільним, тобто це падіння лише під дією сили тяжіння. Отже, тіла у трубці ‒ у стані невагомості.
На космонавта у відкритому космосі, як зображено на фото, діє сила тяжіння, але ні опори, ні підвісу немає, тому вага космонавта дорівнює нулю ‒ стан невагомості.
Відповідь: Б.
ТЕМА: Механіка. Основи динаміки. Рух тіла під дією кількох сил.
Завдання скеровано на перевірку вміння визначати рівнодійну всіх сил, що діють на тіло під час руху.
На аеростат і під час опускання, і під час підйому діятимуть дві сили ‒ сила тяжіння і сила Архімеда (за умовою опором повітря можна знехтувати). Зобразимо ці сили на рисунках ‒ спочатку опускання, а потім, після скидання баласту, підйому.
Запишімо другий закон Ньютона у векторній формі і в проєкціях на вісь
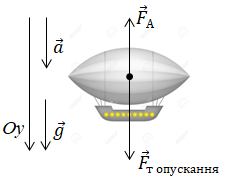
Запишімо другий закон Ньютона у векторній формі і в проєкціях на вісь
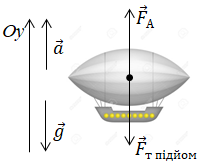
Модуль сили Архімеда залишиться сталим після скидання баласту, тому що об᾽єм
Тож виразімо силу Архімеда в обох ситуаціях і прирівняємо її, так зможемо визначити масу баласту:
розкриємо дужки й виразімо
Відповідь: 10.
ТЕМА: Механіка. Основи динаміки. Невагомість.
Завдання скеровано на перевірку знання і розуміння поняття невагомості.
Стан тіла, за якого вага тіла дорівнює нулю, називають станом невагомості.
У стані невагомості на тіло діє лише сила тяжіння (тіло вільно падає), і навпаки: якщо тіло рухається тільки під дією сили тяжіння, воно перебуває у стані невагомості.
У стані невагомості не тільки тіло не тисне на опору, а й частини тіла не тиснуть одна на одну.
Отже, з усіх умов, зазначених у варіантах відповіді, однозначно правильним є варіант А.
Відповідь: A.
ТЕМА: Механіка. Основи динаміки.
Завдання скеровано на перевірку розуміння руху тіла вздовж похилої площини під дією кількох сил.
Зобразімо схематично транспортер у вигляді похилої площини та брусок на ньому, що рухається вгору разом зі стрічкою транспортера зі швидкістю
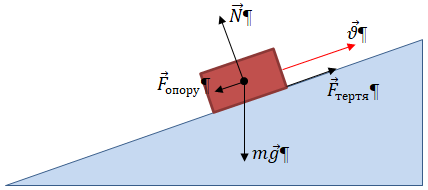
Сила тяжіння
Сила нормальної реакції
Брусок, рухаючись угору разом зі стрічкою транспортера, не зісковзує вниз завдяки силі третя
Сила опору
Відповідь: 1Д, 2Б, 3А, 4Г.
ТЕМА: Механіка. Основи динаміки. Умови рівноваги тіла.
Завдання скеровано на перевірку знання і розуміння умов рівноваги тіла.
Важіль перебуває в рівновазі, якщо сума моментів сил, що обертають його проти годинникової стрілки
У формулі
Отже, для врівноваження важеля тягарець треба підвісити у точці
Відповідь: A.
ТЕМА: Механіка. Основи динаміки. Сила. Гравітаційна взаємодія.
Завдання скеровано на перевірку розуміння принципів гравітаційної взаємодії.
Дано:
Знайти:
Силу тяжіння визначають за формулою
Прискорення вільного падіння можна пов’язати із законом всесвітнього тяжіння:
Сила тяжіння – це сила, із якою Земля чи інше астрономічне тіло притягують до себе тіла, що перебувають на їхній поверхні, тож вона є частковим випадком сили із закону всесвітнього тяжіння.
Тож можна записати рівність виразів для сили тяжіння і закону всесвітнього тяжіння, у якому одне тіло – це планета, а інше – корабель. Вважатимемо, що відстань між центрами мас корабля і планети дорівнює її радіусу:
Тож, якщо поділити обидва вирази на масу корабля, дістаємо:
На планетах із різними радіусами й масами прискорення вільного падіння буде різним.
Прискорення вільного падіння на Землі:
На планеті Z:
За умовою маси планет невідомі, але відомі їхні середні густини. Середню густину планети можна визначити за формулою
Форма планет близька до сферичної внаслідок дії гравітації, тож їхній об’єм можна визначити як об’єм сфери:
Тоді масу планети можна виразити через її середню густину:
Тоді силу тяжіння на Землі можна виразити як
А на планеті Z сила тяжіння
Відповідь: 800.
ТЕМА: Молекулярна фізика і термодинаміка. Квантова фізика.
Завдання скеровано на перевірку розуміння фізичного змісту фізичних сталих.
Розв’язання завдання потребує знання визначень фізичних величин і вміння аналізувати розмірності.
Розмірність сталої Авогадро –
Стала Авогадро – це число, що відповідає кількості атомів (молекул) у будь-якій речовині кількістю
Розмірність сталої Больцмана
Сталу Больцмана використовують для встановлення зв’язку між середньою кінетичною енергією руху молекул і температурою ідеального газу:
Якщо температура змінюється, то змінюється і середня кінетична енергія молекул:
Звідси можна виразити сталу Больцмана:
Розмірність сталої Планка –
За гіпотезою Планка молекули випромінюють енергію порційно, і кількість цієї енергії пропорційна до частоти випромінювання:
Відповідно стала Планка
Гравітаційна стала фігурує в законі Всесвітнього тяжіння:
Якщо маса обох тіл становить 1 кг, відстань між ними – 1 м, то
Тож сила взаємодії таких тіл за модулем дорівнює гравітаційній сталій.
До того ж сила має розмірність
Відповідь: 1Б, 2А, 3Г, 4В.
ТЕМА: Механіка. Основи динаміки. Вага.
Завдання скеровано на перевірку вміння розраховувати вагу тіл, що рухаються з прискоренням.
Якщо тіло перебуває в стані спокою або рухається рівномірно, то його вага за модулем дорівнює силі тяжіння, що діє на нього.
Якщо ж тіло рухається з прискоренням, то його вага відрізнятиметься від значення сили тяжіння.
Якщо прискорення напрямлене вертикально вниз, то вагу можна обчислити за формулою
Униз прискорення напрямлене, коли ліфт рухатиметься з 10-го поверху на 1-й і збільшуватиме швидкість.
Якщо прискорення напрямлене вертикально вгору, то вагу можна обчислити за формулою
Угору прискорення напрямлене, коли ліфт рухається з 1-го поверху на 10-й і збільшує швидкість.
Відповідь: A.
ТЕМА: Сила тяжіння. Сила пружності. Сила кулона. Ядерні сили.
Завдання скеровано на перевірку розуміння впливу сил різної природи на природні явища.
1 електронейтральні нейтрони й позитивно заряджені протони утримуються в ядрах (й альфа-частинках, що є ядрами атомів Гелію, зокрема) завдяки дії ядерних сил
2 куля деформує броню в момент зіткнення. Залежно від величини цієї деформації броня повертається в попередній стан (зазнає пружної деформації), зберігає деформацію після зіткнення (зазнає пластичної деформації) або руйнується. Подальший рух кулі також від цього залежить, адже завдяки силі пружності, що виникає в броні, куля може зрикошетити й змінити напрямок руху чи його швидкість
3 причиною руху Місяця навколо Землі є її сила тяжіння
4 часто рух негативно зарядженого електрона в атомі зумовлений його кулонівською взаємодією з позитивно зарядженим ядром.
Відповідь: 1Г, 2Д, 3А, 4Б.
ТЕМА: Механіка. Основи динаміки. Вага.
Завдання скеровано на перевірку вміння розраховувати вагу тіл, що рухаються з прискоренням.
Вага
Коли тіло рухається лише під дією сили тяжіння, як наприклад камінь, що вільно падає, то воно перебуває в стані невагомості, а отже його вага дорівнює нулю.
Якщо тіло перебуває в стані рівноваги, то його вага за модулем дорівнює силі тяжіння, що діє на нього. Якщо ж тіло рухається з прискоренням, то його вага відрізняється від значення сили тяжіння.
Якщо прискорення напрямлене вертикально вниз, то вагу можна обчислити за формулою
Униз прискорення напрямлене, коли людина починає рухатися з ліфтовою кабіною вниз. Також униз буде напрямлене доцентрове прискорення, коли автомобіль перебуває в найопуклішій частині опуклого мосту.
Якщо прискорення напрямлене вертикально вгору, то вагу можна обчислити за формулою
Тож вага космонавта, що перебуває в ракеті під час її старту із Землі, більша за силу тяжіння, що діє на нього.
Відповідь: Б.
ТЕМА: Механіка. Основи динаміки. Сили. Додавання сил.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з визначення рівнодійної кількох сил.
На кульку, що піднімається вгору в повітрі, діють три сили: сила Архімеда, що виштовхує її з товщі повітря вгору, сила тяжіння, яка притягує кульку до землі, і сила опору повітря, що заважає руху кульки (рис. 1). Оскільки сила Архімеда більша за значенням від сили тяжіння, кулька рухатиметься вгору, а сила опору повітря буде напрямлена вниз.
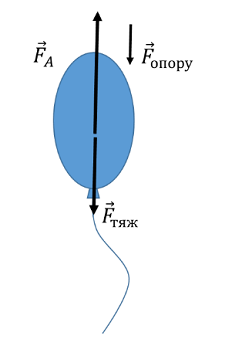
Рис. 1. Сили, що діють на кульку
Рівнодійна
Відповідь: A.
ТЕМА: Сила пружності. Механічні коливання. Коливання вантажу на пружині.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на виявлення зв’язку між періодом коливання і параметрами коливальної системи.
Дано:
Знайти:
Період коливань пружинного маятника визначають за формулою
За умовою
Нехай ціла пружина мала коефіцієнт жорсткості
Закон Гука описують формулами
а
Тоді, підставивши (7) і (8) у (6) і прирівнявши вирази для сили пружності з виразів (6) і (5), можна дістати
Під час розрізання пружини на дві коротші площа перерізу й модуль Юнга не змінюються, тому:
Відповідь: 2.
ТЕМА: Механіка. Основи динаміки. Сила.
Завдання скеровано на оцінювання розуміння природи сил пружності, поверхневого натягу, тертя і гравітаційної сили.
Для правильного розв’язання завдання потрібно розглянути кожен із проявів сил.
A. Відштовхування різнойменних електричних зарядів зумовлено їхньою кулонівською взаємодією.
Б. Амортизатори в автомобілі поглинають результати ударів від нерівностей на поверхні й забезпечують стабільне положення кузова автомобіля. Пружини амортизаторів стискаються і розтискаються під час гальмування і розгону автомобіля, можливість повернутися в попереднє положення їм забезпечує сила пружності.
В. Автомобільні покришки постійно перебувають у контакті з поверхнею. Вони мають забезпечувати тертя, адже лише так можна бути впевненим у керованості автомобіля. Проте тертя – руйнівний процес, тому із часом нерівності поверхні покришок стираються, після чого вони стають непридатними до використання. Тому це прояв саме сили тертя.
Г. Рух астероїда навколо Сонця зумовлено гравітаційним притягуванням між ними.
Д. Поверхневий шар молекул під час видування мильних бульбашок поводиться подібно до тонкої плівки (наприклад, гумової) і тому може втримувати всередині повітря. Існування такого поверхневого шару зумовлено силою поверхневого натягу.
Відповідь: 1Г, 2Б, 3Д, 4В.
ТЕМА: Механіка. Основи динаміки. Невагомість.
Завдання скеровано на оцінювання розуміння поняття «невагомість».
Вага
Невагомість – це стан тіла, за якого його вага дорівнює нулю.
У стані невагомості ні тіло не діє на опори чи підвіси навколо, ні частини тіла не діють одна на одну. Це можливо лише за умови, що на тіло діє тільки сила тяжіння. Адже вона примушує всі тіла (незалежно від їхньої маси) рухатись із тим самим прискоренням – прискоренням вільного падіння.
Також важливо пам’ятати, що маса й вага – це два різні за своєю природою поняття. Вага – це сила, а маса – міра інертності. Маса залишається однаковою незалежно від вибору системи відліку чи сил, які діють на тіло. Тож маса не може дорівнювати нулю в стані невагомості.
Відповідь: A.
ТЕМА: Механіка. Основи динаміки. Сили. Додавання сил.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на рух тіл під дією кількох сил.
Дано:
Знайти:
Корок у пляшці – нерухомий, тому можна зробити висновок, що рівнодійна сил, які діють на нього, дорівнює нулю. Оскільки масу корка не враховують, то дією сили тяжіння можна знехтувати. Тоді на корок діють лише сила атмосферного тиску
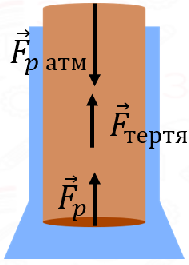
Рис. 1. Схематичне зображення сил, що діють на корок
Силу тиску можна знайти за формулою:
У випадку корка, який можна вважати циліндром, площею для розрахунку обох сил тиску можна вважати площу його основи. Сила тертя діє вздовж усієї площі контакту корка з пляшкою і протидіє його руху. Оскільки атмосферний тиск більший за тиск усередині пляшки, то й сила атмосферного тиску більша, а сила тертя діятиме в тому самому напрямку, що й сила тиску повітря в пляшці.
Тепер можна спроєктувати всі сили, що діють на корок, на одну пряму й записати другий закон Ньютона для корка:
Відповідь: 40.
ТЕМА: Механіка. Основи динаміки. Сила.
Завдання скеровано на оцінювання знання розрахункових формул сили тертя ковзання, сили Ампера, сили поверхневого натягу й сили Архімеда.
Для правильного розв’язання завдання потрібно з’ясувати фізичний зміст формул, наведених у ньому.
A
Б
В
Г
Д
Відповідь: 1В, 2А, 3Б, 4Д.
ТЕМА: Маса. Густина. Сила Ампера.
Завдання скеровано на оцінювання вміння розв’язувати комплексні задачі, що передбачають аналіз за фотографіями результатів експерименту, пов’язаного з вагою і силою Архімеда.
1. Знайти:
На рисунках схематично зображено масу, що відповідає вазі в трьох різних ситуаціях. На рисунку 1 маса, яку вимірює прилад, відповідає вазі склянки з водою:
На рисунку 2 – маса, що відповідає вазі склянки з водою і бруском. Вага – це сила, із якою тіло діє на опору чи підвіс. У цьому випадку на прилад діє вага склянки з водою і сила тиску бруска. Сила тиску бруска на склянку
(і прилад відповідно) чисельно дорівнює виштовхувальній силі, що діє на брусок. Тоді вираз для ваги, якій відповідає маса на рисунку 2:
Тоді можна обчислити силу Архімеда:
2. Знайти:
За визначенням густина дорівнює:
Силу Архімеда можна обчислити за формулою:
Зважаючи на те, що брусок повністю занурено у воду, витіснений об’єм дорівнює об’єму бруска. Тож можна обчислити об’єм бруска:
За вагою бруска можна обчислити його масу:
І густина бруска дорівнюватиме:
Відповідь: 1. 0,12. 2. 8000.
ТЕМА: Механіка. Основи динаміки. Закони Ньютона. Сила тертя.
Завдання скеровано на оцінювання розуміння впливу сили тертя в задачах на основі побутових прикладів.
Під час перетягування каната виграє той, хто може перетягнути стрічку посередині на свій бік. Чим більшою є сила тертя між учасником і підлогою, тим більшу силу треба прикласти, щоби зсунути його з місця. Тому для здобуття перемоги тягнути канат із більшою силою ніж опонент не достатньо, якщо сила тертя з боку підлоги в нього більша.
Сила тертя з боку каната важлива, але вона не визначає переможця, адже за дуже великої сили тертя між канатом й учасником він почне рухатися разом із канатом.
Маса учасників впливає лише на те, наскільки сила тяжіння діятиме на них. Притягування Землі може піти як на користь, так і на шкоду залежно від того в який бік нахилене тіло учасника.
Відповідь: B.
ТЕМА: Механіка. Основи динаміки. Сила. Момент сили. Потенціальна енергія.
Завдання скеровано на оцінювання вміння пояснювати щоденні процеси за допомогою фізичних законів.
У завданні наведено такі формули:
А Вираз для опису роботи сили тяжіння.
Б Вираз для потенціальної енергії деформованого тіла.
В Вираз для визначення сили тертя.
Г Рівняння моментів сил для стану рівноваги.
Д Вираз для закону Архімеда.
1 Під час розтягування гумової нитки виникає сила пружності, тож розтягування можна описати виразом для потенціальної енергії деформованого тіла (Б).
2 Під час падіння поле тяжіння Землі виконує роботу над тілом. Тому цей процес можна описати виразом для роботи сили тяжіння (А).
3 Під час ковзання черевика по підлозі між ними виникає сила тертя ковзання, що можна описати виразом В.
4 Тіло перебуватиме в положенні рівноваги (плаватиме на поверхні, у товщі рідини або на дні), якщо сила Архімеда, що виштовхує його з рідини, дорівнюватиме силі тяжіння, що діє на нього. Тому процес можна описати виразом Д.
Відповідь: 1Б, 2А, 3В, 4Д.
ТЕМА: Механіка. Основи динаміки. Сила пружності. Закон Гука
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на використання закону Гука й потенціальної енергії пружини.
Потенціальну енергію
Оскільки відношення коефіцієнтів жорсткості пружин відоме з умови, потрібно визначити відношення обох видовжень.
Пружини розтягуються силою
Із цих співвідношень випливає, що
Тоді потенціальна енергія для обох пружин:
Відповідь: B.
ТЕМА: Молекулярна фізика і термодинаміка. Механічні властивості твердих тіл.
Завдання скеровано на перевірку поняття «видовження».
Відносне видовження обчислюють за формулою:
Відповідь: Б.
ТЕМА: Механіка. Основи динаміки. Закони Ньютона. Закон всесвітнього тяжіння.
Завдання скеровано на перевірку розуміння закону всесвітнього тяжіння і його застосування для описування реальних ситуацій.
Закон всесвітнього тяжіння – будь-які два тіла притягуються одне до одного із силою, яка прямо пропорційна добутку мас цих тіл й обернено пропорційна квадрату відстані між ними:
Відстань між двома сусідніми цеглинами дорівнює
Відповідь: B.
ТЕМА: Механіка. Основи динаміки. Сила пружності. Закон Гука.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на використання закону Гука.
1. Знайти:
Оскільки прикладена сила – розтягувальна, то довжина пружини збільшувалась. Під час розтягування в пружині виникає сила пружності, що й дорівнює силі розтягування:
Сила пружності пов’язана з абсолютним видовженням і коефіцієнтом жорсткості:
Тоді можна записати вираз для сили пружності в обох випадках:
Зважаючи на те, що максимальна довжина пружини в першому експерименті – 10 см, а в другому – 11 см, то можна записати зв’язок між абсолютними видовженнями в обох випадках (абсолютні видовження подано в метрах):
Тоді
Можна виразити абсолютне видовження
Отже
2. Знайти:
З виразу для сили пружності можна обчислити абсолютне видовження пружини для першого експерименту:
Тож, якщо максимальна довжина пружини в цьому експерименті – 10 см (0,1 м), то можна обчислити початкову довжину:
Відповідь: 1. 200. 2. 8,5.
ТЕМА: Механіка. Основи динаміки. Сила пружності. Закон Гука.
Завдання скеровано на перевірку розуміння понять роботи й потенціальної енергії пружини.
Робота, виконана пружиною під час розтягування чи стискання, дорівнює зміні потенціальної енергії пружини, узятій із протилежним знаком:
Потенціальну енергія пружини можна обчислити за формулою
Для обчислення потенціальної енергії пружини в кожному положенні необхідно перевести в метри видовження, подане в сантиметрах:
Тоді робота, яку пружина виконує під час скорочення від 4 см до 2 см, така:
А робота, яку пружина виконує під час скорочення від 2 см до 0 см, дорівнює:
Знак «мінус» у цьому разі означає, що пружина виконувала роботу, а не зовнішнє тіло виконувало роботу над нею.
Тож
Відповідь: Г.
ТЕМА: Механіка. Основи динаміки. Сили пружності. Закон Гука.
Завдання скеровано на перевірку розуміння залежності сили пружності від видовження тіла під час малих пружних деформацій.
За законом Гука в разі малих пружних деформацій розтягнення або стиснення сила пружності
Між силою пружності й видовженням залежність лінійна, тож графіком функції є пряма. На графіку, наведеному в умові завдання, прямолінійною є лише ділянка
Відповідь: A.
ТЕМА: Механічні коливання і хвилі. Коливання вантажу на пружині. Перетворення енергії під час гармонічних коливань.
Завдання скеровано на оцінку вміння розв’язувати комбіновані задачі, які передбачають обробку й аналіз результатів експерименту, зображених на рисунку, i використання законів збереження енергії в коливальному процесі.
Знайти:
З рисункa 1 можна визначити довжину гумки у двох крайніх положеннях коливання тягарця. У крайніх положеннях тягарець змінює напрямок руху на протилежний, а отже його швидкість
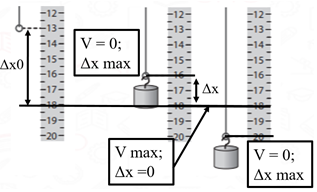
Рис. 1. Крайні положення тягарця
За цими значеннями можна обчислити амплітуду коливань:
Знаючи амплітуду коливань, можна визначити положення рівноваги – таке положення, у якому опиниться гумка під вагою тягарця, коли коливання повністю припиняться:
Під час коливань у положенні рівноваги швидкість найбільша, отже саме цю швидкість потрібно визначити.
Під час коливань зберігається повна механічна енергія системи
Кінетичну енергію можна визначити за формулою
Оскільки для гумової стрічки виконуваний закон Гука, можна обчислити потенціальну енергію за формулою, якою описують потенціальну енергію розтягнутої пружини:
Хоча повна механічна енергія системи зберігається, але значення кінетичної і потенціальної енергії постійно змінюється під час коливань.
У крайніх положеннях швидкість тягарця дорівнює нулю, а отже і його кінетична енергія теж. А от відхилення від положення рівноваги в цих положеннях найбільше, тому потенціальна енергія максимальна.
У положенні рівноваги все навпаки. Швидкість тягарця максимальна, а відхилення дорівнює нулю, отже кінетична енергія приймає найбільше значення, а потенціальна перетворюється на нуль.
Зважаючи на закон збереження енергії і спостереження, описані вище, можна записати таку рівність:
Тоді можна виразити максимальну швидкість:
Відношення
У стані спокою тягарець перебуватиме в положенні рівноваги. Тоді можна записати другий закон Ньютона:
Тоді
Після цього можна підставити отримане відношення у вираз для максимальної швидкості:
Відповідь: 28.
ТЕМА: Механіка. Динаміка. Капілярні явища. Сила Архімеда. Сила пружності. Невагомість.
Завдання скеровано на перевірку розуміння природи фізичних явищ і сил.
1 Капілярні явища зумовлені тим, що рідини в тонких трубках мають велику площу контактування з твердою речовиною. Увігнутий або опуклий меніск утворюється залежно від того, чи змочує рідина поверхню чи не змочує. Унаслідок дії сил поверхневого натягу під деформованою поверхнею виникне надлишковий тиск (тиск Лапласа), який приведе до підняття або опускання стовпчика рідини.
2 Архімедова сила виникає завдяки тому, що в однорідних рідинах на різних рівнях установлюється різний гідростатичний тиск. Що більша глибина, то більший гідростатичний тиск. За законом Паскаля тиск у рідинах і газах поширюється однаково в усіх напрямках. Тоді на верхню поверхню тіла діє менший порівняно з нижньою його поверхнею тиск. Унаслідок такої різниці тисків утворюється сила, що завжди спрямована на виштовхування тіла з рідини – сила Архімеда.
3 Сила пружності – це сила, яка виникає під час деформації тіла й намагається повернути тіло в недеформований стан.
4 Невагомість – це стан тіла, у якому його вага дорівнює нулю. Для тіл на поверхні Землі або поруч із її поверхнею це свідчить про те, що на тіло діє лише сила тяжіння. У такому разі всі тіла рухаються з однаковим прискорення – прискоренням вільного падіння.
Відповідь: 1Г, 2Б, 3А, 4В.
ТЕМА: Механіка. Основи динаміки. Закони Ньютона. Сила тертя.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з використанням законів Ньютона.
Дії сил на брусок зображено на рисунку 1. На нього діють сила тяжіння, сила реакції опори й сила тертя.
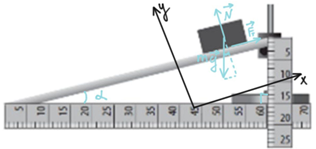
Рис. 1. Дії сил на брусок
Запис другого закону Ньютона для бруска:
Силу тяжіння і силу тертя можна визначити за такими формулами:
де
Оскільки брусок ковзає рівномірно, то його прискорення дорівнює
Тоді
Коефіцієнт тертя можна обчислити за формулою
Можна визначити
Відповідь: A.
ТЕМА: Механіка. Основи динаміки.
Завдання скеровано на перевірку розуміння різних динамічних процесів і вміння описати їх аналітично.
Ситуацію 1, коли відро з водою утримується за допомогою колодязного журавля (важеля), можна описати за допомогою правила моментів A: важіль перебуває в рівновазі, якщо сума моментів сил, які обертають важіль проти ходу годинникової стрілки, дорівнює сумі моментів сил, що обертають важіль за ходом годинникової стрілки.
Отже, умову рівноваги важеля під дією двох обертальних сил (сили тяжіння
У разі деформації тіла, як то стискання пружини (2), із боку тіла починає діяти сила, яка прагне відновити той стан тіла, у якому воно перебувало до деформації. Цю силу називають силою пружності. У разі малих пружних деформацій розтягнення або стиснення сила пружності прямо пропорційна видовженню тіла (Б):
Потужність, яку розвиває транспортний засіб, зручно визначати через силу тяги та швидкість руху. Формула справджується, і якщо в певний інтервал часу тіло рухається рівномірно, а напрямок сили тяги збігається з напрямком переміщення, і за нерівномірного руху: потужність
Отже, ситуації 3 відповідає формула B.
Силу тертя ковзання можна зменшити, змастивши дотичні поверхні, як у ситуації 4, коли деталі механізмів змащують мастилом.
Рідке мастило віддаляє дотичні поверхні одну від одної − сухе тертя замінюється значно слабшим рідким тертям.
Сила тертя ковзання
Відповідь: 1А, 2Б, 3В, 4Г.
ТЕМА: Механіка. Елементи механіки рідин і газів. Архімедова сила.
Завдання скеровано на перевірку вміння розв᾽язувати задачі, коли на тіло діє кілька сил.
Позначмо сили, які діють на тіло, занурене в олію, а потім – у воду.
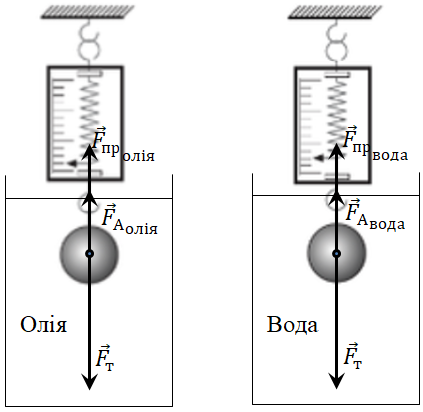
Запишімо рівняння другого закону Ньютона в проєкціях на вертикальну вісь, напрямлену вниз:
Усі тіла внаслідок гравітаційного притягання стискають або прогинають опору або розтягують підвіс. Силу, яка характеризує таку дію тіл, називають вагою і позначають
Прирівняємо праві частини цих формул:
Запишімо, чому дорівнює сила Архімеда у воді та олії:
Відповідь: B.
ТЕМА: Механіка. Основи динаміки. Вага тіла.
Завдання скеровано на перевірку розуміння сили, яку називають вагою.
Усі тіла внаслідок гравітаційного притягання стискають або прогинають опору або розтягують підвіс. Силу, яка характеризує таку дію тіл, називають вагою і позначають
Вантаж і нижній динамометр підвішені до верхнього динамометра й розтягують його пружину. Отже, верхній динамометр покаже загальну вагу вантажа та нижнього динамометра:
Відповідь: B.
ТЕМА: Механіка. Основи динаміки. Сила тертя.
Завдання скеровано на перевірку вміння визначати сили тертя і рівнодійну сил, прикладених до тіл.
Щоб натягнути нитку, якою зв’язано бруски, треба зрушити з місця другий брусок, подолати максимальну силу тертя спокою, протилежно напрямлену до прикладеної горизонтальної сили
Обчислімо силу натягу нитки
Перевірімо, чи рухатиметься за таких умов перший брусок і, відповідно, уся система тіл. Для цього обчислімо максимальну силу тертя спокою, яка мала б діяти на перший брусок, якби він зрушив із місця:
Нитку натягнуто із силою
Відповідь: 2.
ТЕМА: Механіка. Коливання і хвилі.
Завдання скеровано на перевірку розуміння фізичних процесів механіки і знання формул, якими описують ці процеси.
Усім тілам у Всесвіті властива гравітаційна взаємодія, виявом якої є їхнє взаємне притягання. Відповідно до закону всесвітнього тяжіння планети Венера й Марс притягуються одна до одної із силою
Якщо розтягнуту гумову нитку відпустити, то, скорочуючись, вона виконає роботу. Робота сили пружності визначена лише початковим і кінцевим станами гумової нитки, тобто сила пружності ‒ консервативна або потенціальна сила. Величину
Між дотичними поверхнями стрічки транспортера й цеглини діє сила тертя спокою, яка перешкоджає виникненню відносного руху їх. Сила тертя спокою завжди дорівнює за модулем і протилежна за напрямком рівнодійній зовнішніх сил, які намагаються зрушити тіло з місця. Після того як рівнодійна зовнішніх сил зрівняється з максимальною силою тертя спокою, тіло починає ковзання, тобто починає діяти сила тертя ковзання. Отже, максимальна сила тертя спокою дорівнює силі тертя ковзання:
Маленька сталева кулька коливається на довгій нерозтяжній нитці ‒ це модель нитяного (математичного) маятника. Період коливань
Відповідь: 1А, 2Г, 3Д, 4Б.
ТЕМА: Механіка. Основи кінематики. Вільне падіння.
Завдання скеровано на перевірку розуміння вільного падіння тіл.
Якщо б у трубці було повітря, то найважче тіло (дробинка) упало б на дно трубки найшвидше. За умовою завдання повітря з трубки відкачано, тіла падають вільно з однакової висоти.
Вільним називають падіння тіл у безповітряному просторі, тобто це падіння лише під дією сили тяжіння.
Експериментально було доведено, що швидкість будь-якого тіла, яке вільно падає, щосекунди збільшується приблизно на
Тобто в безповітряному просторі (вакуумі) усі тіла ‒ дробинка, корок і пташине перо ‒ незалежно від їхньої маси, об’єму, форми ‒ упадуть на дно трубки одночасно.
Відповідь: Г.
ТЕМА: Механіка. Основи динаміки (закон всесвітнього тяжіння.). Закони збереження в механіці (прості механізми, закон збереження імпульсу). Коливання і хвилі. Оптика. Механічні коливання і хвилі. Коливання вантажу на пружині.
Завдання скеровано на перевірку знання і розуміння механічних процесів, уміння описати їх за допомогою формул і законів.
Взаємодію Землі і Місяця описуємо за допомогою закону всесвітнього тяжіння: будь-які два тіла притягуються одне до одного із силою
Відкручування гайки за допомогою гайкового ключа є прикладом застосування простого механізму ‒ важеля ‒ на практиці. Чим довшою буде ручка гайкового ключа, тим легше ми відкрутимо або сильніше закрутимо гайку, прикладаючи меншу силу. Описати цей процес можна відповідно до правила моментів:
Коливання тіла масою
Зіткнення більярдних куль, як приклад абсолютно пружного удару, опишімо за допомогою закону збереження імпульсу: у замкненій системі тіл векторна сума імпульсів тіл до взаємодії дорівнює векторній сумі імпульсів тіл після взаємодії. Зваживши на те, що імпульс тіла дорівнює добутку маси
Відповідь: 1Д, 2Б, 3В, 4Г.
ТЕМА: Механіка. Основи динаміки. Умови рівноваги тіла.
Завдання скеровано на перевірку розуміння шарнірного з’єднання стержнів і скомпенсованості сил, уміння позначати сили, що діють, шукати їхні проєкції.
За умовою стержні невагомі, один на одного не діють.
У точці
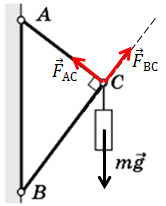
Побудуймо рівнодійну цих сил пружності. Вона буде компенсувати дію сили тяжіння.
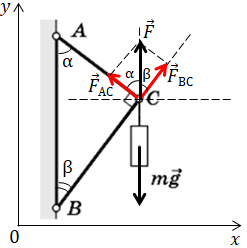
За другим законом Ньютона
Спроєктуймо вектори сил на вісь
Визначімо з прямокутного трикутника
Розв’яжімо систему рівнянь:
1) З другого рівняння системи визначімо силу пружності в стержні
Відповідь: 15.
2) Підставімо в перше рівняння системи значення сили пружності
Відповідь: 20.
Відповідь: 1. 15. 2. 20.
ТЕМА: Механіка. Основи динаміки. Додавання сил. Другий закон Ньютона.
Завдання скеровано на перевірку вміння описати систему зв’язаних тіл за допомогою другого закону Ньютона.
Зробимо схематичний рисунок, який ілюструватиме умову цього завдання. І на рисунку позначимо всі сили, що діють на обидва тіла.
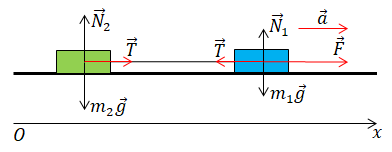
І на перше, і на друге тіло діятимуть сила тяжіння
Запишімо рівняння другого закону Ньютона для кожного з тіл у проєкціях на горизонтальну вісь
Обчислімо горизонтальну силу
Відповідь: B.
ТЕМА: Механіка. Основи динаміки. Рух тіл під дією кількох сил.
Завдання скеровано на перевірку знання і розуміння дії простого механізму ‒ нерухомого блоку, і вміння аналітично описувати рух зв’язаних тіл за допомогою другого закону динаміки Ньютона.
Схематично зобразімо на рисунку сили тяжіння
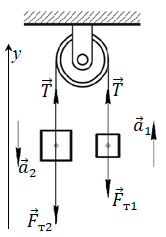
Запишімо для обох предметів другий закон динаміки Ньютона у векторному вигляді:
Запишімо систему рівнянь у проєкціях на вісь
Пояснімо, чому за модулем
Відповідно до умови кінематичного зв’язку, що випливає з нерозтяжності нитки, за будь-який інтервал часу ліва ділянка нитки подовжується саме на стільки, на скільки скорочується права. Таким чином, переміщення обох шматків жерсті весь час однакові за модулем. Звідси випливає, що в шматків однакові й модулі швидкостей, і модулі прискорень, тому
Якщо масами нитки та блока, а також тертям в осі блока можна знехтувати (а це можна зробити, тому що в умові завдання даних про це немає), то сила натягу нитки
Узявши до уваги попередні пояснення
і віднявши від першого рівняння системи друге, дістанемо:
В умові є інформація про матеріал і розміри шматків жерсті, тож виразімо їхні маси через густину
Шматки жерсті виготовлено з однакового матеріалу, тому
Товщина
Отже,
Підставимо отримані вирази для мас у формулу для прискорення:
Відповідь: Г.
ТЕМА: Механіка. Основи динаміки. Сили пружності. Закон Гука.
Завдання скеровано на перевірку розуміння дії тіла на підвіс і застосування знань про з’єднання пружин.
На нижній динамометр діє сила тяжіння, а він підвішений до двох верхніх динамометрів за допомогою гачка, з’єднаного з його пружиною. Отже, у підвісі (тобто в пружині) сила пружності виникає завдяки силі, яку називають вагою. Нижній динамометр покаже значення сили тяжіння, яка за модулем дорівнює силі пружності і протилежно до неї напрямлена, а оскільки динамометр перебуває в стані спокою, то вага дорівнюватиме за модулем силі тяжіння.
Вагу нижнього динамометра розподілено порівну між верхніми динамометрами, оскільки динамометри за умовою однакові. Унаслідок дії нижнього динамометра пружини верхніх динамометрів однаково розтягуються. Отже, верхні динамометри показують значення сил пружності:
Оскільки пружини верхніх динамометрів з’єднані паралельно стержнем, до якого підвішений нижній динамометр, то жорсткості цих пружин додають:
Отже, та сила пружності, що виникає в нижньому динамометрі, дорівнюватиме сумі сил пружності, що виникають у верхніх динамометрах:
А нижній динамометр покаже значення сили тяжіння, яка за модулем дорівнює силі пружності:
Відповідь: A.
ТЕМА: Механіка. Основи динаміки. Вага тіла.
Завдання скеровано на перевірку розуміння ваги тіла й уміння визначати її в різних ситуаціях.
Усі тіла внаслідок гравітаційного притягання стискають або прогинають опору або розтягують підвіс. Силу, яка характеризує таку дію тіл, називають вагою і позначають символом
1) Тіло перебуває в ліфті, що рухається вниз із прискоренням
Вага тіла, яке рухається з прискоренням, напрямленим вертикально вниз, менша, ніж вага
2) Тіло вільно падає біля поверхні Землі. Це означає, що на нього діє лише сила тяжіння, а тіло не діє на опору чи підвіс, тобто воно перебуває в стані невагомості. Тобто вага тіла дорівнює нулю:
3) Тіло зважують на поверхні Місяця, тож вага тіла за модулем дорівнюватиме силі тяжіння:
Але це сила тяжіння, з якою Місяць притягуватиме тіло, а прискорення вільного падіння
Отже, на Місяці вага тіла
4) Тіло рухається в міжпланетному кораблі, тобто далеко від планет. Тому на нього не діє жодна сила тяжіння. За другим законом Ньютона
Вага за модулем дорівнюватиме силі нормальної реакції опори згідно з третім законом Ньютона:
Відповідь: 1Г, 2А, 3Б, 4В.
ТЕМА: Механіка. Основи динаміки. Рух тіла під дією кількох сил.
Завдання скеровано на перевірку знання і розуміння руху тіла під дією кількох сил, і вміння описати цей рух за допомогою другого закону Ньютона.
Позначимо на рисунку сили, які діють на важки до і після перепалювання нитки.
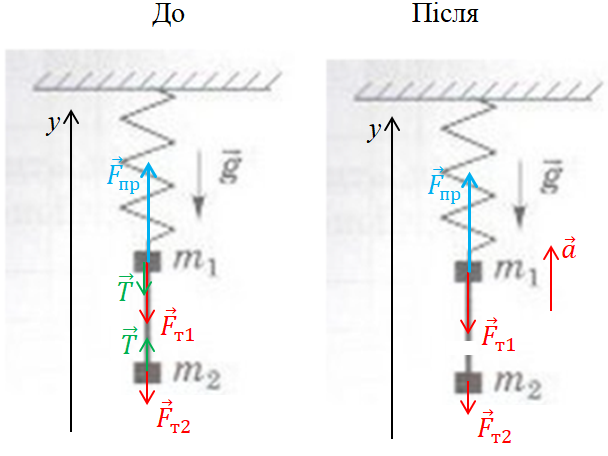
Запишімо другий закон Ньютона для обох випадків.
|
Для першого важка:
Спроєктуймо на вісь
Для другого важка:
Отже, звідси
|
Для першого важка:
Сила тяжіння після перепалювання нитки вже не діє на перший важок, і він рухається вгору з прискоренням
Спроєктуймо на вісь
Другий важок буде падати під дією сили тяжіння |
Підставмо вираз для сили пружності у формулу для прискорення і обчислимо його:
Відповідь:
ТЕМА: Електродинаміка. Робота поля з переміщення заряду.
Завдання скеровано на перевірку знання і розуміння загального поняття роботи у фізиці, а також вміння визначати, від яких параметрів залежить робота різних полів.
Робота у фізиці – характеристика дії сили на тіло, що залежить від величини й напрямку цієї сили та переміщення точки її прикладання.
Запишімо загальну формулу роботи сили. Робота сили дорівнює добутку модуля сили
1. Вихрове електричне поле. Змінне магнітне поле завжди супроводжується появою вихрового електричного поля. Саме вихрове електричне поле діє на вільні заряджені частинки в провіднику й надає їм напрямленого руху, створюючи індукційний струм.
Робота вихрового електричного поля на замкненій траєкторії зазвичай не дорівнює нулю.
Робота вихрового електричного поля з переміщення одиничного позитивного заряду по замкнутому нерухомому провіднику чисельно дорівнює ЕРС індукції в цьому провіднику.
2. Електричне поле – форма матерії, яка існує навколо заряджених тіл і виявляється в дії з деякою силою на заряджене тіло, що перебуває в цьому полі.
Електричне поле є складником єдиного електромагнітного поля. Джерелами електричного поля можуть бути рухомі й нерухомі електричні заряди та змінні магнітні поля.
Електричне поле, створене лише нерухомими зарядами, є незмінним у часі (статичним). Таке поле називають електростатичним.
Нехай в однорідному електричному полі напруженістю
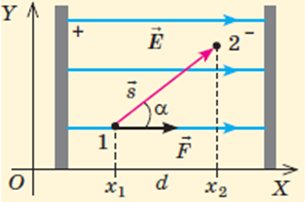
За означенням роботи:
Поле однорідне, тому сила
Отже, робота сил однорідного електростатичного поля в ході переміщення електричного заряду
Формула
3. Гравітаційне поле існує навколо будь-якого тіла і виявляється у взаємному притяганні тіл одне до одного. Визначити силу
Отже, сила, а значить, і робота гравітаційного поля залежатиме від маси частинки, не залежатиме від форми траєкторії, але від відстані (переміщення) залежатиме, тобто від положення початкової та кінцевої точок руху частинки (Г).
4. Магнітне поле – складник електромагнітного поля, основною властивістю якої є дія на рухомі заряджені частинки. Силова характеристика магнітного поля – вектор магнітної індукції

Тобто, ця сила напрямлена перпендикулярно до швидкості руху заряду й напрямку магнітного поля. А напрямок швидкості руху тіла збігається з напрямком його переміщення. Через це робота, що її виконує магнітне поле над частинкою, дорівнює нулю:
Відповідь: 1Д, 2Б, 3Г, 4А.
ТЕМА: Механіка. Основи динаміки. Сила пружності. Закон Гука.
Завдання скеровано на перевірку знання і розуміння закону Гука.
1. Сила пружності
Знак мінус показує, що сила пружності напрямлена в бік, протилежний видовженню.
Запишімо закон Гука для модулів:
Відповідь: 300.
2. Визначімо силу пружності
Відповідь: 30.
Відповідь: 1. 300. 2. 30.
ТЕМА: Коливання і хвилі. Механічні коливання і хвилі. Коливання вантажу на пружині.
Завдання скеровано на перевірку знання суті і розуміння закономірностей коливань тіла на пружині, сил, що діють на тіло в певній ситуації.
Позначмо на рисунку сили, які діють на кульку, що підвішена до пружини й поки не коливається на ній (див. рисунок ліворуч). На кульку діє сила тяжіння
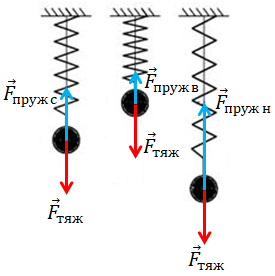
Коли кулька переміститься у верхню точку (див. рисунок посередині), сила пружності
У нижній точці навпаки: сила пружності
Отже, сили, що діють на кульку, будуть урівноважені лише в положенні рівноваги, тобто в середній точці.
Відповідь: Б.
ТЕМА: Механіка. Основи кінематики. Вільне падіння.
Завдання скеровано на перевірку розуміння вільного падіння тіл.
Якщо б у трубці було повітря, то найважче тіло (дробинка) впало б на дно трубки найшвидше. Однак за умовою завдання повітря з трубки відкачано. Тіла падають вільно й з однакової висоти.
Вільним називають падіння тіл у безповітряному просторі, тобто це падіння лише під дією сили тяжіння.
Експериментально доведено, що швидкість будь-якого тіла, яке вільно падає, щосекунди збільшується приблизно на
Без повітря всі тіла ‒ дробинка, корок і пташине перо ‒ незалежно від їхньої маси, об’єму, форми ‒ впадуть на дно трубки одночасно.
Отже, правильна відповідь ‒ Г.
Відповідь: Г.
ТЕМА: Механіка. Основи динаміки. Елементи механіки рідин і газів. Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Капілярні явища.
Завдання скеровано на перевірку знання і розуміння явищ або виникнення сил і вміння пояснити їхній фізичний зміст.
1. Капіляр (від лат. capillaris ‒ волосяний) ‒ трубка з вузьким внутрішнім каналом. З капілярами пов’язані так звані капілярні явища. Капілярний ефект ‒ явище підвищення або зниження рівня рідини в капілярах, як порівняти з тим значенням, яке відповідає закону сполучених посудин.
Під викривленою поверхнею рідини виникає надлишковий (від’ємний або додатний) тиск, який прямо пропорційний поверхневому натягу рідини (тобто силам, що намагаються стягнути цю поверхню, прагнуть зменшити площу поверхні рідини) й обернено пропорційний радіусу кривизни меніска. Завдяки цьому тиску рідина піднімається в капілярах, які змочує (рисунок а), й опускається в капілярах, які не змочує (рисунок б).
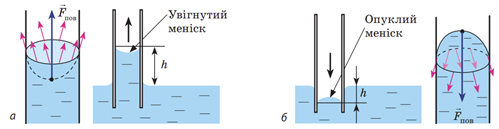
Правильний варіант відповіді ‒ Г.
2. Архімедова (виштовхувальна) сила зумовлена тим, що тиск рідини збільшується з глибиною. На нижню поверхню зануреного в рідину тіла рідина тисне з більшою силою, ніж на верхню. Унаслідок цього рівнодійна сил тиску рідини на всі ділянки поверхні тіла напрямлена вгору ‒ ця рівнодійна і є архімедовою силою.
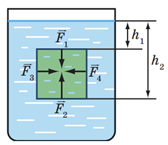
Сили гідростатичного тиску
А от сили гідростатичного тиску
Правильний варіант відповіді ‒ Б.
3. Сила пружності ‒ це сила, яка виникає під час деформації тіла й напрямлена протилежно напрямку зміщення частин цього тіла в процесі деформації. Сила пружності є проявом дії міжмолекулярних сил.
У твердих тілах частинки коливаються біля положень рівноваги й взаємодіють міжмолекулярними силами притягання і відштовхування. У положеннях рівноваги ці сили зрівноважені. У разі деформації тіла у взаємному розташуванні його частинок виникають певні зміни.
Якщо відстань між частинками зростає, то міжмолекулярні сили притягання стають сильнішими за сили відштовхування.
Якщо ж частинки зближуються, то сильнішими стають міжмолекулярні сили відштовхування.
Іншими словами: у разі деформації частинки прагнуть відновити положення рівноваги. Сили, що виникають у разі зміни положення однієї частинки, дуже малі. Однак коли ми деформуємо тіло, то змінюється взаємне розташування величезної кількості частинок. Додавання сил дає помітну рівнодійну, яка протидіє деформації тіла. Це і є сила пружності.
Правильний варіант відповіді ‒ А.
4. Невагомість ‒ це відсутність ваги. Приберіть у тіла опору або підвіс ‒ і воно опиниться в стані невагомості. Опір повітря теж є своєрідною опорою. Невагомість ‒ це такий стан тіла, за якого тіло не діє на опору чи підвіс. Тіло поблизу поверхні Землі перебуває в стані невагомості, якщо на нього діє тільки одна сила ‒ сила тяжіння. На короткий час невагомість легко створити вдома, на вулиці, в класі тощо. Ви можете, наприклад, підстрибнути і на мить опинитися в стані невагомості: у такому разі, поки ви падаєте, опір повітря є нехтовно малим, тож можна вважати, що на вас діє лише сила тяжіння.
Постійно в стані невагомості перебувають космічні орбітальні станції і все, що в них є. Це пов’язано з тим, що космічні кораблі «постійно падають» на Землю через її притягання і водночас залишаються на орбіті завдяки своїй величезній швидкості.
Падіння тіл у безповітряному просторі лише під дією сили тяжіння називають вільним падінням.
Експериментально було доведено, що швидкість будь-якого тіла, яке вільно падає, щосекунди збільшується приблизно на
Правильний варіант відповіді ‒ В.
Відповідь: 1Г, 2Б, 3А, 4В.
ТЕМА: Механіка. Основи динаміки. Рух тіл під дією однієї або кількох сил.
Завдання скеровано на перевірку знання і розуміння руху тіла під дією кількох сил, уміння застосовувати другий закон Ньютона.
За умовою брусок із тягарцями тягнуть прямолінійно рівномірно. Назвімо сили, що діють на цю систему тіл: сила тяжіння
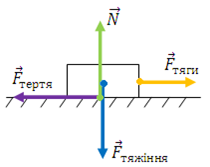
Запишімо другий закон Ньютона:
Вертикально напрямлені сили
Рух рівномірний, а отже, прискорення
Знак мінус, тому що сили напрямлені протилежно.
Визначімо коефіцієнт тертя між бруском і рейкою:
Силу тяги визначімо за показами динамометра на рисунку 1:
Силу тяжіння визначімо за показами динамометра на рисунку 2:
Відповідь: Г.
ТЕМА: Механіка. Основи динаміки. Закон Гука.
Завдання скеровано на перевірку знання і розуміння закону Гука і його застосування до відповідної ситуації.
З’єднаймо послідовно дві однакові за довжиною
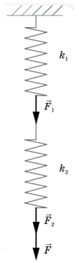
За третім законом Ньютона в пружині виникатиме сила пружності, рівна за модулем прикладеній силі і напрямлена протилежно:
За законом Гука модуль сили пружності прямо пропорційний видовженню тіла
Запишімо тепер рівність сил:
За умовою
Виходячи із цього запису, якщо ми зменшили довжину пружини у 2 рази, то жорсткість пружини повинна збільшитися вдвічі. Лише за цієї умови рівність буде правильною. Отже,
Відповідь: B.
Тема: Механіка. Основи динаміки. Вага тіла.
Завдання скеровано на перевірку знання і розуміння ваги в різних випадках.
Перевантаження ‒ це збільшення ваги. А вага
Єдиний випадок, коли вага тіла за модулем дорівнює силі тяжіння, це якщо тіло перебуває в стані спокою або прямолінійного рівномірного руху:
В усіх інших випадках тіло відчуватиме або збільшення ваги (перевантаження):
Отже, автогонщик не зазнаватиме перевантаження, рухаючись зі сталою швидкістю прямою трасою (рух без прискорення
В усіх інших названих в умові випадках рух автогонщика буде прискореним, і він відчуватиме збільшення ваги (перевантаження).
Відповідь: Б.